Iнтерактивне навчання
- Час: 00:00/00:40:00
- Питання: 0/9
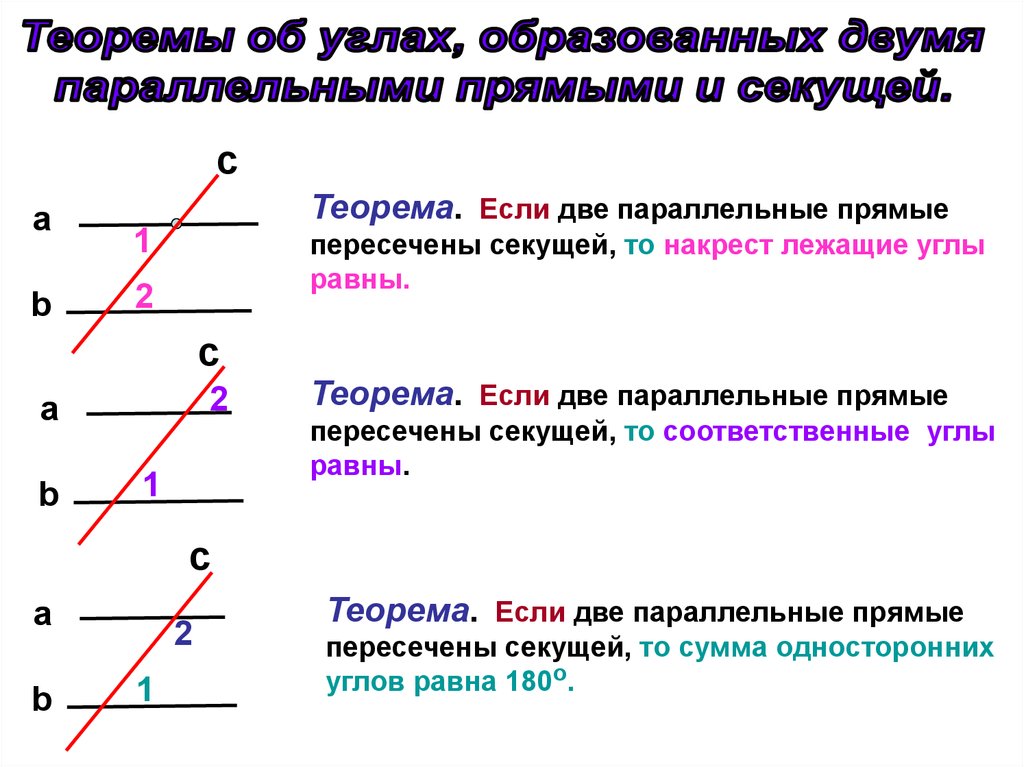
Как называются углы 1 и 2, изображенные на рисунке?
(Кількість балів 1.00)
Укажите рисунок, на котором изображены смежные углы 1 и 2
(Кількість балів 1.00)
- А
- Б
- В
- Г
- А
На рисунке прямые a и b параллельны, прямая c — секущая.

(Кількість балів 1.00)
- А
Угол 5
- Б
Угол 7
- В
Угол 1
- Г
Угол 4
- А
Найдите угол, смежный с углом, равным 50°.
(Кількість балів 1.00)
- А
130°
- Б
25°
- В
50°
- Г
150°
- А
Две прямые пересекаются, причем один из углов, образовавшихся при этом, равен 135°.
 Найдите угол между данными прямыми.
Найдите угол между данными прямыми. (Кількість балів 1.00)
- А
145°
- Б
45°
- В
135°
- Г
55°
- А
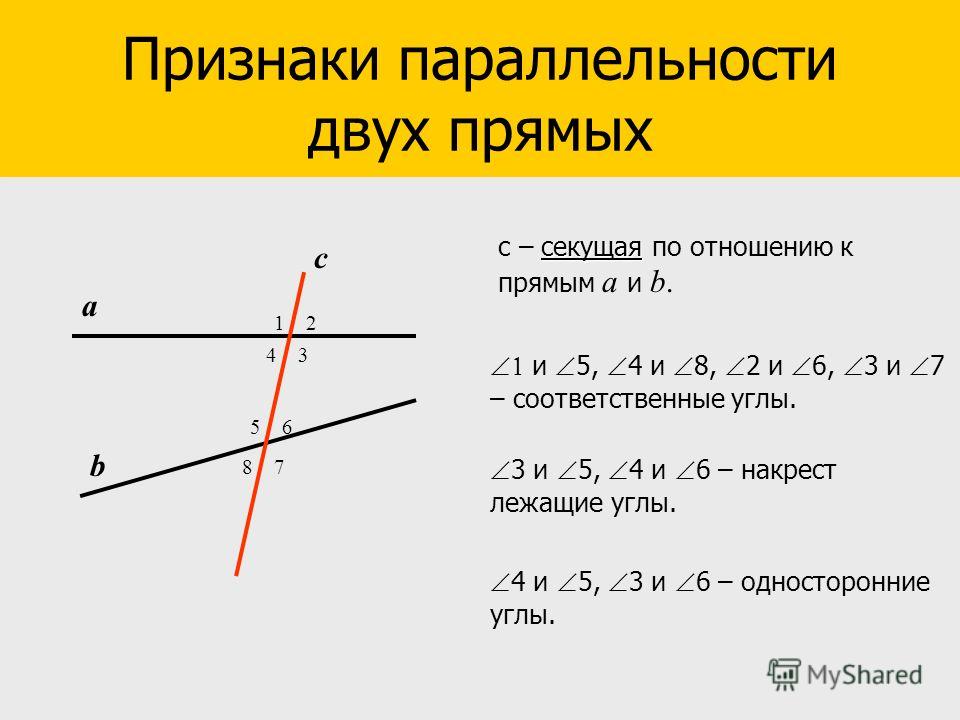
Две прямые пересекаются третьей. Какими могут быть градусные меры соответственных углов, чтобы данные прямые были параллельны?
(Кількість балів 1.00)
- А
180° и 0°
- Б
40° и 35°
- В
145° и 35°
- Г
75° и 75°
- А
При пересечении двух прямых образовались углы, сумма двух из которых равна 80°.
 Найдите угол между данными прямыми.
Найдите угол между данными прямыми. (Кількість балів 2.00)
- °
-
Угол 1 на 30° больше угла 2, (см. рисунок). Найдите угол 2.
(Кількість балів 2.00)
- °
Угол между пересекающимися прямыми a и b на 20° меньше смежного с ним угла. Найдите угол между прямой a и прямой c, проходящей через точку пересечения прямых a и b перпендикулярно прямой b.
(Кількість балів 3.00)
- °
Час вичерпано
Параллельные прямые — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.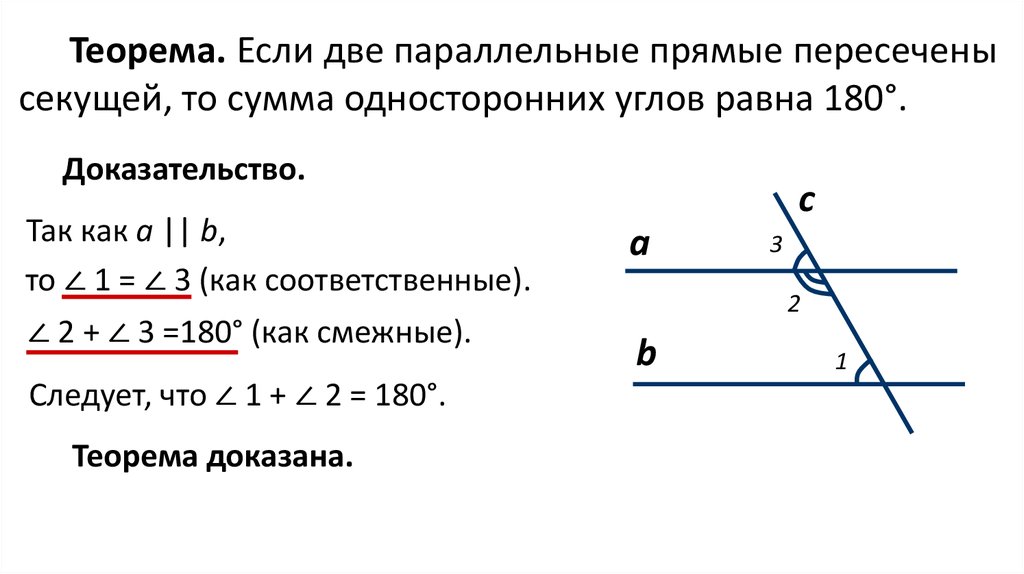
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Определение.
Две прямые на плоскости
называются
параллельными,
если они не пересекаются.
Признаки параллельности прямых
Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны.
c
а
1
2
b
c
Если при пересечении двух прямых
секущей соответственные углы равны,
то прямые параллельны.
Если при пересечении двух прямых секущей
сумма односторонних углов равна 1800, то
прямые параллельны.
1
а
2
b
c
1
2
b
Аксиома параллельности и следствия из неё.

c
А
Через точку, не лежащую на данной
b прямой, проходит только одна прямая,
параллельная данной.
а
с
а
b
Если прямая пересекает одну из
двух параллельных прямых, то она
пересекает и другую.
a II b, c b ⇒ c a
Следствие 1.
Если две прямые параллельны
третьей прямой, то они параллельны.
a II с, b II с ⇒ a II b
Следствие 2.
Если две параллельные прямые пересечены секущей, то
накрест лежащие углы равны.
Дано: a II b, MN- секущая.
Р
1
N
2
M
а
Доказать: 1= 2 (НЛУ)
b
Доказательство:
способ от противного.
Допустим, что 1 2.
Отложим от луча МN угол NМР, равный углу 2.
По построению накрест лежащие углы NМР= 2
РМ II b.
Получили, что через точку М проходит две прямые (а и МР),
параллельные прямой b !!! Это противоречит аксиоме
1= 2.
Теорема доказана.
Теорема об односторонних углах, образованных при пересечении двух
параллельных прямых секущей.
Если две параллельные прямые пересечены секущей, условие
то сумма односторонних углов равна 1800.
заключение теоремы
c
а
3
1
2
b
Дано: а II b, c- секущая.
Доказать: OУ 1+ 2=1800.
Доказательство:
3+ 2 =1800, т. к. они смежные.
11= 3, т. к. это НЛУ при а II b
3 + 2 =1800
Теорема доказана.
Если MN II AB, а угол 2 больше угла 1 на 300, то угол 2 равен…
Решение:
1= х,
2= х+30
Задача
В
1= ВОС,
N
М
2
A
О
1
С
B
они вертикальные.
2= х+30
ВОА=х,
1800, т.к. ОУ при а II b
Составь уравнение…
Найди сам угол.
Теорема о соответственных углах, образованных при пересечении двух
параллельных прямых секущей.
Если две параллельные прямые пересечены секущей,
то соответственные углы равны. заключение теоремы
c
2
а
3
1
b
условие
Дано: а II b, c- секущая.
Доказать: СУ 1 = 2.
Доказательство:
2 = 3, т. к. они вертикальные.
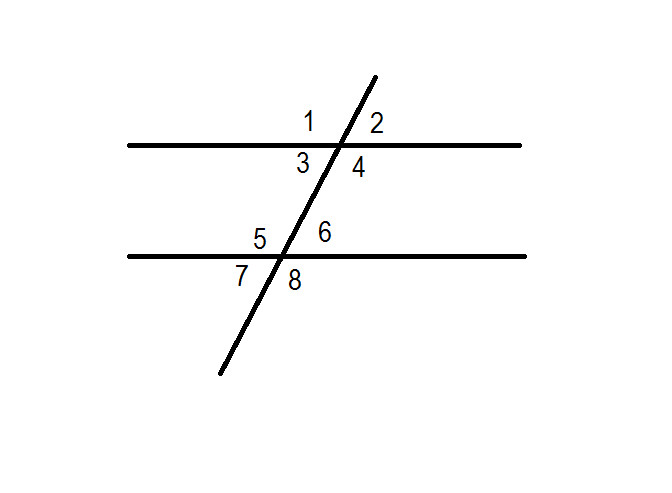
3 = 1, т. к. это НЛУ при а II b
22
11 = 3 =
Теорема доказана.
Свойства углов при параллельных прямых. Дано:
aIIb
1=
a
340
aIIb
aIIb.
1340
2=
b
2 1
a
1=
b 2=
2 1
Сумма углов 1 и 2 равна 760.
a
aIIb
2
b
1
3
1=
3=
1: 2 = 4 : 5.
aIIb
a
2
1
a
440
2
440
Проверить.
1
0
b
1=
2=
b 1=
2=
Дано: а II b, c – секущая.
Один из односторонних углов на
20% меньше другого.
Задача
7 6
8
3
2
b
1
4 5
1=
а
5=
2=
6=
3=
7=
4=
8=
Найти: все углы.
Решение:
2=х,
1 на 20% меньше, т.е. 80%
1=0,8х
2=х
1=0,8х
1800, т.к. ОУ при
а II b
Составь уравнение…
Найди сам все углы…
Проверить.
Тренировочные упражнения
Дано: а II b, с – секущая
1 = 4 2
Найдите:
1
и
2
c
а
Угол 1 в 4 раза больше
угла 2
1
4х
2х
b
Тренировочные упражнения
Угол 1 на 300 больше
угла 2
Дано: а II b, с – секущая
1 – 2 = 300
Найдите:
1
и
2
c
а
1
х+30
2х
b
Тренировочные упражнения
Дано: а II b, с – секущая
2 = 0,8 1
Найдите:
1
и
2
c
а
1х
0,8х
2
Угол 2 составляет 0,8 части
угла 1
b
Тренировочные упражнения
Пусть х – 1 часть
Дано: а II b, с – секущая
1 : 2 = 5 : 4
Найдите:
1
и
2
c
а
5х
1
4х
2
b
Тренировочные упражнения
Дано: а II b, с – секущая
2 составляет 80% от 1
Найдите:
1
и
2
c
а
х
1
0,8х
2
b
AB = BC, A=600,
CD – биссектриса угла ВСЕ.

Докажите, что АВ II CD.
Дано: а II b, с – секущая
1 : 2 = 5 : 4
Найдите:
1
и
2
c
Пусть х – 1 часть
B
D
а
5х
1
600
4х
2
1200
600
A
С
600
E
b
Используя данные рисунка, найдите углы 1, 2 и 3.
с
d
а
1200
1
2
200
1600 b
3
Может ли еще один из семи остальных углов, образованных
при пересечении прямых a и
1100? 600? Почему?
b с прямой d, быть равен
d
m
1100
400
1100
400
а
b
На рисунке АС II ВD и
Найдите СВD.
A
АС = АВ,
M
С
400
2
3
B
1
D
На рисунке АВ II ЕD.
Докажите, что ВСD = B + D
B
Подсказка
A
1
N
2
3
C
Построим CN II AB
4
D
E
На рисунке АВ II ЕD. CВА = 1400, СDE = 1300
Докажите, что ВС СD
Подсказка
B
A
140
400
N
C
Построим CN II AB
130
50 0
D
E
a II b, c – секущая, DM и DN – биссектрисы
смежных углов, образованных прямыми a и c.
 DE = 5,8 см
DE = 5,8 смНа рисунке
Найдите MN.
с
а
400 D
2
3 6
5
1
M
4
E
?
b
N
На рисунке АВ ED и KM ED, ABE = 340
MN – биссектриса КМС
Найдите EMN.
D
K
N
A
0
146
0
73
E
?
340
B
730 C
M
На рисунке АС II BD и KC II MD, ACK = 480
CDK в 3 раза больше EDM
Найдите КDE.
A
B
K
C
480
480
M
3x
D
x
E
English Русский Правила
Линии в геометрии — Типы, Примеры
В геометрии распространенной ошибкой является утверждение, что отрезок и линия — одно и то же.
Сегмент имеет определенное начало и определенный конец, причем каждый конец представлен точкой.
Примеры отрезков включают длину стола, расстояние прямой дороги и т. д.
Мы можем видеть так много прямолинейных примеров вокруг себя, края здания, дороги, по которым мы путешествуем.
1. | Что такое линия? |
| 2. | Нестандартное мышление! |
| 3. | Важные примечания к строкам |
| 4. | Решенные примеры на строках |
| 5. | Интерактивные вопросы по линиям |
Линия – это фигура, образованная соединением двух точек на минимальном расстоянии между ними, причем оба конца уходят в бесконечность.
Хотя линии не имеют определенного начала или конца, в нашей повседневной жизни они представлены такими примерами, как железнодорожные пути или автострады.
Луч — это часть прямой, которая имеет только одну фиксированную точку, а другая точка не имеет конца.
Хотя у лучей есть фиксированное начало и нет определенного конца, в нашей повседневной жизни они представлены такими примерами, как солнечный свет или свет факела.
Отрезок — это часть линии фиксированной длины, или можно сказать, что оба конца отрезка фиксированы. Сегменты, иногда также называемые линейными сегментами.
Сегменты, иногда также называемые линейными сегментами.
Хотя оба сегмента линии имеют фиксированные концы, в нашей повседневной жизни они представлены такими примерами, как край стола, провод или столб.
Think Tank
- Предположим, вы привязали веревку к одной точке на Земле и начали идти с другим концом веревки в руке. Вы идете по прямой, спустя столько месяцев вам каким-то образом удалось вернуться в ту же точку, откуда вы начали. Один из ваших друзей отмечает, что пока вы шли по линии, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
Или мы можем сказать, что если две прямые не имеют точки пересечения, они называются параллельными прямыми.
Пересекающиеся прямые Если две прямые пересекаются в точке, то они называются интересными прямыми.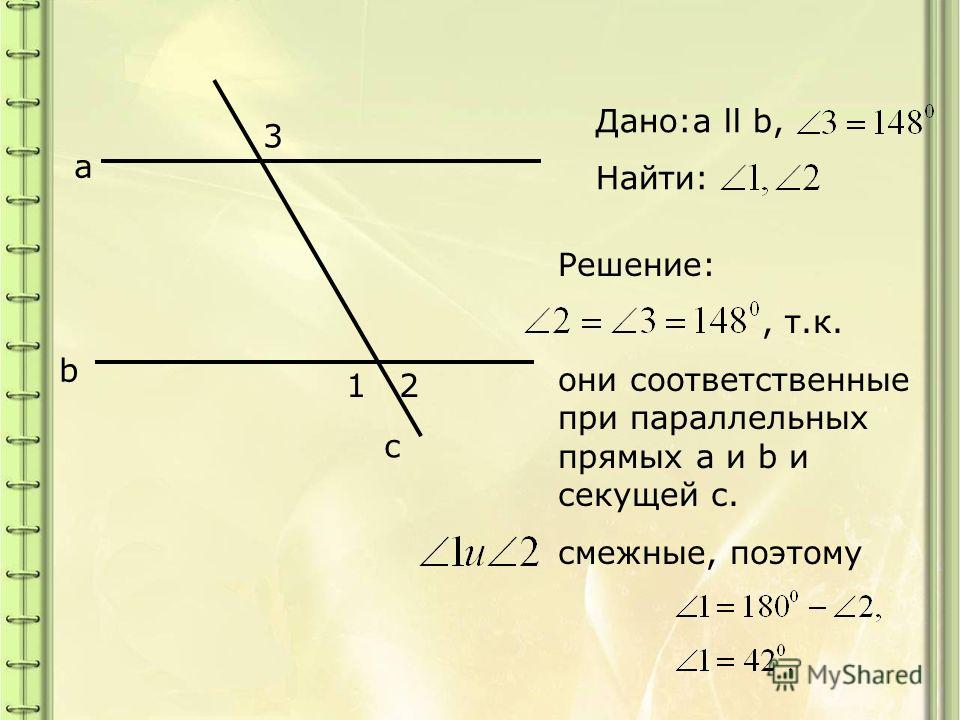
Что такое перпендикулярные линии? 9{\circ}\), то они перпендикулярны друг другу.
Исследуйте типы линий в моделировании ниже.
Горизонтальные и вертикальные линии
Линии классифицируются на основе их выравнивания.
Горизонтальные линииЛинии, проведенные горизонтально, называются горизонтальными линиями.
Вертикальные линииВертикальные линии называются вертикальными.
Наклонные или наклонные линии
Линии, проведенные с наклоном или образующие с горизонтальными или вертикальными линиями угол, отличный от 0, 90, 180, 270, 360 градусов, называются наклонными или наклонными линия.
Важные примечания
- Линия не имеет конечных точек.
- Луч имеет только одну фиксированную точку.
- Отрезок линии — это часть линии фиксированной длины.

- Перпендикулярные линии имеют угол 90 градусов между собой.
- Параллельные линии не пересекаются.
| Пример 1 |
Сэм хочет найти числа, состоящие только из отрезков. Помогите ему выбрать правильные цифры из следующих.
Решение
Давайте обсудим каждый вариант один за другим:
Вариант А состоит из 5 сегментов линии.
Вариант B состоит из 3 прямых сегментов и изогнутой части.
Вариант C представляет собой круг, поскольку он состоит только из изогнутых частей.
Вариант D состоит из 4 сегментов линии.
\(\следовательно\) Варианты A и D верны. |
| Пример 2 |
Найдите правильные типы линий на рисунке ниже.
Решение
Вариант A — пара параллельных прямых
Вариант B — пара непараллельных прямых или линий пересечения.
Вариант C является примером перпендикулярных линий.
| Пример 3 |
Том выбирает точки пересечения линий, указанных на рисунке ниже, он заметил, что есть 5 точек пересечения. Он прав?
Решение
Точки, в которых пересекаются любые из этих прямых: \(\text{A, B, C, D, E, F}\)
Следовательно, всего 6 точек пересечения .
| \(\поэтому\) Том не прав |
Интерактивные вопросы
Вот несколько упражнений для практики.
Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Let’s Summarize
Мы надеемся, что вы наслаждаетесь изучением линий с интерактивными вопросами. Теперь вы сможете легко решать задачи на линии.
О КуэматеВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, это логическое мышление и разумный подход к обучению, в которые мы в Cuemath верим.
Часто задаваемые вопросы по линии
1. Что такое уравнение прямой?
Общее уравнение прямой может быть задано как \(ax + by + c= 0\).
Где \(a, b, c\) — константы, а \(x, y\) — переменные.
2.
 Чему равен угол между двумя перпендикулярными прямыми?
Чему равен угол между двумя перпендикулярными прямыми?Угол между двумя перпендикулярными линиями равен 90 градусов.
3. Что такое секущая?
Секущая — это прямая, пересекающаяся в двух точках с окружностью.
Прямая AB является секущей окружности.
4. Что такое касательная?
Касательная линия — это линия, которая касается окружности в одной точке.
Прямая \(L\) является касательной к окружности в точке \(P\).
5. Какие прямые параллельны?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
смежные, дополнительные, дополнительные, противоположные: задачи с решениями
К Catalin David
Задача 1
Меры угла:
Длина линий
Проем между двумя линиями
Задача 2
Единица измерения углов:
Градусы
Сантиметры
Килограммы
Задача 3
Какая точка является вершиной угла?
Задача 4
Если угол обозначен только одной буквой, то эта буква означает:
Одна из сторон угла
Вершина угла
Задача 5
Если угол обозначается тремя буквами, то буква в середине означает:
Точка на одной из сторон
Вершина угла
Задача 6
Являются ли ∠BAC и ∠ABC одним и тем же углом?
Задача 7
Являются ли ∠BAC и ∠DAE одним и тем же углом?
Задача 8
Мера острого угла:
Равен 90°
Больше 90°
Меньше 90°
Проблема 9
∠BAC:
Тупой
Правый
Острый
Задача 10
Мера прямого угла:
меньше 90°
90°
больше 90°
45°
Задача 11
Угол, стороны которого перпендикулярны, имеет меру:
90°
45°
180°
Задача 12
Какой тип угла ∠ABC?
Правый
Острый
Тупой
Задача 13
Мера тупого угла:
Меньше 90°
Больше 90°
Равно 90°
Проблема 14
∠ABC
Правильно
Острый
Тупой
Проблема 15
∠ABC
Правильно
Острый
Тупой
Задача 16
Угол, обе стороны которого лежат на одной прямой, равен
Острый
Тупой
Прямой
Правый
Задача 17
Размер прямого угла:
90°
180°
120°
0°
Задача 18
А Биссектриса – это полупрямая, которая делит угол на 234 равных угла.
Задача 19
Если угол равен 72°, биссектриса образует два угла по 24°36°12°72° каждый.
Проблема 20
Смежны ли ∠BAC и ∠DEF?
Проблема 21
Смежны ли ∠BAC и ∠DAE?
Проблема 22
Смежны ли ∠BAC и ∠EDC?
Проблема 23
Смежны ли ∠BAC и ∠CAD?
Задача 24
Смежны ли ∠BAC и ∠BAD?
Задача 25
∠ABC имеет меру 42°, а ∠CBD имеет меру 36°. Является ли мера ∠ABD 78°?
Задача 26
∠ABC имеет меру 56°, а ∠ABD имеет меру 100°. Является ли мера ∠DBC 44°?
Задача 27
Два угла являются дополнительными, если сумма их мер равна
180°
90°
45°
60°
Задача 28
Дополнительны ли ∠A и ∠B?
Задача 29
Если OA и OC перпендикулярны, то являются ли ∠AOB и ∠BOC комплементарными?
Задача 30
Мера ∠AOB равна
24°
66°
80°
76°
Задача 31
Если угол имеет меру 40°, то мера дополнительного угла равна 40°80°50°.
Задача 32
Два угла являются дополнительными, если сумма их мер равна
180°
90°
60°
45°
Задача 33
Являются ли ∠AOB и ∠BOC дополнительными?
Да
Нет
Не определено
Задача 34
Какова мера ∠BOC?
90°
135°
45°
145°
Задача 35
Если ∠AOB и ∠COD дополняют друг друга, какова мера ∠BOC?
60°
90°
120°
80°
Задача 36
∠AOB и ∠BOC дополняют друг друга. ∠BOC и ∠COD дополняют друг друга. Равны ли ∠AOB и ∠COD?
Задача 37
∠AOB и ∠BOC дополняют друг друга. ∠BOC и ∠COD дополняют друг друга. Если ∠BOC имеет 30°, какова мера ∠AOD?
120°
150°
180°
Задача 38
Прямые AC и BD пересекаются в точке O. Являются ли углы ∠AOB и ∠COD противоположными?
Являются ли углы ∠AOB и ∠COD противоположными?
Задача 39
Являются ли ∠AOB и ∠COD противоположными углами?
Задача 40
∠AOB и ∠COD — противоположные углы. Имеют ли они одинаковую меру?
Задача 41
∠AOB и ∠COD — противоположные углы. Если ∠AOB=35°, какова мера ∠COD?
15°
66°
150°
35°
Задача 42
∠AOB и ∠COD — противоположные углы. Если ∠AOB = 35°, какова мера ∠DOA?
150°
145°
90°
135°
Задача 43
Пусть a и b — две прямые, пересекаемые прямой c. Найдите два противоположных внутренних угла.
3 и 4
4 и 5
3 и 5
Задача 44
Пусть две прямые a и b пересекает прямая c. Найдите два альтернативных внешних угла.
2 и 8
1 и 3
2 и 5
Задача 45
Пусть две прямые a и b пересекает прямая c.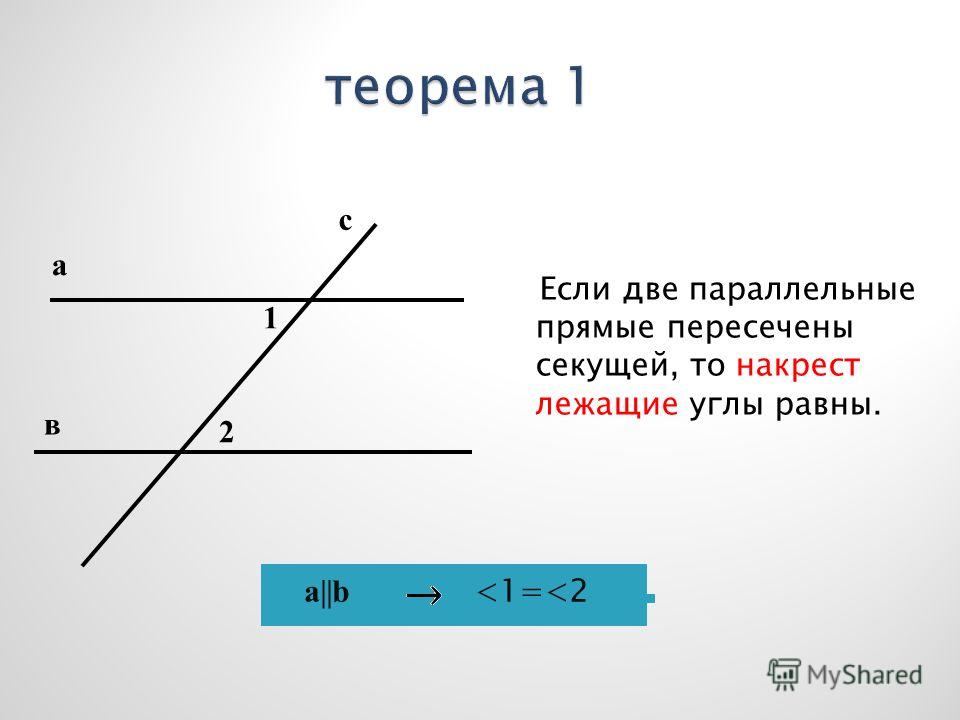

 Найдите угол между данными прямыми.
Найдите угол между данными прямыми.  Найдите угол между данными прямыми.
Найдите угол между данными прямыми. 