Нахождение обратных матриц: Обратная матрица онлайн

Нахождение обратной матрицы.

В этой статье разберемся с понятием обратной матрицы, ее свойствами и способами нахождения. Подробно остановимся на решении примеров, в которых требуется построить обратную матрицу для заданной.

Навигация по странице.

• Обратная матрица — определение.

• Нахождение обратной матрицы с помощью матрицы из алгебраических дополнений.

• Свойства обратной матрицы.

• Нахождение обратной матрицы методом Гаусса-Жордана.

• Нахождение элементов обратной матрицы с помощью решения соответствующих систем линейных алгебраических уравнений.

Обратная матрица — определение.

Понятие обратной матрицы вводится лишь для квадратных матриц, определитель которых отличен от нуля, то есть для невырожденных квадратных матриц.

Определение.

Матрица  называется обратной для матрицы , определитель которой отличен от нуля , если справедливы равенства , где 

E – единичная матрица порядка n на n.

Нахождение обратной матрицы с помощью матрицы из алгебраических дополнений.

Как же находить обратную матрицу для данной?

Во-первых, нам потребуются понятия транспонированной матрицы, минора матрицы и алгебраического дополнения элемента матрицы.

Определение.

Минор k-ого порядка матрицы A порядка m на n – это определитель матрицы порядка k на k, которая получается из элементов матрицы А, находящихся в выбранныхk строках и k столбцах. (k не превосходит наименьшего из чисел m или n).

Минор (n-1)-ого порядка, который составляется из элементов всех строк, кроме i-ой, и всех столбцов, кроме j-ого, квадратной матрицы А порядка n на n обозначим как .

Иными словами, минор  получается из квадратной матрицы 

А порядка n на nвычеркиванием элементов i-ой строки и j-ого столбца.

Для примера запишем, минор 2-ого порядка, который получаетсся из матрицы выбором элементов ее второй, третьей строк и первого, третьего столбцов . Также покажем минор, который получается из матрицы  вычеркиванием второй строки и третьего столбца . Проиллюстрируем построение этих миноров:  и .

Определение.

Алгебраическим дополнением элемента  квадратной матрицы  называют минор (n-1)-ого порядка, который получается из матрицы А, вычеркиванием элементов ее i-ой строки и j-ого столбца, умноженный на .

Алгебраическое дополнение элемента  обозначается как . Таким обрзом, .

Например, для матрицы  алгебраическое дополнение элемента  есть .

Во-вторых, нам пригодятся два свойства определителя, которые мы разобрали в разделе

вычисление определителя матрицы:

На основании этих свойств определителя, определения операции умножения матрицы на число и понятия обратной матрицы справедливо равенство , где  — транспонированная матрица, элементами которой являются алгебраические дополнения .

Матрица  действительно является обратной для матрицы А, так как выполняются равенства . Покажем это

Составим алгоритм нахождения обратной матрицы с использованием равенства .

1. Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).

2. Строим  — матрицу из алгебраических дополнений элементов .

3. Транспонируем матрицу , тем самым получаем .

4. Умножаем каждый элемент матрицы  на число . Этой операцией завершается нахождение обратной матрицы .

5. Проводим проверку результата, вычисляя произведения  и . Если , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.

Разберем алгоритм нахождения обратной матрицы на примере.

Пример.

Дана матрица . Найдите обратную матрицу.

Решение.

Вычислим определитель матрицы А, разложив его по элементам третьего столбца:

Определитель отличен от нуля, так что матрица А обратима.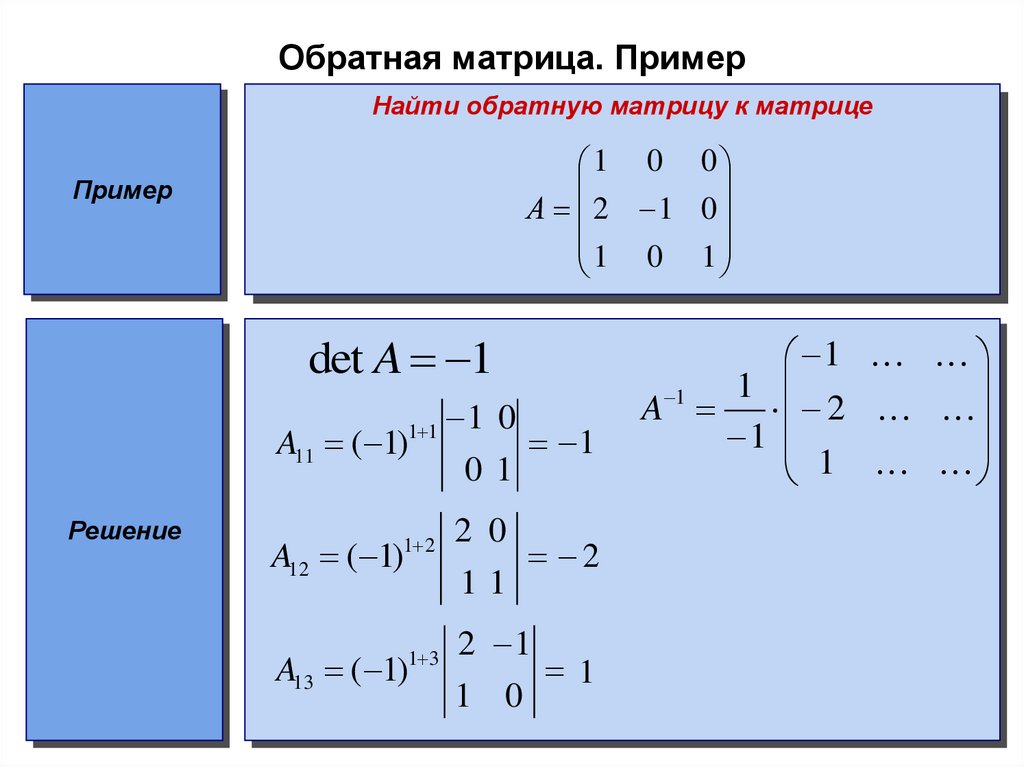

Найдем матрицу из алгебраических дополнений:

Поэтому

Выполним транспонирование матрицы из алгебраических дополнений:

Теперь находим обратную матрицу как :

Проверяем полученный результат:

Равенства  выполняются, следовательно, обратная матрица найдена верно.

Страница не найдена — ПриМат

По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.

Искать:

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2),

{-1}A=I\), где \(I\) – матрица идентичности.

См. также

• Сложение и вычитание матриц
• Как умножить матрицу
• Как умножить матрицу на скаляр
• Как найти определители матрицы

Пошаговое руководство по поиску инверсия матрицы \(2×2\)

Обратное вычисление матрицы \(2×2\) проще по сравнению с матрицами более высокого порядка. Мы можем вычислить обратную матрицу \(2×2\), используя общие шаги вычисления обратной матрицы. 9{-1}\) существует только тогда, когда \(ad-bc≠ 0\).

Следовательно, для вычисления обратной матрицы \(2×2\) надо сначала поменять местами выражения \(a\) и \(d\), поставить знак минус перед выражениями \(b \), и \(с\), и, наконец, разделить его на определитель матрицы.

Обратная матрица \(2×2\) – пример 1:

Найдите обратную матрицу \(A\). \(A= \begin{bmatrix}5 & -1 \\6 & 2 \end{bmatrix}\)

Сначала найдем определитель \(A\): \(|A|=(5)(2) -(-1)(6)=10-(-6)=10+6=16\) 9{-1}= \begin{bmatrix}\frac{1}{3} & -\frac{5}{27}\\ 0& \frac{1}{9}\end{bmatrix}\)

Упражнение для обратной матрицы \(2×2\)

Найдите обратную каждую матрицу.

1. \(\color{blue}{\begin{bmatrix}5 & -2 \\-1 & 2 \end{bmatrix}}\)
2. \(\color{blue}{\begin{bmatrix}4 & 6 \\2 & -4 \end{bmatrix}}\)
3. \(\color{blue}{\begin{bmatrix}3 & 4 \\6 & 8 \end{bmatrix}}\)
4. \ (\color{синий}{\begin{bmatrix}5 и 2 \\-7& -3 \end{bmatrix}}\)
5. \(\color{blue}{\begin{bmatrix}-8 & 3 \\5& 9 \end{bmatrix}}\)

1. \(\color{blue}{\begin{bmatrix}\frac {1}{4} & \frac{1}{4} \\ \frac{1}{8} & \frac{5}{8} \end{bmatrix}}\)
2. \(\color{blue }{\begin{bmatrix}\frac{1}{7} & \frac{3}{14} \\ \frac{1}{14} & -\frac{1}{7} \end{bmatrix}} \)
3. \(\color{blue}{matrix\: is\: единственное число}\)
4. \(\color{blue}{\begin{bmatrix} 3 & 2 \\ -7 & -5 \end{ bmatrix}}\)
5. \(\color{blue}{\begin{bmatrix}-\frac{3}{29} & \frac{1}{29} \\ \frac{5}{87} & \frac{8}{87} \end{bmatrix}}\)

Примеры алгебры | Матрицы | Обратная матрица Nxn

Шаг 1

Найдите определитель.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.1

Выберите строку или столбец с наибольшим количеством элементов. Если элементов нет, выберите любую строку или столбец. Умножьте каждый элемент в столбце на его кофактор и добавьте.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.1.1

Рассмотрим соответствующую таблицу знаков.

Шаг 1.1.2

Кофактором является минор с измененным знаком, если индексы совпадают с положением на таблице знаков.

Шаг 1.1.3

Младший для является определителем с удаленными строкой и столбцом.

Шаг 1.1.4

Умножить элемент на его кофактор.

Шаг 1.1.5

Минор для является определителем с удаленными строкой и столбцом.

Шаг 1.1.6

Умножить элемент на его кофактор.

Шаг 1.1.7

Младший для — это определитель с удаленными строкой и столбцом.

Шаг 1.1.8

Умножить элемент на его кофактор.

Шаг 1.1.9

Сложите термины вместе.

Шаг 1.2

Умножить на .

Шаг 1.3

Оценка .

Нажмите, чтобы увидеть больше шагов…

Шаг 1.3.1

Определитель матрицы можно найти по формуле .

Шаг 1.3.2

Упростим определитель.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.3.2.1

Упростите каждый термин.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.3.2.1.1

Умножить на .

Шаг 1.3.2.1.2

Умножить на .

Шаг 1.3.2.2

Добавить и .

Шаг 1.4

Оценка .

Нажмите, чтобы увидеть больше шагов…

Шаг 1.4.1

Определитель матрицы можно найти по формуле .

Шаг 1.4.2

Упростить определитель.

Нажмите, чтобы увидеть больше шагов…

Шаг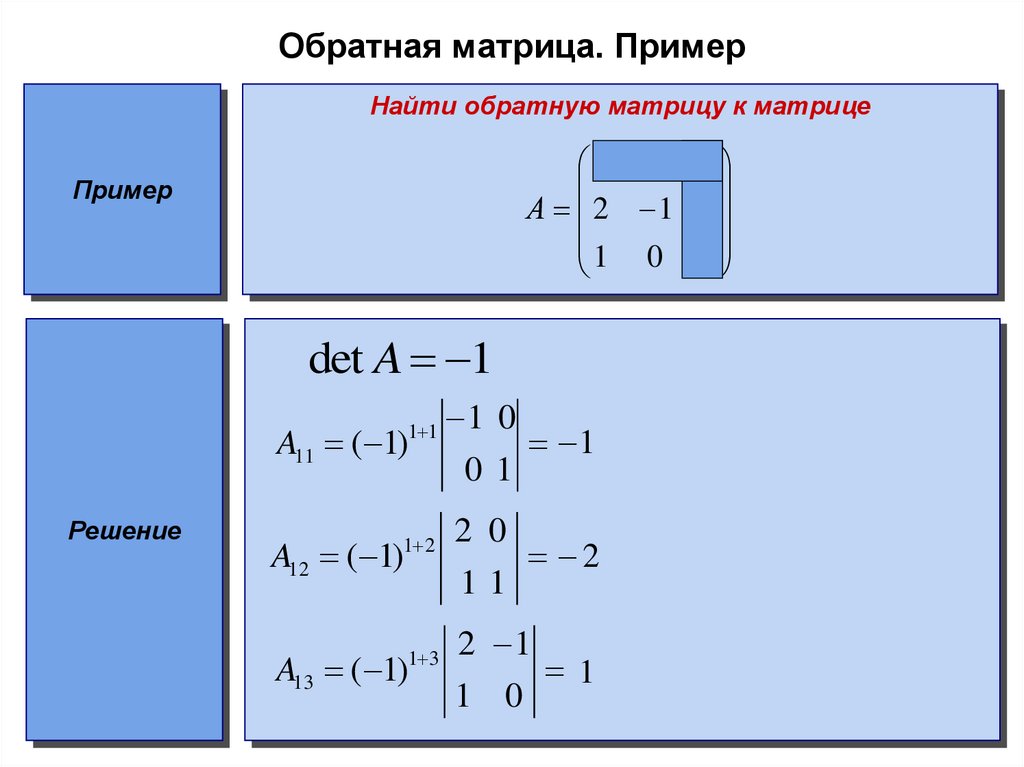 1. 4.2.1

Упростите каждый термин.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.4.2.1.1

Умножить на .

Шаг 1.4.2.1.2

Умножить на .

Шаг 1.4.2.2

Вычесть из .

Шаг 1.5

Упростим определитель.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.5.1

Упростите каждый термин.

Нажмите, чтобы увидеть больше шагов…

Шаг 1.5.1.1

Умножить на .

Шаг 1.5.1.2

Умножить на .

Шаг 1.5.2

Добавить и .

Шаг 1.5.3

Добавить и .

Шаг 2

Поскольку определитель отличен от нуля, существует обратное.

Шаг 3

Создайте матрицу, в которой левая половина является исходной матрицей, а правая половина — ее единичной матрицей.

Шаг 4

Найдите уменьшенную форму эшелона строк.

Нажмите, чтобы увидеть больше шагов. ..

Шаг 4.1

Выполните операцию строки, чтобы сделать запись в .

Нажмите, чтобы увидеть больше шагов…

Шаг 4.1.1

Выполните операцию строки, чтобы сделать запись в .

Шаг 4.1.2

Упрощение .

Шаг 4.2

Умножьте каждый элемент на, чтобы получить запись в .

Нажмите, чтобы увидеть больше шагов…

Шаг 4.2.1

Умножьте каждый элемент на, чтобы получить запись в .

Шаг 4.2.2

Упрощение .

Шаг 4.3

Выполните операцию строки, чтобы сделать запись в .

Нажмите, чтобы увидеть больше шагов…

Шаг 4.3.1

Выполните операцию строки, чтобы сделать запись в .

Шаг 4.3.2

Упрощение .

Шаг 4.4

Умножьте каждый элемент на, чтобы получить запись в .

Нажмите, чтобы увидеть больше шагов…

Шаг 4.