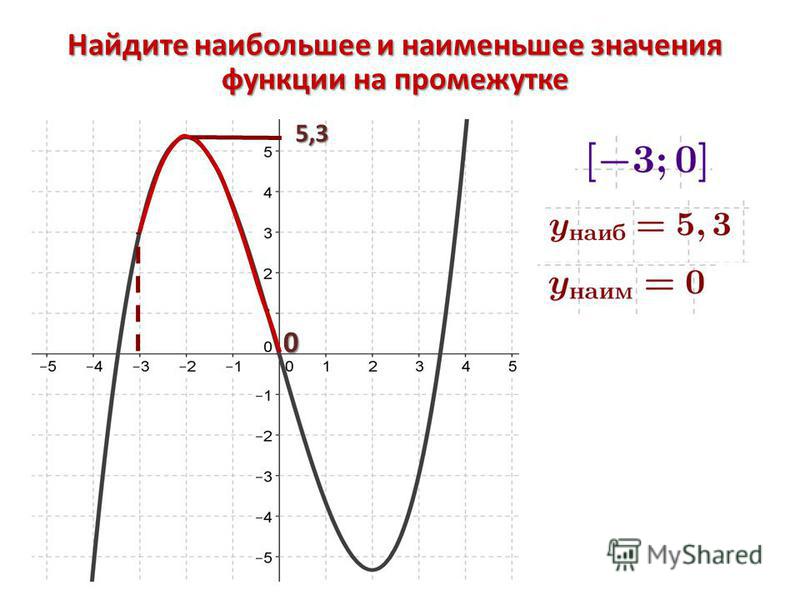
Наименьшее значение функции это: Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Содержание

как обозначается, как найти на отрезке, алгоритм

Содержание:

Что такое наибольшее и наименьшее значение функции
Как записать, каким символом обозначают
Нахождение наибольшего и наименьшего значения функции на промежутке
- Как найти через производную на отрезке $[а; b]$, формулы
Примеры задач с решением

Содержание

Что такое наибольшее и наименьшее значение функции
Как записать, каким символом обозначают
Нахождение наибольшего и наименьшего значения функции на промежутке
- Как найти через производную на отрезке $[а; b]$, формулы
Примеры задач с решением

Что такое наибольшее и наименьшее значение функции

Множество значений каждой функции ограничено, и для представления о ее свойствах часто бывает необходимо вычислить границы этого множества. Функция может обладать такими свойствами, как периодичность, четность и нечетность. Иногда это имеет значение при вычислении наибольшего и наименьшего значений, т. к. равенства, определяющие периодичность, четность и нечетность, ограничивают область определения.

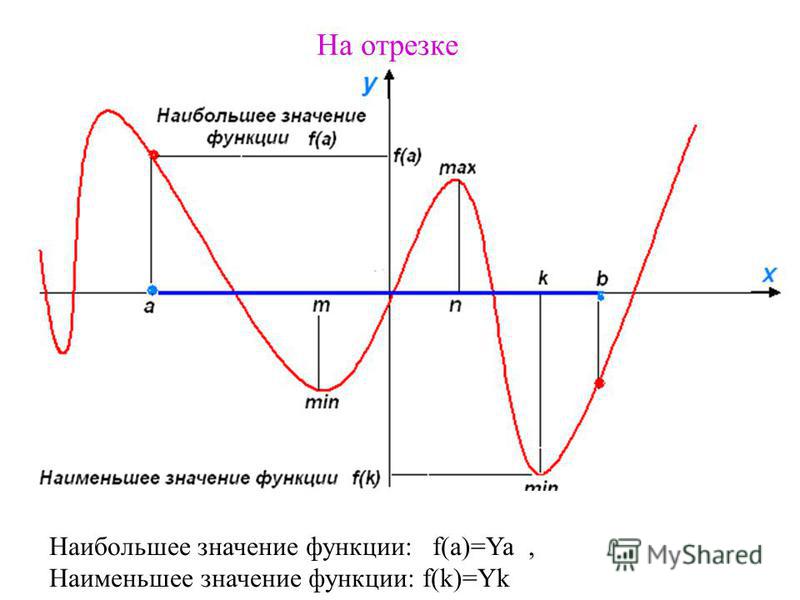
Возьмем в качестве примера функцию, описанную уравнением $y = (f)x$, являющуюся непрерывной на отрезке $[а; b]$. Наибольшим значением функции $f(x)$ будет точка $x_{0}$, принадлежащая этому отрезку, значение которой больше или равно любой из точек $x$, также принадлежащих отрезку $[а; b]$. Аналогично определяется наименьшее значение функции — точка, значение которой меньше или равно любой их точек на отрезке $[а; b]$.

Точки максимума и минимума функции также называют точной верхней и нижней гранью множества значений функции.

Как записать, каким символом обозначают

Обозначение независимой переменной, или аргумента функции — буква х, зависимой переменной, или значения функции — буква у.

Выражение, содержащее х, записывают как $f(x).$

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Максимум функции на множестве $[a;b]$, входящем в область ее определения, можно записать так: $\;\underset{\lbrack a;b\rbrack\;}{y_{max}}$ или ${y_{max}}, y(x_{max})$, указав границы множества отдельно.

Минимум — $\;\underset{\lbrack a;b\rbrack\;}{y_{min}}$ или ${y_{min}}, y(x_{min}).$

Нахождение наибольшего и наименьшего значения функции на промежутке

Если $x_{0}$ — точка экстремума, тогда $f’ (x_{0}) = 0.$

Если в точке $x_{0} f’ (x)$ меняет знак с «+» на «-», то $x_{0}$ — точка максимума.

Если в этой точке $f’ (x)$ меняет знак с «-» на «+», то $x_{0}$ — точка минимума.

Как найти через производную на отрезке $[а; b]$, формулы

Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке $[а; b]:$

Вычислить производную$ f'(x). $
Найти критические точки f(х) на отрезке $[а; b]$: производная будет равна нулю при х, равном искомым точкам.
Найти значения функции в критических точках $f (x_{1}),$ $f (x_{2})$ и т. д.
Вычислить$ f (а)$, $f (b).$
Выбрать наименьшее и наибольшее значение из ряда вычисленных точек, включающем не только критические точки, но и крайние точки отрезка.

Производная — мгновенный частный результат действия функции.

Производная функции $у = f(x)$ в точке $x_{0}$ — это предел отношения приращения функции к точке $x_{0}$ к приращению аргумента, когда приращение аргумента стремится к нулю. Это можно выразить следующей формулой:

$f'(x_{0}) = \lim_{\triangle x \rightarrow 0}\frac{\triangle f}{\triangle x}.$

$\triangle f = f(x_{0}\triangle x) — f(x_{0}).$

Найти производную можно, воспользовавшись специальными таблицами или вычислив ее по правилам:

\((u + v)’ = u’ + v’.

{2} — 24х + 18.\)

Производная равна нулю, если x равен 1 или 3.

3 не принадлежит отрезку, но 1 — принадлежит.

Вычисляем значения критических точек: $f(1) = 11,$ $f(-1) = — 29,$ $f(2) = 7.$

Ответ: на отрезке $[-1; 2]$ $min f(x) = f(-2) = -29$, $max f(x) = f(-1) = 11.$

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши

«Ctrl» и «Enter»

Поиск по содержимому

Курс высшей математики, Т.1

В.И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. — 479 с.

Фундаментальный учебник по высшей математике, выдержавший более двадцати изданий, переведенный на множество языков мира, отличается, с одной стороны, систематичностью и строгостью изложения, а с другой – простым языком, подробными пояснениями и многочисленными примерами. Книга состоит из пяти томов. Тома третий и четвертый – каждый из двух частей.

Для студентов университетов и технических вузов.

ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
1. Величина и ее измерение.
2. Число.
3. Величины постоянные и переменные.
4. Промежуток.
5. Понятие о функции.
6. Аналитический способ задания функциональной зависимости.
7. Неявные функции.
8. Табличный способ.
9. Графический способ изображения чисел.
10. Координаты.
11. График и уравнение кривой.
12. Линейная функция.
13. Приращение. Основное свойство линейной функции.
14. График равномерного движения.
15. Эмпирические формулы.
16. Парабола второй степени.
17. Парабола третьей степени.
18. Закон обратной пропорциональности.
19. Степенная функция.
20. Обратные функции.
21. Многозначность функции.

22. Показательная и логарифмическая функции.

23. Тригонометрические функции.
24. Обратные тригонометрические, или круговые, функции.
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
25. Упорядоченное переменное.
26. Величины бесконечно малые.
27. Предел переменной величины.
28. Основные теоремы.
29. Величины бесконечно большие.
30. Монотонные переменные.
31. Признак Коши существования предела.
32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
33. Примеры.
34. Непрерывность функции.
35. Свойства непрерывных функций.
36. Сравнение бесконечно малых и бесконечно больших величин.
37. Примеры.
38. Число е.
39. Недоказанные предложения.
40. Вещественные числа.
41. Действия над вещественными числами.
42. Точные границы числовых множеств. Признаки существования предела.
43. Свойства непрерывных функций.
44. Непрерывность элементарных функций.
ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
45.

Понятие о производной.
46. Геометрическое значение производной.
47. Производные простейших функций.
48. Производные сложных и обратных функций.
49. Таблица производных и примеры.
50. Понятие о дифференциале.
51. Некоторые дифференциальные уравнения.
52. Оценка погрешностей.
§ 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
53. Производные высших порядков.
54. Механическое значение второй производной.
55. Дифференциалы высших порядков.
56. Разности функций.
§ 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
57. Признаки возрастания и убывания функций.
58. Максимумы и минимумы функций.
59. Построение графиков.
60. Наибольшее и наименьшее значения функций.
61. Теорема Ферма.
62. Теорема Ролля.
63. Формула Лагранжа.
64. Формула Коши.
65. Раскрытие неопределенностей.

66. Различные виды неопределенностей.
§ 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
68. Частные производные и полный дифференциал функции двух независимых переменных.

69. Производные сложных и неявных функций.
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
70. Дифференциал дуги.
71. Выпуклость, вогнутость и кривизна.
72. Асимптоты.
73. Построение графиков.
74. Параметрическое задание кривой.
75. Уравнение Ван-дер-Ваальса.
76. Особые точки кривых.
77. Элементы кривой.
78. Цепная линия.
79. Циклоида.
80. Эпициклоиды и гипоциклоиды.
81. Развертка круга.
82. Кривые в полярных координатах.
83. Спирали.
85. Овалы Кассини и лемниската.
ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
86. Понятие о неопределенном интеграле.
87. Определенный интеграл как предел суммы.
88. Связь определенного и неопределенного интегралов.
89. Свойства неопределенного интеграла.
90. Таблица простейших интегралов.
91. Правило интегрирования по частям.
92. Правило замены переменных. Примеры.
93. Примеры дифференциальных уравнений первого порядка.
§ 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
94.

Основные свойства определенного интеграла.
95. Теорема о среднем.
96. Существование первообразной функции.
97. Разрыв подынтегральной функции.
98. Бесконечные пределы.
99. Замена переменной под знаком определенного интеграла.
100. Интегрирование по частям.
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
101. Вычисление площадей.
102. Площадь сектора.
103. Длина дуги.
104. Вычисление объемов тел по их поперечным сечениям.
105. Объем тела вращения.
106. Поверхность тела вращения.
107. Определение центров тяжести. Теоремы Гульдина.
108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
109. Формула касательных и формула Понселе.
110. Формула Симпсона.
111. Вычисление определенного интеграла с переменным верхним пределом.
112. Графические способы.
113. Площади быстро колеблющихся кривых.
§ 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
115. Разбиение промежутка на части и образование различных сумм.

116. Интегрируемые функции.
117. Свойства интегрируемых функций.
ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
118. Понятие о бесконечном ряде.
119. Основные свойства бесконечных рядов.
120. Ряды с положительными членами. Признаки сходимости.
121. Признаки Коши и Даламбера.
122. Интегральный признак сходимости Коши.
123. Знакопеременные ряды.
124. Абсолютно сходящиеся ряды.
125. Общий признак сходимости.
§ 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
126. Формула Тейлора.
127. Различные виды формулы Тейлора.
128. Ряды Тейлора и Маклорена.
129. Разложение exp(x).
130. Разложение sin x и cos x.
131. Бином Ньютона.
132. Разложение log(1+x).
133. Разложение arctg x.
134. Приближенные формулы.
135. Максимумы, минимумы и точки перегиба.
136. Раскрытие неопределенностей.
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
137. Свойства абсолютно сходящихся рядов.
138. Умножение абсолютно сходящихся рядов.

139. Признак Куммера.
140. Признак Гаусса.
141. Гипергеометрический ряд.
142. Двойные ряды.
143. Ряды с переменными членами. Равномерно сходящиеся ряды.
144. Равномерно сходящиеся последовательности функций.
145. Свойства равномерно сходящихся последовательностей.
146. Свойства равномерно сходящихся рядов.
147. Признаки равномерной сходимости.
148. Степенные ряды. Радиус сходимости.
149. Вторая теорема Абеля.
150. Дифференцирование и интегрирование степенного ряда.
ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
152. О предельном переходе.
153. Частные производные и полный дифференциал первого порядка.
154. Однородные функции.
155. Частные производные высших порядков.
156. Дифференциалы высших порядков.
157. Неявные функции.
158. Пример.
159. Существование неявных функций.
160. Кривые в пространстве и поверхности.
§ 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
161.

Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
162. Необходимые условия максимума и минимума функции.
163. Исследование максимума и минимума функции двух независимых переменных.
164. Примеры.
165. Дополнительные замечания о нахождении максимумов и минимумов функции.
166. Наибольшее и наименьшее значения функции.
167. Относительные максимумы и минимумы.
168. Дополнительные замечания.
169. Примеры.
ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
170. Комплексные числа.
171. Сложение и вычитание комплексных чисел.
172. Умножение комплексных чисел.
173. Деление комплексных чисел.
174. Возвышение в степень.
175. Извлечение корня.
176. Показательная функция.
177. Тригонометрические и гиперболические функции.
178. Цепная линия.
179. Логарифмирование.
180. Синусоидальные величины и векторные диаграммы.
181. Примеры.
182. Кривые в комплексной форме.

183. Представление гармонического колебания в комплексной форме.
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
185. Разложение многочлена на множители.
186. Кратные корни.
187. Правило Горнера.
188. Общий наибольший делитель.
189. Вещественные многочлены.
190. Зависимость между корнями уравнения и его коэффициентами.
191. Уравнение третьей степени.
192. Решение кубического уравнения в тригонометрической форме.
193. Способ итерации.
194. Способ Ньютона.
195. Способ простого интерполирования.
§ 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
196. Разложение рациональной дроби на простейшие.
197. Интегрирование рациональной дроби.
198. Интеграл от выражений, содержащих радикалы.
199. Интегралы вида…
200. Интегралы вида…
201. Интегралы вида…

алгебраическое предварительное исчисление — Наименьшее значение набора изображений функции

спросил 10 лет, 6 месяцев назад

Изменено 10 лет, 6 месяцев назад

Просмотрено 458 раз

$\begingroup$

У меня есть это уравнение, где вопрос говорит:

92}{4a}\right)$$

, поэтому координата $y$ дает наименьшее значение, которое достигает парабола.

$\endgroup$

Функция МАЛЕНЬКИЙ в Excel для поиска и выделения наименьших значений

В этом кратком руководстве мы поговорим о функции МАЛЕНЬКИЙ в Excel, о том, как она работает и как ее использовать для поиска N-го наименьшего числа, даты или времени.

Нужно найти несколько наименьших чисел на листе? Это довольно легко сделать с помощью функции сортировки Excel. Не хотите тратить время на повторную сортировку данных при каждом изменении? Функция НАИМЕНЬШИЙ поможет вам быстро найти наименьшее значение, второе наименьшее значение, третье наименьшее значение и так далее.

МАЛЕНЬКАЯ функция Excel

НАИМЕНЬШИЙ — это статистическая функция, которая возвращает n-е наименьшее значение в наборе данных.

Синтаксис функции МАЛЕНЬКИЙ включает два аргумента, оба из которых обязательны.

МАЛЕНЬКИЙ (массив, к)

Где:

Массив — массив или диапазон ячеек, из которых извлекается наименьшее значение.
K — целое число, указывающее позицию от наименьшего значения до возврата, т.е. k-е наименьшее.

Функция доступна во всех версиях Excel для Office 365, Excel 2021, Excel 2019, Excel 2016, Excel 2013, Excel 2010 и более ранних версиях.

Совет. Чтобы найти k-е наименьшее значение с критериями, используйте формулу Excel МАЛЕНЬКИЙ ЕСЛИ.

Базовая формула МАЛЕНЬКИЙ в Excel

МАЛЕНЬКАЯ формула в ее базовой форме очень проста в построении — вы просто указываете диапазон и позицию от наименьшего элемента, который нужно вернуть.

В списке чисел в B2:B10, предположим, вы хотите извлечь 3 ^rd наименьшее значение. Формула проста:

=МАЛЕНЬКИЙ(B2:B10, 3)

Чтобы вам было проще проверить результат, столбец B отсортирован по возрастанию:

4 вещи, которые вы должны знать о функции SMALL

Следующие примечания по использованию помогут вам лучше понять поведение функции МАЛЕНЬКИЙ и избежать путаницы при построении собственных формул.

Любые пустых ячеек , текст значений и логические значения ИСТИНА и ЛОЖЬ в аргументе массива игнорируются.
Если массив содержит одну или несколько ошибок , возвращается ошибка.
Если в массиве имеется дубликатов , ваша формула может привести к «ничьям». Например, если две ячейки содержат число 1, а функция НАИМЕНЬШИЙ настроена на возврат наименьшего и наименьшего значения 2 ^nd, вы получите 1 в обоих случаях.
Предполагая, что n равно количеству значений в array , МАЛЕНЬКИЙ(массив,1) вернет наименьшее значение, а МАЛЕНЬКИЙ(массив,n) выберет наибольшее значение.

Как использовать функцию МАЛЕНЬКИЙ в Excel — примеры формул

А теперь давайте рассмотрим еще несколько примеров функции МАЛЕНЬКИЙ в Excel, которые выходят за рамки ее основного использования.

Найти последние 3, 5, 10 и т. д. значения

Как вы уже знаете, функция НАИМЕНЬШИЙ предназначена для вычисления n-го наименьшего значения. Этот пример показывает, как это сделать наиболее эффективно.

Предположим, что в приведенной ниже таблице вы хотите найти 3 нижних значения. Для этого наберите в отдельные ячейки (в нашем случае D3, D4 и D5) числа 1, 2 и 3. Затем введите следующую формулу в E3 и перетащите ее вниз через E5:

=МАЛЕНЬКИЙ($B$2:$B$10, D3)

В E3 формула извлекает наименьшее значение, используя число в D3 для аргумента k . Главное — указать правильные ссылки на ячейки, благодаря которым формула правильно копируется в другие ячейки: абсолютная для массив и относительный для k .

Не хотите вручную набирать ранги? Используйте функцию ROWS с расширением диапазона по ссылке , чтобы получить значение k . Для этого мы делаем абсолютную ссылку для первой ячейки (или только блокируем координату строки, например B$2) и относительную ссылку для последней ячейки:

.
=МАЛЕНЬКИЙ($B$2:$B$10, СТРОКИ(B$2:B2))
В результате ссылка на диапазон расширяется по мере того, как формула копируется вниз по столбцу. В D2 ROWS(B$2:B2) дает 1 из k , и формула возвращает наименьшую стоимость. В D3 ROWS(B$2:B3) дает 2, и мы получаем 2 ^nd наименьшую стоимость и так далее.
Просто скопируйте формулу в 5 ячеек, и вы получите 5 нижних значений:

Сумма нижних N значений
Хотите найти сумму наименьших n значений в наборе данных? Если вы уже извлекли значения, как показано в предыдущем примере, самым простым решением будет формула СУММ, например:
.
=СУММ(Е3:Е5)
Или вы можете создать независимую формулу, используя функцию МАЛЕНЬКИЙ вместе с СУММПРОИЗВ:
СУММПРОИЗВ(МАЛЕНЬКИЙ(массив , {1, …, n }))
Чтобы получить сумму трех нижних значений в нашем наборе данных, формула принимает следующий вид:
=СУММПРОИЗВ(МАЛЕНЬКИЙ(B2:B10, {1,2,3}))
Функция СУММ даст тот же результат:
.
=СУММ(МАЛЕНЬКИЙ(B2:B10, {1,2,3}))
Примечание. Если вы используете ячейка ссылается на , а не на константу массива для k , вам нужно нажать Ctrl + Shift + Enter, чтобы сделать ее формулой массива. В Excel 365, который поддерживает динамические массивы, СУММ МАЛЕНЬКИЙ в любом случае работает как обычная формула.
Как работает эта формула:
В обычной формуле МАЛЕНЬКИЙ возвращает одно k-е наименьшее значение в диапазоне. В этом случае мы предоставляем константу массива, такую как {1,2,3}, для аргумента k, заставляя его возвращать массив из трех наименьших значений:
{29240, 43610, 58860}
Функция СУММПРОИЗВ или СУММ складывает числа в массиве и выводит итог. Вот и все!
INDEX MATCH SMALL формула для получения наименьших совпадений
В ситуации, когда вы хотите получить некоторые данные, связанные с наименьшим значением, используйте классическую комбинацию INDEX MATCH с SMALL для значения поиска:
ИНДЕКС( return_array , MATCH(SMALL( lookup_array , n ), lookup_array , 0))
Где:
Return_array — это диапазон, из которого извлекаются связанные данные.
Lookup_array — это диапазон, в котором следует искать наименьшее n-е значение.
N — позиция с наименьшим процентным значением.
Например, чтобы получить название проекта с наименьшей стоимостью, в E3 используется следующая формула:
=ИНДЕКС($A$2:$A$10, ПОИСКПОЗ(МАЛЕНЬКИЙ($B$2:$B$10, D3), $B$2:$B$10, 0))
Где A2:A10 — названия проектов, B2:B10 — затраты, а D3 — ранг от наименьшего.
Скопируйте формулу в ячейки ниже (E4 и E5), и вы получите названия 3 самых дешевых проектов:
Примечания:
Это решение отлично работает для набора данных, в котором нет дубликатов. Однако два или более повторяющихся значения в числовом столбце могут создать «связь» в ранжировании, что приведет к неправильным результатам. В этом случае, пожалуйста, используйте немного более сложную формулу, чтобы разорвать связи.
В Excel 365 эту задачу можно выполнить с помощью новых функций динамического массива. Помимо того, что этот подход намного проще, он автоматически решает проблему связей. Подробную информацию см. в разделе Как отфильтровать нижние значения N в Excel.
Сортировка чисел от меньшего к большему по формуле
Думаю, все знают, как упорядочивать числа с помощью функции сортировки Excel. Но знаете ли вы, как выполнить сортировку с помощью формулы? Пользователи Excel 365 могут легко сделать это с помощью новой функции СОРТИРОВКИ. В Эксель 2019, 2016 и более ранние версии, СОРТИРОВКА не работает, увы. Но немного веры, и МАЛЕНЬКИЙ придет на помощь 🙂
Как и в первом примере, мы используем функцию СТРОКИ с расширением ссылки на диапазон для увеличения k на 1 в каждой строке, где копируется формула:
=МАЛЕНЬКИЙ($A$2:$A$10, СТРОКИ(A$2:A2))
Введите формулу в первую ячейку, а затем перетащите ее в столько ячеек, сколько значений содержится в исходном наборе данных (в данном примере C2:C10):
Совет. Чтобы отсортировать по убыванию , используйте функцию НАИБОЛЬШИЙ вместо МАЛЕНЬКИЙ.
МАЛЕНЬКАЯ формула Excel для даты и времени
Поскольку даты и время также являются числовыми значениями (во внутренней системе Excel даты хранятся в виде порядковых чисел, а время — в виде десятичных дробей), функция МАЛЕНЬКИЙ также может обрабатывать их без каких-либо дополнительных усилий с вашей стороны.
Как вы можете видеть на снимках экрана ниже, основная формула, которую мы использовали для чисел, прекрасно работает и для дат и времени:
=МАЛЕНЬКИЙ($B$2:$B$10, D2)
МАЛЕНЬКАЯ формула для нахождения 3 самых ранних дат:
МАЛЕНЬКАЯ формула для получения самого короткого 3 раза:
В следующем примере показано, как функция МАЛЕНЬКИЙ может помочь вам выполнить более конкретную задачу, связанную с датами.
Поиск предыдущей даты, ближайшей к сегодняшней или указанной дате
В списке дат, предположим, вы хотите найти ближайшую дату до указанной даты. Это можно сделать, используя функцию НАИМЕНЬШИЙ в сочетании с СЧЁТЕСЛИ.
Со списком дат в B2:B10 и целевой датой в E1 следующая формула вернет предыдущую дату, ближайшую к целевой дате:
=МАЛЕНЬКИЙ(B2:B10, СЧЁТЕСЛИ(B2:B10, "<"&E1))
Чтобы извлечь дату, которая находится на две даты раньше даты в E1, т. е. на одну предыдущую дату, формула выглядит следующим образом:
=МАЛЕНЬКИЙ(B2:B10, СЧЁТЕСЛИ(B2:B10, "<"&E1)-1)
Чтобы найти прошлую дату , ближайшую к сегодняшнему дню , используйте функцию СЕГОДНЯ для критериев СЧЁТЕСЛИ:
=МАЛЕНЬКИЙ(B2:B10, СЧЁТЕСЛИ(B2:B10, "<"&СЕГОДНЯ()))
Совет. Чтобы предотвратить ошибки в ситуации, когда дата, соответствующая вашим критериям, не найдена, вы можете обернуть формулу функцией ЕСЛИОШИБКА, например:
=ЕСЛИОШИБКА(МАЛЕНЬКИЙ(B2:B10, СЧЁТЕСЛИ(B2:B10, "<"&E1) )-1), "Не найдено")
Как работают эти формулы:
Общая идея состоит в том, чтобы подсчитать количество дат, меньших целевой даты, с помощью СЧЁТЕСЛИ. И это именно то, что нужно функции МАЛЕНЬКИЙ для к аргумент.
Чтобы лучше понять концепцию, давайте посмотрим на нее под другим углом:
Если 1 августа 2020 года (целевая дата в E1) появится в нашем наборе данных, это будет 7 ^th самая большая дата в списке. Следовательно, есть шесть дат меньше, чем это. Это означает, что 6 ^-й-й наименьшей датой является предыдущая дата, ближайшая к целевой дате.
Итак, сначала вычисляем, сколько дат меньше даты в Е1 (результат 6):
СЧЁТЕСЛИ(B2:B10, "<"&E1)
Затем подставьте количество в аргумент 2 ^nd МАЛЕНЬКОГО:
=МАЛЕНЬКИЙ(B2:B10, 6)
Чтобы получить предыдущую дату (в нашем случае это 5 ^th наименьшая дата), мы вычитаем 1 из результата COUNTIF.
Как выделить нижние значения в Excel
Чтобы выделить наименьшие n значений в таблице с условным форматированием Excel, вы можете использовать либо встроенный параметр Верх/Низ, либо настроить собственное правило на основе формулы МАЛЕНЬКИЙ. Первый метод быстрее и проще в применении, а второй обеспечивает больший контроль и гибкость. Следующие шаги помогут вам создать пользовательское правило:
Выберите диапазон, в котором вы хотите выделить нижние значения. В нашем случае числа находятся в формате B2:B10, поэтому мы выбираем его. Если вы хотите выделить строки целиком, выберите A2:B10.
На вкладке Главная в группе Стили щелкните Условное форматирование > Новое правило .
В диалоговом окне Новое правило форматирования выберите Использовать формулу для определения форматируемых ячеек.
В Форматировать значения, где эта формула верна поле, введите формулу, подобную этой:
=B2<=МАЛЕНЬКИЙ($B$2:$B$10, 3)
Где B2 — это крайняя левая ячейка числового диапазона, который необходимо проверить, $B$2:$B$10 — весь диапазон, а 3 — n нижних значений для выделения.
Обратите внимание на типы ссылок в формуле: крайняя левая ячейка — это относительная ссылка (B2), а диапазон — абсолютная ссылка ($B$2:$B$10).
Нажмите Формат и выберите любой формат, который вам нравится.
Дважды нажмите OK, чтобы закрыть оба диалоговых окна.
Готово! Нижние 3 значения в столбце B выделены:
Дополнительные сведения см. в разделе Условное форматирование Excel на основе формулы.
МАЛЕНЬКАЯ функция Excel не работает
Как вы только что убедились в наших примерах, использовать функцию МАЛЕНЬКИЙ в Excel довольно просто, и вряд ли у вас возникнут трудности с ней. Если ваша формула не работает, скорее всего, это будет #ЧИСЛО! ошибка, которая может возникнуть по следующим причинам:
Массив пуст или не содержит ни одного числового значения.
Значение k меньше нуля (глупая опечатка может стоить вам часов поиска и устранения неисправностей!) или превышает количество значений в массиве.
Вот как можно использовать МАЛЕНЬКУЮ формулу в Excel, чтобы найти и выделить нижние числа в наборе данных.
No related posts.