Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
поставить знаки действия и,если нужно скобки,так что бы получилось верные равенства 33333=198 33333=366 33333=72 33333=243 33333=22
используя рисунок составь и реши задачи соответствующие выражениям (78-35)+10*2
Решено
Поставь знаки и, если нужно скобки в примерах так, чтобы получились данные результаты: 300 20 10 4=334 300 20 10 4=154
2sin^2x+cos4x=0
Найдите значение выражение 4\25+15\4 Напишите решение пожалуйста срочно надо
Пользуйтесь нашим приложением
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Конспект лекц. 1-ый семестр
Лекция 2
Комплексные числа можно рассматривать
как точки плоскости с введённой
прямоугольной системой координат.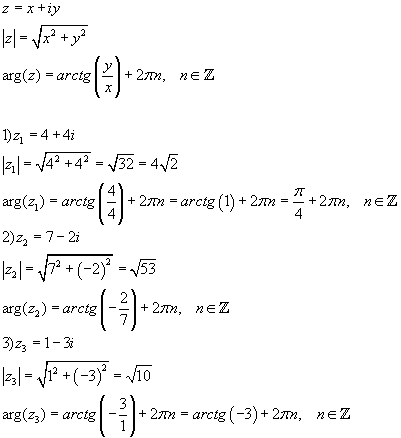 В этом случае
плоскость называют комплексной плоскостью.
В этом случае
плоскость называют комплексной плоскостью.
\
Между комплексными числами и векторами устанавливается взаимно-однозначное соответствие.
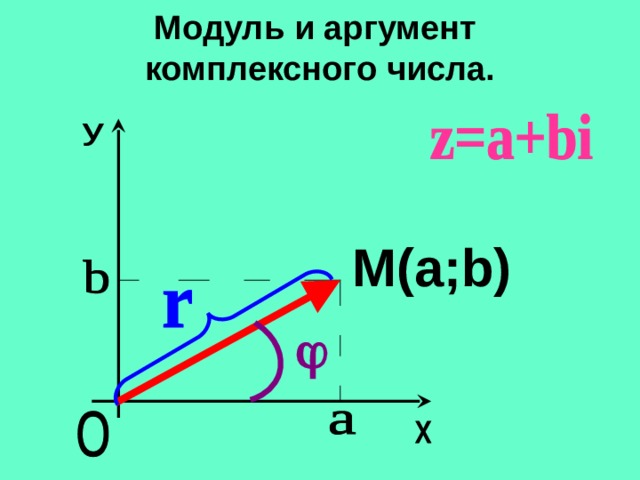
Число называют модулем числа z и обозначают |z|. Модуль комплексного числа определяется однозначно.
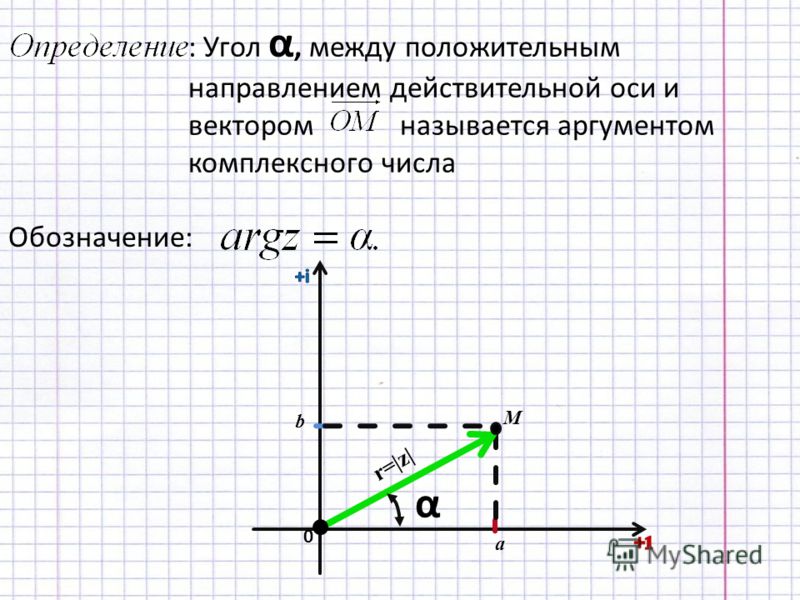
Угол j между вектором и положительным направлением оси 0x называют аргументом числа z и обозначают Arg z. Аргумент комплексного числа определяется неоднозначно. Все аргументы комплексного числа отличаются друг от друга на , . Выделяется так называемое главное значение аргумента , обозначаемое . Обычно главное значение аргумента комплексного числа берут в следующих пределах
.
Если и , то
,
где
при ,
при ,
при .
Если же , то
Аргумент комплексного числа не определён.
Главное значение аргумента определяют так же в пределах
.
Из определения модуля комплексного числа и следует
, ,
где , . Отсюда получаем
. (6)
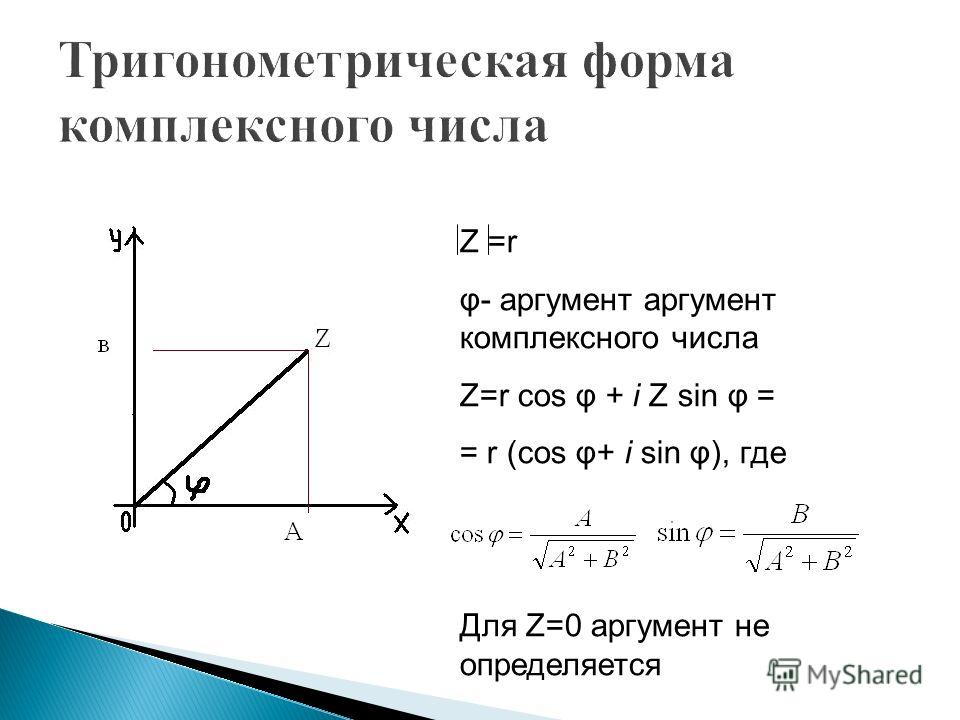
Выражение (6) называется тригонометрической формой комплексного числа z .
Выражение
называется формулой Эйлера. С помощью этой формулы из тригонометрической формы (6) получают показательную форму комплексного числа
. (7)
(7)
Частные случаи
, .
Функция , как функция от j, является периодической с периодом 2p.
Справедливы формулы
, ,
, .
Тригонометрическую и показательнаую формы комплексного числа удобно использовать при выполнении операций умножения и деления комплексных чисел.
Если
, ,
то
, (8)
(9)
или в тригонометрической форме
, (10)
. (11)
Из этих формул следуют формулы Муавра в тригонометрической форме
(12)
и показательной форме
. (13)
(13)
П р и м е р 3. Вычислите комплексное число
Ответ запишите в алгебраической форме.
Р е ш е н и е. Введём обозначения
,.
Тогда
или в тригонометрической форме
,
где и – модуль и главное значение аргумента комплексного числа , и модуль и главное значение аргумента комплексного числа .
Считаем, что . В таком случае для имеем
.
Аналогично для
.
Тогда
Выделяем главное значение аргумента . Оно равно, очевидно, . Наконец, записываем полученный результат
.
О п р е д е л е н и е. Комплексное число называется корнем n-й степени из числа , если .
Любое ненулевое число имеет ровно n различных корней n-й степени и эти корни находятся по формуле
, (14)
где , – арифметический корень n-й степени из положительного числа .
П р и м е р 4. Вычислите .
Р е ш е н и е. В данном случае . Поэтому . Значит, , . Поэтому согласно формуле (14) имеем
, ,
или
.
О п р е д е л е н и е. Многочленом n-ой степени называется функция
,
где – коэффициенты. Очевидно, . Если , т.е.
(15)
то число называется корнем или нулём многочлена , а выражение (15) – алгебраическим уравнением.
П р и м е р 5. Найдите корни уравнения .
Р е ш е н и е. Воспользуемся формулой корней квадратного уравнения
.
Таким образом,
, .
Квадратное уравнение всегда имеет 2 корня. Введём обозначение . Возможны следующие три случая:
– корни вещественные различные,
– корни вещественные одинаковые,
– корни комплексные сопряжённые.
Если коэффициенты алгебраического уравнения вещественные и уравнение имеет комплексный корень , то всегда существует ему комплексно сопряженный корень , т.е. комплексные корни существуют парами.
Основная теорема алгебры. Всякий многочлен степени имеет n корней, при этом корни могут быть вещественными или комплексными, а также простыми или кратными.
Пусть корни уравнения имеют соответственно кратности при этом . Тогда многочлен можно представить в виде
(16)
Выражение (16) называется разложением многочлена на линейные множители. Если коэффициенты многочлена вещественные, то комплексные корни будут попарно сопряженными, т.е. и
.
Здесь . Поэтому, если коэффициенты вещественные, то многочлен
представляется в виде произведения линейных и квадратичных множителей.
О п р е д е л е н и е. Рациональной дробью называется функция где – степенные многочлены. В общем случае рациональную дробь представим в виде
Если , то рациональная дробь называется неправильной, а при правильной.
Например, рациональная дробь
будет неправильной, так как здесь и , а дробь
будет правильная, потому что в этом случае .
Всякую неправильную дробь можно представить в виде суммы целой части (т.е. степенного многочлена) и правильной дроби. Всякая правильная рациональная дробь может быть представлена в виде суммы простейших дробей:
1)
2)
3),
4).
П
р и м е р 6. Разложить на
простейшие рациональную дробь .
Разложить на
простейшие рациональную дробь .
Р е ш е н и е. Заданную дробь представляем в виде суммы простейших дробей первого типа
, (17)
где неопределенные коэффициенты. Эти коэффициенты находятся следующим образом. Правую часть равенства (17) приводим к общему знаменателю
. (18)
Так как дроби в выражения (18) равны и знаменатели этих дробей равны, то и числители тоже будут равны. Приравнивая числители дробей в равенстве (18), получаем
. (19)
Выражение (19) представляет собой равенство двух степенных многочленов, т.е.
. (20)
Два степенных многочлена
равны тогда и только тогда, когда у них равны коэффициенты при соответствующих
степенях . Приравниваем коэффициенты при и получаем , при и получаем . Итак, мы имеем два уравнения относительно и
Приравниваем коэффициенты при и получаем , при и получаем . Итак, мы имеем два уравнения относительно и
Решением этой системы будет . Подставляем найденные значения коэффициентов в выражение (18)
.
Объяснение урока: Аргумент комплексного числа
В этом объяснении мы узнаем, как определить аргумент комплексного числа и как его вычислить.
Когда мы наносим комплексные числа на диаграмму Аргана, мы видим, что комплексные числа имеют много общих свойств с векторами. Например, сложение и вычитание комплексных чисел
геометрически эквивалентны соответствующим операциям над векторами. Мы знаем, что характеристиками вектора являются его направление и величина, поэтому комплексное число должно иметь
эквивалентные характеристики. Напомним, что величина комплексного числа называется его модулем. Направление комплексного числа на диаграмме Аргана является аргументом комплексного числа.
Напомним, что величина комплексного числа называется его модулем. Направление комплексного числа на диаграмме Аргана является аргументом комплексного числа.
Определение: Аргумент комплексного числа
Аргумент комплексного числа — это угол в радианах между положительной действительной осью в Аргане диаграмма и отрезок линии между началом координат и комплексным числом, измеренный против часовой стрелки. Аргумент обозначается как arg(𝑧) или Арг(𝑧).
Аргумент 𝜃 комплексного числа по соглашению задается в диапазоне -𝜋𝜃≤𝜋. Однако мы можем обсудить и сложный число с аргументом больше 𝜋 или меньше -𝜋. Аргумент комплексного числа в диапазоне ]−𝜋,𝜋] называется главным аргументом. Другие соглашения используют диапазон 0≤𝜃2𝜋 для основного аргумента, но это менее распространено.
Если нам дана декартова форма комплексного числа 𝑎+𝑏𝑖, мы можем использовать тригонометрию прямоугольного треугольника, чтобы найти аргумент комплексного числа. Например, рассмотрим
комплексное число, указанное на диаграмме Аргана выше. Поскольку это комплексное число лежит в первой четверти, мы можем видеть, что аргумент этого комплексного числа является углом в прямоугольном треугольнике,
стороны — это синие, зеленые и фиолетовые сегменты линий. В этом случае тангенс этого угла равен отношению противлежащего к прилежащему; следовательно,
загар𝜃=𝑏𝑎.
Поскольку это комплексное число лежит в первой четверти, мы можем видеть, что аргумент этого комплексного числа является углом в прямоугольном треугольнике,
стороны — это синие, зеленые и фиолетовые сегменты линий. В этом случае тангенс этого угла равен отношению противлежащего к прилежащему; следовательно,
загар𝜃=𝑏𝑎.
Затем мы можем вычислить 𝜃, применив функцию арктангенса к обеим частям этого уравнения: 𝜃=𝑏𝑎.tan
Этот метод можно использовать всякий раз, когда комплексное число находится в первом квадранте. В нашем первом примере мы найдем главный аргумент комплексного числа в первом квадранте с помощью с помощью тригонометрии прямоугольного треугольника.
Пример 1. Нахождение аргумента комплексного числа в радианах
Найдите аргумент комплексного числа 4+3𝑖 в радианах. Дайте правильный ответ с точностью до двух знаков после запятой.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью аргана
диаграмма и линия между началом координат и комплексным числом, измеренная против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению дается в
диапазон ]−𝜋,𝜋].
Мы также помним, что аргумент комплексного числа по соглашению дается в
диапазон ]−𝜋,𝜋].
Начнем с нанесения комплексного числа на диаграмму Аргана.
Мы обозначили аргумент комплексного числа на приведенной выше диаграмме Аргана 𝜃. Мы видим, что аргументом этого комплексного числа является угол в правой треугольник, сторонами которого являются синий, зеленый и фиолетовый отрезки. Применяя тригонометрию прямоугольного треугольника, получаем таннапротив соседнего𝜃==34.
Затем мы можем применить функцию арктангенса к обеим частям этого уравнения, чтобы найти 𝜃=34=0,6435….arctanradians
Следовательно, argradians(4+3𝑖)=0,64 с точностью до двух знаков после запятой.
В предыдущем примере мы смогли вычислить аргумент комплексного числа 𝑎+𝑏𝑖, вычислив арктангенс 𝑏𝑎. Однако это не относится ко всем комплексным числам, как будет показано в следующем примере.
Пример 2. Нахождение главного аргумента комплексного числа
Учитывая, что 𝑍=−12+√32𝑖, найдите главный аргумент 𝑍.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линия между началом координат и комплексным числом, измеренная против часовой стрелки. Кроме того, мы помним, что главный аргумент комплексного числа — это аргумент, лежащий в диапазоне ]−𝜋,𝜋].
Начнем с нанесения комплексного числа на диаграмму Аргана, как показано ниже.
Мы обозначили аргумент комплексного числа на приведенной выше диаграмме Аргана 𝜃, а дополнительный угол 𝜙. Мы видим, что 𝜙 — угол в прямоугольном треугольнике, сторонами которого являются синий, зеленый и фиолетовый отрезки. Применяя тригонометрию прямоугольного треугольника, получаем tanoppositeadjacent𝜙==.√
Затем мы можем применить функцию арктангенса к обеим частям этого уравнения, чтобы найти 𝜙=⎛⎜⎜⎝⎞⎟⎟⎠=√3=𝜋3.arctanrctanradians√
Затем мы можем вычислить аргумент, вычитая 𝜙 из 𝜋:
арградианцы(𝑍)=𝜋−𝜙=𝜋−𝜋3=2𝜋3.
Заметим, что этот аргумент лежит в диапазоне ]−𝜋,𝜋]; следовательно, это главный аргумент.
Мы заключаем, что главный аргумент данного комплексного числа равен 2𝜋3.
В предыдущем примере мы видели, что аргумент комплексного числа 𝑎+𝑏𝑖 не всегда равен арктангенсу 𝑏𝑎. На самом деле, если бы мы наивно пытались вычислить аргумент 𝑧, оценивая 𝛼=⎛⎜⎜⎝⎞⎟⎟⎠,арктан√ мы бы закончили с 𝛼=−√3=−𝜋3.arctanradians
Этот аргумент представляет угол по часовой стрелке от положительной действительной оси в 𝜋3 радиана, что поместит комплексное число в четвертый квадрант. Из диаграммы Аргана в предыдущем примере видно, что это не аргумент комплексного числа. Однако мы можем получить правильное значение arg(𝑧), добавив 𝜋 к 𝛼.
Этот эффект показывает, что нам нужно быть осторожными при вычислении аргумента комплексного числа, которое не лежит в первом квадранте. Кроме того, мы видим, что существуют разные подходит для получения arg(𝑧).
Мы описываем два разных метода вычисления аргумента комплексного числа. Какой бы метод мы ни выбрали, нанесение числа на диаграмму Аргана будет чрезвычайно полезным.
и поможет нам избежать типичных ошибок при вычислении аргумента.
Какой бы метод мы ни выбрали, нанесение числа на диаграмму Аргана будет чрезвычайно полезным.
и поможет нам избежать типичных ошибок при вычислении аргумента.
Практическое руководство. Нахождение аргумента комплексного числа с помощью функции арктангенса
Чтобы найти аргумент arg(𝑧) комплексного числа 𝑧=𝑎+𝑏𝑖, нам нужно рассмотреть, в каком квадранте оно находится. аргумент Комплексное число 𝑧=𝑎+𝑏𝑖 можно получить с помощью функции арктангенса в каждом квадранте следующим образом:
- Если 𝑧 лежит в первом или четвертом квадранте, аргарктан(𝑧)=𝑏𝑎.
- Если 𝑧 лежит во втором квадранте, аргарктан(𝑧)=𝑏𝑎+𝜋.
- Если 𝑧 лежит в третьем квадранте, аргарктан(𝑧)=𝑏𝑎−𝜋.
Если комплексное число не лежит в квадранте, то оно либо чисто действительное, либо чисто мнимое. Если оно чисто мнимое (𝑎=0), то argforargfor(𝑧)=𝜋2𝑏>0,(𝑧)=−𝜋2𝑏0.
Если чисто действительный (𝑏=0), то argforargfor(𝑧)=0𝑎>0,(𝑧)=𝜋𝑎0.
Наконец, если 𝑎=𝑏=0, аргумент не определен.
Эти точки показаны на следующей диаграмме.
Основное преимущество описанного выше метода заключается в том, что нам дана формула, которой нужно следовать в каждой ситуации. Однако этот метод также требует, чтобы мы либо запоминали каждое правило, либо имели доступную ссылку на правила. Альтернативный метод нахождения аргумента комплексного числа — использовать тригонометрию прямоугольного треугольника, чтобы сначала определить положительный острый угол между действительной осью и отрезком линии между началом координат и комплексным числом на диаграмме Аргана. Найдя положительный острый угол, мы можем найти аргумент комплексного числа геометрически.
Как найти аргумент комплексного числа с использованием положительных острых углов
Мы определяем угол 𝜃 как положительный острый угол между линией, соединяющей 𝑧 с началом координат, и действительной осью, как показано на диаграмме.
Мы можем затем рассчитать аргумент 𝑧 в разных квадрантах следующим образом:
- Квадрант 1 : arg (𝑧) = 𝜃
- Квадрант 2 : arg (𝑧) = 𝜋 —
- Квадрант 3 : arg(𝑧)=𝜃−𝜋
- Квадрант 4 : arg(𝑧)=−𝜃
Два разных метода получения аргумента комплексного числа приведут к одному и тому же ответу. Второй метод, использующий положительный острый угол, более интуитивен и требует меньшего запоминания. Используя этот метод, мы сначала вычисляем положительный острый угол, а затем используем его для нахождения аргумента комплексного числа, которое представляет собой угол против часовой стрелки от положительной вещественной оси, лежащий в диапазоне ]−𝜋,𝜋].
Второй метод, использующий положительный острый угол, более интуитивен и требует меньшего запоминания. Используя этот метод, мы сначала вычисляем положительный острый угол, а затем используем его для нахождения аргумента комплексного числа, которое представляет собой угол против часовой стрелки от положительной вещественной оси, лежащий в диапазоне ]−𝜋,𝜋].
В следующем примере мы применим этот метод для нахождения аргумента комплексного числа, лежащего в третьем квадранте.
Пример 3: связь между комплексным сопряжением и аргументом
Рассмотрим комплексное число 𝑧=−4−5𝑖.
- Вычислить arg(𝑧), давая ответ с точностью до двух знаков после запятой в интервале от −𝜋 до 𝜋.
- Вычислите arg𝑧, давая ответ с точностью до двух знаков после запятой в интервале от −𝜋 до 𝜋.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Часть 1
Начнем с нанесения комплексного числа на диаграмму Аргана, как показано ниже.
Мы обозначили острый угол 𝜙, который связан с аргументом комплексного числа 𝑧. Если мы можем найти угол 𝜙, аргумент этого числа можно получить, прибавив 𝜋 к этому углу. Однако мы видим, что этот аргумент не будет лежать в диапазоне ]−𝜋,𝜋]. Затем мы должны вычесть из этого полученного угла полный оборот 2𝜋, что приводит к соотношению arg(𝑧)=(𝜙+𝜋)−2𝜋=𝜙−𝜋.
Мы видим, что 𝜙 — это угол в прямоугольном треугольнике, стороны которого являются синими, зелеными и фиолетовыми отрезками. Применяя тригонометрию прямоугольного треугольника, получаем таннапротив соседнего𝜙==54.
Затем мы можем применить функцию арктангенса к обеим частям этого уравнения, чтобы найти 𝜙=54=0,8960….arctanradians
Следовательно, чтобы вычислить arg(𝑧), мы вычитаем 𝜋 из 𝜙, что дает
арградианы, округленные до десятичных знаков (𝑧) = 𝜙−𝜋=−2,2455…=−2,25,2.
Часть 2
Напомним, что сопряженное 𝑧 получается заменой знака мнимой части комплексного числа 𝑧. Следовательно, 𝑧=−4+5𝑖. Теперь нанесем 𝑧 на диаграмму Аргана.
Как и в предыдущей части, мы найдем аргумент 𝑧, сначала вычислив 𝜙: 𝜙=54=0,8960….arctanradians
Поскольку 𝜙 и arg𝑧 являются дополнительными, мы можем получить arg𝑧, вычитая 𝜙 из 𝜋: арградианы, округленные до десятичных знаков𝑧=𝜋−𝜙=2,2455…=2,25,2.
В предыдущем примере мы вычислили аргументы комплексного числа и его сопряженного числа. Заметим, что аргумент комплексно-сопряженного числа в этом примере является отрицательным значением аргумента исходного комплексного числа. Это демонстрирует общее правило рассуждения.
Свойство: Аргумент сопряженного комплексного числа
Для любого ненулевого комплексного числа 𝑧 и его сопряженного 𝑧 (также обозначаемого 𝑧∗), аргарг(𝑧)=−𝑧.
В следующем примере мы покажем, как умножение и деление комплексных чисел связаны с аргументами комплексных чисел.
Пример 4. Аргументы произведений и частных
Рассмотрим комплексные числа 𝑧=1+√3𝑖 и 𝑤=2−2𝑖.
- Найдите arg(𝑧) и arg(𝑤).
- Вычислить аргумент(𝑧𝑤). Как это соотносится с arg(𝑧) и arg(𝑤)?
- Вычислить аргумент𝑧𝑤. Как это соотносится с arg(𝑧) и arg(𝑤)?
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Часть 1
Начнем с построения 𝑧 и 𝑤 на диаграмме Аргана.
Напомним, что аргумент комплексного числа 𝑧=𝑎+𝑏𝑖, лежащего в первом или четвертом квадранте, определяется выражением аргарктан(𝑧)=𝑏𝑎.
Поскольку 𝑧 и 𝑤 лежат в первом и четвертом квадрантах соответственно, мы можем использовать арктангенс, чтобы найти их аргументы следующим образом:
argarctanradians(𝑧)=√31=𝜋3
а также
argarctanradians(𝑤)=−22=−𝜋4.
Часть 2
Начнем с расчета 𝑧𝑤 следующим образом: 𝑧𝑤=1+√3𝑖(2−2𝑖).
Умножая через скобки, получаем 𝑧𝑤=2−2𝑖+2√3𝑖−2𝑖√3.
Используя 𝑖=−1 и собирая действительные и мнимые члены, получаем 𝑧𝑤=2+2√3+2√3−2𝑖.
Поскольку и действительная, и мнимая части положительны, 𝑧𝑤 лежит в первом квадранте диаграммы Аргана, и мы можем вычислить аргумент, вычислив арктангенс следующим образом: аргарктан(𝑧𝑤)=2√3−22+2√3.
Отменяя множитель 2 сверху и снизу, имеем аргарктан(𝑧𝑤)=√3−11+√3.
Мы можем упростить дробь, умножив и числитель, и знаменатель на сопряженную часть знаменателя: аргарктан(𝑧𝑤)=√3−11−√31+√31−√3.
Умножая через скобки, получаем argarctanarctanarctanradians(𝑧𝑤)=−1+2√3−31−3=−4+2√3−2=2−√3=𝜋12.
Сравнивая это с arg(𝑧) и arg(𝑤), мы находим, что argargarg(𝑧𝑤)=(𝑧)+(𝑤).
Часть 3
Начнем с вычисления 𝑧𝑤 следующим образом: 𝑧𝑤=1+√3𝑖2−2𝑖.
Чтобы записать это комплексное число в декартовой форме, 𝑎+𝑏𝑖, нам нужно умножить и числитель, и знаменатель на сопряженное значение знаменателя, то есть 2+2𝑖:
𝑧𝑤=1+√3𝑖(2+2𝑖)(2−2𝑖)(2+2𝑖).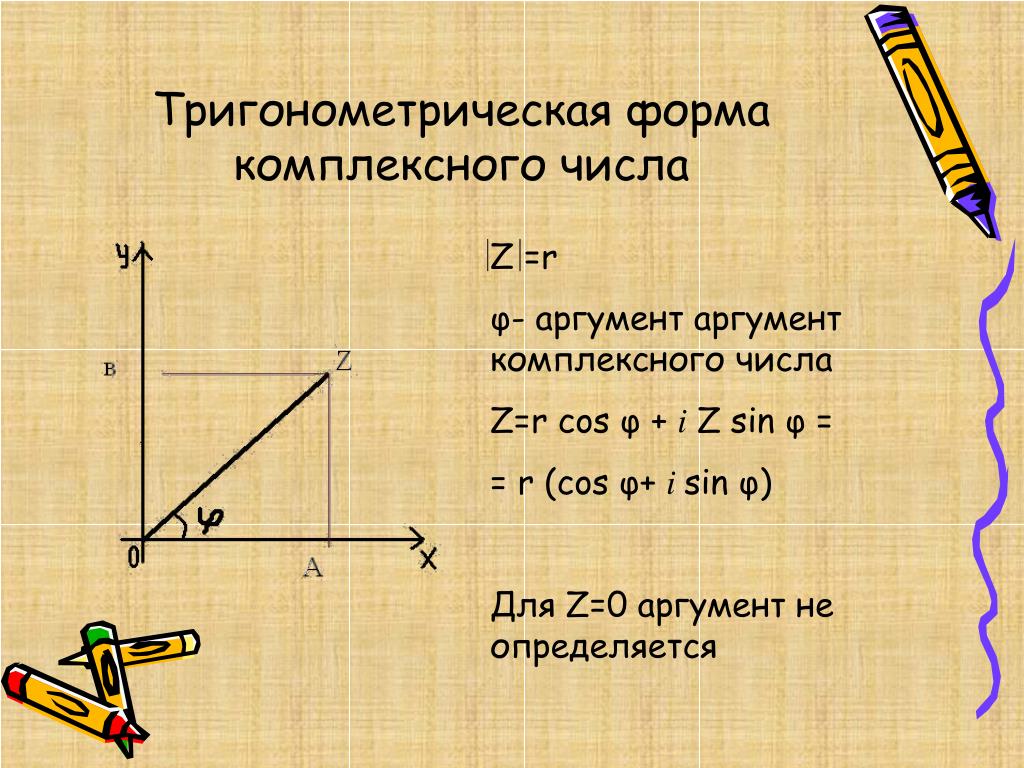
Умножая через скобки, имеем 𝑧𝑤=2+2𝑖+2𝑖√3+2𝑖√34+4.
Используя 𝑖=−1 и собирая действительные и мнимые термины, 𝑧𝑤=141−√3+141+√3𝑖.
С Re𝑧𝑤0 и Im𝑧𝑤>0, комплексное число 𝑧𝑤 лежит во втором квадранте. Напомним, что если комплексное число 𝑧=𝑎+𝑏𝑖 лежит в второй квадрант, аргарктан(𝑧)=𝑏𝑎+𝜋.
Отсюда имеем argarctan𝑧𝑤=1+√31−√3+𝜋.
Сокращая общий множитель 14, имеем аргарктан𝑧𝑤=1+√31−√3+𝜋.
Вычисляя арктангенс, получаем arg𝑧𝑤=−5𝜋12+𝜋=7𝜋12.
Наконец, сравнивая это с arg(𝑧) и arg(𝑤), мы находим, что argargarg𝑧𝑤=(𝑧)−(𝑤).
В предыдущем примере мы наблюдали связь между умножением/делением комплексных чисел и их аргументами. Это соотношение, показанное в примере, справедливо для общих комплексных чисел.
Свойство: Аргументы и умножение/деление комплексных чисел
Для любых ненулевых комплексных чисел 𝑧 и 𝑧, argargargargargarg(𝑧𝑧)=(𝑧)+(𝑧),𝑧𝑧=(𝑧)−(𝑧).
Следующий пример продемонстрирует, как мы можем решать задачи, применяя свойства Аргумент.
Пример 5. Использование умножения комплексных чисел для определения аргумента
Комплексное число умножается на другое комплексное число 𝑧, а затем на комплексно-сопряженное число 𝑧. Как аргумент полученного комплексного числа связан с аргументом исходного комплексного числа?
Ответ
Напомним, что аргумент произведения пары комплексных чисел равен сумме аргументов двух комплексных чисел.
Начнем с комплексного числа 𝑤; затем он умножается на 𝑧 и 𝑧. Следовательно, результат 𝑤𝑧𝑧. Нас спрашивают, как аргумент полученного комплексного числа связан с аргументом исходного комплексного числа. Следовательно, мы должны рассмотреть arg𝑤𝑧𝑧. Используя мультипликативные свойства аргумента, мы можем переписать это следующим образом: аргаргаргарг𝑤𝑧𝑧=(𝑤)+(𝑧)+𝑧.
Мы также знаем, что аргумент комплексного числа равен отрицательному значению аргумента его сопряженного числа. Следовательно, мы можем заменить arg𝑧 выше на −(𝑧)arg, чтобы написать
аргаргаргаргарг𝑤𝑧𝑧=(𝑤)+(𝑧)−(𝑧)=(𝑤).
Следовательно, аргумент комплексного числа после его умножения на другое комплексное число 𝑧, а затем на комплексно-сопряженное число 𝑧 не меняется.
В нашем последнем примере мы рассмотрим связь между аргументом и степенями.
Пример 6. Нахождение аргумента степеней комплексных чисел в алгебраической форме
Рассмотрим комплексное число 𝑧=7+7𝑖.
- Найдите аргумент 𝑧.
- Следовательно, найдите аргумент 𝑧.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Часть 1
Напомним, что аргумент комплексного числа 𝑧=𝑎+𝑏𝑖, лежащего в первой или четвертой четверти, определяется формулой аргарктан(𝑧)=𝑏𝑎.
Поскольку комплексное число лежит в первом квадранте, мы можем вычислить его аргумент, оценив арктангенс его мнимой части над его действительной частью следующим образом:
аргарктанарктанрадиан(𝑧)=77=(1)=𝜋4.
Часть 2
Напомним, что для любых двух ненулевых комплексных чисел 𝑧 и 𝑧, аргаргарг(𝑧𝑧)=(𝑧)+(𝑧).
Если оба комплексных числа равны 𝑧, это означает argarg𝑧=2(𝑧).
Используя аналогичную логику, мы можем найти, что argargargarg𝑧=3(𝑧),𝑧=4(𝑧).
Следовательно, argargradians𝑧=4(𝑧)=4×𝜋4=𝜋.
В предыдущем примере мы видели связь между степенью комплексного числа и его аргументом. Используя ту же логику, что и в этом примере, мы можем видеть, что это соотношение выполняется для общих комплексных чисел для любой степени положительного целого числа.
Свойство: Аргумент степени комплексного числа
Для любого ненулевого комплексного числа 𝑧 и степени положительного целого числа 𝑛 аргумент 𝑧 задается формулой argarg(𝑧)=𝑛(𝑧).
В этом объяснении мы рассмотрели, как аргумент комплексного числа связан с сопряжениями, умножением и делением комплексных чисел. Однако мы намеренно исключили сложение и вычитание комплексных чисел, поскольку между этими операциями и аргументами комплексных чисел нет простой связи. Мы закончим это объяснение, проиллюстрировав двумя разными способами, почему мы не ожидаем найти простую связь между сложением/вычитанием и аргументами комплексных чисел.
Мы закончим это объяснение, проиллюстрировав двумя разными способами, почему мы не ожидаем найти простую связь между сложением/вычитанием и аргументами комплексных чисел.
Во-первых, напомним, что сложение и вычитание комплексных чисел геометрически эквивалентны соответствующим векторным операциям и, следовательно, подчиняются правилам треугольника или параллелограмма. При этом мы видим, что знания только аргументов (углов) комплексных чисел будет недостаточно, чтобы найти аргумент результирующего комплексного числа. Это один из способов понять, почему нет простой связи между этими операциями и аргументами комплексных чисел.
В качестве альтернативного способа понять, почему такой простой связи не существует, рассмотрим три комплексных числа 𝑧=1+𝑖, 𝑧=2+√3(1+𝑖) и 𝑧=1−𝑖 нанесен на диаграмму Аргана ниже.
Мы видим, что argarg(𝑧)=(𝑧)=𝜋4 и что arg(𝑧)=−𝜋4. Кроме того, 𝑧+𝑧=2, аргумент которого равен 0, тогда как
𝑧+𝑧=3+√3+1+√3𝑖,
аргумент которого явно не равен нулю. На самом деле мы можем вычислить точное значение аргумента следующим образом:
argarctan(𝑧+𝑧)=1+√33+√3.
На самом деле мы можем вычислить точное значение аргумента следующим образом:
argarctan(𝑧+𝑧)=1+√33+√3.
Умножая числитель и знаменатель на сопряженное знаменателю, мы можем упростить дробь: аргарктан(𝑧+𝑧)=1+√33−√33+√33−√3.
Умножая через скобки, получаем argarctan(𝑧+𝑧)=3−√3+3√3−33−3.
Наконец, мы можем упростить и вычислить арктангенс, чтобы получить argarctanarctanradians(𝑧+𝑧)=2√36=√33=𝜋6.
Чтобы обобщить наши вычисления, вспомним, что комплексные числа 𝑧 и 𝑧 имеют один и тот же аргумент, 𝜋4. Если бы существовала простая связь между аргументами комплексных чисел и суммой, аргументы 𝑧+𝑧 и 𝑧+𝑧 были бы одинаковыми. Однако мы получили аргумент(𝑧+𝑧)=0,(𝑧+𝑧)=𝜋6.
Это показывает, что знания аргументов двух комплексных чисел недостаточно для вычисления аргумента их суммы.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые моменты
- Аргумент комплексного числа 𝑧 определяется как угол в радианах между положительной действительной осью на диаграмме Аргана и отрезком прямой от начала координат до комплексного числа, измеренный против часовой стрелки.

- Аргумент комплексного числа 𝑧=𝑎+𝑏𝑖 можно получить с помощью функции арктангенса в каждом квадранте следующим образом:
- Если 𝑧 лежит в первом или четвертом квадранте, аргарктан(𝑧)=𝑏𝑎.
- Если 𝑧 лежит во втором квадранте, аргарктан(𝑧)=𝑏𝑎+𝜋.
- Если 𝑧 лежит в третьем квадранте, аргарктан(𝑧)=𝑏𝑎−𝜋.
- Аргумент имеет следующие свойства:
- Аргарг (𝑧) = — 𝑧,
- Аргаргарг (𝑧𝑧) = (𝑧)+(𝑧) ,
- Аргаргарг = (𝑧)+(𝑧) 𝑧)−(𝑧),
- аргарг(𝑧)=𝑛(𝑧).
- Между сложением комплексных чисел и их аргументами нет простой связи.
Аргумент комплексных чисел. Решаемые примеры
В математике комплексные плоскости играют чрезвычайно важную роль. Мы также называем это z-плоскостью, состоящей из взаимно перпендикулярных линий, известных как оси. Действительные числа представлены горизонтальной линией и поэтому известны как действительная ось, тогда как мнимые числа представлены вертикальной линией и поэтому известны как мнимая ось. В основном мы используем комплексные плоскости для представления геометрической интерпретации комплексных чисел. Это похоже на декартову плоскость, которая имеет как действительную, так и мнимую части комплексного числа вместе с осями X и Y. Комплексные числа разветвляются на две основные концепции, т. е. величину и аргумент. Но пока мы сосредоточимся только на аргументе комплексных чисел и изучим его определение, формулы и свойства. 9{2}\] = −1. Комплексные числа называются продолжением одномерных числовых линий. На комплексной плоскости комплексное число, обозначаемое a + bi, обычно представляется в виде точки (a, b). Мы должны отметить, что комплексное число, не имеющее абсолютно никакой реальной части, например –i, -5i и т. д., называется чисто мнимым. Кроме того, комплексное число, не имеющее абсолютно никакой мнимой части, называется действительным числом.
В основном мы используем комплексные плоскости для представления геометрической интерпретации комплексных чисел. Это похоже на декартову плоскость, которая имеет как действительную, так и мнимую части комплексного числа вместе с осями X и Y. Комплексные числа разветвляются на две основные концепции, т. е. величину и аргумент. Но пока мы сосредоточимся только на аргументе комплексных чисел и изучим его определение, формулы и свойства. 9{2}\] = −1. Комплексные числа называются продолжением одномерных числовых линий. На комплексной плоскости комплексное число, обозначаемое a + bi, обычно представляется в виде точки (a, b). Мы должны отметить, что комплексное число, не имеющее абсолютно никакой реальной части, например –i, -5i и т. д., называется чисто мнимым. Кроме того, комплексное число, не имеющее абсолютно никакой мнимой части, называется действительным числом.
Что такое аргумент комплексных чисел?
Аргумент комплексного числа — это угол, который наклонен от действительной оси к направлению комплексного числа, представленного на комплексной плоскости. Мы можем обозначить его как «θ» или «φ» и измерить в стандартных единицах «радиан».
Мы можем обозначить его как «θ» или «φ» и измерить в стандартных единицах «радиан».
На приведенной выше диаграмме комплексное число обозначено точкой P. Длина OP представляет собой величину или модуль числа, а угол, под которым OP наклонен к положительной действительной оси, известен как аргумент числа точка P.
Как найти аргументы комплексного числа?
Есть несколько шагов, которые необходимо выполнить, если мы хотим найти аргумент комплексного числа. Эти шаги приведены ниже:
Шаг 1) Сначала мы должны найти как действительные, так и мнимые части комплексного числа, которое нам дано, и обозначить их x и y соответственно. 9{-1}\] сам по себе.
Шаг 4) Окончательное значение вместе с единицей «радиан» является требуемым значением комплексного аргумента для данного комплексного числа.
С помощью этого метода вы теперь узнаете, как узнать аргумент комплексного числа.
Аргумент комплексных чисел Примеры
1. Найдите аргумент -1+i и 4-6i
Ответ: Сначала нам нужно найти два комплексных числа в комплексной плоскости. Это облегчит нам определение квадрантов, в которых лежат ангелы, и даст приблизительное представление о величине каждого угла.
Для, z = —+i
Мы можем видеть, что Аргументом z является второй квадрант угла, а тангенс представляет собой отношение мнимой части к действительной части, в таком случае −1 . Таким образом, тангенс исходного угла будет равен 1. Запишите значение второго квадранта угла так, чтобы его исходный угол мог иметь тангенс, равный 1. Если исходный угол содержит тангенс, равный 1, то значение исходного угла будет π/4, поэтому угол второго квадранта равен π − π/4 или 3π/4. 9{-1}\](tan π/3)
arg (z) = π/3
Следовательно, аргумент комплексного числа равен π/3 радиан.
Комплексные числа
Комплексные числа — это те числа, которые используются для нахождения квадратного корня из отрицательных чисел. Комплексные числа были впервые введены греческим математиком по имени Герой Александрийский, который пытался найти квадратный корень из отрицательных чисел, но не смог его решить. Эта проблема была решена итальянским математиком по имени Джероламо Кардано, который нашел отрицательные корни кубических и квадратичных полиномиальных выражений, используя комплексные числа. Комплексные числа широко используются в научных исследованиях, гидродинамике, квантовой механике и обработке сигналов.
Комплексное число может быть определено как сумма мнимого числа и действительного числа. Он записывается как + ib, который можно обозначить через z. Здесь a и b — действительные числа. Говорят, что значение a является действительной частью, которая обозначается Re(z), а b называется мнимой частью, записываемой как Im(z).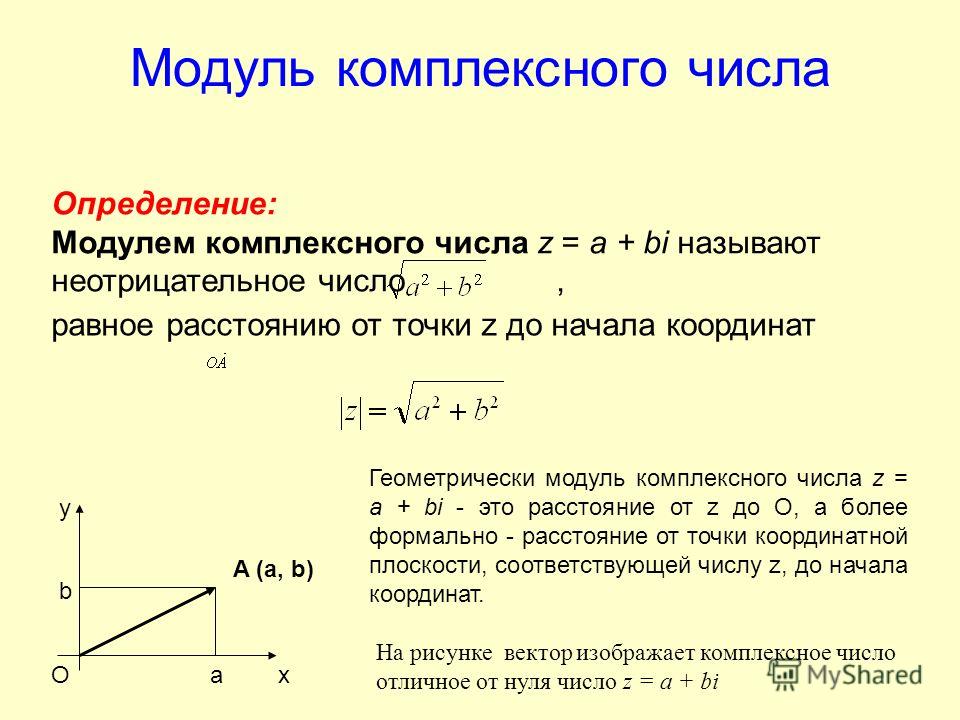 ib также является мнимым числом. Например, 2 + 3i и -2 -5i являются примерами комплексных чисел. Написанное здесь i называется йотой и используется для представления мнимой части комплексных чисел. Также полезно находить квадратный корень из отрицательных чисел.
ib также является мнимым числом. Например, 2 + 3i и -2 -5i являются примерами комплексных чисел. Написанное здесь i называется йотой и используется для представления мнимой части комплексных чисел. Также полезно находить квадратный корень из отрицательных чисел.
Что означает аргумент комплексных чисел?
Когда в геометрическом представлении линия, представляющая комплексное число и начало координат, образует угол с положительной осью X в направлении против часовой стрелки, это называется аргументом комплексных чисел. Это представлено инверсией тангенса мнимого числа в комплексном числе, которое делится на действительную часть комплексного числа.
Argz(θ) = Tan−1(b/a)
Как найти модуль (абсолютное значение) и аргумент (угол) комплексных чисел?
Комплексная плоскость играет важную роль в математике. Есть два понятия, связанные с комплексными числами: модуль и аргумент. Следующее пошаговое руководство поможет вам научиться находить модуль и аргумент комплексных чисел.
Одна из самых важных особенностей чисел, вещественных или сложных, заключается в том, что они имеют «абсолютное значение». Имейте в виду, что если действительное число положительное или отрицательное, его абсолютное значение \(|x|\) равно самому себе. Если \(x\) отрицательно, его абсолютное значение \(|x|\) является его отрицанием, которое является положительным значением \(x\). Потому что \(|3|\) равно \(3\), а \(| –4|\) равно \(4\). Удаляет знак у вещественного числа.
См. также
- Тождества комплексных чисел
- Как решить комплексную плоскость
Пошаговое руководство по модулю и аргументу комплексных чисел
В комплексной плоскости \(C\) расстояние от \( z\) до \(0\) называется абсолютным значением \(|z|\). Это облегчит понимание абсолютного значения действительных чисел. Абсолютное значение \(|x|\) действительного числа \(x\) можно рассматривать как расстояние от \(x\) до \(0\) на прямой с действительными числами, так что это облегчит задачу. понять, что такое абсолютное значение. 92}}\)
понять, что такое абсолютное значение. 92}}\)
Аргумент комплексного числа определяется как угол, образованный между действительной осью и комплексным числом, представленным на комплексной плоскости, где действительная ось является началом комплексного числа. Обозначается символами «\(θ\)» или «\(φ\)». Он измеряется в радианах, которые являются стандартной единицей измерения.
Точка \(P\) обозначает комплексное число на этой диаграмме. Длина \(OP\) известна как величина или модуль числа, а угол, под которым \(OP\) наклонен от положительной действительной оси, является аргументом точки \(P\). 9n)=n\ arg (z)}\)
- \(Z_1\) и \(Z_2\) — два комплексных числа, которые, как мы можем предположить, обладают следующими свойствами:
\(\color{blue} { arg (\frac {z_1}{z_2})=arg (z_1)-arg(z_2)}\)
\(\color{blue}{arg\ (z_1 z_2)= arg (z_1) + arg (z_2 )}\)
Как лучше всего найти аргумент комплексного числа?- По заданному комплексному числу определите действительную и мнимую составляющие.
 {–1}(\frac {y}{x})}\). 92}\)\(=\sqrt {25+9}\)\(=\sqrt {34}\)
{–1}(\frac {y}{x})}\). 92}\)\(=\sqrt {25+9}\)\(=\sqrt {34}\)Модуль и аргумент комплексных чисел – Пример 3:
Если \(arg ({z_1}) =\frac{7π }{6}\) и \(arg ({z_2})=\frac{-π }{2}\), найдите \(arg ( z_1 z_2)\).
Чтобы найти \(arg ( z_1 z_2)\) используйте эту формулу: \(\color{blue}{arg\ (z_1 z_2)= arg (z_1) + arg (z_2)}\)
\(arg ( z_1 z_2)\) \(= \frac{7π }{6} + \frac{-π }{2} = \frac{7π }{6} – \frac{π }{2} =\frac{ 7π -3 π {6}=\frac {4π}{6}=\frac{2π}{3}\)
Упражнения на модуль и аргумент комплексных чисел
Найдите модуль комплексного числа.
- \(\color{blue}{ z= {2+i}}\)
- \(\color{blue}{ z= {10-6i}}\)
Найти аргумент комплекса количество.
- \(\color{blue}{z= {\sqrt{3}-i}}\)
- \(\color{blue}{z= {-4-4i}}\)
- \(\color{blue}{ |z| =\sqrt {5}}\)
- \(\color{blue}{ |z| =8}\)
- \(\color{blue}{ θ= \frac{-π}{6}}\)
- \(\color{blue}{ θ=\frac{π}{4}}\)
Комплексные числа и формулы, символы
Комплексные числа сами по себе очень абстрактны, и чтобы лучше понять их свойства, мы необходимо провести параллели между ними и другими менее абстрактными величинами.
 Один из способов сделать это — рассматривать комплексное число как вектор и находить сходные свойства, такие как величина (также известная как модуль) комплексного числа, его направление и фаза . Рекомендуется просмотреть статью о комплексных числах, прежде чем продолжить эту статью!
Один из способов сделать это — рассматривать комплексное число как вектор и находить сходные свойства, такие как величина (также известная как модуль) комплексного числа, его направление и фаза . Рекомендуется просмотреть статью о комплексных числах, прежде чем продолжить эту статью!Краткий обзор комплексных чисел: формула и символы
Представлять комплексные числа в виде точек на плоскости XY — очень плодотворная идея. Но эта плоскость не является правильной декартовой плоскостью с нормальными декартовыми координатами, а мы будем называть ее комплексной плоскостью. Также иногда известный как плоскость Аргана, в честь математика Жана-Роберта Аргана.
Комплексные числа очень естественно нанесены на эту плоскость. Пусть есть комплексная плоскость вида где . Здесь a называется действительной частью, а b называется мнимой частью. Координаты z на комплексной плоскости будут (a, b). Ось у называется воображаемой осью, а ось х — действительной осью. Линия «r» в этой статье называется конечным плечом.

Комплексные числа состоят из действительной и мнимой частей, StudySmarter Originals
Модуль комплексного числа
Обозначим расстояние точки от начала координат как r, и мы можем использовать теорему Пифагора для вычисления его расстояние от начала координат, которое составляет
Это расстояние r известно как Модуль z , следовательно, мы получаем,
, где обозначает модуль z.
Модуль комплексного числа — это расстояние этой точки от начала координат на комплексной плоскости. В противном случае квадрат модуля комплексного числа равен сумме квадратов его действительной и мнимой частей. ()
Вычислить модуль комплексного числа z=3+4i
Решение:
Шаг 1: Из определения модуля комплексного числа,
0 Шаг 74 Рядом с числом 74 всегда мнимая часть. Из вопроса 3 и 4 — действительная и мнимая части соответственно:
Таким образом, модуль z=3+4i равен 5
Отношение между комплексным числом, его сопряженным и его модулем
Пусть комплексное число, тогда его сопряженное (вспомните раздел статьи о комплексных числах о сопряженных числах)!
Шаг 1: Если мы умножаем конъюгаты вместе, например,:
Шаг 2: , и когда мы расширяем скобки, мы получаем
и AS, поэтому
.
 : Подставив в уравнение на шаге 2, мы получим
: Подставив в уравнение на шаге 2, мы получимПравая часть — это просто квадрат модуля! Итак, у нас
Другими словами,
Модуль и фазовый угол
Вернемся к геометрическому представлению комплексного числа,
Фаза комплексного числа — это угол между положительной осью концевое плечо, StudySmarter Originals
Пусть будет углом, образованным z с положительной осью x. Мы называем этот угол фазовым углом z, также известным как аргумент z. В полярной форме z выражается как
и из графика мы можем использовать тригонометрические отношения, чтобы сказать, что
Решая для мы получаем
ВАЖНО! Для целей этой статьи -1 на тангенсе равно , а не , как экспонента (т. е. не является обратной величиной тангенса — котангенса). Это используется, потому что оно представляет функцию арктангенса , арктангенс, на большинстве калькуляторов.

Альтернативный способ вычисления фазового угла — использование синуса и косинуса.
Подставляя переменные из рисунка 2 выше, мы получаем:
Мы только что узнали, что r — это модуль, . Подставив это выражение для r в приведенное выше уравнение, мы получим
Используя теорему Пифагора, мы можем определить r через a и b:
получить (как и для синуса):
Основные аргументы комплексных чисел
Можно заметить, что при изменении угла и т. д. комплексное число остается прежним. Таким образом, будет не уникальное значение, а бесконечно много. Следовательно, мы называем первое значение основного аргумента z Arg(z).
Вычислить главный аргумент комплексного числа.
Решение:
Шаг 1: Мы знаем, что . Из вопроса имеем. Таким образом, мы имеем значение тангенса как
Шаг 2: Решая для , получаем
Таким образом, главный аргумент Arg(z) равен .
 Это означает, что мы можем прибавить или вычесть кратные 360 градусов к 45 и получить то же самое комплексное число!
Это означает, что мы можем прибавить или вычесть кратные 360 градусов к 45 и получить то же самое комплексное число!Теорема де Муавра
Теорема де Муавра является фундаментальной для комплексных чисел. Теорема формулируется следующим образом:
Теорема: Пусть два различных комплексных числа и их полярные формы
и
Тогда произведение будет комплексным числом с фазой как .
Важное следствие теоремы Муавра: Мы определили как фазовый угол комплексного числа z. Теперь мы увидим, как фазовый угол изменяется в зависимости от степени, возведенной в z. Умножим z на себя n раз. У нас есть новое комплексное число с другим фазовым углом. Следствием приведенной выше теоремы является то, что
упрощается до
с фазовым углом . Это верно для всех целочисленных значений n, т. е.
. Это следствие помогает нам найти аргумент комплексного числа, возведенного в степень, намного эффективнее, чем перемножать все члены.

Примеры модуля и фазы
Не расширяя комплексное число, найдите его аргумент.
Решение:
Шаг 1 : Преобразование комплексного числа в его полярную форму:
Step2 : по сравнению с общей формой мы выводим, что
дает нам принцип принципа следующим образом:
Шаг3 : подключение к значению Н. .
Следовательно, основной аргумент — радианы.
Применение комплексных чисел
Концепция комплексных чисел не является полностью чистой и абстрактной, но имеет применение повсюду.
Одним из самых простых способов применения комплексных чисел является нахождение корней квадратного уравнения. Это также одно из мест, где возникла концепция комплексного числа.
Найдите корень квадратного уравнения.
Решение:
Шаг 1: Используя квадратную формулу, чтобы найти корни этого уравнения:
Шаг 2: При упрощении, мы получаем:
часть, потому что мы не знаем квадратный корень из отрицательного числа?
Здесь мы используем наши знания об использовании, которые упрощают данную форму в:
С которым теперь можно обращаться по законам комплексных чисел.

Целая отрасль математики, известная как комплексный анализ, основана на изучении комплексных чисел и применении их свойств в других областях математики.
Очень популярное уравнение в физике также использует комплексные числа, Уравнение Шрёдингера:
Волновое уравнение, используемое для моделирования орбит электронов вокруг ядра атома.
Применений множество, от дифференциального уравнения цепи индуктор-конденсатор (LC) до моделирования принимаемых сигналов.
Модуль и фаза. Ключевые выводы
- Модуль комплексного числа — это его расстояние от начала координат на комплексной плоскости.
- Комплексное число связано с его модулем и сопряжено уравнением
- Фазовый угол или аргумент комплексного числа представляет собой угол r (отрезок линии, соединяющий начало координат с комплексным числом) с положительной осью x.
- Фазовый угол комплексного числа z=a+ib равен .
- Теорема де Муавра описывает, как можно легко вычислить комплексное число, возведенное в целую степень, без использования биномиальной теоремы.

- Важное следствие теоремы Муавра гласит, что (аргумент комплексного числа, возведенного в степень n, в n раз больше аргумента исходного комплексного числа
Аргумент комплексного числа в разных квадрантах
Аргумент комплексного числа в разных квадрантах:
Пусть (r, θ) — полярные координаты точки.
P = P(x, y) в комплексной плоскости, соответствующей комплексному числу
z = x + iy
cos θ = смежная сторона/сторона гипотенузы ==> OM/MP ==> x/r
sin θ = противолежащая сторона/сторона гипотенузы ==> PM/OP ==> y/r
x = r cos θ и y = r sin θ
tan θ = y/x
θ = tan−1 y /x
называется амплитудой или аргументом z = x + iy
, обозначается amp z или arg z и измеряется как угол, который линия OP образует с положительной осью x (в направлении против часовой стрелки).
Как найти аргумент комплексного числа?
Обычно у нас есть два метода нахождения аргумента комплексного числа
(i) Используя формулу θ = tan−1 y/x
, где x и y — действительная и мнимая части комплексного числа соответственно.

Эта формула применима, только если x и y положительны.
Но для нахождения аргумента любого комплексного числа используется следующий метод.
Аргумент комплексного числа в разных квадрантах
Чтобы найти модуль и аргумент для любого комплексного числа, мы должны приравнять их к полярной форме
r (cos θ + i sin θ)
Здесь r обозначает модуль, а θ обозначает аргумент
Давайте см. несколько примеров задач, чтобы понять, как найти модуль и аргумент комплексного числа.
Аргумент комплексного числа в разных квадрантах — Примеры
Пример 1:
Найдите модуль и аргумент комплексного числа
— √2 + i √2
Решение:
— √2 + i √2 = r (cos θ + i sin θ) —-(1)
r 9 (- √2) ² + √2²] = √(2 + 2) = √4 = 2
r = 2
Примените значение r в первом уравнении
— √2 + i √ 2 = 2 (cos θ + i sin θ)
— √2 + i √2 = 2 cos θ + i 2 sin θ
Приравнивание действительной и мнимой частей по отдельности
2 cos θ = — √2
cos θ = — √2/2
cos θ = — 1/ √2
2 SIN θ = √2
SIN θ = √2/ 2
SIN θ = 1/ √2
Поскольку sin θ положительный, а cos θ отрицательный, искомое и θ лежит во втором квадранте.

θ = Π — α
Здесь α не что иное, как углы sin и cos, для которых мы получаем значение θ = (4Π-Π)/4 ==> 3 Π/4
Модуль = 2 и аргумент = 3Π/4
Отсюда — √2 + i √2 = 2 (cos 3Π/4 + i sin 3Π/4)
Пример 2:
Найти модуль и аргумент комплексного числа
1 + i √3
Решение:
1 + i √3 = r (cos θ + i sin θ) —-(1)
r = √ [(1 ) ² + √3] (1 + 3) = √4 = 2
r = 2
Применить значение r в первом уравнении √3 = 2 cos θ + i 2 sin θ
Приравнивание действительной и мнимой частей по отдельности
2 cos θ = 1
cos θ = 1 /2
2 sin θ = √3
sin θ = √3 /2
Поскольку sin θ и cos θ положительны, искомое и θ лежит в первом квадранте.
θ = α
Здесь α не что иное, как углы sin и cos, для которых мы получаем значения 1/2 и √3 /2 соответственно.

θ = Π/3
Модуль = 2 и аргумент = Π/3
Следовательно — √2 + i √2 = 2 (cos Π/3 + i sin Π/3)
4 Пример 3 :
Найдите модуль и аргумент комплексного числа
-1 — i √3
Решение :
-1 — i √3 = r (cos θ) — + i- sin θ -(1)
r = √ [(-1 ) ² + (-√3)²] = √(1 + 3) = √4 = 2
r = 2
Примените значение r в первом уравнении
-1 — i √3 = 2 (cos θ + i sin θ)
-1 — i √3 = 2 cos θ + i 2 sin θ
Приравнивая действительную и мнимую части по отдельности
4
2 cos θ = -1
cos θ = -1 /2
2 sin θ = — √3
sin θ = — √3 /2
Поскольку sin θ и cos θ отрицательны, искомое и θ лежит в третьем квадранте.
θ = -Π + α
Здесь α есть не что иное, как углы sin и cos, для которых мы получаем значения √3 /2 и 1/2 соответственно.

θ = — Π + α
= — Π + Π/3 ==> (-3Π+Π)/3 ==> -2Π/3
Модуль = 2 и аргумент = -2Π/3
Отсюда — 1 — i √3 = 2 (cos (-2Π/3) + i sin (-2Π/3))
аргумент комплексного числа.
Помимо материалов, представленных в этом разделе, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Счет, математика и статистика — Набор академических навыков
Модуль и аргумент
Главное меню ContentsToggle 1 Диаграмма Аргана 1.1 Определение 1.2 Рабочий пример 2 Модуль и аргумент 2.1 Определение 3 Рабочие примеры 4 Видео пример 5 Рабочая тетрадь 6 Проверьте себя 7 Внешние ресурсы
Диаграмма Аргана
Определение
Диаграмма Аргана имеет горизонтальную ось, называемую реальной осью , и вертикальную ось, называемую воображаемой осью .

В координатах $(a,b)$ нанесено комплексное число $z = a + bi$, где $a$ — действительная часть комплексного числа, а $b$ — мнимая часть.
|center
Рабочий пример
Пример 1
Нанесите следующие комплексные числа на диаграмму Аргана.
\begin{align} z_1 &= 3+i \\ z_2 &= -2-4i \\ z_3 &=-1+3i \\ z_4 &= -2i \end{align}
Решение
Модуль и аргумент
Определение
Любое комплексное число $z$ может быть представлено точкой на диаграмме Аргана. Мы можем соединить эту точку с началом координат с помощью отрезка. Длина отрезка называется модулем комплексного числа и обозначается $\lvert z \rvert$. Угол, измеренный от положительной действительной оси к отрезку, называется 92}\]
При вычислении аргумента комплексного числа необходимо сделать выбор между взятием значений в диапазоне $[-\pi,\pi]$ или в диапазоне $[0,\pi]$. Оба эквивалентны и одинаково действительны. На этой странице мы будем использовать соглашение $-\pi \lt \theta \lt \pi$.

«Наивный» способ вычисления угла к точке $(a,b)$ заключается в использовании $\arctan(\frac{b}{a})$, но поскольку $\arctan$ принимает значения только в диапазон $[-\frac{\pi}{2},\frac{\pi}{2}]$, это даст неверный результат для координат с отрицательной $x$-компонентой. Это можно исправить, добавив или вычтя $\pi$, в зависимости от того, в каком квадранте диаграммы Аргана находится точка.
- Первый квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right)$.
- Второй квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right) + \pi$.
- Третий квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right) -\pi$.
- Четвертый квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right)$.
При принятии решения о том, какую формулу использовать, рекомендуется нарисовать диаграмму Аргана комплексного числа.
Примечание: обратите внимание на случай, когда $a=0$, т.е. комплексное число не имеет вещественной части. В этом случае метод $\arctan$ не работает, но аргументом является либо $\frac{\pi}{2}$, либо $-\frac{\pi}{2}$ для чисел с положительными и отрицательными мнимых частей соответственно.
 2}\\ &=\sqrt{16}\\ &=4 \end{align } 92}\\ &=\sqrt{4+25}\\ &=\sqrt{29} \end{align}
2}\\ &=\sqrt{16}\\ &=4 \end{align } 92}\\ &=\sqrt{4+25}\\ &=\sqrt{29} \end{align}Поскольку $z$ находится во втором квадранте диаграммы Аргана, нам нужно добавить $\pi $ к результату, полученному из $\arctan \left(\frac{5}{-2}\right)$.
\begin{align} \arg z &= \arctan \left(\frac{5}{-2}\right) + \pi \\ &=-1,19 + \pi \\ &= 1,95 \text{ радианы (до 2 д.п.)} \end{align}
Пример 4
Найдите модуль и аргумент комплексного числа $z = -4-3i$.
Решение
|центр 92}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ &=5 \end{align}
Поскольку $z$ лежит в третьем квадранте диаграммы Аргана, нам нужно чтобы вычесть $\pi$ из результата $\arctan \left(\frac{-3}{-4}\right)$.
\begin{align} \arg z &= \arctan \left(\frac{-3}{-4}\right) — \pi\\ &= \arctan \left(\frac{3}{4} \right) — \pi\\ &= 0,64 — \pi \\ &= -2,50 \text{ радианы (до 2 d.p.)} \end{align}
Примечание: В качестве альтернативы ответ мог быть дан в диапазон $0 \lt \theta \lt 2\pi$, где мы бы добавили $\pi$ вместо вычитания и получили ответ $\arg z = 3,67$ радиан (к 2 д.
 п.) 92}\\ &=\sqrt{1+16}\\ &=\sqrt{17} \end{align}
п.) 92}\\ &=\sqrt{1+16}\\ &=\sqrt{17} \end{align}Поскольку $z$ лежит в четвертом квадранте диаграммы Аргана, нам не нужно изменять результат $\arctan \left(\frac{-4}{1}\right)$, чтобы найти аргумент.
\begin{align} \arg z &= \arctan \left(\frac{-4}{1}\right)\\ &= \arctan \left(-4\right) \\ &= -1.33 \ text{ радианы (до 2 д.п.)} \end{align}
Пример видео
Профессор Робин Джонсон рисует комплексные числа $z=-1-i$ и $z=-4+3i$ на диаграмме Аргана, и находит их модуль и аргумент.
Рабочая тетрадь
Эта рабочая тетрадь, созданная HELM, является хорошим пособием по повторению, содержащим ключевые моменты для исправления и множество рабочих примеров.
- Диаграммы Аргана и полярная форма
Проверь себя
Проверь себя: тест Numbas по нахождению модуля и аргумента
Внешние ресурсы
- Брошюра с диаграммой Аргана в math center.



 {–1}(\frac {y}{x})}\). 92}\)\(=\sqrt {25+9}\)\(=\sqrt {34}\)
{–1}(\frac {y}{x})}\). 92}\)\(=\sqrt {25+9}\)\(=\sqrt {34}\) Один из способов сделать это — рассматривать комплексное число как вектор и находить сходные свойства, такие как величина (также известная как модуль) комплексного числа, его направление и фаза . Рекомендуется просмотреть статью о комплексных числах, прежде чем продолжить эту статью!
Один из способов сделать это — рассматривать комплексное число как вектор и находить сходные свойства, такие как величина (также известная как модуль) комплексного числа, его направление и фаза . Рекомендуется просмотреть статью о комплексных числах, прежде чем продолжить эту статью!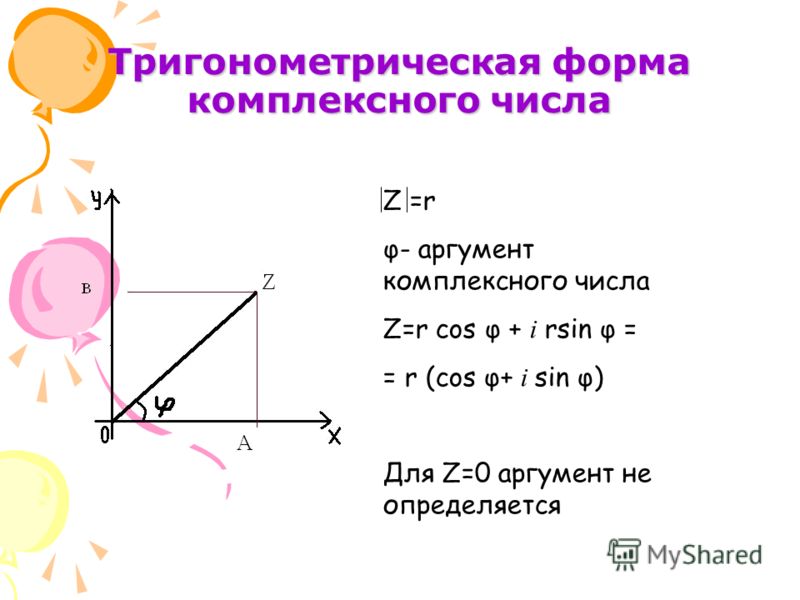
 : Подставив в уравнение на шаге 2, мы получим
: Подставив в уравнение на шаге 2, мы получим
 Это означает, что мы можем прибавить или вычесть кратные 360 градусов к 45 и получить то же самое комплексное число!
Это означает, что мы можем прибавить или вычесть кратные 360 градусов к 45 и получить то же самое комплексное число!






 2}\\ &=\sqrt{16}\\ &=4 \end{align } 92}\\ &=\sqrt{4+25}\\ &=\sqrt{29} \end{align}
2}\\ &=\sqrt{16}\\ &=4 \end{align } 92}\\ &=\sqrt{4+25}\\ &=\sqrt{29} \end{align} п.) 92}\\ &=\sqrt{1+16}\\ &=\sqrt{17} \end{align}
п.) 92}\\ &=\sqrt{1+16}\\ &=\sqrt{17} \end{align}