4.1. Экстремум функции двух переменных. Необходимые и достаточные условия существования экстремума
Пусть функция двух переменных задана в некоторой области .
Точка называется Точкой максимума функции , если существует такая окрестность этой точки, что для всех точек этой окрестности, отличных от , выполняется неравенство (рис. 7).
Точка называется Точкой минимума функции , если существует такая окрестность этой точки, что для всех точек этой окрестности, отличных от , выполняется неравенство (рис. 8).
Как и в случае функции одной переменной, точка максимума (или минимума) не следует смешивать с точкой, в которой функция принимает наибольшее (или наименьшее) значение в области .
Значение функции в точке максимума (точке минимума) называют Максимумом (Минимумом) функции или экстремумом.
Теорема (необходимый признак существования экстремума). Если есть точка экстремума функции , то
,
В предположении, что указанные частные производные существуют в точке .
Таким образом, Обращение в нуль в точке Частных производных первого порядка функции (если они существуют) является Необходимым условием существования в точке экстремума этой функции.
Функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует. Например, функция , очевидно, имеет минимум в точке , но в этой точке частные производные и не существуют.
Точки, в которых частные производные первого порядка , обращаются в ноль или не существуют, называются Критическими точками этой функции.
Из изложенного выше следует, что точка экстремума функции следует искать среди ее критических точек. Однако не всякая критическая точка будет точкой экстремума функции.
Теорема (достаточный признак существования экстремума). Пусть — критическая точка функции .
Обозначим , , и составим .
Тогда, если , то — точка экстремума, причем
— точка максимума в случае ,
— точка минимума в случае ,
Если , то в точке — экстремума нет,
Если , то требуется дополнительные исследования (сомнительный случай).
Пример 19. Найти экстремумы функции .
Решение. Найдем частные производные первого порядка:
, .
Приравнивая эти производные к нулю, после элементарных преобразований получим систему уравнений:
Складывая и вычитая почленно уравнения системы, получим:
или или
Решая эту систему уравнений (равносильную данной), находим четыре критические точки: , , , .
Теперь найдем частные производные второго порядка:
, , ,
Составим выражение .
Так как
1. — точка минимума;
2. В точке Экстремума нет;
3. В точке Экстремума нет;
4. — точка максимума.
Итак, данная функция имеет два экстремума:
В точке — минимум ,
В точке — максимум .
| < Предыдущая | Следующая > |
|---|
Экстремумы функций двух переменных
По аналогии с
понятием экстремума для функций одного
переменного введем следующее определение.
Пусть точка
входит в область определения функции
с некоторой ее окрестностью (т.е. со
всеми точками некоторого круга с центром
в этой точке). Точка
называется
точкой максимума (минимума)
функции
,
если значение функции в этой точке
больше или равно (меньше или равно)
значений функции во всех ближайших к
точках, т.е. (
)
для всех точек
из какой-либо окрестности точки
.
Точки максимума и минимума функции
называются точками экстремума этой функции. В практических задачах
принятие оптимального решения сводится
обычно к поиску экстремумов некоторой
функции. Как же ищутся точки экстремуму
для функции двух переменных? Если
вспомнить, то точки экстремума функции
одного переменного находились среди
ее критических точек (т.е. точек, в которых
производная не существовала или
обращалась в 0). По аналогии, назовем
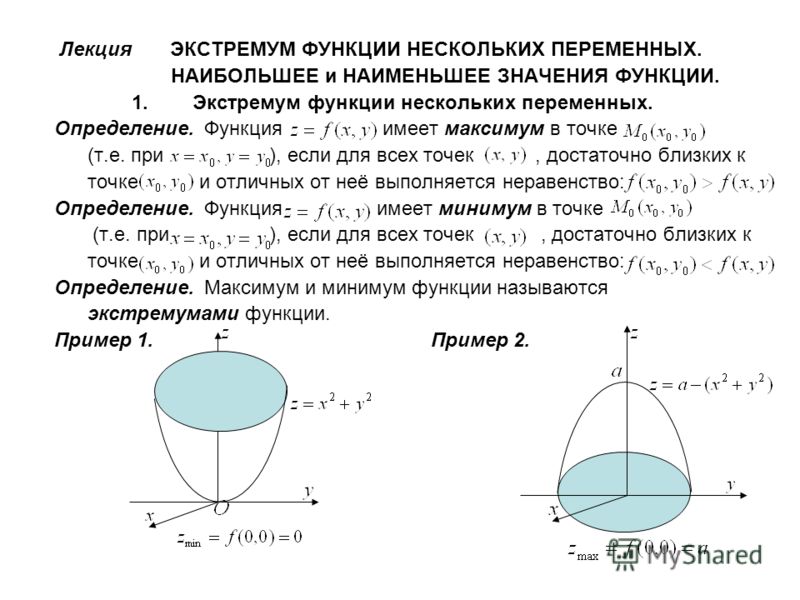Точки,
в которых обе частные производные
существуют и одновременно обращаются
в 0, называются стационарными
точками функции. Таким образом, критические
точки функции состоят из ее стационарных
точек и точек, в которых не существует
хотя бы одна из ее частных производных.
Важную роль таких точек обеспечиваетТеорема 1(необходимое условие экстремума). Пусть в точке функция имеет экстремум и в ней существуют обе частные производные. Тогда они необходимо обращаются в 0: , .
Эта теорема
позволяет сделать тот же вывод, что был
сделан для функции одного переменного: все экстремумы функции находятся
только среди ее критических точек.
Однако точно так же, как и в случае
функции одного переменного, не всякая
критическая точка функции
двух переменных обязательно
является точкой ее экстремума. Например,
для функции начало координат
является критической точкой, так как в
ней обращаются в 0 обе частные производные: , .
Однако эта точка не является ни точкой
максимума, ни точкой минимума, поскольку
значение функции в начале координат,
очевидно, равно 0, а в любой сколь угодно
малой окрестности начала координат
(т.е. в любом круге с центром в начале
координат) есть точки, в которых функция
принимает как отрицательные (в точках
II
и IV
четверти), так и положительные (I
и III
четверть) значения (т.е. как меньшие
значения, чем в точке
,
так и большие ).
Поэтому снова (как и в случае функций одного переменного) необходим алгоритм, позволяющий определить, является ли данная критическая точка точкой экстремума или нет. А если является, то максимумом или минимумом? Такой алгоритм дает
Теорема 2 (достаточное условие экстремума). Пусть – стационарная точка функции , в некоторой окрестности которой существуют и непрерывны все частные производные второго порядка. Пусть , , , а .
Тогда
а) Если ,
то в точке
экстремум есть
( при минимум, при максимум).
б) Если , то в точке экстремума нет.
Приведенные выше рассуждения позволяют предложить следующую схему нахождения экстремумов функции двух переменных
Находим выражения для частных производных и .
Находим критические точки функции; это либо стационарные точки, в которых обе частные производные обращаются в 0 (координаты таких точек есть решения системы ), либо точки, в которых не существует хотя бы одна из найденных частных производных (в этих точках не определено хотя бы одно из выражений для найденных частных производных и ).
Находим выражения для вторых производных , и .
Дальнейшие пункты схемы делаются отдельно для каждой из найденных стационарных точек, входящих в состав найденных критических точек. Пусть исследуется стационарная точка .
Подставляя координаты и исследуемой точки в выражения для вторых производных, находим числа
, , .
Находим значение .
Делаем вывод о характере исследуемой точки в соответствии с заключением приведенной теоремы: если , то в точке экстремум есть ( при минимум, при максимум), а если , то в точке экстремума нет.
Если оказалась точкой экстремума, то находим соответствующее экстремальное значение функции , подставляя в выражение для функции координаты и этой точки.
Большим недостатком теоремы является то, что она не отвечает на вопрос о характере стационарной точки в случае, когда . В этом случае характер этой точки выявляется дополнительным исследованием. Такое исследование требуется и в том случае, когда исследуется критическая точка, не являющаяся стационарной (т.е. к ней не применима теорема 2). Приведем иллюстрирующий эту ситуацию
Пример 1 . Найти точки экстремума функции .
Решение. В соответствии с приведенной схемой находим выражения для частных производных: , аналогично . Оба получившихся выражения для производных и можно, очевидно, вычислить при любых значениях и , а потому частные производные существуют для всех точек координатной плоскости . Тогда критическими могут быть только стационарные точки, т.е. точки, в которых обе производные обращаются в 0. Для нахождения координат таких точек решаем систему , т.е. . Решением такой системы является, очевидно, единственная пара чисел: , . Поэтому единственной критической точкой является начало координат . В соответствии с дальнейшими пунктами схемы находим вторые производные: , и . Подставляя координаты и критической точки в выражения для вторых производных, получим: , . Отметим, что выражение для (а мы получили, что ) не содержит и , а просто равно числу 0. Это говорит о том, что эта производная является постоянной, т.е. принимает одно и то же значение (равное 0)
в любой точке.
Поэтому такое же значения она принимает
и в критической точке
,
а потому .
Тогда число .
Таким образом, в данном примере как раз
возник тот случай, в котором приведенная
схема не отвечает на вопрос о наличии
или отсутствии экстремума в критической
точке
,
а потому для ответа на этот вопрос
требуются (как сказано выше) дополнительные
исследования. Проведем их. Значение
исследуемой функции
в точке
равно .
С другой стороны, значение этой функции
в любой другой точке строго больше 0: ,
если хотя бы одно из чисел
или
отлично от 0 (это следует из того, что
четвертая степень любого отличного от
0 числа строго положительна). Таким
образом, значение функции в точке
меньше значения функции в любой другой
точке. Тогда по определению точка
является точкой Следующий пример
также демонстрирует бессилие приведенной
схемы в случае, если ,
однако, дополнительные исследования
приводят уже к другому выводу.
Пример 2. Найти точки экстремума функции .
Решение. Функция
очень похожа на функцию в предыдущем
примере, поэтому все выкладки можно
делать короче. Имеем , .
Для нахождения координат критических
точек решаем систему
,
т.е. . Решением такой системы снова является
единственная пара чисел:
,
.
Поэтому опять единственной критической
точкой является начало координат
.
Далее, , , .
Тогда , ,
,
а потому опять
.
Снова возник тот случай, в котором
приведенная схема не отвечает на вопрос
о наличии или отсутствии экстремума в
критической точке
,
а потому для ответа на этот вопрос опять
требуются дополнительные исследования.
Проведем их. Значение исследуемой
функции
в точке
равно .
С другой стороны, какую бы маленькую
окрестность точки
(т.е. кружок с центром в начале координат)
мы ни взяли, в ней всегда найдутся точки
из I
и III
четверти. Но в точках первой четверти
(обе координаты таких точек положительны)
значение исследуемой функции
строго больше 0 (сумма кубов двух
положительных чисел положительна), а в
точках третей четверти (обе координаты
таких точек отрицательны) значение этой
функции
строго меньше 0 (сумма кубов двух
отрицательных чисел отрицательна).
Таким образом, в любой окрестности точки
всегда есть точки, значения в которых
как больше значения функции в этой
точке, так и меньше. Поэтому по определению
точка
не может быть точкой экстремума. А так
как на подозрении в наличии экстремума
у нас была только эта точка (напомним –
все экстремумы только среди критических
точек!), то можно сделать вывод, что у
данной функции вообще экстремумов нет.
Далее рассмотрим примеры, где указанная схема работает до конца.
Пример 3 . Найти точки экстремума функции .
Решение. В
соответствии с приведенной схемой
находим выражения для частных производных: ,
аналогично .
Оба получившихся выражения для производных
определены при любых значениях
и
,
а потому частные производные существуют
для всех точек координатной плоскости
.
Поэтому критическими могут быть только
стационарные точки, т.е. точки, в которых
обе производные обращаются в 0. Для
нахождения координат таких точек решаем
систему
,
т.
е. . Выражаем из первого уравнения и подставляем во второе: ,
откуда получаем .
Поэтому .
Итак, единственным решением системы
является пара чисел:
, ,
а потому единственной критической
точкой является точка .
В соответствии с дальнейшими пунктами
схемы, находим вторые производные: , .
Выражения для вторых производных не
содержат
и
,
а просто равны некоторым числам. Поэтому
каждая вторая производная является
постоянной, т.е. принимает одно и то же
значение в
любой точке.
Поэтому такие же значения они принимают
и в исследуемой критической точке
: , .
Тогда число .
Поскольку число ,
то (в соответствии с описанной схемой)
исследуемая критическая точка
действительно является точкой экстремума.
Поскольку выше получилось ,
то это точка минимума. Минимальное
значение функции – ее значение в этой
точке, поэтому .
Итак, функция
имеет одну точку минимума
,
причем .
Пример 4 . Найти точки экстремума функции .
Решение.
Находим
частные производные: , .
Обе производные определены при любых
значениях
и
,
а потому критическими могут быть только
стационарные точки. Для нахождения
координат таких точек решаем систему
,
т.е. . Получившаяся система решается очень
просто (в отличии от системы в предыдущем
примере, которая решалась просто
«просто»), поскольку в первом уравнении
есть только иксы, а во втором только
игреки, а потому из каждого уравнения
можно сразу найти соответствующее
неизвестное: , .
Итак, единственной критической точкой
является точка .
В соответствии с дальнейшими пунктами
схемы, далее находим вторые производные: , ,
а потому , .
Тогда число ,
поэтому критическая точка
является точкой экстремума. Поскольку
выше получилось ,
то это точка максимума. Максимальное
значение функции – ее значение в этой
точке, поэтому .
Итак, исследуемая функция
имеет одну точку максимума
,
причем .
Пример 5 . Найти точки экстремума функции .
Решение. Частные
производные первого порядка: ,
аналогично .
Критическими снова могут быть только
стационарные точки. Для нахождения
координат таких точек решаем систему
,
т.е. . Деля обе части первого уравнения на
2, второго – на 4 и перенося числа в правую
часть, получим следующую систему для
определения координат стационарных
точек: . Оказывается, что эта система несовместна,
т.е. не имеет ни одного решения. Это
можно доказать с помощью теоремы
Кронекера- Капели (эта теорема была в
разделе «Основы линейной алгебры»),
убедившись, что ранги основной и
расширенной матриц системы не совпадают.
Если эти методы уже забылись, то можно
действовать и «школьными» приемами.
Для этого выразим из первого уравнения и подставим во второе: , , .
Последнее уравнение, очевидно, решений
не имеет, так как не существует такого
числа, которое, будучи умноженным на 0,
даст .
Поэтому и вся система решений не имеет.
Что же это означает? Решения этой системы
давали нам координаты критических
точек.
Отсутствие решений системы
говорит об отсутствии критических точек
у исследуемой функции. Но поскольку
все экстремумы функции находятся только
среди ее критических точек, то у данной
функции экстремумов нет.
Пример 6 . Найти точки экстремума функции .
Решение. Находим частные производные: , . Ищем координаты критических точек: , т.е. . Ясно, что система имеет единственное решение , . Поэтому единственной критической точкой является начало координат . Далее, , , . Тогда , , , а потому . Итак, , потому по приведенной выше теореме экстремумов в точке нет. Но эта точка была единственной точкой, в которой мог быть экстремум (все экстремумы – только среди критических точек функции!) . Поэтому у данной функции экстремумов нет.
Пример 7 . Найти точки экстремума функции .
Решение. Выражения
для частных производных: , .
Оба получившихся выражения для производных
определены при любых значениях
и
,
а потому частные производные существуют
для всех точек координатной плоскости
.
Поэтому критическими могут быть только
стационарные точки, для нахождения
координат которых решаем систему
,
т.е. . Сокращая уравнения на 3, получим .
Выражаем из первого уравнения и подставляем во второе: , , .
Произведение может обратиться в 0 только
при тех значениях
,
которые обращают в 0 хотя бы один из
сомножителей. Поэтому либо
,
либо ,
т.е. .
Таким образом, уравнение имеет два
корня: и .
Учитывая полученную ранее связь
,
получим соответствующие значения
: , .
Потому система имеет 2 решения: ,
и
,
,
а исследуемая функция имеет, соответственно,
две критические точки: и .
В соответствии с дальнейшими пунктами
схемы, находим выражения для вторых
производных: , .
Далее, в соответствии с приведенной схемой исследуем обе критические точки и по отдельности.
1. Исследуем
критическую точку
. Вычисляем в этой точке значения вторых
производных: , .
Тогда число .
Поскольку число ,
то (в соответствии с описанной схемой)
исследуемая критическая точка не является
точкой экстремума.
2. Исследуем критическую точку . Вычисляем в этой точке значения вторых производных: , . Тогда число . Поскольку число , то (в соответствии с описанной схемой) исследуемая критическая точка является точкой экстремума. Поскольку , то − точка минимума. Значение функции в точке минимума: .
Итак, функция имеет единственную точку минимума , причем .
Пример 8 . Найти точки экстремума функции .
Решение. Выражения
для частных производных: ={производная произведения: }=
,
аналогично {первый
множитель не содержит
, а потому при вычислении производной
по этой переменной считается постоянным
множителем и выносится за знак
производной}= .
Оба получившихся выражения для производных
определены при любых значениях
и
,
а потому частные производные существуют
для всех точек координатной плоскости
.
Поэтому критическими могут быть только
стационарные точки, для нахождения
координат которых решаем систему
,
т.
е. . Поскольку не обращается в 0 ни при каких значениях
показателя степени
,
то, разделив обе части первого уравнения
на
,
а второго на ,
получим систему, равносильную исходной: .
Подставляя
в первое уравнение, получим .
Итак, единственным решением системы
является пара чисел:
,
,
а потому единственной критической
точкой является точка .
Далее, находим вторые производные: , , .
Вычисляем значения вторых производных
в исследуемой критической точке
: , .
Тогда число .
Поэтому исследуемая критическая точка действительно является точкой экстремума.
Поскольку ,
то это точка минимума. Минимальное
значение функции .
Итак, функция
имеет одну точку минимума
,
причем .
П ример 9. Необходимо построить открытый бассейн в форме прямого параллелепипеда объемом , на облицовку дна и стен которого пойдет наименьшее количество материала.
Решение. Обозначим
размеры бассейна (длину, ширину и глубину
в метрах) через
,
и
(см.
рисунок). Понятно, что чем меньше
необходимая площадь облицовки, тем меньше будет использовано
облицовочного материала. Таким образом,
встает следующая задача. Подобрать
такие числа
,
и
− размеры параллелепипеда (бассейна),
чтобы его объем
был равен ,
а суммарная площадь основания и боковой
поверхности (это как раз дно и стены
бассейна) была бы наименьшей. Выразим
эту площадь через размеры параллелепипеда.
Указанная площадь (обозначим ее )
складывается из площади прямоугольника-основания
(равной ),
площадей передней и задней стенок
(равных каждая) и площадей левой и правой стенок
(по каждая). Таким образом, площадь облицовки
следующим образом зависит трех переменных
– размеров бассейна
,
и
: или .
Требуется найти точку минимума этой
функции. Поскольку мы изучили методы
отыскания экстремумов функции двух (а не трех) переменных, то от одной
переменной надо избавиться. Это можно
сделать, если понять, что размеры бассейна
,
и
не могут быть выбраны независимо друг
от друга.
Если выбраны его длина
и ширина
,
то глубина
не может быть выбрана произвольно, так
как выбираемая при этом глубина должна
быть такой, чтобы обеспечить требование
о необходимом объеме получающегося
бассейна:
.
Поскольку объем параллелепипеда равен
произведению всех его измерений, то
должно выполняться требование: ,
откуда .
Поэтому если выбраны длина
и ширина
бассейна, то глубина
однозначно определена: .
Подставляя это выражение в полученную
выше формулу
для площади, получаем площадь как
функцию двух переменных
и
: .
Раскрывая скобки, получим более удобное
для исследования выражение: или .
По смыслу задачи (
и
− размеры бассейна) эту функцию мы
рассматриваем только при положительных
значениях переменных
и
: , .
Поэтому областью определения этой
функции является I
четверть без точек, лежащих на осях
координат. Найдем экстремумы этой
функции двух переменных по привычной схеме. Находим
первые производные: .
Таким образом, или . Аналогично можно получить выражение
для другой частной производной: или .
Находим критические точки. Производная
не существует для всех точек, у которых
первая координата
,
т.е. для всех точек, лежащих на оси .
Аналогично, производная
не существует для всех точек, у которых
вторая координата
,
т.е. для всех точек, лежащих на оси .
Однако все эти точки не входят в область
определения исследуемой функции, а
потому не являются критическими точками
функции и не интересуют нас как
потенциальные точки экстремума. Найдем
теперь те критические точки функции,
которые являются ее стационарными
точками. Для нахождения координат этих
точек решаем систему ,
т.е. . Из первого уравнения выразим и подставим во второе уравнение: , , , или .
Откуда получаем либо
,
либо ,
т.е и .
Первое решение
нас опять не интересует по причине его
несоответствия области определения
функции. Подставляя
в полученную выше связь
,
получим .
Таким образом, у функции имеется
единственная критическая точка .
Далее (в соответствии со схемой поиска
экстремумов функции) находим выражения
для вторых производных: или .
Аналогично, , .
Исследуем критическую точку
на экстремум. Находим значения вторых
производных в этой точке: , , .
Тогда число ,
поэтому в точке
имеется экстремум, а так как , то это действительно точка минимума
(то, чего нам бы и хотелось!). Минимальное
значение функции площади
есть ее значение в точке минимума
: .
Таким образом, оптимальная длина и
ширина бассейна , .
Оптимальная глубина бассейна
находим из связи этого размера с длиной
и шириной
.
Поэтому .
Итак, оптимальные размеры бассейна .
При этом площадь облицовки минимальна
и составляет .
Экстремумы функций двух переменных
Экстремумы функций двух переменныхТест второй производной
Ясно, что f ( x , y ) имеет локальный максимум при критической точка ( p , q ), только если каждый вертикальный срез z = f ( x , y ) имеет максимум в ( p ,
7 q .
Точно так же f ( x , y ) имеет локальный минимум в критической точке ( p , q ) только в том случае, если каждый вертикальный срез z = f 90,7 x
08 (
08 г )
имеет минимум при ( p , q ).
Однако для f ( x , y ) возможно иметь минимум в одном срез и максимум в другом срезе.
Если это так, то мы говорим, что f ( x , y ) имеет седло at ( p , q ), потому что результирующая поверхность напоминает седло для лошади.
Чтобы определить, получаем ли мы максимум, минимум или седловую точку в критической точки ( p , q ), рассмотрим вертикальный срез z ( t ) = f ( р + мт , q + нт ). Поскольку x = p + mt и y = q + nt подразумевает, что x ‘ ( t ) = м и y ‘ ( t ) = n , первая производная от z ( t ) равна
|
| ||||||||||||||||||||||||||||||||||||||
| (2) |
Если f xx ( p,q ) = 0, то мы можем выбрать значения m и n такой
что z » отрицательно в некоторых срезах и положительно в
другие, таким образом, подразумевая, что z=f ( x,y ) имеет седло в точке ( p,q ).
Если f xx ( p,q ) ¹ 0, то завершение квадрата в м дает
| (3) |
ИЗ . (т. е. расширение (3) приведет к (2) ).Если D ( p,q ) > 0, то z » (0) имеет то же самое знак как f xx ( p,q ) во всех направлениях u = < m,n > , таким образом, подразумевается максимум, если < 0 и минимум, если f xx ( p,q ) > 0. Однако если Д ( р, к ) < 0, тогда выбор m= 1, n =0 дает z » (0) > 0, тогда как выбор m = f xx ( p,q ) / f xx ( p,q 9 3) n дает z » (0) < 0, что подразумевает седло. Эти наблюдения приводят к следующей теореме:
Тест второй производной: Если ( p , q ) является критической точкой функции f ( x , y ), вторые производные которой существуют при ( p , q ), тогдаОднако, если D ( p , q ) = 0, то нет информации о f ( x , y ) получается.
Дискриминант
2 nd der
Результат
D ( p , q ) > 0,
f xx ( p , q ) > 0
ф ( х , y ) has a local minimum at ( p , q )
D ( p , q ) > 0,
f xx ( p , q ) < 0
f ( x , y ) has a local maximum at ( p , q )
D ( p , q ) < 0,
f ( x , y ) имеет седло на ( p , q )
ПРИМЕР 2 Найдите экстремумы и седловые точки f ( x , y ) = x 2 — y6 2 98 20457 .Решение: Поскольку f x = 2 x и f y = -2 y , единственная критическая точка равно (0,0) . Однако f xx = 2, f yy = -2, и f xy = 901, так что дискриминант f равен
Таким образом, f ( x , y ) = x 2 — y 2 имеет седло в (0,0) .
D = F XX F YY -( F XY ) 2 = (2) -2) -0 9045) 2 = (2) -0 9048) 2 = (2) -0 9048). < 0
Пример 3 Найдите точки экстремы и седла F ( x , Y ) = x 3 -3 XY + Y 3 .Решение: В примере 1 мы показали, что критические точки f ( 0,0) и ( 1,1) . Поскольку f x ( x , y ) = 3 x 2 -3 y и f y ( x , y ) = -3 x +3 y 2 , второй производные от f ( x , y ) равны
77 70196 При (0,0) имеем D ( 0,0) = 0 — 9 = -9 < 0. Таким образом, f имеет седло в (0,0) . В (1,1) мы есть
888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888989н. Таким образом, дискриминант равен
F XX = 6 x , F XY = -3, F YY = 6 Y
.
D ( x , y ) = (6 x ) (6 Y ) -(-3) 2 = 36 XY -9 Однако f xx ( 1,1) = 6 > 0, поэтому f имеет локального минимума в (1,1) .
D ( 1,1) = 36·1·1 — 9 = 27 > 0
7ПРИМЕР 4 Найдите локальные экстремумы и седловые точкиПервые производные равны
f ( x , y ) = x sin( xy )
Настройка f y = 0 дает либо x = 0, либо cos( xy ) = 0, последний из которых подразумевает, что
F x = SIN ( XY ) + XY COS ( XY ), F Y = x 2 COS (. для любого целого числа n . В таких точках у нас было бы f x ( x , y ) либо как 1, либо -1 (но не 0). Однако если y = 0, то
ху = п 2
+ п р откуда следует, что как f x = 0, так и f y = 0 в точке (0, 0) (и нигде более).
f x ( x ,0) = 0 + y и F XX (0,0) = F XY (0,0) = F YY (0,0) = 0.
2 y cos( xy ) — xy 2 sin( xy )
f yx = 2 x cos( xy ) — x 2 y 909 18 xy6
— x 3 sin( xy ) Экспорт кленовой графики
Хотя в примере 4 кажется, что в точке (0,0) есть седло, нет способ определения этого с помощью теста второй производной. Действительно, г ( x,y ) = x 4 + y 4 положительно везде, кроме г (0,0) = 0, поэтому очевидно, что g ( x,y ) имеет минимум в точке (0,0). Но г хх ( 0,0) = г ху ( 0,0) = г 8 уу
) = 0 означает, что D (0,0) = 0, поэтому этот минимум нельзя определить с помощью тест второй производной.
Проверьте свое чтение: Соответствует ли p ( x , y ) = — х 4 — у 4 есть ли какие-либо локальные экстремумы, которые можно определить с помощью теста второй производной?Деловой расчет
Частные производные говорят нам кое-что о том, где поверхность имеет локальные максимумы и минимумы.
Вторые производные
Когда вы находите частную производную функции двух переменных, вы получаете другую функцию двух переменных — вы можете взять и ее частные производные. Мы делали это раньше, в настройке с одной переменной. В случае с одной переменной вторая производная давала информацию о том, как изогнут график. В случае с двумя переменными вторые частные производные дают некоторую информацию о том, как искривляется поверхность, когда вы путешествуете по поперечным сечениям, но это не очень полная информация обо всей поверхности.
Представьте, что у вас есть поверхность, взъерошенная вокруг точки, как это происходит рядом с пуговицей на мягком диване, или защемленным куском ткани, или морщинистой кожей возле большого пальца, когда вы сжимаете кулак.
вогнутая вверхиливогнутая внизне может описать все, что может произойти. на поверхности.Удивительно, однако, все еще существует второй тест производной, который может помочь вам решить, является ли точка локальным максимумом или минимумом или ни тем, ни другим, поэтому мы все еще хотим найти вторые производные.
Вторые частные производные
Предположим, что \( f(x,y) \) является функцией двух переменных. Тогда у него есть четыре вторых частных производных : \[ \begin{выравнивание*} f_{xx}=&\frac{\partial}{\partial x}\left(f_x\right)=\left(f_x\right)_x & f_{xy}=&\frac{\partial}{\partial y }\влево(f_x\вправо)=\влево(f_x\вправо)_y\\ f_{yx}=&\frac{\partial}{\partial x}\left(f_y\right)=\left(f_y\right)_x & f_{yy}=&\frac{\partial}{\partial y }\влево(f_y\вправо)=\влево(f_y\вправо)_y \end{выравнивание*} \] \( f_{xy} \) и \( f_{yx} \) называются 92\).
Мы должны начать с нахождения (первых) частных производных: \[ \begin{выравнивание*} f_x(x,y)=& 2x-4y \\ f_y(x,y)=& -4x+8y \end{выравнивание*} \]
Теперь мы готовы взять вторые частные производные: \[ \begin{выравнивание*} f_{xx}(x,y)=& \frac{\partial}{\partial x}(2x-4y)=2 \\ f_{xy}(x,y)=& \frac{\partial}{\partial y}(2x-4y)=-4 \\ f_{yx}(x,y)=& \frac{\partial}{\partial x}(-4x+8y)=-4 \\ f_{yy}(x,y)=& \frac{\partial}{\partial y}(-4x+8y)=8 \end{выравнивание*} \]
Вы могли заметить, что в последнем примере две смешанные частные производные равны. Оказывается, это не совпадение — это теорема!
Теорема о смешанных частных производных
Если \( f \), \( f_x \), \( f_y \), \( f_{xy} \) и \( f_{yx} \) непрерывны (без разрывов в своих графиках), то \[ f_{xy}=f_{yx}. \]
На самом деле, пока \(f\) и все ее подходящие частные производные непрерывны, смешанные частные производные равны, даже если они имеют более высокий порядок, и даже если функция имеет более двух переменных.
Если бы мы решили поступить иначе, то оказались бы в том же месте. В конце концов…
Локальные максимумы, локальные минимумы и седловые точки
Кратко рассмотрим задачи макс-мин с одной переменной.
Локальный максимум — это точка на кривой, которая выше всех соседних точек. Локальный минимум ниже, чем все близлежащие точки. Мы знаем, что локальный максимум или минимум могут возникать только в критических точках, где производная равна нулю или не определена. Но мы также знаем, что не все критические точки являются максимальными или минимальными, поэтому нам также необходимо проверить их с помощью теста первой производной или второй производной.
Ситуация с функцией двух переменных почти такая же. Как и в случае с одной переменной, первым шагом является поиск критических точек, мест, где обе частные производные либо равны нулю, либо не определены
.Определение (локальный максимум и минимум)
- \(f\) имеет локальный максимум в точке \((a, b)\), если \(f(a, b) \geq f(x, y)\ ) для всех точек \((x, y)\) вблизи \((a, b)\).
- \(f\) имеет локальных минимумов в точках \((a, b)\), если \(f(a, b) \leq f(x, y)\) для всех точек \((x, y )\) вблизи \((a, b)\).
Критическая точка для функции \(f(x, y)\) — это точка \((x, y)\) (или \((x, y, f(x, y))\) ), где верны оба следующих утверждения:
- \( f_x=0 \) или не определено, и
- \( f_y=0 \) или не определено.
Как и в случае с одной переменной, локальный максимум или минимум \(f\) может иметь место только в критической точке.
Как и в случае с одной переменной, не все критические точки являются локальными максимумами или минимумами. Для функции двух переменных критическая точка может быть локальным максимумом, локальным минимумом или седловой точкой.
Точка на поверхности является локальным максимумом, если она выше всех соседних точек; точка является локальным минимумом, если она ниже всех ближайших точек.
Седловая точка — это точка на поверхности, которая является минимумом на одних путях и максимумом на некоторых других.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Тест второй производной
Как и в случае с одной переменной, нам понадобится способ проверки критических точек, чтобы увидеть, являются ли они локальными максимумами или минимумами. Существует второй тест производной для функций двух переменных, который может помочь, но, как и в случае с одной переменной, не всегда дает ответ.
Признак второй производной для функций двух переменных
- Найдите все критические точки \(f(x,y)\).
Вычислить \[ D(x,y)=\left(f_{xx}\right)\left(f_{yy}\right)-\left(f_{xy}\right)\left(f_{yx}\ справа),\] и оцениваем его в каждой критической точке.
Если \(D \gt 0\), то \(f\) имеет локальный максимум или минимум в критической точке. Чтобы узнать какой, посмотрите на знак \( f_{xx} \):
- Если \( f_{xx}\gt 0 \), то \(f\) имеет локальный минимум в критической точке.
- Если \( f_{xx}\lt 0 \), то \(f\) имеет локальный максимум в критической точке.
- Если \(D \lt 0\), то \(f\) имеет седловую точку в критической точке.
- Если \(D = 0\), может быть локальный максимум, локальный минимум или ни то, ни другое (т. е. тест не дает результатов).
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5 92-6y=3y(y-2)=0 \), когда \(y = 0\) или когда \(y = 2\).
Сложив их вместе, мы получим четыре критические точки: (0, 0), (-2, 0), (0, 2) и (-2, 2).
Теперь, чтобы классифицировать их, мы будем использовать тест второй производной. Нам понадобятся все вторые частные производные: \[f_{xx}=6x+6,\ f+{yy}=6y-6,\ f_{xy}=f_{yx}=0.\]
Тогда \ [ D(x,y)=(6x+6)(6y-6)-(0)(0)=(6x+6)(6y-6). \]
Теперь рассмотрим каждую критическую точку по очереди:
- В точке (0, 0): \( D(0,0)=(6(0)+6)(6(0)-6)=( 6)(-6)=-36 \lt 0 \), поэтому в точке (0, 0) есть седловая точка.
- При (-2, 0): \( D(-2,0)=(6(-2)+6)(6(0)-6)=(-6)(-6)=36 \gt 0 \) и \( f_{xx}(-2,0)=6(-2)+6=-6 \lt 0 \), поэтому в точке (-2, 0) имеется локальный максимум.
- В точке (0, 2): \( D(0,2)=(6(0)+6)(6(2)-6)=(6)(6)=36 \gt 0 \) и \( f_{xx}(0,2)=6(0)+6=6 \gt 0 \), поэтому в точке (0, 2) есть локальный минимум.
- При (-2, 2): \( D(-2,2)=(6(-2)+6)(6(2)-6)=(-6)(6)=-36 \lt 0 \), так что есть еще одна седловая точка в (-2, 2).
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5 92}{4} \) для нахождения \(x\) дает нам две критические точки: (0,0) и \( \left(\frac{4}{9},\frac{4}{3}\ верно) \).
Теперь их протестировать. Первое вычисление \[ \begin{выравнивание*} D(x,y)=& (f_{xx})(f_{yy})-(f_{xy})(f_{yx}) \\ =& (54x)(2y)-(-4)(-4) \\ =& 108xy-16 \end{align*} \] Затем оцените \( D \) в двух критических точках:
- В (0,0): \(D(0,0) = -16 \lt 0\), поэтому в (0, 0) есть седловая точка.
- В \( \left(\frac{4}{9}, \ frac {\ sqrt [3] {4}} {3} \ right) \): \ (D \ left (\ frac {4} {9}, \ frac {\ sqrt [3] {4}} {3}\right) =16(\sqrt[3]{4}-1)\gt 0\) и \(f_{xx}\left(\frac{4}{9},\frac{\sqrt [3]{4}}{3}\right) \gt 0 \), поэтому существует локальный минимум в точке \( \left(\frac{4}{9},\frac{\sqrt[3]{4 }}{3}\справа) \).
Прикладная оптимизация
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Пример 5
Компания производит два продукта. Уравнения спроса на эти два продукта приведены ниже. \(p_1\), \(p_2\), \(q_1\) и \(q_2\) – это цены и количество товаров 1 и 2.
888) 8888) 8888).
Вторые производные
Таким D ( 0,0) = 0, поэтому
тест второй производной не дает информации об экстремумах или седлах
из f ( x , y ) = x sin( xy ) at (0,0) .
Помните, что даже в случаях с одной переменной были критические точки, которые не были ни максимумами, ни минимумами — это также верно для функций многих переменных. На самом деле, как и следовало ожидать, ситуация еще сложнее.
Прямо в этот момент, в каждом направлении, в котором вы двигаетесь, будет происходить что-то другое — оно может увеличиваться, уменьшаться, изгибаться вверх, изгибаться вниз… Простая фраза вроде 
92} \]
Он так называется, потому что по форме немного напоминает седло, на котором можно ездить верхом. Седловую точку можно увидеть, сжав кулак — между костяшками указательного и среднего пальцев можно увидеть место, минимальное, когда вы идете поперек костяшек, и максимальное, когда вы идете по руке к пальцам. 92+10 \), а над началом координат находится седловая точка. Линии показывают, как выглядит поверхность над осями \(x\)- и \(y\)-. Обратите внимание, что точка над началом координат, где линии пересекаются, является локальным минимумом в одном направлении и локальным максимумом в другом направлении.
