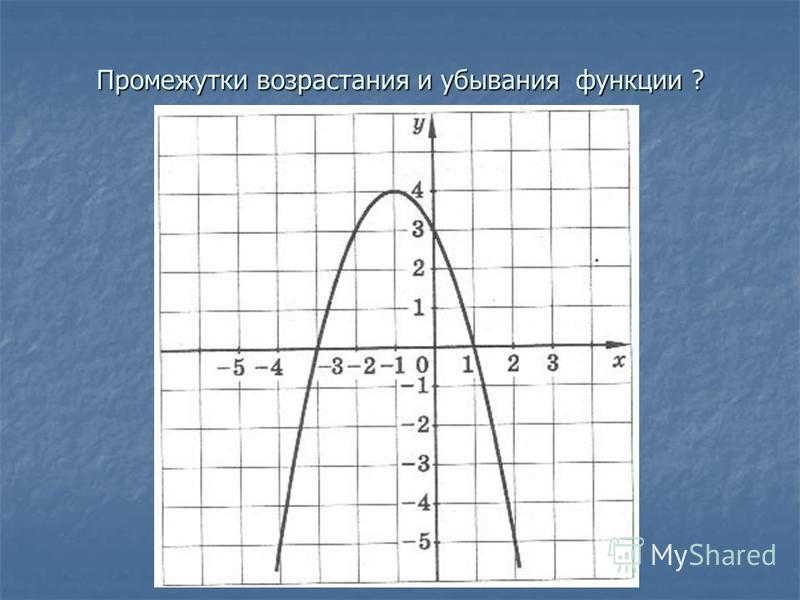
Признаки возрастания и убывания функции. | План-конспект урока по алгебре (10 класс) по теме:
Цели урока:
- ввести признак возрастания, убывания функции и показать его применение при решении заданий;
- развить познавательную активность, интерес к предмету;
- воспитать точность, логичность в мышлении.
Оборудование:
- портреты И. Ньютона, Г. Лейбница;
- карточки с заданиями.
Домашнее задание к уроку: повторить п. 5. Возрастание и убывание функций.
Ход урока
1. Организационный момент.
2. Математическая разминка.
Ученики выполняют задания устно. Ответы проверяются с помощью таблицы «ответ – буква». Записывают только буквы, из которых получаются фамилии ученых.
Задания: найдите y'(x) или y'(x0).
I вариант II вариант
- y = 5x² + 4, x0 = 6 Н 1. y = 0,5x² – 6x + 1/5 Л
- y = 15cosx + 3 Ь 2.
y = 11 + 8sinx Е - y = -0,5x² + 6x + 17 Ю 3. y = 2√x + 4x, x0 = 9 Й
- y = 1/x + 2√x Т 4. y = 4/x – √x Б
- y = 2x + cosx О 5. y = 7,9 + 2x², x0 = 0 Н
- y = 60x + 4,8 Н 6. y = sinx – cosx, x0 = 0 И
- y = 3,5x² – 12, x0 = 1/7 И 7. y = cosx + 2sinx, x0 = 0 Ц
y = 11 + 8sinx ЕОтветы:
Б: -4/х² – 1/(2√х)
Е: 8соsх
И: 1
Й: 4,3
Л: х – 6
Н: 60
О: 2 – sinх
Т: -1/х² + 1/√х
Ц: 2
Ь: -15sinx
Ю: -x + 6
3. Историческая справка.
Весь мир его узнал по изданным трудам,
Был даже край родной с ним вынужден считаться,
Уроки мудрости давал он мудрецам,
Он был мудрее их: умел он сомневаться.
Вольтер «Надпись к портрету Лейбница»
Готфрид Лейбниц Исаак Ньютон
(1646 – 1716) (1643 – 1727)
Краткий рассказ двух учащихся о жизни этих ученых и их вкладе в изучение математического анализа (учащиеся сами находят информацию, работая с дополнительной литературой и другими информационными ресурсами).
Вывод: они одновременно разработали основы математического анализа; если Ньютон исходил из задач механики, то Лейбниц – из геометрических задач.
4. Индивидуальные задания.
Во время математической разминки 2 человека работают с индивидуальными заданиями у доски.
1 задание. Решить неравенство методом интервалов: х4 – 4х2 > 0.
2 задание. Указать промежутки возрастания, убывания функций:
у = 2/х; у = х2 – 4; у = -х2 + 3х +6; у = 0,2х5 – 4/3 х3
Выполнив первые три задания, получаем проблему: как найти промежутки монотонности для четвертой функции?
Итак, сформулируйте тему и цель нашего урока.(Учащиеся сами проговаривают тему и ставят цели).
5. Введение нового материала (в ходе фронтальной беседы с элементами исследования).
? Какая функция называется возрастающей, убывающей?
? Для функций, графики которых изображены на рисунках, укажите промежутки возрастания, убывания (на рисунках графики различных функций).
Разбор второго индивидуального задания.
? Как определить промежутки возрастания, убывания функции у = 0,2х5 – 4/3 х3
Для этого исследуем график некоторой функции (предложен на рисунке).
На каждом из промежутков (-∞;х1), (х1;х2), (х2;х3), (х3;+∞) построим касательные.
Задание. Проанализировать расположение касательных по отношению к оси абсцисс (угол наклона) и определить знаки значений производной.
Учащиеся самостоятельно делают вывод.
Вывод:
- Достаточный признак возрастания функции. Если f ‘(x) > 0 в каждой точке интервала У, то функция f возрастает на У.
- Достаточный признак убывания функции. Если f ‘(x) < 0 в каждой точке интервала У, то функция f убывает на У.
Учащиеся вместе с учителем составляют план исследования функции на возрастание (убывание).
План:
- Найти область определения.
- Найти производную функции.
- Найти точки, в которых производная равна нулю или не существует.
- Определить знаки производной.
- Вывод о «поведении» функции.
Пример.
у = 0,2х5 – 4/3 х3
- определена при любом х
- у ‘ = х4 – 4х2
- у ‘ существует во всех точках.
у ‘ = 0; х4 – 4х2 = 0;
х2(х – 2)(х + 2) = 0
у ‘ + – – + х
у
- Функция возрастает на луче (–∞; –2] и на луче [2; +∞).
Функция убывает на отрезке [–2; +2].
- Практика под руководством учителя.
Учащиеся выполняют задания по порядку (каждый в своем темпе), учитель проверяет, дает рекомендации каждому индивидуально.
На «3» – №280 (б, г)
На «4» + №283 (а, б)
На «5» + исследовать функцию на монотонность
у = 0,25х4 – 2х3 + 5,5х2 – 6х + 2π
7. Итог урока и д/з на выбор : №281(а,б) или № 284 (а,в)
х1
х2
х
у
0
y = f(х)
x3
y = f(х)
х1
х2
х
у
0
x3
β1
β2
α1
α2
10.
Признак возрастания и убывания функции.Одна из основных задач исследования функции – нахождение промежутков ее возрастания и убывания.
Достаточный признак возрастания функции:
Если f/ (x)>0 в точке интервала (а,в), то функция f (x) возрастает на (а,в).
Достаточный признак убывания функции:
Если f/ (x)<0 в точке интервала (а,в), то функция f (x) убывает на (а,в).
Пример: Найти промежутки возрастания и убывания функции:
y= -x2 + 2x – 3
Решение: Область определения функции – все множество действительных чисел ( т.к. нет «подводных камней»)
D (y) = R
Найдем критические точки функции:
y/ = -2x + 2 = 0
x = 1
+ 1 —
Ответ: f (x) возрастает при x ( — ; 1 ],
f
(x)
убывает при x
[1;
+
).
11. Критические точки функции, экстремумы.
Определение: Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками.
Теорема Ферма: ( необходимое условие экстремума )
Если точка является точкой экстремума функции f (x) и в этой точке существует производная, то она равна нулю.
Признак максимума:
Если функция f непрерывна в точке х0, а f/ (x) >0 на интервале
( а; х0), и f/ (x) <0 на интервале (х0, в), то точка х0
является точкой максимума функции f .Признак минимума:
Если функция f непрерывна в точке х0, а f/ (x) <0 на интервале
( а;
х0),
и f/ (x)
>0 на интервале (х0,
в), то точка
х0 является точкой минимума функции f
.
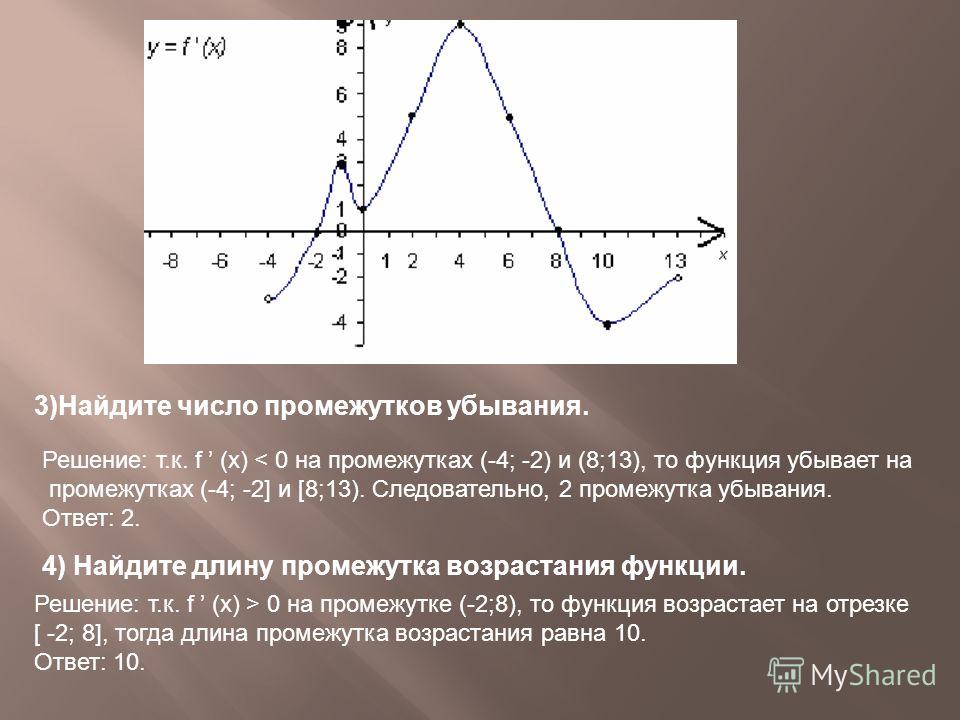
Упрощенно: Если в точке х0 производная меняет знак
с «+» на «-», то х0 – точка максимума
с «-» на «+», то х0 – точка минимума
12. Схема исследования функции.
Область определения функции
Четность-нечетность
( функция называется четной, если выполняется условие
f (-x) = f (x), график симметричен относительно оси ОУ; функция называется нечетной, если выполняется условие
f (-x) = -f (x), график симметричен относительно начала координат)
3. Точки пересечения с осями координат:
с ОХ: у=0, решить уравнение f(х)=0
с ОУ: х=0, у=f (0)
4. Промежутки возрастания, убывания, экстремумы, значение
функции в точках экстремума.
5. Построить график.
Пример: Исследовать функцию и построить график:
у= х2 + х – 2
D (y) = (- ; + )
y (-x) = (-x)2 + (-x) – 2 = x2 – x – 2 – общего вида
с ОХ: у=0 х2 + х – 2 = 0
х1,2= -2; 1
точки пересечения с осью ОХ (-2; 0 ), ( 1; 0)
с ОУ: х=0 у= -2
точка пересечения с ОУ (0; -2)
у/ = 2x + 1 = 0
x = — — — +
y(- ) = — — 2 = -2
Построим график функции:
у
2/x+1 увеличивается или уменьшаетсяПодписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Мэрайя В.
ответил 20.05.22
Репетитор
5 (10)
Учитель математики средней школы с опытом работы от 3 лет
Об этом репетиторе ›
Об этом репетиторе ›
Я хотел записать для вас видео, но оно не работает, поэтому я стараюсь его напечатать.
Чтобы найти интервалы, на которых функция убывает или возрастает, нужно сначала найти критические точки
1) f(x)=x 2 /(x+1)
- критические числа/точка, где наклон касательной (первая производная) либо равен 0, либо не определен (горизонтальный наклон или вертикальная асимптота)
- Используйте правило частных, чтобы найти первую производную
- резюмируется здесь: низкий d (высокий) — высокий d (низкий), по всему низкому квадрату.
- d ƒ(x)/dx=(x 2 +2x)/(x+1) 2 =[x(x+2)]/(x+1) 2
- Это функция для определения наклона линии, поэтому установите его равным 0.
- Чтобы получить dƒ/dx=0, только числитель может быть равен нулю
- х(х+2)=0
- х=0 или х=-2
- Но в знаменателе есть ограниченное значение, если x=-1, то функция не определена
- подставьте значения x обратно в исходную функцию, чтобы найти значение y точек. из графика вы увидите, что x=-1 является вертикальной асимптотой.
- см. график по этой ссылке https://www.desmos.com/calculator/93lf5vxwqh
- f(0)=0 2 /(0+1)=0 f(-2)=(-2) 2 /(-2+1)=-4
- критические точки (0,0) и (-2,-4)
- функция возрастает, когда d f(x)/dx>0 на интервале, и уменьшается, когда d f(x)/dx<0 на интервале.
- на приведенном выше графике вы можете увидеть, когда функция уменьшается и увеличивается, если подумать о том, какой знак касательной будет двигаться слева направо.Вы также можете выбрать точки слева и справа от критических точек для проверки и подставить значения x в функцию первой производной для проверки или предоставления доказательств.
- Из графика
- наклон касательной положительный (возрастающий) от (-∞,-2), затем отрицательный (убывающий) от (-2,-1) и снова отрицательный (убывающий) от (-1,0) и положительный (прирост) от (0,∞)
Голосовать за 0 голос против
Подробнее
Отчет
Ранголи Г. ответил 20.05.22
Репетитор
5 (23)
Кандидат математических наук со стажем преподавания более 10 лет
Об этом репетиторе ›
Об этом репетиторе ›
youtube.com/embed/yf4XYLOU7nQ» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Открыто или Закрыто? | Преподавание исчисления
Примерно в это время года вы встречаете кого-то, надеюсь, одного из ваших учеников, который спрашивает: «Если я найду, где функция возрастает, интервал будет открытым или закрытым?»
У вас есть ответ?
Самое время рассказать об определениях и теоремах.
Начнем с вопроса, что означает возрастание функции. Вот определение:
Функция возрастает на отрезке тогда и только тогда, когда для всех (любых, любых) пар чисел x 1 < x 2 в промежутке, f ( x 1 ) < f ( 6 5 5 2 9090 x 900 ).
(Для убывания на отрезке второе неравенство меняется на формулировку.)
- Обратите внимание, что функции увеличиваются или уменьшаются на интервалах, а не в отдельных точках. Мы вернемся к этому через минуту.
- Численно это означает, что для каждой возможной пары точек точка с большим значением x всегда дает большее значение функции.
- Графически это означает, что при движении вправо по графику график идет вверх.
- Аналитически это означает, что мы можем доказать неравенство в определении.
В качестве примера этой последней точки рассмотрим функцию f ( x ) = x 2 .
Пусть x 2 = x 1 + h where h > 0. Then in order for f ( x 1 ) < f (
Это может быть правдой, только если , Таким образом, x 2 увеличивается, только если .
Теперь, конечно, мы редко, если вообще когда-либо, идем на все это. А для функции, возрастающей на нескольких интервалах, еще больше проблем. Обычный способ найти, где функция возрастает, — посмотреть на ее производную.
Обратите внимание, что выражение очень похоже на числитель исходного предельного определения производной x 2 at x = x 1 , а именно . Если ч > 0, где функция возрастает, числитель положителен и производная тоже положительна. Оборачивая это, мы получаем теорему, которая гласит: если для всех x в интервале, то функция возрастает на интервале.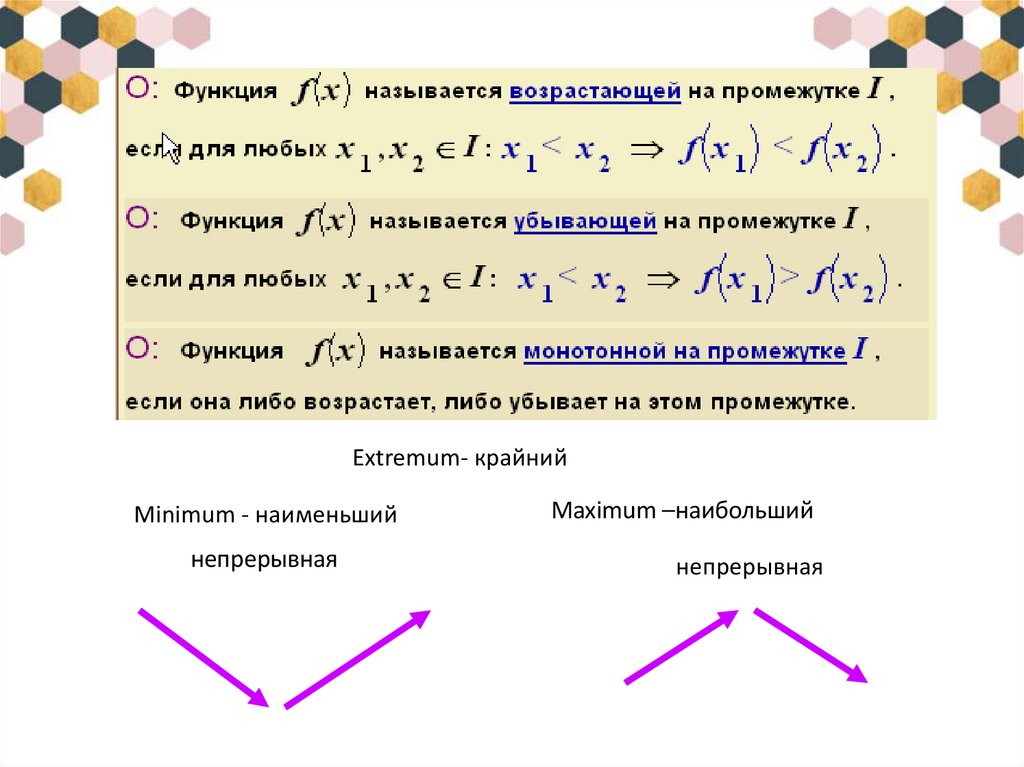
Это значительно упрощает поиск места возрастания функции: мы упрощаем поиск места, где ее производная положительна.
Есть только небольшая проблема в том, что теорема не говорит, что произойдет, если где-то на интервале производная равна нулю. Если это так, мы должны вернуться к определению возрастания на интервале или использовать какой-либо другой метод. Например, функция x 3 везде возрастает, хотя ее производная в начале координат равна нулю.
Рассмотрим другой пример. Функция sin( x ) возрастает на интервале (среди прочего) и убывает на . Некоторых смущает, что в обоих промежутках и что производная функции равна нулю на х = . Это не проблема. Sin() больше, чем все остальные значения, это оба интервала, поэтому по определению, а не по теореме, интервалы правильные.
Обычно верно, что если функция непрерывна на отрезке [ a , b ] и возрастает на открытом интервале ( a , b ), то она должна возрастать на отрезке [ a , b ] a , b ].