Тензорное исчисление
Тензорное исчисление
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. ЛИНЕЙНОЕ ПРОСТРАНСТВО § 1. Понятие линейного пространства § 2. Линейная зависимость векторов § 3. Размерность и базис линейного пространства § 4.  § 5. Векторное и смешанное произведения векторов § 6. Преобразования ортонормированного базиса. Основная задача тензорного исчисления § 7. Некоторые вопросы аналитической геометрии в пространстве ГЛАВА II. ПОЛИЛИНЕЙНЫЕ ФОРМЫ И ТЕНЗОРЫ § 2. Билинейные формы § 3. Полилинейные формы. Общее определение тензора § 4. Алгебраические операции над тензорами § 5. Симметричные и антисимметричные тензоры ГЛАВА III. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ ВЕКТОРНОГО ПРОСТРАНСТВА И ТЕНЗОРЫ ВТОРОЙ ВАЛЕНТНОСТИ § 2. Матрица линейного преобразования § 3. Определитель матрицы линейного преобразования. Ранг матрицы § 4. Линейные преобразования и билинейные формы § 5. Умножение линейных преобразований и умножение матриц § 6. Обратное линейное преобразование и обратная матрица § 7. Группа линейных преобразований и ее подгруппы ГЛАВА XIV. ПРИВЕДЕНИЕ К ПРОСТЕЙШЕМУ ВИДУ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ § 1.  Собственные векторы и собственные значения линейного преобразования§ 2. Приведение к простейшему виду матрицы линейного преобразования в случае различных собственных значений § 3. Многочлены от матриц и теорема Гамильтона—Кэли § 4. Свойства собственных векторов и собственных значений симметричного линейного прейбразования § 5. Приведение к диагональному виду матрицы симметричного линейного преобразования § 6. Приведение квадратичной формы к каноническому виду § 7. Представление невырожденного линейного преобразования в виде произведения симметричного и ортогонального преобразований ГЛАВА V. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА § 1. Общее уравнение поверхности второго порядка. Его инварианты § 2. Приведение к простейшему виду общего уравнения поверхности второго порядка § 3. Определение типа поверхности второго порядка при помощи инвариантов § 5. Приложение теории инвариантов к классификации поверхностей второго порядка § 6. 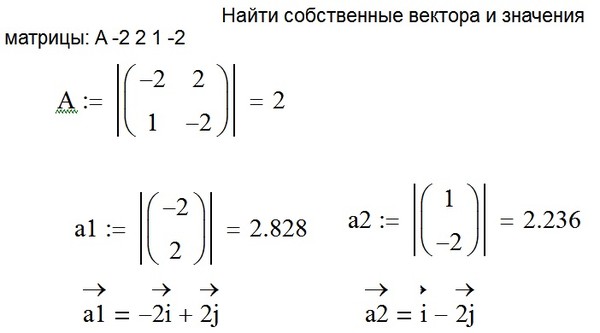 Центральные и нецентральные поверхности второго порядка§ 7. Примеры ГЛАВА VI. ПРИЛОЖЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К НЕКОТОРЫМ ВОПРОСАМ МЕХАНИКИ И ФИЗИКИ § 2. Некоторые свойства кристаллов, связанные с тензорами второй валентности § 3. Тензоры напряжений и деформации § 4. Дальнейшие свойства кристаллов ГЛАВА VII. ОСНОВЫ ТЕНЗОРНОГО АНАЛИЗА § 1. Тензорное поле и его дифференцирование § 2. Механика деформируемой среды § 3. Ортогоналыше криволинейные системы координат § 4. Подвижной репер ортогональной криволинейной системы координат и тензорные поля § 5. Дифференцирование тензорного поля в криволинейных координатах ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И УПРАЖНЕНИЙ ЛИТЕРАТУРА |
Собственные векторы и собственные значения линейного преобразования Основные теоретические сведения
Определение. Ненулевой вектор ,
удовлетворяющий условию ,
называется собственным вектором
преобразования .
Число
– собственное значение этого
преобразования, причем собственный
вектор
соответствует собственному значению
.
Между всеми линейными преобразованиями пространства и всеми квадратными матрицами порядка существует взаимно-однозначное соответствие, зависящее от выбранного в пространстве базиса . Говорят, что матрица , задает линейное преобразование в базисе , если
.
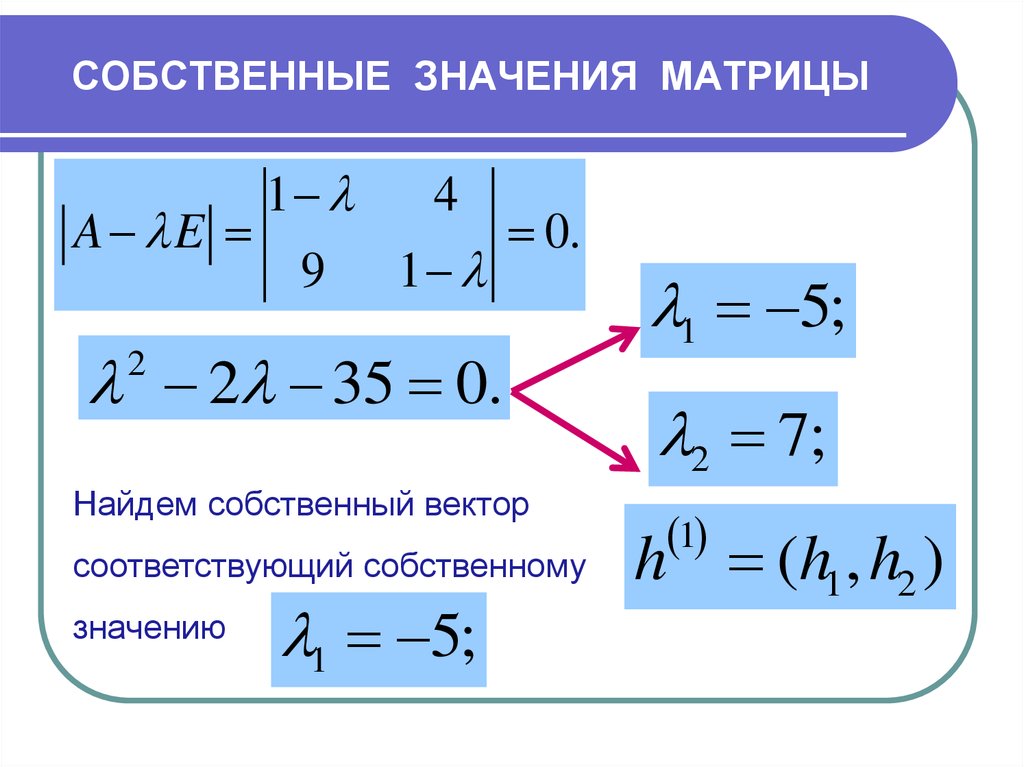
Определение. Определитель называется характеристическим многочленом матрицы :
,
а его корни – характеристическими корнями.
Характеристические корни линейного преобразования являются собственными значениями этого преобразования.
Примеры решения задач
Задача 1. Найти собственные значения и собственные векторы матрицы:
1) .
Решение. Составим характеристическое уравнение или ; .
Собственные значения ; .
Найдем собственный вектор:
При .
Следовательно,
решение этой системы ; .
Собственный вектор .
Пусть , тогда собственный вектор .
При система примет вид
.
Решение системы: , . Собственный вектор при имеет вид .
Ответ. , ; ; .
2) .
Решение. Собственные значения – решения характеристического уравнения:
или , являются кратными: .
Найдем собственный вектор, соответствующий собственному значению . Решением системы уравнений
является ; ; , т.е. собственный вектор . При имеем или .
Ответ. ; .
3) .
Решение. Характеристическое уравнение:
,
разложением по третьему столбцу получим: , ; тогда при так как –
любое число, обозначим .
,
если , тогда , собственный вектор: .
4) .
Решение. Характеристическое уравнение для этой матрицы имеет вид:
.
Собственные числа ; . Для каждого составим систему:
: :
Решение первой системы: , , , , т.е. собственный вектор . Вторая система равносильна системе следовательно, ее решение: ; ; ; .. Собственный вектор – . При , собственные векторы примут вид , .
Ответ. ; ; , .
Задачи для самостоятельного решения
Найти собственные числа и собственные векторы матриц.
1. . | 2. . |
3. . | 4. . |
5. . | 6. . |
7. . | 8. . |
9. | 10. . |
.Ответы: 1. , ; , ; , .
2.
, ; , .3. , .
4. , ; , .
5. , ; , .
6. , .
7. , .
8. , ; , ; , .
9. , ; , .
10. , .
Определение. Квадратичной формой называется многочлен
,
где – действительные постоянные, – переменные.
Матрица называется матрицей квадратичной формы.
Пример. Записать матрицу квадратичной формы
.
Решение. Диагональные элементы матрицы квадратичной формы равны коэффициентам при квадратах переменных, т.е. 1; 2; 5, а другие – половинам соответствующих коэффициентов квадратичной формы.
Перепишем ее в виде:
,
поэтому
.
Определение. Каноническим видом квадратичной формы называется
,
т.е. все при .
Квадратичная форма может быть приведена к каноническому виду произвольными неособенными линейными преобразованиями переменных, например, способом Лагранжа. Таких преобразований бесконечно много. Однако хотя коэффициенты и не совпадают, число положительных и отрицательных коэффициентов одно и то же. В системе координат с ортонормированным базисом преобразования должны быть ортогональными.
В канонической квадратичной форме число коэффициентов , отличных от нуля, равно рангу квадратичной формы
.
Примеры решения задач
Задача 1. Методом Лагранжа (выделения полных квадратов) привести к каноническому виду квадратичную форму
.
Решение. Первое преобразование: , , . Тогда получим
.
Второе преобразование: ; ;
и форма принимает канонический вид:
, , .
Ответ. .
Задача 2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду.
Решение. Диагональные элементы матрицы квадратичной формы: 3, 2, 1, остальные элементы: ; ; . Составим характеристическое уравнение
;
;
или .
Корни: ; ; . Найдем собственные векторы
:
при ;
:
или ;
:
, .
Нормируем систему векторов , , ; ; ; .
Следовательно, , , .
Формулы преобразования координат:
, ,
.
Квадратичная
форма: .
Ответ. , ,
, .
Задача 3. Привести к каноническому виду квадратичную форму:
.
Решение. Характеристическое уравнение
,
, .
Решение характеристического уравнения: ; . Канонический вид: .
Найдем матрицу ортогонального преобразования
:
, ; ;
: .
, так как
Корень кратности два, следовательно, этому собственному значению соответствуют два собственных вектора. Первый выбираем произвольно. Пусть ; , , тогда .
Второй выбираем так, чтобы , т.е. .
, ,
– любое; , , .
Матрица преобразования:
.
Формулы преобразования координат:
;
; .
Подставляем в исходную матрицу квадратичную форму:
.
Ответ. .
Задачи для самостоятельного решения
Методом Лагранжа привести к каноническому виду квадратичные формы:
1. ;
2. ;
3. ;
Ответ: 1) ;
2) ;
3) .
Найти ортогональное преобразование, приводящее следующие формы к каноническому виду, и написать этот канонический вид:
4. .
Ответ. ,
5. .
Ответ. ,
6. .
Ответ. ,
7. .
Ответ. ,
Собственные значения и собственные векторы линейных преобразований
Определение
Пусть $T:V \to V$ — линейное преобразование векторного пространства $V$ в себя.
- Мы говорим, что $\lambda$ является собственным значением $T$, если существует ненулевой вектор $\mathbf{v}\in V$ такой, что $T(\mathbf{v})=\lambda \ mathbf{v}$.
- Для каждого собственного значения $\lambda$ оператора $T$ ненулевые векторы $\mathbf{v}$, удовлетворяющие $T(\mathbf{v})=\lambda \mathbf{v}$, называются собственными векторами 92$, состоящее из собственных векторов.
(б) Найдите матрицу $T$ относительно базиса $B=\{\mathbf{v}_1, \mathbf{v}_2\}$. - Пусть $P_1$ — векторное пространство всех вещественных многочленов степени $1$ или меньше. Рассмотрим линейное преобразование $T: P_1 \to P_1$, определенное как $T(ax+b)=(3a+b)x+a+3$ для любого $ax+b\in P_1$.
(a) По базису $B=\{1, x\}$ найти матрицу линейного преобразования $T$.
(b) Найдите базис $B’$ векторного пространства $P_1$ такой, что матрица $T$ относительно $B’$ является диагональной матрицей. 9{\infty}=(a_1, a_2, \dots)$.
Пусть $U$ — подпространство в $V$, состоящее из всех вещественных последовательностей, удовлетворяющих линейному рекуррентному соотношению $a_{k+2}-5a_{k+1}+3a_{k}=0$ при $k=1 , 2, \точки$. Пусть $T$ — линейное преобразование из $U$ в $U$, определяемое равенством
\[T\big((a_1, a_2, \dots)\big)=(a_2, a_3, \dots). \] Пусть $B=\{\mathbf{u}_1, \mathbf{u}_2\}$ — базис $U$, где
\begin{align*}
\mathbf{u}_1&=(1, 0 , -3, -15, -66, \точки)\\
\mathbf{u}_2&=(0, 1, 5, 22, 95, \точки). 9{\infty}$, удовлетворяющих линейному рекуррентному соотношению $a_{k+2}-5a_{k+1}+3a_{k}=0$, и выразить его через $a_1, a_2$.
9{\infty}$, удовлетворяющих линейному рекуррентному соотношению $a_{k+2}-5a_{k+1}+3a_{k}=0$, и выразить его через $a_1, a_2$.Найти собственные значения и собственные векторы линейного преобразования $T: M_{2\times 2}\to M_{2\times 2}$
Пример — отличная идея! Давайте возьмем другую карту, чтобы проиллюстрировать, как напрямую вычислять собственные значения и собственные векторы:
$$T \begin{pmatrix}
а и б \\
CD
\end{pmatrix}= \begin{pmatrix}
2a-b-c и -a+3b-c-d\\
-a-b+3c-d и -b-c+2d
\end{pmatrix}.$$
Есть несколько способов найти собственные значения и собственные векторы. Как предлагает Бабба, мы можем применить определение, т. е. найти скаляры $\lambda$ и $2 \times 2$ матрицы $M$ такие, что $TM = \lambda M$. То есть решить
$$\begin{pmatrix}
2a-b-c и -a+3b-c-d\\
-a-b+3c-d и -b-c+2d
\end{pmatrix} = \lambda\begin{pmatrix}
а и б \\
CD
\end{pматрица}. \тег{$\звезда$}$$
Это приводит к четырем однородным линейным уравнениям относительно $a, b, c, d$ с неизвестным параметром $\lambda$ (поскольку уравнения $a, b, c, d, \lambda$, система, к сожалению, нелинейна , но если мы рассматриваем $\lambda$ как неизвестную константу, мы все еще можем использовать методы линейной алгебры).
Уравнения:
$$\begin{случаи}
2а — б — с = \лямбда а \\
-а + 3b — с — d = \лямбда б \\
-а — б + 3с — д = \лямбда с \\
-b — c + 2d = \лямбда d
\end{случаи} \iff \begin{случаи}
(2 — \lambda)a — b — c = 0 \\
-а + (3 — \lambda)b — c — d = 0 \\
-а — b + (3 — \lambda)c — d = 0 \\
-b — c + (2 — \lambda)d = 0.
\end{случаи}$$
Мы можем поместить это в расширенную матрицу
$$\left[\begin{массив}{cccc|c}
2 — \лямбда&-1&-1&0&0\\
-1 и 3 — \лямбда & -1 & -1 & 0 \\
-1 & -1 & 3 — \ лямбда & -1 & 0 \\
0 и -1 и -1 и 2 — \лямбда и 0
\end{массив}\right].$$
Теперь напомним, что эта матрица имеет больше, чем просто единственное решение (т.е. больше, чем просто $a = b = c = d = 0$, что соответствует матрице $0$ как решению в $(\star)$), если и только если матрица коэффициентов имеет ненулевой определитель. Нам нужны собственные векторы и собственные значения, поэтому нам нужны ненулевые решения. То есть $\lambda$ будет собственным значением тогда и только тогда, когда
$$\det\begin{bmatrix}
2 — \лямбда&-1&-1&0\
-1 и 3 — \лямбда & -1 & -1 \\
-1 и -1 и 3 — \лямбда & -1 \\
0 и -1 и -1 и 2 — \лямбда
\end{bmatrix} = 0.