Средняя линия трапеции
МБОУ «Воргинская средняя школа» 2019-2020гг
«Прикладная математика»
Выполнила: Прокопенкова Марина, 8 А класс,
МБОУ «Воргинская средняя школ»
Руководитель: Суслов Григорий Александрович
учитель математики МБОУ «Воргинская средняя школа»
«Геометрия полна приключений,
потому что за каждой задачей скрывается приключение мысли…»
В.Произволов
Дано : ABCD –равнобедренная трапеция, FE -высота, FE= а AC ┴ BD
Найти : MN
FE =FO+OE= а
F
C
D
FO+OE=DF+AE,
DF+AE =½( AB + CD )= a
M
N
MN =
B
MN=a
A
E
«А есть ли еще средние линии
в трапеции?»
Цель исследования:
установить, сколько средних линий имеет трапеция
Обьект исследования: трапеция
Предмет исследования: средние линии трапеции
Задачи исследования:
- подобрать данные о средних линиях трапеции
- изучить особенные особенности средних линий в трапеции
- исследовать задачи о средних линиях трапеции, действующие в математической литературе
- разобрать конкретные вопросы о средних линиях трапеции
Гипотеза: Если знать в совершенстве основные особенности средних линий трапеции, то их применение будет хорошим подспорьем ученикам в практическом направлении материала
Актуальность, новизна и практическая значимость:
Наше исследование актуально и ново, поскольку в школьной программе по математике данное направление не рассматривалось более глубоко и основательно.
В процессе собственных информационных поисков получены не известные факты для школьников о второй средней линии трапеции.
Данные исследования будут полезны при подготовке к математическим олимпиадам и конкурсам, более углубленного изучения геометрии, а также поможет обычным школьникам стать более успешными в математике, поскольку данная тема является важной при подготовке к ОГЭ.
Вторая средняя линия трапеции :
MN= ½ ( AB + CD )
F
C
D
B
A
E
В точке, в которой пересекаются две средние линии,
они делятся пополам
K
KO = OS
MO = ON
B
KN || BD и KN =½ BD
C
MS || BD, MS =½ BD
МК || АС, MK =½ AC
O
NS || AC, NS =½ AC
A
S
D
Диагонали трапеции и вторая средняя линия
пересекаются в одной точке
~
Дано : ВК=КС
Доказать : AS=SD
~
K
C
B
BK=KC
O
AS=SD
D
A
S
Прямая, содержащая вторую среднюю линию трапеции проходит через точку пересечения прямых, содержащих боковые стороны
△ A O D △ B O C
~
OK = ½ (ОВ+ОС),
OS = ½ ( OA + OD ),
OS = ½ ( k ∙ OB + k ∙ OC )= ½ k ( OB + OC )= k OK
O OS
Средние линии равнобедренной трапеции перпендикулярны
MN FE
В равнобокой трапеции вторая средняя линия перпендикулярна ее основаниям
FE AB
FE CD
F
C
D
Если средние линии трапеции равны, то ее диагонали перпендикулярны
N
M
AC BD
B
A
E
M
Задача 1. (Кушнир И. А.)
(Кушнир И. А.)
В трапеции ABCD сумма углов при меньшем основании равна 270º. Найти длину второй средней линии, если основания AD и BC соответственно равны а и в (а в)
N
C
B
NF = MF – MN =
(a – b)/2
D
A
F
Задача 2 (Кушнир И.А.)
Доказать, что площадь трапеции равна произведению второй средней линии на сумму перпендикуляров, проведенных к этой средней линии (или её продолжению) из двух противоположных вершин трапеции
Дано: ABCD – трапеция, EF – вторая средняя линия, СN EF, AM EF.
Доказать:
E
BC
N
Доказательство: Рассмотрим △ AEF и△ ECF
M
D
A
F
Задача 3. (Кушнир И. А.)
В трапеции ABCD сумма углов при основании AD равна 90º. Докажите, что отрезок, соединяющий середины оснований, равен полуразности оснований
Докажите, что отрезок, соединяющий середины оснований, равен полуразности оснований
AD, BC – гипотенузы прямоугольных
△ AMD и △BMC
Решение: AF=FD, BN=NC
M
C
N
B
D
A
F
FN =½ AD –½ BC =½ (AD – BC)
Задача 1 (составлена самостоятельно)
Верно ли утверждение:
если прямая проходит через точку пересечения диагоналей
и середину одного основания трапеции, то и второе основание
она делит пополам?
K
C
B
Диагонали трапеции и вторая средняя линия пересекаются в одной точке
O
D
A
S
Задача 2 (составлена самостоятельно)
В трапеции ABCD вторая средняя линия KS = 4 см, основания равны 12 см и 8 см, угол между средними линиями 30º.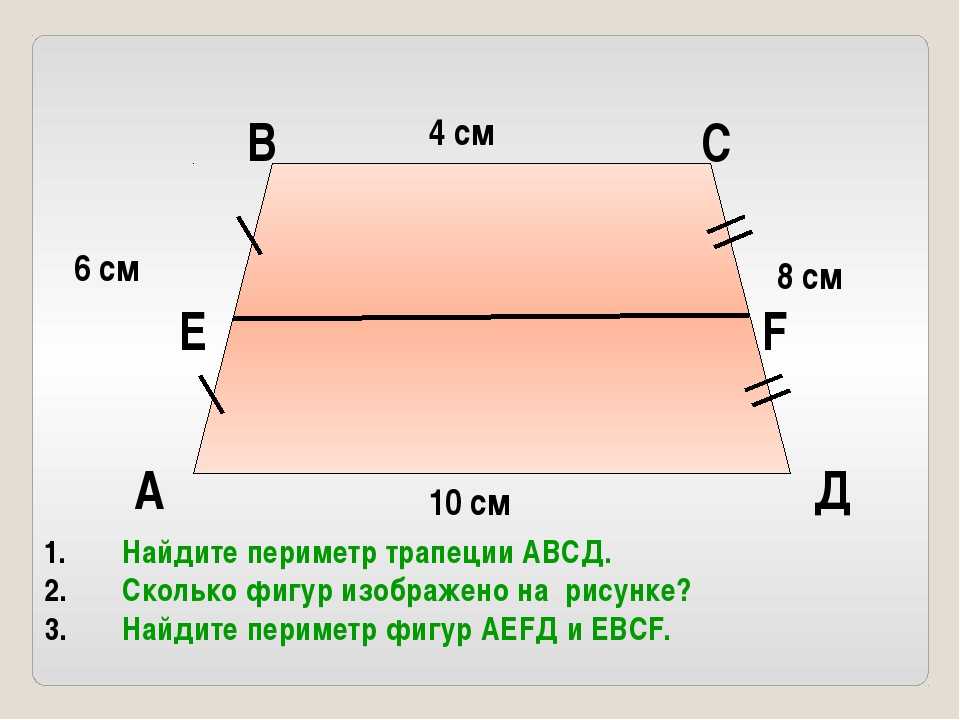
Найти площадь трапеции.
△ KHS — прямоугольный
K
C
B
N
O
M
KH =2 см
S
H
A
D
Задача 3
С помощью чертежной линейки построить вторую среднюю линию трапеции
K
B
C
O
D
A
S
Задача 4
Найдите среднюю линию трапеции АВС D , если ВС= 1 6см и ее вторая средняя линия делится диагональю в отношении 1:2.
Рассмотрим ∆КОС и ∆ SOA . Они подобны по стороне и прилежащим углам. Значит Так как точка К середина отрезка ВС, то КС= 8 см, а А S = 1 6 c м. Следовательно, AD = 3 2 c м.
C
K
B
O
A
D
S
Задача 5 Вторая средняя линяя равнобокой трапеции перпендикулярна её основаниям.
△ АОD и △ ВОС равнобедренные
ОМ и ОК медианы
M
KM ┴BC, KM┴AD
ВЫВОДЫ:
2. Изучены особенные свойства средней линии
3. Рассмотрены практическое решение
математических задач с использованием свойств средней линии трапеции.
4. Составлены собственные математические задачи и их решение.
5. Получены новые для меня знания и умения, повысилась заинтересованность к изучению математики.
«Геометрия полна приключений,
потому что за каждой задачей скрывается приключение мысли…»
В.Произволов
Тест Средняя линия трапеции по теме геометрии (8 класс)
Последний раз тест пройден 23 часа назад.
Для учителя
Вопрос 1 из 10
Основания трапеции относятся как 4:5, а средняя линия равна 9. Найдите меньшее основание.
8
10
2
18
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Средняя линия трапеции равна 11, а одно из ее оснований больше другого на 2. Найдите большее основание трапеции
10
12
22
18
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Периметр трапеции равен 112, а сумма непараллельных сторон равна 70.
 Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.42
21
14
84
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Основания трапеции равны 6,5 и 8,5 см. Найдите длину ее средней линии.
14
15
7,5
30
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Средняя линия трапеции равна 10, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
8
12
20
16
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Основания трапеции относятся как 2:3 , а средняя линия равна 10.
 Найдите меньшее основание.
Найдите меньшее основание.12
20
2
8
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Средняя линия трапеции равна 10, а одно из ее оснований больше другого на 2. Найдите большее основание трапеции a.
20
11
9
18
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции. a.
30
10
15
5
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Основания трапеции равны 6,3 и 8,7 см.
 Найдите длину ее средней линии.
Найдите длину ее средней линии.7,5
15
30
14
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Средняя линия трапеции равна 20, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
8
16
22
18
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Андрей Московский
9/10
Сабина Мамедова
10/10
Игорь Заградский
10/10
Рейтинг теста
3.8
Средняя оценка: 3.8
Всего получено оценок: 429.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Как найти середины катетов трапеции?
Медиана трапеции — это отрезок, соединяющий середины двух катетов.
Как решить среднюю линию трапеции?
Как найти середину ног?
https://www.youtube.com/watch?v=uKEJBh4wMZc
Что из следующего соединяет середины катетов трапеции?
Медиана трапеции — это отрезок, соединяющий середины двух катетов.
По какой формуле найти площадь трапеции?
Чтобы найти площадь трапеции, умножьте сумму оснований (параллельных сторон) на высоту (перпендикулярное расстояние между основаниями), а затем разделите на 2 .
Как найти середину катета трапеции?
Как вы используете среднюю теорему для решения задачи?
Что такое теорема о среднем отрезке трапеции?
Теорема о среднем отрезке трапеции утверждает, что отрезок, соединяющий середины катетов трапеции, параллелен основаниям и равен половине их суммы .
Как найти средний сегмент?
Применяется ли теорема о средней точке к трапеции?
| Заявление | Причина |
|---|---|
| 6. В ∆PQS отрезок MU соединяет середины сторон QS и PS. Следовательно, MU = 12PQ. | 6. По теореме о средней точке. |
Как найти недостающую длину трапеции?
- Определите, какая сторона отсутствует.
- Сложите все остальные стороны и запишите результат.
- Вычтите это число из периметра. В результате получается длина недостающей стороны.
Как называется отрезок, соединяющий середины двух сторон треугольника?
Середина треугольника — это отрезок, соединяющий середины двух сторон треугольника.
Каковы середины отрезков АВ и ВС соответственно?
В ΔABC D и E являются серединами AB и BC соответственно. Теорема о средней точке: говорят, что отрезок прямой в треугольнике, соединяющий середины двух сторон треугольника, параллелен его третьей стороне, а также составляет половину длины третьей стороны.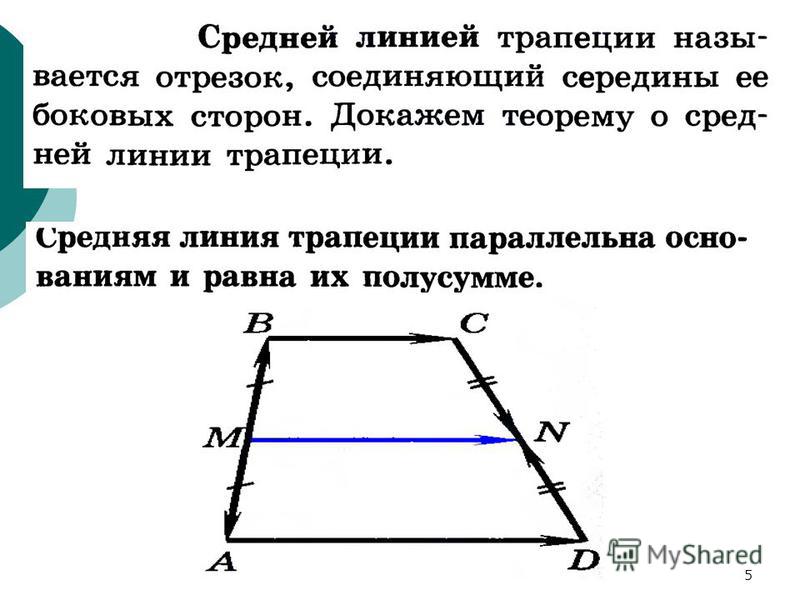
Какой отрезок соединяет середины двух сторон треугольника?
Средняя линия — это отрезок, соединяющий середины двух сторон треугольника. Поскольку у треугольника три стороны, каждый треугольник имеет три середины. Средняя линия треугольника параллельна третьей стороне треугольника и составляет половину длины третьей стороны.
Какова мера среднего сегмента Ed?
Каждый средний сегмент равен половине длины стороны, которой он параллелен ; сумма длин средних сегментов равна половине периметра треугольника.
Какая теорема используется при нахождении медианы трапеции Modu?
Длина медианы равна среднему значению двух оснований, поэтому ее можно найти по формуле: ((длина одного основания) + (длина другого основания)) / 2 .
Как доказать теорему о средней линии?
Доказательство этой теоремы — это просто использование свойств подобных треугольников и соответствующих углов для логического вывода, что оба свойства в теореме верны . Если в треугольнике ABC соединить середины D и E любых двух сторон, то верны следующие факты: AD = BD и CD = BE.
Если в треугольнике ABC соединить середины D и E любых двух сторон, то верны следующие факты: AD = BD и CD = BE.
Что такое b1 и b2 в трапеции?
Трапеция – это четырехсторонняя фигура, у которой ровно одна пара параллельных сторон. Две параллельные стороны являются основаниями; мы будем называть их b1 (основание один) и b2 (основание два) . Две другие стороны называются ножками. ОНИ НЕ ПАРАЛЛЕЛЬНЫ.
Что находит формула средней точки?
2.5. Чтобы найти середину любого диапазона, сложите два числа вместе и разделите на 2 . В данном случае 0 + 5 = 5, 5/2 = 2,5.
Почему работает формула площади трапеции?
Площадь этого параллелограмма равна его высоте (половина высоты трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна половине высоты × (основание1 + основание2). Поскольку параллелограмм состоит из того же «материала», что и трапеция, это тоже площадь трапеции .
Что такое формула площади?
Площадь = длина × длина .
Что такое средний сегмент?
линия, соединяющая середины двух сторон треугольника .
Что делает трапецию равнобедренной?
Равнобедренная трапеция может быть определена как трапеция, у которой непараллельных сторон и углы при основании имеют одинаковую меру . Другими словами, если две противоположные стороны (основания) трапеции параллельны, а две непараллельные стороны имеют одинаковую длину, то это равнобедренная трапеция.
Какие стороны равнобедренной трапеции?
В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (бока) имеют равную длину (свойства общие с параллелограммом). Диагонали также имеют одинаковую длину.
Что такое медиана равнобедренной трапеции?
Медиана трапеции — это отрезок, соединяющий середины непараллельных сторон (катетов) . Теорема: Медиана трапеции параллельна каждому основанию, а длина медианы равна половине суммы длин двух оснований.
Как найти недостающую длину?
- если катет a отсутствует, то преобразовать уравнение к виду, когда a находится на одной стороне, и извлечь квадратный корень: a = √(c² – b²)
- если катет b неизвестен, то. b = √(c² – a²)
- для гипотенузы c отсутствует формула. c = √(a² + b²)
Какая теорема утверждает, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче?
Теорема о средней линии утверждает, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче.
Середина трапеции Какова длина сегмента?
Пояснение: Средняя линия трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции. Этот сегмент имеет два особых свойства. Она параллельна основаниям трапеции. Длина среднего отрезка равна средней длины двух оснований .
Что такое теорема о средней точке треугольника?
Теорема о средней точке утверждает, что « Отрезок в треугольнике, соединяющий середины двух сторон треугольника, называется параллельным его третьей стороне и также составляет половину длины третьей стороны ».
Как написать формулу трапеции?
Формула, используемая для нахождения площади трапеции, выглядит следующим образом: Площадь трапеции = ½ (a + b) h ; где a’ и ‘b’ — основания (параллельные стороны), а ‘h’ — высота трапеции.
Как найти длину середины треугольника?
Как найти периметр средней точки?
- Используйте формулу расстояния, чтобы найти расстояние между всеми тремя сторонами. Добавьте все три стороны. …
- Используйте формулу средней точки, чтобы найти среднюю точку расстояния между тремя заданными точками.
- Найдите расстояние между 3 средними точками, найденными в части 2 выше. Добавьте все 3 стороны. …
- Отношение = (периметр 1)/(периметр 2)
Как найти объем прямой трапециевидной призмы?
Объем трапециевидной призмы – это емкость призмы. Формула объема трапециевидной призмы: площадь основания × высота призмы в кубических единицах .
Как найти площадь и периметр трапеции?
Площадь равна высоте, умноженной на среднее значение оснований; периметр это сумма сторон . Трапеция – это четырехугольник с одной парой параллельных сторон. Параллельные стороны называются основаниями, а длины оснований будем обозначать как b1 и b2.
Что такое прямая трапеция в математике?
Прямоугольная трапеция это трапеция с двумя прямыми углами .
Как написать площадь?
Площадь измеряется в квадратных единицах, таких как квадратные дюймы, квадратные футы или квадратные метры. Чтобы найти площадь прямоугольника, умножьте длину на ширину. Формула: A = L * W , где A — площадь, L — длина, W — ширина, а * означает умножение.
Какова площадь диска радиусом R?
Диск — плоский круглый объект с круговой границей. Площадь диска радиуса r определяется по формуле: A=πr2 .
Как пользоваться формулой площади?
Простейшие (и наиболее часто используемые) расчеты площади для квадратов и прямоугольников.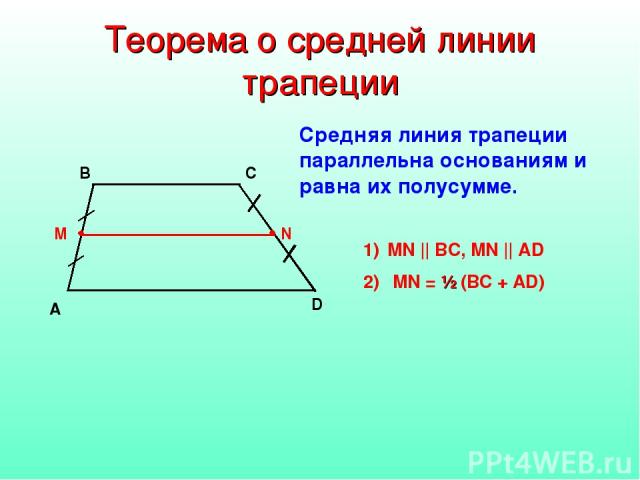

 Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции. Найдите меньшее основание.
Найдите меньшее основание. Найдите длину ее средней линии.
Найдите длину ее средней линии.