Найти точки пересечения графика с осями координат: Найдите координаты точек пересечения с осями координат графика функции y=2x 4

примеры решения. Случай двух нелинейных функций

Найти точки пересечения функции с осями координат. Как найти координаты точек пересечения графика функции: примеры решения. Случай двух нелинейных функций

В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.

Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.

Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами

и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.

Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.

Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.

Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.

Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией».

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций. 2 – 3x – 2 = 0$.

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

$x_1=2; x_2 = -\frac{1}{2}$

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — \frac{1}{2} = \frac{1}{2}$.

Точки пересечения будут $(2;3)$ и $(-\frac{1}{2}; \frac{1}{2})$.

Третий способ

Перейдём к третьему способу — графическому , но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

1. Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
2. Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
3. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.

Случай двух линейных функций

Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.

Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 \neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ — это коэффициент угла наклона. Если $ k_1 \neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.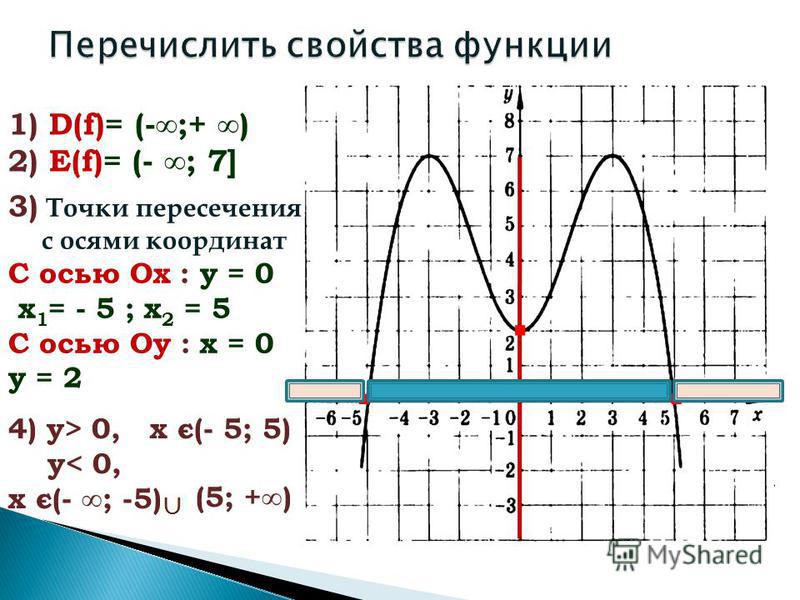

Пример 1

Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций.

Решение

Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 \neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x — x = 3+5 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2\cdot 8 — 5 = 16 — 5 = 11 $$ Итак, $ M (8;11) $ — является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. 2-2\cdot 0 + 1 = 1 $$ $ M (0;1) $ — точка пересечения графиков функций

Ответ

$$ M (0;1) $$

Как найти координаты точек пересечения графика функции: примеры решения

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Первый способ

2. Второй способ

3. Третий способ

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$.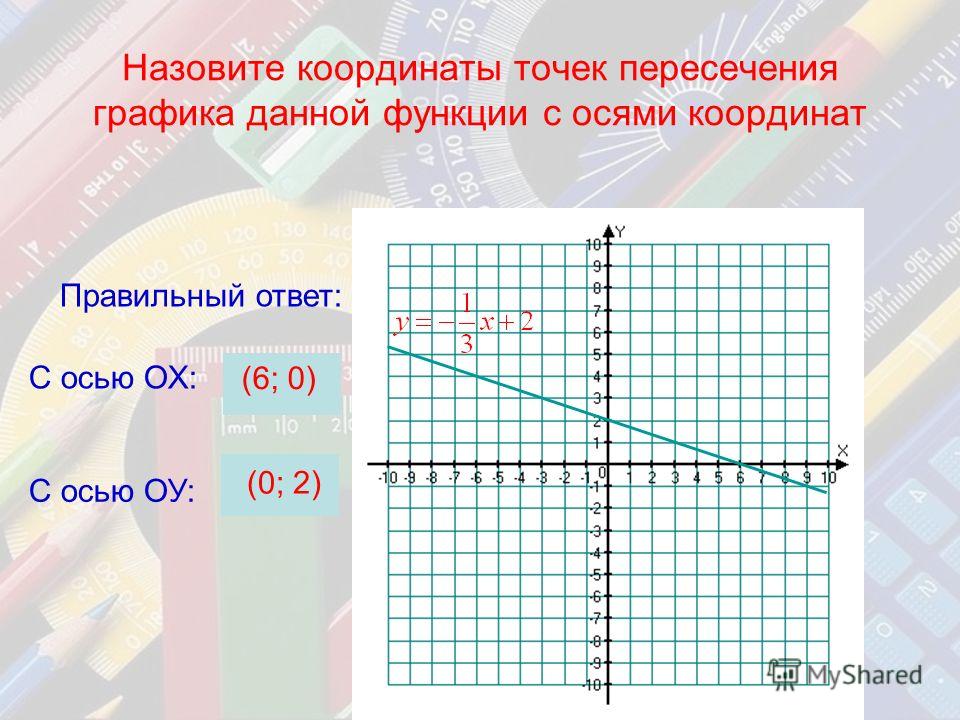 2 – 3x – 2 = 0$.

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

$x_1=2; x_2 = -\frac{1}{2}$

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — \frac{1}{2} = \frac{1}{2}$.

Точки пересечения будут $(2;3)$ и $(-\frac{1}{2}; \frac{1}{2})$.

Третий способ

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Пример 3

Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 07.05.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Функции: графики и пересечения

Горячая математика

Предполагать ф ( Икс ) а также грамм ( Икс ) две функции, которые принимают на вход действительное число и выводят действительное число.

Тогда точки пересечения ф ( Икс ) а также грамм ( Икс ) это те числа Икс для которого ф ( Икс ) знак равно грамм ( Икс ) .

Иногда точные значения можно легко найти, решив уравнение ф ( Икс ) знак равно грамм ( Икс ) алгебраически.

Пример 1:

Каковы точки пересечения функций ф ( Икс ) а также грамм ( Икс ) если ф ( Икс ) знак равно Икс + 6 а также грамм ( Икс ) знак равно − Икс ?

Точки пересечения ф ( Икс ) а также грамм ( Икс ) это те числа Икс для которого ф ( Икс ) знак равно грамм ( Икс ) .

То есть, Икс + 6 знак равно − Икс .

Решить для Икс .

Икс + 6 знак равно − Икс 2 Икс + 6 знак равно 0 2 Икс знак равно − 6 Икс знак равно − 3

Теперь вы можете использовать значение Икс найти соответствующий у -координата точки пересечения.

Подставьте значение Икс в любой из двух функций.

грамм ( − 3 ) знак равно − ( − 3 ) знак равно 3

Уравнения также можно решить графически, нанеся две функции на координатную плоскость и указав точку их пересечения.

В других случаях точные значения найти сложно. Возможно, вам придется использовать технологию для их оценки.

Пример 2:

Найдите точку (точки) пересечения двух функций.

ф ( Икс ) знак равно | Икс − 5 | грамм ( Икс ) знак равно журнал Икс

Здесь решить алгебраически не так просто. Решения уравнения | Икс − 5 | знак равно журнал Икс не являются красивыми рациональными числами.

График функций на координатная плоскость .

Вы можете использовать графическую утилиту, чтобы найти, что координаты точек пересечения приблизительно ( 4,36 , 0,64 ) а также ( 5,76 , 0,76 ) .

Загрузите наши бесплатные приложения для обучения и книги для подготовки к экзаменам

Объяснение урока: Точка пересечения двух прямых на координатной плоскости

В этом объяснении мы узнаем, как найти точку пересечения между две прямые линии в системе координат и использовать эту концепцию, чтобы найти уравнения линий.

Начнем с того, что вспомним, что мы подразумеваем под пересечением двух линий.

Определение: точка пересечения двух прямых

Точка пересечения двух различных непараллельных прямых — это единственная точка где они встречаются или пересекаются. Это упорядоченная пара значений 𝑥 и 𝑦 где линии встречаются на графике и удовлетворяет уравнениям обеих линий.

Отдельные параллельные линии — это линии на плоскости, которые всегда находятся на одном и том же расстоянии отдельно. У них не будет точек пересечения.

На схеме ниже 𝐴𝐵 и 𝑃𝑄 пересекаются в пункт 𝐹.

Как найти точку пересечения двух линий на координатной плоскости

Мы можем найти точку пересечения двух линий на координатной плоскости используя два метода, графический или алгебраический метод. Например, если мы были две линии, представленные 𝑦=𝑥+1 и 𝑦+2𝑥=4, тогда мы могли бы построить график это следующим образом.

Конкретную точку пересечения можно найти графически с помощью исследуя график, чтобы отметить точку (𝑥,𝑦), где линии встречаются или Пересекать. Однако для более сложных уравнений алгебраическое решение может быть предпочтительнее. Для алгебраического решения мы признаем, что точка, лежащая на обе линии должны удовлетворять обоим уравнениям.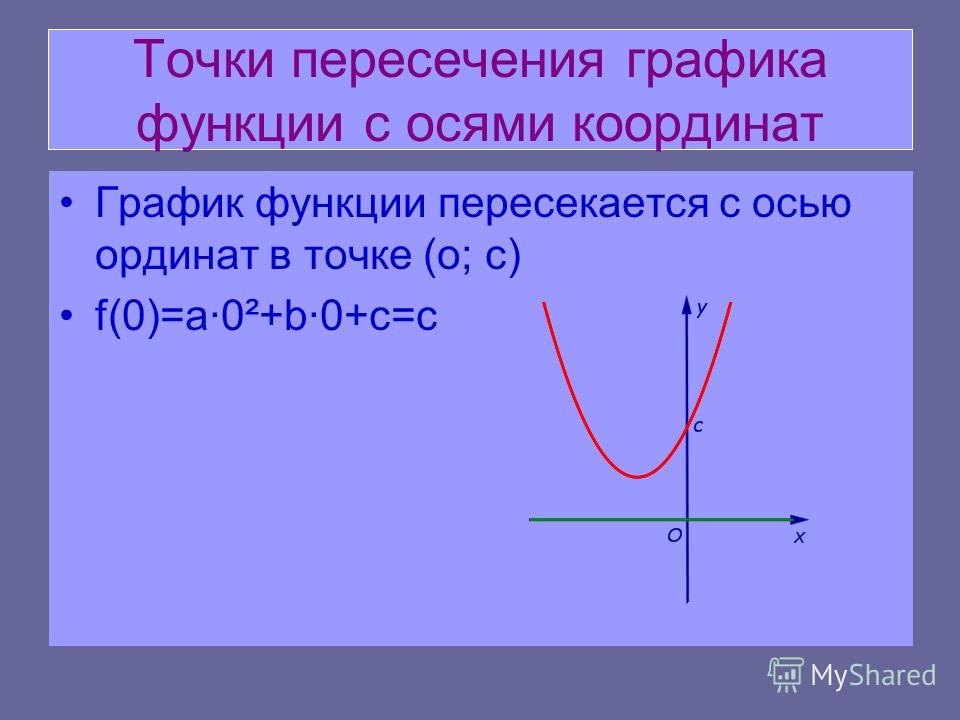 Это то же самое, что решить система двух линейных уравнений с двумя неизвестными.

В первом примере мы увидим, как можно использовать графическое решение для нахождения точка пересечения горизонтальной и вертикальной линий.

Пример 1: Нахождение точки пересечения горизонтальной и вертикальной прямой

В какой точке провести линии 𝑥=7 и 16𝑦=−1 пересекаются?

Ответ

Точка пересечения двух различных линий — это точка пересечения этих линий. Один из способов ответить на этот вопрос — нарисовать обе линии. Начнем с рисования график 𝑥=7. Любое уравнение, которое просто имеет 𝑥-переменная и отсутствие 𝑦-переменной будет вертикальная линия.

Далее рассмотрим граф 16𝑦=−1. Это может будет полезно, если мы изменим это, чтобы сделать 𝑦 подлежащим. Итак, умножив обе части уравнения, 16𝑦=−1, по 6 имеем 𝑦=−6.

Уравнение только с 𝑦-переменной представляет собой горизонтальную линию. Поскольку 𝑦=−6, горизонтальная линия проходит через −6 на 𝑦-ось.

Чтобы найти точку пересечения двух прямых, 𝑥=7 и 16𝑦=−1, ищем точку, где они пересечься или встретиться. Изучая график, точка пересечения находится в точке координировать (7,−6).

В следующем примере мы увидим, как можно использовать алгебраический метод для нахождения точка пересечения двух прямых.

Пример 2. Нахождение точки пересечения двух прямых

Определите точку пересечения двух прямых, представленных уравнения 𝑥+3𝑦−2=0 и −𝑦+1=0.

Ответ

Мы можем вспомнить, что точкой пересечения двух различных прямых является точку пересечения линий. Чтобы найти эту точку пересечения или точка пересечения линий, мы можем использовать либо алгебраический, либо графический подход.

Точка пересечения лежит на обеих линиях, поэтому она должна удовлетворять уравнения обеих линий. Следовательно, мы можем найти точку пересечения решая эти уравнения как одновременные, находя значения 𝑥 и 𝑦, где (𝑥,𝑦) — точка пересечения.

Мы можем написать наши уравнения:

𝑥+3𝑦−2=0,−𝑦+1=0.

(1)(2)

Чтобы решить эту задачу методом подстановки, переставляем вторую уравнение, −𝑦+1=0, добавляя 𝑦 к обоим стороны уравнения, чтобы дать −𝑦+1=01=𝑦𝑦=1.

Подставив 𝑦=1 в уравнение (1), и переставляем, имеем 𝑥+3(1)−2=0𝑥+1=0𝑥=−1.

У нас есть решение 𝑥=−1 и 𝑦=1. Следовательно точка пересечения может быть задана как (−1,1).

В качестве альтернативного метода или проверки алгебраического метода мы рассмотрим графики двух линий.

Мы установили, что линия −𝑦+1=0 может быть переставлен как 𝑦=1. Следовательно, линия будет горизонтальной. линия, проходящая через 1 на оси 𝑦.

Мы можем набросать уравнение 𝑥+3𝑦−2=0, найдя два точки на линии. Например, мы могли бы найти 𝑦-перехват, подставив 𝑥=0 и 𝑥-перехват, подставив 𝑦=0.

Замена 𝑦=0 на 𝑥+3𝑦−2=0 и упрощая, имеем 𝑥+3(0)−2=0𝑥−2=0𝑥=2.

Подстановка 𝑥=0 и упрощение дает 0+3𝑦−2=03𝑦−2=03𝑦=2𝑦=23.

Теперь мы установили, что прямая проходит через точки (2,0) и 0,23. Может быть немного сложно построить набор координат с нецелыми значениями, например 0,23; так, мы можем предпочесть найти другой набор координат на линии 𝑥+3𝑦−2=0.

Замена 𝑥=−4 на 𝑥+3𝑦−2=0 и упрощая, имеем (−4)+3𝑦−2=0−6+3𝑦=03𝑦=6𝑦=2.

Это дает нам третью координату (−4,2) на линии 𝑥+3𝑦−2=0. Мы можем построить эти три координаты и нарисуйте эту линию рядом с графиком −𝑦+1=0, как показано.

Изучив график, мы можем подтвердить приведенное выше алгебраическое решение, так как точка пересечения находится в (−1,1).

В предыдущем примере использовались два разных метода: алгебраический и графический. Оба метода имеют преимущества, и часто графический метод — хороший способ проверить результат алгебраического. Однако стоит отмечая, что графический метод может быть не совсем точным, особенно в случаи, когда решение является нецелочисленным результатом. С другой стороны, алгебраическая решение всегда даст точный результат.

В следующем примере мы увидим, как можно найти пересечение между двумя строк, где один задан в векторной форме.

Пример 3. Нахождение векторной формы линии, проходящей через пересечение двух других прямых

Найдите векторное уравнение прямой, параллельной 𝑦-ось и проходит через точку пересечения двух прямые ⃑𝑟=𝑘(−6,−4) и −3𝑥+5𝑦=−5.

Ответ

Напомним, что пересечение двух прямых — это точка, в которой они встретиться или пересечься. Чтобы найти векторное уравнение прямой, нам понадобится точку на прямой и ее направление. Так как линия параллельна 𝑦-ось, это вертикальная линия и имеет вектор направления (0,1). Следовательно, нам нужно найти точку на прямой. Эта точка будет точкой пересечения.

Мы можем написать строку с векторным уравнением ⃑𝑟=𝑘(−6,−4) как единица в декартовой форме. Для любых точек 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) в системе координат с вектор направления ⃑𝑑=(𝑎,𝑏), для любого скаляра 𝑘, (𝑥,𝑦)=(𝑥,𝑦)+𝑘(𝑎,𝑏).

Следовательно, взяв ⃑𝑟=(𝑥,𝑦), мы можем записать уравнение ⃑𝑟=𝑘(−6,−4) в параметрическом форма как 𝑥=−6𝑘,𝑦=−4𝑘.

Затем мы можем исключить 𝑘, переставив каждое уравнение выше, чтобы сделать 𝑘 предметом. Это дает нам 𝑥−6=𝑘,𝑦−4=𝑘.

Таким образом, мы можем положить левую часть каждого уравнения равной, например что −𝑥6=−𝑦4.

Перестановка, у нас есть 4𝑥=6𝑦4𝑥−6𝑦=02𝑥−3𝑦=0.

Далее строку −3𝑥+5𝑦=−5 можно переставить так: −3𝑥+5𝑦+5=0, и мы можем найти точку пересечения двух прямых в Декартова форма с использованием одновременного метода:

−3𝑥+5𝑦+5=0,2𝑥−3𝑦=0.

(3)(4)

Второе уравнение можно преобразовать так, чтобы 𝑥 предмет, следующим образом: 2𝑥=3𝑦𝑥=32𝑦.

Затем мы подставляем это значение в уравнение (3), чтобы получить −332𝑦+5𝑦+5=0−92𝑦+5𝑦+5=012𝑦+5=012𝑦=−5𝑦=−10.

Теперь мы можем подставить это значение 𝑦=−10 в 𝑥=32𝑦 дать 𝑥=32(-10)=-15.

Таким образом, точка пересечения двух прямых находится в точке (−15,−10).

Теперь у нас есть направление вектора, ⃑𝑑, в качестве единицы вектор (0,1) и положение вектор точки пересечения как (−15,−10).

Записав это уравнение в виде ⃑𝑟=⃑𝑟+𝑘⃑𝑑, где 𝑘 как любое скалярное кратное, мы имеем ⃑𝑟=(−15,−10)+𝑘(0,1).

В следующем примере мы будем использовать заданный угол, чтобы найти направление линия через пересечение двух других линий.

Пример 4. Нахождение уравнения прямой линии, проходящей через пересечение из двух других линий

Определите уравнение прямой, проходящей через точку пересечения две прямые, уравнения которых равны 5𝑥+2𝑦=0 и 3𝑥+7𝑦+13=0 при создании угол 135∘ с положительной 𝑦-осью.

Ответ

Напомним, что пересечение двух различных прямых — это точка, в которой они пересекаются. Нам дана информация об угле, который искомый линия проходит с положительной 𝑦-осью; однако мы будем также нужно найти точку на прямой, чтобы написать уравнение эта линия. Так как точка пересечения других прямых лежит на этой линии, то это будет идеальная точка для выбора.

Начнем с поиска пересечения линий 5𝑥+2𝑦=0 и 3𝑥+7𝑦+13=0. В точка пересечения, 𝑥- и 𝑦-значения в каждом уравнении будут равны. Мы можем найти эти значения, используя метод замещения.

Взять уравнение 5𝑥+2𝑦=0 и переставить так, чтобы получилось 𝑥 предмет, у нас есть 5𝑥=−2𝑦𝑥=−25𝑦.

Затем мы можем подставить 𝑥=−25𝑦 в уравнение 3𝑥+7𝑦+13=0 и переставить, чтобы получить 3−25𝑦+7𝑦+13=0−65𝑦+7𝑦+13=0295𝑦=−13𝑦=−6529.

Чтобы найти значение 𝑥, подставим 𝑦=−6529 в наше переставленное уравнение, 𝑥=−25𝑦. Это дает нам 𝑥=−25×−6529𝑥=2629.

Точка пересечения (𝑥,𝑦) может быть дается как 2629,−6529.

Нам нужно найти уравнение прямой, проходящей через эту точку 2629,−6529 при составлении угла 135∘ с положительная 𝑦-ось. Мы можем нарисовать линию с углом 135∘ к оси 𝑦. Поскольку угол положительный, измерение проводится против часовой стрелки.

Чтобы найти наклон линии, нам нужно вычислить положительный угол, который линия образует с положительной направление оси 𝑥. Мы можем использовать углы на прямой и соответствующие углы, полученные из параллельных линии и трансверсали.

Мы помним, что сумма углов на прямой равна 180∘. Следовательно, линия будет составлять угол 180−135=45∘∘∘ к положительной оси 𝑦, измеряется по часовой стрелке.

Следовательно, линия будет составлять угол 𝜃=90−45=45∘∘∘ с положительной 𝑥-осью, измеренной в направление против часовой стрелки.

Если линия образует угол 𝜃 с положительной 𝑥-ось, то ее наклон tan𝜃.

Наклон, 𝑚, 𝑚=45=1.tan∘

Мы можем использовать форму точки и наклона линии, чтобы написать уравнение этого линия. В таком виде уравнение прямой, проходящей через (𝑥,𝑦) с наклоном 𝑚 определяется выражением 𝑦−𝑦=𝑚(𝑥−𝑥).

Итак, прямая, проходящая через точку 2629,−6529, с наклоном 1, составляет 𝑦−−6529=1𝑥−2629𝑦+6529=𝑥−2629.

Добавление 2629 к обеим частям этого уравнения дает 𝑦+9129=𝑥.

Тогда, умножая члены на 29, мы имеем 29𝑦+91=29𝑥.

Записав это уравнение в виде 𝑎𝑥+𝑏𝑦+𝑐=0, вычтем 29𝑦 и 91 с обеих сторон уравнения, чтобы дать 29𝑥−29𝑦−91=0.

Теперь мы можем рассмотреть, как мы можем написать общее уравнение прямой линии проходящей через точку пересечения двух данных прямых.

Мы понимаем, что существует бесконечное число прямых линий, проходящих через через любую конкретную точку. Следовательно, мы можем определить уравнение, которое представляет все прямые, проходящие через точку пересечения двух линии следующим образом.

Определение: уравнение прямой линии, проходящей через точку пересечения двух заданных прямых

Уравнение, представляющее все прямые, проходящие через точку пересечения точка двух прямых 𝑎𝑥+𝑏𝑦+𝑐=0 и 𝑎𝑥+𝑏𝑦+𝑐=0 𝑚(𝑎𝑥+𝑏𝑦+𝑐)+𝑙(𝑎𝑥+𝑏𝑦+𝑐)=0, где 𝑚,𝑙∈ℝ.

Если 𝑚=0, имеем уравнение второй строки.

Если 𝑙=0, имеем уравнение первой строки.

При 𝑚≠0 и 𝑙≠0 имеем уравнение прямой проходящие через точку пересечения, исключая исходные линии. Следовательно, мы можем записать приведенное выше уравнение в виде 𝑎𝑥+𝑏𝑦+𝑐+𝑘(𝑎𝑥+𝑏𝑦+𝑐)=0, для любого 𝑘∈ℝ.

В следующем примере мы увидим, как мы можем применить это уравнение в алгебраический метод нахождения уравнения прямой, проходящей через данную точку и точка пересечения двух прямых.

Пример 5. Нахождение уравнения прямой, проходящей через пересечение Две другие прямые

Каково уравнение прямой, проходящей через 𝐴(−1,3) и пересечение строк 3𝑥−𝑦+5=0 и 5𝑥+2𝑦+3=0?

1. 23𝑥+17𝑦+17=0
2. 8𝑥+𝑦+8=0
3. 17𝑥−2𝑦+23=0

Ответ

Начнем с точки пересечения двух прямых. точку, где они пересекаются.

Мы можем написать общее уравнение прямой, проходящей через точка пересечения двух прямых 𝑎𝑥+𝑏𝑦+𝑐=0 и 𝑎𝑥+𝑏𝑦+𝑐=0 как 𝑎𝑥+𝑏𝑦+𝑐+𝑘(𝑎𝑥+𝑏𝑦+𝑐)=0, для любого 𝑘∈ℝ.

Подстановка значений 𝑎, 𝑏 и 𝑐 в качестве значений из строка 3𝑥−𝑦+5=0 и 𝑎, 𝑏 и 𝑐 значения из строки 5𝑥+2𝑦+3=0 имеем

3𝑥−𝑦+5+𝑘(5𝑥+2𝑦+3)=0.

(5)

Поскольку прямая проходит через точку с координатами (−1,3), мы можем подставить 𝑥=−1 и 𝑦=3 в уравнение (5) выше. Это дает нам 3(−1)−3+5+𝑘[5(−1)+2(3)+3]=0−1+4𝑘=04𝑘=1𝑘=14.

Теперь мы можем подставить 𝑘=14 в уравнение (5). Это дает нам 3𝑥−𝑦+5+14(5𝑥+2𝑦+3)=03𝑥−𝑦+5+54𝑥+24𝑦+34=0174𝑥−24𝑦+234=017𝑥−2𝑦+23=0.

Следовательно, уравнение прямой, проходящей через 𝐴(−1,3) и пересечение прямых 3𝑥−𝑦+5=0 и 5𝑥+2𝑦+3=0 17𝑥−2𝑦+23=0.

В качестве альтернативного метода мы можем найти уравнение прямой, используя два отдельные точки на линии. Поэтому используем точку пересечения и точку 𝐴, чтобы найти уравнение прямой.

Мы можем найти пересечение 3𝑥−𝑦+5=0 и 5𝑥+2𝑦+3=0 при одновременном решении уравнений используя метод исключения. Использование метода исключения. Мы можем пронумеровать наши уравнения как

3𝑥−𝑦+5=0,5𝑥+2𝑦+3=0.

(6)(7)

Чтобы исключить 𝑥- или 𝑦-переменные, их абсолютные значения должны быть одинаковыми в оба уравнения. Заметим, что мы можем умножить уравнение (6) на 2, чтобы иметь одинаковое абсолютное значение 2𝑦 в каждом уравнении. Таким образом, у нас есть

6𝑥−2𝑦+10=0,5𝑥+2𝑦+3=0.

(8)(9)

Затем мы исключаем 𝑦, добавляя два уравнения (8) и (9): 6𝑥−2𝑦+10=0+5𝑥+2𝑦+3=011𝑥+13=0

Затем переставляем 11𝑥+13=0, вычитая 13 с обеих сторон уравнение, а затем деление на 11 дает нам 11𝑥=−13𝑥=−1311.

Теперь мы нашли 𝑥-координату точки пересечение, поэтому подставляя это в любое из уравнений (6) или (7) позволит нам найти 𝑦-координату. Замена 𝑥=−1311 в уравнение (6), и, упрощая, имеем 3−1311−𝑦+5=0−3911−𝑦+5=01611−𝑦=0𝑦=1611.

Это дает нам точку пересечения −1311,1611.

Теперь нам нужно найти уравнение прямой, проходящей через точки 𝐴(−1,3) и −1311,1611.

Напомним, что строка, содержащая координату (𝑥,𝑦), с наклоном 𝑚, задается в форме точка–наклон как 𝑦−𝑦=𝑚(𝑥−𝑥). 

Чтобы использовать эту форму, нам нужно вычислить наклон 𝑚 линия, соединяющая две точки (𝑥,𝑦) и (𝑥,𝑦), который задается формулой 𝑚=𝑦−𝑦𝑥−𝑥.

Мы можем обозначить −1311,1611 как (𝑥,𝑦) и (−1,3) как (𝑥,𝑦). Подставляя их, мы имеем 𝑚=3−−1−=3−−1+=−+==172. 

Теперь у нас есть наклон линии, равный 172, вместе с двумя точками которые лежат на линии. Нам нужна только одна из этих точек, чтобы иметь возможность использовать форма уравнения точка-наклон рядом с наклоном.

Таким образом, подставляя 𝐴(−1,3) вместо точки (𝑥,𝑦) и наклон 𝑚=172 в уравнение 𝑦−𝑦=𝑚(𝑥−𝑥), имеем 𝑦−3=172(𝑥−(−1))𝑦−3=172(𝑥+1).

Распределение 172 по скобкам справа, а затем добавление 3 к обеим частям уравнения дает нам 𝑦−3=172𝑥+172𝑦=172𝑥+232.

Это верное уравнение для линии. Однако мы также можем записать это в общий вид уравнения прямой, 𝑎𝑥+𝑏𝑦+𝑐=0, где 𝑎,𝑏,𝑐∈ℝи.

Мы умножаем все члены на 2, а затем вычитаем 2𝑦 из обе части уравнения, что дает 2𝑦=17𝑥+230=17𝑥−2𝑦+23.

Это подтверждает ответ, который мы нашли с помощью первого метода; уравнение линия 17𝑥−2𝑦+23=0.

Теперь мы можем суммировать ключевые моменты.

Ключевые точки

• Точка пересечения двух отдельных линий — это точка, где они встречаются или пересекаются. Это упорядоченная пара значений 𝑥 и 𝑦, где линии пересекаются на графике и что удовлетворяет уравнениям обеих прямых.
• Отдельные параллельные линии — это линии на плоскости, которые всегда одинаковы расстояние друг от друга. У них не будет точек пересечения.
• Мы можем найти пересечение двух линий либо графически, либо алгебраически. Алгебраические решения всегда дадут точный результат.
• Чтобы найти точку пересечения двух непараллельных прямых, алгебраически решим систему двух уравнений.

  No related posts.