Найти точку касания прямой и графика функции: Точка касания прямой параллельно заданной — задание. Алгебра, 10 класс.

Уравнение касательной. Условие касания. | Методическая разработка по алгебре (10 класс) на тему:

Урок по алгебре и началам математического анализа

 в 10 классе (физ-мат.)

Тема: «Уравнение касательной. Условие касания».

Тип урока: урок применения знаний, умений и навыков при  решении проблемы.

Цель урока: Закрепить ранее полученные знания,  научиться самостоятельно решать более сложные задачи и на основе их  анализа делать выводы.

 Образовательные:
                  -закрепить знания и   навыки по теме «Уравнение касательной»;

-сформировать умения учащихся решать более сложные задачи;

-подготовить учащихся к самостоятельной деятельности.

Развивающие:

— способствовать развитию мыслительных операций: анализ, аналогия, сравнение, обобщение, внимание, монологической и диалогической речи;

— способствовать развитию у учащихся поиска и распознавания полезной информации ( на основе наблюдения и оценки выявленных закономерностей).

Воспитательные:

             — содействовать воспитанию активной личности,

              способной  самостоятельно  делать обобщения и вывод.

Структура урока:

1. Организационно-мотивационный момент.
2. Актуализация ЗУН.
3. Углубление ЗУН на примерах более сложных задач.

4. Обобщение, вывод, рефлексия.

5. Домашнее задание, подведение итогов.

№	Этап урока	Действия учителя	Действия ученика	Результат
1.	Организационно мотивационный	Установка на сотрудничество с учащимися и успех в предстоящей работе, постановка  цели и проблемы	Слушают и оценивают предложение учителя, определяют смысл  проблемы	Повышение самооценки, включение в работу
2.	Актуализация ЗУН	Предлагает вспомнить знания и умения, которыми уже владеют дети, по этой теме, корректирует допущенные ошибки	Вспоминают, сравнивают, аргументируют, обобщают те знания, которые уже имеют	Самооценка  и взаимопроверка имеющихся знаний, ликвидация пробелов
3.	Углубление материала по теме	Организует  индивидуальную и фронтальную работу, предлагает участие в обсуждении и  анализе. Помогает увидеть проблему в конкретном задании, оценивает и корректирует выполняемые учащимися задачи, помогает обобщить полученные результаты	Применяют к составлению уравнений касательных условия параллельности и перпендикулярности. На основе задач с параметром видят решение поставленной проблемы	Поиск и выделение необходимой информации на основе наблюдения и оценки
4.	Обобщение, вывод, рефлексия	Помогает обобщить весь материал, помогает увидеть  самое важное для решения проблемы	Обобщают, систематизируют, формулируют решение проблемы на основе полученных знаний, делают вывод	Составлено условие касания прямой и графика функции, сделан вывод
5.	Домашнее задание, подведение итогов	Комментирует и объясняет домашнее задание, помогает подвести итог, оценивает	Записывают и оценивают, подводят итог	№ 43.56(а) № 43.58(а) № 43.62(а)

Ход урока:

На прошлом уроке мы с вами вывели уравнение касательной и научились решать некоторые виды задач на составление уравнения касательной.

Давайте ещё раз повторим:

Согласны ли вы с утверждением, что «Касательная – это прямая, имеющая с данной кривой одну общую точку?»  (слайд 3,4)

• Что же такое касательная? (слайд 5,6)
• Какова связь между производной в точке касания и уравнением касательной? ( слайд 7,8,9,10)
• Назовите уравнение касательной  (слайд 11)
• Как мы его получили?

Решение  задач на повторение :

Цель: повторить алгоритм решения задач на составление уравнения касательной, выявить пробелы у учащихся и их  ликвидировать.

Слайд 12 – устно проговорить алгоритм решения, проговорить сходства и различия в решении задач разных видов.

 Решение по вариантам:

Задача №1.

Написать уравнения всех касательных к графику функции f(x)=x2+4x+6, проходящих через точку М(-3;-1).

Ответ:  y=-6x–19,     y=2x+5.

Ответ:  y=-6x–19,     y=

Задача №2.

Правильно ли составлено уравнение касательной к графику функции         f(x)=x3-3×2+1, если угловой коэффициент касательной k = -3. y= -3x+7.

Правильный ответ: y= -3x+2

Как расположены графики таких прямых y= -3x+7, y= -3x+2.

Делаем вывод, что у параллельных прямых коэффициенты равны, а если прямые перпендикулярны?

Слайд 15

Углубление материала:

Цель: вспомнить условия параллельности и перпендикулярности прямых и применить их при  составлении уравнений касательных; в задачах с параметром выяснить необходимые и достаточные условия для существования касательной к графику функции.

Задача №3.

Составьте уравнение касательной к графику функции y = x3-x2-x+1, которая параллельна прямой y=2x-1.

Задача №4.

Составьте уравнение касательной к графику функции y=x2+4x+1, перпендикулярной прямой y= -1/4x+8.

Ответ: y = 4x+1

Задача №5.

При каких значениях а прямая y=3x-2 является касательной к графику функции y = x2+ax+2?

Ответ: a=-1, a=7.

Задача №6.

При каких значениях b прямая y =3x +b является  касательной к графику функции y = ?

Ответ: b = .

Вывод, рефлексия:

Цель: решить поставленную проблему ,  сформулировать условие касания прямой к графику функции и сделать вывод.

Для того, чтобы прямая y = kx+b была касательной к графику функции y = f(x), необходимо и достаточно существование хотя бы одного числа x0(одной точки касания), для которой выполняется система

Способы написания уравнения касательной:

1. Находим общие точки графиков, т.е. решение уравнения f(x) = kx+b, а затем для каждого из его решений вычислить f’(x0). Там где f’(x0) = k  , имеет место касание, а в других пересечение.
2. Находим корни уравнения f’(x0) = k и для каждого из них проверим, выполняется ли равенство f(x0) = kx0 + b. При его выполнении получаются абсциссы точек касания.

Вывод:

 Если в точке x0 существует производная, то в точке с этой абсциссой есть касательная к графику функции y = f(x)   и наоборот,  если в точке x0  нет производной функции y =f(x), то в точке с этой абсциссой нет касательной к графику функции y =f(x) с  угловым коэффициентом k=f’(x0).

Касательная к графику функции задается уравнением. Касательная к графику функции в точке

Инструкция

Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).

Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.

Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате. Определите значение функции f(a), подставив в уравнение функции величину абсциссы.

Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».

Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.

Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.

Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.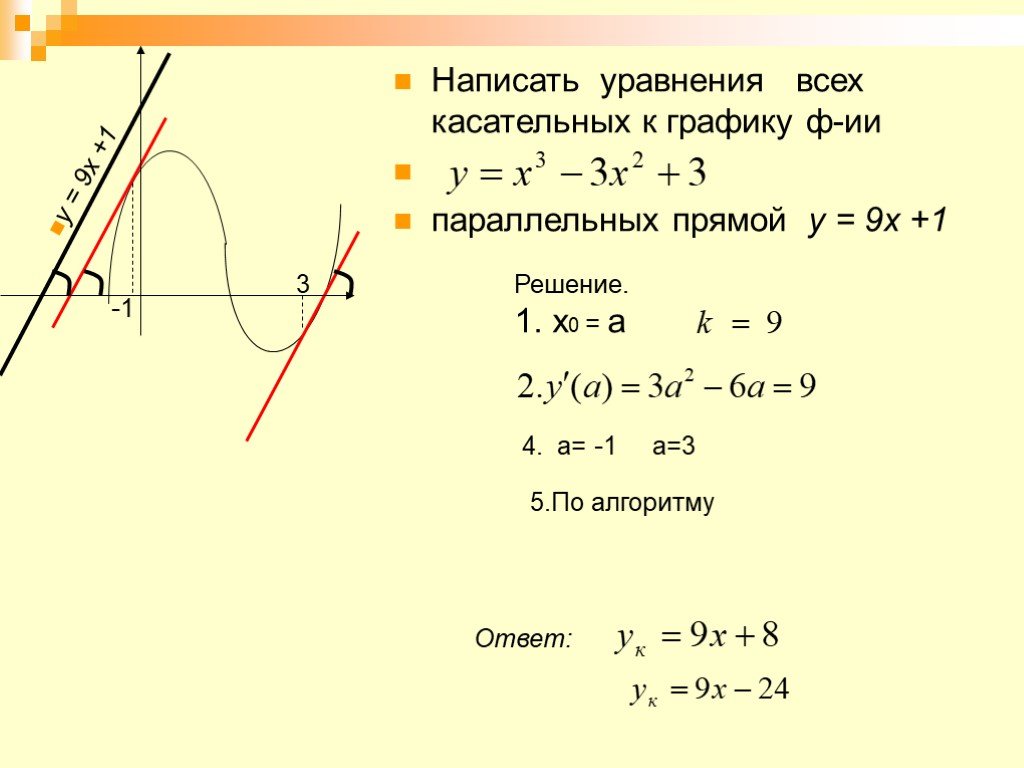

2+5x-7 в произвольной точке x_0 равен y»(x_0). Но y»=-2x+5, значит, y»(x_0)=-2x_0+5. Угловой коэффициент прямой y=-3x+4, указанной в условии, равен -3. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что =-2x_0 +5=-3.

Получаем: x_0 = 4.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 7
Тема: Геометрический смысл производной. Касательная к графику функции

Условие

Показать решение

Решение

По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через \alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \pi -\alpha, который является тупым.

Как известно, tg(\pi -\alpha) и будет значением производной функции f(x) в точке x_0.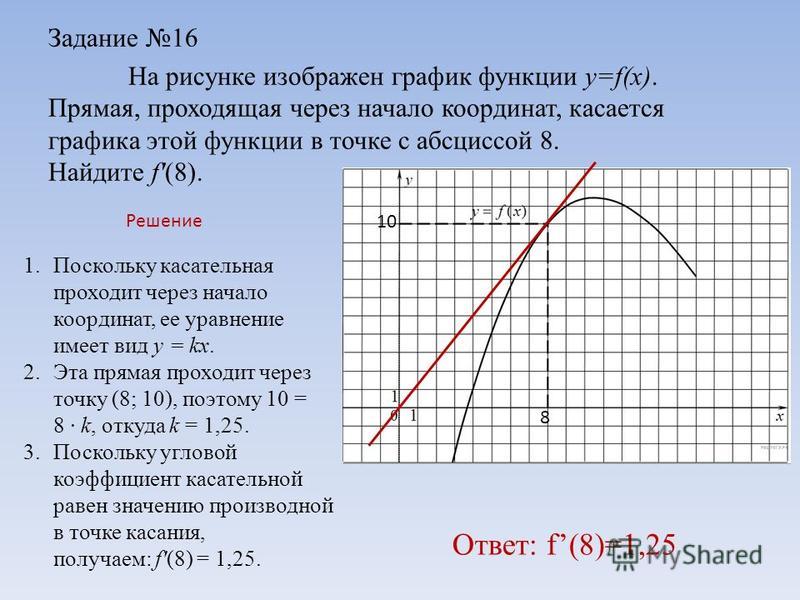

2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1, тогда b=-2-32x_0=-34.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 7
Тема: Геометрический смысл производной. Касательная к графику функции

Условие

На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых касательная к графику функции параллельна прямой y=6.

Показать решение

Решение

Прямая y=6 параллельна оси Ox . Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 4 .

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С.

2-4x+9 в произвольной точке x_0 равен y»(x_0). Но y»=2x-4, значит, y»(x_0)=2x_0-4. Угловой коэффициент касательной y=4x-7, указанной в условии, равен 4 . Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что 2x_0-4=4. Получаем: x_0=4.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 7
Тема: Геометрический смысл производной. Касательная к графику функции

Условие

На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.

Показать решение

Решение

По рисунку определяем, что касательная проходит через точки A(1; 1) и B(5; 4). Обозначим через C(5; 1) точку пересечения прямых x=5 и y=1, а через \alpha угол BAC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол \alpha.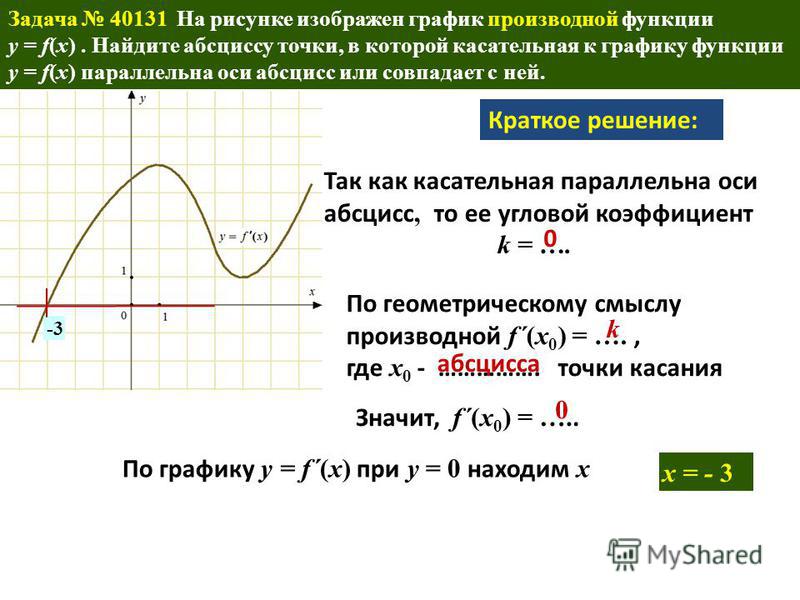

Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0). Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.

А что будет, если производная в точке x 0 не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример — функция y = |x | в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b , где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x 0 , достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x 0) · (x − x 0) + f (x 0)

Здесь f ’(x 0) — значение производной в точке x 0 , а f (x 0) — значение самой функции.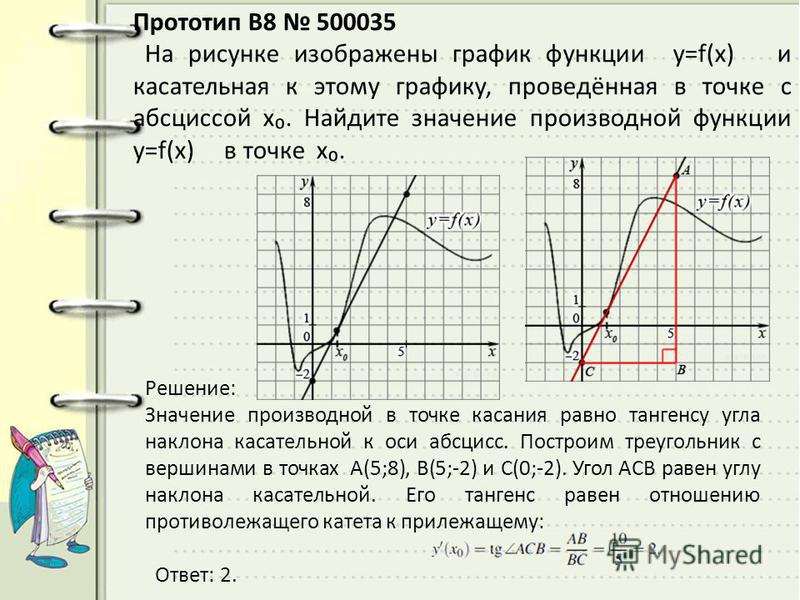

Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.

Уравнение касательной: y = f ’(x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ’(x 0) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x 0) = f (2) = 2 3 = 8;
Теперь найдем производную: f ’(x ) = (x 3)’ = 3x 2 ;
Подставляем в производную x 0 = 2: f ’(x 0) = f ’(2) = 3 · 2 2 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x ) = (2sin x + 5)’ = 2cos x ;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Уравнение касательной:

y = 0 · (x − π /2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.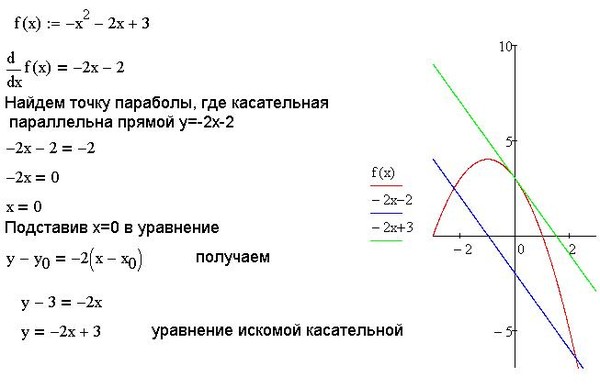 к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.

Касательная — это прямая , которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой .

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

y = kx + b .

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

y — y 0 = k (x — x 0 ) .

Значение производной f «(x 0 ) функции y = f (x ) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f (x 0 ) .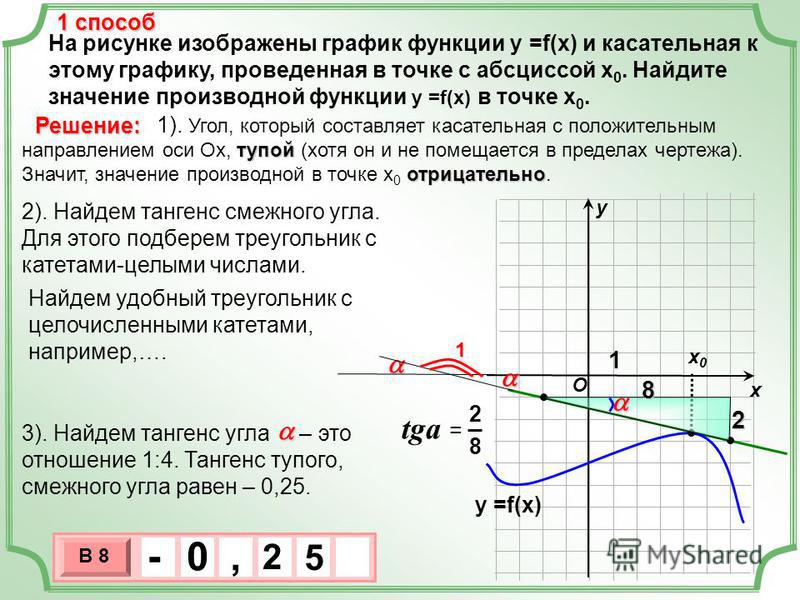 В этом состоит геометрический смысл производной

.

Таким образом, можем заменить k на f «(x 0 ) и получить следующее уравнение касательной к графику функции :

y — y 0 = f «(x 0 )(x — x 0 ) .

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде . Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали :

(x — x 0 ) + f «(x 0 )(y — y 0 ) = 0

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение.

Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Найдём производную функции:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.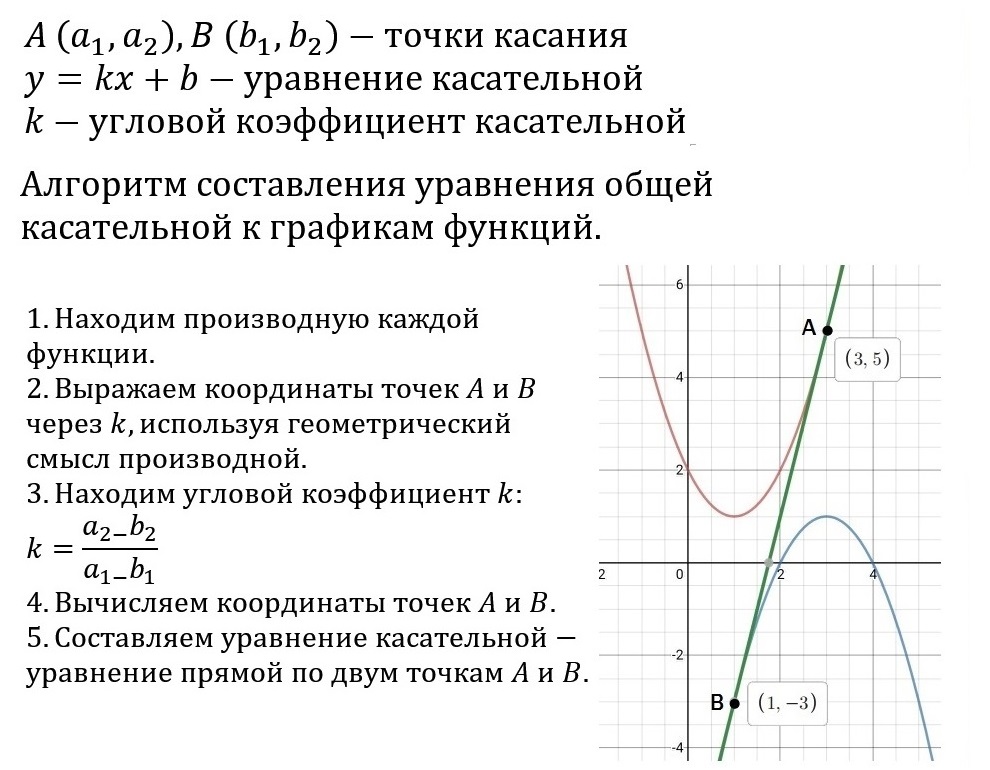

Пример 2.

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса (2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции. 2 Результатом будет значение {x}, которое можно подставить в уравнение прямой, чтобы найти значение {y}. Или; подставив уравнение линии в уравнение окружности, чтобы найти значение {x}, а затем снова подставив это значение в уравнение линии, чтобы найти значение {y}. Надеюсь, это поможет. 92 И прямые линии у=мх+с С ними вы можете просто подставить второе уравнение в первое, заменив все y на mx+c. После упрощения вы должны получить квадратное выражение, и его решение даст вам координату x. Используя это, вы подключаете его обратно к y=mx+c, чтобы получить координату y. Есть и другие способы сделать это, которые требуют различных фрагментов информации. Если подскажете, что дано в вопросе, то могу подсказать более подходящий способ

Awais Naveed

Ответим по очереди на каждую из этих частей: Во-первых, как найти касательную кривой. Большинство кривых, которые вы увидите на экзаменах GCSE и A-Level, представляют собой многочлены. Чтобы получить касательную линию в стандартной форме y=mx+c (где m — градиент, а c — точка пересечения с осью y), нам сначала нужно найти градиент. Мы можем либо дифференцировать кривую (по сути, вы рассчитываете коэффициент каждого члена со степенью x и отнимаете единицу от степени) и подставляете точку касания в уравнение, либо вы можете провести касательную линию от точки и вычислить градиент с использованием 2 точек на линии. Градиент — это разница координат y/разность координат x. Затем, чтобы вычислить точку пересечения y, мы можем заменить точку касания в уравнении y=mx+c вашим недавно рассчитанным градиентом m. Теперь вычисляем касательные к окружности. Уравнение касательной к окружности: y-b=m(x-a). Мы можем использовать описанные выше методы для вычисления градиента, а (a,b) является центром круга. Надеюсь, это поможет. 92 = 0 следуйте инструкциям выше + используйте квадратные формулы для завершения.

Ник Грей

точка соприкосновения = точки пересечения чтобы найти это, вы можете приравнять оба уравнения окружности и касательной затем переставьте, чтобы найти значение x, и подставьте, чтобы найти значения y вы можете сделать это, например, с помощью одновременных уравнений.

Fowzi Begum

Найдите градиент линии от центра круга до нужной точки на круге, затем используйте его, чтобы найти градиент касательной. Наконец, используйте y=mx+c с этим градиентом и точкой на окружности, которой он касается.

Talha Ghannam

•

Математика

Вопрос от Дарианы

Переставьте b+g, чтобы g стало предметом или формулой

Математика

Вопрос от неизвестного Затем он летит по азимуту 300 °, пока не окажется точно к северу от своего начального положения. На каком расстоянии от исходного положения находится самолет?

Математика

Вопрос задан 19THAVR

Найдите целое число x, удовлетворяющее обоим неравенствам x+4>5 и 3x-4<5

Нужна помощь по математике?

Получение квалифицированной помощи от репетитора — отличный способ улучшить свои оценки по математике.

интегрирование — Как найти уравнение функции $f$, имеющее конкретную касательную к графику этой функции в определенной точке?

спросил 2 года, 6 месяцев назад

Изменено 2 года, 6 месяцев назад

Просмотрено 161 раз

$\begingroup$

как найти уравнение функции $f$, которая имеет конкретную касательную к графику этой функции, например: уравнение касательной к функции $f$ может быть $y=\frac{1}{2}−\ дробь{3x}{2}$; и есть точка, которая лежит и на графике $f$, и на графике этой касательной, т.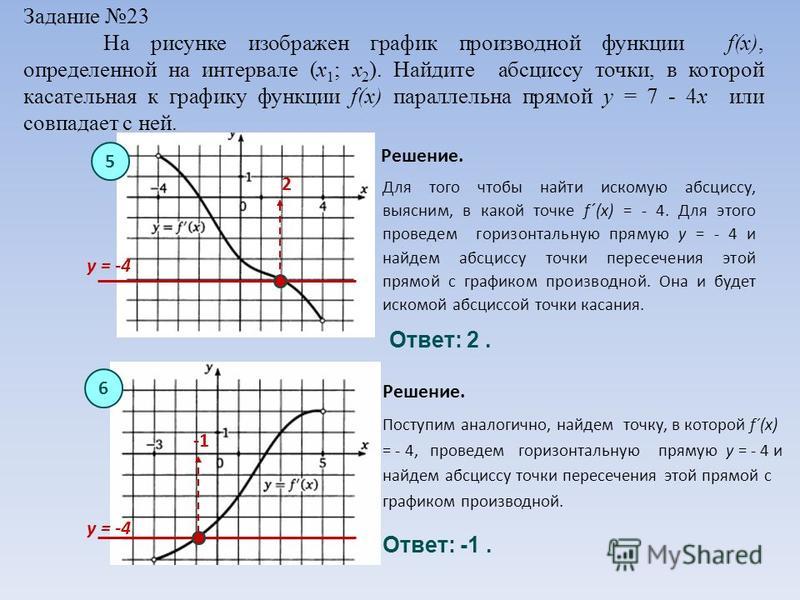 е.: $\exists (1,−1) \in y \wedge \exists (1, -1) \in f$ | $y$ является касательной к нелинейной $f$ в точке $(1, -1)$, где $y=\frac{1}{2}−\frac{3x}{2}$. Как найти уравнение $f$?

Другой пример может выглядеть так: пример Мы ищем уравнение пурпурной функции; красная линия — это касательная функция фиолетового цвета, а точка, в которой они встречаются, — это конкретная точка.

• интегрирование
• функции
• производные
• графические функции
• касательная

$\endgroup$

2

$\begingroup$ 92 г(х) $$ для некоторой функции $g(x)$.

Обратите внимание, что $g(x)$ может быть любой функцией, которая не разрушается при $x = h$. Могут быть и другие ограничения, но это технические детали, в которые, вероятно, не стоит вдаваться.

$\endgroup$

3

$\begingroup$

Касательная — это прямая, имеющая степень 1.