Неравенства линейные примеры 9 класс: Линейные неравенства, примеры решения, урок в 9 классе, презентация

Содержание

Решение линейных и квадратных неравенств 9 класс онлайн-подготовка на Ростелеком Лицей

Определение линейного неравенства

Линейные неравенства – это неравенства вида и они решаются двумя способами: эквивалентными преобразованиями либо с помощью графика функции. Рассмотрим второй способ на примерах:

Решение линейного неравенства графическим способом

1. Решить неравенство

Построим график функции. Графиком является прямая, она пересекает ось oy в точке 1, ось ox в т. Корень функции разбивает ось ox на два различных промежутка. На первом промежутке функция отрицательна, на втором – положительна.

Этого достаточно, чтобы решить линейное неравенство.

Ответ:

Линейные неравенства эффективно решаются путем выбора интервалов, на которых функция сохраняет знак, т.е. до корня и после корня. Решением линейного неравенства, как правило, является луч.

Решение квадратного неравенства графическим способом

Рассмотрим квадратное неравенство

Оно решается с помощью свойств квадратичной функции

Рассмотрим на примере.

2. Решить неравенство

Рассмотрим функцию Построим ее график, для этого вначале найдем корни. По теореме Виета

Схематически изобразим параболу и определим интервалы знакопостоянства и знаки на них. Ветви параболы направлены вверх.

Вне интервала корней функция положительна, внутри интервала корней – отрицательна.

Ответ:

Рассмотрим квадратичную функцию и её свойства в общем виде.

Квадратичная функция в общем виде, D>0

Функция имеет вид

значит, корни квадратного трехчлена различны,

Графиком квадратичной функции является парабола, пересекающая ось ox в точках с абсциссами

ветви параболы направлены вверх.

Вне интервала корней функция имеет положительный знак, внутри интервала корней – отрицательный.

Что можно сказать о функции, если Прежде всего, что она разлагается на линейные множители:

Также для нее справедлива теорема Виета:

Найдем координаты вершины параболы.

Для квадратичной функции есть два возможных варианта неравенств:

Множество значений функции – луч от в положительном направлении. Точка пересечения с осью oy – т..

Квадратичная функция в общем виде, D=0

Как и в предыдущем случае, многочлен раскладывается на множители.

График функции – парабола, ветви направлены вверх.

Парабола касается оси ox в одной точке, которая и является вершиной параболы.

Рассмотрим возможные варианты неравенств:

Множество значений функции:

График функции пересекается с осью oy в т.

Квадратичная функция в общем виде, D<0

Рассмотрим функцию

означает, что уравнение не имеет корней, трехчлен нельзя разложить на множители и не выполняется теорема Виета.

Найдем координаты вершины:

Схематически изобразим график – параболу, ветви направлены вверх.

В этом случае часто допускается стандартная ошибка – нет корней, значит, нет решений. Корней нет у квадратного уравнения, а решением неравенства является любое действительное число.

Множество значений функции

Для более глубокого рассмотрения рекомендуется самостоятельно изучить случаи, когда

Необходимо построить графики и расписать решения стандартных неравенств самостоятельно.

Решение задач

Мы подробно рассмотрели свойства квадратичной функции, которые лежат в основе решения задач.

Рассмотрим примеры.

1. Найти область определения функции.

Область определения функции задается неравенством т.к. трехчлен находится под корнем и в знаменателе.

Умножим обе части неравенства на .

Рассмотрим функцию найдем ее корни.

По теореме Виета

Изобразим график функции. Точки -2 и 1 выколотые, т.к. неравенство строгое.

Поставленному условию удовлетворяет промежуток внутри интервала корней.

Ответ:

Мы увидели на примере, что многие задачи сводятся к решению квадратного уравнения.

Решение неравенства с параметром

2. При каких значениях p данное уравнение имеет

два различных корня?

один корень?

не имеет корней?

Если p принимает конкретное значение, мы имеем конкретный квадратный трехчлен с конкретным значением дискриминанта,

Найдем дискриминант.

Рассмотрим функцию

Найдем корни по теореме Виета.

Рассмотрим ось p и график функции Графиком является парабола, ветви направлены вверх.

Функция сохраняет положительный знак вне интервала корней, отрицательный знак – внутри интервала.

Ответ: Уравнение имеет

1. два различных корня, когда

2. один корень, когда

3. не имеет корней, когда

19. Заключение

Мы рассмотрели решение линейных и квадратичных неравенств, некоторые свойства квадратичной функции, которые используются при решении квадратных неравенств.

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованные ссылки на интернет-ресурсы

1. Портал Естественных Наук (Источник).

2. Центр образования «Технология обучения» (Источник).

3. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).

4. Виртуальный репетитор (Источник).

5. Раздел College.ru по математике (Источник).

Рекомендованное домашнее задание

1.Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.№№ 8; 9; 15.

Линейные и квадратные неравенства. 9 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Рациональные неравенства
Алгебра 9 класс
Неравенства
Неравенства
линейные
квадратные
рациональные
Линейные неравенства
Линейным неравенством с одной
переменной х называется неравенство
вида ах + b > 0, ах + b<0 где а≠0.
Решение неравенства – значение

переменной х, которое обращает
неравенство в верное числовое
неравенство.
Множество частных решений
называют общим решением.
Пример 1: Являются ли числа 3, -5 решением
данного неравенства 4х + 5 < 0.
При х = 3, 4∙3+5=17, 17>0
Значит х=3 не является решением
данного неравенства.

При х=-5, 4∙(-5)=-15, -15<0
Значит х=-5 является решением
данного неравенства.
Два неравенства f(х)<g(х) и r(х)<s(х) называют
равносильными, если они имеют одинаковые
решения.
Правила
(преобразования неравенств, приводящие к
равносильным неравенствам):
1. Любой член неравенства можно перенести из одной
части неравенства в другую с противоположным
знаком (не меняя при этом знака неравенства)
Например: 3х + 5 < 7х
3х + 5 -7х < 0
2: а) обе части неравенства можно умножить

или разделить на одно и то же положительное
число, не меняя при этом знака неравенства.
б) если обе части неравенства умножить или
разделить на одно и то же выражение,
положительное при любых значениях
переменной, и сохранить знак неравенства, то
получится неравенство, равносильное данному.
Например: а)8х – 12 > 4х2 ( :4)
2х – 3 > х2
б)(2х + 1)(х2 + 2) < 0 ( ( х2 + 2))
(2х + 1) < 0
3.а) Обе части неравенства можно умножить или
разделить на одно и то же отрицательное число,
изменив при этом знак неравенства на
противоположный ( < на >, > на <).

б) если обе части неравенства умножить или
разделить на одно и то же выражение,
отрицательное при всех значениях переменной, и
изменить знак исходного неравенства на
противоположный, то получится неравенство,
равносильное данному.
Например: а) — 6х3 + 3х – 15 < 0
2х3 – х + 5 > 0
б) (3х – 4 )(-х2 – 2) > 0
3х – 4 < 0
(: (-3))
(: (-х2 – 2))
Решите неравенство:
5х + 3(2х – 1)>13х — 1
Решение: 5х + 6х – 3 >13х – 1
5х + 6х – 13х > 3 – 1
-2х > 2 (: (-2))
х < -1
-1
\\\\\\\\\\\\\\\\\
Ответ: х < -1 или (-∞; -1)
Квадратные неравенства
Неравенства вида
ах2 + bх + с > 0, где а ≠ 0, а,b,с некоторые числа, называются
квадратными.
Методы решения
графический
интервалов
Квадратные неравенства
Для каждой из функций, графики которых
изображены, определите знаки a и Д
а) а<0, Д >0;
Б)а >0, Д >0;
В)а >0, Д < 0;
г)а < 0, Д < 0;
д)а > 0, Д =0;
Найдите значения x, при которых у>0, y<0.

А) y<0 при любом х (х є R)

Б) y<0 при х≠-1
В) у>0 при х <0 и при х>1, y<0 при 0 < х <1
Г) у< 0 при х <-1 и при х>0, y> 0 при -1 < х<0
д) y> 0 при любом х (х є R)
Расположение графика квадратичной у=aх2+bx+c
относительно оси абсцисс в зависимости от функции
дискриминанта и коэффициента а
D>0
D=0
D<0
а>0
x
x
x
а <0
x
x
x
Построим график функции
Рассмотрим график функции y=x²+x-6 1
1
, y0 6
1. Координат вершины параболы x0
2
4
2. Нули функции x1 3, x2 2
y
y=0 при х=-3 и х=2, т.к.
при х= -3 и х= 2
x²+x-6=0.
3. у<0 при -3 < х < 2, т.к.
при -3 < х < 2 x²+x-6 <0.
у>0 при х< — 3 и х> 2
при х< — 3 и х> 2 x²+x-6 >0.
определение
-3
2 x
Неравенства вида ax²+bx+c ≥ 0 ,
ax²+bx+c > 0 или ax²+bx+c ≤ 0,
ax²+bx+c < 0 , где а≠0, называют
квадратными неравенствами
2 + bx +c
Рассмотреть
функцию
у=ах
Алгоритм решения квадратного неравенства
Найти нули функции (решить уравнение
ах2 + bx +c=0)
2.

Определить направление ветвей параболы
1.
3.
4.
Схематично построить график функции.
Учитывая знак неравенства, выписать ответ.
Решить неравенство
2х² -7х+5 < 0
1. 2х² -7х+5=0
D=(-7)²-4*2*5=9
x1 1, x2 2.5
2. а>0,
ветви параболы
направлены вверх
Ответ: ( 1; 2,5)
1
2.
5
x
Решите неравенство
а) x² -2x -3 >0
Ответ:(-∞ ; -1 ) U ( 3 +∞)
б) x² -2x -3 ≥ 0
Ответ:(-∞ ; -1 ] U [ 3 +∞)
в) x² -2x -3 < 0
Ответ:( -1; 3 )
г) x² -2x -3 ≤ 0
Ответ:[ -1; 3 ]
1
3
х
Решить неравенство
— 4x²+2х≥0
4x²-2х ≤ 0
1. 2х(2х -1) =0
Х1 =0
х2 =0,5
2. а <0
Ветви направлены
вниз
Ответ:[ 0 ; 0,5 ]

0
0,5
Решить неравенство
1. х² +4≥0
х² +4 =0
х² = -4, корней нет.
а>0, ветви параболы
направлены вверх
Ответ:(-∞ ; +∞)
2) х² +4 < 0
Ответ: {Ǿ}
Решить неравенство
а) ( x 2) 2 0
( x 2) 0, x 2
2
а <0, ветви направлены вниз
Ответ: Х =2
б) ( x 2) 2 0
Ответ: {Ǿ}
в) ( x 2) 2 0
Ответ: х≠2
г) ( x 2) 2 0
Ответ:(-∞ ; +∞).

2
Домашнее задание:
П. 6, 7. Теория и контрольные вопросы.
Разобрать и законспектировать примеры
данного пункта.
№ 95, 99.

English Русский Правила

Алгебра. Урок 8. Неравенства, системы неравенств.

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Линейные неравенства

Таблица числовых промежутков
Алгоритм решения линейного неравенства
Примеры решения линейных неравенств

Квадратные неравенства

Алгоритм решения квадратного неравенства
Примеры решения квадратных неравенств

Дробно рациональные неравенства

Алгоритм решения дробно рационального неравенства
Примеры решения дробно рациональных неравенств

Системы неравенств

Алгоритм решения системы неравенств
Примеры решения систем неравенств

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

> больше,

≥ больше или равно,

< меньше,

≤ меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

ax<bax≤bax>bax≥b

где a и b – любые числа, причем a≠0,x – переменная.

Примеры линейных неравенств:

3x<5x−2≥07−5x<1x≤0

Решить линейное неравенство – получить выражение вида:

x<cx≤cx>cx≥c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Если знак неравенства строгий >,<, точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Если знак неравенства нестрогий ≥,≤, точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.

Смысл жирной точки в том, что сама точка входит в ответ.

Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

Неравенство	Графическое решение	Форма записи ответа
x<c		x∈(−∞;c)
x≤c		x∈(−∞;c]
x>c		x∈(c;+∞)
x≥c		x∈[c;+∞)

Алгоритм решения линейного неравенства

Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:

ax<bax≤bax>bax≥b

Пусть получилось неравенство вида ax≤b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.

Если a>0 то неравенство приобретает вид x≤ba.

Если a<0, то знак неравенства меняется на противоположный, неравенство приобретает вид x≥ba.

Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.

Примеры решения линейных неравенств:

№1. Решить неравенство 3(2−x)>18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6−3x>18

−3x>18−6−3x>12|÷(−3)

Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как −3<0, знак неравенства поменяется на противоположный. x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x∈(−∞;−4)

№2. Решить неравество 6x+4≥3(x+1)−14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6x+4≥3x+3−14

6x−3x≥3−14−4

3x≥−15 | ÷3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3>0, знак неравенства после деления меняться не будет.

x≥−153⇒x≥−5 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x∈[−5; +∞)

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

Примеры:

№1. Решить неравенство 6x−1≤2(3x−0,5).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6x−1≤6x−1

6x−6x≤−1+1

0≤0

Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.

Ответ:

x – любое число
x∈(−∞;+∞)
x∈ℝ

№2. Решить неравенство x+3(2−3x)>−4(2x−12).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x+6−9x>−8x+48

−8x+8x>48−6

0>42

Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.

Ответ: x∈∅

Квадратные неравенства

Квадратные неравенства – это неравенства вида: ax2+bx+c>0ax2+bx+c≥0ax2+bx+c<0ax2+bx+c≤0 где a, b, c — некоторые числа, причем a≠0,x — переменная.

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Решить уравнение ax2+bx+c=0 и найти корни x1 и x2.

Отметить на числовой прямой корни трехчлена.

Если знак неравенства строгий >,<, точки будут выколотые.

Если знак неравенства нестрогий ≥,≤, точки будут жирные (заштрихованный).

Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение ax2+bx+c вместо x.

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Выбрать подходящие интервалы (или интервал).

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.

Записать ответ.

Примеры решения квадратных неравенств:

№1. Решить неравенство x2≥x+12.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

x2≥x+12

x2−x−12≥0

x2−x−12=0

a=1,b=−1,c=−12

D=b2−4ac=(−1)2−4⋅1⋅(−12)=1+48=49

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−1)±492⋅1=1±72=[1+72=82=41−72=−62=−3

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:

x2−x−1=62−6−1=29>0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪.

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ: x∈(−∞;−3]∪[4;+∞)

№2. Решить неравенство −3x−2≥x2.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

−3x−2≥x2

−x2−3x−2≥0

−x2−3x−2=0

a=−1,b=−3,c=−2

D=b2−4ac=(−3)2−4⋅(−1)⋅(−2)=9−8=1

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−3)±12⋅(−1)=3±1−2=[3+1−2=4−2=−23−1−2=2−2=−1

x1=−2,x2=−1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:

−x2−3x−2=−(0)2−3⋅0−2=−2<0

Это значит, что знак на интервале, в котором лежит точка 0 будет −.

Поскольку знак неравенства ≥, выбираем в ответ интервал со знаком +.

Точки -2 и -1 будут в квадратных скобках, так как они жирные.

Ответ: x∈[−2;−1]

№3. Решить неравенство 4<x2+3x.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

4<x2+3x

−x2−3x+4<0

−x2−3x+4=0

a=−1,b=−3,c=4

D=b2−4ac= (−3)2−4⋅(−1)⋅4=9+16=25

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−3)±252⋅(−1)=3±5−2=[3+5−2=8−2=−43−5−2=−2−2=1

x1=−4,x2=1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:

−x2−3x+4=−(2)2−3⋅2+4=−6<0

Это значит, что знак на интервале, в котором лежит точка 2, будет -.

Поскольку знак неравенства <, выбираем в ответ интервалы со знаком −.

Точки -4 и 1 будут в круглых скобках, так как они выколотые.

Ответ: x∈(−∞;−4)∪(1;+∞)

№4. Решить неравенство x2−5x<6.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

x2−5x<6

x2−5x−6<0

x2−5x−6=0

a=1,b=−5,c=−6

D=b2−4ac=(−5)2−4⋅1⋅(−6)=25+25=49

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−5)±492⋅1=5±72=[5+72=122=65−72=−22=−1

x1=6,x2=−1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:

x2−5x−6=102−5⋅10−6=100−50−6= 44>0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Поскольку знак неравенства <, выбираем в ответ интервал со знаком -.

Точки -1 и 6 будут в круглых скобках, так как они выколотые

Ответ: x∈(−1;6)

№5. Решить неравенство x2<4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

x2<4

x2−4<0

x2−4=0

(x−2)(x+2)=0⇔[x−2=0x+2=0 [x=2x=−2

x1=2,x2=−2

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:

x2−4=32−4=9−4=5>0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Поскольку знак неравенства <, выбираем в ответ интервал со знаком −.

Точки -2 и 2 будут в круглых скобках, так как они выколотые.

Ответ: x∈(−2;2)

№6. Решить неравенство x2+x≥0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x2+x=0.

x2+x≥0

x2+x=0

x(x+1)=0⇔[x=0x+1=0[x=0x=−1

x1=0,x2=−1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:

x2+x=12+1=2>0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Поскольку знак неравенства ≥, выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.

Ответ: x∈(−∞;−1]∪[0;+∞)

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x−1x+3<03(x+8)≤5×2−1x>0x+20x≥x+3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0

Приравнять числитель дроби к нулю f(x)=0. Найти нули числителя.

Приравнять знаменатель дроби к нулю g(x)=0. Найти нули знаменателя.

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Нанести нули числителя и нули знаменателя на ось x.

Вне зависимости от знака неравенства
при нанесении на ось xнули знаменателя всегда выколотые.

Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.

Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.

Расставить знаки на интервалах.

Выбрать подходящие интервалы и записать ответ.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x−1x+3>0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.

Приравниваем числитель к нулю f(x)=0.

x−1=0

x=1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

Приравниваем знаменатель к нулю g(x)=0.

x+3=0

x=−3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):x−1x+3 = 2−12+3=15>0,

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x∈(−∞;−3)∪(1;+∞)

№2. Решить неравенство 3(x+8)≤5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Привести неравенство к виду f(x)g(x)≤0.

3(x+8)≤5

3(x+8)−5\x+8≤0

3x+8−5(x+8)x+8≤0

3−5(x+8)x+8≤0

3−5x−40x+8≤0

−5x−37x+8≤0

Приравнять числитель к нулю f(x)=0.

−5x−37=0

−5x=37

x=−375=−375=−7,4

x=−7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

Приравнять знаменатель к нулю g(x)=0.

x+8=0

x=−8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f(x)g(x):

−5x−37x+8=−5⋅0−370+8=−378<0

Это значит, что знак на интервале, в котором лежит точка 0 будет -.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства ≤, выбираем в ответ интервалы со знаком -.

В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ: x∈(−∞;−8)∪[−7,4;+∞)

№3. Решить неравенство x2−1x>0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.

Приравнять числитель к нулю f(x)=0.

x2−1=0

(x−1)(x+1)=0⇒[x−1=0x+1=0[x=1x=−1

x1=1,x2=−1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

Приравнять знаменатель к нулю g(x)=0.

x=0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):

x2−1x=22−12=4−12=32>0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x∈(−1;0)∪(1;+∞)

Системы неравенств

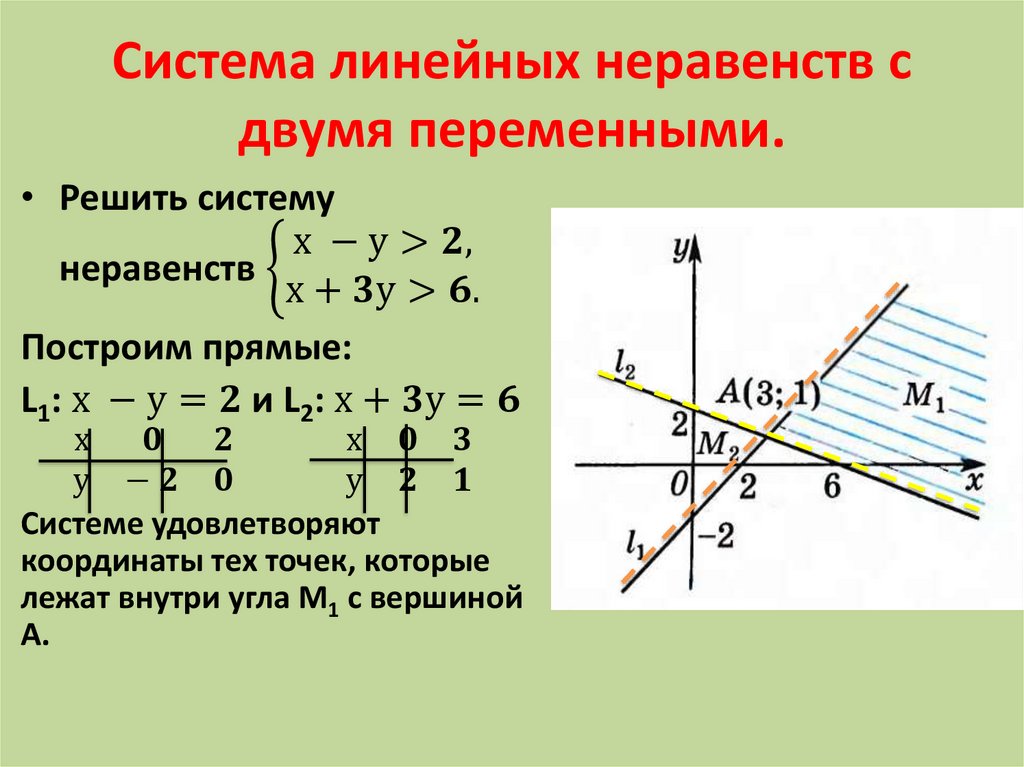
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

{x+4>02x+3≤x2

Алгоритм решения системы неравенств

Решить первое неравенство системы, изобразить его графически на оси x.

Решить второе неравенство системы, изобразить его графически на оси x.

Нанести решения первого и второго неравенств на ось x.

Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Примеры решений систем неравенств:

№1. Решить систему неравенств {2x−3≤57−3x≤1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2x−3≤5

2x≤8|÷2, поскольку 2>0, знак неравенства после деления сохраняется.

x≤4;

Графическая интерпретация:

Точка 4 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

7−3x≤1

−3x≤1−7

−3x≤−6|÷(−3), поскольку −3<0, знак неравенства после деления меняется на противоположный.

x≥2

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.

Ответ: x∈[2;4]

№2. Решить систему неравенств {2x−1≤51<−3x−2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2x−1≤5

2x≤6|÷2, поскольку 2>0, знак неравенства после деления сохраняется.

x≤3

Графическая интерпретация:

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

1<−3x−2

3x<−1−2

3x<−3|÷3, поскольку 3>0, знак неравенства после деления сохраняется.

x<−1

Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.

Ответ: x∈(−∞;−1)

№3. Решить систему неравенств {3x+1≤2xx−7>5−x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

3x+1≤2x

3x−2x≤−1

x≤−1

Графическая интерпретация решения:

Решаем второе неравенство системы

x−7>5−x

x+x>5+7

2x>12| ÷2, поскольку 2>0, знак неравенства после деления сохраняется.

x>6

Графическая интерпретация решения:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

Ответ: x∈∅

№4. Решить систему неравенств {x+4>02x+3≤x2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

x+4>0

x>−4

Графическая интерпретация решения первого неравенства:

Решаем второе неравенство системы

2x+3≤x2

−x2+2x+3≤0

Решаем методом интервалов.

−x2+2x+3=0

a=−1,b=2,c=3

D=b2−4ac=22−4⋅(−1)⋅3=4+12=16

D>0 — два различных действительных корня.

x1,2=−b±D2a=−2±162⋅(−1)=−2±4−2=[−2−4−2=−6−2=3−2+4−2=2−2=−1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪.

Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.

Ответ: x∈(−4;−1]∪[3;+∞)

Скачать домашнее задание к уроку 8.

Системы линейных неравенств с одной переменной

Примеры решения систем линейных неравенств с одной переменной

Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.

Рассмотрим простейший пример. Система состоит из двух неравенств, которые уже решены.

Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.

Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:

Но дело в том, что неравенства x > 4 и x < 9 соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями как им захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.

Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.

Значит решениями системы являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x < 9 строгие. Ответ можно записать в виде числового промежутка:

x ∈ ( 4 ; 9 )

Также, нужно изобразить множество решений системы на координатной прямой.

Для системы линейных неравенств решение на координатной прямой изображают так:

Сначала указывают границы обоих неравенств:

На верхней области отмечают множество решений первого неравенства x > 4

На нижней области отмечают множество решений второго неравенства x < 9

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:

Для проверки можно взять любое число из этого промежутка и подставить его в исходную систему . Возьмем, например, число 6

Видим, что решение 6 удовлетворяет обоим неравенствам. Возьмём ещё какое-нибудь число из промежутка (4; 9), например, число 8

Видим, что решение 8 удовлетворяет обоим неравенствам.

Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:

Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.

Пример 2. Решить систему неравенств

Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.

Решениями же обоих неравенств являются все числа, которые больше 17.

Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка.

Для начала отметим на координатной прямой границы обоих неравенств:

На верхней области отметим множество решений первого неравенства x > 17

На нижней области отметим множество решений второго неравенства x > 12

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:

x ∈ ( 17 ; +∞ )

Пример 3. Решить систему неравенств

Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок

Получили систему . На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.

Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства (x > 6 и x > 3). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы

x ∈ ( 6 ; + ∞ )

Пример 4. Решить систему неравенств

Решим каждое неравенство по отдельности:

Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка:

Пример 5. Решить неравенство

Решим каждое неравенство по отдельности:

Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка:

Когда решений нет

Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.

Пример 1. Решить неравенство

Решим каждое неравенство по отдельности:

Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.

Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:

На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система

Ответ: решений нет.

Пример 2. Решить систему неравенств

Решим каждое неравенство по отдельности:

Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:

Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система

Ответ: решений нет.

Пример 3. Решить систему неравенств

Решим каждое неравенство по отдельности:

Получили неравенства 0 < −0,2 и a > 5. Первое неравенство не является верным и не имеет решений. Решением второго неравенство a > 5 являются все числа, которые больше 5. Но поскольку первое неравенство не будет верным ни при каком a, то можно сделать вывод, что у неравенств нет общих решений. А значит не имеет решений исходная система

Ответ: решений нет.

Задания для самостоятельного решения

Задание 1. Решите неравенство:

Решение:

Показать решение

Задание 2. Решите неравенство:

Решение:

Показать решение

Задание 3. Решите неравенство:

Решение:

Показать решение

Задание 4. Решите неравенство:

Решение:

Показать решение

Задание 5. Решите неравенство:

Решение:

Показать решение

Задание 6. Решите неравенство:

Решение:

Показать решение

Задание 7. Решите неравенство:

Решение:

Показать решение

Задание 8. Решите неравенство:

Решение:

Решений нет

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Линейные неравенства подборка заданий. можно познакомиться с функциями и производными

Теперь можно разбираться, как решаются линейные неравенства a·x+b

Основной способ их решения заключается в использовании равносильных преобразований, позволяющих прийти при a≠0 к элементарным неравенствам

, ≥), p — некоторое число, которые и являются искомым решением, а при a=0 – к числовым неравенствам вида a

, ≥), из которых делается вывод о решении исходного неравенства. Его мы и разберем в первую очередь.

Также не помешает взглянуть на решение линейных неравенств с одной переменной и с других позиций. Поэтому, мы еще покажем, как можно решить линейное неравенство графически и методом интервалов.

Используя равносильные преобразования

Пусть нам нужно решить линейное неравенство a·x+b, ≥). Покажем, как это сделать, используя равносильные преобразования неравенства .

Подходы при этом различаются в зависимости от равенства или неравенства нулю коэффициента a при переменной x . Рассмотрим их по очереди. Причем при рассмотрении будем придерживаться схемы из трех пунктов: сначала будем давать суть процесса, дальше – алгоритм решения линейного неравенства, наконец, приводить решения характерных примеров.

Начнем с алгоритма решения линейного неравенства a·x+b, ≥) при a≠0 .

Во-первых, число b переносится в правую часть неравенства с противоположным знаком. Это позволяет перейти к равносильному неравенству a·x, ≥).
Во-вторых, проводится деление обеих частей полученного неравенства на отличное от нуля число a . При этом, если a – положительное число, то знак неравенства сохраняется, а если a — отрицательное число, то знак неравенства изменяется на противоположный. В результате получается элементарное неравенство, равносильное исходному линейному неравенству, оно и является ответом.

Остается разобраться с применением озвученного алгоритма на примерах. Рассмотрим, как с его помощью решаются линейные неравенства при a≠0 .

Пример.

Решите неравенство 3·x+12≤0 .

Решение.

Для данного линейного неравенства имеем a=3 и b=12 . Очевидно, коэффициент a при переменной x отличен от нуля. Воспользуемся соответствующим алгоритмом решения, приведенным выше.

Во-первых, переносим слагаемое 12 в правую часть неравенства, не забывая изменить его знак, то есть, в правой части окажется −12 . В результате приходим к равносильному неравенству 3·x≤−12 .

И, во-вторых, делим обе части полученного неравенства на 3 , так как 3 – число положительное, то знак неравенства не изменяем. Имеем (3·x):3≤(−12):3 , что то же самое x≤−4 .

Полученное элементарное неравенство x≤−4 равносильно исходному линейному неравенству и является его искомым решением.

Итак, решением линейного неравенства 3·x+12≤0 является любое действительное число, меньшее или равное минус четырем. Ответ можно записать и в виде числового промежутка , отвечающего неравенству x≤−4 , то есть, как (−∞, −4] .

Приобретя сноровку в работе с линейными неравенствами, их решения можно будет записывать кратко без пояснений. При этом сначала записывают исходное линейное неравенство, а ниже – равносильные ему неравенства, получающиеся на каждом шаге решения:
3·x+12≤0 ;
3·x≤−12 ;
x≤−4 .

Ответ:

x≤−4 или (−∞, −4] .

Пример.

Укажите все решения линейного неравенства −2,7·z>0 .

Решение.

Здесь коэффициент a при переменной z равен −2,7 . А коэффициент b отсутствует в явном виде, то есть, он равен нулю. Поэтому, первый шаг алгоритма решения линейного неравенства с одной переменной выполнять не нужно, так как перенос нуля из левой части в правую не изменит вид исходного неравенства.

Остается разделить обе части неравенства на −2,7 , не забыв изменить знак неравенства на противоположный, так как −2,7 – отрицательное число. Имеем (−2,7·z):(−2,7)

А теперь кратко:
−2,7·z>0 ;
z

Ответ:

Пример.

Решите неравенство .

Решение.

Нам нужно решить линейное неравенство с коэффициентом a при переменной x , равным −5 , и с коэффициентом b , которому отвечает дробь −15/22 . Действуем по известной схеме: сначала переносим −15/22 в правую часть с противоположным знаком, после чего выполняем деление обеих частей неравенства на отрицательное число −5 , изменяя при этом знак неравенства:

В последнем переходе в правой части используется , затем выполняется .

Ответ:

Теперь переходим к случаю, когда a=0 . Принцип решения линейного неравенства a·x+b

На чем это основано? Очень просто: на определении решения неравенства . Каким образом? Да вот каким: какое бы значение переменной x мы не подставили в исходное линейное неравенство, мы получим числовое неравенство вида b

Сформулируем приведенные рассуждения в виде алгоритма решения линейных неравенств 0·x+b, ≥) :

Рассматриваем числовое неравенство b, ≥) и

если оно верное, то решением исходного неравенства является любое число;
если же оно неверное, то исходное линейное неравенство не имеет решений.

А теперь разберемся с этим на примерах.

Пример.

Решите неравенство 0·x+7>0 .

Решение.

Для любого значения переменной x линейное неравенство 0·x+7>0 обратится в числовое неравенство 7>0 . Последнее неравенство верное, следовательно, любое число является решением исходного неравенства.

Ответ:

решением является любое число или (−∞, +∞) .

Пример.

Имеет ли решения линейное неравенство 0·x−12,7≥0 .

Решение.

Если подставить вместо переменной x любое число, то исходное неравенство обратиться в числовое неравенство −12,7≥0 , которое неверное. А это значит, что ни одно число не является решением линейного неравенства 0·x−12,7≥0 .

Ответ:

нет, не имеет.

В заключение этого пункта разберем решения двух линейных неравенств, оба коэффициента которых равны нулю.

Пример.

Какое из линейных неравенств 0·x+0>0 и 0·x+0≥0 не имеет решений, а какое – имеет бесконечно много решений?

Решение.

Если вместо переменной x подставить любое число, то первое неравенство примет вид 0>0 , а второе – 0≥0 . Первое из них неверное, а второе – верное. Следовательно, линейное неравенство 0·x+0>0 не имеет решений, а неравенство 0·x+0≥0 имеет бесконечно много решений, а именно, его решением является любое число.

Ответ:

неравенство 0·x+0>0 не имеет решений, а неравенство 0·x+0≥0 имеет бесконечно много решений.

Методом интервалов

Вообще, метод интервалов изучается в школьном курсе алгебры позже, чем проходится тема решение линейных неравенств с одной переменной. Но метод интервалов позволяет решать самые разные неравенства, в том числе и линейные. Поэтому, остановимся на нем.

Сразу заметим, что метод интервалов целесообразно применять для решения линейных неравенств с отличным от нуля коэффициентом при переменной x . В противном случае вывод о решении неравенства быстрее и удобнее сделать способом, разобранным в конце предыдущего пункта.

Метод интервалов подразумевает

введение функции, отвечающей левой части неравенства, в нашем случае – линейной функции y=a·x+b ,
нахождение ее нулей, которые разбивают область определения на промежутки,
определение знаков, которые имеют значения функции на этих промежутках, на основе которых делается вывод о решении линейного неравенства.

Соберем эти моменты в алгоритм , раскрывающий как решать линейные неравенства a·x+b, ≥) при a≠0 методом интервалов:

Находятся нули функции y=a·x+b , для чего решается a·x+b=0 . Как известно, при a≠0 оно имеет единственный корень, который обозначим x 0 .
Строится , и на ней изображается точка с координатой x 0 . Причем, если решается строгое неравенство (со знаком ), то эту точку делают выколотой (с пустым центром), а если нестрогое (со знаком ≤ или ≥), то ставят обычную точку. Эта точка разбивает координатную прямую на два промежутка (−∞, x 0) и (x 0 , +∞) .
Определяются знаки функции y=a·x+b на этих промежутках. Для этого вычисляется значение этой функции в любой точке промежутка (−∞, x 0) , и знак этого значения и будет искомым знаком на промежутке (−∞, x 0) . Аналогично, знак на промежутке (x 0 , +∞) совпадает со знаком значения функции y=a·x+b в любой точке этого промежутка. Но можно обойтись без этих вычислений, а выводы о знаках сделать по значению коэффициента a : если a>0 , то на промежутках (−∞, x 0) и (x 0 , +∞) будут знаки − и + соответственно, а если a>0 , то + и −.
Если решается неравенство со знаками > или ≥, то ставится штриховка над промежутком со знаком плюс, а если решаются неравенства со знаками

Рассмотрим пример решения линейного неравенства методом интервалов.

Пример.

Решите неравенство −3·x+12>0 .

Решение.

Коль скоро мы разбираем метод интервалов, то им и воспользуемся. Согласно алгоритму, сначала находим корень уравнения −3·x+12=0 , −3·x=−12 , x=4 . Дальше изображаем координатную прямую и отмечаем на ней точку с координатой 4 , причем эту точку делаем выколотой, так как решаем строгое неравенство:

Теперь определяем знаки на промежутках. Для определения знака на промежутке (−∞, 4) можно вычислить значение функции y=−3·x+12 , например, при x=3 . Имеем −3·3+12=3>0 , значит, на этом промежутке знак +. Для определения знака на другом промежутке (4, +∞) можно вычислить значение функции y=−3·x+12 , к примеру, в точке x=5 . Имеем −3·5+12=−3

Так как мы решаем неравенство со знаком >, то изображаем штриховку над промежутком со знаком +, чертеж принимает вид

По полученному изображению делаем вывод, что искомым решением является (−∞, 4) или в другой записи x

Ответ:

(−∞, 4) или x

Графическим способом

Полезно иметь представление о геометрической интерпретации решения линейных неравенств с одной переменной. Чтобы его получить, давайте рассмотрим четыре линейных неравенства с одной и той же левой частью: 0,5·x−10 и 0,5·x−1≥0 , их решениями являются соответственно x2 и x≥2 , а также изобразим график линейной функции y=0,5·x−1 .

Несложно заметить, что

решение неравенства 0,5·x−1
решение неравенства 0,5·x−1≤0 представляет собой промежуток, на котором график функции y=0,5·x−1 находится ниже оси Ox или совпадает с ней (другими словами, не выше оси абсцисс),
аналогично решение неравенства 0,5·x−1>0 есть промежуток, на котором график функции выше оси Ox (эта часть графика изображена красным цветом),
и решение неравенства 0,5·x−1≥0 является промежутком, на котором график функции выше или совпадает с осью абсцисс.

Графический способ решения неравенств , в частности линейных, и подразумевает нахождение промежутков, на которых график функции, соответствующей левой части неравенства, располагается выше, ниже, не ниже или не выше графика функции, соответствующей правой части неравенства. В нашем случае линейного неравенства функция, отвечающая левой части, есть y=a·x+b , а правой части – y=0 , совпадающая с осью Ox .

Учитывая приведенную информацию, несложно сформулировать алгоритм решения линейных неравенств графическим способом :

Строится график функции y=a·x+b (можно схематически) и

при решении неравенства a·x+b
при решении неравенства a·x+b≤0 определяется промежуток, на котором график ниже или совпадает с осью Ox ,
при решении неравенства a·x+b>0 определяется промежуток, на котором график выше оси Ox ,
при решении неравенства a·x+b≥0 определяется промежуток, на котором график выше или совпадает с осью Ox .

Пример.

Решите неравенство графически.

Решение.

Построим эскиз графика линейной функции . Это прямая, которая убывает, так как коэффициент при x – отрицательный. Еще нам понадобится координата точки его пересечения с осью абсцисс, она является корнем уравнения , который равен . Для наших нужд можно даже не изображать ось Oy . Так наш схематический чертеж будет иметь такой вид

Так как мы решаем неравенство со знаком >, то нас интересует промежуток, на котором график функции выше оси Ox . Для наглядности выделим эту часть графика красным цветом, а чтобы легко определить соответствующий этой части промежуток, подсветим красным цветом часть координатной плоскости, в которой расположена выделенная часть графика, так, как на рисунке ниже:

Интересующий нас промежуток представляет собой часть оси Ox , оказавшуюся подсвеченной красным цветом. Очевидно, это открытый числовой луч . Это и есть искомое решение. Заметим, что если бы мы решали неравенство не со знаком >, а со знаком нестрогого неравенства ≥, то в ответ пришлось бы добавить , так как в этой точке график функции совпадает с осью Ox .y=0·x+7 , что то же самое y=7 , задает на координатной плоскости прямую, параллельную оси Ox и лежащую выше нее. Следовательно, неравенство 0·x+7

А графиком функции y=0·x+0 , что то же самое y=0 , является прямая, совпадающая с осью Ox . Следовательно, решением неравенства 0·x+0≥0 является множество всех действительных чисел.

Ответ:

второе неравенство, его решением является любое действительное число.

Неравенства, сводящиеся к линейным

Огромное количество неравенств с помощью равносильных преобразований можно заменить равносильным линейным неравенством, другими словами, свести к линейному неравенству. Такие неравенства называют неравенствами, сводящимися к линейным .

В школе почти одновременно с решением линейных неравенств рассматривают и несложные неравенства, сводящиеся к линейным. Они представляют собой частные случаи целых неравенств , а именно в их левой и правой части находятся целые выражения, которые представляют собой или линейные двучлены , или преобразуются к ним путем и . Для наглядности приведем несколько примеров таких неравенств: 5−2·x>0 , 7·(x−1)+3≤4·x−2+x , .

Неравенства, которые подобны по виду указанным выше, всегда можно свести к линейным. Это можно сделать путем раскрытия скобок, приведения подобных слагаемых, перестановки слагаемых местами и переноса слагаемых из одной части неравенства в другую с противоположным знаком.

Например, чтобы свести неравенство 5−2·x>0 к линейному, достаточно переставить слагаемые в его левой части местами, имеем −2·x+5>0 . Для сведения второго неравенства 7·(x−1)+3≤4·x−2+x к линейному нужно немного больше действий: в левой части раскрываем скобки 7·x−7+3≤4·x−2+x , после этого приводим подобные слагаемые в обеих частях 7·x−4≤5·x−2 , дальше переносим слагаемые из правой части в левую 7·x−4−5·x+2≤0 , наконец, приводим подобные слагаемые в левой части 2·x−2≤0 . Подобным образом и третье неравенство можно свести к линейному неравенству.

Из-за того, что подобные неравенства всегда можно свести к линейным, некоторые авторы даже называют их тоже линейными. Но все же будем их считать сводящимися к линейным.

Теперь становится понятно, почему подобные неравенства рассматривают вместе с линейными неравенствами. Да и принцип их решения абсолютно такой же: выполняя равносильные преобразования, их можно привести к элементарным неравенствам, представляющим собой искомые решения.

Чтобы решить неравенство подобного вида можно его предварительно свести к линейному, после чего решить это линейное неравенство. Но рациональнее и удобнее поступать так:

после раскрытия скобок собрать все слагаемые с переменной в левой части неравенства, а все числа – в правой,
после чего привести подобные слагаемые,
а дальше – выполнить деление обеих частей полученного неравенства на коэффициент при x (если он, конечно, отличен от нуля). Это даст ответ.

Пример.

Решите неравенство 5·(x+3)+x≤6·(x−3)+1 .

Решение.

Сначала раскроем скобки, в результате придем к неравенству 5·x+15+x≤6·x−18+1 . Теперь приведем подобные слагаемые: 6·x+15≤6·x−17 . Дальше переносим слагаемые с левую часть, получаем 6·x+15−6·x+17≤0 , и снова приводим подобные слагаемые (что приводит нас к линейному неравенству 0·x+32≤0 ) и имеем 32≤0 . Так мы пришли к неверному числовому неравенству, откуда делаем вывод, что исходное неравенство не имеет решений.

Ответ:

нет решений.

В заключение отметим, что существует и масса других неравенств, сводящихся к линейным неравенствам, или к неравенствам рассмотренного выше вида. Например, решение показательного неравенства 5 2·x−1 ≥1 сводится к решению линейного неравенства 2·x−1≥0 . Но об этом будем говорить, разбирая решения неравенств соответствующего вида.

Список литературы.

Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.

Линейными называются неравенства левая и правая часть которых представляет собой линейные функции относительно неизвестной величины. К ним относятся, например, неравенства:

2х-1 -х+3; 7х 0;

5 >4 — 6x 9- x .

1) Строгие неравенства: ax +b>0 либо ax + b

2) Нестрогие неравенства: ax +b≤0 либо ax + b ≫ 0

Разберем такое задание . Одна из сторон параллелограмма составляет 7см. Какой должна быть длина другой стороны, чтобы периметр параллелограмма был больше 44 см?

Пусть искомая сторона составит х см. В таком случае периметр параллелограмма будет представлен (14 + 2х) см. Неравенство 14 + 2х > 44 является математической моделью задачи о периметре параллелограмма. Если в этом неравенстве заменить переменную х на, например, число 16, то получим верное числовое неравенство 14 + 32 > 44. В таком случае говорят, что число 16 является решением неравенства 14 + 2х > 44.

Решением неравенства называют значение переменной, которое обращает его в верное числовое неравенство.

Следовательно, каждое из чисел 15,1; 20;73 выступают решением неравенства 14 + 2х > 44, а число 10, например, не является его решением.

Решить неравенство означает установить все его решения или доказать, что решений не существует.

Формулировка решения неравенства сходна с формулировкой корня уравнения. И все же не принято обозначать «корень неравенства».

Свойства числовых равенств помогали нам решать уравнения. Точно так же свойства числовых неравенств помогут решать неравенства.

Решая уравнение, мы меняем его другим, более простым уравнением, но равнозначным заданному. По схожей схеме находят ответ и неравенства. При смене уравнения на равнозначное ему уравнение пользуются теоремой о перенесении слагаемых из одной части уравнения в противоположную и об умножении обеих частей уравнения на одно и то же отличное от нуля число. При решении неравенства есть существенное различие его с уравнением, которое заключается в том, что всякое решение уравнения можно проверить просто подстановкой в исходное уравнение. В неравенствах такой способ отсутствует, так как бесчисленное множество решений подставить в исходное неравенство не представляется возможным. Поэтому есть важное понятие, вот эти стрелочки — это знак эквивалентных, или равносильных, преобразований. Преобразование называются равносильными, или эквивалентными , если они не изменяет множества решений.

Сходные правила решения неравенств.

Если какое-либо слагаемое переместить из одной части неравенства в другую, заменив при этом его знак на противоположный, то получим неравенство, эквивалентное данному.

Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, эквивалентное данному.

Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, заменив при этом знак неравенства на противоположный, то получим неравенство, эквивалентное данному.

Используя эти правила вычислим нижеследующие неравенства.

1) Разберем неравенство 2x — 5 > 9 .

Это линейное неравенство , найдем его решение и обсудим основные понятия.

2x — 5 > 9 2x > 14 (5 перенесли в левую часть с противоположным знаком), далее поделили все на 2 и имеем x > 7 . Нанесем множество решений на ось x

Нами получен положительно направленный луч. Отметим множество решений либо в виде неравенства x > 7 , либо в виде интервала х(7; ∞). А что выступает частным решением этого неравенства? Например, x = 10 — это частное решение этого неравенства, x = 12 — это тоже частное решение этого неравенства.

Частных решений много, но наша задача — найти все решения. А решений, как правило, бесчисленное множество.

Разберем пример 2:

2) Решить неравенство 4a — 11 > a + 13 .

Решим его: а переместим в одну сторону, 11 переместим в другую сторону, получим 3a 3 неравенство имеет вид a.

4a — 11 > a + 13 3a a .

Тоже отобразим множество a , но уже на оси а .

Ответ либо пишем в виде неравенства a а (-∞;8), 8 не включается.

Урок и презентация на тему: «Примеры линейных неравенств и их решение»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 9 класса
Образовательный комплекс 1C: «Алгебраические задачи с параметрами, 9–11 классы» Программная среда «1С: Математический конструктор 6.1»

Линейные уравнения (повторение)

Ребята, мы переходим к изучению курса алгебры за 9 класс. Во время изучения нашего курса мы научимся решать много новых увлекательных задач.

Давайте немного повторим.
Вы помните, что такое линейное уравнение?
Мы называем уравнение вида $ax+b=0$ — линейным, здесь коэффициенты а и b из множества действительных чисел, то есть практически любое число. Кстати, а почему оно называется линейным? Правильно, если нарисуем график решения нашего уравнения, то получается линия.

Как мы решали наше уравнение? То, что с х, мы оставляли слева от знака равно, а без х переносили на право, не забывая менять знак, то есть получали уравнение вида: $ax=-b$.
После делили на коэффициент при х и получали решение уравнения: $x=-\frac{b}{a}$.
Ну что же, давайте перейдем к первой теме нашего курса.

Мы с вами вспомнили линейные уравнения, теперь давайте введем понятие линейного неравенства. Думаю вы догадались, что определения не будут сильно отличаться.
Линейным неравенством с одной переменной называют неравенства вот такого вида: $ax+b>0$, где а и b значения из множества действительных чисел $(a≠0)$. Вообще можно записать 4 вида неравенств :
$ax+b>0\\ ax+b
Значения переменной x, при котором наше неравенство становится верно — называется решением. Стоит заметить, что существует два вида решений: частное и общее. Общим решением называют все множество частных решений.

Давайте введем несколько правил при решении линейных неравенств:
Члены неравенства можно так же, как и в линейных уравнениях переносить из одно части в другую, не меняя знак неравенства.
Неравенство $3х
Неравенство можно умножить и разделить на одно и тоже число большее нуля, не изменив при этом знак неравенства. Ребята, не забывайте что обязательно надо умножать или делить обе части неравенства!
Неравенство $3x
Неравенство можно умножить или разделить на отрицательное число, не забыв при этом изменить знак неравенства на противоположный. Знак, ≤ на≥, и соответственно наоборот.
Умножим неравенство $3x-7 0$.

Если неравенство от переменой x разделить или умножить на выражение $p(x)$, зависящее от х, и которое положительно при любом х, не изменив знак неравенства, то получится неравенство, равносильное изначальному.

Если неравенство от переменой x разделить или умножить на выражение $p(x)$, зависящее от х, b которое отрицательно при любом х, поменяв знак неравенства, то получится неравенство, равносильное изначальному.

1. Решить неравенство: $3x-6
Решение:
Способ решения аналогичен линейным уравнениям, перенесем -6 направо от знака неравенства $3x Мы можем разделить наше неравенство на любое положительное число, не меняя знака. Давайте раздели на 3 и получим решение: $x Ответ: $x
2. Решить неравенство: $-3x+6
Решение:
Выполним начальные действия: $-3x Разделим неравенство на -3, не забыв изменить знак: $x>2$.
Ответ: $x>2$.

3. Решить неравенство: $\frac{x}{4}+\frac{(3x-2)}{8}>x-\frac{1}{16}$.

Решение:
Умножим наше неравенство на 16, получаем: $4x+2(3x-2)>16x-1$.
Выполним необходимые действия: $4x+6x-4-16x>-1$.
$-6x>3$.
Разделим неравенство на -6, поменяв его знак: $x Ответ: $x
4. Решить неравенство: $|2x-2|
Решение:
Разделим неравенство на 2. Получим: $|x-1| Решением нашего неравенство можно представить в виде отрезка координатной прямой. Середина отрезка будет находиться в точке $x=1$, а границы удалены на 2.
Нарисуем наш отрезок:
Открытый интервал $(-1;3)$ – решение нашего неравенства.

Задачи на линейные неравенства

1. Решить неравенство:
a) $2x+5 b) $-4x-9>11.$
c) $-5x+10
2. Решить неравенство: $\frac{2x}{9}+\frac{2x-4}{3}≤x-\frac{1}{18}$.

3. Решить неравенство:
$a) |3x-5| b) $|5x|

Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.

Понятие системы неравенств

Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.

Системы неравенств и системы уравнений

В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.

Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.

Виды неравенств

Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).

Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.

Свойства неравенств

К свойствам неравенств относятся следующие положения:

Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t 1 ≤ t 2 , то t 2 ≥ t 1).
Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t 1 ≤ t 2 , то t 1 + число ≤ t 2 + число).
Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t 1 ≥ t 2 , t 3 ≥ t 4 , то t 1 + t 3 ≥ t 2 + t 4).
Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t 1 ≤ t 2 , t 3 ≤ t 4 , t 1 , t 2 , t 3 , t 4 ≥ 0 то t 1 · t 3 ≤ t 2 · t 4).
Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
Все неравенства обладают свойством транзитивности (например, если t 1 ≤ t 2 и t 2 ≤ t 3 , то t 1 ≤ t 3).

Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.

Решение систем неравенств. Общие сведения. Способы решения

Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.

Графический способ

Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.

Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.

Алгебраический способ

Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.

Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.

Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.

Способ подстановки

Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х 4 — х 2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х 2 «, далее модель переписывают в новом виде. В нашем случае получится t 2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.

Метод интервалов

Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:

Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
Неравенства выписываются отдельно, определяется решение каждого из них.
Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.

Какой способ использовать?

Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.

Если что-то не получается

Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.

Решебник?

А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.

Выводы

Алгебра — это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.

Линейные уравнения с параметром. Анализ решений

Уравнения с параметром. Задача 18 (С6)

Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где $p(a)$ и $q(a)$- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все $x$ при всех значениях параметра $a$. Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение:

$x=\frac{q(a)}{p(a)}$ при $p(a)≠0.$

Если же $p(a)=0$ и $q(a)=0$, то решением данного уравнения является любое число. И последний случай, когда $p(a)=0$,а $q(a)≠0$, то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с $x$ в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:

Пример 1

Решить уравнение $ax-5a=7x-3$ при всех возможных $a$.

Перенесем все одночлены с $x$ влево, а оставшиеся члены – вправо. И вынесем $x$ за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда $(a-7)≠0$. Тогда мы можем поделить все уравнение на $a-7$ и выразить: $$x=\frac{5a-3}{a-7}.$$ Второй случай, когда $(a-7)=0$, получим уравнение $$x*0=32,$$ которое не имеет решений. 2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ.

Ответ: При $a=0$ решениями уравнения будут все действительные числа, кроме $x=0.$ Если $a≠0,$ то решений нет.

Показательные и логарифмические уравнения

Решение показательных и логарифмических уравнений с параметром

Неравенства с параметром в задании 18 ЕГЭ

При решении неравенств нужно понимать, какие преобразования будут равносильными, и какие нет. Разберем несколько примеров простейших неравенств с параметром.

Графический метод решения задания с параметром

Применение графического метода для решения задачи с параметром 18(С6) ЕГЭ по профильной математике. Подробно разбираем как решать уравнения и неравенства с параметром при помощи графиков.

Графический метод решения параметра при помощи семейства кривых

В статье подробно разобран второй графический метод решения уравнений и неравенств с параметрами. Детально разобраны несколько примеров.

Симметрия в задачах с параметром

Использование свойств функции при решении заданий с параметром из ЕГЭ по математике профильного уровня. Симметрия функций и приемы решения.

Финансовая математика в ЕГЭ. Экономическая задача в задании 15

Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.

Метод координат. Задача 14 ЕГЭ

Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.

Как сдать ЕГЭ по математике

Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.

линейных неравенств с двумя переменными| Графики и уравнения | Примеры

В этом мини-уроке мы узнаем о бесконечных множествах, упорядоченных парах, построении графиков линейных неравенств с двумя переменными, больше или равно, меньше или равно, линейных неравенствах с двумя переменными и построении графиков неравенств с двумя переменными.

Но вот интересная мелочь: знаете ли вы, что Томас Харриот был человеком, который ввел понятие неравенств в своей книге «Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas» в 1631 году.

План урока

1.	Что такое линейное неравенство с двумя переменными?
2.	Советы и рекомендации
3.	Важные замечания о линейных неравенствах с двумя переменными
4.	Решенные примеры линейных неравенств с двумя переменными
5.	Интерактивные вопросы о линейных неравенствах с двумя переменными

Что такое линейные неравенства с двумя переменными?

Когда одно выражение больше или меньше другого выражения, возникает неравенство.

Линейные неравенства определяются как выражения, в которых два значения сравниваются с использованием символов неравенства. Символы, представляющие неравенства :

Не равно ($\neq$)
Меньше чем ($<$)
Больше чем ($>$)
Меньше или равно ($\leq$)
Больше или равно to ($\geq$)

Линейные неравенства с двумя переменными представляют собой отношения неравенства между двумя алгебраическими выражениями, которые включают две разные переменные.

Линейное неравенство двух переменных формируется, когда символы, отличные от равенства, такие как больше или меньше, используются для связи двух выражений и двух переменных.

Вот несколько примеров линейных неравенств с двумя переменными:

\[\begin{array}{l}2x< 3y + 2\\7x - 2y > 8\\3x + 4y + 3 \le 2y — 5\ \y + x \ge 0\end{массив}\]

Как решать линейные неравенства с двумя переменными?

Решением линейного неравенства с двумя переменными, например Ax + By > C, является упорядоченная пара (x, y), которая дает истинное утверждение, когда значения x и y подставляются в неравенство.

Решение линейных неравенств аналогично решению линейных уравнений; разница, которую он имеет, связана с символом неравенства.

Мы решаем линейные неравенства так же, как и линейные уравнения.

Шаг 1. Упростите неравенство с обеих сторон, как с левой, так и с правой стороны, в соответствии с правилами неравенства.
Шаг 2: Получив значение, мы имеем:

строгих неравенств, в которых две стороны неравенства не могут быть равны друг другу.
нестрогих неравенств, в которых две части неравенств также могут быть равны.

Рассмотрим следующее неравенство:

\[2x +3y > 7\]

Когда мы говорим о нахождении решения этого неравенства , мы говорим обо всех тех парах значений из x и y , для которых это неравенство доволен. Это означает, например, что $x = 4,\;y = 3$ является одним из возможных решений этого конкретного неравенства. Однако $x = 0,\;y = 0$ не является таковым, потому что при подстановке x и y равными 0 в левой части неравенства получается меньше 7,

Мы видели, что любое линейное уравнение с двумя переменными имеет бесконечно много решений. Теперь вам может быть очевидно, что и для любого линейного неравенства у нас будет бесконечно много решений. Все эти решения составят наборов решений линейного неравенства.

Советы и рекомендации

PEMDAS и BODMAS играют решающую роль в решении неравенств.
Если число отрицательное с любой стороны знака (не с обеих сторон), направление остается прежним.

Как построить график неравенства с двумя переменными?

Линейные неравенства с двумя переменными имеют бесконечные множества или бесконечно много упорядоченных парных решений.

Эти упорядоченные пары или наборы решений можно изобразить в соответствующей половине прямоугольной координатной плоскости.

Чтобы построить график неравенств с двумя переменными,

Укажите тип неравенства (больше, меньше, больше или равно, меньше или равно).
Нарисуйте граничную линию — штриховой (в случае строгого неравенства) или сплошной линией (в случае нестрогого неравенства).
Выберите тестовую точку, скорее всего (0,0) или любую другую точку, которая не находится на границе.
Закрасьте область соответствующим образом. Если контрольная точка решает неравенство, заштрихуйте содержащую ее область. В противном случае заштрихуйте противоположную сторону граничной линии.
Проверка с большим количеством контрольных точек в регионе и за его пределами.

Пример: начертите линейное равенство \[2x + 3y > 7\]

Нарисуйте прямую, соответствующую линейному уравнению $2x + 3y = 7$.
Определите любые две точки (решения) этого уравнения: две возможные точки на графике можно взять как $A\left( { — 1,\;3}\right),\,\,B\left( {2 ,\;1} \right)$ и нанесите их на график.
Определите некоторые конкретные решения линейного неравенства \[2x + 3y > 7\], которые могут быть следующими \begin{equation}(2,3), (3,1), (4.5,0), (0, 3), (1.5,2)\end{уравнение}
Нанесите эти пять точек на один график.

Все пять точек (соответствующих пяти решениям) лежат на выше линии .

Возьмем любую точку , лежащую выше линии. Его координаты, например $\left( {{x_0},\;{y_0}} \right),$, будут удовлетворять неравенству: \[2{x_0} + 3{y_0} >7\]
Это означает, что множество решений неравенства состоит из всех точек, лежащих выше прямой .
Положим x = 0, y = 0, что дает 2(0) + 3(0) > 7, что далее дает 0 > 7. Это неверно для данного неравенства. Итак, заштрихуйте полуплоскость, которая не включает точку (0,0).

Важные примечания

Неравенства можно решать путем сложения, вычитания, умножения или деления обеих частей на одно и то же число.
Деление или умножение обеих сторон на отрицательные числа изменит направление неравенства.
Упорядоченные пары вне заштрихованной области не решают линейных неравенств.
Меньше и больше являются строгими неравенствами, тогда как меньше или равно и больше или равно не являются строгими неравенствами.
Любая прямая разделит плоскость, в которой она лежит, на две полуплоскости.
Наборы решений линейных неравенств соответствуют полуплоскостям, а наборы решений линейных уравнений соответствуют прямым.

Решенные примеры

Пример 1

Помогите Бобу определить, является ли (2,1/5) решением уравнения \[2x + 5y < 10\]

Решение

Положим эти значения (2,1/5) на ) в данном линейном неравенстве.

Это дает \begin{equation}
2(2)+5(1 / 5)<10
\end{уравнение}

\begin{уравнение}4 + 1 < 10\end{уравнение}

\begin{equation}5 < 10\end{equation} что верно.

$\следовательно$ Таким образом, (2,1/5) является решением \[2x + 5y < 10\]

Пример 2

Мать Брука передает ему 7 долларов на шоколад. Она говорит ему, чтобы он потратил всего 7 долларов или меньше.

Молочный шоколад стоит 2 доллара, а шоколад с орехами – 33 доллара.

Пусть x — количество шоколадных конфет, а y — количество шоколадных конфет с орехами.

Составьте неравенство, соответствующее приведенной выше ситуации, и начертите неравенство.

Решение

\[2x + 3y ≤ 7\] будет неравенством, соответствующим приведенной выше ситуации.

В этом случае мы построим сплошную линию как границу, соединяющую точки, удовлетворяющие линейному уравнению \[2x + 3y=7\]

Для \[2x + 3y=7\]

Нанесите эти точки на график. Они будут лежать ниже сплошной линии.

Теперь положим x = 0, y = 0

Это дает 2(0) + 3(0) ≤ 7, что удовлетворяет неравенству.

Итак, заштрихуйте полуплоскость на графике линейного неравенства ниже, которая включает точку (0,0).

х	2	5	-7
и	1	-1	7

Пример 3

Постройте график множества решений для \[y > -5x + 2 \]

Решение:

\[y > -5x + 2 \] форма пересечения неравенства в наклоне; наклон=-5, точка пересечения=2.

В этом случае мы построим пунктирную линию из-за того, что равенство меньше или равно, как границу, соединяющую точки, удовлетворяющие линейному уравнению \[y = -5x + 2\]

Для \[y = — 5x + 2\]

х	0	1	2	-1
и	2	-3	-8	7

Для неравенства \[y > -5x + 2 \]

Определить конкретные решения линейного неравенства \[y > -5x + 2 \], которые могут быть следующими: \begin {уравнение} (1,2), (3,-2), (4,3), (4,5), (3,6)\end{уравнение}
Нанесите эти точки на график. Они будут лежать выше пунктирной линии.

Для \[y > -5x + 2 \] поместите x=0, y=0

Это дает 0>-5(0)+2

, что далее дает 0>2

Это неверно для данного неравенства. Итак, заштрихуйте полуплоскость на графике линейного неравенства ниже, которая не включает точку (0,0).

Интерактивные вопросы

Вот несколько заданий для практики.

Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Подведем итоги

Надеемся, вам понравилось узнавать о том, что такое линейные неравенства с двумя переменными, решать линейные неравенства с двумя переменными, графически изображать неравенства с двумя переменными, бесконечные множества, упорядоченные пары, больше или равно &, меньше или равно с интерактивными вопросами . Теперь вы сможете легко находить ответы на линейные неравенства с двумя переменными и знать о решениях линейных неравенств.

Мини-урок был посвящен увлекательной концепции линейных неравенств с двумя переменными. Математическое путешествие вокруг линейных неравенств с двумя переменными начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, чтобы это было не только понятно и легко для понимания, но и осталось с ними навсегда. В этом заключается магия Cuemath.

О Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.

Часто задаваемые вопросы o

n Линейные неравенства с двумя переменными

1.

Система линейных неравенств с двумя переменными относится к набору не менее двух линейных неравенств с одними и теми же переменными.

2. Как отличить линейные неравенства с двумя переменными от линейных уравнений с двумя переменными?

График линейных уравнений включает сплошную линию в любой ситуации, тогда как в случае линейных неравенств график включает либо пунктирную, либо сплошную линию. Кроме того, линейные неравенства включают заштрихованные области, а линейные уравнения — нет.

3. Что является примером линейного неравенства?

Примером линейного неравенства может быть любое линейное уравнение, но с такими символами, как <, >, ≤ или ≥ вместо =.

4. Какие символы используются в линейных неравенствах?

В линейных неравенствах используются символы <, ≤, > и ≥.

5. Что означают линейные неравенства?

Линейное неравенство — это неравенство, имеющее линейную функцию, состоящую из одного из символов неравенства.

6. Как определить линейное неравенство?

Когда две части уравнения имеют знак, отличный от равного.

7. Для чего используются линейные неравенства?

Система линейных неравенств часто используется для определения максимального или минимального значения ситуации с несколькими ограничениями.

8. Какие 5 символов неравенства?

Пять символов неравенства: ≠ = не равно, > = больше, < = меньше, ≥ = больше или равно & ≤ = меньше или равно.

9. Что означает R в неравенствах?

В неравенствах R соответствует действительным числам и включает все действительные числа.

4.7 Решение линейных неравенств | Уравнения и неравенства

4.6 Буквенные уравнения

4. 8 Краткое содержание главы

4.7 Решение линейных неравенств (EMA3H)

Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен $\текст 1}$. Ниже приведены примеры линейных неравенств.

Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений. Единственный разница возникает, когда есть умножение или деление, которое включает знак минус. Например, мы знайте, что $8>6$. Если обе части неравенства разделить на $-\text{2}$, то получим $-4>-3$, что неверно. Следовательно, знак неравенства необходимо поменять местами, что дает $-4<-3$.

Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение.

Решите $2x + 2 = 1$:

Если мы представим этот ответ на числовой прямой, мы получим:

Теперь найдем $x$ в неравенстве $2x + 2 \le 1$:

Если мы представим этот ответ на числовой прямой, мы получим:

Мы видим, что для уравнения существует только одно значение $х$, для которого уравнение верно. Однако, для неравенства существует диапазон значений, для которых неравенство верно. Это главное отличие между уравнением и неравенством.

Помните: когда мы делим или умножаем обе части неравенства на отрицательное число, направление изменения неравенства. Например, если $x<1$, то $-x>-1$. Также обратите внимание, что мы не можем разделить или умножить на переменную.

Следующее видео знакомит с линейными неравенствами.

Видео: 2FGH

Интервальное обозначение (EMA3J)

Примеры:

$\влево(4;12\вправо)$	Круглые скобки означают, что номер не включен. В этот интервал входят все действительные числа больше, но не равны $\text{4}$ и меньше, но не равны $\текст{12}$.
$\влево(-\infty ;-1\вправо)$	Круглые скобки всегда используются для положительной и отрицательной бесконечности. Этот интервал включает все действительные числа меньше, но не равны $-\text{1}$.
$\влево[1;13\вправо)$	Квадратная скобка указывает, что число включено. В этот интервал входят все действительные числа больше или равные $\text{1}$ и меньше, но не равные $\текст{13}$.

Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.

Мы представим приведенный выше ответ в интервальной нотации как $\left(-\infty ; -\frac{1}{2}\right]$

Рабочий пример 17: Решение линейных неравенств

Найдите $r$:

\[6 — г > 2\]

Ответ представить в числовой строке и в интервальной записи.

Переставить и решить для $r$

Умножение на $-\text{1}$ и обратный знак неравенства

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Рабочий пример 18: Решение линейных неравенств

Найдите $q$:

\[4q + 3 < 2(q + 3)\]

Ответ представить в числовой строке и в интервальной записи.

Развернуть скобу

Переставить и решить для $q$

Разделить обе стороны на $\text{2}$

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Рабочий пример 19: Решение сложных линейных неравенств

Найдите $x$:

\[5 \le x + 3 < 8\]

Ответ представить в числовой строке и в интервальной записи.

Вычесть $\text{3}$ из всех частей неравенства

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Учебник Упражнение 4.6

$x < -1 \text{ и } x \ge 6 ; x \in \mathbb{R}$

$3 < x < 6 ; x \in \mathbb{R}$

$x \neq 3 ; x \neq 6 ; x \in \mathbb{R}$

$x > -10 ; x \in \mathbb{R}$

$3x + 4 > 5x + 8$

\начать{выравнивать*} 3х+4&>5х+8\ 3х — 5х & > 8 — 4\ -2х > 4\ 2х<-4\ х < -2 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $(-\infty; -2)$

$3(x — 1) — 2 \le 6x + 4$

\начать{выравнивать*} 3(х — 1) — 2 & \le 6x + 4 \\ 3х — 5 и \ле 6х + 4\ 3х — 6х &\ле 4+5\ -3х\ле 9\ х \ge -\frac{9}{3} \\ х \ гэ -3 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $[-3; \infty)$

$\dfrac{x — 7}{3} > \dfrac{2x — 3}{2} $

\начать{выравнивать*} \frac{x — 7}{3} & > \frac{2x — 3}{2} \\ 2(х — 7) & > 3(2х — 3) \\ 2х — 14 > 6х — 9\ -4х > 5\ х < -\фракция{5}{4} \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $(-\infty; -\frac{5}{4})$

$-4(x — 1) < x + 2$

\начать{выравнивать*} -4 (х — 1) & < х + 2 \\ -4x + 4 & < х + 2 \\ -5х < -2\ х > \ гидроразрыва {2} {5} \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $(\frac{2}{5}; \infty)$

$\dfrac{1}{2}x + \dfrac{1} {3}(x — 1) \ge \dfrac{5}{6}x — \dfrac{1}{3}$

\начать{выравнивать*} \frac{1}{2}x + \frac{1}{3}(x — 1) & \ge \frac{5}{6}x — \frac{1}{3} \\ \frac{1}{2}x + \frac{1}{3}x — \frac{1}{3} & \ge \frac{5}{6}x — \frac{1}{3} \ \ \frac{1}{2}x + \frac{1}{3}x — \frac{5}{6}x & \ge \frac{1}{3} — \frac{1}{3} \ \ \frac{3}{6}x + \frac{2}{6}x — \frac{5}{6}x & \ge 0 \\ 0x\ge 0 \конец{выравнивание*}

Неравенство верно для всех действительных значений $x$.

$-2 \le x — 1 < 3$

\[\begin{массив}{ccccc} -2 & \le & x — 1 & < & 3 \\ -1 & \le & x & < & 4 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: $[-1; 4)$

$-5 < 2x - 3 \le 7$

\[\begin{массив}{ccccc} -5&<&2x - 3&\le&7\ -2 & < & 2x & \le & 10 \\ -1 & < & х & \ле & 5 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: $(-1; 5]$

$7(3x + 2) — 5(2x — 3) > 7$

\начать{выравнивать*} 7 (3x + 2) — 5 (2x — 3) & > 7 \\ 21х + 14 — 10х + 15 и > 7\ 11х&>-22\ х & > -2 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $(-2; \infty)$

$\dfrac{5x — 1}{-6} \ge \dfrac{1 — 2x}{ 3}$

\начать{выравнивать*} \frac{5x — 1}{-6} & \ge \frac{1 — 2x}{3} \\ 5x — 1 & \ge -2(1 — 2x) \\ 5x — 1 & \ge -2 + 4x \ 5x — 4x & \ge -1\ х & \ ge -1 \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $[-1; \infty)$

$3 \ле 4 — х \ле 16$

\[\begin{массив}{ccccc} 3&\ле&4 — х&\ле&16\ -1&\le&-x&\le&12\ 1 & \ge & x & \ge & -12 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: $[1; 12]$

$\dfrac{-7y}{3} — 5 > -7$

\начать{выравнивать*} \frac{-7y}{3} — 5 & > -7 \\ -7у — 15 и > -21\ -7у&>-6\ у & < \ гидроразрыва {6} {7} \конец{выравнивание*}

Представлено на числовой прямой:

В интервальной записи: $(-\infty;\frac{6}{7})$

$1 \le 1 — 2y < 9$

\[\begin{массив}{ccccc} 1&\le&1 — 2у&<&9\ 0&\le&-2y&<&8\ 0 & \ge & y & > & -4 \\ -4 & < & у & \ле & 0 \конец{массив}\]

Представлено в числовой строке:

В интервальных обозначениях: $(-4;0]$

$-2 < \dfrac{x - 1}{-3} < 7$

\[\begin{массив}{ccccc} -2 & < & \dfrac{x - 1}{-3} & < & 7 \\ 6&>&х-1&>&-21\ 7&>&х&>&-20\ -20 & < & х & < & 7 \конец{массив}\]

Представлено на числовой прямой:

В интервальной записи: $(-20;7)$

$2x -1 < 3(x+11)$

\begin{align*} 2 х -1 &< 3(х +11) \\ 2 х -1 &< 3 х +33 \\ 2 х -3 х &< 33 +1 \ -1 х &< 34\ \поэтому х &> -34 \end{выравнивание*}

\[\left(-34;\infty\right)\]

$x -1 < -4(x-6)$

\begin{align*} х-1 &<-4(х-6) \\ х -1 &< -4 х +24 \\ х +4 х &< 24 +1 \\ 5 х &< 25\ \поэтому х &< 5 \end{align*}

\[\left(-\infty;5\right)\]

$\dfrac{x-1}{8} \leq \dfrac{2(x-2)}{3}$

\начать{выравнивать*} \frac{x-1}{8} &\leq \frac{2(x-2)}{3} \\ 3(х-1) &\leq 16(х-2) \\ 3x-3 &\leq 16x-32\ 3x -16x &\leq -32 +3\ -13x &\leq -29\ \поэтому х &\geq\frac{29}{13} \конец{выравнивание*}

$\; x \in \left[ \frac{29}{13} ;\infty\right)$.

$\dfrac{x+2}{4} \leq \dfrac{-2(x-4)}{7}$

\начать{выравнивать*} \frac{x+2}{4} &\leq \frac{-2(x-4)}{7} \\ 7(х+2) &\leq -8(х-4) \\ 7x+14 &\leq -8x+32 \\ 7x +8x &\leq 32 -14\ 15x &\leq 18\\ \поэтому х &\leq\frac{6}{5} \конец{выравнивание*}

$\; x \in \left(-\infty; \frac{6}{5} \right]$.

$\dfrac{1}{5}x — \dfrac{5}{ 4}(x+2) > \dfrac{1}{4}x + 3$

\begin{align*} \frac{1}{5}x — \frac{5}{4}(x+2) &> \frac{1}{4}x +3 \\ 4x — 25(x+2) &> 5x +60 \\ 4х — 25х-50 &> 5х +60\ 4х — 25 х -5х &> 60 + 50\\ -26x &> 110\\ \следовательно, x &< -\frac{55}{13} \end{выравнивание*}

Интервал: \[\left(-\infty;-\frac{55}{13}\right)\]

$\dfrac{1}{5}x — \dfrac{2}{5}(x+3) \geq \dfrac{4}{2}x +3$

\begin{align*} \frac{1}{5}x — \frac{2}{5}(x+3) &\geq \frac{4}{2}x +3 \\ 2x — 4(x+3) &\geq 20x +30 \\ 2x — 4x-12 &\geq 20x+30\ 2x — 4 x -20x &\geq 30 + 12\\ -22x &\geq 42\\ \поэтому x &\leq -\frac{21}{11} \end{выравнивание*}

Интервал: \[\left(-\infty;-\frac{21}{11}\right]\]

$4x +3 < -3 \quad\text{or}\quad 4x +3 > 5$

Решите неравенство: \[\begin{массив}{rclcrcl} 4x +3 &<& -3 &\text{or}& 4x +3 &>& 5 \\ 4x &<& -3-3 &\text{or}& 4x &>& 5-3 \\ х &<& \frac{-3-3}{4} &\text{or}& x &>& \frac{5-3}{4} \\ x &<& - \frac{3}{2} &\text{or}& x &>& \frac{1}{2} \\ \конец{массив}\]

\[\left(-\infty; — \frac{3}{2}\right) \cup \left(\frac{1}{2}; \infty\right)\]

$4 \ ge -6x -6 \ge -3$

Решите неравенство: \[\begin{массив}{rcccl} 4 &\ge&-6x -6 &\ge&-3 \\ 4+6 &\ge& -6x &\ge& -3+6 \\ \frac{4+6}{-6} &\le& x &\le& \frac{-3+6}{-6} \\ — \frac{5}{3} &\le& x &\le& — \frac{1}{2} \\ \конец{массив}\]

\[\left[- \frac{5}{3}; — \frac{1}{2}\right]\]

$6b — 3 > b + 2 , ~b \in \mathbb{Z}$

\начать{выравнивать*} 6b — 3 > b + 2 , ~b \in \mathbb{Z}\\ 5б > 5\ б > 1 \конец{выравнивание*}

$3a — 1 < 4a + 6 , ~a \in \mathbb{N}$

\начать{выравнивать*} 3а — 1 < 4а + 6\ -а < 7\ а > -7 \конец{выравнивание*}

Однако нам говорят, что $a \in \mathbb{N}$ и, следовательно, $a > 0$.

$\dfrac{b-3}{2} + 1 < \dfrac{b}{4} - 4 , ~b \in \mathbb{R}$

\начать{выравнивать*} \frac{b-3}{2} + 1 < \frac{b}{4} - 4 \\ 2б - 6 + 4 < б - 16\ б < -14 \конец{выравнивание*}

$\dfrac{4a +7}{3} — 5 > a — \dfrac{2}{3} , ~a \in \mathbb{N}$

\начать{выравнивать*} \frac{4a +7}{3} — 5 > a — \frac{2}{3} \\ 4а + 7 — 15 > 3а — 2\ а > 6 \конец{выравнивание*}

4.6 Буквенные уравнения

Оглавление

4. 8 Краткое содержание главы

Решение линейных уравнений и неравенств

Давайте начнемРешение словесных описаний линейных уравненийДва метода решения линейных уравненийОтсутствующие фрагменты информацииРешение линейных неравенств с помощью графикаСловарный запасЗанятие в дневнике

Стандарты TEKS и ожидания учащихся

A(5) Линейные функции, уравнения и неравенства. Учащийся применяет стандарты математического процесса для решения линейных уравнений с помощью технологий и без них и оценивает обоснованность их решений. Студент должен:

A(5)(A) решать линейные уравнения с одной переменной, в том числе те, для которых необходимо применение дистрибутивного свойства и для которых переменные включены с обеих сторон

A(5)(B) решать линейные неравенства с одной переменной, в том числе те, для которых необходимо применение распределительного свойства и для которых переменные включены с обеих сторон Используйте различные методы для решения уравнений и неравенств с одной и двумя переменными.

Основные вопросы

Какие шаги необходимы для алгебраического решения линейного уравнения или неравенства?

Что представляет собой пересечение двух линейных уравнений на графике?

Как представить линейное неравенство на графике?

Словарь

Уравнение
Неравенство
Пересекающиеся линии
Система линейных уравнений
Переменная

При задании ситуации сначала необходимо написать уравнение. Есть два метода, которые можно использовать для решения линейного уравнения.

Пример задачи

Lawns Beautiful взимала с миссис Гарсия 119 долларов за растения плюс 25 долларов в час за ландшафтного дизайнера, завершающего благоустройство ее двора. Общая сумма составила 253 доллара. Как долго дизайнер работал над благоустройством двора миссис Гарсия?

Первое, что вы должны сделать, это написать уравнение, которое представляет ситуацию.

Задача заключается в том, чтобы определить, сколько времени дизайнер работал над ландшафтным дизайном. Следовательно, х = часы.
Миссис Гарсия заплатила 119 долларов за растения.
С нее также брали 25 долларов в час. Это можно представить выражением 25 x .
Всего она потратила 253 доллара.
Уравнение, описывающее эту ситуацию: 119 + 25 x = 253.

Построение уравнения на графике

Еще один способ решить уравнение — построить график обеих частей уравнения и найти пересечение.

Точка пересечения (5.36, 253). Эта точка представляет собой значение x-, 5,36, которое представляет собой общее количество часов, и значение y-, 253, которое представляет собой общую сумму потраченных денег.

Используйте любой метод, чтобы ответить на вопросы следующего теста, чтобы решить проблему.

Когда линейное уравнение имеет две переменные ( x , y ), решением является любая точка, которая удовлетворяет уравнению, лежащему на прямой. Есть два способа определить, является ли точка решением уравнения.

Например: Является ли (-2, 3) решением уравнения 3 x + y = 3?

Метод 1: Алгебраически
Подставьте данные значения для x и y в уравнение.

3 x + y = 3
3(-2) + 3 = 3
-6 + 3 ≠ 3
-3 ≠ 3

Поскольку уравнение неверно, мы знаем, что (-2, 3 ) НЕ является решением уравнения.

Метод 2: Графика/Таблица

Решите уравнение в y = форма: y = -3 x + 3

Введите уравнение в «Y1» вашего графического калькулятора.

Таблица показывает, что когда x = -2, y = 9, то (-2, 3) НЕ является решением уравнения.

Определите, какой метод вы предпочитаете, и решите задачи в следующем упражнении. Если вам нужен графический калькулятор, используйте инструмент Equation Grapher Tool.

Чтобы использовать инструмент Equation Grapher:

Введите уравнение Y 1=.
Пресс-график.
Проверьте таблицу Function Value справа для данной заказанной пары.

Иногда вам могут дать частично упорядоченную пару и уравнение, и вас попросят определить значение отсутствующей переменной.

Существует два разных метода нахождения пропущенного значения в упорядоченной паре уравнений.

Пример: Если (−1, y ) является решением уравнения 2 x – 7 y = 40, чему равно y ?

Алгебраически вам просто нужно подставить -1 вместо x в уравнении и найти y .

Вы также можете ввести уравнение (решенное для y ) в свой графический калькулятор и просмотреть сгенерированную таблицу значений.

Например, если мы посмотрим на уравнение для последнего примера (2 x – 7 y = 40) и перепишите его так, чтобы оно было решено для y , уравнение будет y=27x — 407

. Введите это в свой графический калькулятор в разделе «Y1». Посмотрите в ТАБЛИЦУ значение y , когда x = -1.

Глядя на таблицу, мы видим, что когда x = -1, y = -6.

Выберите метод, который вы предпочитаете, чтобы решить практические задачи в упражнении ниже.

Посмотрите следующее видео, чтобы узнать о решении линейных неравенств с помощью графика. Выполните каждое из трех действий в видео, чтобы проверить свое понимание.

Печать
Поделиться

Часть 2: Неравенства | Пособие для начинающих по математике для 9-х классов

Неравенства

Понимание неравенства и умение решать вопросы такого типа — это фундаментальные знания, которые все учащиеся должны знать до 10-го класса. Прочтите это руководство, если вы хотите закрепить свои способности или даже если вы изучаете это в первый раз!

Результат программы NSW

В этой статье рассматриваются следующие результаты программы:

Сравнение относительных значений целых чисел, включая запись сравнения с использованием символов ( < и > )
Списки заказов

В этом разделе вы узнаете, что математика — это краткий способ записи операторов, сравнивающих размер чисел.

В этой статье мы обсудим

Как работают неравенства
Решение уравнений с неравенствами
Распространенные ошибки при отображении неравенств
Сравнение различных форм отображения чисел (например, экспоненциальное представление, смешанные дроби)

Предполагаемые знания

Учащиеся должны уметь решать простые алгебраические уравнения. Они также должны понимать, как преобразовать определенное число между различными формами, например. дробь в смешанную дробь в десятичную.

$\frac{7}{4}=1\frac{3}{4}=1,75$

Учащиеся также должны уметь преобразовывать индексные и экспоненциальные записи и обратно.

Что такое неравенство?

Проще говоря, неравенства — это система выражения одного числа как меньшего или большего, чем другое число. Для этого обычно используются два символа:

< (меньше) и
> (больше)

Уловка, чтобы запомнить это, заключается в том, что две строки «открываются» до большего числа. и «замыкается» в сторону меньшего числа.

Пример: Заполните пропуск

Заполните пропуск соответствующим знаком неравенства:

$5$ _____ $8$

Решение

Поскольку мы знаем, что 5 меньше 8 , мы бы использовали знак «меньше».

$5<8$

Дополнительно!

Существует еще одна форма записи, которая будет использоваться в старших классах:

≤ (меньше или равно)

и ≥ (больше или равно)

Решение уравнений с неравенствами

Вы должны уметь решать уравнения с неравенствами. Давайте посмотрим, как это сделать.

Линейные уравнения

Обычно при решении линейных уравнений вы ожидаете найти единственное значение $x$.

Например:

\begin{align*}
2x-1=5 \\
2x=6 \\
∴x=3 \\
\end{align*}

Однако уравнения со знаком неравенства (а не знак равенства) означает, что вы ищете значение(я) $x$, которое удовлетворяло бы «неравенству».

$2x-1>5$

Здесь вы хотите найти все значения x, при которых $2x-1$ больше, чем $5$.

К счастью, эти типы уравнений можно решать так же, как и обычные уравнения. Однако есть одно дополнительное правило, о котором мы поговорим позже.

т. е. Обрабатывать знак неравенства как знак равенства .

Пока рассмотрим:

\begin{align*}
2x-1>5 \\
2x>6 \\
x>3 \\
\end{align*}

Приравнивая знак неравенства к знаку равенства, вы ответили на вопрос. Для любого значения $x$, большего чем $3$, наше исходное неравенство будет выполнено.
Например, если $x=4$, $2(4)-1=7$, что равно $>5$.

Как обсуждалось ранее, существуют особые случаи, когда знак неравенства меняет направление при нахождении $x$. Это происходит, когда вы умножаете или делите обе части неравенства на отрицательное число.

Рассмотрим:

\begin{align*}
-2x-1>5 \\
-2x>6 \\
\end{align*}

Теперь, чтобы найти $x$, мы должны разделить обе части на $-2$. Поскольку мы делим обе части на отрицательное число, мы должны поменять знак (изменить между < и > ).

$x< -3$

Помните:

Если вы умножаете или делите обе части на минус, вы должны перевернуть знак.

Типичные ошибки

Типичные ошибки, которые допускают учащиеся при решении неравенств:

Забыл перевернуть знак при умножении или делении на отрицательное число
Неверное решение неравенства из-за концентрации внимания на переворачивании знака.

Например, если мы вернемся к предыдущему примеру:

\begin{align*}
-2x-1>5 \\
-2x>6 \\
x< 3
\end{align*}
(Здесь отрицательное было забыто)

Списки упорядочения

Обычный вопрос о неравенстве, тестируемый в 9-м классе, заключается в упорядочении значений в порядке возрастания или убывания.

Эти вопросы потребуют от вас сравнения значений чисел в различных формах (десятичные числа, дроби, индексы и т. {-1}, 0,333 , \frac{1}{3} , \frac{3}{8}\)

Примечание. Если вы решите преобразовать все числа в дроби, вы должны убедиться, что все дроби имеют общий знаменатель, прежде чем сравнивать значения. Как только все дроби имеют общий знаменатель, числа можно расположить в соответствии со значением числителей.

Пример:

Упорядочить следующие значения в порядке убывания:

$\frac{1}{3}, \frac{-1}{5}, \frac{1}{4}$

Решение

LCM ( Наименьшее общее кратное ) из $3,4$ и $5$ равно $60$. Следовательно:

Исходная форма	$\frac{1}{3}$	$-\frac{1}{5}$	$\frac{1}{4}$
Скорректированная форма	$\frac{20}{60}$	$\frac{-12}{60}$	$\frac{15}{60}$
Порядок (по убыванию)	$1$	$3$	$2$

Наш окончательный ответ:

$\frac{1}{3},\frac{1}{4},-\frac{1}{5}$

Распространенные ошибки

Распространенные ошибки, которые учащиеся допускают при упорядочении списков: полагая, что если знаменатель одной дроби больше другой, то и эта дробь должна быть больше. например Утверждая, что $\frac{1}{4}$ больше, чем $\frac{1}{3}$ (это не так).

Запись преобразованной формы чисел при перечислении окончательного порядка вместо использования исходной формы.

Контрольные вопросы

1. Заполните пропуск соответствующим символом:

$\frac{2}{5}$, _____ , $0,28$

2. Упорядочьте следующие значения по убыванию порядок:

$136 \text{%} \ ; \frac{5}{3} ; 1.34$

3. Заполните пропуск соответствующим символом:

$1 \frac{5}{ 6}$_____ $ 1 \frac{11}{12}$

4. Решить:

$3x-1>4$

5. Упорядочить следующие значения в порядке возрастания: 9{-3}\)_____ $0,003$

9. Решить:

$-5(2-x) < -10(x-1)$

10. Упорядочить следующие значения в порядке убывания :

$-3.14 ; -\frac{22}{7} ; -3.14\text{%} ; -π$

Решения

1. Преобразовать $\frac{2}{ 5}$ в десятичной форме.

$\frac{2}{5}=0,4>0,28$

2. Преобразовать все в десятичную форму

$136 \text{% }=1,36, \frac{5}{3}=1,67 , 1.34$

Итак, порядок убывания:

$\frac{5}{3},136 \text{% },1.34$

3. Преобразовать обе смешанные дроби в неправильный вид.

$\frac{11}{6}$ _____ $\frac{23}{12}$

Затем сделайте LCM из $12$.

$\frac{22}{12}< \frac{23}{12}$

\begin{align*}
3x-1>4 \\
3x>5 \\
x>\frac{5}{3} \\
\end{align*}

5. Преобразовать все в целое число

$4444.4; 4356; 4444; 40000$

Затем расположить в порядке возрастания: 94\)

6. Использование НОК из $12$

$– \frac{1}{3}$_____ $-\frac{1}{4}$ аналогично $ -\frac{4}{12}$ _____$-\frac{3}{12}$
Из-за отрицательных значений $-\frac{3}{12}$ больше, чем $-\ frac{4}{12}$
∴$-\frac{1}{3}< -\frac{1}{4}$

\begin{align*}
-2( x+3) < & \ -8 \\
x+3> & \ 4 \\
\end{align*}

Деление на минус переворачивает знак

\begin{align*}
x>1 \\
\end{выравнивание*} 9{-3}<0. 003\)

\begin{align*}
-5(2-x)< & \ -10(x-1) \\
2-x> & \ 2(x -1) \\
2-x> & \ 2x-2 \\
-3x> & \ -4 \\
x< & \ \frac{4}{3} \\
\end{align*}

10. Преобразовать в десятичную форму:

$
-3,14 ; -22/7 ; -3,14 \text{%} ; -π \\
-3,14; -3,142857; -0,0314; -3,14159
$

$-3.14 \text{%},-3.14,-π,-\frac{22}{7}$

Дополнительные сложные примеры (из серии Maths MAX для 9-го класса)

Вопросы

Вопросы из серии Maths MAX для 9-го класса, том. 2 Уравнения

Ответы

Решения 9-го класса Maths MAX Series Vol. 2 Уравнения

Резюме

Вот несколько моментов, которые мы хотим, чтобы вы вынесли из этого:

Неравенства говорят вам, является ли число < (меньше) или > (больше) другим числом
При решении уравнений неравенства относитесь к неравенству как к знаку равенства. Если вы умножаете/делите уравнение на отрицательное значение, не забудьте также изменить направление знака неравенства, например. < до >
При сравнении дробей не забудьте преобразовать в HCF:
$\frac{1}{3}=\frac{4}{12}$ и $\frac{1}{4}=\frac{3 {12}$
, поэтому $\frac{1}{3}>\frac{1}{4}$

Запутались в индексах и индексах?

В нашей следующей статье мы расскажем вам об индексах и сурдах.

© Matrix Education и www.matrix.edu.au, 2022. Несанкционированное использование и/или копирование этого материала без письменного разрешения автора и/или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указаны с соответствующим и конкретным указанием на исходный контент.

Решение неравенств – объяснение и примеры

Что такое неравенство в математике?

Слово неравенство означает математическое выражение, в котором стороны не равны друг другу. По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.

В основном существует пять символов неравенства, используемых для представления уравнений неравенства.

Символы неравенства

Эти символы неравенства: меньше ( < ), больше ( > ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ не равно ( ≠ ).

Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, удовлетворяющих условиям данной переменной.

Операции над неравенствами

Операции над линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила для этих операций приведены ниже.

Хотя мы использовали символ < для иллюстрации, вы должны отметить, что те же самые правила применяются к >, ≤ и ≥.

Символ неравенства не меняется, если к обеим сторонам неравенства добавляется одно и то же число. Например, если a< b, то a + c < b +
Вычитание обеих частей неравенства на одно и то же число не меняет знак неравенства. Например, если a< b, то – c < b – c.
Умножение обеих частей неравенства на положительное число не меняет знак неравенства. Например, если a< b и c — положительное число, то a * c < b *
Деление обеих частей неравенства на положительное число не меняет знак неравенства. Если a< b и если c – положительное число, то a/c < b/c
Умножение обеих частей уравнения неравенства на отрицательное число изменяет направление символа неравенства. Например, если a < b и c — отрицательное число, тогда a * c > b *
Аналогично, деление обеих частей уравнения неравенства на отрицательное число изменяет символ неравенства. Если a < b и c — отрицательное число, то a /c > b/c

Как решать неравенства?

Как и линейные уравнения, неравенства можно решать, применяя аналогичные правила и шаги, за некоторыми исключениями. Единственным отличием при решении линейных уравнений является операция, включающая умножение или деление на отрицательное число. Умножение или деление неравенства на отрицательное число изменяет символ неравенства.

Линейные неравенства решаются с помощью следующих операций:

Сложение
Вычитание
Умножение
Деление
Распределение имущества

Решение линейных неравенств со сложением

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример 1

Решите 3x — 5 ≤ 3 — x.

Решение

Начнем со сложения обеих частей неравенства на 5

3x – 5 + 5 ≤ 3 + 5 − x

3x ≤ 8 – x

Затем добавьте обе стороны на x.

3x + x ≤ 8 – x + x

4x ≤ 8

Наконец, разделите обе части неравенства на 4, чтобы получить;

x ≤ 2

Example 2

Calculate the range of values of y, which satisfies the inequality: y − 4 < 2y + 5.

Solution

Add обе части неравенства на 4.

y – 4 + 4 < 2y + 5 + 4

y < 2y + 9

Вычесть обе части на 2y.

y – 2y < 2y – 2y + 9

Y < 9 Умножьте обе части неравенства на −1 и измените направление символа неравенства. y > − 9

Решение линейных неравенств с вычитанием

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример 3

Решите x + 8 > 5.

Решение

Изолируйте переменную x, вычитая 8 из обеих частей неравенства.

х + 8 – 8 > 5 – 8 => х > −3

Следовательно, х > −3.

Пример 4

Решение 5x + 10> 3x + 24.

Раствор

Подряд 10 с обеих сторон.

5x + 10 – 10 > 3x + 24 – 10

5x > 3x + 14.

Теперь мы вычитаем обе части неравенства в 3 раза.

5x – 3x > 3x – 3x + 14

2x > 14

x > 7

Решение линейных неравенств с умножением ниже, чтобы понять эту концепцию

. Пример 50003

4(x/4) > 5 x 4

x > 20

Example 6

Solve -x/4 ≥ 10

Solution:

Multiply both сторон неравенства на 4.

4(-x/4) ≥ 10 x 4

-x ≥ 40

Умножьте обе части неравенства на -1 и измените направление символа неравенства на обратное.

x ≤ – 40

Решение линейных неравенств с делением

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример 7

Решение неравенства: 8x — 2> 0.

Раствор

Сначала добавьте обе стороны неравенства на 2

— Добавьте обе стороны неравенства на 2

— Добавьте обои. + 2 > 0 + 2

8x > 2

Теперь решите, разделив обе части неравенства на 8, чтобы получить;

х > 2/8

х > 1/4

Пример 8

Решение следующего неравенства:

−5x> 100

Раствор

Дивизирование оба стороны на неравенство и неравность на неравности и неравности. символ

= -5x/-5 < 100/-5

= x < - 20

Решение линейных неравенств с использованием свойства распределения

Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.

Пример

Решение: 2 (x — 4) ≥ 3x — 5

Решение

2 (x — 4) ≥ 3x — 5

Применить свойство распределительного.

⟹ 2x — 8 ≥ 3x — 5

Добавить обе стороны на 8.

⟹ 2x — 8 + 8 ≥ 3x — 5 + 8

⟹ 2x ≥ 3x + 3

Обетающую сторону по 3.

⟹ 2x – 3x ≥ 3x + 3 – 3x

⟹ -x ≥ 3

⟹ x ≤ – 3

Пример 10

Студент набрал 60 баллов за первый тест и 45 баллов за второй тест итогового экзамена. Сколько минимальных баллов должен набрать учащийся в третьем тесте, чтобы в среднем было не менее 62 баллов?

Решение

Пусть в третьем тесте набрано x баллов.

(60 + 45 + x)/3 ≥ 62
105 + x ≥ 196
x ≥ 93
Таким образом, учащийся должен набрать 93 балла, чтобы поддерживать средний балл не менее 62 баллов.

Пример 11

Джастину требуется не менее 500 долларов для проведения вечеринки по случаю его дня рождения. Если он уже накопил 150 долларов и до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?

Решение

Пусть минимальная сумма сэкономлена ежемесячно = x

150 + 7x ≥ 500

Решение для x

150 — 150 + 7x ≥ 500 — 150

x ≥ 500003

С. $50 или больше

Пример 12

Найдите два последовательных нечетных числа, которые превышают 10 и имеют сумму менее 40.

Решение

Следовательно, следующее число будет x + 2

x > 10 ………. больше 10

x + (x + 2) < 40 ……сумма меньше 40

Решите уравнения.

2x + 2 < 40

x + 1< 20

x < 19

Объедините два выражения.

10 < x < 19

Таким образом, последовательные нечетные числа равны 11 и 13, 13 и 15, 15 и 17, 17 и 19. и визуализировать числа — это числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными вдоль через равные сегменты или интервалы. Числовая линия имеет нейтральную точку посередине, известную как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа.

Линейные уравнения также могут быть решены графическим методом с использованием числовой прямой. Например, чтобы изобразить x > 1 на числовой прямой, вы обводите цифру 1 на числовой прямой и рисуете линию, идущую от круга в направлении чисел, которая удовлетворяет утверждению о неравенстве. Пример 13 и заполните или заштрихуйте круг. Наконец, нарисуйте линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства.

Пример 14

x ≥ 1

Example 15

–2 < x < 2

Example 16

–1 ≤ x ≤ 2

Пример 17

–1 < x ≤ 2

Обзор для математического экзамена 9 — единица 6 — линейные уравнения и неравенство

Похожие документы

Второй модуль практического теста: Законы о степенях и экспонентах

Класс: Дата: Вторая часть Практический тест: Законы о степенях и экспонентах Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос 1 Запишите основание ( 6) 5 a 6 b 6 c 6 5 d 5

Дополнительная информация

Обзор закона экспоненты 3 + 3 0.

Имя: Класс: Дата: Обзор закона Eponent Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос Выражение + 0 равно 0 Упростить 6 6 8 6 6 6 0 Упростить ( ) (

Дополнительная информация

Решение линейных уравнений с одной переменной. Примеры работы

Решение линейных уравнений с одной переменной Примеры работы Решите уравнение 30 x 1 22x Решите уравнение 30 x 1 22x Наша цель состоит в том, чтобы изолировать x на одной стороне. Мы сделаем это, добавив (или вычтя) количества

Дополнительная информация

Планы алгебры. 7 класс. Апрель 2012 г. Автор: Даниэль Браун; Розанна Гаудио; Лори Марано; Мелисса Пино; Бет Орландо и Шерри Виотто

Планы раздела по алгебре, 7 класс, апрель 2012 г. Автор: Даниэль Браун; Розанна Гаудио; Лори Марано; Мелисса Пино; Бет Орландо и Шерри Виотто Лист планирования модуля по алгебре Большие идеи по алгебре (доктор Смолл)

Дополнительная информация

Летнее задание для поступающих в 7-й класс средней школы Фэйрхоуп учащихся продвинутого уровня математики

Летнее задание для поступающих в седьмой класс средней школы Фэйрхоуп, учащихся продвинутого уровня по математике. Исследования показывают, что большинство учащихся теряют около двух месяцев математических способностей за лето, когда они не занимаются 9-м классом.0003

Дополнительная информация

Уравнения без решений Давайте посмотрим на следующее уравнение: 2 +3=2 +7

5.4 Решение уравнений с бесконечным числом решений или без них До сих пор мы рассматривали уравнения, у которых есть ровно одно решение. В уравнениях других типов, таких как

, может быть не только решение. Дополнительная информация

1.6. Решение линейных неравенств ПРИМЕР 1 ПРИМЕР 2. Нарисуйте график простого неравенства. График составных неравенств

.6 Решите линейные неравенства Прежде чем решать линейные уравнения. Теперь Вы будете решать линейные неравенства. Почему? Таким образом, вы можете описать диапазоны температур, как в упр. 54. Ключевой словарный запас составного линейного неравенства

Дополнительная информация

Определение 8.1. Два неравенства эквивалентны, если они имеют одно и то же множество решений. Добавьте или вычтите одно и то же значение с обеих сторон неравенства.

8 Понятия о неравенствах: эквивалентные неравенства Линейные и нелинейные неравенства Неравенства абсолютного значения (разделы 4.6 и 1.1) 8. 1 Эквивалентные неравенства Определение 8.1 Два неравенства эквивалентны

Дополнительная информация

IV. АЛГЕБРАИЧЕСКИЕ ПОНЯТИЯ

IV. АЛГЕБРАИЧЕСКИЕ ПОНЯТИЯ Алгебра — это язык математики. Большую часть наблюдаемого мира можно охарактеризовать как имеющую закономерность, когда изменение одной величины приводит к изменению другой

Дополнительная информация

1.6. Кусочные функции. УЗНАТЬ О математике. Представление проблемы с помощью графической модели

1.6 Кусочные функции ВАМ ПОТРЕБУЕТСЯ Калькулятор на миллиметровой бумаге ЦЕЛЬ Понимать, интерпретировать и графически изображать ситуации, описываемые кусочными функциями. УЗНАЙТЕ О МАТЕМАТИКЕ Городская парковка

Дополнительная информация

Стандартные основные вопросы по математике

Общие основные примеры вопросов по математике программы тестирования штата Нью-Йорк, класс 7 Материалы, содержащиеся в данном документе, предназначены для использования учителями штата Нью-Йорк. Настоящим предоставляется разрешение учителям и

Дополнительная информация

Примеры вопросов диагностики системы муниципальных колледжей Северной Каролины и вступительного экзамена

Примеры вопросов диагностики системы муниципальных колледжей Северной Каролины и вступительного экзамена 01 The College Board. College Board, ACCUPLACER, WritePlacer и логотип желудя являются зарегистрированными товарными знаками College

. Дополнительная информация

План урока — процент от числа/увеличение и уменьшение

План урока – Проценты от числа/Увеличение и уменьшение Ресурсы главы – Урок 4-11 Нахождение процентов от чисел – Урок 4-11 Нахождение процентов от чисел Ответы – Урок 4-12 Проценты от увеличения и

Дополнительная информация

Практическая математическая алгебра

Практическая математическая алгебра Пэм Мидер и Джуди Сторер, иллюстрации Джули Мазур Содержание Учителю. .. v Тема: Соотношение и пропорция 1. Продвижение конфет… 1 2. Оценка популяций диких животных… 6 3.

Дополнительная информация

Практический тест EOC по алгебре № 2

Класс: Дата: Алгебра EOC Практический тест № 2 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. 1. Какая из следующих прямых перпендикулярна прямой y =

Дополнительная информация

7. Решение линейных неравенств и составных неравенств.

7. Решение линейных неравенств и составных неравенств Шаги решения линейных неравенств очень похожи на шаги решения линейных уравнений. Большие различия умножаются и делятся на

Дополнительная информация

Уравнения абсолютного значения и неравенства

. Уравнения абсолютного значения и неравенства. ЗАДАЧИ 1. Решить уравнение абсолютного значения с одной переменной. Решите абсолютное неравенство одной переменной ПРИМЕЧАНИЕ Технически мы имеем в виду расстояние между

Дополнительная информация

Обзор теста по математике PERT

PERT Mathematics Test Review Prof. Miguel A. Montañez ESL/Math Seminar Math Test? НЕТ!!!!!!! Я не силен в математике! Я не могу получить высшее образование из-за математики! Я ненавижу математику! Полезные сайты Веб-сайт отдела математики Wolfson

Дополнительная информация

Часть 1. Выражения, уравнения и неравенства: упрощение и решение

Раздел 7. Алгебраические манипуляции и решение. Часть 1. Выражения, уравнения и неравенства: упрощение и решение. Прежде чем приступить к математике, давайте поговорим о словах

Дополнительная информация

Алгебра I Восстановление кредита

Algebra I Credit Recovery ОПИСАНИЕ КУРСА: Цель этого курса — помочь учащимся освоить работу с математическими выражениями, уравнениями, графиками и другими темами и их оценку,

Дополнительная информация

2.

2.3. Нахождение полиномиальных функций. Введение: Как это обычно бывает при изучении нового понятия в математике, новое понятие является противоположностью предыдущего. Вспомни, как ты впервые узнал

Дополнительная информация

CAHSEE о партнерстве Калифорнийского университета в Дэвисе и университетах Target

Калифорнийский университет в Дэвисе, Партнерство между школами и университетами CAHSEE по учебной программе по целевой математике Опубликовано Калифорнийским университетом в Дэвисе, Программа партнерства между школами и университетами 006 Директор Сара Р. Мартинес,

Дополнительная информация

Имя: Класс: Дата: ID: A

Класс: Дата: Словесные задачи на наклон 1. Стоимость школьного банкета 9 долларов.5 плюс 15 долларов за каждого присутствующего. Напишите уравнение, которое определяет общую стоимость как функцию количества людей, пришедших на мероприятие. Что

Дополнительная информация

Алгебра 2: обзор Q1 и Q2

Имя: Класс: Дата: ID: A Алгебра 2: Обзор Q1 и Q2 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. 1. Каков график y = 2(x 2) 2 4? а. в. б. д. Короткий

Дополнительная информация

Графики линейных уравнений с двумя переменными

Математика 123 Раздел 3.2 — Построение графика линейных уравнений с использованием точек пересечения — Страница 1 Построение графика линейного уравнения с двумя переменными I. Построение графика A. График линии — это просто набор точек решения

Дополнительная информация

HFCC Math Lab Beginning Algebra 13 ПЕРЕВОД АНГЛИЙСКОГО В АЛГЕБРУ: СЛОВА, ФРАЗЫ, ПРЕДЛОЖЕНИЯ

HFCC Math Lab Beginning Algebra 1 ПЕРЕВОД С АНГЛИЙСКОГО В АЛГЕБРУ: СЛОВА, ФРАЗЫ, ПРЕДЛОЖЕНИЯ Прежде чем решать текстовые задачи по алгебре, вы должны уметь менять слова, фразы и предложения

Дополнительная информация

ПРИМЕРЫ ПРИСВОЕНИЯ УРОВНЕЙ ГЛУБИНЫ ЗНАНИЙ АНАЛИЗ СООТВЕТСТВИЯ CCSSO TILSA ИЗУЧЕНИЕ СООТВЕТСТВИЯ 21-24 мая 2001 г.

ПРИМЕРЫ ПРИСВОЕНИЯ УРОВНЕЙ ГЛУБИНЫ ЗНАНИЙ АНАЛИЗ СООТВЕТСТВИЯ CCSSO TILSA СООТВЕТСТВИЕ ИССЛЕДОВАНИЮ 21-24 мая 2001 г., версия 2.0 Уровень 1 Отзыв Отзыв факта, информации или процедуры Пример 1:1 8 класс

Дополнительная информация

1.6. Кусочные функции. УЗНАТЬ О математике. Представление проблемы с помощью графической модели

1. Кусочные функции ВАМ ПОТРЕБУЕТСЯ Калькулятор на миллиметровой бумаге ЦЕЛЬ Понимать, интерпретировать и графически изображать ситуации, описываемые b кусочными функциями. УЗНАЙТЕ О МАТЕМАТИКЕ Городская парковка использует

Дополнительная информация

Урок 4: Решение линейных уравнений и построение графиков

Урок 4: Решение линейных уравнений и построение графиков Избранное содержание Стандарты Контрольные показатели Адресовано: A-2-M Моделирование и разработка методов решения уравнений и неравенств (например, с использованием диаграмм, графиков,

Дополнительная информация

Мозговая игра.

Имя Дата Класс Период Игра для ума 3.4 Решение и построение графиков неравенств МАТЕРИАЛЫ игровые карточки КАК ИГРАТЬ Поработайте с другим учеником. Перемешайте карточки, полученные от учителя. Затем положите их лицевой стороной вниз

Дополнительная информация

Прентис Холл: Математика средней школы, курс 1 2002 г. Соответствует: Стандарты обучения математике Нью-Йорка (средний уровень)

Стандарты обучения математике Нью-Йорка (средний уровень) Математическое мышление Основная идея: учащиеся используют МАТЕМАТИЧЕСКОЕ ОБСУЖДЕНИЕ для анализа математических ситуаций, выдвижения предположений, сбора доказательств и построения

Дополнительная информация

Определите, представляет ли уравнение функцию

Вопрос: Что такое линейная функция? Термин линейная функция состоит из двух частей: линейной и функциональной. Чтобы понять, что эти термины означают вместе, мы должны сначала понять, что такое функция.

Дополнительная информация

12. Уравнения двух прямых и . Чему равно значение х в решении этой системы уравнений?

Название: Период: Рабочий лист решения систем уравнений со текстовыми задачами Для всех задач определите переменные, напишите систему уравнений и решите для всех переменных. Направления от TAKS, так что все

Дополнительная информация

Формулы и решение задач

2.4 Формулы и решение задач 2.4 ЦЕЛИ. Решите буквальное уравнение для одной из его переменных 2. Преобразуйте словосочетание в уравнение 3. Используйте уравнение для решения приложения Формулы чрезвычайно

Дополнительная информация

Алгебра. Урок 5.1 Использование букв в качестве цифр.

5 ГЛАВА Урок алгебры 5.1 Использование букв в качестве чисел Напишите выражение для каждой ситуации. 1. Прибавить 8 к w 2. Вычесть 10 из a 3. Суммировать p и 3_4 4. Вычесть 6y из 5 5. Умножить 6 на g 6. Разделить

Дополнительная информация

Как понять и решить алгебраические уравнения

Текст курса алгебры в колледже Барнетт, Рэймонд А., Майкл Р. Зиглер и Карл Э. Байлин. College Algebra, 8-е издание, McGraw-Hill, 2008 г., ISBN: 978-0-07-286738-1 Описание курса Этот курс содержит

Дополнительная информация

Дипломная программа средней школы New Summit School по алгебре II

Программа Описание курса: Алгебра II рассчитана на два семестра. Студенты, завершившие этот курс, получат 1,0 единицу по завершении. Необходимые материалы: 1. Учебный текст Glencoe Algebra 2: Integration,

Дополнительная информация

Приобретение плана урока для концепции, темы или навыка — не на день

Приобретение План урока Концепция: Линейные системы Имя(а) автора: Математический кадровый комитет средней школы штата Делавэр Класс: Девятый класс Сроки: Два 45-минутных периода Требования: Написание алгебраических выражений

Дополнительная информация

5 систем уравнений

Понятия систем уравнений: Решения систем уравнений — Графические и алгебраические системы решения — Метод подстановки Системы решения — Метод исключения с использованием —мерных графов для аппроксимации

Дополнительная информация

ТЕСТ ГЛАВА 6, УРАВНЕНИЯ, НЕРАВЕНСТВА, РЕШЕНИЕ ЗАДАЧ.

ТЕСТ ГЛАВА 6, УРАВНЕНИЯ, НЕРАВЕНСТВА, РЕШЕНИЕ ЗАДАЧ. Множитель x 2-5x + 6. 2. Множитель x 2-4x — 5. 3. Решить: (x + 2)(x — 3) = 0 x(x — 3)(x + 4) = 0 4. Решить разложением: х 2 + х + 2 = 0. 5. Решить по

Дополнительная информация

2) Основываясь на информации в таблице, какой выбор НАИЛУЧШЕ показывает ответ на 1 906? 906 899 904 909

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ) Умножение числа на дает какой тип. даже. 0. четный., 0. странно.., 0. даже ) Основываясь на информации в таблице, какой выбор НАИЛУЧШЕ показывает ответ на 0? 0 0 0 )

Дополнительная информация

Учащиеся, которые в настоящее время сдают экзамен по математике по алгебре 2 штата Мэн, восток, проблемы с обзором

Учащиеся, которые в настоящее время изучают алгебру, Восточная математика штата Мэн. Проблемы с обзором вступительной группы У фактической рабочей группы есть 100 вопросов за 3 часа. Команда размещения является бесплатным ответом, студенты должны ответить на вопросы и написать

Дополнительная информация

МАКМИЛЛАН/МАКГРОУ-ХИЛЛ. МАТЕМАТИКА СОЕДИНЯЕТ И ВОЗДЕЙСТВУЕТ МАТЕМАТИКА ВАШИНГТОНСКИЕ МАТЕМАТИЧЕСКИЕ СТАНДАРТЫ. ОСНОВНЫЕ ТРЕБОВАНИЯ К АКАДЕМИЧЕСКОМУ ОБУЧЕНИЮ (EALR)

MACMILLAN/McGRAW-HILL MATH СОЕДИНЯЕТ И ВЛИЯЕТ МАТЕМАТИКА НА МАТЕМАТИЧЕСКИЕ СТАНДАРТЫ ШТАТА ВАШИНГТОН, ОСНОВНЫЕ ТРЕБОВАНИЯ К АКАДЕМИЧЕСКОМУ ОБРАЗОВАНИЮ (EALR) И ОЖИДАНИЯ УРОВНЯ КЛАССА (GLE) / Издание, Copyright

Дополнительная информация

Геометрия Глава 2 Учебное пособие

Геометрия Глава 2 Учебное пособие Краткий ответ (по 2 балла за каждый) 1. (1 балл) Назовите свойство равенства, подтверждающее утверждение: Если g = h, то. 2. (1 балл) Назовите свойство конгруэнтности, которое оправдывает

Дополнительная информация

Программы итоговой оценки IOWA. Выпущенные материалы ALGEBRA I. Авторские права принадлежат Университету Айовы, 2010 г.

Выпущенные материалы программ итоговой оценки штата Айова. Авторские права принадлежат Университету Айовы, 2010 г. АЛГЕБРА I 1 Салли работает продавцом автомобилей и получает 2000 долларов в месяц. Она также зарабатывает 500 долларов за

. Дополнительная информация

Прямой перевод — это процесс перевода английских слов и фраз в числа, математические символы, выражения и уравнения.

Раздел 1 Математика имеет свой собственный язык. Чтобы иметь возможность решать многие типы текстовых задач, нам нужно уметь переводить английский язык на математический язык. процесс перевода

Дополнительная информация

Пример темы WritePlacer.

. Знание другого языка способствует лучшему пониманию культурного разнообразия народов мира. Люди, владеющие иностранными языками, с большей готовностью оценивают ценности других людей

Дополнительная информация

Алгебра 1 Если вы согласны с этим размещением, то у вас нет дальнейших действий, чтобы сдать часть алгебры 1 вступительного теста по математике.

Уважаемые родители! По результатам теста для поступления в старшие классы (HSPT) ваш ребенок должен сдать алгебру 1 этой осенью. Если вас устраивает это место размещения, вам больше нечего делать

Дополнительная информация

Системы линейных уравнений с тремя переменными

5.3 Системы линейных уравнений с тремя переменными 5.3 ЗАДАЧИ 1. Найти упорядоченные тройки, связанные с тремя уравнениями 2. Решить систему методом сложения 3. Графически интерпретировать решение 4.

Дополнительная информация

Экзамены Keystone: ориентиры оценки по алгебре I и допустимый контент. Пенсильвания

Keystone Exams: Algebra I Assessment Anchors и Pennsylvania Algebra 1 СТАНДАРТЫ 2010 МОДУЛЬ 1 Операции, линейные уравнения и неравенства ТОЧКА ОЦЕНКИ A1.1.1 Операции с действительными числами и

Дополнительная информация

Индикатор 2: Используйте различные алгебраические концепции и методы для решения уравнений и неравенств.

Учебные цели по математике для 3-го класса Алгебра: Индикатор 1: Использование процедур для преобразования алгебраических выражений. 3.А.1.1. Учащиеся могут объяснить взаимосвязь между повторяющимся сложением и умножением.

Дополнительная информация

Дроби и линейные уравнения

Дроби и линейные уравнения Операции с дробями Хотя вы можете выполнять операции с дробями с помощью калькулятора, для этого рабочего листа вы должны выполнять операции вручную. Вы должны показать все шаги

Дополнительная информация

ПЛАН КУРСОВ КОЛЛЕДЖА HIBBING COMMUNITY

ОПИСАНИЕ КУРСОВ КОЛЛЕДЖА HIBBING COMMUNITY НОМЕР И НАЗВАНИЕ КУРСА: — Начальная алгебра КРЕДИТЫ: 4 (Урок 4 / Лаборатория 0) ПРЕДВАРИТЕЛЬНЫЕ ТРЕБОВАНИЯ: МАТЕМАТИКА 0920: Фундаментальная математика с оценкой C или выше, вступительный экзамен,

Дополнительная информация

Решение систем методом исключения

1 декабря 2008 г. Решение систем методом исключения стр. 1 Решение систем методом исключения Вот еще один метод решения системы двух уравнений. Иногда этот метод проще, чем построение графика

Дополнительная информация

Алгебра 2 Глава 5 Практический тест (обзор)

Имя: Класс: Дата: Алгебра 2 Глава 5 Практический тест (повторение) Множественный выбор Определите вариант, который лучше всего дополняет утверждение или отвечает на вопрос. Определите, является ли функция линейной или

Дополнительная информация

3.2. Решение квадратных уравнений. Введение. Предпосылки. Результаты обучения. Стиль обучения

Решение квадратных уравнений 3.2 Введение Квадратное уравнение — это уравнение, которое можно записать в виде ax 2 + bx + c = 0, где a, b и c — числа, а x — неизвестное, значение (значения) которого мы хотим найти.

Дополнительная информация

Линейные уравнения и неравенства

Линейные уравнения и неравенства Раздел 1.1 Prof. Wodarz Math 109 — Fall 2008 Содержание 1 Линейные уравнения 2 1.1 Стандартная форма линейного уравнения ……………. 2 1.2 Решение линейных уравнений… ……………….

Дополнительная информация

7-дневный план занятий по целочисленной арифметике для 7-го класса Брайана М.

Семидневный план целочисленной арифметики 7-го класса, Брайан М. Фишер Лакаванна. .3 Ресурсы

Дополнительная информация

Наука управления 250: математические методы бизнес-анализа, три часа семестра

Наука управления 250: Математические методы бизнес-анализа Три часа семестра Д-р Лора Суонсон Офис: FH, Rm. 3121 Домашняя страница: http://www.siue.edu/~lswanso Рабочий телефон: (618) 650-2710 Электронная почта:

Дополнительная информация

План урока с дополнительным кредитным заданием. Следующее задание является необязательным и может быть выполнено для получения до 5 баллов на ранее сданном экзамене.

Дополнительный кредит Задание План урока Следующее задание является необязательным и может быть выполнено, чтобы получить до 5 баллов на ранее сданном экзамене. Дополнительное кредитное задание состоит в том, чтобы создать машинописный урок

. Дополнительная информация

РУКОВОДСТВО ПО ОБЗОРУ ОБЩЕСТВЕННОГО КОЛЛЕДЖА ОКРУГА КОУЛИ Compass Algebra Level 2

СООБЩЕСТВО ОКРУГА КОУЛИ РУКОВОДСТВО ПО ОБЗОРУ КОЛЛЕДЖА Compass Algebra Level Это учебное пособие предназначено для студентов, пытающихся сдать экзамен по алгебре колледжа. Существует три уровня учебных пособий по математике. 1. Если х и у 1, то что

Дополнительная информация

8.9 Пересечение прямых и конических

8.9 Пересечение линий и конусов Центральный круг хоккейной площадки имеет радиус 4,5 м. Диаметр центрального круга лежит на центральной красной линии. центральная (красная) линия центральный круг ИССЛЕДОВАНИЕ &

Дополнительная информация

4 Проценты Примечания к главам

4 Проценты Примечания к главам Концепции и навыки спецификации GCSE Найти процент от количества (N o): 4. Использовать проценты для решения задач (N m): 4., 4.2, 4., 4.4 Использовать проценты в реальных жизненных ситуациях:

Дополнительная информация

Алгебра I Примеры вопросов. 1 Какой упорядоченной пары нет в наборе решений (1) (5,3) (2) (4,3) (3) (3,4) (4) (4,4)

1 Какая упорядоченная пара не входит в набор решений (1) (5,3) (2) (4,3) (3) (3,4) (4) (4,4) y 1 > x + 5 и у 3x 2? 2 5 2 Если для нахождения корней уравнения используется квадратичная формула x 2 6x 19 = 0,

Дополнительная информация

Вес (фунты) 3 5 8 10 Стоимость ($) 9 15 24 30

Имя: Класс: Дата: ID: R CCA Week 12 Test ОБЗОР 7R 1. Посмотрите на таблицу ниже. Вес (фунты) 3 5 8 10 Стоимость ($) 915 24 30 Определить константу пропорциональности. 2. Элизабет прошла тест из 25 вопросов.

Дополнительная информация

ОБЗОРНЫЕ ЛИСТЫ ВВОДНАЯ ФИЗИЧЕСКАЯ МАТЕМАТИКА 52

ОБЗОРНЫЕ ЛИСТЫ ВВЕДЕНИЕ В ФИЗИЧЕСКИЕ НАУКИ МАТЕМАТИКА 52 Краткое изложение понятий, необходимых для успешного изучения математики На следующих листах перечислены ключевые понятия, изучаемые в указанном курсе математики.

Дополнительная информация

Решение рациональных уравнений и неравенств

8-5 Решение рациональных уравнений и неравенств TEKS 2A.10.D Рациональные функции: определение решений рациональных уравнений с использованием графиков, таблиц и алгебраических методов. Задача Решить рациональные уравнения

Дополнительная информация

Практический тест EOC по алгебре № 4

Класс: Дата: Алгебра EOC Практический тест № 4 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. 1. Для f(x) = 3x + 4 найдите f(2) и x такие, что f(x) = 17,9.0003

Дополнительная информация

Алгебра 1. Практическая рабочая тетрадь с примерами. Макдугал Литтел. Концепции и навыки

McDougal Littell Algebra 1 Понятия и навыки Ларсон Босвелл Канольд Жесткая практическая рабочая тетрадь с примерами Практическая рабочая тетрадь обеспечивает дополнительную практику с проработанными примерами для каждого урока.

Дополнительная информация

Математика 121 — Программа онлайн-колледжа по алгебре, весна 2015 г.

Math 121 — Online College Algebra Syllabus Spring 2015 Преподаватель: Майкл Азлин Офис: Hume 218 Часы работы: M/W: 10:00 11:30, T/Th: 9:00 10:30 или по апп. /Th часов в течение тестовых недель)

Дополнительная информация

Математика 143 — Алгебра колледжа (онлайн)

Math 143 — College Algebra (онлайн) 3 кредита Срок: Преподаватель: весна 2010 г. Ken Floyd (208) 732-6583 Местонахождение офиса: Часы работы: Shields 206E 13-14 PM, M-F E-mail: [email protected] 10 утра — полдень суббота

Дополнительная информация

Алгебра I Примечания учителя Выражения, уравнения и формулы Обзор

Большие идеи Написать и оценить алгебраические выражения Использовать выражения для написания уравнений и неравенств Решать уравнения Представлять функции в виде словесных правил, уравнений, таблиц и графиков Повторить эти концепции

Дополнительная информация

2.

HFCC Learning Lab ЗАДАЧИ НА ПРОЦЕНТНЫЕ СЛОВА Арифметика — 11 Многие задачи на проценты можно решить с помощью пропорции. Чтобы использовать этот метод, вы должны быть знакомы со следующими представлениями о процентах:

Дополнительная информация

Решение специальных систем линейных уравнений

5. Решение специальных систем линейных уравнений Основной вопрос Может ли система линейных уравнений не иметь решения или решений может быть бесконечно много? Использование таблицы для решения задачи Работайте с партнером. Вы инвестируете

Дополнительная информация

Вы с друзьями отправляетесь в любимый ресторан

19 Анализ затрат, объема и прибыли Цели обучения 1 Определить, как изменения объема влияют на затраты 2 Использовать анализ CVP для расчета точки безубыточности 3 Использовать анализ CVP для планирования прибыли и построить график CVP

Дополнительная информация

Алгебра I.

В наш технологический век математика важнее, чем когда-либо. Когда учащиеся заканчивают школу, они все чаще используют математику в своей работе и повседневной жизни, работая с компьютерным оборудованием,

Дополнительная информация

Результаты исследования серии «Переход к алгебре»

Результаты исследования серии «Переход к алгебре» Результаты до и после тестирования Опросы учителей Интервью с фокус-группами учителей Интервью с фокус-группами учащихся Опрос учащихся в конце года Следующие

Дополнительная информация

Стандартные основные вопросы по математике

Программа тестирования штата Нью-Йорк Математика Общие основные примеры вопросов Оценка Содержащиеся здесь материалы предназначены для использования учителями штата Нью-Йорк. Настоящим разрешение предоставляется учителям и

Дополнительная информация

Давайте рассмотрим содержание и навыки, оцениваемые с помощью вопросов Heart of Algebra.

Глава 9 Сердце алгебры Сердце алгебры сосредоточено на овладении линейными уравнениями, системами линейных уравнений и линейными функциями. Умение анализировать и составлять линейные уравнения, неравенства,

Дополнительная информация

ОСНОВНОЕ СОДЕРЖАНИЕ МОДУЛЬ Алгебра I — Линейные уравнения и неравенства T-71. Приложения. F = мс + б.

ОСНОВНОЕ СОДЕРЖАНИЕ МОДУЛЬ Алгебра I – Линейные уравнения и неравенства T-71 Приложения Формула y = mx + b иногда встречается с другими символами. Например, вместо x мы могли бы использовать букву C.

Дополнительная информация

Онлайн-учебные материалы по математике в соответствии со стандартами обучения и структурой учебного плана по алгебре I 2009 г.

Provider York County School Division Программа курса URL-адрес http://yorkcountyschools.org/virtuallearning/coursecatalog.aspx Название курса Алгебра I AB Последнее обновление 2010 г. — A.1 Учащийся представит вербальный

Дополнительная информация

Математика 830-Элементарная алгебра

Математика 830 — Элементарная алгебра Вт, четверг: 13:00–14:45 Преподаватель: доктор Леми Накамура Комната: 3507 Офис: 3621 Section 1979 Телефон: 760-757-2121 доб. 6219 Весна 2010 Электронная почта: [email protected] Офис

Дополнительная информация

Предварительные требования: TSI Math Complete и средняя школа по алгебре II и геометрии или MATH 0303.

Программа курса Math 1314 College Algebra Дата пересмотра: 8-21-15 Описание каталога: Углубленное изучение и применение полиномиальных, рациональных, радикальных, экспоненциальных и логарифмических функций и систем

Дополнительная информация

Целочисленные операции.

7 класс Математика, 1 четверть, Раздел 1.1 Обзор операций с целыми числами Количество учебных дней: 15 (1 день = 45 минут) Содержание для изучения Опишите ситуации, в которых противоположности объединяются, чтобы получить ноль.

Дополнительная информация

Свойства чисел со знаком Раздел 1.2 Коммутативные свойства Если a и b — любые числа,

1 Резюме ОПРЕДЕЛЕНИЕ/ПРОЦЕДУРА ПРИМЕР ССЫЛКА От арифметики к алгебре Раздел 1.1 Сложение x y означает сумму x и y или x плюс y. Некоторые другие слова Сумма x и 5 равна x 5. указывает на сложение

Дополнительная информация

JMS, MAT150 НАСТОЯЩАЯ ПРОГРАММА, РАСПИСАНИЕ КУРСА, ЗАДАНИЯ И ДАТЫ ЭКЗАМЕНОВ Летом 2014 ГОДА МОГУТ ИЗМЕНЯТЬСЯ В СООТВЕТСТВИИ С ОБСТОЯТЕЛЬСТВАМИ.

SCOTTSDALE COMMUNITY COLLEGE MATHEMATIC DEPARTMENT MAT150, COLLEGE ALGEBRA CLASS# 16015 ВРЕМЯ: 12:10 14:20 ДНИ: Пн, Вт, Пт, Чт РАСПОЛОЖЕНИЕ: CM 465 ПРЕПОДАВАТЕЛЬ: Дж. Майкл Синклер Голосовая почта: 480-731-8866

Дополнительная информация

Решение систем подстановок линейных уравнений

Решение систем линейных уравнений с подстановками Результат (цель обучения) Учащиеся будут точно решать систему уравнений алгебраически с помощью подстановок. Студент/Класс Цель Студенты думают

Дополнительная информация

Что измеряет число m в y = mx + b? Чтобы выяснить это, предположим, что (x 1, y 1 ) и (x 2, y 2 ) — две точки на графике y = mx + b.

МОДУЛЬ ОСНОВНОГО СОДЕРЖАНИЯ Алгебра. Линейные уравнения и неравенства T-37/H-37 Что измеряет число m в y = mx + b? Чтобы выяснить это, предположим, что (x 1, y 1 ) и (x 2, y 2 ) — две точки на графике

. Дополнительная информация

Издательство АГС-Потребительская математика. Армирующие мероприятия. Дополнительные практические задачи. Групповые исследования. AGS Publishing-Потребительская математика

ПРЕДМЕТЫ: ПОТРЕБИТЕЛЬСКАЯ МАТЕМАТИКА УРОВЕНЬ(И) ОЦЕНОК: 12 ПЕРЕСМОТР: ИЮЛЬ 2007 ГОДА ФИЛОСОФИЯ: Этот курс разработан как годовой курс, который будет посвящен методологии и применению в реальном мире и предоставит учащимся

Дополнительная информация

9 класс комплект 1 заметки по математике, чтобы сопровождать 9Книга Х.

Часть 1: 9-й класс, комплект 1 «Заметки по математике», прилагаемый к книге 9H. уравнения 1. (стр. 1), 1.6 (стр. 44), 4.6 (стр. 196) последовательности 3. (стр. 115) Учащиеся используют книгу Elmwood Press Essential Maths Дэвида Реймера (9H

Дополнительная информация

Неделя 2: Экспоненциальные функции

Неделя 2: Экспоненциальные функции. Цели: Знакомство с экспоненциальными функциями. Изучение сложного процента и введение числа. Рекомендуемая литература в учебнике: Глава 4: 4.1 и Глава 5: 5.1. Практические задачи:

Дополнительная информация

Урок 9: Сдавать в аренду с выкупом или не сдавать в аренду?

Все о кредите Урок 9: сдавать в аренду с выкупом или не сдавать в аренду? Стандарты и ориентиры (см. стр. C-61) Описание урока Учащиеся повторяют элементы контракта. Обсуждают характеристики

Дополнительная информация

Прентис Холл. Калифорнийское издание алгебры 1 — классическое издание (Смит / Чарльз) 2008 г. 8 класс

Prentice Hall 8 класс Калифорнийское издание алгебры 1 — Classics Edition (Smith/Charles) 2008 К О Р Е Л А Т И Д К Карта Калифорнии для программы базового уровня для 8 класса ОПИСАНИЕ ПРОГРАММЫ Prentice

Дополнительная информация

Десятичные числа и проценты

Десятичные числа и проценты Образцы рабочих листов для выбранных аспектов Пол Харлинг b Распознавание числовых отношений между координатами в первом квадранте связанных точек Ключевой этап 2 (AT2) на линии

Дополнительная информация

Административное обучение – основной учебный план ОБЛОЖКА

Административная программа — основной учебный план. Дополнительная информация

F.IF.7b: Корневая, кусочная, ступенчатая и абсолютная функции графа

F.IF.7b: Корневая, кусочная, ступенчатая и абсолютная функции графика F.IF.7b: Корневая, кусочная, ступенчатая и абсолютная функции графика Анализ функций с использованием различных представлений. 7. Графические функции выражены

Дополнительная информация

Колледж Алгебра МАТЕМАТИКА 1111/11

Колледж Алгебра МАТЕМАТИКА 1111 Весна 2011 Преподаватель: Гордон Шумард Класс: CRN Дни Временной курс Номер/сек Местоположение 12293 T R 8:00–9:15 MATH 1111/09 Burruss Building- 109 12294 T R 9:30–10:45 MATH 1111/11

Дополнительная информация

Урок SPIRIT 2.0: Точка пересечения

SPIRIT 2.0 Урок: точка пересечения ================================Заголовок урока======== ===================== Название урока: Точка пересечения Дата проекта: 17.

\(\влево(4;12\вправо)\)	Круглые скобки означают, что номер не включен. В этот интервал входят все действительные числа больше, но не равны \(\text{4}\) и меньше, но не равны \(\текст{12}\).
\(\влево(-\infty ;-1\вправо)\)	Круглые скобки всегда используются для положительной и отрицательной бесконечности. Этот интервал включает все действительные числа меньше, но не равны \(-\text{1}\).
\(\влево[1;13\вправо)\)	Квадратная скобка указывает, что число включено. В этот интервал входят все действительные числа больше или равные \(\text{1}\) и меньше, но не равные \(\текст{13}\).

Исходная форма	\(\frac{1}{3}\)	\(-\frac{1}{5}\)	\(\frac{1}{4}\)
Скорректированная форма	\(\frac{20}{60}\)	\(\frac{-12}{60}\)	\(\frac{15}{60}\)
Порядок (по убыванию)	\(1\)	\(3\)	\(2\)

Решение линейных и квадратных неравенств 9 класс онлайн-подготовка на Ростелеком Лицей

Определение линейного неравенства

Решение линейного неравенства графическим способом

Решение квадратного неравенства графическим способом

Квадратичная функция в общем виде, D>0

Квадратичная функция в общем виде, D=0

Квадратичная функция в общем виде, D<0

Решение задач

Решение неравенства с параметром

19. Заключение

Линейные и квадратные неравенства. 9 класс

Алгебра. Урок 8. Неравенства, системы неравенств.

Системы линейных неравенств с одной переменной

Примеры решения систем линейных неравенств с одной переменной

Когда решений нет

Задания для самостоятельного решения

Линейные неравенства подборка заданий. можно познакомиться с функциями и производными

Используя равносильные преобразования

Методом интервалов

Графическим способом

Неравенства, сводящиеся к линейным

Сходные правила решения неравенств.

Урок и презентация на тему: «Примеры линейных неравенств и их решение»

Задачи на линейные неравенства

Понятие системы неравенств

Системы неравенств и системы уравнений

Виды неравенств

Свойства неравенств

Решение систем неравенств. Общие сведения. Способы решения

Графический способ

Алгебраический способ

Способ подстановки

Метод интервалов

Какой способ использовать?

Если что-то не получается

Решебник?

Выводы

Линейные уравнения с параметром. Анализ решений

линейных неравенств с двумя переменными| Графики и уравнения | Примеры

1.

2. Как отличить линейные неравенства с двумя переменными от линейных уравнений с двумя переменными?

3. Что является примером линейного неравенства?

4. Какие символы используются в линейных неравенствах?

5. Что означают линейные неравенства?

6. Как определить линейное неравенство?

7. Для чего используются линейные неравенства?

8. Какие 5 символов неравенства?

9. Что означает R в неравенствах?

4.7 Решение линейных неравенств | Уравнения и неравенства

4.7 Решение линейных неравенств (EMA3H)

Интервальное обозначение (EMA3J)

Рабочий пример 17: Решение линейных неравенств

Переставить и решить для \(r\)

Умножение на \(-\text{1}\) и обратный знак неравенства

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Рабочий пример 18: Решение линейных неравенств

Развернуть скобу

Переставить и решить для \(q\)

Разделить обе стороны на \(\text{2}\)

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Рабочий пример 19: Решение сложных линейных неравенств

Вычесть \(\text{3}\) из всех частей неравенства

Представьте ответ в числовой строке

Представить ответ в интервальной нотации

Решение линейных уравнений и неравенств

Часть 2: Неравенства | Пособие для начинающих по математике для 9-х классов

Неравенства

Результат программы NSW

В этой статье мы обсудим

Предполагаемые знания

Что такое неравенство?

Пример: Заполните пропуск

Решение

Дополнительно!

Решение уравнений с неравенствами

Линейные уравнения

Например:

Помните: