Нижнетреугольная матрица | это… Что такое Нижнетреугольная матрица?
ТолкованиеПеревод
- Нижнетреугольная матрица
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.
Пример верхнетреугольной матрицы
Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.
Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:
Любую ненулевую матрицу путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.

Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.
Свойства
- Определитель треугольной матрицы равен произведению элементов на её главной диагонали .
- Определитель унитреугольной матрицы равен единице.
- Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается UT(n, k) или UTn (k).
- Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT(n, k) или LTn (k).
- Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UTn (k ) по умножению, которая обозначается SUT(n, k) или SUTn (k).
 Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLTn (k).
Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLTn (k). - Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.
- Группа UTn разрешима, а её унитреугольная подгруппа SUTn нильпотентна.
См. также
- Система линейных алгебраических уравнений
- Элементарные преобразования матрицы
Wikimedia Foundation. 2010.
Поможем написать курсовую
- Нижнетериберская ГЭС
- Нижние Адими
Полезное
Треугольная матрица — frwiki.wiki
В линейной алгебре , треугольные матрицы являются квадратными матрицами , в которой треугольная часть значений, разделенная на главной диагонали , равна нуль.
Резюме
- 1 Предварительное замечание
- 2 верхнетреугольные матрицы
- 3 нижние треугольные плашки
- 4 Свойства треугольных матриц
- 5 Примечания и ссылки
- 6 Статьи по теме
Предварительное замечание
В дальнейшем мы будем рассматривать унитарное кольцо R, которое не обязательно коммутативно , R -модули слева и R-модули справа. Читатель, незнакомый с некоммутативными кольцами и левыми или правыми модулями, может предположить, что кольцо R коммутативно, и не читать отрывки, в которых сделано противоположное предположение. Если кольцо R коммутативно, R -модули слева и R -модули справа совпадают и являются просто R- модулями. Точно так же читатель, не знакомый с модулями, может предположить, что R является полем, и не читать отрывки, в которых сделано противоположное предположение. Если R — поле, то R -модули слева (соответственно справа) являются R- векторными пространствами слева (соответственно справа). Наконец, если читатель не знаком с некоммутативными полями и левым и правым векторными пространствами, он может предположить, что R является коммутативным полем, и не читать отрывки, в которых сделаны противоположные предположения. Если R — коммутативное поле, то R -модули слева и справа совпадают с пространствами R- векторов.
Наконец, если читатель не знаком с некоммутативными полями и левым и правым векторными пространствами, он может предположить, что R является коммутативным полем, и не читать отрывки, в которых сделаны противоположные предположения. Если R — коммутативное поле, то R -модули слева и справа совпадают с пространствами R- векторов.
Верхние треугольные матрицы
Пусть R — унитарное кольцо . По определению, более высокая треугольная матрица с коэффициентами в
- Взнак равно(вя,j)знак равно(в1,1в1,2⋯⋯в1,нет0в2,2в2,нет⋮⋱⋱⋮⋮⋱⋱⋮0⋯⋯0внет,нет){\ displaystyle A = (a_ {i, j}) = {\ begin {pmatrix} a_ {1,1} & a_ {1,2} & \ cdots & \ cdots & a_ {1, n} \\ 0 & a_ {2, 2} &&& a_ {2, n} \\\ vdots & \ ddots & \ ddots && \ vdots \\\ vdots && \ ddots & \ ddots & \ vdots \\ 0 & \ cdots & \ cdots & 0 & a_ {n, n} \\ \ end {pmatrix}}}
A является верхнетреугольным тогда и только тогда, когда :
- ∀я>j,вя,jзнак равно0{\ displaystyle \ forall i> j, \ quad a_ {i, j} = 0}
Плашки нижние треугольные
Пусть R — унитарное кольцо.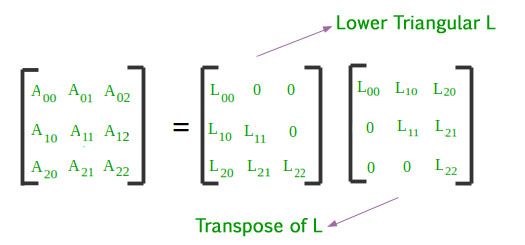 По определению нижнетреугольная матрица с коэффициентами в R является квадратной матрицей с коэффициентами в R , значения которых над главной диагональю равны нулю:
По определению нижнетреугольная матрица с коэффициентами в R является квадратной матрицей с коэффициентами в R , значения которых над главной диагональю равны нулю:
- Взнак равно(вя,j)знак равно(в1,10⋯⋯0в2,1в2,2⋱⋮⋮⋱⋱⋮⋮⋱0внет,1внет,2⋯⋯внет,нет){\ displaystyle A = (a_ {i, j}) = {\ begin {pmatrix} a_ {1,1} & 0 & \ cdots & \ cdots & 0 \\ a_ {2,1} & a_ {2,2 } & \ ddots && \ vdots \\\ vdots && \ ddots & \ ddots & \ vdots \\\ vdots &&& \ ddots & 0 \\ a_ {n, 1} & a_ {n, 2} & \ cdots & \ cdots & a_ {n, n} \\\ конец {pmatrix}}}
A является нижним треугольником тогда и только тогда, когда:
- ∀я<j,вя,jзнак равно0.{\ displaystyle \ forall i <j, \ quad a_ {i, j} = 0.}
Свойства треугольных матриц
- Транспонирования из верхней треугольной матрицы является нижней треугольной матрицей, и наоборот.
- И нижняя, и верхняя треугольная матрица являются диагональной матрицей .
 {*} \ end {pmatrix}}} в частности, LL * = 0 — то есть сумма квадратов модулей коэффициентов L равна нулю — поэтому L = 0. Следовательно, L * L = 0. Таким образом, B нормален, следовательно (по индукции гипотеза) диагональ, поэтому и A тоже.
{*} \ end {pmatrix}}} в частности, LL * = 0 — то есть сумма квадратов модулей коэффициентов L равна нулю — поэтому L = 0. Следовательно, L * L = 0. Таким образом, B нормален, следовательно (по индукции гипотеза) диагональ, поэтому и A тоже.- Если A и B две нижние (соответственно верхние) треугольные матрицы порядка n, то A + B и — A тоже. В абелевой группе (M n ( R ), +) матриц с n строками и n столбцами с коэффициентами в R матрицы нижнего треугольника (соответственно более высокие) образуют подгруппу .
- Если A нижний треугольник (соответственно верхний), то λ A и A λ также для любого скаляра λ. Таким образом, матрицы нижнего (соответственно верхнего) треугольника образуют подбимодуль RR — бимодуля M n ( R ).
- Если A и B две нижние (соответственно верхние) треугольные матрицы порядка n, то и AB .

- Поскольку в M n (R) единичная матрица диагональна и, следовательно, как верхнетреугольная, так и нижняя треугольная, две предыдущие точки показывают, что набор верхних (соответственно нижних) треугольных матриц является подкольцом M n ( R ). Если кольцо R коммутативно, это подкольцо является даже (в общем случае некоммутативной) подалгеброй в M n ( R ).
- Если A = ( a i, j ) i, j и B = ( b i, j ) i, j являются верхними (соответственно нижними) треугольными матрицами M n ( R ), i -й диагональный коэффициент матрицы
- Если кольцо R коммутативно, определитель треугольной матрицы с коэффициентами в R является произведением ее диагональных коэффициентов:Det((вя,j)(я,j)∈[[1;нет]]2)знак равно∏язнак равно1нетвя,я.
 {n} a_ {i, i}.}(Если матрица верхнетреугольная, разверните в соответствии с минорами первого столбца и рассмотрите индукцией по размеру матрицы. Если матрица имеет нижнюю треугольную форму, разверните в соответствии с минорами первой строки.)
{n} a_ {i, i}.}(Если матрица верхнетреугольная, разверните в соответствии с минорами первого столбца и рассмотрите индукцией по размеру матрицы. Если матрица имеет нижнюю треугольную форму, разверните в соответствии с минорами первой строки.) - Если R является коммутативным полем и А является треугольной матрицей с коэффициентами в R , то собственные значения из A являются ее диагональными коэффициентами. (Действительно матрица Х Id — также треугольной формы, таким образом, в соответствии с предыдущим пунктом, определитель этой матрицы, то есть в характеристический полином от А , равно произведению X — в г, г , где a i, i пересекает диагональные коэффициенты матрицы A. )
- Если является верхним (соответственно опустить) треугольную матрицу , принадлежащие М п ( R ) , и если все диагональные коэффициенты А являются обратимыми в кольце R , то матрица А является обратимым в кольце М п (R).
 В этом случае его обратная матрица также является верхнетреугольной матрицей (соответственно нижней). Это следует из предпоследней точки диагональных коэффициентов обратных А затем обратные диагональные коэффициенты А и обратимы в
В этом случае его обратная матрица также является верхнетреугольной матрицей (соответственно нижней). Это следует из предпоследней точки диагональных коэффициентов обратных А затем обратные диагональные коэффициенты А и обратимы в - Обратное к первому утверждению предыдущего пункта неверно во всей общности в том смысле, что мы можем найти кольцо R , натуральное целое число n и треугольную матрицу, принадлежащую M n ( R ), которая обратима в M n ( R ), но не все диагональные коэффициенты обратимы.
 (Позже мы увидим, что такое кольцо не может быть полем и не может быть коммутативным.)
(Позже мы увидим, что такое кольцо не может быть полем и не может быть коммутативным.)
Контрпример
Пусть R — кольцо и a , b — элементы R такие, что ab = 1 и ba ≠ 1.
(Случай выполнен: возьмем в качестве R кольцо эндоморфизмов векторного пространства, допускающего бесконечный счетный базис v 0 , v 1 …, умножение в этом кольце есть композиция ∘, определенная формулой f ∘ g : x ↦ f ( g ( х )).
Возьмем для более в левом операторе сдвига , который применяется V 0 до 0 , и для всех I , по крайней мере , равным 1, применимо v я к V я -1 . Возьмем в качестве b эндоморфизм правого сдвига, который для всех i переводит v i в v i +1 .
 Тогда a ∘ b = id, но b ∘ a ( v 0 ) = 0, следовательно, b ∘ a ≠ id.) Из соотношений ab = 1 и ba ≠ 1 следует, что a и b не обратимы. Нижнетреугольная матрица
Взнак равно(в01б){\ displaystyle A: = {\ begin {pmatrix} a & 0 \\ 1 & b \\\ end {pmatrix}}}обратима, поскольку расчет показывает, что матрица
Bзнак равно(б1-бв-1в){\ displaystyle B: = {\ begin {pmatrix} b & 1-ba \\ — 1 & a \\\ end {pmatrix}}}
восстанавливается в левом и правом обратной А . Тем не менее , диагональные элементы А являются и б , которые , как мы уже видели, не обратимы в R . Мы также видим, что обратная матрица A не является нижнетреугольной (что, учитывая свойство диагонали произведения двух нижнетреугольных матриц, также следует из того факта, что диагональные коэффициенты матрицы A не обратимы).
Тогда a ∘ b = id, но b ∘ a ( v 0 ) = 0, следовательно, b ∘ a ≠ id.) Из соотношений ab = 1 и ba ≠ 1 следует, что a и b не обратимы. Нижнетреугольная матрица
Взнак равно(в01б){\ displaystyle A: = {\ begin {pmatrix} a & 0 \\ 1 & b \\\ end {pmatrix}}}обратима, поскольку расчет показывает, что матрица
Bзнак равно(б1-бв-1в){\ displaystyle B: = {\ begin {pmatrix} b & 1-ba \\ — 1 & a \\\ end {pmatrix}}}
восстанавливается в левом и правом обратной А . Тем не менее , диагональные элементы А являются и б , которые , как мы уже видели, не обратимы в R . Мы также видим, что обратная матрица A не является нижнетреугольной (что, учитывая свойство диагонали произведения двух нижнетреугольных матриц, также следует из того факта, что диагональные коэффициенты матрицы A не обратимы). - С другой стороны, если кольцо R коммутативно, если треугольная матрица с коэффициентами в R обратима, ее диагональные коэффициенты обратимы.
 Действительно, тогда определитель этой матрицы обратим. Мы видели, что определитель этой матрицы является произведением ее диагональных коэффициентов, поэтому произведение диагональных коэффициентов обратимо, поэтому каждый диагональный коэффициент обратим.
Действительно, тогда определитель этой матрицы обратим. Мы видели, что определитель этой матрицы является произведением ее диагональных коэффициентов, поэтому произведение диагональных коэффициентов обратимо, поэтому каждый диагональный коэффициент обратим. - Аналогично, если R — поле (не обязательно коммутативное), если треугольная матрица с коэффициентами в R обратима, ее диагональные коэффициенты обратимы, то есть (поскольку R — поле) не равны нулю.
Демонстрация
Есть, например , А обратимый верхняя треугольная матрица размера п коэффициентов в теле R . Если по абсурдности, то я -й диагональ коэффициент А равен нуль, то I первые столбцы A генерируются, в R- векторного пространства на правом R н , с помощью I — 1 первых векторов канонического базиса это пространство, следовательно, связано , поэтому семейство векторов-столбцов A не является базисом R- векторного пространства справа R n .
 Отсюда следует, что матрица A необратима в R ; противоречие.
Отсюда следует, что матрица A необратима в R ; противоречие.Примечания и ссылки
- ↑ Если R коммутативно, это частный случай теоремы Кэли-Гамильтона . Но мы можем продемонстрировать это гораздо более элементарно и для любого R , как в этом упражнении, исправленном из урока «Матрица» в Викиверситете .
- ↑ (in) Джин Х. Голуб и Чарльз Ф. Ван Лоан (in) , Matrix Computations , Johns Hopkins University Press ,, 3 е изд. , 694 с. ( ISBN 978-0-8018-5414-9 , читать онлайн ) , стр.
 318, Проблема P7.1.1.
318, Проблема P7.1.1. - ↑ (in) Юсеф Саад (in) , Итерационные методы для разреженных линейных систем: второе издание , SIAM ,, 2- е изд. , 528 с. ( ISBN 978-0-89871-534-7 , читать онлайн ) , стр. 20.
- ↑ Умножение матриц слева или справа на скаляры наделяет аддитивную группу M n ( R ) структурой R -модуля слева или справа (эти две структуры совпадают, если кольцо R коммутативно).
- ↑ Бурбаки Н.
 См., Например, Бурбаки 1970 , стр. II.150.
См., Например, Бурбаки 1970 , стр. II.150.
Статьи по Теме
Теорема Ли-Колчина
Матрицы
Форма Квадрат · Треугольник · Диагональ · Трехдиагональ · Элементарно · В шахматном порядке · Подвал · Случайно · Циркуланте · Ганкель · Теплиц · Вандермонд · Гессенберг Преобразованный Транспонированный · Комбинированный · Помощник · Обратный · Адъюгированная матрица Отношение эквивалент · аналогичный · конгруэнтный Имущество Обращение · диагонализуемость · Полуодин · триангулируемость · сбалансированность · перекос · эрмитов · нормальный · ортогональный · унитарный · симплектический · адамар · положительный самосопряженный · определенный положительный · доминантная диагональ · нильпотентная Семья Нет · Идентичность · Пусто · Кастельжау · Картан · Гильберт · Мюллер · Паули · Дирак · Домохозяин Партнер Обмен · Переключение · Сопутствующий · Сильвестр · смежность · Лапласиан · Гессиан · Якобиан · Генератор · Контроль · Корреляция · Грамм · ковариация-дисперсия · Инерция · Джонс · Прибыль · Стохастик Полученные результаты Разложения LU · QR · Холецкий · Шур · Полярный · Сингулярные значения Диагонализация · Тригонализация · Редукция Жордана · Факторы инвариантов Статьи по Теме CKM · Теория матриц · Линейная алгебра · Мультилинейная алгебра · Сложение матриц · Палитра, включающая умножение матриц <img src=»https://fr.
 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>Объяснение верхней треугольной и нижней треугольной матрицы (с примерами Python) | Миша Св
В этой статье мы обсудим интуицию и шаги для вычисления верхней треугольной матрицы и нижней треугольной матрицы с использованием Python.
Image by AuthorСодержание:
- Введение
- Верхняя треугольная матрица, объяснение
- Нижняя треугольная матрица, объяснение
- Специальные формы треугольной матрицы
- Извлечь верхнюю треугольную матрицу в Python
- Извлечь нижнюю треугольную матрицу в Python
Треугольные матрицы — не самые популярные понятия в линейной алгебре, однако они очень полезны, а их свойства помогают нам понять и другие частные случаи матриц. как операции с матрицами.
Чтобы продолжить следовать этому руководству, нам понадобится следующая библиотека Python: numpy.
Если они у вас не установлены, откройте «Командную строку» (в Windows) и установите их, используя следующий код:
pip install numpy
Верхнетреугольная матрица (или правотреугольная матрица) — это частный случай квадратной матрицы, в которой все значения ниже главной диагонали равны нулю.

Например, рассмотрим матрицу 4×4 U :
Image by AuthorЭта матрица является верхнетреугольной, поскольку все значения ниже ее главной диагонали (которая равна [3, 1, 9, 2]) равны нулю.
Далее это можно обобщить до квадратной матрицы размером n × n .
Image by AuthorНижняя треугольная матрица (или левотреугольная матрица) — это частный случай квадратной матрицы, в которой все значения выше главной диагонали равны нулю.
Например, рассмотрим матрицу 4×4.
Далее это можно обобщить до квадратной матрицы размера \(n \times n\).
Изображение автораСуществует несколько специальных форм треугольных матриц:
Матрица, имеющая одновременно верхнюю и нижнюю треугольную формы, является диагональной матрицей, поскольку на главной диагонали находятся только ненулевые элементы.
Например:
Изображение автораЕсли матрица является верхнетреугольной или нижнетреугольной, где все значения главной диагонали равны 1, такая матрица называется (верхней или нижней) унитреугольной.

Пример верхней унитреугольной матрицы:
Изображение автораПример нижней унитреугольной матрицы:
Изображение автораЕсли матрица является верхнетреугольной или нижнетреугольной, где все значения главной диагонали равны 1, такая матрица называется строго (верхней или нижней) треугольной .
Строго верхняя треугольная матрица:
Изображение автораСтрого нижняя треугольная матрица:
Изображение автораЕсли матрица является унитреугольной матрицей, где все элементы вне главной диагонали равны нулю, за исключением одного столбца, такая матрица называется атомарная (верхняя или нижняя) треугольная матрица.
Пример атомарной верхней треугольной матрицы:
Изображение автораПример атомарной нижней треугольной матрицы:
Изображение автораЧтобы создать единичную матрицу в Python, мы будем использовать библиотеку NumPy. И первым шагом будет его импорт:
NumPy имеет множество полезных функций, и для этой операции мы будем использовать функцию triu(), которая будет извлекать верхний треугольник матрицы.

Давайте создадим образец матрицы:
Образец матрицы:
[[3 2 5 7]
[2 1 3 4]
[3 1 9 8]
[8 7 3 2]]Последний шаг чтобы извлечь верхнюю треугольную матрицу с помощью Python:
И вы должны получить:
[[3 2 5 7]
[0 1 3 4]
[0 0 9 8]
[0 0 0 2]]что выглядит идентично образцу верхней треугольной матрицы, используемой в разделе пояснений.
Чтобы создать идентификационную матрицу в Python, мы будем использовать библиотеку NumPy. И первым шагом будет его импорт:
В NumPy есть много полезных функций, и для этой операции мы будем использовать функцию tril(), которая извлечет нижний треугольник матрицы.
Давайте создадим образец матрицы:
Образец матрицы:
[[2 6 5 7]
[7 3 9 4]
[9 4 8 2]
[6 2 1 5]]Последний шаг для извлечения нижней треугольной матрицы с использованием Python:
И вы должны получить:
[[2 0 0 0]
[7 3 0 0]
[9 4 8 0]
[6 2 1 5]], что выглядит идентично использованному образцу нижней треугольной матрицы в разделе пояснений.

В этой статье мы обсудили шаги и интуицию для вычисления верхней треугольной матрицы и нижней треугольной матрицы с использованием Python.
Не стесняйтесь оставлять комментарии ниже, если у вас есть какие-либо вопросы или предложения по некоторым изменениям, и ознакомьтесь с другими моими статьями по линейной алгебре.
Первоначально опубликовано на https://pyshark.com 24 января 2022 г.
Больше контента на Подпишитесь на нашу бесплатную еженедельную рассылку . Получите эксклюзивный доступ к возможностям письма и советам в нашем сообществе Discord .
Определение треугольных матриц — веб-формулы
· Изгиб векторного поля
· Дивергенция векторного поля
· Градиент скалярного поля
· Свойства транспонирования
· Транспонирование матрицы· Декартова координата
· Цилиндрическая координата
· Сферическая координата
· Преобразование декартовой системы координат в цилиндрическую
· Преобразование декартовой системы координат в сферическую
· Преобразование цилиндрической системы координат в декартову
· Преобразование сферической системы координат в декартову
· Теорема о расходимости/теорема Гаусса
· Теорема Стокса
· Определение матрицыТекущее местоположение > Математические формулы > Линейная алгебра > Определение треугольных матриц
Не забудьте попробовать наше бесплатное приложение — Agile-журнал , который поможет вам отслеживать время, потраченное на различные проекты и задачи, 🙂
Попробуй сейчас
Треугольные матрицы: Квадратная матрица с элементами sij = 0 для j < i называется верхней треугольной матрицей.
 Другими словами, квадратная матрица является верхнетреугольной, если все ее элементы ниже главной диагонали равны нулю.
Другими словами, квадратная матрица является верхнетреугольной, если все ее элементы ниже главной диагонали равны нулю.
Пример верхней треугольной матрицы 2 × 2:
Квадратная матрица с элементами s ij = 0 для j > i называется нижней треугольной матрицей. Другими словами, квадратная матрица является нижней треугольной, если все ее элементы выше главной диагонали равны нулю.Пример нижней треугольной матрицы 3 × 3:
· Диагональные матрицы являются как верхними, так и нижними треугольными, поскольку они имеют нули выше и ниже главной диагонали.
· Матрица, обратная нижней треугольной, также является нижней треугольной.
· Произведение двух или более нижнетреугольных матриц также является нижнетреугольным.
· Транспонирование нижней треугольной матрицы является верхней треугольной.
· Матрица, обратная верхнетреугольной, также является верхнетреугольной.
· Произведение двух или более верхнетреугольных матриц также является верхнетреугольным.


 Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLTn (k).
Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLTn (k).

 {n} a_ {i, i}.}(Если матрица верхнетреугольная, разверните в соответствии с минорами первого столбца и рассмотрите индукцией по размеру матрицы. Если матрица имеет нижнюю треугольную форму, разверните в соответствии с минорами первой строки.)
{n} a_ {i, i}.}(Если матрица верхнетреугольная, разверните в соответствии с минорами первого столбца и рассмотрите индукцией по размеру матрицы. Если матрица имеет нижнюю треугольную форму, разверните в соответствии с минорами первой строки.) В этом случае его обратная матрица также является верхнетреугольной матрицей (соответственно нижней). Это следует из предпоследней точки диагональных коэффициентов обратных А затем обратные диагональные коэффициенты А и обратимы в
В этом случае его обратная матрица также является верхнетреугольной матрицей (соответственно нижней). Это следует из предпоследней точки диагональных коэффициентов обратных А затем обратные диагональные коэффициенты А и обратимы в  (Позже мы увидим, что такое кольцо не может быть полем и не может быть коммутативным.)
(Позже мы увидим, что такое кольцо не может быть полем и не может быть коммутативным.) Тогда a ∘ b = id, но b ∘ a ( v 0 ) = 0, следовательно, b ∘ a ≠ id.) Из соотношений ab = 1 и ba ≠ 1 следует, что a и b не обратимы. Нижнетреугольная матрица
Взнак равно(в01б){\ displaystyle A: = {\ begin {pmatrix} a & 0 \\ 1 & b \\\ end {pmatrix}}}обратима, поскольку расчет показывает, что матрица
Bзнак равно(б1-бв-1в){\ displaystyle B: = {\ begin {pmatrix} b & 1-ba \\ — 1 & a \\\ end {pmatrix}}}
восстанавливается в левом и правом обратной А . Тем не менее , диагональные элементы А являются и б , которые , как мы уже видели, не обратимы в R . Мы также видим, что обратная матрица A не является нижнетреугольной (что, учитывая свойство диагонали произведения двух нижнетреугольных матриц, также следует из того факта, что диагональные коэффициенты матрицы A не обратимы).
Тогда a ∘ b = id, но b ∘ a ( v 0 ) = 0, следовательно, b ∘ a ≠ id.) Из соотношений ab = 1 и ba ≠ 1 следует, что a и b не обратимы. Нижнетреугольная матрица
Взнак равно(в01б){\ displaystyle A: = {\ begin {pmatrix} a & 0 \\ 1 & b \\\ end {pmatrix}}}обратима, поскольку расчет показывает, что матрица
Bзнак равно(б1-бв-1в){\ displaystyle B: = {\ begin {pmatrix} b & 1-ba \\ — 1 & a \\\ end {pmatrix}}}
восстанавливается в левом и правом обратной А . Тем не менее , диагональные элементы А являются и б , которые , как мы уже видели, не обратимы в R . Мы также видим, что обратная матрица A не является нижнетреугольной (что, учитывая свойство диагонали произведения двух нижнетреугольных матриц, также следует из того факта, что диагональные коэффициенты матрицы A не обратимы).  Действительно, тогда определитель этой матрицы обратим. Мы видели, что определитель этой матрицы является произведением ее диагональных коэффициентов, поэтому произведение диагональных коэффициентов обратимо, поэтому каждый диагональный коэффициент обратим.
Действительно, тогда определитель этой матрицы обратим. Мы видели, что определитель этой матрицы является произведением ее диагональных коэффициентов, поэтому произведение диагональных коэффициентов обратимо, поэтому каждый диагональный коэффициент обратим.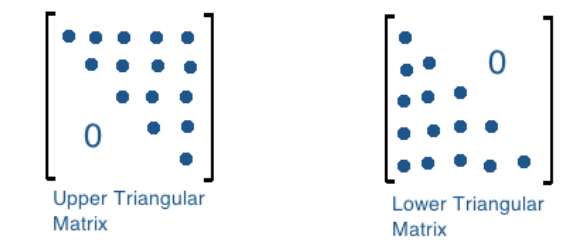 Отсюда следует, что матрица A необратима в R ; противоречие.
Отсюда следует, что матрица A необратима в R ; противоречие. 318, Проблема P7.1.1.
318, Проблема P7.1.1.