Нормальное распределение
Числовые случайные величины могут быть либо дискретными, либо непрерывными (подробнее см. Типы данных). Дискретные случайные величины (т.е. величины, возникающие в результате подсчета событий) были рассмотрены ранее (см. Биномиальное распределение, Гипергеометрическое распределение, Распределение Пуассона). В этой и нескольких следующих заметках мы изучим непрерывные случайные величины, которые возникают в результате измерений. Непрерывная случайная величина может принимать любое значение, принадлежащее числовой оси или интервалу. [1] Примером такой случайной величины может служить вес какой-нибудь коробки, время загрузки Web-страницы, расходы на рекламу, доходы от продаж, время обслуживания клиента и время между двумя приходами клиентов в банк.
Математическое выражение, описывающее распределение значений непрерывной случайной величины, называется плотностью непрерывного распределения вероятностей (рис. 1). На панели А представлена плотность нормального распределения.

Рис. 1. Три непрерывных распределения
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
В этой заметке описывается одно из наиболее важных распределений в статистике — нормальное распределение, которое также называют гауссовым. То, что это одно из наиболее часто используемых распределений, косвенно подтверждается, в частности тем, что ранее я уже писал на эту тему :), см. Нормальное распределение. Построение графика в Excel. Концепция шести сигм. Страница с этой заметкой является третьей по посещаемости из более чем 370 на сайте.
Плотность нормального распределения изображена на рис. 1а. Можно вычислить вероятность того, что нормально распределенная случайная величина лежит в заданном интервале. Однако вероятность того, что она принимает наперед заданное значение, равна нулю. Это отличает непрерывные случайные величины (измеряемые) от дискретных (подсчитываемых). Например, время измеряется, а не подсчитывается. Следовательно, можно вычислить вероятность того, что Web-страница будет загружаться от 7 до 10 с.
Определение вероятностей или вычисление математического ожидания и стандартного отклонения непрерывной случайной величины требуют знания интегрального исчисления и не будут здесь рассматриваться. Однако использование функций Excel позволяет легко преодолеть эти трудности.
Важность нормального распределения в статистике обусловлена тремя причинами:
- Оно описывает (точно или приблизительно) распределение многих непрерывных случайных величин.
- С помощью нормального распределения можно аппроксимировать разнообразные дискретные распределения.
- Нормальное распределение лежит в основе классической теории статистических выводов, поскольку оно тесно связано с центральной предельной теоремой.

Нормальное распределение:
- Имеет колоколообразную (а значит, симметричную) форму.
- Его математическое ожидание, медиана и мода совпадают друг с другом.
- Половина нормально распределенных значений лежит в интервале, длина которого равна 4/3 стандартного отклонения. Это значит, что межквартильный размах находится в интервале от 2/3 стандартного отклонения левее среднего значения до 2/3 стандартного отклонения правее среднего значения.
На практике многие случайные величины являются лишь приближенно нормальными. Иначе говоря, их свойства лишь аппроксимируют теоретические свойства нормального распределения, перечисленные выше. Рассмотрим в качестве примера таблицу на рис. 2.
Рис. 2. Толщина 10 000 медных дисков
Здесь перечислены результаты измерения толщины 10 000 медных дисков. Толщина представляет собой непрерывную случайную величину, распределение которой аппроксимируется нормальным.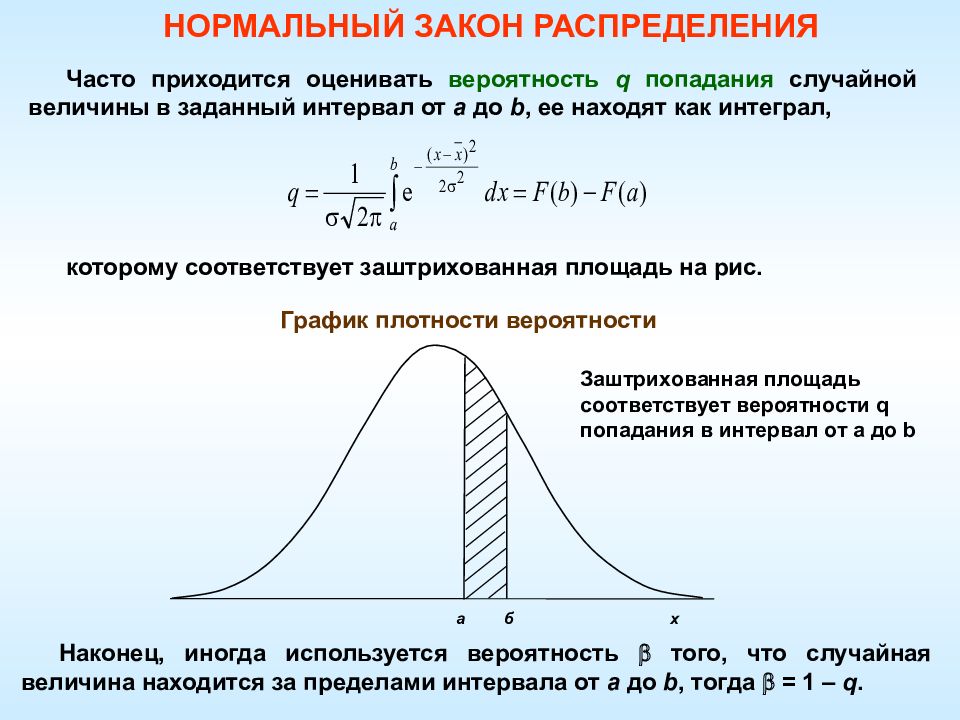 Основная масса значений этой величины лежит в интервале от 0,0190 до 0,0192 дюймов и распределена симметрично относительно этого интервала, формируя колоколообразную кривую. Как следует из таблицы, разбиение числовой прямой на интервалы образует группы взаимоисключающих и исчерпывающих событий, сумма вероятностей которых равна единице. Таким образом, распределение вероятностей можно интерпретировать как распределение относительных частот (подробнее см. Представление числовых данных в виде таблиц и диаграмм и последний раздел заметки Определение среднего значения, вариации и формы распределения. Описательные статистики), соответствующих средним точкам интервалов.
Основная масса значений этой величины лежит в интервале от 0,0190 до 0,0192 дюймов и распределена симметрично относительно этого интервала, формируя колоколообразную кривую. Как следует из таблицы, разбиение числовой прямой на интервалы образует группы взаимоисключающих и исчерпывающих событий, сумма вероятностей которых равна единице. Таким образом, распределение вероятностей можно интерпретировать как распределение относительных частот (подробнее см. Представление числовых данных в виде таблиц и диаграмм и последний раздел заметки Определение среднего значения, вариации и формы распределения. Описательные статистики), соответствующих средним точкам интервалов.
На рис. 3 изображена гистограмма относительных частот и полигон распределения толщины 10 000 медных дисков. Как видим, первые три условия нормального распределения выполняются, а четвертое — нет. Толщина диска не может быть отрицательной или равной нулю. Из таблицы (рис. 2) следует, что из 10 000 медных дисков только 48 толще 0,0202 дюйма и такое же количество дисков тоньше 0,0180 дюйма. Таким образом, вероятность случайно выбрать слишком толстый или слишком тонкий диск равна 0,0048+0,0048=0,0096, т.е. меньше 1 из 100.
Таким образом, вероятность случайно выбрать слишком толстый или слишком тонкий диск равна 0,0048+0,0048=0,0096, т.е. меньше 1 из 100.
Рис. 3. Гистограмма относительных частот и полигон распределения ширины 10 000 медных дисков
Плотность нормального распределения:
где е — основание натурального логарифма, константа равная 2,71828, μ — математическое ожидание генеральной совокупности, σ — стандартное отклонение генеральной совокупности, X — произвольное значение непрерывной случайной величины, –∞ < X < +∞.
Поскольку величины е и π являются математическими константами, плотность нормального распределения зависит только от двух параметров — математического ожидания μ и стандартного отклонения σ (рис. 4). Разным комбинациям этих параметров соответствуют разные плотности нормального распределения. Распределения А и Б имеют одинаковое математическое ожидание μ, но разные стандартные отклонения.
Рис. 4. Три нормальных распределения, соответствующие разным комбинациям параметров μ и σ
К сожалению, вычислить математическое выражение, заданное формулой (1), довольно сложно. Чтобы упростить задачу, значения плотности нормального распределения, как правило, табулируют. Поскольку количество возможных комбинаций параметров μ и σ бесконечно, для вычислений понадобилось бы бесконечное количество таблиц. Однако, если нормировать данные, все распределения можно свести к одной таблице. Используя формулу преобразования, любую нормально распределенную случайную величину X
Величина Z равна разности между величиной X и математическим ожиданием генеральной совокупности μ, деленной на стандартное отклонение σ:
(2) Z = (Х – μ)/σ
Математическое ожидание стандартизованного нормального распределения равно нулю, а стандартное отклонение — единице. Плотность стандартизованного нормального распределения можно получить, подставив формулу (2) в формулу (1):
Плотность стандартизованного нормального распределения можно получить, подставив формулу (2) в формулу (1):
Таким образом, любое множество нормально распределенных величин можно преобразовать в стандартизованную форму. Проиллюстрируем процедуру нормирования. Например, время загрузки Web-страницы распределено нормально, причем его математическое ожидание равно р = 7 с, а стандартное отклонение σ = 2 с. Как показывает рис. 5, каждому значению переменной X соответствует нормированное значение Z, полученное с помощью формулы преобразования (2). Следовательно, время загрузки, равное 9 с, на одну стандартную единицу превышает математическое ожидание: Z = (9 – 7) / 2 = +1, а время загрузки равное 1 с на три стандартные единицы (стандартных отклонения) меньше математического ожидания: Z = (1 – 7) / 2 = –3.
Рис. 5. Преобразование шкал для загрузки Web-сайта; μ = 7, σ = 2
Таким образом, стандартное отклонение становится единицей измерения.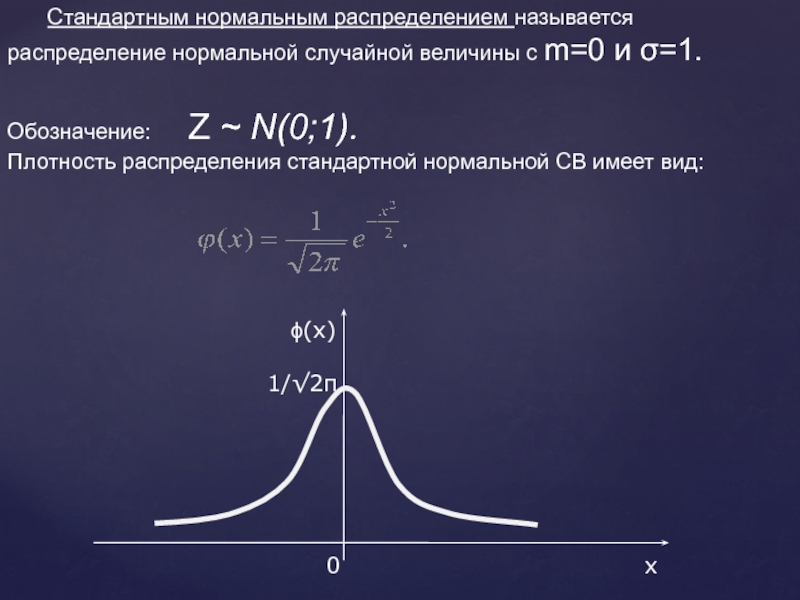 Иначе говоря, время загрузки, равное 9 с, на 2 с (т.е. на одно стандартное отклонение) превышает математическое ожидание, а время, равное 1 с, на 6 с (т.е. на три стандартных отклонения) меньше математического ожидания. Допустим теперь, что среднее время загрузки другого Web-сайта равно 4 с, а стандартное отклонение 1 с (рис. 6).
Иначе говоря, время загрузки, равное 9 с, на 2 с (т.е. на одно стандартное отклонение) превышает математическое ожидание, а время, равное 1 с, на 6 с (т.е. на три стандартных отклонения) меньше математического ожидания. Допустим теперь, что среднее время загрузки другого Web-сайта равно 4 с, а стандартное отклонение 1 с (рис. 6).
Рис. 6. Преобразование шкал для загрузки Web-сайта; μ = 4, σ = 1
Сравнивая рисунки 5 и 6, легко обнаружить, что время загрузки, равное 5 с, на одно стандартное отклонение больше среднего времени загрузки: Z = (5 – 4) / 1 = +1, а время загрузки, равное 1 с, на три стандартных отклонения меньше математического ожидания: Z = (1 – 4) / 1 = –3. На рис. 5 и 6 показаны полигоны относительных частот, соответствующие времени загрузки двух Web-сайтов. Поскольку результаты измерений образуют полную генеральную совокупность, сумма вероятностей, т.е. площадь фигуры, лежащей под кривой, должна быть равной единице.
Предположим, нам необходимо определить вероятность того, что время загрузки Web-сайта (μ = 7, σ = 2, рис.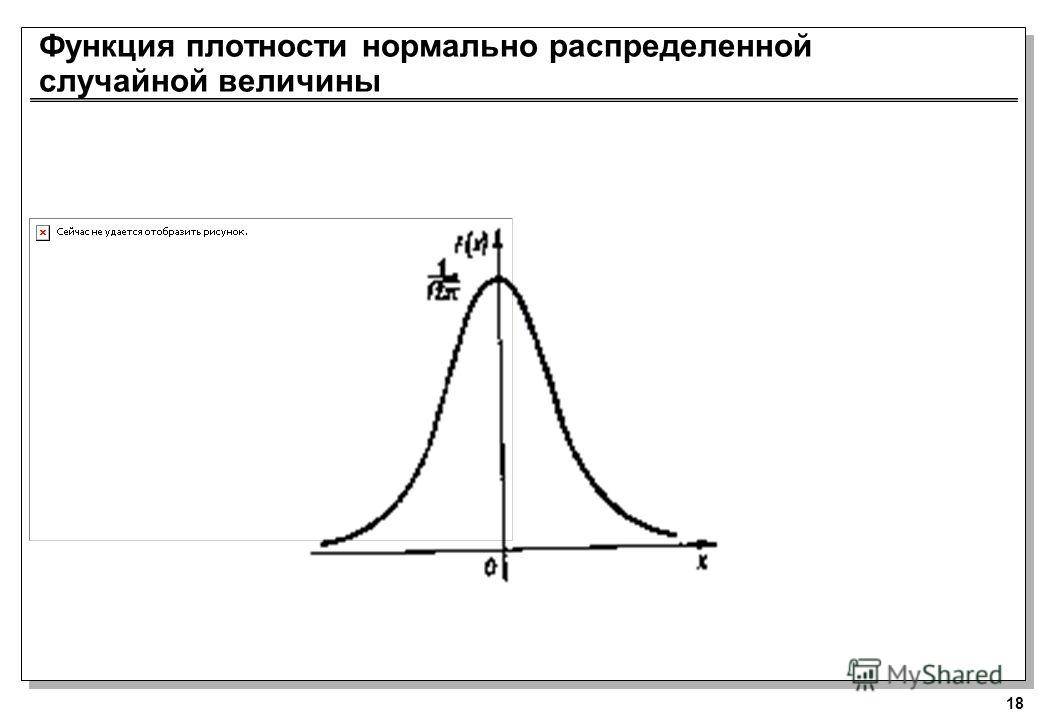 5) меньше 9 с. Поскольку это время на одно стандартное отклонение превышает математическое ожидание, следует найти вероятность того, что время загрузки не превышает величины, равной математическому ожиданию плюс одно стандартное отклонение. В Excel2013 для работы с нормально распределенными случайными величинами используется довольно много функций. Для решения нашей задачи идеально подходит =НОРМ.СТ.РАСП(z;интегральная) (рис. 7). В Excel до версии 2007 используется функция =НОРМСТРАСП(z). В ней только один параметр, так как второй параметр (интегральная) по умолчанию равен ИСТИНА.
5) меньше 9 с. Поскольку это время на одно стандартное отклонение превышает математическое ожидание, следует найти вероятность того, что время загрузки не превышает величины, равной математическому ожиданию плюс одно стандартное отклонение. В Excel2013 для работы с нормально распределенными случайными величинами используется довольно много функций. Для решения нашей задачи идеально подходит =НОРМ.СТ.РАСП(z;интегральная) (рис. 7). В Excel до версии 2007 используется функция =НОРМСТРАСП(z). В ней только один параметр, так как второй параметр (интегральная) по умолчанию равен ИСТИНА.
Рис. 7. Расчет вероятности того, что время загрузки Web-сайта (μ = 7, σ = 2, рис. 5) меньше 9 с
Параметр z – это координата X на нормированной оси (рис. 8). Мы же с помощью функции =НОРМ.СТ.РАСП() определили вероятность того, что случайная величина будет левее Х.
Рис. 8. Площадь фигуры, ограниченной интегральной кривой стандартизованного нормального распределения
С другой стороны, для распределения с параметрами μ = 4, σ = 1 (рис. 6) время загрузки, равное 5 с, на одно стандартное отклонение превышает математическое ожидание, т.е. 4 с. Следовательно, вероятность того, что Web-страница загрузится быстрее, чем за 5 с, также равна 0,8413. На рис. 9 показано, как два отличающихся распределения преобразуются в одно и тоже стандартизованное распределение.
6) время загрузки, равное 5 с, на одно стандартное отклонение превышает математическое ожидание, т.е. 4 с. Следовательно, вероятность того, что Web-страница загрузится быстрее, чем за 5 с, также равна 0,8413. На рис. 9 показано, как два отличающихся распределения преобразуются в одно и тоже стандартизованное распределение.
Рис. 9. Преобразование шкал для площадей фигур, ограниченных интегральными кривыми двух нормальных распределений
Рассмотрим несколько примеров.
Пример 1. Определите вероятность того, что время загрузки (μ = 7, σ = 2) превысит 9 с.
Решение. Вероятность того, что время загрузки не превысит 9 с, равна 0,8413, следовательно, искомая вероятность равна 1 – 0,8413 = 0,1587.
Пример 2. Определите вероятность того, что время загрузки (μ = 7, σ = 2) лежит в интервале 7–9 с.
Решение. Р(7 < Х < 9) = P(X < 9) – P(X < 7). Можно было бы, как и выше, сначала привести нормальное распределение к стандартному виду, а потом воспользоваться функцией =НОРМ. СТ.РАСП (рис. 10).
СТ.РАСП (рис. 10).
Рис. 10. Определение вероятности Р(7 < Х < 9)
Однако в Excel есть функция и для нестандартизированного нормального распределения (рис. 11).
Рис. 11. Определение вероятности того, что время загрузки (μ = 7, σ = 2) лежит в интервале от 7 до 9 с
Обратите внимание, что, поскольку математическое ожидание и медиана нормального распределения совпадают между собой, вероятность того, что загрузка продлится меньше 7 с, равна 0,5, то есть, =НОРМ.РАСП(7;7;2;ИСТИНА) = 0,5.
Пример 3. Определите вероятность того, что время загрузки (μ = 7, σ = 2) лежит в интервале 5–9 с.
Решение. Р(5 < Х < 9) = P(X < 9) – P(X < 5) =НОРМ.РАСП(9;7;2;ИСТИНА)-НОРМ.РАСП(5;7;2;ИСТИНА) = 0,6826 (рис. 12).
Рис. 12. Определение вероятности Р(5 < Х < 9)
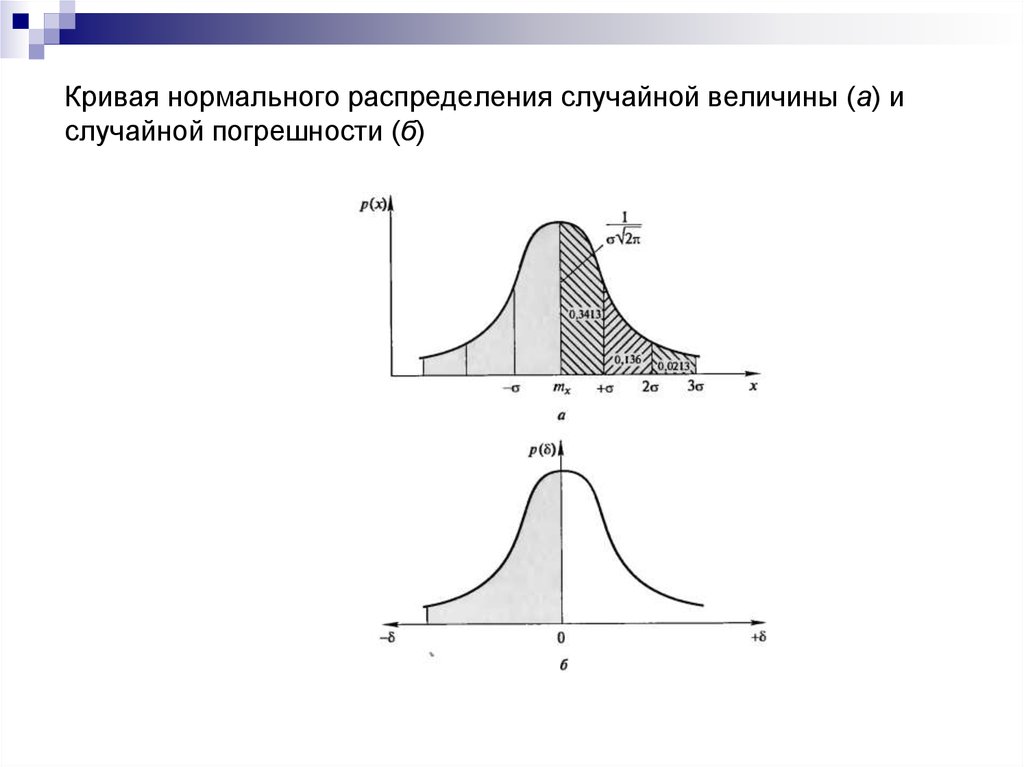
Полученный результат довольно важен. Для любого нормального распределения вероятность того, что случайно выбранное число лежит в окрестности математического ожидания на расстоянии, не превышающем одно стандартное отклонение, равно 0,6826. В окрестности математического ожидания на расстоянии, не превышающем двух стандартных отклонений, лежит чуть более 95% нормально распределенных величин (рис. 13).
В окрестности математического ожидания на расстоянии, не превышающем двух стандартных отклонений, лежит чуть более 95% нормально распределенных величин (рис. 13).
Рис. 13. Вероятность случайной величины попасть в пределы σ-окрестности
В окрестности математического ожидания на расстоянии, не превышающем трех стандартных отклонений, расположено 99,7% всех нормально распределенных величин. Следовательно, 99,73% результатов измерений времени загрузки Web-страницы лежат в интервале от 1 до 13 с. Таким образом, весьма маловероятно (0,0027, или 27 шансов из 10 000), что время загрузки Web-страницы будет меньше 1 с или больше 13 с. Вот почему на практике считают, что интервал длиной 6σ, центром которого является математическое ожидание, содержит практически все значения нормально распределенной случайной величины.
В примерах 1–3 мы вычислили вероятности, связанные с разными значениями измеренной величины. Примеры 4 и 5 посвящены обратной задаче: как определить значение переменной, соответствующей заданной вероятности?
Пример 4. Найдите значение переменной Х, соответствующей интегральной вероятности, равной 0,1. Сколько секунд длится загрузка Web-страницы в 10% случаев?
Найдите значение переменной Х, соответствующей интегральной вероятности, равной 0,1. Сколько секунд длится загрузка Web-страницы в 10% случаев?
Решение. Поскольку предполагается, что в 10% случаев Web-страница загружается не более чем за X с, площадь фигуры, ограниченной гауссовой кривой и осью абсцисс, равна 0,1 (рис. 14). Для обратной задачи в Excel до версии 2007 существуют две функции =НОРМСТОБР() – возвращает обратное значение стандартного нормального распределения, и =НОРМОБР() – возвращает обратное нормальное распределение (не стандартизированное). В версии Excel, начиная с 2010, им соответствуют функции: =НОРМ.СТ.ОБР() и =НОРМ.ОБР(). В нашем примере =НОРМ.ОБР(0,1;7;2) = 4,4 с (рис. 15).
Рис. 14. Интегральная вероятность, равная 0,1
Рис. 15. Использование функции =НОРМ.ОБР()
В общем случае формула для определения величины X может быть выведена на основе формулы (2) Z = (Х – μ)/σ:
(4) Х = μ + Zσ
Пример 5.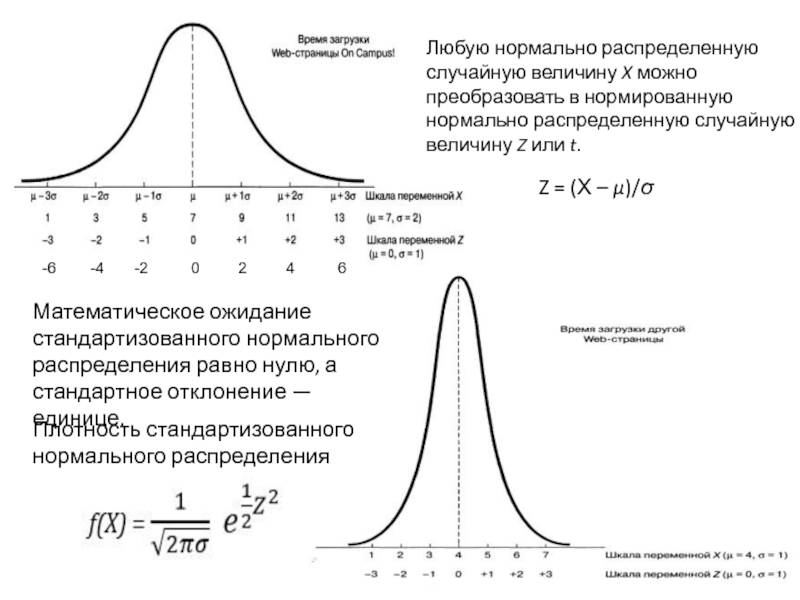 Для стандартного нормального распределения определите нижнюю и верхнюю границы интервала с центром в математическом ожидании, который содержит 90% значений случайной величины.
Для стандартного нормального распределения определите нижнюю и верхнюю границы интервала с центром в математическом ожидании, который содержит 90% значений случайной величины.
Решение. Нижняя граница Z соответствует такой интегральной вероятности р(Z), которая меньше (1 – 90%) / 2, то есть меньше 5%. Верхняя граница Z соответствует такой интегральной вероятности р(Z), которая больше (1 – 90%) / 2 + 90%, то есть больше 95%.
Рис. 16. Определение величин Z, соответствующих значениям ±45%
Таким образом, с вероятностью 90% случайная величина попадает в окрестность ±1,65σ математического ожидания. 90%-ные интервалы находят широкое применение в оценочных суждениях; см., например, Дуглас Хаббард. Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе.
Предыдущая заметка Распределение Пуассона
Следующая заметка
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 346–363
Статистика для менеджеров. – М.: Вильямс, 2004. – с. 346–363
Теория вероятностей
Теория вероятностей
ОглавлениеГлава 1. Введение ВведениеПРЕДИСЛОВИЕ 1.1. Предмет теории вероятностей Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5.  4. Плотность распределения 4. Плотность распределения5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.3. Статистический ряд. Гистограмма 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8.  Системы случайных величин Системы случайных величин8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений.  Общая запись нормального закона для системы произвольного числа случайных величин Общая запись нормального закона для системы произвольного числа случайных величинГлава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации Глава 12. Законы распределения функций случайных аргументов 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин.  Композиция законов распределения Композиция законов распределения12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14.  3. Доверительный интервал. Доверительная вероятность 3. Доверительный интервал. Доверительная вероятность14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов Глава 15. Основные понятия теории случайных функций 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15.  7.2. Производная от случайной функции 7.2. Производная от случайной функции15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17.  7. Эргодическое свойство стационарных случайных функций 7. Эргодическое свойство стационарных случайных функций17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19.  3. Поток событий. Простейший поток и его свойства 3. Поток событий. Простейший поток и его свойства19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 7. Таблица значений функции Таблица 8. Значения распределение Пуассона |
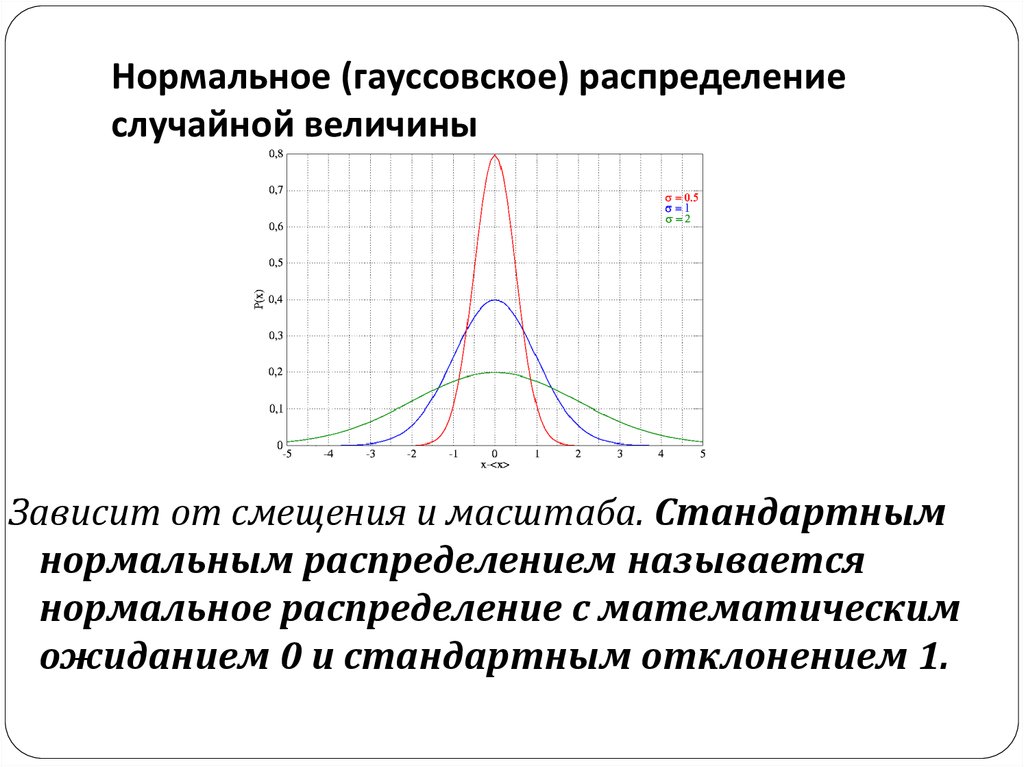
Нормальное распределение
Нормальное распределение определяется следующим уравнением:
Нормальное уравнение . Значение
случайная величина Y равна:
Значение
случайная величина Y равна:
Y = { 1/[ σ * sqrt(2π) ] } * e -(x — μ) 2 /2σ 2
где X — нормальная случайная величина, μ — среднее, σ — стандартное отклонение, π приблизительно равно 3,14159, а e равно приблизительно 2,71828.
Случайная величина X в нормальном уравнении называется нормальная случайная величина . Нормальное уравнение – это функция плотности вероятности для нормального распределения.
Нормальная кривая
График нормального распределения зависит от двух факторов — среднего и среднеквадратичное отклонение. Среднее значение распределения определяет положение центр графика, а стандартное отклонение определяет высоту и ширина график. Все нормально распределения выглядят как симметричная колоколообразная кривая, как показано ниже.
Меньшее стандартное отклонение
Большее стандартное отклонение
Когда стандартное отклонение мало, кривая длинная и узкая; и когда стандартное отклонение
большой, изгиб короткий и широкий (см. выше)
выше)
Вероятность и нормальная кривая
Нормальное распределение — это непрерывное распределение вероятностей. Это имеет несколько последствий для вероятности.
- Вероятность того, что X меньше а равно площади под нормальной кривой ограниченный a и минус бесконечность (как указано заштриховал область на рисунке ниже).
Кроме того, каждая нормальная кривая (независимо от ее среднего или стандартного отклонение) соответствует следующему «правилу».
В совокупности эти точки известны как эмпирическое правило или правило 68-95-99.7 . Понятно, что при нормальном распределение, большинство результатов будут в пределах 3 стандартных отклонений от Значение.
Чтобы найти вероятность, связанную с нормальным случайным
переменная, используйте графический калькулятор, онлайн нормальное распределение
калькулятор или таблица нормального распределения. В приведенных ниже примерах
мы иллюстрируем использование Stat Trek’s
Калькулятор нормального распределения,
бесплатный инструмент, доступный на этом сайте. На следующем уроке мы покажем
использование таблиц нормального распределения.
В приведенных ниже примерах
мы иллюстрируем использование Stat Trek’s
Калькулятор нормального распределения,
бесплатный инструмент, доступный на этом сайте. На следующем уроке мы покажем
использование таблиц нормального распределения.
Калькулятор нормального распределения
Калькулятор нормального распределения решает распространенные статистические задачи на основе нормального распределение. Калькулятор вычисляет кумулятивные вероятности на основе трех простые входы. Простые инструкции помогут быстро найти точное решение и легко. Если что-то непонятно, часто задаваемые вопросы и образец проблемы дают прямое объяснение. калькулятор бесплатный. Его можно найти в главном меню Stat Trek на вкладке Stat Tools. Или вы можете нажать кнопку ниже.
Калькулятор нормального распределения
Проверьте свои знания
Задача 1
Средняя лампочка, произведенная корпорацией Acme, работает 300 дней при
стандартное отклонение 50 дней. Предполагая, что срок службы лампы в норме
распределены, какова вероятность того, что лампочка Acme прослужит не более
365 дней?
Предполагая, что срок службы лампы в норме
распределены, какова вероятность того, что лампочка Acme прослужит не более
365 дней?
Решение: Учитывая средний балл 300 дней и стандартное отклонение 50 дней, мы хотим найти кумулятивную вероятность того, что срок службы лампы меньше или равно 365 дням. Таким образом, мы знаем следующее:
- Стандартное отклонение равно 50 дням.
Мы вводим эти значения в Калькулятор нормального распределения и вычисляем кумулятивная вероятность.
Ответ: P(X < 365) = 0,. Следовательно, вероятность того, что лампочка перегорит в течение 365 дней, составляет около 90%.
Задача 2
Предположим, что результаты теста IQ распределены нормально. Если тест имеет среднее 100 и стандартное отклонение 10, какова вероятность того, что человек кто пройдет тест, наберет от 90 и 110?
Решение: Здесь мы хотим узнать вероятность того, что результат теста упадет
между 90 и 110. «Хитрость» в решении этой проблемы заключается в том, чтобы осознать
следующий:
«Хитрость» в решении этой проблемы заключается в том, чтобы осознать
следующий:
P(90 < X < 110) = P( X < 110) - P( X < 90)
Мы используем калькулятор нормального распределения, чтобы вычислить обе вероятности на правая часть вышеприведенного уравнения.
Мы используем эти результаты для вычисления нашего окончательного ответа следующим образом:
P(90 < X < 110) = P( X < 110) - P( X < 90)
P(90 < X < 110) = 0,84 - 0,16
P( 90 < X < 110) = 0,68
Таким образом, около 68% результатов тестов будут находиться между 90 и 110.
Последний урок Следующий урок
Вероятностные вычисления для общих нормальных случайных величин
Цель обучения
- Научиться вычислять вероятности, связанные с любой нормальной случайной величиной.
Если X является любой нормально распределенной нормальной случайной величиной, то рисунок 12. Если X является нормально распределенной случайной величиной со средним значением μ и стандартным отклонением σ , затем P(a , где Z обозначает стандартную нормальную случайную величину. и могут быть любыми десятичными числами или −∞; b может быть любым десятичным числом или ∞. Новые конечные точки (a−μ)∕σ и (b−μ)∕σ представляют собой z -оценки a и b , как определено в разделе 2.4.2 главы 2 «Описательная статистика». Рисунок 5.14 «Вероятность для интервала конечной длины» геометрически иллюстрирует смысл равенства: две заштрихованные области, одна под кривой плотности для X и другая под кривой плотности для Z имеют одинаковую площадь. Однако вместо того, чтобы рисовать обе колоколообразные кривые, мы всегда будем рисовать одну общую колоколообразную кривую с осями x и осью z под ней. Рис. 5.14 Вероятность для интервала конечной длины Пусть X — нормальная случайная величина со средним значением μ = 10 и стандартным отклонением σ = 2,5. Вычислите следующие вероятности. Решение: См. рис. 5.15 «Вычисление вероятности для общей нормальной случайной величины». Рис. 5.15 Расчет вероятности для общей нормальной случайной величины См. рис. 5.16 «Вычисление вероятности для общей нормальной случайной величины». Рис. 5.16 Расчет вероятности для общей нормальной случайной величины Срок службы протектора определенной автомобильной шины нормально распределен со средним значением 37 500 миль и стандартным отклонением 4 500 миль. Решение: Пусть X обозначает срок службы случайно выбранной шины. Чтобы упростить работу с числами, мы выберем в качестве единиц измерения тысячи миль. Таким образом, μ = 37,5, σ = 4,5, и задача состоит в том, чтобы вычислить P(30 P(30 Обратите внимание, что две z -оценки были округлены до двух знаков после запятой, чтобы использовать Рисунок 12.2 «Совокупная нормальная вероятность». Баллы на стандартизированном вступительном экзамене в колледж ( CEE ) обычно распределяются со средним значением 510 и стандартным отклонением 60. Выборочный университет рассматривает для поступления только абитуриентов с баллами CEE выше 650. Решение: Пусть X обозначает оценку, полученную на CEE случайно выбранным человеком. Затем X нормально распределяется со средним значением 510 и стандартным отклонением 60. Вероятность того, что X лежат в определенном интервале, равна доле всех экзаменационных баллов, попадающих в этот интервал. Таким образом, решение задачи равно P ( X > 650), выраженное в процентах. На рис. 5.18 «Вычисление вероятности для результатов экзамена» показано следующее вычисление: Рис. 5.18 Расчет вероятностей для результатов экзамена баллов, которые превышают 650, составляют 0,0099, следовательно, 0,99% или около 1%. X — нормально распределенная случайная величина со средним значением 57 и стандартным отклонением 6. X — нормально распределенная случайная величина со средним значением −25 и стандартным отклонением 4. Найдите указанную вероятность. X — нормально распределенная случайная величина со средним значением 112 и стандартным отклонением 15. X — нормально распределенная случайная величина со средним значением 72 и стандартным отклонением 22. Найдите указанную вероятность. X — нормально распределенная случайная величина со средним значением 500 и стандартным отклонением 25. Найдите указанную вероятность. X — нормально распределенная случайная величина со средним значением 0 и стандартным отклонением 0,75. X — нормально распределенная случайная величина со средним значением 15 и стандартным отклонением 1. Используйте рисунок 12.2 «Совокупная нормальная вероятность», чтобы найти первую указанную вероятность. Найдите вторую вероятность, используя симметрию кривой плотности. Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление. X — нормально распределенная случайная величина со средним значением 100 и стандартным отклонением 10. X — нормально распределенная случайная величина со средним значением 67 и стандартным отклонением 13. Вероятность того, что X принимает значение в объединении интервалов (−∞,67−a]∪[67+a,∞) и будет обозначаться как P(X≤67−a или X≥67+a). X — нормально распределенная случайная величина со средним значением 288 и стандартным отклонением 6. Вероятность того, что X примет значение в объединении интервалов (−∞,288−a]∪[288+a,∞), будет равна обозначается P(X≤288−a или X≥288+a). Используйте рисунок 12.2 «Суммарная нормальная вероятность», чтобы найти следующие вероятности этого типа. Количество X напитка в банке с маркировкой 12 унций нормально распределено со средним значением 12,1 унции и стандартным отклонением 0,05 унции. Банка выбирается случайным образом. Продолжительность супоросности свиней имеет нормальное распределение со средним значением 114 дней и стандартным отклонением 0,75 дня. Найдите вероятность того, что помет родится в течение одного дня после среднего числа 114. Систолическое артериальное давление X у взрослых в регионе нормально распределено со средним значением 112 мм рт.ст. и стандартным отклонением 15 мм рт.ст. Человек считается «предгипертоником», если его систолическое артериальное давление составляет от 120 до 130 мм рт. Найти вероятность того, что артериальное давление у случайно выбранного человека будет предгипертоническим. Высоты X взрослых женщин распределены нормально со средним значением 63,7 дюйма и стандартным отклонением 2,71 дюйма. Ромео, 69 летРост 0,25 дюйма, желает встречаться только с женщинами, которые ниже его ростом, но не более чем на 4 дюйма его роста. Высоты X взрослых мужчин распределены нормально со средним значением 69,1 дюйма и стандартным отклонением 2,92 дюйма. Джульетта, рост которой 63,25 дюйма, желает встречаться только с мужчинами, которые выше ее, но в пределах 6 дюймов от нее. Найдите вероятность того, что следующий встречный мужчина будет иметь такой же рост. Обычная хоккейная шайба должна весить от 5,5 до 6 унций. Вес X шайб, изготовленных с помощью определенного процесса, нормально распределяется со средним значением 5,75 унции и стандартным отклонением 0,11 унции. Найти вероятность того, что шайба, изготовленная таким способом, будет соответствовать стандарту веса. Стандартный мяч для гольфа не может весить более 1,620 унций. Продолжительность времени, в течение которого батарея в сотовом телефоне Ипполиты будет держать заряд, достаточный для приемлемой работы, нормально распределяется со средним значением 25,6 часа и стандартным отклонением 0,32 часа. Ипполита вчера забыла зарядить свой телефон, так что в тот момент, когда она впервые захотела воспользоваться им сегодня, прошло 26 часов 18 минут с момента последней полной зарядки телефона. Найти вероятность того, что телефон будет работать исправно. Сумма неипотечного долга на домохозяйство для домохозяйств с определенным доходом в одной части страны обычно распределяется со средним значением 28 350 долларов США и стандартным отклонением 3 425 долларов США. Масса тела при рождении доношенных детей в определенном регионе распределяется нормально со средним значением 7,125 фунта и стандартным отклонением 1,29.0 фунтов. Найдите вероятность того, что случайно выбранный новорожденный будет весить менее 5,5 фунтов (историческое определение недоношенности). Расстояние от спинки сиденья до передней части коленей сидящих взрослых мужчин нормально распределяется со средним значением 23,8 дюйма и стандартным отклонением 1,22 дюйма. Расстояние от спинки сиденья до спинки следующего вперед сиденья на всех сиденьях самолетов бюджетной авиакомпании составляет 26 дюймов. Найдите долю взрослых мужчин, летающих этой авиакомпанией, колени которых касаются спинки переднего сиденья. Расстояние от сиденья до макушки головы сидящих взрослых мужчин нормально распределяется со средним значением 36,5 дюйма и стандартным отклонением 1,39 дюйма. Срок службы конкретной марки и типа автомобильной шины нормально распределяется со средним значением 57 500 миль и стандартным отклонением 950 миль. Станок производит большие крепежные детали, длина которых должна быть в пределах 0,5 дюйма от 22 дюймов. Длины нормально распределены со средним значением 22,0 дюйма и стандартным отклонением 0,17 дюйма. Время, затрачиваемое учащимися на экзамен по алгебре (если его не заставляют останавливаться перед его завершением), обычно распределяется со средним значением 28 минут и стандартным отклонением 1,5 минуты. Рост взрослых мужчин в возрасте от 18 до 34 лет распределяется нормально со средним значением 69,1 дюйма и стандартным отклонением 2,92 дюйма. Одним из требований для зачисления в армию является то, что мужчины должны быть ростом от 60 до 80 дюймов. Обычная хоккейная шайба должна весить от 5,5 до 6 унций. В альтернативном производственном процессе средний вес произведенных шайб составляет 5,75 унции. Вес шайб имеет нормальное распределение, стандартное отклонение которого можно уменьшить за счет все более строгого (и дорогого) контроля производственного процесса. Найдите максимальное допустимое стандартное отклонение, при котором не более 0,005 всех шайб не соответствуют стандарту веса. (Подсказка: распределение симметрично и находится в середине интервала допустимых весов.) Количество бензина X , подаваемое насосом-дозатором, когда он регистрирует 5 галлонов, является нормально распределенной случайной величиной. 2 «Совокупная нормальная вероятность» также может быть использован для вычисления вероятности формы P(a
2 «Совокупная нормальная вероятность» также может быть использован для вычисления вероятности формы P(a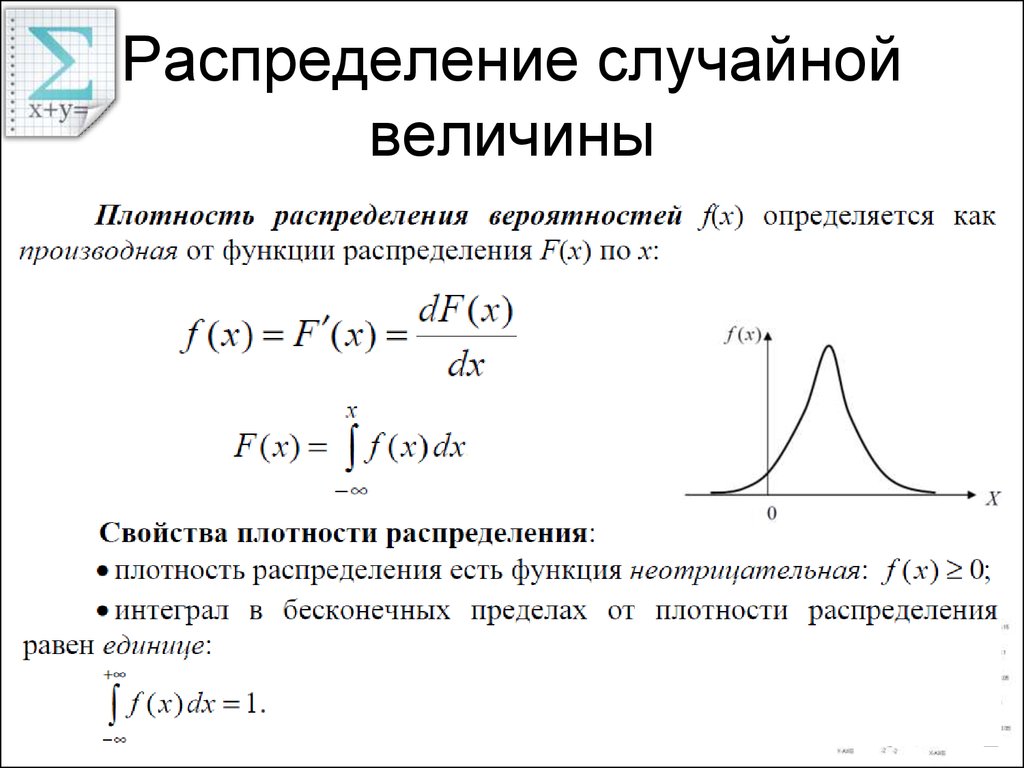
Пример 9
Пример 10
 Найдите вероятность того, что срок службы случайно выбранной шины составит от 30 000 до 40 000 миль.
Найдите вероятность того, что срок службы случайно выбранной шины составит от 30 000 до 40 000 миль. Пример 11
 Найдите процент всех лиц кто взял CEE кто соответствует 9 университету0054 CEE требование рассмотрения для приема.
Найдите процент всех лиц кто взял CEE кто соответствует 9 университету0054 CEE требование рассмотрения для приема. Упражнения
Базовый
 Найдите указанную вероятность.
Найдите указанную вероятность. Найдите указанную вероятность.
Найдите указанную вероятность. Найдите указанную вероятность.
Найдите указанную вероятность. Используйте рисунок 12.2 «Совокупная нормальная вероятность», чтобы найти первую указанную вероятность. Найдите вторую вероятность, используя симметрию кривой плотности. Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление.
Используйте рисунок 12.2 «Совокупная нормальная вероятность», чтобы найти первую указанную вероятность. Найдите вторую вероятность, используя симметрию кривой плотности. Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление. Используйте рисунок 12.2 «Суммарная нормальная вероятность», чтобы найти следующие вероятности этого типа. Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление. Из-за симметричности кривой плотности вам нужно использовать рисунок 12.2 «Суммарная нормальная вероятность» только один раз для каждой части.
Используйте рисунок 12.2 «Суммарная нормальная вероятность», чтобы найти следующие вероятности этого типа. Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление. Из-за симметричности кривой плотности вам нужно использовать рисунок 12.2 «Суммарная нормальная вероятность» только один раз для каждой части. Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление. Из-за симметричности кривой плотности вам нужно использовать рисунок 12.2 «Суммарная нормальная вероятность» только один раз для каждой части.
Нарисуйте кривую плотности с заштрихованными соответствующими областями, чтобы проиллюстрировать вычисление. Из-за симметричности кривой плотности вам нужно использовать рисунок 12.2 «Суммарная нормальная вероятность» только один раз для каждой части. Приложения

 Найдите вероятность того, что следующая женщина, которую он встретит, будет иметь такой же рост.
Найдите вероятность того, что следующая женщина, которую он встретит, будет иметь такой же рост. Весы X мячей для гольфа, изготовленных с помощью определенного процесса, нормально распределяются со средним значением 1,361 унции и стандартным отклонением 0,09 унции. Найдите вероятность того, что мяч для гольфа, изготовленный таким способом, будет соответствовать стандарту веса.
Весы X мячей для гольфа, изготовленных с помощью определенного процесса, нормально распределяются со средним значением 1,361 унции и стандартным отклонением 0,09 унции. Найдите вероятность того, что мяч для гольфа, изготовленный таким способом, будет соответствовать стандарту веса. Найдите вероятность того, что случайно выбранное такое домохозяйство имеет неипотечный долг от 20 000 до 30 000 долларов.
Найдите вероятность того, что случайно выбранное такое домохозяйство имеет неипотечный долг от 20 000 до 30 000 долларов. Расстояние от сиденья до крыши автомобиля определенной марки и модели составляет 40,5 дюймов. Найдите долю взрослых мужчин, которые, сидя в этой машине, будут иметь над головой хотя бы один дюйм (расстояние от макушки до крыши).
Расстояние от сиденья до крыши автомобиля определенной марки и модели составляет 40,5 дюймов. Найдите долю взрослых мужчин, которые, сидя в этой машине, будут иметь над головой хотя бы один дюйм (расстояние от макушки до крыши). Дополнительные упражнения
 0054 p происходит из части (а).
0054 p происходит из части (а).
 Найдите вероятность того, что все они удовлетворят требованиям по высоте. Подсказка: здесь есть биномиальная случайная величина, значение которой p происходит из части (а).
Найдите вероятность того, что все они удовлетворят требованиям по высоте. Подсказка: здесь есть биномиальная случайная величина, значение которой p происходит из части (а).

