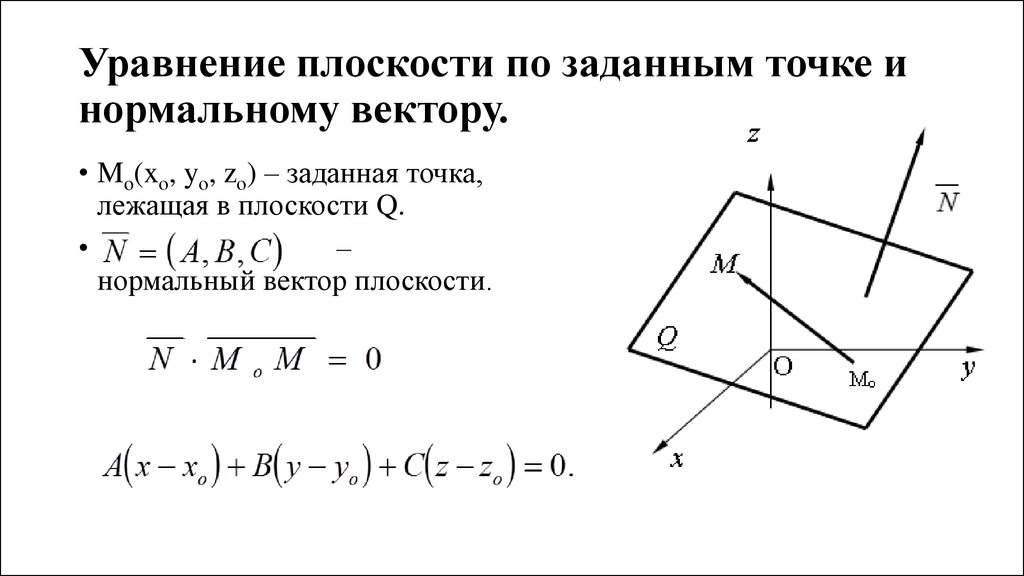
описание, примеры, решение задач, описание нормального уравнения прямой
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
Фиксируем на плоскости систему координат Оху, где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n→. Его начало обозначено точкой O. координатами являются cos α и cos β, углы которых расположены между вектором n→ и положительными осями Оx и Oy. Это запишется так: n→=(cos α, cos β). Прямая проходит через точку A с расстоянием равным p, где p≥0 от начальной точки O при положительном направлении вектора n→.
Если р=0, тогда A считается совпадающей с точкой координат. Отсюда имеем, что OA=p. Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M (x, y) расположена на прямой тогда и только тогда, когда числовая проекция вектора OM→ по направлению вектора n→ равняется p, значит при выполнении условия npn→OM→=p.
OM→ является радиус-вектором точки с координатами M (x, y), значит OM→=(x, y).
Применив определение скалярного произведения векторов, получим равенство вида: n→, OM→=n→·npn→OM→=1·npn→OM→=npn→OM→=p
Тогда это же произведение будет иметь вид в координатной форме: n→, OM→=cos α·x+cos β·y
Отсюда cos α·x+cos β·y=p или cos α·x+cos β·y-p=0. Было выведено нормальное уравнение прямой.
Определение 1Уравнение вида cos α·x+cos β·y-p=0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой Ax+By+C=0, где A и B имеют значения, при которых длина вектора n→=(A, B) равна 1, а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α·x+cos β·y-p=0 задает в системе координат Оху на плоскости прямую с наличием нормального вектора единичной длины n→=(cos α, cos β), которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n→.
Если дано уравнение прямой вида -12·x+32·y-3=0, то на плоскости задается прямая, у которой нормальный вектор с координатами -12, 32. Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n→=-12, 32.
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному.
Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой Ax+Bx+C=0 к нормальному необходимо обе части умножить на нормирующий множитель,
Привести уравнение прямой 3x-4y-16=0 к нормальному виду.
Решение
Из общего уравнения видно, что А=3, В=-4, С=-16. Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1A2+B2=132+(-4)2=15
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 15·(3x-4y-16)=0⇔35·x-45·y-165=0.
Нормальное уравнение по заданной прямой найдено.
Ответ: 35·x-45·y-165=0.
Пример 2Получить нормальное уравнение прямой y=13x.
Решение
По условию имеем, что общее уравнение прямой 13x-y=0. Очевидно, что С=0, значит знак нормирующего множителя не имеет значения.
1A2+B2=1132+(-1)2=310
Обе части умножаем на нормированный множитель, получаем, что нормальное уравнение прямой имеет вид 110x-310y=0.
Ответ: 110x-310y=0.
Нахождение расстояния от точки до прямой на плоскости
В данном пункте рассмотрим важное приложение нормального уравнения прямой – нахождение расстояния от заданной точки до заданной прямой на плоскости.
Расстояние от точки M0(x0, y0) до прямой с нормальным уравнением cos α·x+cos β·y-p=0 задается буквой p. Вычисление расстояния р производится по формуле p=cos α·x0+cos β·y0-p. Для того, чтобы найти расстояние от точки до прямой, нужно сделать подстановку координат этой точки в левую часть уравнения и работать с абсолютной величиной полученного значения. С подробным выводом формулы можно ознакомиться в статье нахождения расстояния от точки до прямой. Имеется альтернативный способ его вычисления.
Пример 3Найти расстояния от точки с координатами M0(-2, 1) к прямой с нормальным уравнением 23x-52y-1=0.
Решение
По условию имеем, что x0=-2, y0=1, cos α=23, cos β=-53, p=1.
Применим формулу для вычисления расстояния от точки до прямой. Получим, что:
p=cos α·x0+cos β·y0-p=23·-2-53·1-1=-7+53=7+53
Ответ: 7+53.
Пример 4Вычислить расстояние от точки с координатами M0(-2, -3) до прямой x-1-2=y+33.
Решение
Начнем решение с приведения уравнения заданной прямой к нормальному виду. Для начала необходимо привести к общему виду. Получим:
x-1-2=y+33⇔3·(x-1)=-2·(y+3)⇔3x+2y+3=0
Проведем вычисление нормирующего множителя по формуле: -1A2+B2=-132+22=-113.
Следующим действием будет умножение обоих частей уравнения 3x+2y+3=0 на нормирующий множитель.
Получаем: -313·x-213·y-313=0
Было произведено получение нормального уравнения прямой. Чтобы найти расстояние, необходимо использовать абсолютную величину и подставить в формулу для нахождения искомого значения.
Тогда p=-313·(-2)-213·(-3)-313=913=913.
Ответ: 913.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нормальное уравнение прямой на плоскости
Пусть дана некоторая прямая L. Проведём через начало координат прямую n, перпендикулярно данной и назовём её нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L. На нормали введём направление от точки O к точке N.
Обозначим через угол, на которой нужно повернуть против часовой стрелки ось Ox до совмещения её положительного направления с направлением нормали, через p длину отрезка ON.
Тогда уравнение
. (1)
будет нормальным уравнением прямой.
С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости
до прямой. Пусть — точка, не лежащая
на прямой, заданной нормальным уравнением.
Требуется определить расстояние d от точки до прямой. Это расстояние
определяется по формуле
. (2)
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
— общее уравнение прямой, а
— её нормальное уравнение.
Так как оба уравнения определяют одну и ту же прямую, их коэффициенты пропорциональны.
Очевидно, для получения нормального уравнения следует все члены общего уравнения умножить на постоянный множитель , вычисляемый по формуле
. (3)
В этой формуле берётся знак, противоположный знаку C в общем уравнении прямой.
Таким образом, получаем уравнение
, (4)
которое и будет нормальным уравнением прямой на плоскости.
Пример 1. Привести общее уравнение прямой к нормальному виду.
Решение. Вычисляем нормирующий множитель:
(знак, противоположный C).
Умножаем все члены общего уравнения на нормирующий множитель и получаем:
.
Нет времени вникать в решение? Можно заказать работу!
Пример 2. Привести общее уравнение прямой к нормальному виду.
Решение. Вычисляем нормирующий множитель:
(знак, противоположный C).
Умножаем все члены общего уравнения на нормирующий множитель и получаем:
.
Пример 3. Найти расстояние от точки до прямой .
Решение. Приведём данное уравнение к нормальному виду. Вычисляем нормирующий множитель:
(знак, противоположный C).
Умножаем все члены общего уравнения на нормирующий множитель и получаем нормальное уравнение:
.
По формуле (2) находим искомое расстояние:
.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Прямая и плоскость
Всё по теме «Прямая на плоскости
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой на плоскости
Уравнение прямой в отрезках
Каноническое уравнение прямой на плоскости
Параметрические уравнения прямой на плоскости
Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Видео-урок: Уравнение прямой в пространстве: Декартовы и векторные формы
Стенограмма видео
В этом видео мы увидим, как
найти уравнение прямой в пространстве.
Значит, мы рассматриваем
координаты в трех измерениях, а не только в двух измерениях. Посмотрим, как мы можем написать это
уравнение в декартовой форме, которую иногда называют общей формой. И мы также увидим, как мы можем писать
это в векторной форме. Начнем с того, что посмотрим на
векторная форма.
Векторная форма линии может быть
описывается как 𝐫 равно 𝐫 меньше нуля плюс 𝑡𝐯, где 𝐫, 𝐫 меньше нуля и 𝐯 все
векторы. 𝐫 — вектор положения любого
общая точка на линии. 𝐫 ниже нуля — это вектор положения
заданной точки на прямой. 𝐯 — вектор направления или
вдоль линии. А 𝑡 — скалярное кратное. Векторная форма может использоваться как в двух
измерения и трехмерность. Отличие в том, что в трех
размеры, все наши векторы будут иметь 𝑥-, 𝑦- и 𝑧-компоненты. Когда мы описываем строку в
векторной форме, помните, что мы думаем о том, как перейти от исходной точки к
конкретная точка.
И тогда мы движемся по этому
линия в скалярных кратных вектору 𝐯.
Теперь рассмотрим вопрос где нам нужно написать векторное уравнение прямой по заданной точке на прямой и вектор направления.
Приведите векторное уравнение линия через точку три, семь, минус семь с нулевым вектором направления, минус пять, семь.
Мы должны помнить, что когда мы
нужно написать уравнение в векторной форме, оно будет в виде 𝐫 равно 𝐫 sub
ноль плюс 𝑡𝐯, где 𝐫 — вектор положения общей точки на прямой, 𝐫
к югу от нуля — это вектор положения данной точки на линии, а 𝐯 — это направление
вектор. 𝑡 — скалярное кратное. Если мы посмотрим на информацию, которая
нам дано в вопросе, мы видим, что у нас есть вектор направления. И у нас есть точка на линии
который можно записать в виде вектора положения. По мере того, как мы перемещаемся от источника к
точка три, семь, минус семь, то мы можем записать это как положение
вектор три, семь, минус семь.
Затем мы можем просто подключить эти два вектора в векторную форму. 𝐫 равно вектору положения три, семь, минус семь плюс 𝑡, умноженный на вектор направления ноль, минус пять, Семь. И так это ответ на векторное уравнение прямой.
В следующем вопросе мы посмотрите, как мы можем вычислить вектор направления по двум точкам.
Найти вектор направления прямая, проходящая через 𝐴 один, минус два, семь и 𝐵 четыре, минус один, три.
В этом вопросе нам дается
векторы положения двух точек в пространстве, 𝐴 и 𝐵, и нас просят найти
вектор направления. Когда мы хотим найти направление
вектор 𝐀𝐁, 𝐴 — начальная точка, а 𝐵 — конечная точка, мы вычитаем
отправная точка от конечной точки. Для того, чтобы найти направление
вектора, мы можем вычесть каждую из 𝑥-, 𝑦- и 𝑧-компонент в 𝐴 из компонентов в
𝐵.
Для начала у нас будет четыре
вычесть один, давая нам три. Тогда у нас будет отрицательный
вычесть минус два, что эквивалентно минус один плюс два, что равно
один. И, наконец, у нас будет три
вычесть семь, что даст нам минус четыре. Итак, мы получили ответ на
вектор направления 𝐝 как три, один, минус четыре.
Однако в этом вопросе мы не обязательно нужно было найти вектор направления 𝐀𝐁. Мы могли бы также найти вектор направления 𝐁𝐀. В этом случае мы получили бы вектор, обратный 𝐝, равен отрицательным трем, отрицательным единицам, четырем, что также были действительным ответом.
В следующем вопросе мы увидим немного более сложный пример, где нам нужно найти векторное уравнение медианы треугольника, нарисованного в трехмерном пространстве.
Точки 𝐴 минус восемь,
минус девять, минус два; 𝐵 ноль, минус семь, шесть; и 𝐶 минус восемь,
отрицательная единица, отрицательная четверка образуют треугольник.
Определить в векторной форме
уравнение медианы, взятое из 𝐶.
В этом вопросе у нас три точки 𝐴, 𝐵 и 𝐶, заданные в трехмерном пространстве. Нам говорят, что эти три точки образуют треугольник. Нам говорят, что есть медиана взято из 𝐶, поэтому было бы полезно напомнить, что медиана — это отрезок соединение вершины с серединой противоположной стороны. Например, если мы нарисовали это двумерного треугольника 𝐴𝐵𝐶 медиана из 𝐶 будет выглядеть так.
Пожалуй, лучший способ начать это
вопрос в том, сможем ли мы найти точку, которая является серединой 𝐴𝐵. Обозначим это буквой
𝑀. Формула для нахождения середины
две точки в пространстве очень похожи на то, что мы могли бы использовать для двух координат
в двухмерном пространстве. Чтобы найти середину 𝑀 𝑥 одного,
𝑦 один, 𝑧 один и 𝑥 два, 𝑦 два, 𝑧 два, имеем, что 𝑀 равно 𝑥 один плюс
𝑥 два плюс два, 𝑦 один плюс 𝑦 два плюс два, 𝑧 один плюс 𝑧 два плюс два.
Когда мы наполняем наши ценности этим
формулы, нам нужно убедиться, что мы используем значения для 𝐴 и 𝐵, поскольку, в конце концов, мы
нужно найти середину 𝐴𝐵.
Обратите внимание, что при подключении
наши ценности, неважно, какую точку мы используем с нашей 𝑥 одной, 𝑦 одной, 𝑧 одной
значений или 𝑥 два, 𝑦 два, 𝑧 два значения. Итак, у нас есть середина 𝑀
равно минус восемь плюс ноль больше двух, минус девять плюс минус семь больше
два и минус два плюс шесть на два. Упрощая это, мы имеем это 𝑀
равно минус четыре, минус восемь, два. Теперь мы можем очистить место, чтобы
можно начать думать о векторной форме уравнения этой медианы. Векторная форма уравнения может
быть записано в виде 𝐫 равно 𝐫 меньше нуля плюс 𝑡𝐯, где 𝐫 — позиция
вектор общей точки на прямой, 𝐫 ниже нуля — это вектор положения заданного
точка на линии, а 𝐯 — вектор направления.
𝑡 — скалярное кратное.
Давайте подумаем, что произойдет если мы смоделируем эти три точки в трехмерном пространстве. У нас был бы треугольник 𝐴𝐵𝐶 и медиана, которая будет отрезком 𝐶𝑀. Поэтому, когда дело доходит до написания медиана в векторной форме, вектор положения может быть точкой 𝐶. Но нам еще нужно проработать вектор направления 𝐂𝐌. Чтобы найти вектор 𝐂𝐌, мы вычесть начальную точку 𝐶 из конечной точки 𝑀. Итак, у нас есть минус четыре вычесть минус восемь, минус восемь вычесть минус один, а два вычесть минус четыре. Упрощая это, мы имеем, что вектор 𝐂𝐌 равен четырем, минус семь, шесть.
Теперь у нас есть вся информация
что нам нужно подключить к векторной форме линии. 𝐫 ниже нуля будет позиция
вектор, представляющий точку 𝐶. Вектор 𝐯 будет представлен
вектор 𝐂𝐌. Поэтому ответ на
уравнение медианы из 𝐶 равно 𝐫 отрицательной восьмерке, отрицательной единице, отрицательной
четыре плюс 𝑡 четыре, минус семь, шесть.
До сих пор в этом видео мы смотрели при уравнениях прямых в векторной форме. Теперь подумаем, как мы изменимся. линия, заданная в векторной форме, соответствует линии в декартовой форме. Вас может смутить терминологии декартовой формы, но линия в двух измерениях в декартовой форме может быть записанное в виде 𝑦 равно 𝑚𝑥 плюс 𝑏, где 𝑚 — наклон или градиент, а 𝑏 является 𝑦-перехватом. Но, конечно, по-другому трехмерном пространстве, так как нам нужно уравнение, описывающее 𝑥-, 𝑦- и 𝑧-переменные.
Итак, чтобы найти уравнение прямой
в декартовой форме, мы можем сказать, что данное уравнение линии с направлением
вектор 𝐯 равен 𝑙, 𝑚, 𝑛, который проходит через точку 𝑥 под единицу, 𝑦 под единицу,
𝑧 sub один, то это дается 𝑥 минус 𝑥 sub один больше 𝑙 равно 𝑦 минус 𝑦 sub
единица над 𝑚 равна 𝑧 минус 𝑧 меньше единицы над 𝑛, где 𝑙, 𝑚 и 𝑛 не равны нулю
действительные числа.
Таким образом, мы можем видеть, как эта информация
уравнения с точкой и направлением, т. е. в векторной форме, может быть
превратился в один в декартовой форме. Сейчас мы рассмотрим два
вопросы, где мы могли бы применить эту формулу.
Приведите декартово уравнение строка 𝐫 равна минус три, минус два, минус два плюс 𝑡 четыре, два, четыре.
В этом вопросе нам дано это
уравнение в векторной форме. Минус три, минус два,
отрицательные два — это вектор положения данной точки, а четыре, два, четыре — это
вектор направления. Чтобы изменить уравнение в
векторную форму в уравнение в декартовой форме, есть формула, которую мы можем применить. Уравнение прямой с
вектор направления 𝐯 равен 𝑙, 𝑚, 𝑛, который проходит через 𝑥 под единицу, 𝑦 под единицу, 𝑧
подгруппа определяется как 𝑥 минус 𝑥 подгруппа над 𝑙 равна 𝑦 минус 𝑦 подгруппа над 𝑚
равно 𝑧 минус 𝑧 меньше единицы над 𝑛, где 𝑙, 𝑚 и 𝑛 ненулевые вещественные числа
числа.
Теперь нам нужно взять направление вектор четыре, два, четыре, чтобы иметь значения 𝑙, 𝑚 и 𝑛 соответственно. Мы можем сделать то же самое и обозначить координата 𝑥 под единица, 𝑦 под единица, 𝑧 под единица со значениями минус три, минус два, минус два. Подставив эти значения в формула, мы имеем 𝑥 минус минус три больше четырех равно 𝑦 минус минус два больше два равно 𝑧 минус минус два больше четырех. Упрощая числители, имеем 𝑥 плюс три больше четырех равно 𝑦 плюс два больше двух равно 𝑧 плюс два больше четыре. И это ответ на Декартово уравнение заданной прямой.
Посмотрим на финал вопрос.
Найдите декартову форму уравнение прямой, проходящей через точки отрицательная семерка, отрицательная три, минус семь и минус три, минус 10, минус четыре.
В этом вопросе, хотя мы
спросил декартову форму уравнения, может быть полезно подумать о том, что
эта линия будет похожа на векторную форму.
Если рассматривать наши две точки как
𝐴 и 𝐵 и мы хотели найти вектор направления 𝐀𝐁, тогда мы вычли бы
все точки на нашей отправной точке 𝐴 из тех, что на 𝐵. Таким образом, у нас будет 𝐀𝐁 равно
минус три вычесть минус семь, что эквивалентно минус три плюс
семь, что дает нам четыре. Минус 10 вычесть минус три
эквивалентно минус 10 плюс три, что составляет минус семь. И тогда у нас будет минус четыре
вычесть минус семь, что дает нам три.
Теперь, когда у нас есть вектор направления
и точка на прямой, мы можем найти декартову форму уравнения прямой
соединяя эти два пункта. Мы должны помнить, что
уравнение прямой с направляющим вектором 𝐯, равным 𝑙, 𝑚, 𝑛, проходящей через
точка 𝑥 подгруппа, 𝑦 подгруппа, 𝑧 подгруппа определяется как 𝑥 минус 𝑥 подгруппа над 𝑙
равно 𝑦 минус 𝑦 меньше единицы над 𝑚 равно 𝑧 минус 𝑧 меньше единицы больше 𝑛.
Обратите внимание, что 𝑙, 𝑚 и 𝑛
ненулевые действительные числа.
Теперь мы можем использовать вектор направления из 𝐀𝐁 для значений 𝑙, 𝑚 и 𝑛 и точки минус семь, минус три, минус семь для значений 𝑥 меньше единицы, 𝑦 меньше единицы и 𝑧 меньше единицы. Заполнение этих значений в формула, у нас есть 𝑥 вычесть минус семь из четырех равных 𝑦 вычесть минус три на минус семь равно 𝑧 вычесть минус семь на три. Упрощение числителей дает нам ответ в декартовой форме 𝑥 плюс семь больше четырех равно 𝑦 плюс три больше минус семь равно 𝑧 плюс семь на три.
Теперь мы можем суммировать ключевые моменты
этого видео. Во-первых, мы увидели уравнение
линия, заданная в векторной форме как 𝐫, равна 𝐫 ниже нуля плюс 𝑡𝐯. 𝐫 — вектор положения
общая точка на линии, 𝐫 к югу от нуля — это вектор положения данной точки на
линия, а 𝐯 — вектор направления.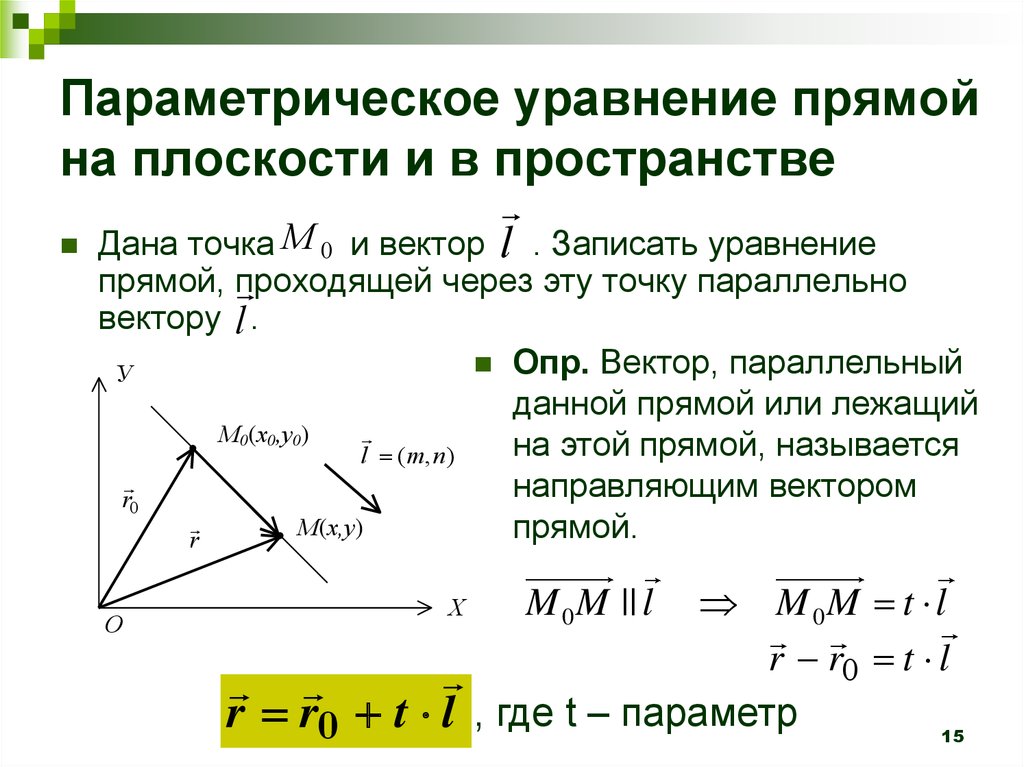
𝑡 — скалярное кратное. Чтобы найти вектор направления 𝐀𝐁, мы
вычесть начальную точку 𝐴 из конечной точки 𝐵.
Наконец, мы увидели, что уравнение линии с направляющим вектором 𝐯, равным 𝑙, 𝑚, 𝑛, которая проходит через 𝑥 подединицу, 𝑦 подгруппа, 𝑧 подгруппа определяется как 𝑥 минус 𝑥 подгруппа над 𝑙 равно 𝑦 минус 𝑦 подгруппа над 𝑚 равна 𝑧 минус 𝑧 подгруппа над 𝑛, где 𝑙, 𝑚 и 𝑛 не равны нулю действительные числа. Эта окончательная формула очень полезна для замены уравнения прямой, заданного в векторной форме, уравнением, заданным в Картезианская форма.
Объяснение урока: Уравнение прямой в пространстве: Декартова и векторная формы
В этом объяснении мы научимся находить декартову и векторную формы уравнения прямой в пространстве.
Когда мы рассматриваем уравнения в пространстве, у нас есть координаты в трех измерениях, как (𝑥,𝑦,𝑧), а не в двух измерениях, как (𝑥,𝑦).
В векторной форме мы считаем, что линия определяется любой точкой на линии и направлением. Чтобы найти уравнение, представляющее линия, 𝐿, в трех измерениях, мы выбираем точку, 𝑃, на линии и ненулевой вектор, ⃑𝑑, параллельный линии, где ⃑𝑟 — вектор положения 𝑃.
Поскольку ⃑𝑑 параллелен 𝐿, то добавление любой постоянной, кратной ⃑𝑑 к ⃑𝑟, даст вектор положения точки на прямой. Таким образом, вектор положения ⃑𝑟 на прямой можно найти путем движения к точке 𝑃(𝑥,𝑦,𝑧) на прямой вдоль вектора ⃑𝑟, а затем следуя постоянному множителю вектора ⃑𝑑 .
Затем мы можем установить векторную форму линии следующим образом.
Определение: векторная форма линии
Вектор положения ⃑𝑟 любой общей точки на линии, которая содержит точку 𝑃(𝑥,𝑦,𝑧) в векторе положения ⃑𝑟 ⃑𝑟=⃑𝑟+𝑡⃑𝑑, где ⃑𝑑 — вектор направления линии или вдоль нее, а 𝑡 — любое кратное скаляру.
Теперь мы увидим пример того, как мы можем написать векторное уравнение линии, зная точку на линии и направление
вектор.
Пример 1. Нахождение векторного уравнения прямой по заданной точке и ее направлению Вектор
Задайте векторное уравнение прямой, проходящей через точку (3,7,−7) с вектором направления (0,−5,7).
Ответ
Мы помним, что вектор можно записать в виде ⃑𝑟=⃑𝑟+𝑡⃑𝑑, где ⃑𝑟 — вектор положения любой общей точки на прямой с вектором направления ⃑𝑑, содержащим точку в векторе положения ⃑𝑟. Значение 𝑡 представляет собой скалярное кратное.
Нам задан вектор направления (0,−5,7).
Поскольку точка (3,7,−7) лежит на прямой, мы можем установить ⃑𝑟 как вектор положения этой точки (3,7,−7).
Таким образом, подстановка вектора положения ⃑𝑟=(3,7,−7) и заданного вектора направления как ⃑𝑑=(0,−5,7) в векторное уравнение прямой дает решение ⃑𝑟=(3,7,−7)+𝑡(0,−5,7).
Мы можем найти вектор направления 𝐴𝐵 прямой между двумя точками 𝐴 и 𝐵, вычитая положение
вектор начальной точки, 𝐴, из вектора положения конечной точки, 𝐵. Для этого мы вычитаем каждую из 𝑥-, 𝑦- и 𝑧-компонентов позиционного вектора 𝐴 из позиционного вектора 𝐵.
Давайте посмотрим на примере того, как мы можем это сделать.
Пример 2. Нахождение вектора направления прямой через две точки
Найдите вектор направления прямой, проходящей через 𝐴(1,−2,7) и 𝐵(4,−1,3).
Ответ
Вектор направления прямой — это ненулевой вектор, параллельный прямой. Чтобы найти вектор направления, ⃑𝑑, прямой линии между точками 𝐴 и 𝐵, мы замечаем, что эта линия должна иметь то же направление, что и вектор от 𝐴 до 𝐵. Мы можем найти этот вектор, вычитая каждую из 𝑥-, 𝑦- и 𝑧-компонентов 𝑂𝐴 из 𝑂𝐵.
Следовательно, имеем ⃑𝑑=(4−1,−1−(−2),3−7)=(3,1,−4).
Мы можем дать решение, что вектор направления прямой, проходящей через 𝐴(1,−2,7) и 𝐵(4,−1,3), равен (3,1,−4).
В качестве примечания: нам не был задан вектор направления как 𝐴𝐵; таким образом, вектор 𝐵𝐴=(−3,−1,4) также был бы допустимым вектором направления. Действительно, любое ненулевое кратное любого из этих векторов направления будет правильным.
Нам часто нужно найти середину линии, соединяющей две точки в пространстве.
Мы можем сделать это, используя тот же процесс
для трех измерений, как мы делаем для линии в двух измерениях. Нахождение среднего значения каждой из 𝑥-, 𝑦- и 𝑧-координат обеих конечных точек позволяет нам определить координаты середины трехмерного отрезка прямой.
Резюме: середина двух точек в 3D
Середина 𝑀 любых двух точек (𝑥, 𝑦, 𝑧) и (𝑥,𝑦,𝑧) определяется выражением 𝑀=𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
В следующем вопросе мы увидим, как эту формулу можно использовать для нахождения медианы треугольника, нарисованного в пространстве.
Пример 3. Нахождение векторного уравнения одной медианы треугольника
Точки 𝐴(−8,−9,−2), 𝐵(0,−7,6) и 𝐶(−8,−1,−4) образуют треугольник. Определить в векторной форме уравнение медианы, взятое из 𝐶.
Ответ
Медиана треугольника — это отрезок, соединяющий вершину с серединой противоположной стороны. Мы можем рассмотреть двумерное представление средней точки, 𝑀,
на противоположной стороне от вершины 𝐶, что при соединении с вершиной 𝐶,
образует медиану 𝐶𝑀.
Мы помним, что векторное уравнение прямой можно записать в виде ⃑𝑟=⃑𝑟+𝑡⃑𝑑, где ⃑𝑟 — вектор положения любой общей точки на прямой с вектором направления ⃑𝑑, содержащим точку в векторе положения ⃑𝑟. Значение 𝑡 представляет собой скалярное кратное.
Чтобы найти векторную форму уравнения медианы, мы можем начать с нахождения середины 𝑀 𝐴𝐵.
Середина 𝑀 двух точек (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) находится по формуле 𝑀=𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
Итак, для 𝐴(−8,−9,−2) и 𝐵(0,−7,6) мы имеют 𝑀=−8+02,−9+(−7)2,−2+62.
Оценка дает нам 𝑀=(−4,−8,2).
Вектор 𝐶𝑀 будет вектором направления медианы. Чтобы найти 𝐶𝑀, мы вычитаем 𝑥-, 𝑦- и 𝑧-компоненты 𝑂𝐶, (−8,−1,−4), из 𝑂𝑀, (−4,−8,2), что дает 𝐶𝑀=(−4−(−8),−8−(−1),2−(−4))=(4,−7,6).
Теперь мы можем применить векторную форму уравнения ⃑𝑟=⃑𝑟+𝑡⃑𝑑, где 𝑡 — скалярное кратное, как ⃑𝑟=𝑂𝐶+𝑡𝐶𝑀.
Подставляя в 𝑂𝐶=(−8,−1,−4) и 𝐶𝑀=(4,−7,6), мы получаем решение для векторной формы медианы, проведенной из 𝐶 как
⃑𝑟=(−8,−1,−4)+𝑡(4,−7,6).
Альтернативное решение можно найти, используя вектор направления 𝑀𝐶 медианы. В этом случае вектор форма уравнения будет использовать вектор положения 𝑂𝑀, чтобы дать уравнение в форме ⃑𝑟=𝑂𝑀+𝑡𝑀𝐶, где 𝑡 — скалярное кратное.
Замена 𝑂𝑀=(−4,−8,2) и 𝑀𝐶=(−4,7,−6) дает ⃑𝑟=(−4,−8,2)+𝑡(−4,7,−6).
Уравнение прямой можно записать несколькими способами. Имеем векторное уравнение прямой, записанное в виде ⃑𝑟=⃑𝑟+𝑡⃑𝑑, где ⃑𝑟 — вектор положения любой общей точки на прямой с вектором направления ⃑𝑑, содержащим точку в векторе положения ⃑𝑟. Значение 𝑡 представляет собой скалярное кратное.
Мы также можем представить вектор ⃑𝑟 как (𝑥,𝑦,𝑧) и вектор направления ⃑𝑑 как (𝑎,𝑏,𝑐). Таким образом, мы можем записать векторную форму альтернативно как ⃑𝑟=(𝑥,𝑦,𝑧)+𝑡(𝑎,𝑏,𝑐).
Представив ⃑𝑟 в виде (𝑥,𝑦,𝑧) и упростив компоненты в правой части, мы можем записать это уравнение как (𝑥,𝑦,𝑧)=(𝑥+𝑎𝑡,𝑦+𝑏𝑡,𝑧+𝑐𝑡).
Когда два вектора равны, их компоненты равны.
Это означает, что у нас есть
𝑥=𝑥+𝑎𝑡𝑦=𝑦+𝑏𝑡𝑧=𝑧+𝑐𝑡.
Этот набор уравнений дает нам параметрические уравнения линии. Чтобы найти точку на прямой в таком виде, мы могли бы выберите любое значение 𝑡 и подставьте его в каждое из уравнений.
Мы также можем изменить этот набор уравнений, чтобы найти значение 𝑡 в каждом случае, предполагая, что 𝑎, 𝑏 и 𝑐 отличны от нуля: 𝑡=𝑥−𝑥𝑎,𝑡=𝑦−𝑦𝑏,𝑡=𝑧−𝑧𝑐.
Поскольку значение 𝑡 будет одинаковым в каждом уравнении, мы можем положить эти выражения в правой части равными друг друга: 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐.
Это декартово уравнение прямой.
Определение: декартово уравнение прямой
Уравнение прямой с направляющим вектором ⃑𝑑=(𝑎,𝑏,𝑐), где 𝑎, 𝑏 и 𝑐 — ненулевые действительные числа, проходящей через точку (𝑥, 𝑦,𝑧) определяется выражением 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐.
Мы по-прежнему можем использовать декартову форму уравнения прямой, если одна или две переменные 𝑎, 𝑏 или 𝑐 равны 0. Например, предположим, что 𝑎=0, а 𝑏 и 𝑐 не равны нулю.
В этом случае 𝑡 не будет существовать в параметрическом уравнении для 𝑥, поэтому мы можем решить только параметрические уравнения для 𝑦 и 𝑧. Приравняем их друг к другу и запишем параметрическое уравнение для 𝑥; таким образом, мы имеем два уравнения:
𝑥=𝑥,𝑦−𝑦𝑏=𝑧−𝑧𝑐.
Теперь мы рассмотрим пример того, как мы можем изменить линию, заданную в векторной форме, на линию, заданную в декартовой форме.
Пример 4. Нахождение декартова уравнения прямой по ее векторному уравнению
Приведите декартово уравнение прямой ⃑𝑟=(−3,−2,−2)+𝑡(4,2,4).
Ответ
Поскольку у нас есть уравнение прямой в векторной форме, мы можем заметить, что у нас есть вектор положения точки (−3,−2,−2). У нас также есть вектор направления (4,2,4).
Можно использовать тот факт, что уравнение прямой с направляющим вектором ⃑𝑑=(𝑎,𝑏,𝑐), где 𝑎, 𝑏 и 𝑐 — ненулевые действительные числа, проходящей через точку (𝑥,𝑦,𝑧) задается 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐.
Затем мы подставляем значения (𝑥,𝑦,𝑧)=(−3,−2,−2) и (𝑎,𝑏,𝑐)=(4,2,4) в эту форму.
Это дает 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐𝑥−(−3)4=𝑦−(−2)2=𝑧−(−2)4.
Упрощая числители, решение декартова уравнения эта линия 𝑥+34=𝑦+22=𝑧+24.
В последнем примере мы можем увидеть, как мы используем две точки на прямой в пространстве, чтобы найти ее декартово уравнение.
Пример 5. Нахождение декартова уравнения прямой через две точки
Найдите декартову форму уравнения прямой, проходящей через точки (−7,−3,−7) и (−3,−10, −4).
Ответ
Один из методов, который мы можем использовать, чтобы найти декартово уравнение линии, проведенной в пространстве, заключается в рассмотрении ее в аналогичном путь к векторной форме; то есть линия, описываемая точкой на линии и вектором направления.
Имея две точки 𝐴(−7,−3,−7) и 𝐵(−3,−10,−4), мы можем найти вектор направления 𝐴𝐵, вычитая 𝑥-, 𝑦- и 𝑧- компоненты вектора положения ⃑𝐴 от компонентов вектора положения ⃑𝐵.
Это дает нам 𝐴𝐵=(−3,−10,−4)−(−7,−3,−7)=(−3−(−7),−10−(−3),−4−(−7)) =(4,−7,3).
Можно использовать тот факт, что уравнение прямой с направляющим вектором ⃑𝑑=(𝑎,𝑏,𝑐), где 𝑎, 𝑏 и 𝑐 — ненулевые действительные числа, проходящей через точку (𝑥,𝑦,𝑧) задается
𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐.