Нормальный закон распределения это: Нормальное распределение (Normal Distribution) · Loginom Wiki

Теория вероятностей

Теория вероятностей

Вентцель Е.С. Теория вероятностей: Учеб. для вузов. — 6-е изд. стер. — М.: Высш. шк., 1999.— 576 c. Книга представляет собой один из наиболее известных учебников по теории вероятностей и предназначена для лиц, знакомых с высшей математикой и интересующихся техническими приложениями теории вероятностей. Она представляет также интерес для всех тех, кто применяет теорию вероятностей в своей практической деятельности. В книге уделено большое внимание различным приложениям теории вероятностей (теории вероятностных процессов, теории информации, теории массового обслуживания и др.). Оглавление Глава 1. Введение ПРЕДИСЛОВИЕ 1. 1. Предмет теории вероятностей Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5. 4. Плотность распределения 5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.3. Статистический ряд. Гистограмма 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8. Системы случайных величин 8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений. 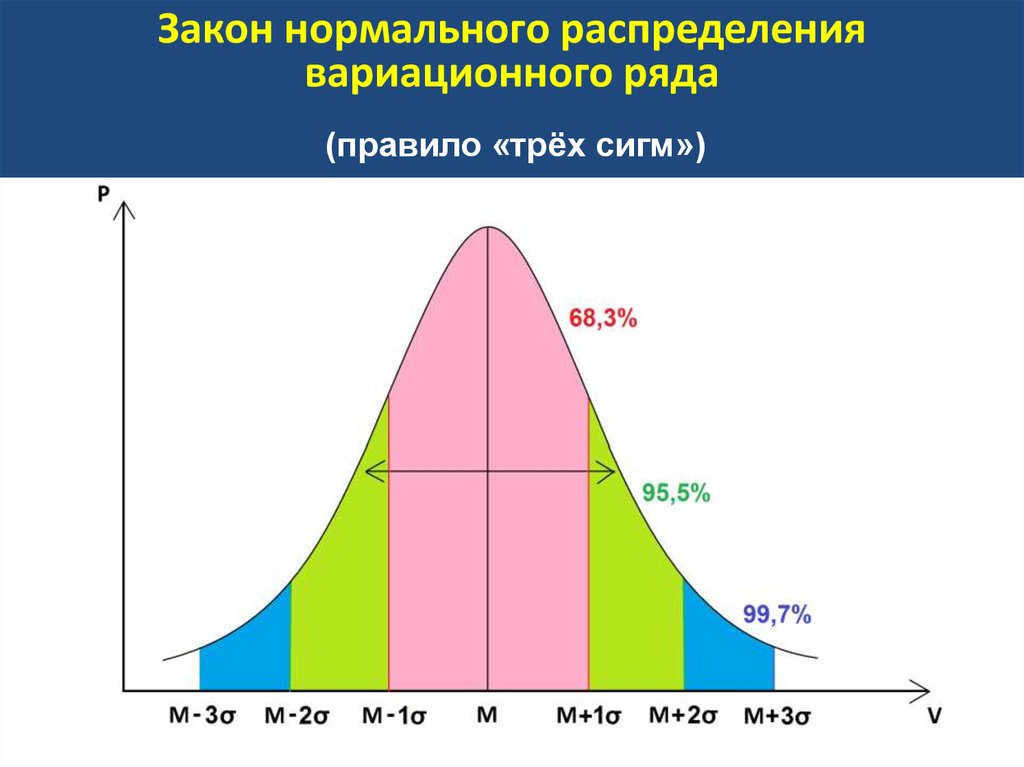Общая запись нормального закона для системы произвольного числа случайных величин Глава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации Глава 12. Законы распределения функций случайных аргументов 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин. 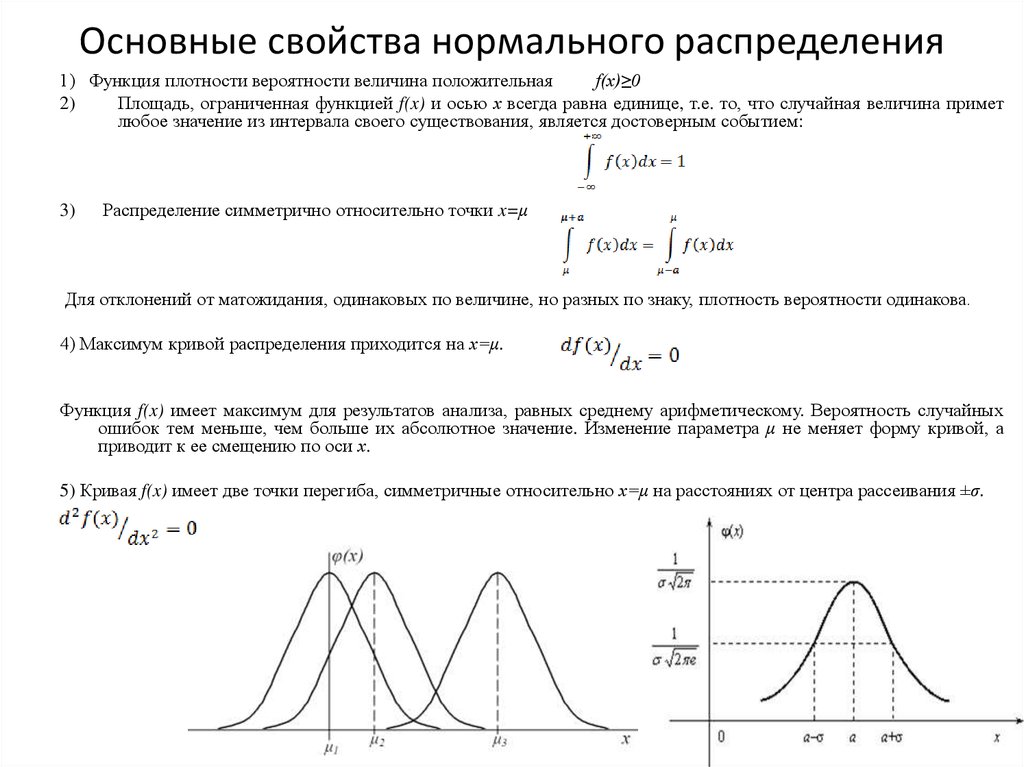Композиция законов распределения 12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14. 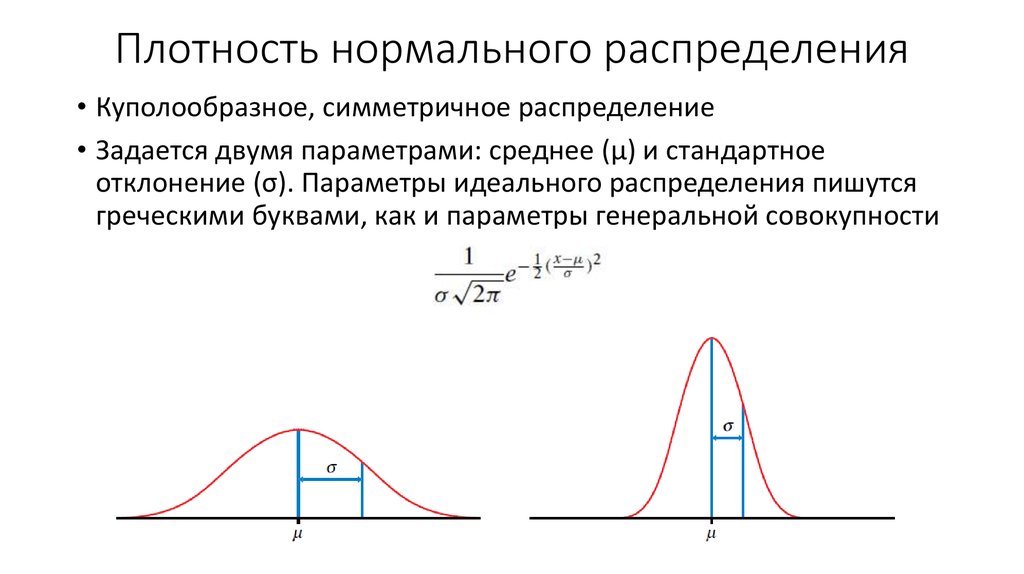3. Доверительный интервал. Доверительная вероятность 14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов Глава 15. Основные понятия теории случайных функций 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15. 7.2. Производная от случайной функции 15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 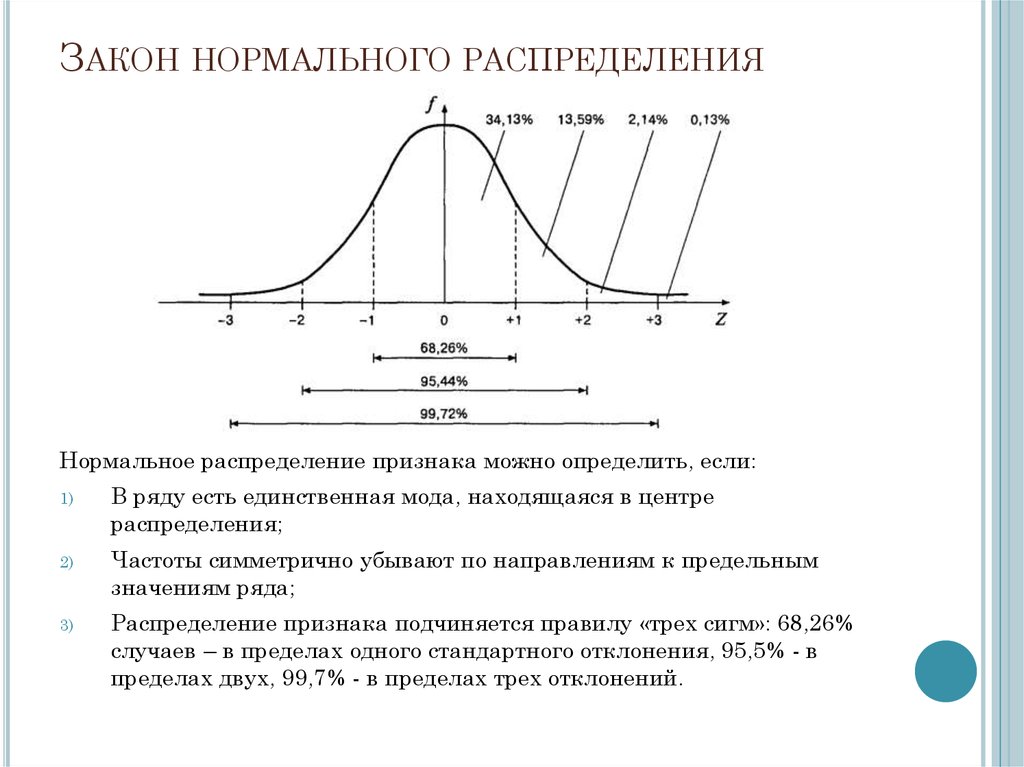17. 7. Эргодическое свойство стационарных случайных функций 17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19. 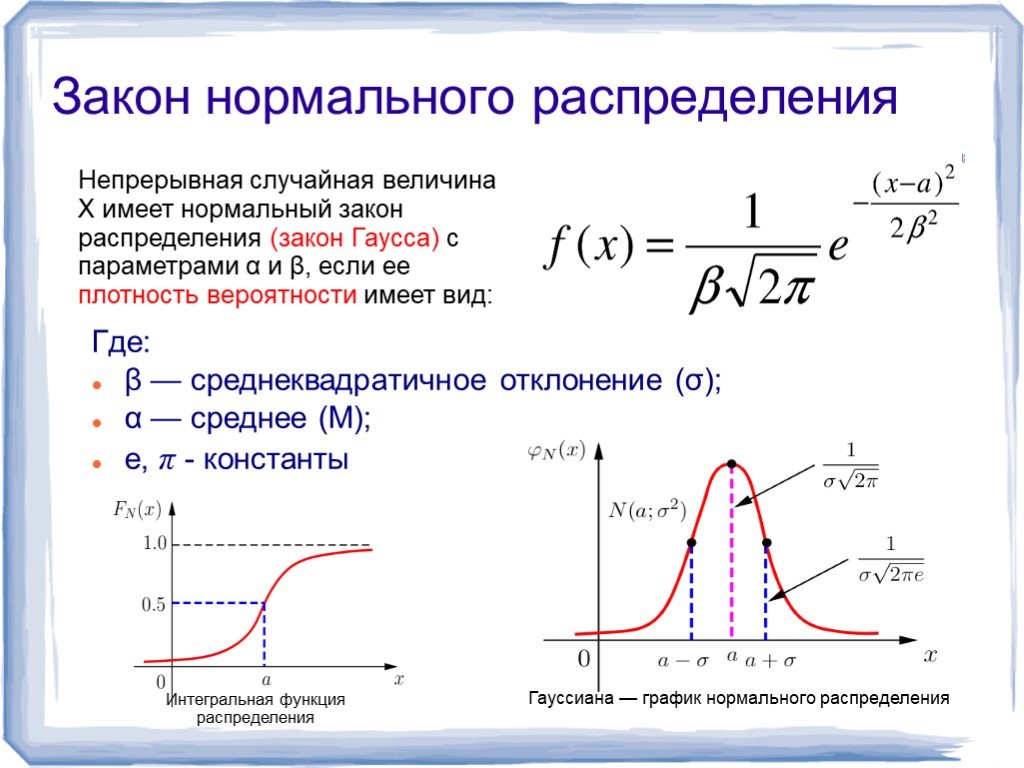3. Поток событий. Простейший поток и его свойства 19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 7. Таблица значений функции Таблица 8. Значения распределение Пуассона

Закон нормального распределения

Значение для исследований в области физической культуры и спорта (ФКиС)

Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основополагающую роль в математической статистике.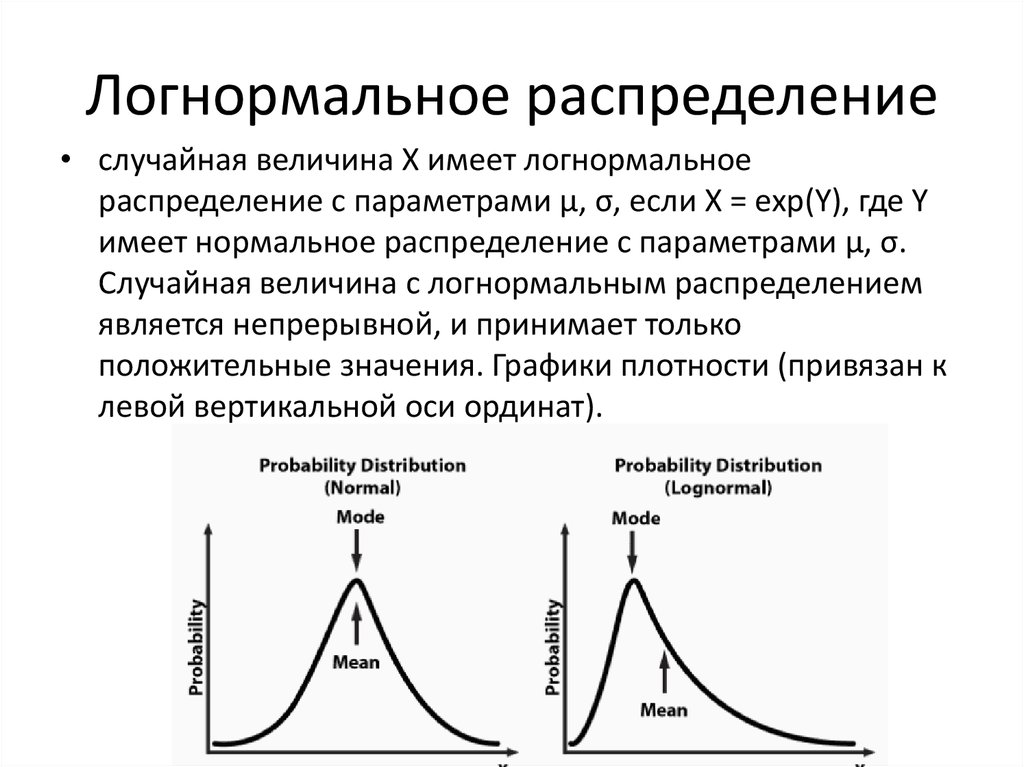 Причинами это являются:

1. Многие эмпирические распределения можно успешно описать с помощью нормального закона распределения. Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
2. Нормальное распределение обладает рядом благоприятных математических свойств, обеспечивших его широкое применение в статистике.
3. Корректное использование критериев проверки статистических гипотез предполагает знание закона распределения экспериментальных данных. Так, например, использование t – критерия Стьюдента и  F-критерия Фишера требует нормального распределения экспериментальных данных.
4. Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения.

Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.

Более подробно о методах статистической обработки данных рассказано в книгах:

• Факторный анализ в педагогических исследованиях в области физической культуры и спорта
• Компьютерная обработка данных экспериментальных исследований
• Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта

История изучения нормального распределения

Блез Паскаль и Пьер Ферма

Первые исследования по теории вероятностей проводили математик, механик, физик Блез Паскаль и математик Пьер Ферма в середине XVII века. Эти исследования выполнялись по  просьбе Шевалье де Мере, азартного игрока в кости, который пытался понять природу выигрыша. В дальнейшем эти исследования заложили основы теории вероятностей (Дж. Гласс, Дж. Стэнли, 1976).

Якоб Бернулли

Дальнейшее развитие теория вероятностей получила в XVIII веке.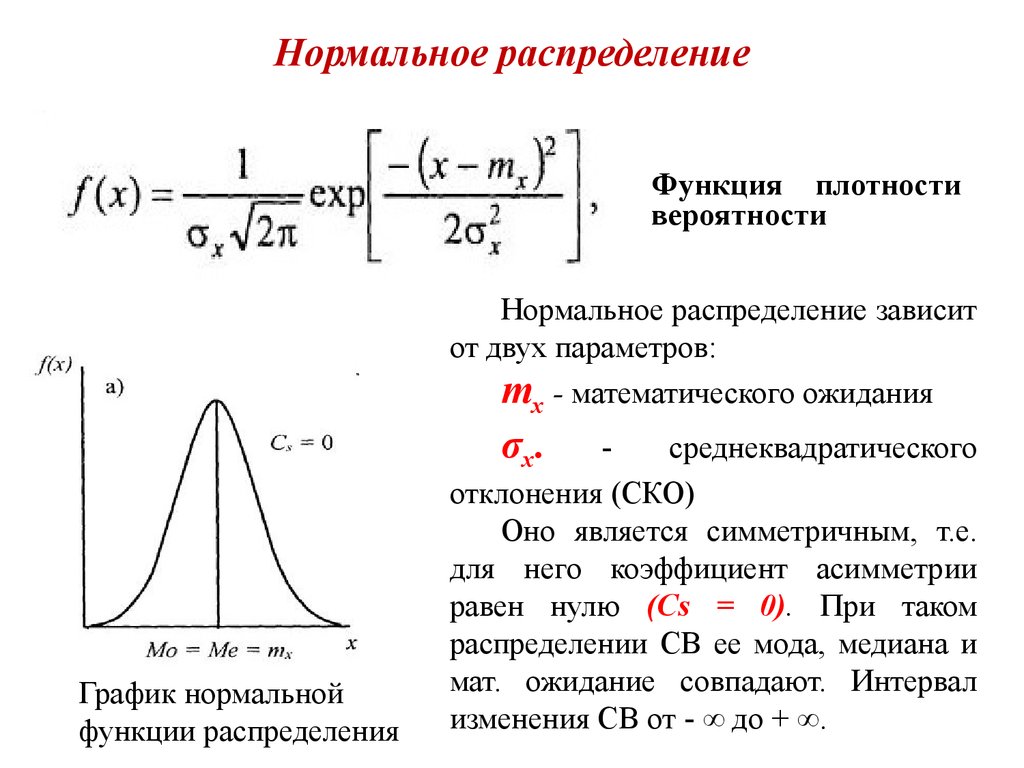 В 1713 году была опубликована  книга швейцарского математика Якоба Бернулли «Искусство предположений». В этой книге был рассмотрен ряд вопросов теории вероятностей.  Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей, а также  изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).

Джеймс Стирлинг

В последствии (в 1730 г.) шотландский математик Джеймс Стирлинг опубликовал формулу, аппроксимирующую произведение первых n чисел. Это позволило упростить решение ряда задач, которые встречаются в теории вероятностей. Однако все еще эти задачи оставались трудно разрешимыми.

Абрахам де Муавр

Эту задачу решил английский математик Абрахам де Муавр. В работе «Доктрина случайностей», которая была издана в 1738 году он привел формулу, аппроксимирующую  биномиальное распределение события, вероятность которого была равна 0,5  (рис.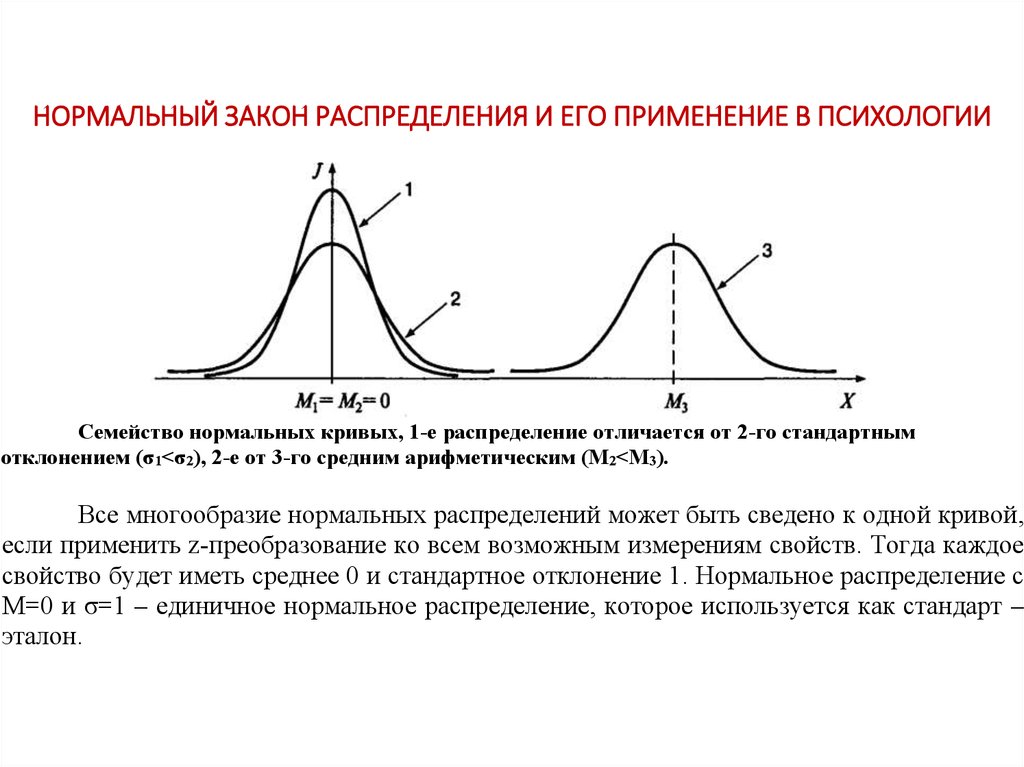 1).  То есть он нашел уравнение кривой, проходящей через точки графика, изображенного на рис. 1. Эта была формула, которую впоследствии стали называть формулой нормального распределения вероятностей. Появление  формулы нормального распределения значительно упростило расчеты вероятностей событий.

Пьер-Симон де Лаплас

В начале XIX века (в 1812 г.) французский математик, механик, физик и астроном Пьер-Симон де Лаплас  обобщил результаты А. Муавра для произвольного биномиального распределения.

Рис.1. Биномиальное распределение

Карл Фридрих Гаусс

Одновременно с П. Лапласом в 1809 году немецкий математик, механик, физик и астроном Карл Фридрих Гаусс в сочинении «Теория движения небесных тел» использовал формулу нормального распределения для описания случайных ошибок, возникающих в результате многократных измерений  движений небесных тел. К.Ф. Гаусс внес настолько большой вклад в разработку теории нормального распределения, что впоследствии это распределение стали назвать гауссово распределение или распределение Гаусса-Лапласса.

Адольф Кетле

В начале ХХ века бельгийский математик, астроном и социолог Адольф Кетле  одним из первых применил  нормальный закон распределения случайной величины к анализу биологических и социальных процессов. Изучая распределение солдат американской армии по росту, Адольф Кетле  обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1911).

В настоящее время нормальное распределение широко используется в биологии, медицине, экономике и других областях науки.

Формула нормального распределения

Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:

где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.

Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0  и σ=1.  Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.2).

Рис.2. График плотности вероятностей нормального распределения при μ=0  и σ=1.

 

Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при  μ=3 график сместится вправо вдоль оси Х  (рис.3).

Рис.3. График плотности вероятностей нормального распределения при μ=3  и σ=1.

Если мы оставим μ=0 , а изменим параметр σ, например σ=3, то получим распределение с большим размахом (рис. 4).

Рис.4. График плотности вероятностей нормального распределения при μ=0  и σ=3.

Свойства нормального распределения

1. Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
2. Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
3. Медиана и мода нормального распределения совпадают и равны µ.
4. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.

Нормированное отклонение

В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:

Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.

Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».

Нормированное нормальное распределение

Рис.5. Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.

Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.

Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры:   µ=0; σ = 1 (рис. 1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле: U= (X-μ)/σ.

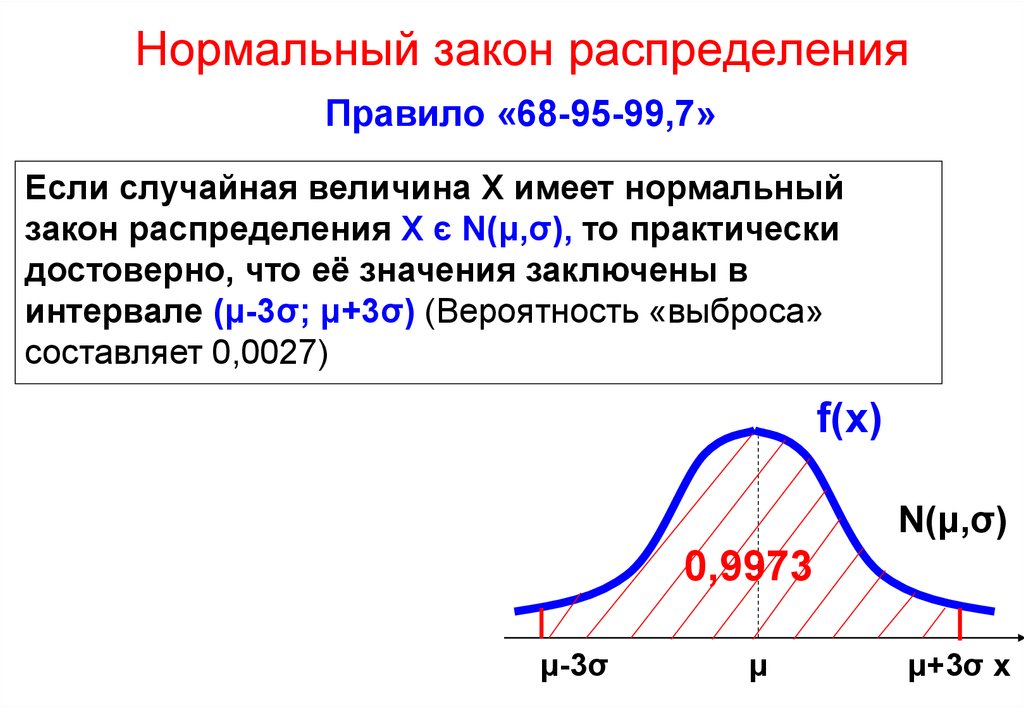
Для нормированного нормального распределения характерно, что в интервал µ±σ попадают 68 % всех результатов, в интервал µ±2σ попадают 95% всех результатов, в интервал µ±3σ попадают 99 % всех результатов.

В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М. Зациорским (рис. 6) предложено использовать следующую систему оценок результатов.  Если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.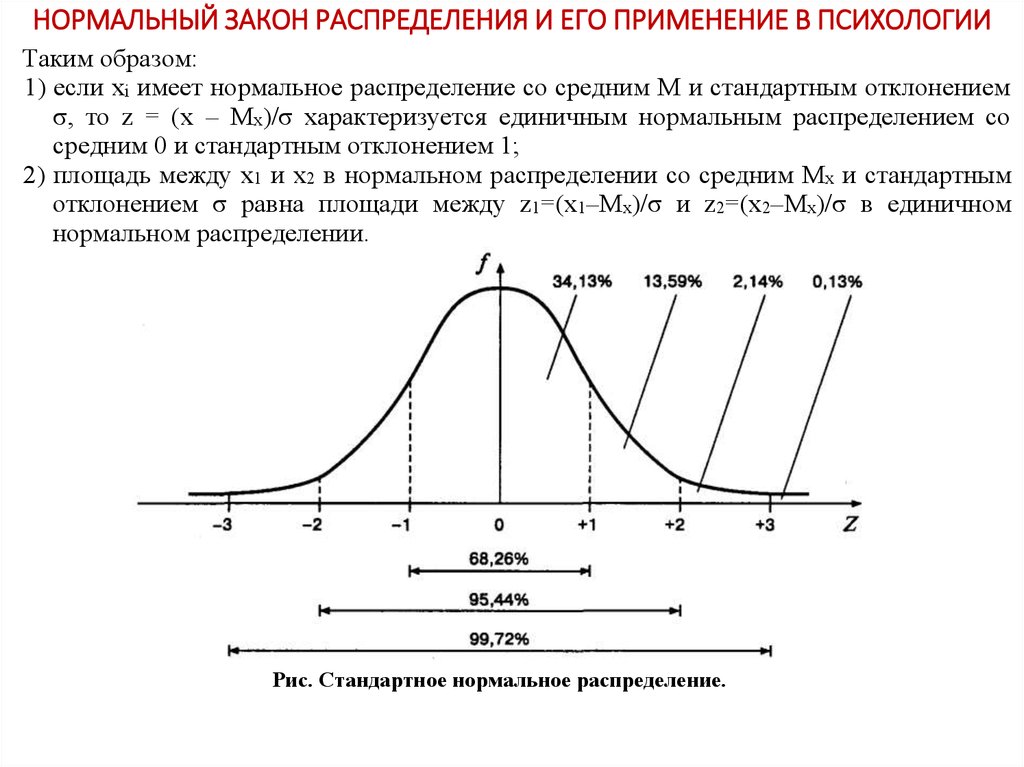

Рис.6. Использование нормального распределения для разработки системы оценок результатов

Критерии согласия

Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.

Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).

Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:

• если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки;
• если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова.
• в статистическом пакете Statgraphics Centurion существует специальная опция — критерии проверки нормальности распределения. В этой опции есть 4 критерия, посредством которых можно сделать вывод о соответствии эмпирического распределения нормальному закону.

Литература

1. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
2. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии.- М.: Прогресс, 1976.-495 с.
3. Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
4. Кетле А. (1835) Социальная физика, или опыт исследования о развитии человеческих способностей.  Т.1, 1911.- С. 38-39.
5. Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Что такое нормальное распределение? – Определение TechTarget

К

• Рахул Авати

Что такое нормальное распределение?

Нормальное распределение — это тип непрерывного распределения вероятностей, при котором большинство точек данных сгруппированы в направлении середины диапазона, а остальные симметрично сужаются к любому из крайних значений.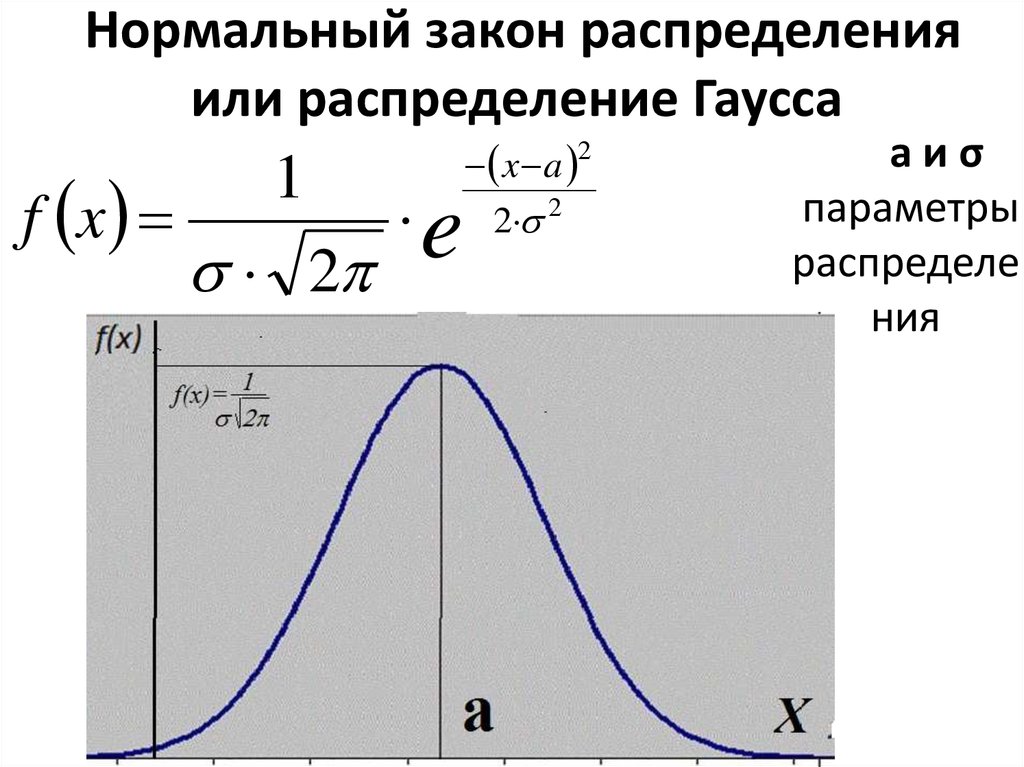 Середина диапазона также известна как 9.0023 означает дистрибутива.

Нормальное распределение также известно как распределение Гаусса или вероятность колоколообразная кривая . Он симметричен относительно среднего и указывает на то, что значения, близкие к среднему, встречаются чаще, чем значения, которые дальше от среднего.

Объяснение нормального распределения

Графически нормальное распределение представляет собой колоколообразную кривую из-за ее расширяющейся формы. Точная форма может варьироваться в зависимости от распределения значений в совокупности. Совокупность — это весь набор точек данных, которые являются частью распределения.

Независимо от формы, колоколообразная кривая нормального распределения всегда симметрична относительно среднего значения. Симметричное распределение означает, что вертикальная разделительная линия, проведенная через максимальное/среднее значение, даст два зеркальных изображения по обе стороны от линии, в которых половина населения меньше среднего, а половина больше. Однако обратное не всегда верно; то есть не все симметричные распределения являются нормальными. На кривой нормального распределения пик всегда находится посередине, а среднее значение, мода и медиана одинаковы.

Колоколообразная кривая нормального распределения всегда симметрична относительно среднего значения.

Основные примеры нормального распределения: рост и вес

Высота — это простой пример значений, которые следуют нормальному шаблону распределения. Большинство людей среднего роста — каким бы он ни был для данного населения. Если рост этих людей представлен в графическом формате вместе с ростом людей, которые выше и ниже среднего, распределение всегда будет нормальным. Это связано с тем, что люди среднего роста будут сгруппированы ближе к середине, а те, кто выше и ниже, будут дальше.

Далее, эти последние группы будут состоять из очень небольшого числа людей. Количество очень высоких или очень низких людей будет еще меньше, поэтому они будут дальше всего от среднего.

Точно так же вес может подчиняться нормальному распределению, если известен средний вес рассматриваемой совокупности. Как и в случае с ростом, отклонениями в весе будут те, кто весит больше или меньше среднего. Чем больше отклонение от среднего, тем дальше будут эти точки данных на графике распределения.

Важность нормального распределения

Нормальное распределение является одним из наиболее важных распределений вероятностей для независимых случайных величин по трем основным причинам.

Во-первых, нормальное распределение описывает распределение значений многих природных явлений в широком диапазоне областей, включая биологию, физические науки, математику, финансы и экономику. Он также может точно представлять эти случайные величины.

Помимо роста и веса, нормальное распределение также используется для представления многих других величин, включая следующие:

• ошибка измерения
• кровяное давление
• балла IQ
• цены активов
• ценовое действие

Во-вторых, нормальное распределение важно, поскольку его можно использовать для аппроксимации других типов распределения вероятностей, таких как биномиальное, гипергеометрическое, обратное (или отрицательное) гипергеометрическое, отрицательное биномиальное и распределение Пуассона.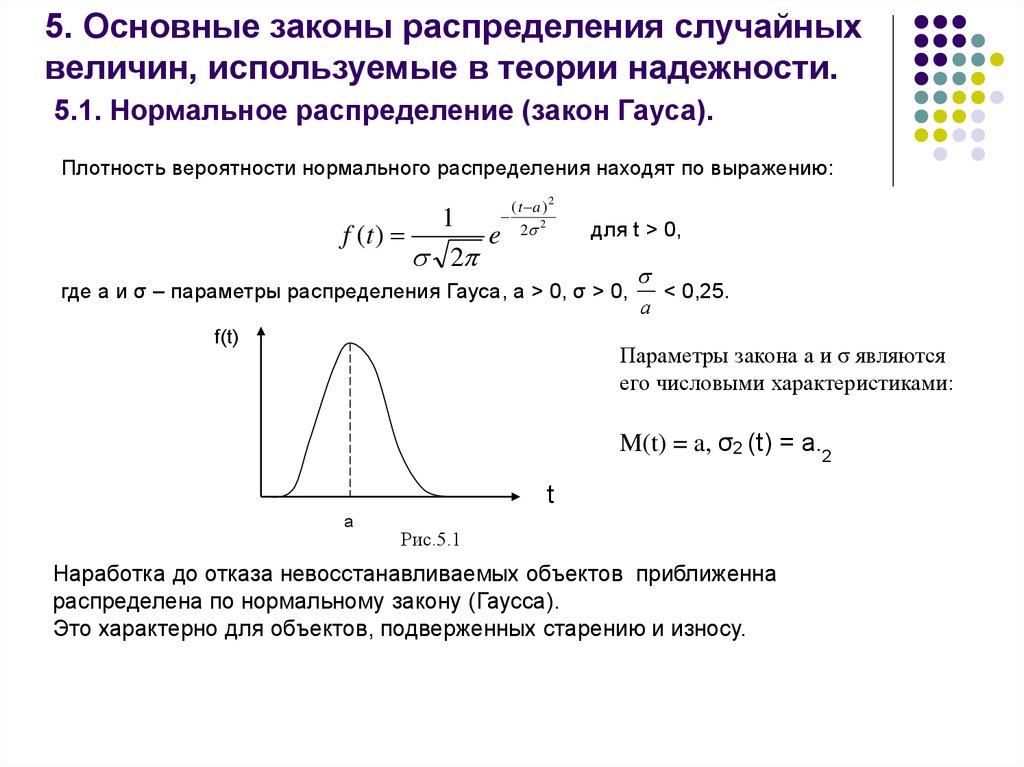

В-третьих, нормальное распределение является ключевой идеей центральной предельной теоремы, или CLT, которая утверждает, что средние значения, вычисленные из независимых, одинаково распределенных случайных величин, имеют приблизительно нормальное распределение. Это верно независимо от типа распределения, из которого отбираются переменные, если оно имеет конечную дисперсию.

Формула нормального распределения и эмпирическое правило

Формула нормального распределения представлена ​​ниже.

Формула нормального распределения.

Здесь x — значение переменной; f(x) представляет функцию плотности вероятности; мк (мю) — среднее значение; σ (сигма) — стандартное отклонение.

Эмпирическое правило нормального распределения описывает, где будет появляться большая часть данных в нормальном распределении, и утверждает следующее:

• 68,2% наблюдений появятся в пределах +/-1 стандартного отклонения от среднего;
• 95,4% наблюдений будут находиться в пределах +/-2 стандартных отклонения; и
• 99,7% наблюдений будут находиться в пределах +/-3 стандартных отклонения.

Все точки данных, выходящие за пределы трех стандартных отклонений (3σ), указывают на редкие случаи.

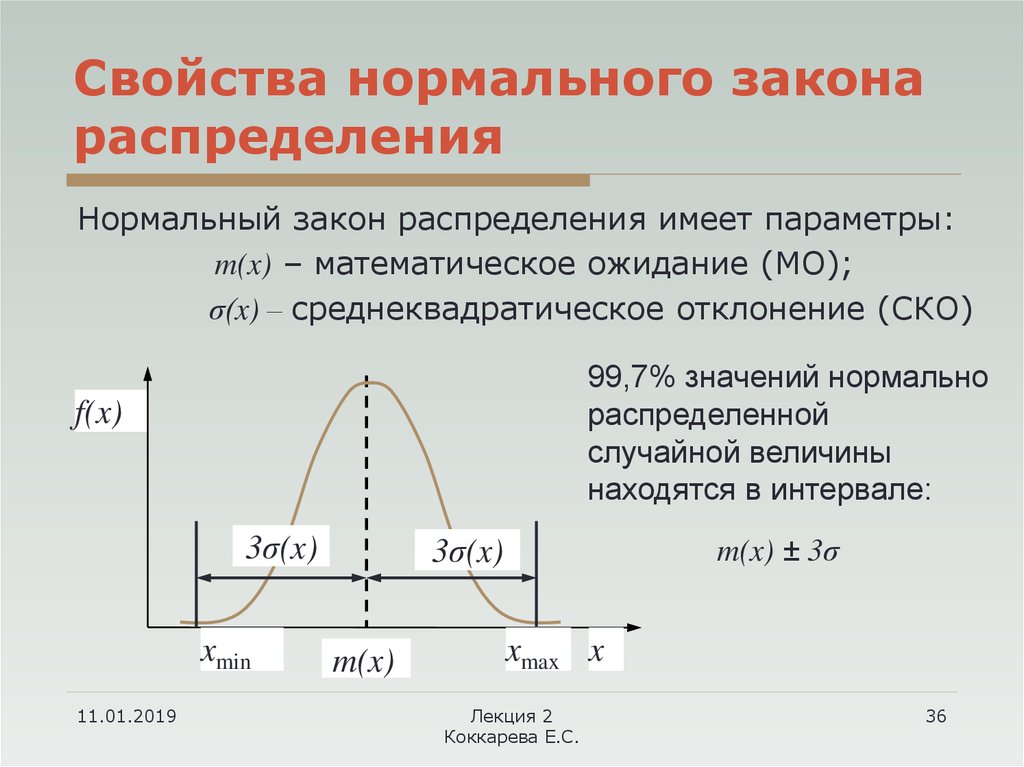
Параметры нормального распределения

Поскольку среднее значение, мода и медиана в нормальном распределении одинаковы, нет необходимости вычислять их отдельно. Эти значения представляют собой наивысшую точку распределения или пик. Все остальные значения в распределении затем падают симметрично вокруг среднего значения. Ширина среднего определяется стандартным отклонением.

Фактически, для описания нормального распределения требуются только два параметра: среднее значение и стандартное отклонение.

1. Среднее

Среднее значение — это центральное самое высокое значение кривой нормального распределения. Все остальные значения в распределении либо группируются вокруг него, либо находятся на некотором расстоянии от него. Изменение среднего значения на графике сдвинет всю кривую по оси X либо влево, либо вправо. Однако его симметричность все равно будет сохраняться.

2. Стандартное отклонение

Обычно стандартное отклонение является мерой изменчивости распределения. В колоколообразной кривой он определяет ширину распределения и показывает, насколько далеко от среднего значения падают другие значения. Кроме того, он представляет типичное расстояние между средним значением и наблюдениями.

Изменение стандартного отклонения изменит распределение значений вокруг среднего значения. Меньшее отклонение уменьшит разброс — ужесточит распределение — в то время как большее отклонение увеличит разброс и создаст более широкое распределение. По мере того, как распределение становится шире, становится более вероятным, что значения будут дальше от среднего.

Асимметрия и эксцесс в нормальном распределении

Асимметрия представляет собой степень симметрии распределения. Поскольку нормальное распределение совершенно симметрично, его асимметрия равна нулю. В других распределениях с асимметрией меньше или больше нуля левый хвост (левая асимметрия) или правый хвост (правая асимметрия) будут соответственно длиннее.

Эксцесс измеряет толщину каждого хвоста распределения по отношению к хвостам нормального распределения. Для нормального распределения эксцесс всегда равен 3. В распределении с эксцессом больше 3 хвостовые данные превышают хвосты нормального распределения, что приводит к явлению, называемому курдючные . На финансовых рынках толстые хвосты описывают хвостовой риск — вероятность убытка из-за какого-то редкого события. Распределения с эксцессом менее 3 показывают более тонкие хвосты, чем хвосты нормального распределения.

См. также: статистический анализ, гистограмма, зависимая переменная, данные, специалист по данным, большие данные, классификация данных, интеллектуальный анализ данных, контекст данных и анализ временных рядов в ИТ-средах.

Последнее обновление: декабрь 2022 г.

Продолжить чтение О нормальном распределении

• Общие методы обработки данных, которые необходимо знать и использовать

• Навыки работы с данными для машинного обучения и искусственного интеллекта

• Введение в типы и методы ведения журнала IoT

• Случайные процессы имеют различное практическое применение

• Специалист по данным и бизнес-аналитик: в чем разница?

нейроморфные вычисления

Нейроморфные вычисления — это метод компьютерной инженерии, при котором элементы компьютера моделируются по образцу систем человеческого мозга и нервной системы.

Сеть

• коллизия в сети

  В полудуплексной сети Ethernet коллизия возникает в результате попытки двух устройств в одной сети Ethernet передать. ..

• краеугольный камень домкрат

  Гнездо трапецеидального искажения — это гнездовой разъем, используемый для передачи аудио, видео и данных. Он служит гнездом для соответствующей вилки…

• инкапсуляция (объектно-ориентированное программирование)

  В объектно-ориентированном программировании (ООП) инкапсуляция — это практика объединения связанных данных в структурированную единицу вместе с …

Безопасность

• Общая система оценки уязвимостей (CVSS)

  Общая система оценки уязвимостей (CVSS) — это общедоступная платформа для оценки серьезности уязвимостей безопасности в …

• WPA3

  WPA3, также известный как Wi-Fi Protected Access 3, представляет собой третью версию стандарта сертификации безопасности, разработанного Wi-Fi …

• брандмауэр

  Брандмауэр — это устройство сетевой безопасности, которое предотвращает несанкционированный доступ к сети. Проверяет входящий и исходящий трафик…

ИТ-директор

• Agile-манифест

  The Agile Manifesto — это документ, определяющий четыре ключевые ценности и 12 принципов, в которые его авторы верят разработчикам программного обеспечения…

• Общее управление качеством (TQM)

  Всеобщее управление качеством (TQM) — это система управления, основанная на вере в то, что организация может добиться долгосрочного успеха, …

• системное мышление

  Системное мышление — это целостный подход к анализу, который фокусируется на том, как взаимодействуют составные части системы и как…

HRSoftware

• непрерывное управление производительностью

  Непрерывное управление эффективностью в контексте управления человеческими ресурсами (HR) — это надзор за работой сотрудника . ..

• вовлечения сотрудников

  Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.

• кадровый резерв

  Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.

Служба поддержки клиентов

• Облачная служба Salesforce

  Salesforce Service Cloud — это платформа управления взаимоотношениями с клиентами (CRM), позволяющая клиентам Salesforce предоставлять услуги и …

• БАНТ

  BANT — это аббревиатура от «Budget, Authority, Need, Timing».

• бесконтактная оплата

  Бесконтактный платеж — это беспроводная финансовая транзакция, при которой покупатель совершает покупку, перемещая жетон безопасности в . ..

Что он говорит вам и примеры

Что такое симметричное распределение?

Симметричное распределение имеет место, когда значения переменных появляются с постоянной частотой, и часто среднее значение, медиана и мода находятся в одной и той же точке. Если провести линию, пересекающую середину графика, она покажет две стороны, которые зеркально отражают друг друга.

В графической форме симметричные распределения могут выглядеть как нормальное распределение (то есть кривая нормального распределения). Симметричное распределение является основной концепцией технической торговли, поскольку предполагается, что поведение цены актива соответствует симметричной кривой распределения во времени.

Симметричным распределениям можно противопоставить асимметричные распределения, которые представляют собой распределения вероятностей, которые демонстрируют асимметрию или другие нерегулярности в своей форме.

Ключевые выводы

• Симметричное распределение — это такое распределение, при котором разделение данных посередине дает зеркальные изображения.
• Кривые Белла являются часто цитируемым примером симметричного распределения.
• Наличие симметричного распределения полезно для анализа данных и создания выводов на основе статистических методов.
• В финансах процессы генерации данных с симметричным распределением могут помочь в принятии торговых решений.
• Однако данные о ценах в реальном мире, как правило, демонстрируют асимметричные качества, такие как правая асимметрия.

О чем говорит симметричное распределение?

Симметричные распределения используются трейдерами для установления области стоимости акции, валюты или товара в установленный период времени. Эти временные рамки могут быть внутридневными, например, 30-минутными интервалами, или более долгосрочными с использованием сессий или даже недель и месяцев. Колоколообразная кривая может быть построена вокруг ценовых точек, достигнутых в течение этого периода времени, и ожидается, что большая часть ценового действия — примерно 68% ценовых точек — будет находиться в пределах одного стандартного отклонения от центра кривой.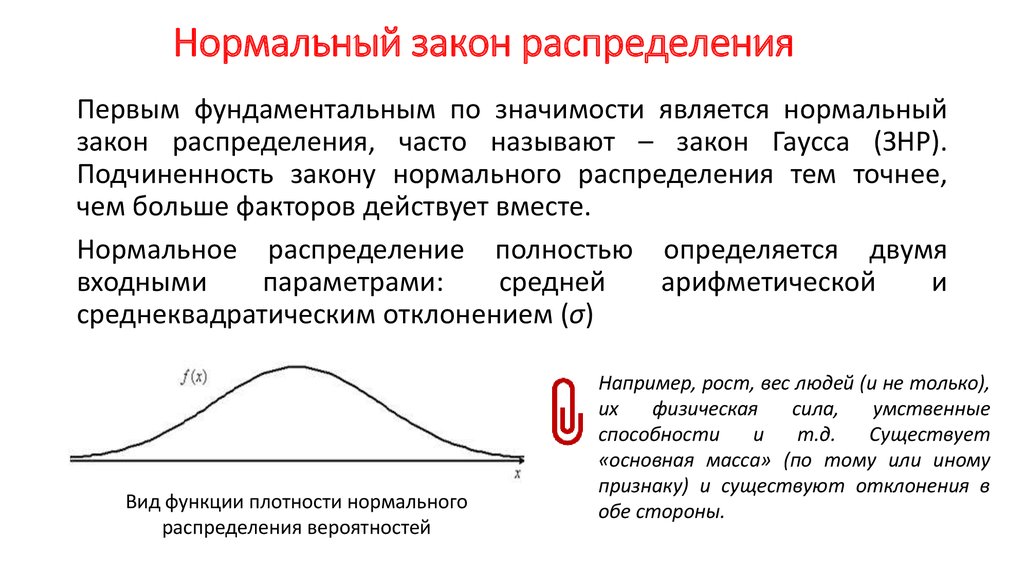 Кривая применяется к оси Y (цена), поскольку она является переменной, тогда как время в течение всего периода просто линейно. Таким образом, область в пределах одного стандартного отклонения от среднего значения — это область стоимости, в которой цена и фактическая стоимость актива наиболее точно совпадают.

Если ценовое действие выводит цену актива за пределы области стоимости, это предполагает, что цена и стоимость не совпадают. Если разрыв находится в нижней части кривой, актив считается недооцененным. Если он находится на вершине кривой, актив должен быть переоценен. Предполагается, что актив вернется к среднему значению с течением времени. Когда трейдеры говорят о возврате к среднему, они имеют в виду симметричное распределение движения цены во времени, которое колеблется выше и ниже среднего уровня.

Центральная предельная теорема утверждает, что распределение выборки приближается к нормальному распределению (т. е. становится симметричным) по мере увеличения размера выборки, независимо от распределения населения, в том числе асимметричного.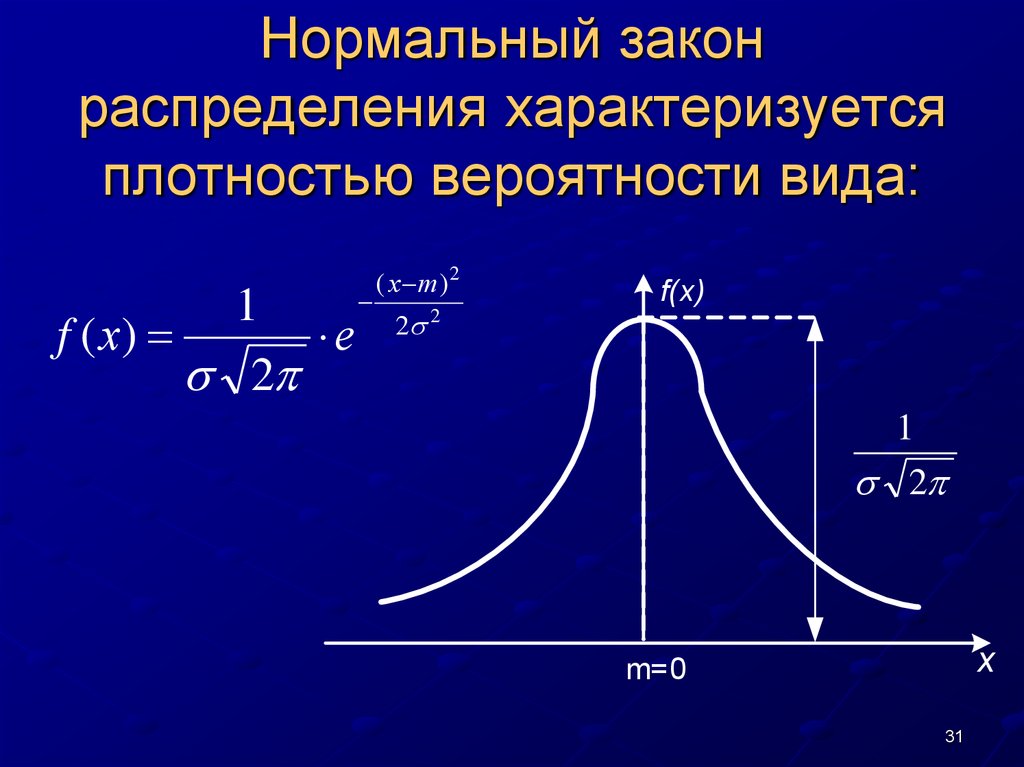

Пример использования симметричного распределения

Симметричное распределение чаще всего используется, чтобы поместить ценовое действие в контекст. Чем дальше ценовое действие отклоняется от области стоимости на одно стандартное отклонение с каждой стороны от среднего, тем выше вероятность того, что базовый актив недооценен или переоценен рынком. Это наблюдение предложит потенциальные сделки для размещения на основе того, насколько ценовое действие отклонилось от среднего значения за используемый период времени. Однако на больших временных масштабах существует гораздо больший риск упустить фактические точки входа и выхода.

Изображение Джули Бэнг © Investopedia, 2019 

Симметричные распределения и асимметричные распределения

Противоположностью симметричного распределения является асимметричное распределение. Распределение является асимметричным, если оно не является симметричным с нулевой асимметрией; другими словами, он не перекашивается.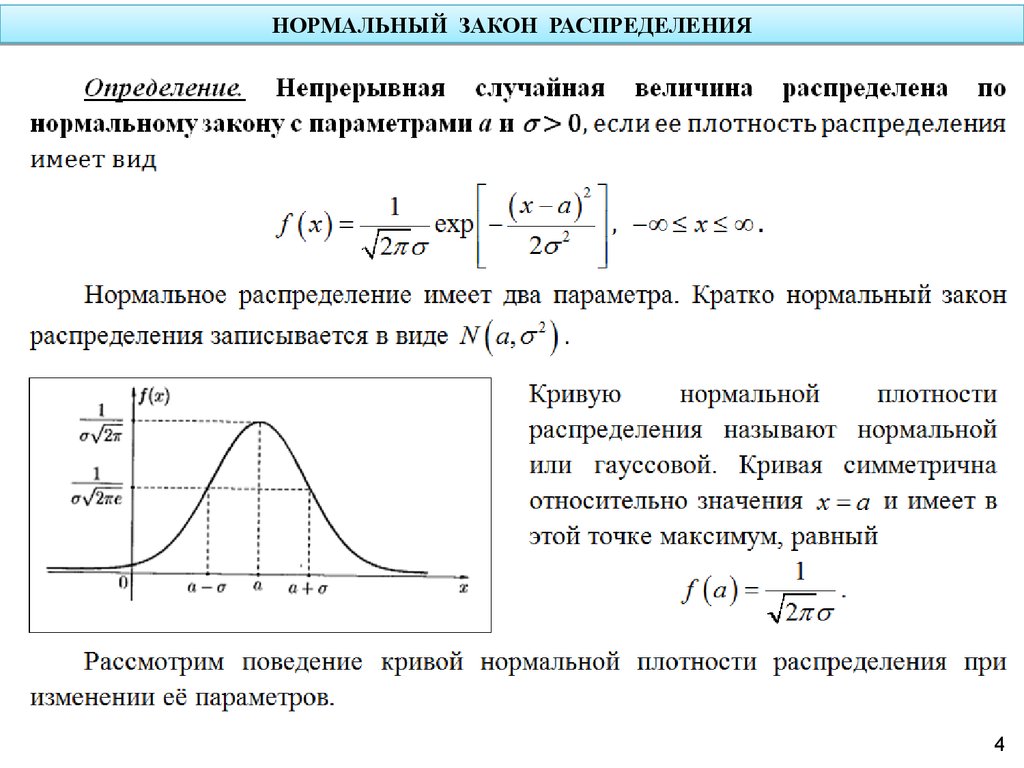 Асимметричное распределение либо смещено влево, либо смещено вправо. Распределение с асимметрией влево, известное как отрицательное распределение, имеет более длинный левый хвост. Распределение с асимметрией вправо или распределение с асимметрией в положительном направлении имеет более длинный правый хвост. Определение того, является ли среднее значение положительным или отрицательным, важно при анализе асимметрии набора данных, поскольку это влияет на анализ распределения данных. Логарифмически нормальное распределение — это обычно цитируемое асимметричное распределение с асимметрией вправо.

Асимметрия часто является важным компонентом анализа трейдером потенциального дохода от инвестиций. Симметричное распределение доходов равномерно распределяется вокруг среднего значения. Асимметричное распределение с положительной асимметрией вправо указывает на то, что исторические доходы, которые отклонялись от среднего, были в основном сосредоточены на левой стороне кривой нормального распределения.

И наоборот, отрицательная асимметрия влево показывает, что историческая доходность отклоняется от среднего значения, сконцентрированного на правой стороне кривой.

Нормальный против искаженного.

Изображение Сабрины Цзян © Investopedia 2020

Ограничения использования симметричных распределений

Обычный инвестиционный рефрен заключается в том, что прошлые результаты не гарантируют будущих результатов; тем не менее, прошлые результаты могут проиллюстрировать закономерности и предоставить информацию трейдерам, которые хотят принять решение о позиции. Симметричное распределение является общим эмпирическим правилом, но независимо от используемого периода времени часто будут периоды асимметричного распределения на этой временной шкале. Это означает, что, хотя колоколообразная кривая обычно возвращается к симметрии, могут быть периоды асимметрии, которые устанавливают новое среднее значение для центра кривой. Это также означает, что торговля, основанная исключительно на области значений симметричного распределения, может быть рискованной, если сделки не подтверждаются другими техническими индикаторами.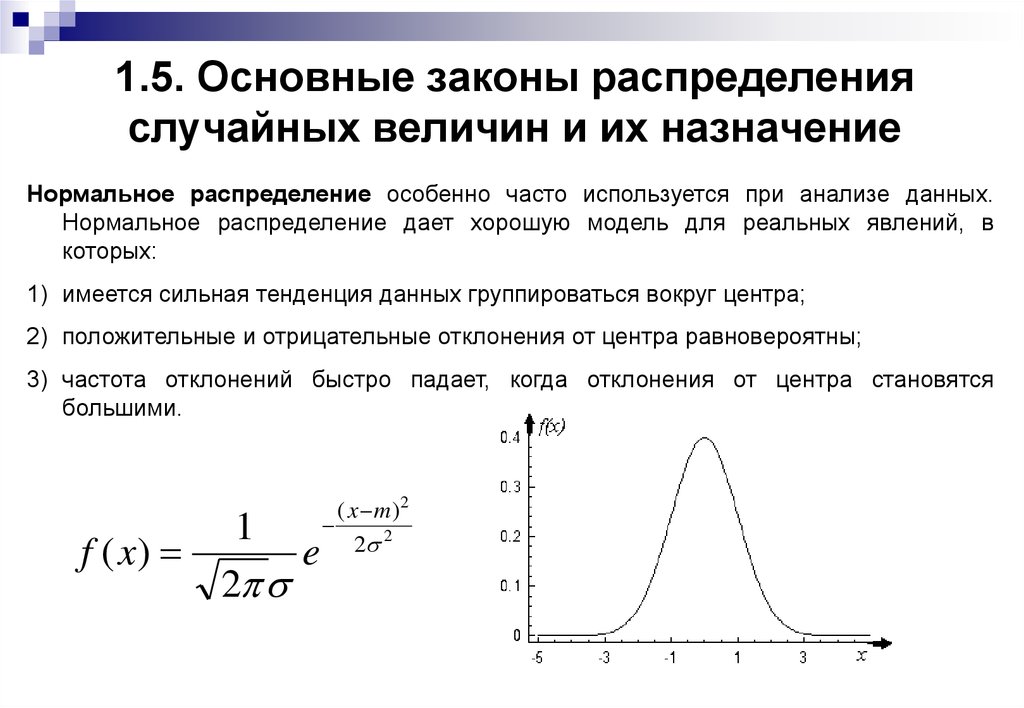

Какая связь между средним, медианой и модой в симметричном распределении?

При симметричном распределении все три описательных статистики обычно имеют одно и то же значение, например, при нормальном распределении (колоколообразная кривая). Это справедливо и для других симметричных распределений, таких как равномерное распределение (где все значения идентичны; изображается просто горизонтальной линией) или биномиальное распределение, учитывающее дискретные данные, которые могут принимать только одно из двух значений (например, нулевое или один, да или нет, правда или ложь и т. д.).

В редких случаях симметричное распределение может иметь две моды (ни одна из которых не является средним или медианным), например, такая, которая выглядит как две идентичные вершины холмов, равноудаленные друг от друга.

Является ли медиана симметричной?

Медиана описывает точку, в которой 50 % значений данных находятся выше, а 50 % — ниже. Таким образом, это средняя точка данных.

No related posts.