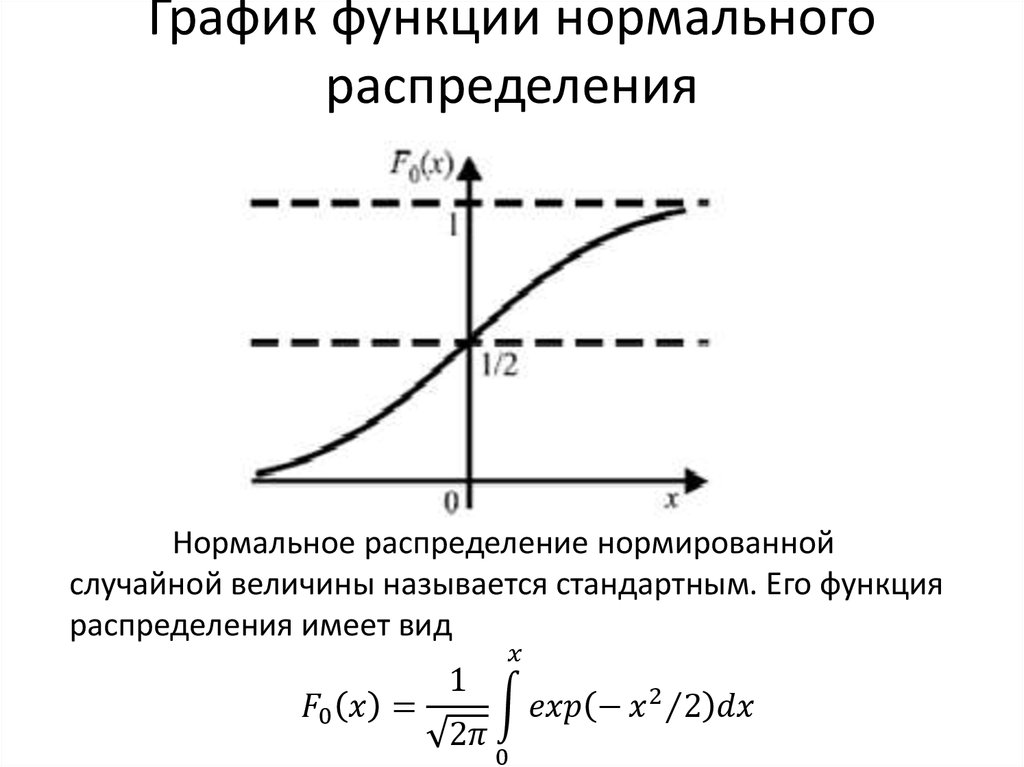
4.10.2. Нормированное нормальное распределение
Формула (4.23) описывает целое семейство нормальных кривых, зависящих, как было сказано выше, от двух параметров —и, которые могут принимать любые значения, поэтому возможно бесконечно много нормально распределенных совокупностей.
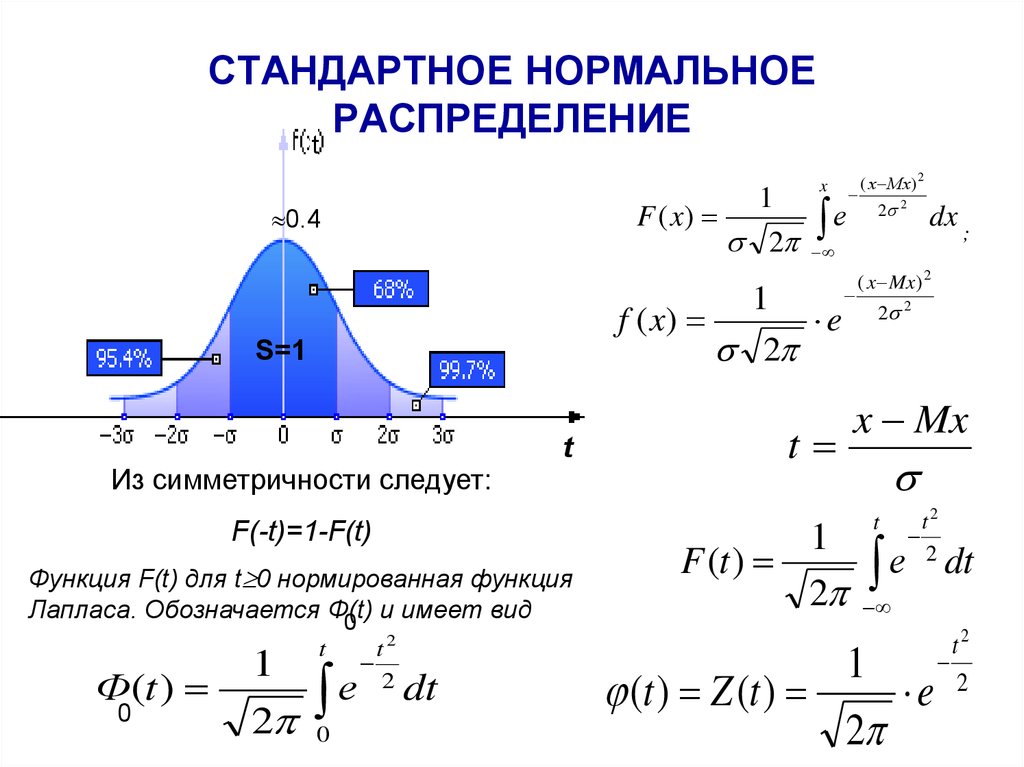
Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая по достаточно сложной формуле (4.23), используют так называемое нормированное (или стандартное) нормальное распределение N(0;1), для которого составлены подробные таблицы.
Нормированное нормальное распределение имеет параметры и. Это распределение получается, еслипронормировать нормально распределенную величину X по формуле:
(4.24)
Плотность распределения вероятностей нормированного нормального распределения записывается в виде:
На
кривой нормированного нормального
распределения (рис.
Рис. 4.11. Нормированное нормальное распределение
Таблица значений — ординат нормальной кривой приведена в специальных таблицах. Значения для некоторых характерных нормированных отклонений представлены в табл. 4.1.
Таблица 4.1
Ординаты нормальной кривой
Нормированное отклонение, u | 0 | ±0,5 | ±1,0 | ±2,0 | ±3,0 |
Ордината нормальной кривой, | 0,399 | 0,352 | 0,242 | 0,054 | 0,004 |
Очень
часто исследователя интересует вопрос:
какова вероятность того, что изучаемый
признак генеральной совокупности
находится в заданных границах (например,
вероятность того, что результат измерения
IQ для группы испытуемых окажется в
пределах 115 — 125)? Если предполагается
нормальное распределение признака в
генеральной совокупности, то получить
ответ на этот вопрос очень просто.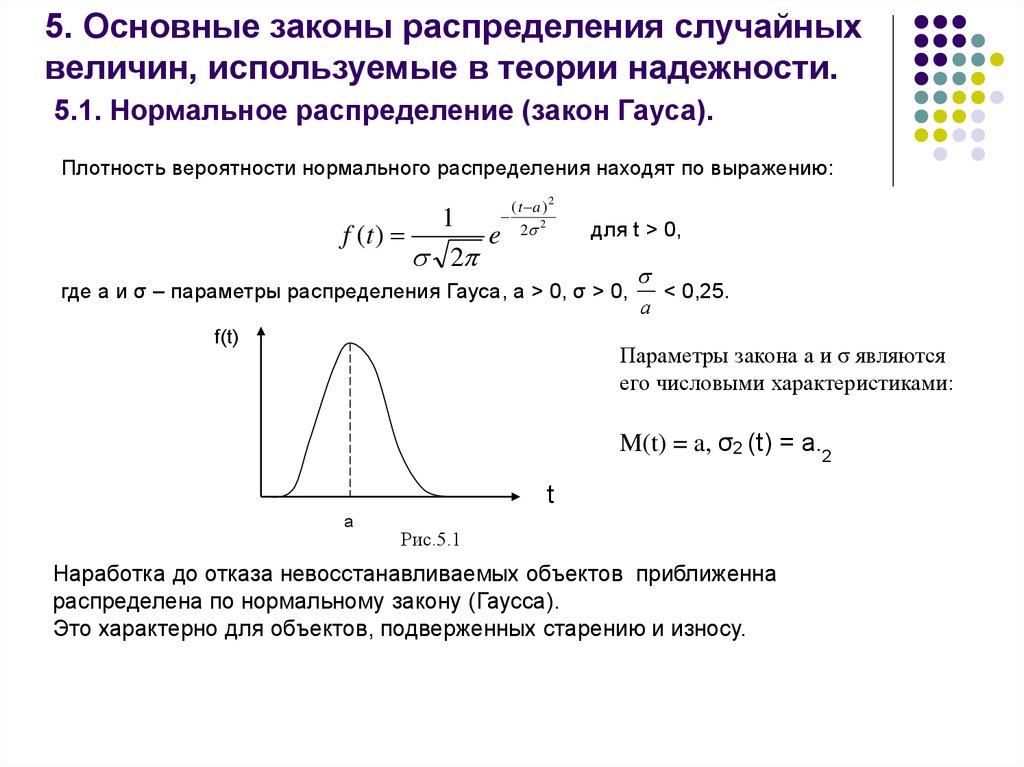
Как говорилось ранее, вероятность попадания нормально распределенной случайной величины в заданный интервал можно определить по функции распределения:или с помощью функции плотности вероятностей:.
Итак, вероятность попадания с.в. U—>N(0;1) в заданный интервал:
,
где Ф — принятое обозначение для функции нормированного нормального распределения которое имеет следующий вид:
, (4.25)
при этом .
Часто представляет интерес вероятность попадания с.в. U—>N(0;1) в симметричный интервал. Тогда
Учитывая свойства функции Лапласа, получаем:
Интеграл, входящий в выражение (4.25), не выражается в элементарных функциях, поэтому для вычисления функции Ф(u) используют вспомогательную функцию — функцию Лапласа (интеграл вероятностей):
(4. 26)
26)
который табулируется. Функция Лапласа является нечетной, т.е. Ф0(-u)=–Ф0(u).
В книгах по теории вероятности приведена либо таблица значений функции Лапласа , либо.
Чтобы найти вероятность попадания нормально распределенной случайной величины в заданный интервалс помощью функции Лапласа, сначала с.в. Х нормализуется (см. 4.24), а затем используется следующая формула:
=(4.27)
Пример 4.14. Вычислить если.
Решение.
Нормальное распределение
Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое
задается плотностью
.
Нормальное распределение задается двумя параметрами:
– математическим ожиданием,
– средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой
(кривой Гаусса).
Нормированным называют нормальное распределение с параметрами
.
Плотность нормированного распределения задается формулой
.
Вероятность попадания в заданный интервал нормальной случайной величины
Как уже было установлено,
вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу ,
равна определенному интегралу от плотности распределения, взятому в соответствующих
пределах:
Для нормально распределенной случайной величины соответственно получим:
.
Преобразуем последнее выражение, введя новую переменную . Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.

Для замены переменной в определенном интеграле еще необходимо заменить дифференциал и пределы интегрирования, предварительно выразив переменную из формулы замены:
;
;
– нижний предел интегрирования;
– верхний предел интегрирования;
(для нахождения пределов интегрирования по новой переменной в формулу замены переменной были подставлены и – пределы интегрирования по старой переменной ).
Подставим все в последнюю из формул для нахождения вероятности:
где – функция Лапласа.
,
где – математическое ожидание, – среднее квадратическое отклонение данной случайной величины.
Примеры решения задач
Пример 1. Случайная величина
имеет нормальное распределение с математическим ожиданием
и средним квадратическим отклонением .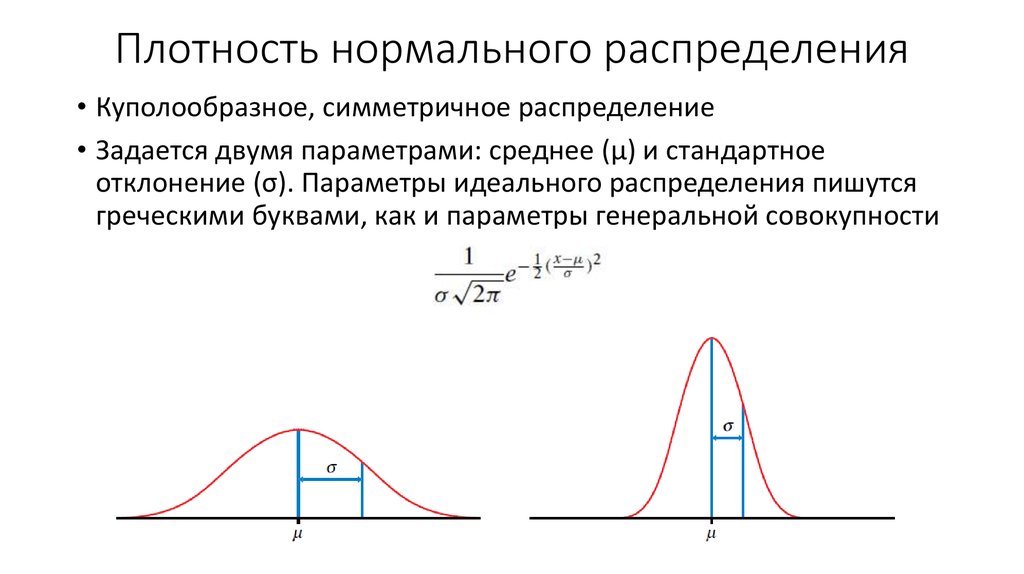 Найти вероятность того, что случайная величина
примет значение, принадлежащее интервалу .
Найти вероятность того, что случайная величина
примет значение, принадлежащее интервалу .
Решение.
Известно, что вероятность
того, что нормально распределенная случайная величина
примет значение, принадлежащее интервалу ,
равна:
,
где
– математическое ожидание,
– среднее квадратическое отклонение.
Ответ: .
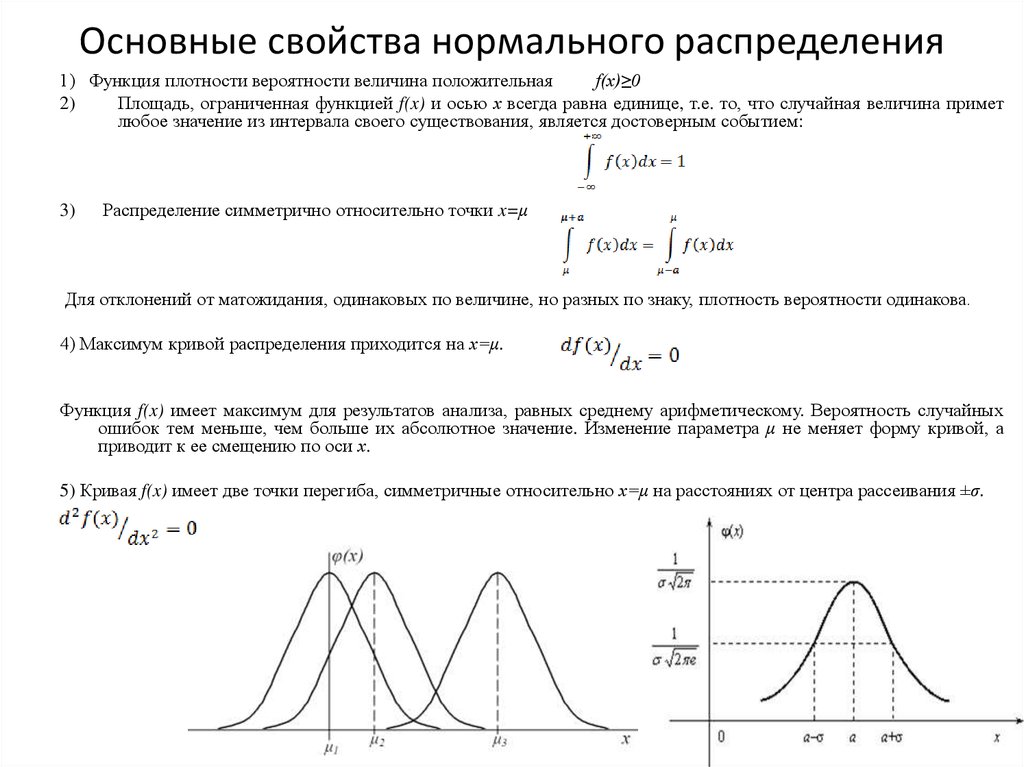
Вычисление вероятности заданного отклонения
Вычислим вероятность того,
что отклонение нормально распределенной случайной величины
от своего математического ожидания по абсолютной величине не превысит ,
то есть вероятность осуществления неравенства .
Заменим неравенство с модулем равносильным ему двойным неравенством:
Теперь мы можем воспользоваться формулой для нахождения вероятности попадания
в заданный интервал нормальной случайной величины, где границами интервала являются
:
(в последних преобразованиях использовано свойство нечетности функции Лапласа:
).
Вывод: вероятность того, что отклонение нормально распределенной случайной величины
от своего математического ожидания по абсолютной величине не превысит ,
равна:
где – математическое ожидание, – среднее квадратическое отклонение.
Примеры решения задач
Пример 1. Случайная величина имеет нормальное распределение с математическим ожиданием и средним квадратическим отклонением . Найти вероятность того, что случайная величина отклонится от своего математического ожидания по абсолютной величине не больше, чем на .
Решение.
Известно, что вероятность
того, что отклонение нормально распределенной случайной величины от
своего математического ожидания по абсолютной величине не превысит ,
равна:
,
где
– математическое ожидание, –
среднее квадратическое отклонение.
По условию .
Следовательно,
.
Ответ: .
Правило трех сигм
Вычислим вероятность того,
что отклонение нормально распределенной случайной величины
от своего математического ожидания по абсолютной величине не превысит .
Воспользуемся формулой для нахождения вероятности заданного отклонения, в которую
в качестве
подставим :
.
Таким образом, вероятность того, что отклонение случайной величины
по абсолютной величине будет меньше утроенного среднего квадратического отклонения,
равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит
,
составляет всего 0,0027. Такое событие, исходя их принципа невозможности маловероятных
событий, можно считать практически невозможным.
Вывод (правило трех сигм): если случайная величина распределена
нормально, то абсолютная величина ее отклонения от математического ожидания
не превосходит утроенного среднего квадратического отклонения.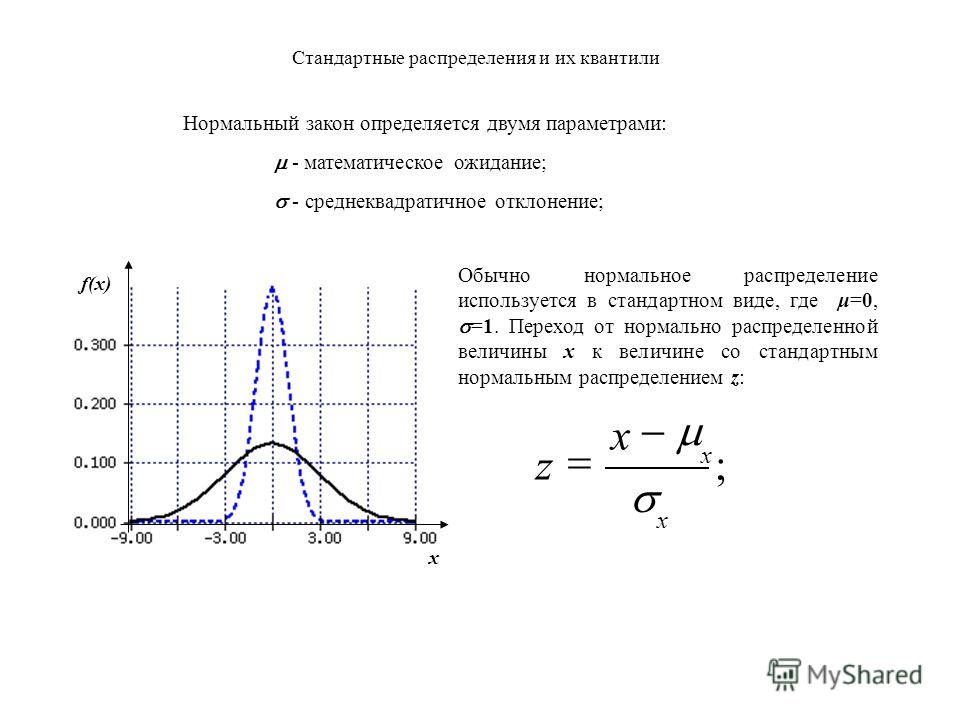
Понятие о теореме Ляпунова
Известно, что нормально распределенные случайные величины широко распределены на практике. Объяснение этому было дано А.М.Ляпуновым в центральной предельной теореме: если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.
| $F_X(x)$ | $=P(X \leq x)$ |
| $=P( \sigma Z+\mu \leq x) \hspace{20pt} \big(\textrm{где} Z \sim N(0,1)\big)$ | |
| $=P\left(Z \leq \frac{x-\mu}{\sigma}\right)$ | |
$=\Phi\left(\frac{x-\mu}{\sigma}\right).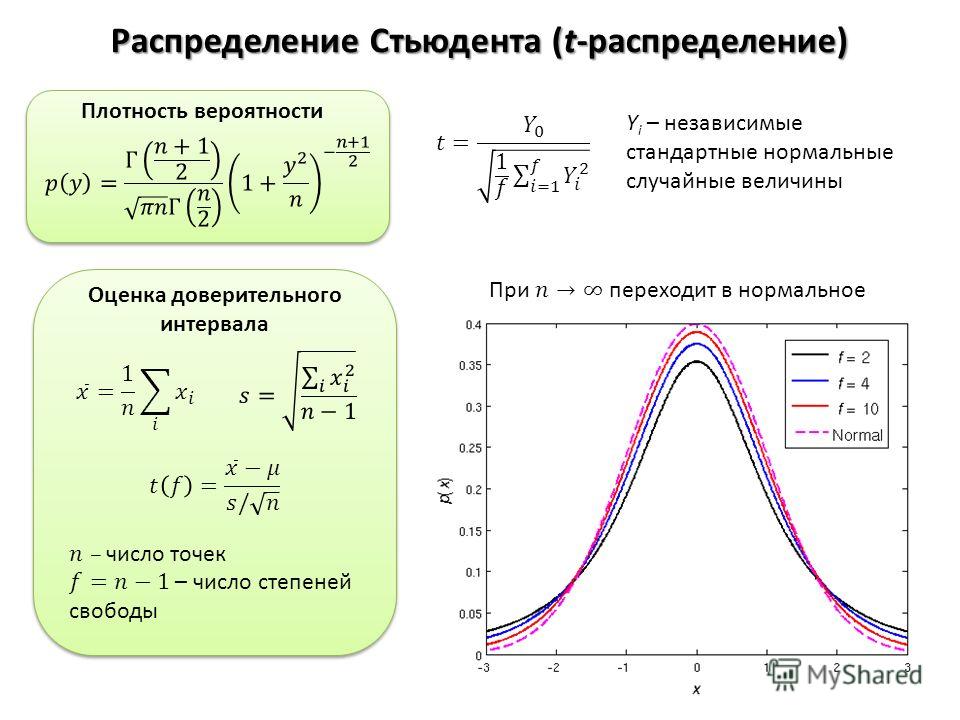 $ $ |
Чтобы найти PDF, мы можем взять производную от $F_X$,
| $f_X(x)$ | $=\frac{d}{dx} F_X(x)$ 92}\справа\},$$
$$F_X(x)=P(X \leq x)=\Phi\left(\frac{x-\mu}{\sigma}\right),$$
$$P(a На рис. 4.8 показана PDF нормального распределения для нескольких значений $\mu$ и $\sigma$. Рис.4.8 – PDF нормального распределения. Пример
Важным и полезным свойством нормального распределения является то, что линейное преобразование нормального случайная величина сама по себе является нормальной случайной величиной. В частности, справедлива следующая теорема: 92_Х).$$ ← предыдущая следующая → Печатная версия книги доступна на Amazon здесь. |
5.2: Стандартное нормальное распределение
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 525
Цели обучения
- Узнать, что такое стандартная нормальная случайная величина.

- Научиться вычислять вероятности, связанные со стандартной нормальной случайной величиной.
Определение: стандартная нормальная случайная величина
Стандартная нормальная случайная величина — это нормально распределенная случайная величина со средним значением \(\mu =0\) и стандартным отклонением \(\sigma =1\). Он всегда будет обозначаться буквой \(Z\).
Функция плотности для стандартной нормальной случайной величины показана на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): кривая плотности для стандартной нормальной случайной величины. Чтобы вычислить вероятности для \(Z\), мы не будем напрямую работать с ее функцией плотности, а вместо этого будем считывать вероятности из рисунка \(\PageIndex{ 2}\). Таблицы представляют собой таблицы кумулятивных вероятностей; их записи представляют собой вероятности вида \(P(Z Пример \(\PageIndex{1}\) Найдите указанные вероятности, где, как всегда, \(Z\) обозначает стандартную нормальную случайную величину. Решение : \[P(Z< 1,48)=0,9306\] Пример \(\PageIndex{2}\) Найти указанные вероятности. Решение : Пример \(\PageIndex{3}\) Найти указанные вероятности. Решение : В следующем примере показано, что делать, если значение \(Z\), которое мы хотим найти в таблице, там отсутствует. Пример \(\PageIndex{4}\) Найти указанные вероятности. Решение : Последний пример этого раздела объясняет происхождение пропорций, приведенных в эмпирическом правиле. Пример \(\PageIndex{5}\) Найти указанные вероятности. Решение : Анонимный Эта страница под названием 5.2: Стандартное нормальное распространение распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
 Таким образом, \(P(Z<-0,25)=0,4013\).
Таким образом, \(P(Z<-0,25)=0,4013\).
Рисунок \(\PageIndex{4}\): вычисление вероятности для правой полупрямой
Рисунок \(\PageIndex{5}\): вычисление вероятности для интервала конечной длины В символах \[P(0,5
В символах \[P(0,5
Рисунок \(\PageIndex{6}\): Вычисление вероятности для интервала конечной длины Мы получаем значение \(0,8708\) площади области под кривой плотности слева от \(1,13\) без каких-либо проблем, но когда мы ищем число \(4,16\) в таблице, оно нет там. Мы можем видеть из последней строки чисел в таблице, что площадь слева от \(4,16\) должна быть настолько близка к 1, что до четырех знаков после запятой она округляется до \(1,0000\). Следовательно, \[P(1,13
Мы получаем значение \(0,8708\) площади области под кривой плотности слева от \(1,13\) без каких-либо проблем, но когда мы ищем число \(4,16\) в таблице, оно нет там. Мы можем видеть из последней строки чисел в таблице, что площадь слева от \(4,16\) должна быть настолько близка к 1, что до четырех знаков после запятой она округляется до \(1,0000\). Следовательно, \[P(1,13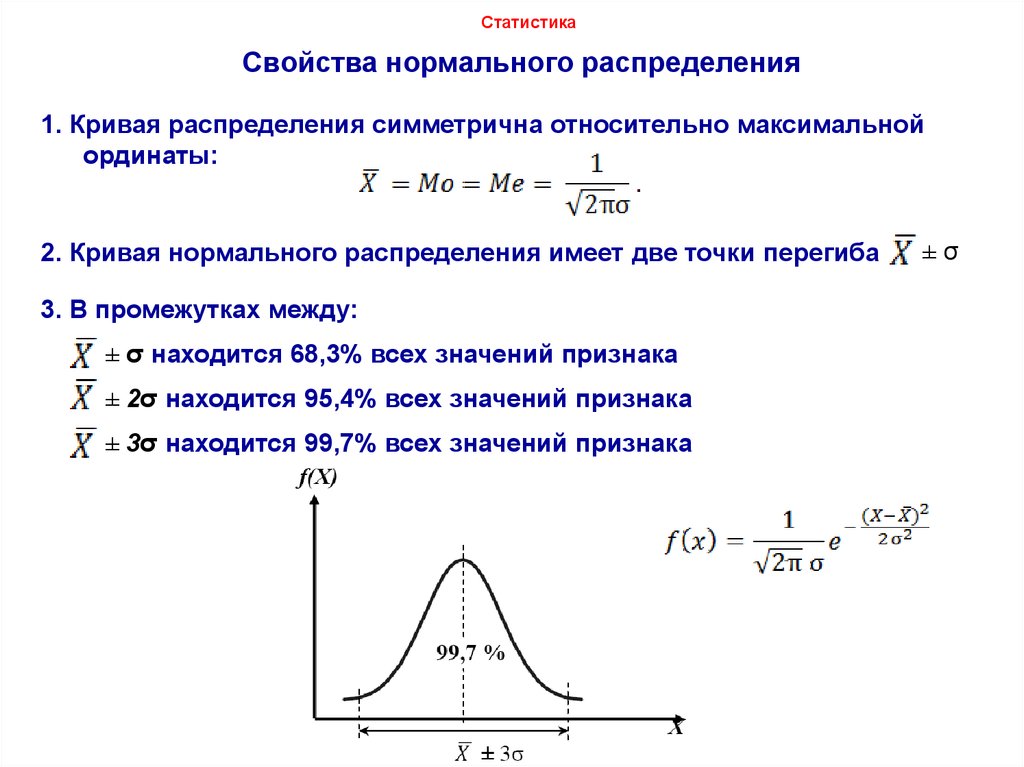


 2}{2}\ справа\} ду.$$
Этот интеграл не имеет решения в замкнутой форме. Тем не менее из-за важности
нормальное распределение, значения $F_Z(z)$ сведены в таблицы, и многие калькуляторы и
пакеты программного обеспечения имеют эту функцию. Обычно мы обозначаем стандартную нормальную CDF через $\Phi$. 92}{2}\right\} du.$$
2}{2}\ справа\} ду.$$
Этот интеграл не имеет решения в замкнутой форме. Тем не менее из-за важности
нормальное распределение, значения $F_Z(z)$ сведены в таблицы, и многие калькуляторы и
пакеты программного обеспечения имеют эту функцию. Обычно мы обозначаем стандартную нормальную CDF через $\Phi$. 92}{2}\right\} du.$$