Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .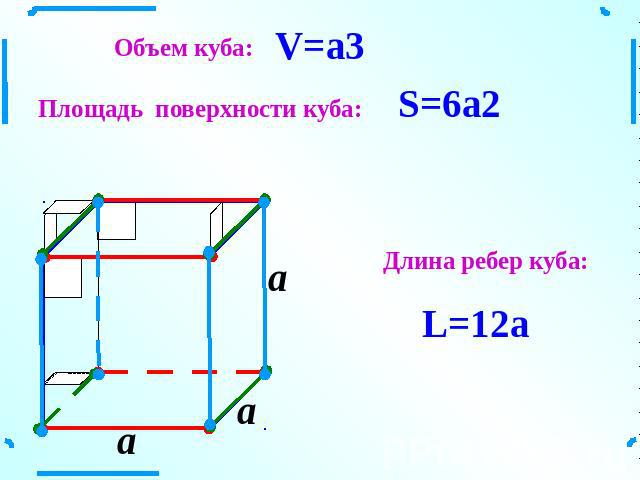
Решено
На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?
у мальчика тетрадей в клетку на 15 больше чем в линейку сколько всего у него тетрадей если тетрадей в клетку в 4 раза больше чем в линейку
как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз
Решено
из 100 кг свеклы получают…
Пользуйтесь нашим приложением
| ГОСТы, СНиПы Карта сайта TehTab. Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Инженерные приемы и понятия / / Отношение объема к площади поверхности любого физического тела. Один из важнейших инженерных приемов.
| |||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама на сайте | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||
Как найти площадь поверхности куба
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
SAT Math Help » Геометрия » Твердая геометрия » Кубики » Как найти площадь поверхности куба
Какова площадь поверхности куба с объемом 1728 в 3 ?
Possible Answers:
72 in 2
432 in 2
1728 in 2
144 in 2
864 in 2
Correct answer:
864 в 2
Объяснение:
Эта проблема относительно проста. Мы знаем, что объем куба равен s 3 , где s — длина данной стороны куба. Следовательно, чтобы найти наши размеры, нам просто нужно решить s 3 = 1728. Извлекая кубический корень, получаем s = 12.
Следовательно, чтобы найти наши размеры, нам просто нужно решить s 3 = 1728. Извлекая кубический корень, получаем s = 12.
Поскольку все стороны куба одинаковы, площадь поверхности куба в 6 раз больше площади одной грани. Для наших размеров одна грань имеет площадь 12 * 12 или 144 в 2 . Таким образом, общая площадь поверхности составляет 6 * 144 = 864 в 2 .
Сообщить об ошибке
Комната имеет размеры 18 на 15 на 9 футов. Последним размером является высота комнаты. В нем есть одна дверь размером 3 фута на 7 футов и два окна, каждое 2 фута на 5 футов. Нет отделки пола, стен, дверей и окон. Какова общая открытая площадь стены?
Possible Answers:
594 ft 2
1093ft 2
2389ft 2
553 ft 2
1134ft 2
Correct answer:
553 ft 2
Объяснение:
Если разбить на части, это простая задача.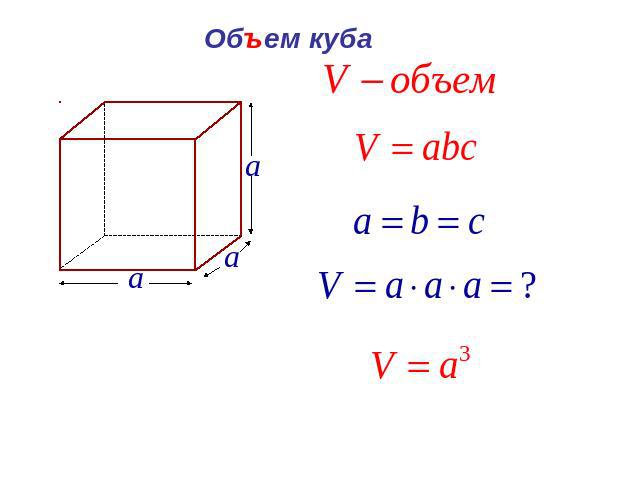 Сначала необходимо выделить размеры стен. Если высота комнаты 9 футов, мы знаем, что 18 x 15 обозначает площадь пола и потолка. Исходя из этого, мы знаем, что комната имеет следующие размеры по стенам: 18 х 9и 15 x 9. Так как каждой из них по две, мы можем рассчитать общую площадь стен, не считая дверей и окон, удвоив сумму этих двух площадей:
Сначала необходимо выделить размеры стен. Если высота комнаты 9 футов, мы знаем, что 18 x 15 обозначает площадь пола и потолка. Исходя из этого, мы знаем, что комната имеет следующие размеры по стенам: 18 х 9и 15 x 9. Так как каждой из них по две, мы можем рассчитать общую площадь стен, не считая дверей и окон, удвоив сумму этих двух площадей:
2 * (18 * 9 + 15 * 9) = 2 * (162 + 135) = 2 * 297 = 594 фута 2
Теперь нам просто нужно вычислить площадь, «вынутую» из стен:
Для двери: 3 * 7 = 21 фут 2
Для окон: 2 * (2 * 5) = 20 футов 2
Таким образом, общая площадь стены составляет: 594 – 21 – 20 = 553 фута 2
Сообщить об ошибке
Некоторый куб имеет длину стороны 25 м. Сколько квадратных плиток, каждая площадью 5 м 2 , необходимо, чтобы полностью покрыть поверхность куба?
Возможные ответы:
100
750
1000
500
200
Правильный ответ:
7505
Пояснение:
Куб со стороной 25 м имеет площадь поверхности:
25 м * 25 м * 6 = 3750 м 2
(Площадь поверхности куба равна площади одной грани куба, умноженной на 6 сторон. Другими словами, если сторона куба равна s, , то площадь поверхности куба равна 6 s 2. )
Другими словами, если сторона куба равна s, , то площадь поверхности куба равна 6 s 2. )
Каждая квадратная плитка имеет площадь 5 м 2 .
Следовательно, общее количество квадратных плиток, необходимых для полного покрытия поверхности куба, составляет:
3750 м 2 /5 м 2 = 750
Примечание: объем куба со стороной с равен с 3 . Следовательно, если спросить, сколько мини-кубов со стороной n нужно заполнить исходный куб, ответ будет таким:
s 3 /n 3
постройте кубическую комнату вокруг конуса так, чтобы высота и диаметр конуса были на 3 дюйма меньше, чем размеры куба. Если объем конуса 486π футов 3 , какова площадь поверхности куба?
Возможные ответы:
69 984 в 2
486 в 2
726 в 2
513. 375 в 2
375 в 2
513.375 в 2
513.375 в 2
513.375.
73 926 в 2
Пояснение:
Для начала нам нужно найти размеры конуса.
Базовая форма объема конуса: V = (1/3) πr 2 h
Используя наши данные, мы знаем, что h = 2r , потому что высота конуса соответствует его диаметру (на основе подсказки).
486 π = (1/3) πr 2 * 2 R = (2/3) πr 3
Установите обе стороны (3/2 π ): 729 = r 3
Извлеките кубический корень из обеих сторон: r = 9
Обратите внимание, что это футов . Ответы в квадратных дюймах. Поэтому переведите единицы измерения в дюймы: 9 * 12 = 108, а затем добавьте к этому 3 дюйма: 108 + 3 = 111 дюймов.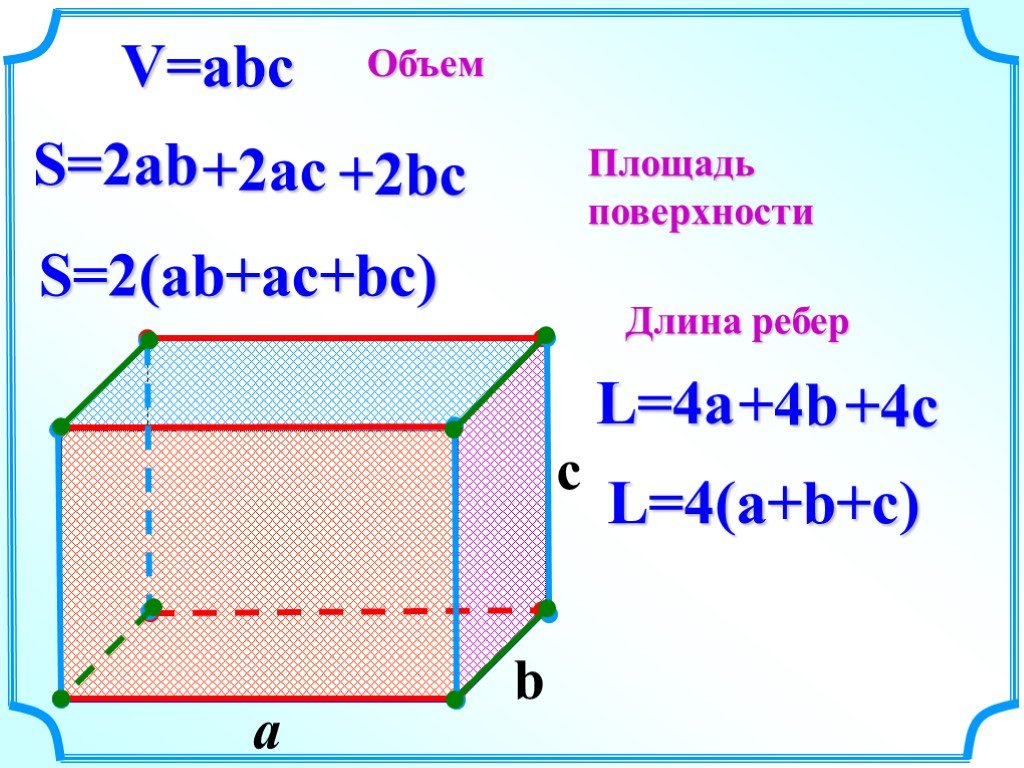
Площадь поверхности куба определяется как: A = 6 * с 2 , или для наших данных A = 6 * 111 2 = 73 9026 9000 4 в отчете3 2 Ошибка
Если объем куба 216 кубических единиц, то какова площадь его поверхности в квадратных единицах?
Возможные ответы:
36
64
216
54
108
Правильный ответ:
216
Объяснение:
Объем куба находится по формуле V = , где V — объем, а s — длина каждой стороны. Мы можем установить V равным 216, а затем найти s .
Чтобы найти s , мы можем найти кубический корень из обеих сторон экватора. Нахождение кубического корня числа равносильно возведению этого числа в третью степень.
Это означает, что длина стороны куба равна 6. Мы можем использовать эту информацию, чтобы найти площадь поверхности куба, которая равна . Формула площади поверхности исходит из того факта, что каждая грань куба имеет площадь , а в кубе 6 граней.
Мы можем использовать эту информацию, чтобы найти площадь поверхности куба, которая равна . Формула площади поверхности исходит из того факта, что каждая грань куба имеет площадь , а в кубе 6 граней.
площадь поверхности =
Площадь поверхности квадрата составляет 216 квадратных единиц.
Ответ: 216.
Сообщить об ошибке
У вас есть куб со стороной 4,5 дюйма. Какова площадь поверхности куба?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь одной стороны куба:
У куба 6 граней, поэтому общая площадь поверхности куба равна
Сообщить об ошибке
Куб имеет площадь поверхности 24 Если мы удвоим высоту куба, каков будет объем новой прямоугольной коробки?
Возможные ответы:
Правильный ответ:
Объяснение:
У нас есть куб с площадью поверхности 24, что означает, что площадь каждой стороны равна 4. Следовательно, длина каждой стороны равна 2. Если мы удвоим высоту, объем станет равным .
Следовательно, длина каждой стороны равна 2. Если мы удвоим высоту, объем станет равным .
Сообщить об ошибке
Куб имеет площадь поверхности 10 м 2 . Если все стороны куба удвоятся в длину, какова новая площадь поверхности?
Possible Answers:
320m 2
20m 2
640m 2
80m 2
40m 2
Correct answer:
40m 2
Объяснение:
Уравнение площади поверхности исходного куба: 6s 2 . Если длина всех сторон удвоится, новое уравнение будет 6(2s) 2 или 6 * 4s 2 . Это делает новую площадь поверхности в 4 раза больше, чем у старой. 4х10 = 40м 2
Сообщить об ошибке
Какова площадь поверхности куба со стороной 30?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу площади поверхности куба.
Заменить сторону.
Сообщить об ошибке
Площади шести кубов образуют арифметическую прогрессию. Два самых маленьких куба имеют длины сторон 10 и 12 соответственно. Укажите площадь поверхности самого большого куба.
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь поверхности куба можно вычислить, возведя длину стороны в квадрат и умножив ее на шесть. Таким образом, два самых маленьких куба имеют площади поверхности
и
Площади поверхностей образуют арифметическую последовательность с этими двумя площадями поверхностей в качестве первых двух членов, поэтому их общая разница составляет
.
Площадь поверхности самого большого, или шестой малой, кубика,
Отчет о ошибке
← Предыдущие 1 2 Далее →
Уведомление о авторском здании
ВСЕ
1 216 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
Понимание площади поверхности и объема
Наставник: Итак, если мы знаем, что можем найти площадь двумерной фигуры, как вы думаете, это можно ли найти площадь трехмерной фигуры? В самом деле, кто может сказать мне, что такое три объемная фигура есть?
Ученик: Трехмерная фигура подобна шару или кубу — она не плоская.
Наставник: Это верно. Теперь кто-нибудь может сказать что-нибудь о том, что может означать нахождение площади такая фигура?
Ученик: Когда вы говорите «найти площадь», вы имеете в виду внешнюю или внутреннюю часть?
Наставник: Ну, это зависит. На самом деле нет такой вещи, как нахождение «площади» куба. Вместо, у нас есть термины «объем» и «площадь поверхности». Сначала поговорим об объеме. Когда ты сказал «найти площадь» квадрата, вы имеете в виду внешнюю сторону или внутренности включены?
Ученик: Мы просто смотрим на то место, которое он занимает на бумаге; мы предполагаем, что ребра квадрата имеют ширина нуля.
Наставник: Точно! Теперь представьте, сколько места занимает куб в трех измерениях. Мы вызов, который измеряет объем куба.
Ученик: Как вы измеряете объем?
Наставник: Точно так же, как вы измеряете и умножаете длину и ширину прямоугольника, чтобы найти его площадь, вы
умножьте длину, ширину и высоту трехмерного объекта, такого как куб, чтобы найти его объем. умножение трех переменных дает ему три измерения, таким образом, объем, а не просто
область. Как вы думаете, в каких единицах измеряется объем?
умножение трех переменных дает ему три измерения, таким образом, объем, а не просто
область. Как вы думаете, в каких единицах измеряется объем?
Ученик: Ну, если есть три слагаемых, все в дюймах, то это будут дюймы * дюймы * дюймы, что в дюймах в кубе.
Наставник: Чем это отличается от юнитов при нахождении площади?
Ученик: Ну, площадь «возводится в квадрат», потому что вы просто умножаете дюймы на дюймы.
Наставник: Точно! Площадь «в квадрате», а объем в «кубе». Как вы думаете, как это связано с их значение?
Ученик: Вы находите площадь квадрата или другого двумерного объекта, но вы находите объем трехмерные объекты, такие как кубы!
Наставник: Хорошо, теперь мы знаем, как измерить, сколько места занимает объект. Но как насчет вне объекта, как вы упоминали ранее? Как вы думаете, что такое «площадь поверхности»?
Ученик: Звучит так, как будто это только внешние стороны — область, которая находится на поверхности, которую я могу
трогать.

 02.16
02.16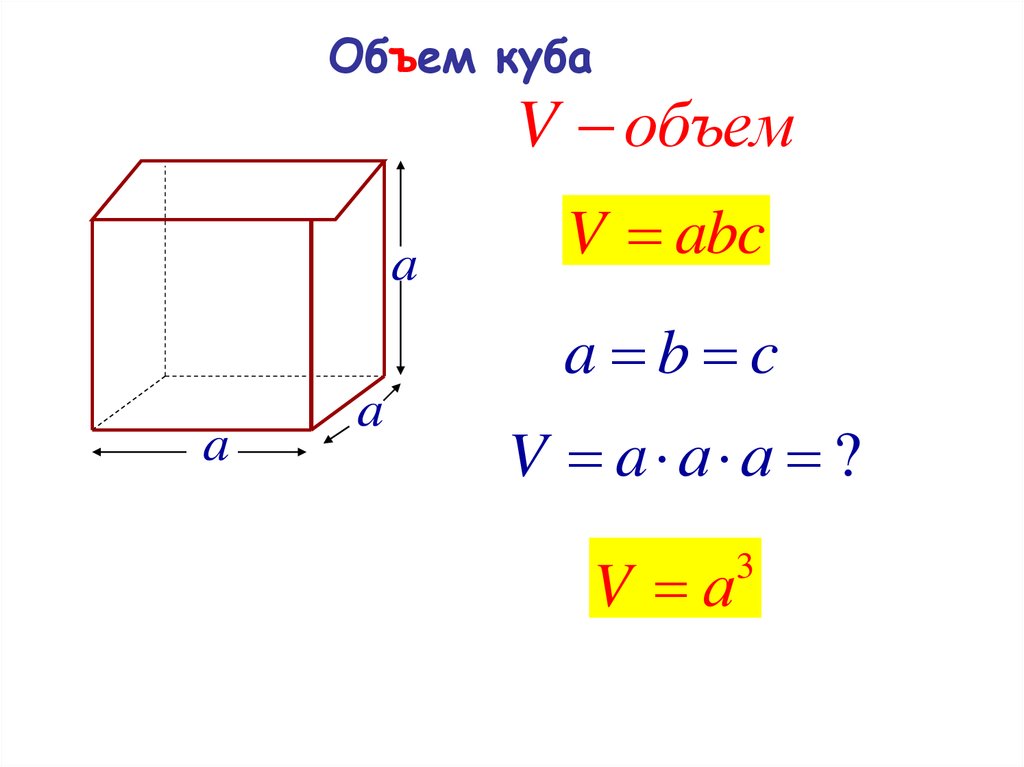
 Объем этого куба равен 27 м3 (3х3х3). Каждая сторона имеет площадь 9 м2 , а вся площадь поверхности этого кубика равна 54 м2. Отношение объема к площади поверхности равно 27:54 = 1/2 = 3/6.
Объем этого куба равен 27 м3 (3х3х3). Каждая сторона имеет площадь 9 м2 , а вся площадь поверхности этого кубика равна 54 м2. Отношение объема к площади поверхности равно 27:54 = 1/2 = 3/6. Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).
Этот факт применим не только к телам кубической формы, но и к любым другим телам, естественно при сохранении формы ( или пропорций, если Вам так больше нравится).