Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеСЛОВО К УЧАЩИМСЯГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел.  8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами.  30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49.  3.112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени.  130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения.  149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными.  169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188.  Неравенства и системы неравенств с двумя переменными.§ 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21.  Производная и ее применения209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226.  Правила вычисления первообразных.227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22.  23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники.  49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76.  Понятие движения.§ 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ |
Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности. | ||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
| |||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||
ru: главная страница / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.
Расчет объема прямоугольного бака.
Расчет объема и общей площади поверхности правильной пирамиды.
Расчет объема и общей площади поверхности конуса.
Поскольку радиус полукруга равен 6 см, диаметр равен 12 см.
Вычислить объем бойлера и общую площадь его поверхности.
Введите свой запрос:линейная алгебра — Очень просто — Объем параллелепипеда
Задавать вопрос
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 680 раз
$\begingroup$
Я пытаюсь понять, почему объем параллелепипеда со сторонами $s,u,w$ равен $ V = s \cdot(u \times w)$.
Даже единицы измерения не складываются. Длина векторов $s,u,w$ измеряется в сантиметрах, объем измеряется в кубических см.
$u\times w$ — вектор. Это вектор, ортогональный к $u$ и $w$, но все же вектор, поэтому его длина снова измеряется в см. Таким образом, в целом $V=s \cdot(u \times w)$ означает, что $V$ равно произведению $2$ векторов, поэтому единицей измерения $V$ являются сантиметры в квадрате, а не в кубе.
Я пытаюсь понять, как $|u\times w|$ может равняться площади параллелограмма. Это равносильно утверждению: «Время, необходимое мне для решения проблемы, равно расстоянию между Нью-Йорком и Лондоном».
- линейная алгебра
- векторные пространства
- определитель
- объем
$\endgroup$
1
$\begingroup$
92$ — независимо от того, что $u\times v$ является вектором. Векторы не обязательно должны иметь единицы длины — они могут иметь любые единицы измерения, которые нам нравятся. Таким образом, если $\|u\times v\|$ — это площадь параллелограмма, то площадь параллелепипеда будет просто равна этой площади, умноженной на высоту параллелепипеда («основание умножить на высоту» — формула, которую мы здесь используем ). Так как $\|s\|\cos(\theta)$ — это высота параллелепипеда (нарисуйте рисунок, чтобы убедиться в этом сами), объем будет равен $\|s\|\cos(\theta)\ |и\раз v\| = \|s\|\|u\times v\|\cos(\theta)$.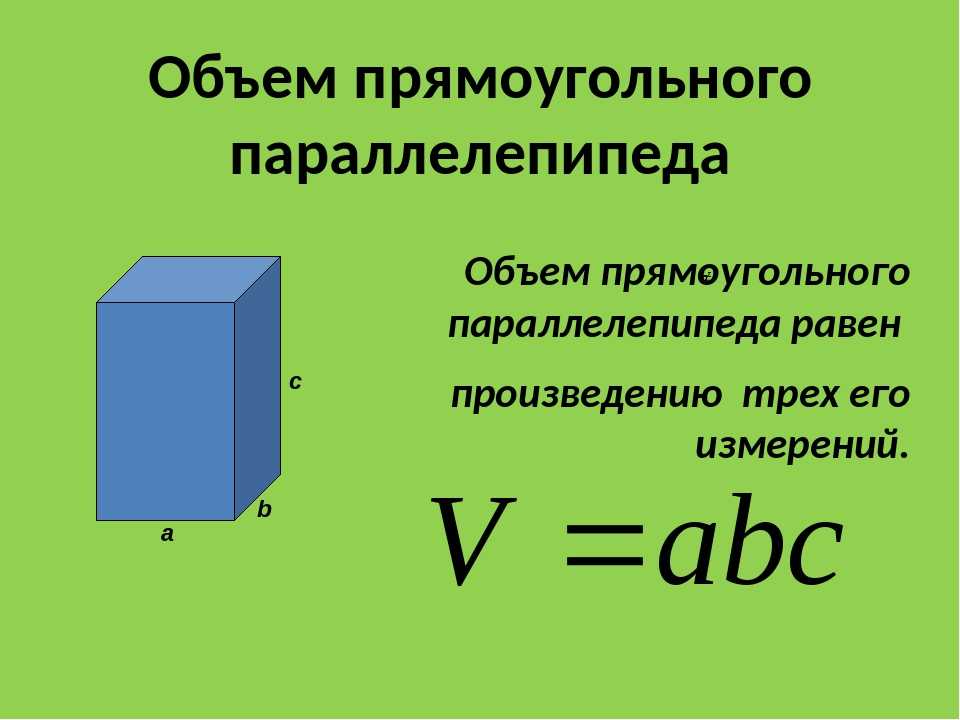
Но это всего лишь скалярное произведение $s$ и $u\times v$.
$\endgroup$
4
$\begingroup$
Я думаю, очевидный парадокс в этом вопросе проистекает из ошибочного убеждения, что вектор имеет связанные единицы длины. Это неправильно. В трехмерном пространстве вектор $(1,2,3)$ можно рассматривать как состоящий из упорядоченных троек сантиметров (не то же самое, что сантиметры в кубе). У нас также могут быть координаты в сантиметрах, секундах, литрах, но это все равно упорядоченная тройка. 92}$ действительно в сантиметрах, потому что каждый из $1,2,3$ в сантиметрах, так что если возвести в квадрат в квадратных сантиметрах, то к сумме применяется квадратный корень, который возвращает нас к сантиметрам.
Если единицами измерения были сантиметры, секунды, литры, то длина вектора больше не имеет значимых единиц.
$\endgroup$
$\begingroup$
Перекрестное произведение имеет размеры площади $ |A|\cdot|B| \sin\тета $.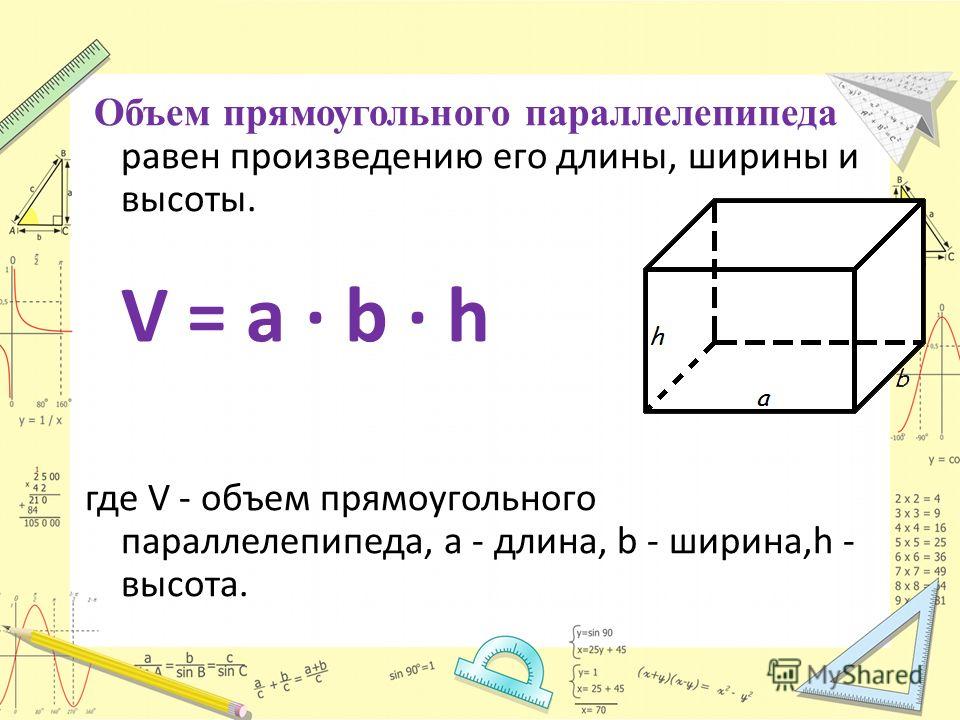
Просто потому, что это вектор, он не всегда должен быть прямой линией. Мы говорим область указана количество. Площадь или даже объем могут быть вектором.
Как мы принимаем углы, угловые скорости, угловые ускорения как векторы? Силы как векторы? Ток и напряжение как векторы? Каждая из них имеет физическую величину и направление.
Тройное произведение является скалярным без направления.
Объем параллелепипеда равен 2+1 = 3.
$\endgroup$
Узнайте все, что вам нужно знать о параллелепипеде
Трехмерная фигура, состоящая из шести параллелограммов, известна как «параллелепипед». Параллелепипед — это термин, происходящий от греческого слова parallelepipdon, что переводится как «тело с параллельными телами». Параллелограмм имеет уникальную взаимозависимую связь с параллелепипедом точно так же, как куб связан с квадратом. Параллелепипед — это многоугольник с шестью гранями в форме параллелограмма, восемью вершинами и двенадцатью ребрами.
В следующей статье мы рассмотрим свойства параллелепипеда и различные формулы, связанные с его площадью поверхности и объемом.
- Определение параллелепипеда в геометрии состоит в том, что параллелепипед представляет собой трехмерную форму с шестью гранями, каждая из которых имеет форму прямоугольника или квадрата
- Он состоит из шести граней, восьми вершин и двенадцати края. В параллелепипеде есть несколько исключений. Наиболее известны куб, прямоугольный параллелепипед и ромбоид.
- Куб — это параллелепипед, все четыре стороны которого имеют квадратную форму. Кубоид и ромбоид, с другой стороны, являются параллелепипедами с прямоугольными и ромбовидными гранями соответственно
- Трехмерная форма, или призма, образована в основном шестью гранями параллелограмма, при этом основание параллелограмма служит основой для всей конструкции.
- Она будет определена как многогранник. Три пары параллельных граней соединяются вместе, образуя трехмерную фигуру с шестью гранями.
Основные и наиболее важные характеристики отличают его от других трехмерных фигур. Основные свойства параллелепипеда приведены ниже; они:
- Параллелепипед — это трехмерная фигура
- Всего он состоит из шести граней
- Параллелепипед имеет 12 ребер и восемь вершин
- Параллелограммы — это формы всех граней параллелепипеда
- две диагонали на каждой из его граней, которые называются диагоналями граней
- По крайней мере, в параллелепипеде 12 диагоналей граней
- Диагонали, соединяющие вершины параллелепипеда, которые не все лежат на одной грани, равны называется диагоналями тела или пространства
- Призму с основанием в виде параллелограмма называют геометрическим параллелепипедом
- Параллелепипед имеет две грани, каждая из которых является зеркальным отражением другой грани
Площадь поверхности параллелепипеда определяется как общая площадь, покрытая всеми его поверхностями.
Он равен сумме всех своих сторон. Обычно площадь поверхности параллелепипеда выражается в квадратных единицах, таких как in2 (дюймы в квадрате), cm2 (метры в квадрате), ft2 (футы в квадрате) и так далее.
Площадь поверхности параллелепипеда можно разделить на две категории:
- Площадь боковой поверхности
- Общая площадь поверхности
Площадь боковой поверхности (LSA): Когда мы говорим «площадь боковой поверхности параллелепипеда, ” мы имеем в виду площадь боковых или боковых граней параллелепипеда с любой стороны. Чтобы вычислить LSA параллелепипеда, мы должны сначала найти сумму площадей, покрываемых четырьмя боковыми гранями.
Общая площадь поверхности (TSA): параллелепипеды имеют общую площадь поверхности, определяемую как сумма всех граней, составляющих параллелепипед. Для параллелепипеда мы должны найти сумму площадей, покрытых его шестью гранями, чтобы вычислить его общую площадь поверхности, TSA.
Формула для расчета площади поверхности параллелепипеда приведена ниже.
Для LSA параллелепипеда это P x H. В то же время TSA параллелепипеда равен LSA + 2 B = (P H) + (2 B), где «B» представляет собой площадь основания, «H ” представляет высоту параллелепипеда, а “P” представляет базовый периметр.
Каков объем параллелепипеда?
Когда параллелепипед определяется как пространство, занимаемое фигурой на трехмерной плоскости, говорят, что он имеет объем. Объем параллелепипеда измеряется в кубических единицах, таких как дюймы, сантиметры, метры, футы и ярды.
Формула для расчета объема параллелепипеда приведена ниже.
Формула для расчета объема параллелепипеда: B x H. B представляет собой площадь основания, а H представляет собой высоту параллелепипеда.
Заключение Параллелепипед – одна из самых распространенных и выдающихся геометрических фигур. Его влияние видно почти во всех присутствующих фигурах. Свойства параллелепипеда уникальны, что делает их актуальными с точки зрения геометрии.