| 2.10. Геометрический смысл смешанного произведения. Задачи, решаемые с помощью смешанного произведения |  Векторная алгебра > 2.10. Геометрический смысл смешанного произведения. Задачи, решаемые с помощью смешанного произведения Векторная алгебра > 2.10. Геометрический смысл смешанного произведения. Задачи, решаемые с помощью смешанного произведения
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| gif»> | ||||||||||||||||||||||||||||||||||||||||||||||||||
2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
Любой вектор в декартовой системе координат может быть представлен в виде
Где координаты вектора Орты координатных осей.
Вектор с началом в точке и концом в точке Имеет вид:
,
то есть .
Длина отрезка называется Длиной (модулем) вектора, обозначается = и вычисляется по формуле
.
Сумма векторов и определяется формулой
Произведение вектора На число определяется формулой
.
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т. е.
.
Скалярное произведение векторов и вычисляется по формуле:
.
Векторным произведением векторов и называется вектор, обозначаемый и удовлетворяющий следующим условиям:
1) длина вектора равна площади параллелограмма, построенного на векторах и , т. е. ;
2) вектор перпендикулярен векторам и ;
3) векторы образуют правую тройку, то есть они ориентированы по отношению друг к другу соответственно как орты .
Модуль векторного произведения векторов и численно равен площади параллелограмма, построенного на этих векторах:
Векторное произведение векторов и вычисляется по формуле:
.
Смешанным произведением векторов называется скалярное произведение вектора на вектор , то есть .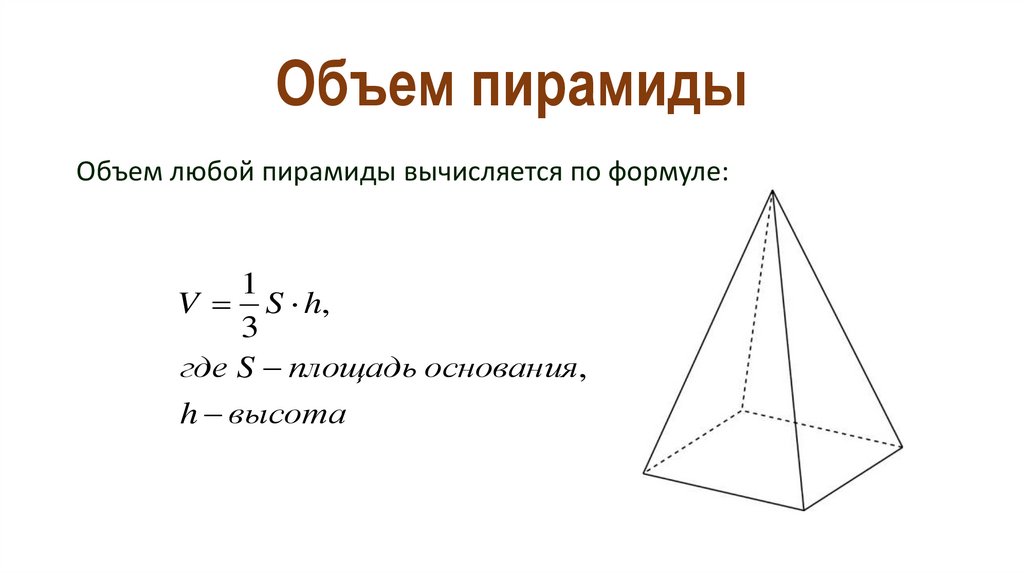
Модуль смешанного произведения векторов численно равен объему параллелепипеда, построенного на этих векторах:
Пусть Тогда
.
Уравнение любой плоскости может быть записано в виде:
где .
Вектор , перпендикулярный плоскости, называется Нормальным Вектором плоскости.
Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид
Угол между плоскостями и определяется следующим образом:
.
Расстояние от точки До плоскости, определяемой уравнением , находится по формуле
.
Прямая В пространстве может быть задана уравнениями двух плоскостей
,
Пересекающихся по этой прямой, или Каноническими уравнениями прямой
,
Которые определяют прямую, проходящую через точку и параллельную вектору . Вектор называется Направляющим вектором прямой.
Уравнения прямой, проходящей через две точки и , имеют вид:
.
Угол между Двумя прямыми и определяется следующим образом:
.
Угол между прямой и плоскостью определяется следующим образом:
.
Если Точка Делит отрезок АВ, где ,, в Отношении, то координаты точки М определяются по формулам:
.
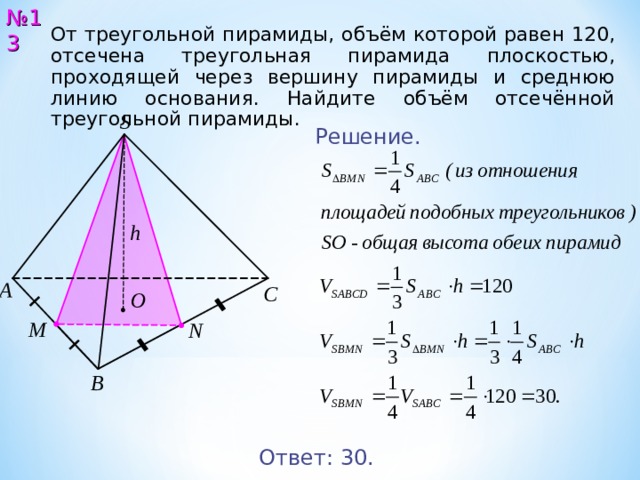
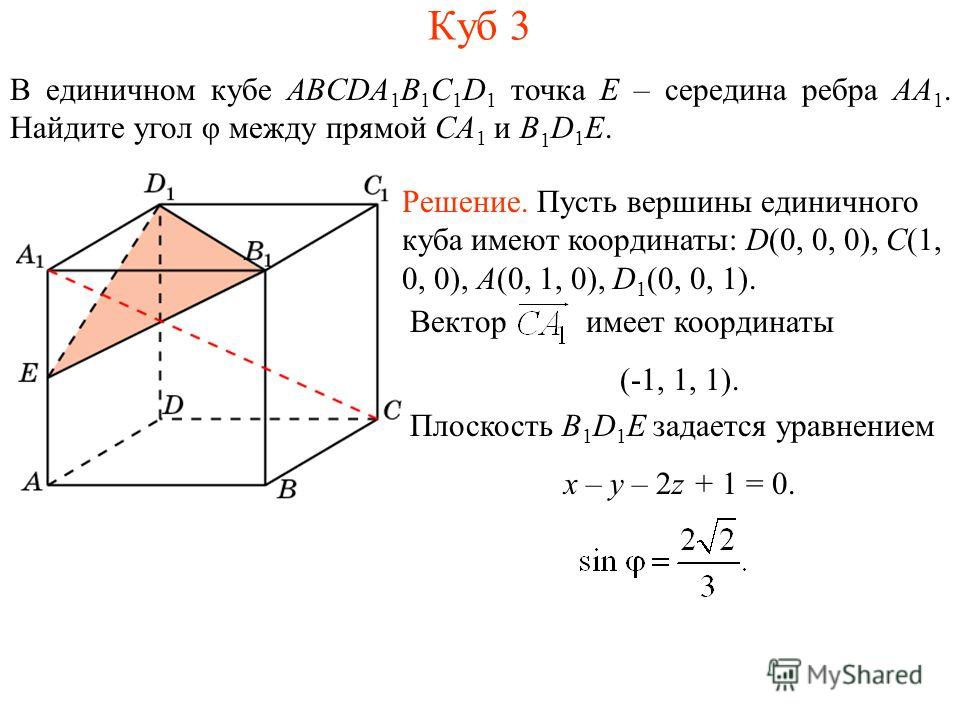
Задание 1. Даны координаты вершин пирамиды : ,. Найти: 1) длину ребра ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды; 6) уравнения прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.
Решение. 1) Для определения длины ребра найдем координаты вектора : . Тогда длина ребра будет равна длине вектора :
.
2) Найдем угол между ребрами и . Для этого, как и раньше, найдем координаты вектора , определяющего ребро . Получим и .
Тогда угол между ребрами и можно найти из определения скалярного произведения двух векторов:
.
Следовательно, .
3) Чтобы найти угол между ребром и гранью , определим нормальный вектор Плоскости . Из определения векторного произведения двух векторов имеем:
,
Т. е. и . Тогда , .
Так как нормальный вектор перпендикулярен плоскости , то угол между ребром и гранью определяется как .
4) Площадь грани можем найти по формуле . Следовательно, Кв. ед.
5) Объем пирамиды, построенной на векторах, равен 1/6 объема параллелепипеда, построенного на этих же векторах. Для определения объема параллелепипеда воспользуемся свойством смешанного произведения векторов. В результате имеем:
Таким образом, куб. ед.
6) Составим уравнения прямой . Для этого воспользуемся уравнениями прямой, проходящей через две заданные точки И :
.
Получаем:
.
7) Уравнение плоскости можно найти по формуле:, где , . Следовательно, уравнение плоскости имеет вид: или после упрощения .
8) Чтобы составить уравнение высоты , опущенной из вершины на грань , воспользуемся формулой:
,
Где , — направляющий вектор высоты Пирамиды . Так как вектор Перпендикулярен грани , то в качестве Можно взять вектор — нормальный вектор плоскости .
Так как вектор Перпендикулярен грани , то в качестве Можно взять вектор — нормальный вектор плоскости .
Следовательно, имеем: или .
9) Сделаем теперь чертеж:
| < Предыдущая | Следующая > |
|---|
Объем пирамиды – формула, вывод, определение, примеры
Объем пирамиды – это пространство, которое она занимает (или) определяется как количество единичных кубов, которые могут в нее поместиться. Пирамида — это многогранник, так как его грани состоят из многоугольников. Существуют различные типы пирамид, такие как треугольная пирамида, квадратная пирамида, прямоугольная пирамида, пятиугольная пирамида и т. д., которые названы в честь их основания, то есть, если основание пирамиды квадратное, она называется квадратной пирамидой. Все боковые грани пирамиды представляют собой треугольники, где одна сторона каждого треугольника сливается со стороной основания.
| 1. | Что такое объем пирамиды? |
| 2. | Объем формулы пирамиды |
| 3. | Формулы объема различных типов пирамид |
| 4. | Часто задаваемые вопросы о Томе Пирамиды |
Что такое объем пирамиды?
Объем пирамиды — это пространство, заключенное между ее гранями. Измеряется в кубических единицах, таких как см 3 , m 3 , in 3 и т. д. Пирамида представляет собой трехмерную фигуру, у которой ее основание (многоугольник) соединено с вершиной (вершиной) с помощью треугольных граней. Расстояние по перпендикуляру от вершины до центра основания многоугольника называется высотой пирамиды. Название пирамиды происходит от ее основания. Например, пирамида с квадратным основанием называется квадратной пирамидой.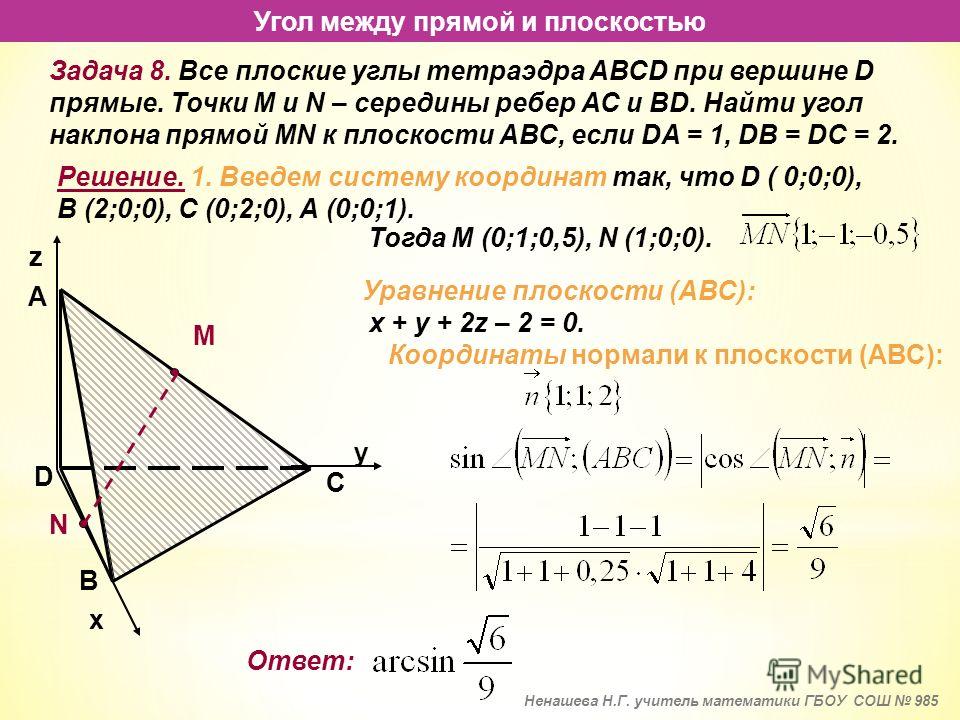 Таким образом, площадь основания играет главную роль в определении объема пирамиды. Объем пирамиды есть не что иное, как одна треть произведения площади основания на ее высоту.
Таким образом, площадь основания играет главную роль в определении объема пирамиды. Объем пирамиды есть не что иное, как одна треть произведения площади основания на ее высоту.
Объем формулы пирамиды
Рассмотрим пирамиду и призму, каждая из которых имеет площадь основания «В» и высоту «h». Мы знаем, что объем призмы получается путем умножения ее основания на высоту. т. е. объем призмы равен Bh. Объем пирамиды равен одной трети объема соответствующей призмы (т. е. их основания и высоты равны). Таким образом,
Объем пирамиды = (1/3) (Bh), где
- B = Площадь основания пирамиды
- h = Высота пирамиды (которую также называют «высотой»)
Примечание: Треугольник, образованный наклонной высотой (s), высотой (h) и половиной длины стороны основания (x/2), является прямоугольным треугольником, поэтому мы можем применить Теорема Пифагора для этого. Таким образом, (x/2) 2 + h 2 = s 2 . Мы можем использовать это при решении задач нахождения объема пирамиды по ее наклонной высоте.
Мы можем использовать это при решении задач нахождения объема пирамиды по ее наклонной высоте.
Формулы объема различных типов пирамид
Из предыдущего раздела мы узнали, что объем пирамиды равен (1/3) × (площадь основания) × (высота пирамиды). Таким образом, чтобы вычислить объем пирамиды, мы можем использовать формулы площадей многоугольников (поскольку мы знаем, что основание пирамиды является многоугольником), чтобы вычислить площадь основания, а затем, просто применив приведенную выше формулу, мы можно вычислить объем пирамиды. Здесь вы можете увидеть формулы объема различных типов пирамид, таких как треугольная пирамида, квадратная пирамида, прямоугольная пирамида, пятиугольная пирамида и шестиугольная пирамида, и то, как они получены.
Решенные примеры на объем пирамиды
Пример 1: Пирамида Хеопса в Египте имеет размер основания около 755 футов × 755 футов, а ее высота составляет около 480 футов.
 Вычислите ее объем.
Вычислите ее объем.Решение:
Пирамида Хеопса представляет собой квадратную пирамиду. Его базовая площадь (площадь квадрата) составляет
B = 755 × 755 = 570 025 квадратных футов.
Высота пирамиды, h = 480 футов.
Используя формулу объема пирамиды,
Объем пирамиды, V = (1/3) (Bh)
V = (1/3) × 570025 × 480
V = 91 204 000 кубических футов.
Ответ: Объем пирамиды Хеопса составляет 91 204 000 кубических футов.
Пример 2: Пирамида имеет правильный шестиугольник со стороной 6 см и высотой 9 см. Найдите его объем.
Решение:
Длина стороны основания (правильного шестиугольника), a = 6,
Площадь основания (площадь правильного шестиугольника) равна,
B = (3√3/2) × a 2
B = (3√3/2) × 6 2 ≈ 93,53 см 2 .
Высота пирамиды h = 9 см.
Объем шестиугольной пирамиды равен,
V = (1/3) (Bh)
V = (1/3) × 93,53 × 9
V = 280,59 см 3
3 :
3 Объем пирамиды 280,59 см 3 .

Пример 3: Тим построил прямоугольную палатку (имеющую форму прямоугольной пирамиды) для ночлега. Основание палатки представляет собой прямоугольник со стороной 6 единиц × 10 единиц и высотой 3 единицы. Какой объем палатки?
Решение:
Площадь основания (площадь прямоугольника) палатки равна B = 6 × 10 = 60 квадратных единиц.
Высота палатки h=3 ед.
Объем палатки по формуле объема пирамиды,
В = (1/3) (Bh)
В = (1/3) × 60 × 3
В = 60 кубических единиц.
Ответ: Объем палатки = 60 куб.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Запись на бесплатный пробный урок
Практические вопросы по объему пирамиды
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о томе пирамиды
Что означает объем пирамиды?
Объем пирамиды — это пространство, которое занимает пирамида. Объем пирамиды, площадь основания которой равна «B», а высота — «h», составляет (1/3) (Bh) кубических единиц.
Объем пирамиды, площадь основания которой равна «B», а высота — «h», составляет (1/3) (Bh) кубических единиц.
Каков объем пирамиды с квадратным основанием?
Если «B» — площадь основания, а «h» — высота пирамиды, то ее объем равен V = (1/3) (Bh) кубических единиц. Рассмотрим квадратную пирамиду, основание которой представляет собой квадрат длины «x». Тогда площадь основания равна B = x 2 и, следовательно, объем пирамиды с квадратным основанием равен (1/3)(x 2 h) кубических единиц.
Каков объем пирамиды с треугольным основанием?
Чтобы найти объем пирамиды с треугольным основанием, во-первых, нам нужно найти площадь ее основания «B», которую можно найти, применив подходящую формулу площади треугольника. Если h — высота пирамиды, то ее объем находится по формуле V = (1/3) (Bh).
Каков объем пирамиды с прямоугольным основанием?
Пирамида, основание которой представляет собой прямоугольник, является прямоугольной пирамидой.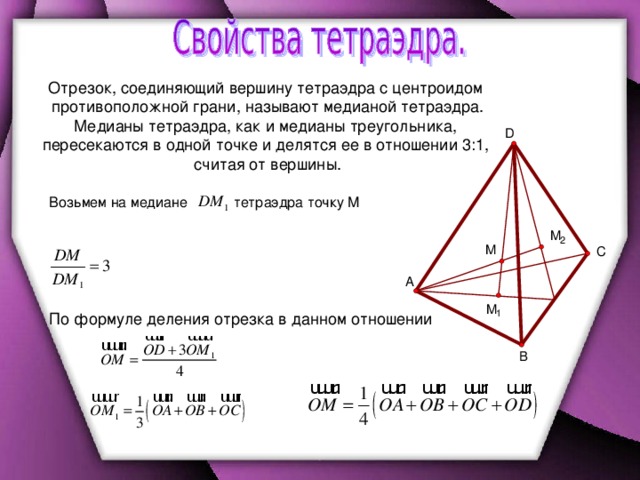 Его базовая площадь «B» находится путем применения формулы площади прямоугольника. т. е. если «l» и «w» — размеры основания (прямоугольника), то его площадь равна B = lw. Если «h» — высота пирамиды, то ее объем равен V = (1/3) (Bh) = (1/3) lwh кубических единиц.
Его базовая площадь «B» находится путем применения формулы площади прямоугольника. т. е. если «l» и «w» — размеры основания (прямоугольника), то его площадь равна B = lw. Если «h» — высота пирамиды, то ее объем равен V = (1/3) (Bh) = (1/3) lwh кубических единиц.
По какой формуле найти объем пирамиды?
Объем пирамиды находится по формуле V = (1/3) Bh, где B — площадь основания, а h — высота пирамиды. Поскольку мы знаем, что основанием пирамиды является любой многоугольник, мы можем применить формулы площади многоугольников, чтобы найти «B».
Как найти объем пирамиды с наклонной высотой?
Если «x» — длина основания, «s» — высота наклона, а «h» — высота правильной пирамиды, то они удовлетворяют уравнению (теореме Пифагора) (x/2) 2 + ч 2 = с 2 . Если нам даны «x» и «s», то мы можем сначала найти «h», используя это уравнение, а затем применить формулу V = (1/3) Bh, чтобы найти объем пирамиды, где «B» — это объем пирамиды.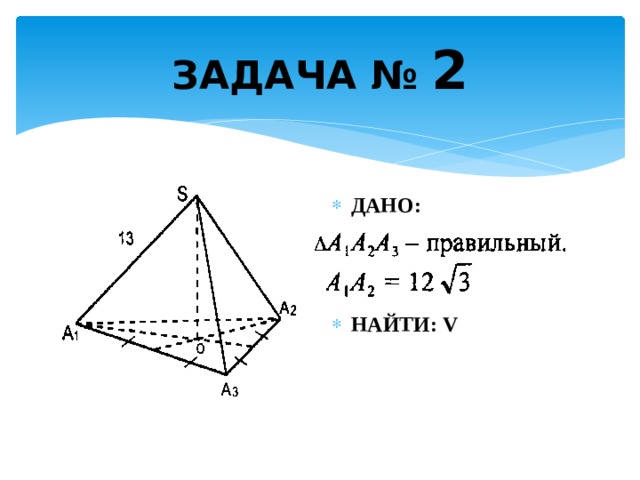 площадь основания пирамиды.
площадь основания пирамиды.
Почему в формуле объема пирамиды стоит 1/3?
Куб единичной длины можно разделить на три конгруэнтные пирамиды. Значит, объем пирамиды равен 1/3 объема куба. Следовательно, мы имеем 1/3 объема пирамиды.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по объему пирамиды
Расчет объема призмы и пирамиды с векторами
Энциклопедия>Числа и количества>Векторы>Три измерения>Вычисления векторов>Как рассчитать объем призмы и пирамиды с векторами
Вы можете использовать векторное произведение и скалярное произведение, чтобы найти объем квадратной призмы (параллелепипеда), пирамиды или тетраэдра (пирамиды с треугольным основанием), натянутого на три вектора. Для этого вы сначала находите векторное произведение двух векторов, затем скалярное произведение этого векторного произведения и третьего вектора и, наконец, умножаете полученное число на число, принадлежащее фигуре, которую вы хотите найти объем .
Для квадратной призмы ни на что умножать не нужно.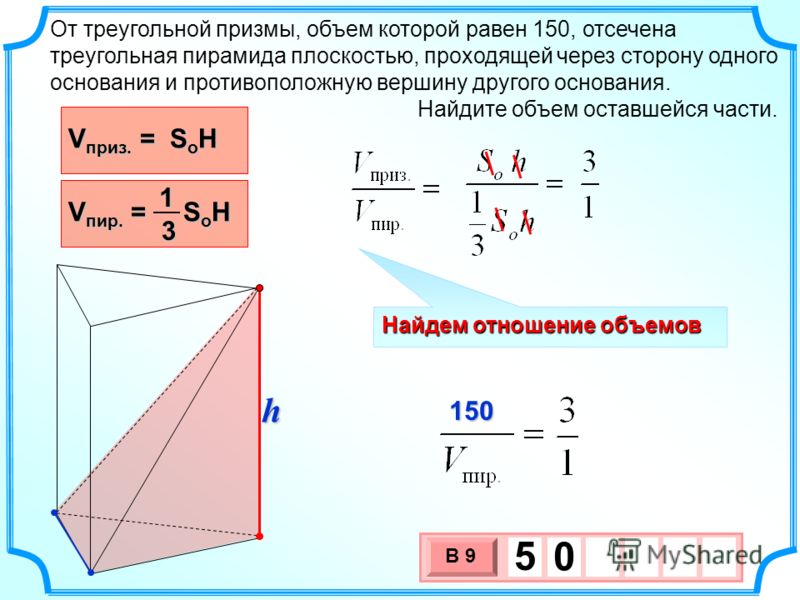 Для пирамиды с квадратным основанием множитель равен 13, а для тетраэдра множитель равен 16.
Для пирамиды с квадратным основанием множитель равен 13, а для тетраэдра множитель равен 16.
Внимание! Иногда вы получаете отрицательное число. Отрицательный объем не имеет смысла, поэтому всегда следует использовать абсолютное значение ответа, например, V= |−14|=14.
Формула
Объем квадратной призмы
| ВФ= | (u→×v→)⋅w→| |
Пример 1
Найдите объем квадратной призмы, натянутой на (1,3,−2), (−3,2,4) и (1,1,1).
Теперь вам нужно найти векторное произведение двух векторов, а затем найти скалярное произведение этого векторного произведения и неиспользованного вектора. Перекрестное произведение первых двух векторов равно (16,2,11). Затем вы находите скалярное произведение этого и (1,1,1),
| (16,2,11)⋅ (1,1,1)=16+2+11=29, |
, что дает нам объем 29. Если бы вы получили отрицательный ответ, вам пришлось бы использовать его абсолютное значение в качестве объема.
Формула
Объем пирамиды
| ПО=13 | (u→×v→)⋅w→| |
Внимание! Эта формула применима только тогда, когда основание пирамиды квадратное. Когда основание представляет собой треугольник, фигура называется тетраэдром, который имеет свою формулу.
Пример 2
Найдите объем пирамиды, натянутой на (1,3,−2), (−3,2,4) и (1,1,1).
Вы начинаете с нахождения векторного произведения двух векторов, а затем находите скалярное произведение этого векторного произведения и неиспользованного вектора. Затем вы умножаете ответ на 13. Перекрестное произведение двух первых векторов равно (16,2,11). Скалярный продукт этого и (1,1,1) равен 29, который вы умножаете на 13:
| 13⋅29=293 |
Объем равен 293. Если бы вы получили отрицательный ответ, вам пришлось бы взять его абсолютное значение в качестве объема.
Формула
Объем тетраэдра
| VT=16 | (u→×v→)⋅w→| |
Пример 3
Найдите объем тетраэдра, натянутого на (1,3,−2), (−3,2,4) и (1,1,1).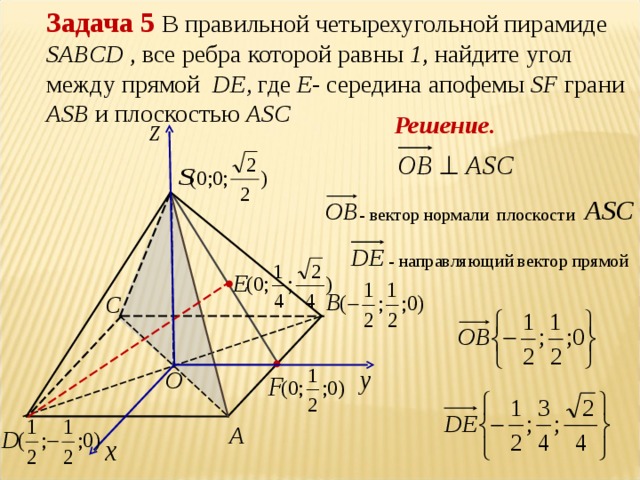

 16 a
Рис. 16 b
16 a
Рис. 16 b Поскольку площадь треугольника , где — площадь параллелограмма, построенного на векторах
и , а высоты тетраэдра и параллелепипеда, построенных на
векторах совпадают, то
Поскольку площадь треугольника , где — площадь параллелограмма, построенного на векторах
и , а высоты тетраэдра и параллелепипеда, построенных на
векторах совпадают, то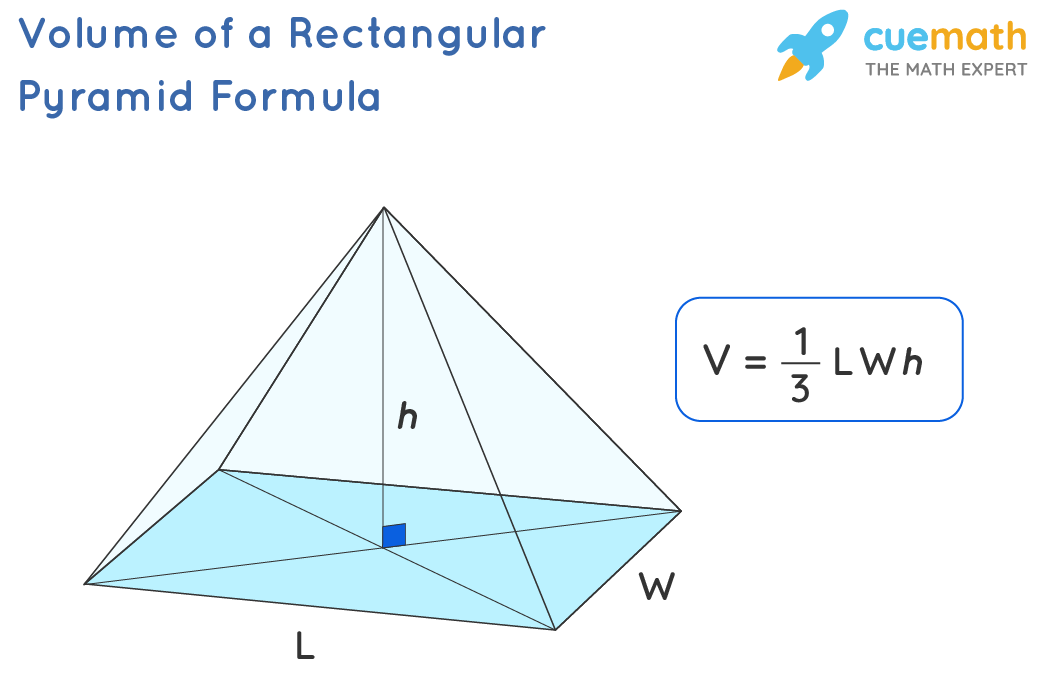 Вычислите ее объем.
Вычислите ее объем.