Объем трапеции формула: Расчет объема трапеции онлайн калькулятор

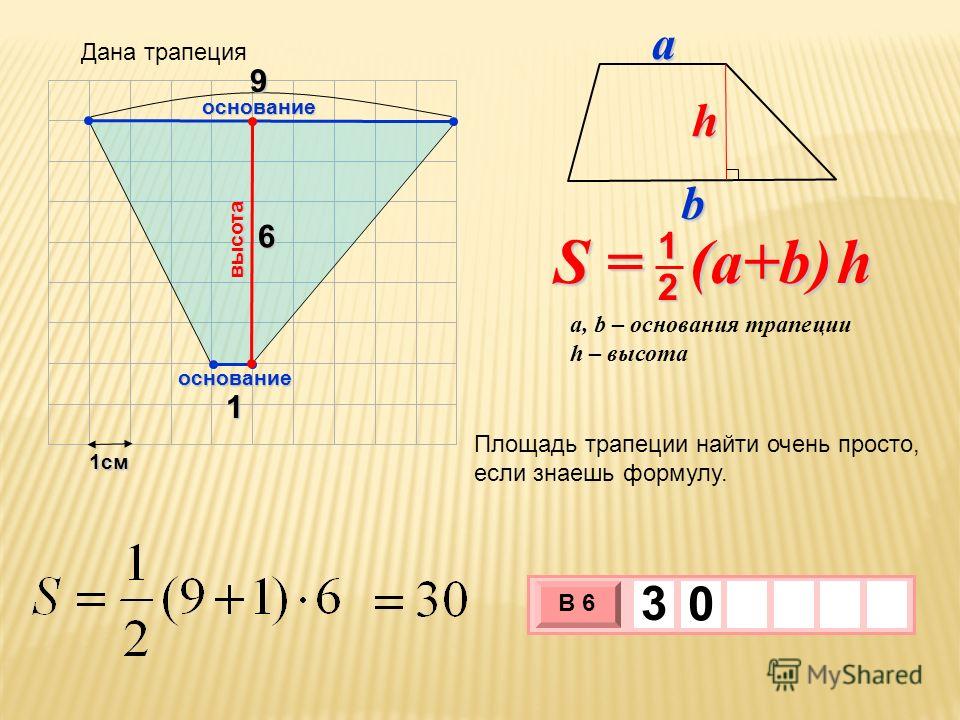
Все основные формулы для объема тела

 

1. Формулы длины диагоналей прямоугольной трапеции по теореме Пифагора

 

a — нижнее основание

b — верхнее основание

c=h — боковая сторона, равная высоте трапеции

d₁ , d₂ — диагонали трапеции

 

Формулы диагоналей трапеции:

Остальные формулы диагоналей как для произвольной трапеции

---

---

 

Формулы площади произвольной трапеции

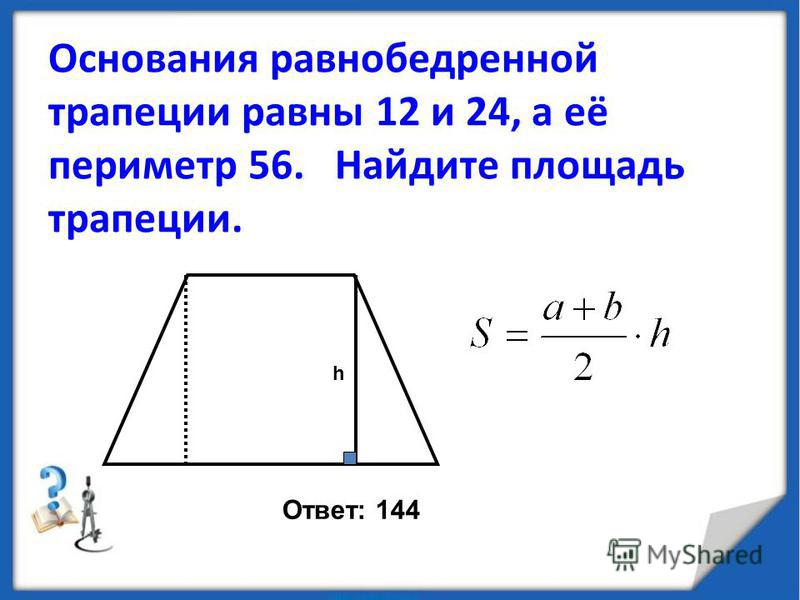
Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формулы длины диагонали равнобедренной трапеции через ее стороны

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

d — диагональ трапеции

 

Формула диагонали трапеции (d ):

 

 

2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α, β — углы трапеции

d — диагональ трапеции

 

Формулы диагонали трапеции (d ):

 

---

 

3. Формула длины диагонали равнобедренной трапеции

 

a — нижнее основание

b — верхнее основание

α, β — углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d — диагональ трапеции

 

Формулы диагонали трапеции (d ):

Справедливо для данного случая :

---

 

4.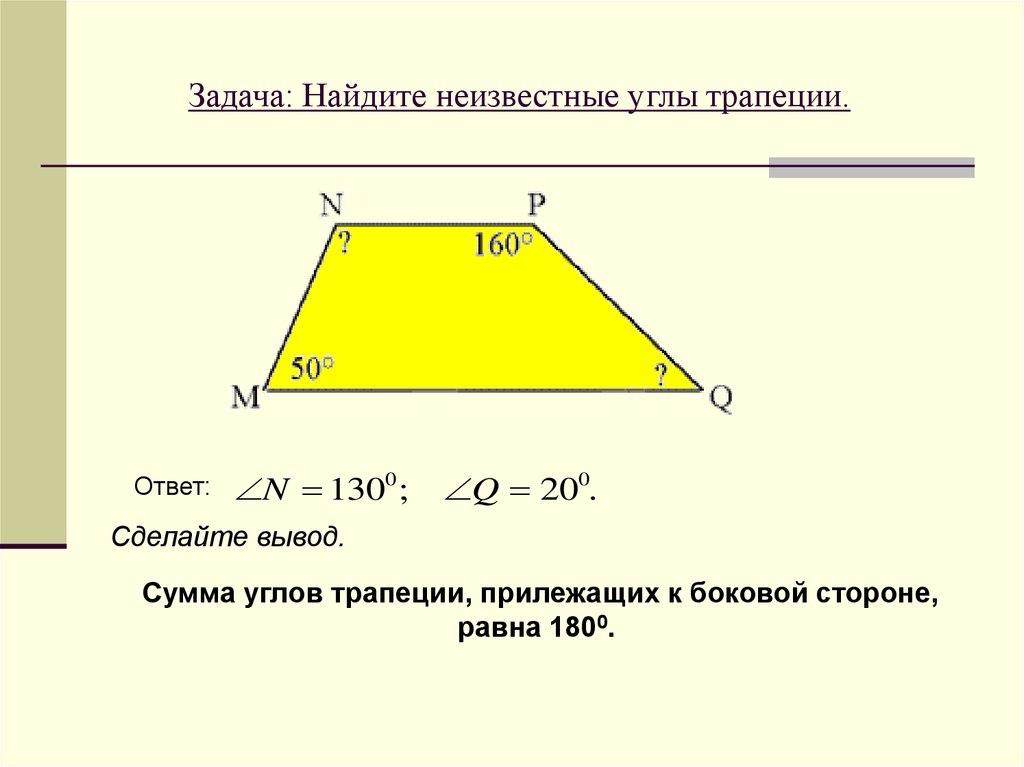 Формулы длины диагонали трапеции через высоту и стороны

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

h — высота трапеции

α — угол при нижнем основании

d — диагональ трапеции

 

Формулы диагонали трапеции (d ):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

Найти длину диагонали трапеции

зная все четыре стороны

или две стороны и угол

или высоту, сторону и угол

или площадь, другую диагональ и угол

и еще много других формул.

 

1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны

 

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

d₁ , d₂ — диагонали трапеции

 

Формулы диагоналей трапеции по теореме косинусов:

 

 

Формулы диагоналей трапеции через четыре стороны:

 

 

2. Формула длины диагоналей трапеции через высоту

 

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

d₁ , d₂ — диагонали трапеции

 

Формулы диагоналей трапеции через высоту:

 

---

 

3. Формула длины диагонали трапеции через другую диагональ

 

a — нижнее основание

b — верхнее основание

α, β

— углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d₁ , d₂ — диагонали трапеции

 

Формулы диагоналей трапеции :

Справедливо для данного случая :

---

 

4.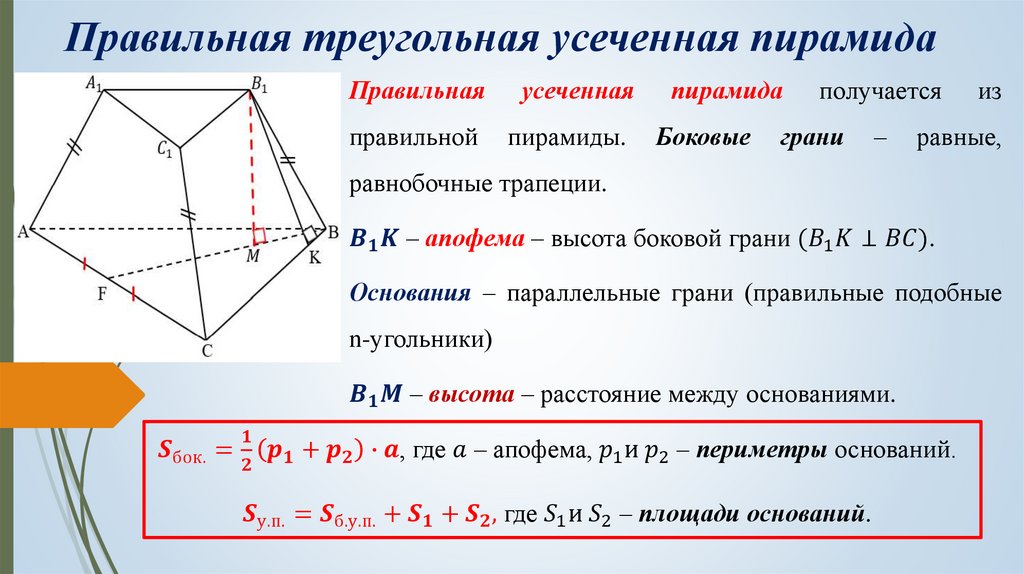 Формулы длины диагонали трапеции через сумму квадратов диагоналей

 

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

d₁ , d₂ — диагонали трапеции

 

Формула суммы квадратов диагоналей :

 

Формулы диагоналей трапеции :

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула средней линии трапеции через основания (для всех видов трапеции)

 

a — нижнее основание

b — верхнее основание

m — средняя линия

 

 

Формула средней линии, (m ):

 

 

 

2.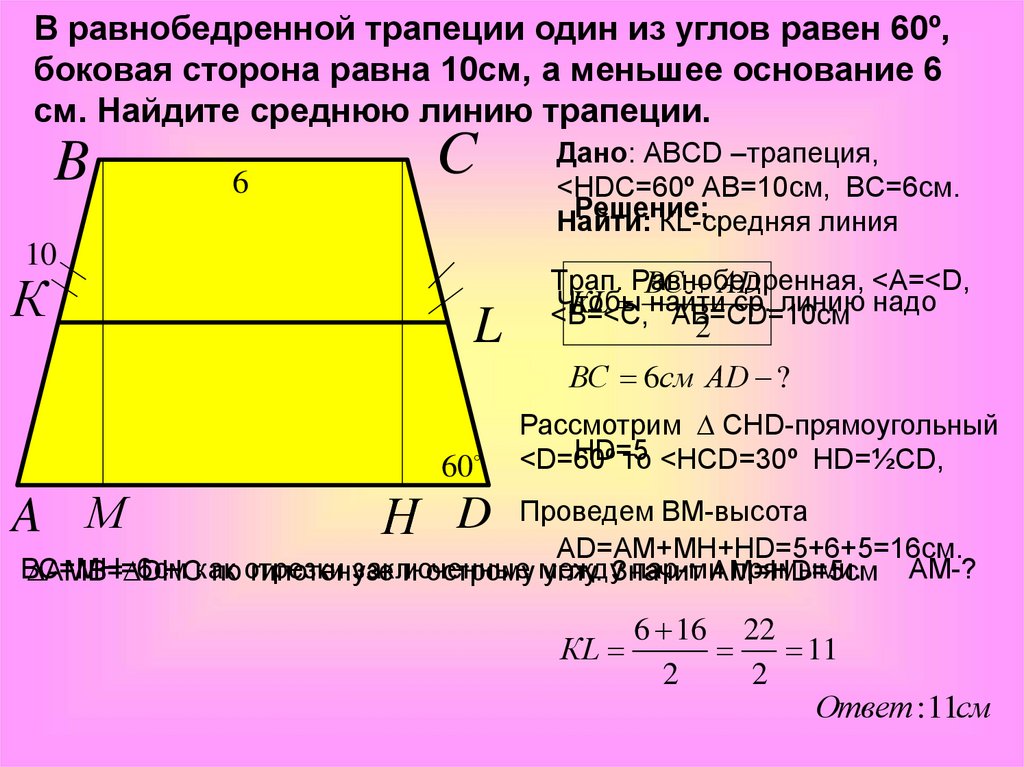 Формулы средней линии через основания, высоту и угол при нижнем основании

 

a, b — основания трапеции

c — боковая сторона под прямым углом к основаниям

d — боковая сторона

α — угол при основании

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m ):

---

 

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

 

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m ):

---

 

4.

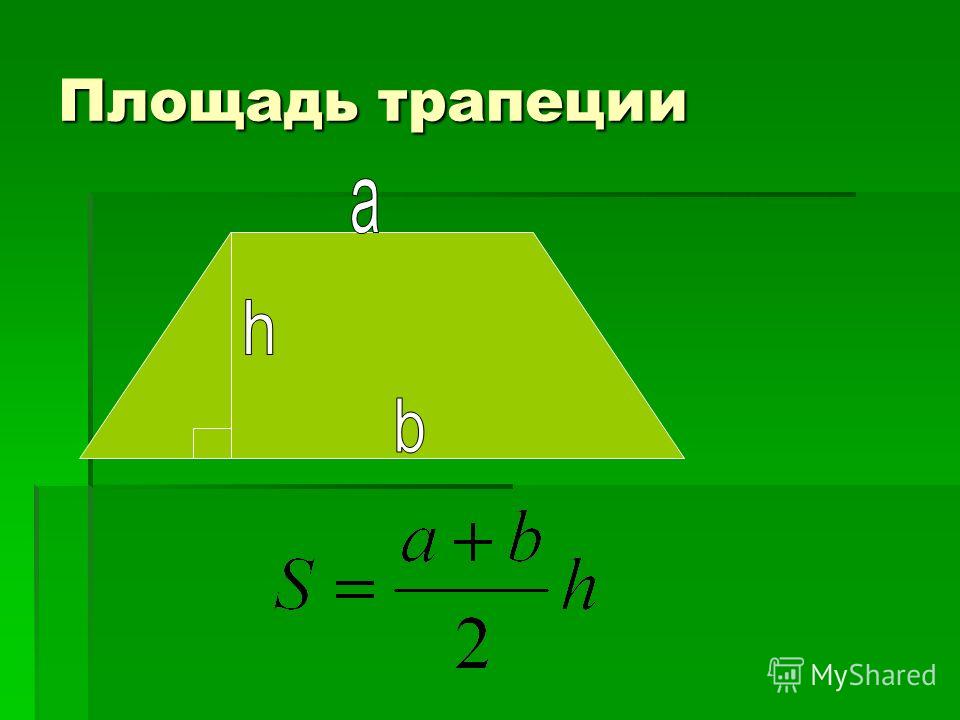Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)

 

S — площадь трапеции

h — высота трапеции

m — средняя линия

 

 

Формула средней линии трапеции, (m ):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании

a — нижнее основание

b — верхнее основание

d — боковая сторона

α — угол при нижнем основании

h — высота трапеции

c — боковая сторона под прямым углом к основаниям

 

 

Формулы длины боковой стороны (с) :

 

 

2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали  и угол между ними

 

a — нижнее основание

b — верхнее основание

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

c — боковая сторона под прямым углом к основаниям

 

 

Формулы длины боковой стороны (с):

---

 

3. Формулы боковой стороны (с) прямоугольной трапеции через площадь

 

a — нижнее основание

b — верхнее основание

m — средняя линия трапеции

c — боковая сторона под прямым углом к основаниям

 

 

Формула длины боковой стороны (с) :

---

 

4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании

a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

α — угол при нижнем основании

h — высота трапеции

d — боковая сторона

 

 

Формулы длины боковой стороны (d) :

---

 

5. Формула боковой стороны (d) прямоугольной трапеции через площадь

 

a — нижнее основание

b — верхнее основание

m — средняя линия трапеции

α — угол при нижнем основании

d — боковая сторона

 

 

Формула длины боковой стороны (d) :

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула длины оснований прямоугольной трапеции через среднюю линию

 

a — нижнее основание

b — верхнее основание

m — средняя линия

 

 

Формулы длины оснований :

 

 

2. Формулы длины оснований через боковые стороны и угол при нижнем основании

 

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α — угол при нижнем основании

 

 

Формулы длины оснований :

---

 

3. Формулы длины оснований трапеции через диагонали  и угол между ними

 

a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

 

 

Формулы длины оснований :

---

 

4. Формулы длины оснований трапеции через площадь

 

a — нижнее основание

b — верхнее основание

c — боковая сторона под прямым углом к основаниям

h — высота трапеции

 

 

Формулы длины оснований :

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула средней линии равнобедренной трапеции через основания

 

a — нижнее основание

b — верхнее основание

m — средняя линия

 

 

Формула средней линии, (m ):

 

 

2. Формулы средней линии через основание, высоту и углы при нижнем основании

 

a — нижнее основание

b — верхнее основание

c — боковая сторона

α — угол при нижнем осровании

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m ):

---

 

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

 

d — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

 

Формула средней линии трапеции, (m ):

---

 

4. Формула средней линии трапеции через площадь и высоту

 

S — площадь трапеции

h — высота трапеции

α — угол при нижнем осровании

m — средняя линия

 

Формула средней линии трапеции, (m ):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула высоты равнобедренной трапеции через стороны и углы при основании

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α — угол при нижнем основании

h — высота трапеции

 

Формулы длины высоты, (h ):

 

 

2. Формула высоты равнобедренной трапеции через диагонали и углы между ними

 

_d — диагонали трапеции

α , β — углы между диагоналями

a , b — основания

h — высота трапеции

m — средняя линия

 

Формулы длины высоты, (h ):

---

 

3. Формула высоты равнобедренной трапеции через площадь

 

S — площадь трапеции

a , b — основания

h — высота трапеции

m — средняя линия

 

Формулы длины высоты, (h ):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула длины основания равнобедренной трапеции через среднюю линию

 

a — нижнее основание

b — верхнее основание

m — средняя линия

 

 

Формулы длины основания:

 

 

2. Формулы длины сторон через высоту и угол при нижнем основании

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α — угол при основании трапеции

h — высота трапеции

 

Формулы всех четырех сторон трапеции:

 

---

 

3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

d — диагонали

α , β — углы между диагоналями

h — высота трапеции

 

Формулы длины сторон трапеции:

справедливо для данной ситуации:

---

 

4. Формулы длины сторон равнобедренной трапеции через площадь

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α , β — углы при основаниях

m — средняя линия

h — средняя линия

 

Формулы длины сторон равнобедренной трапеции через площадь:

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

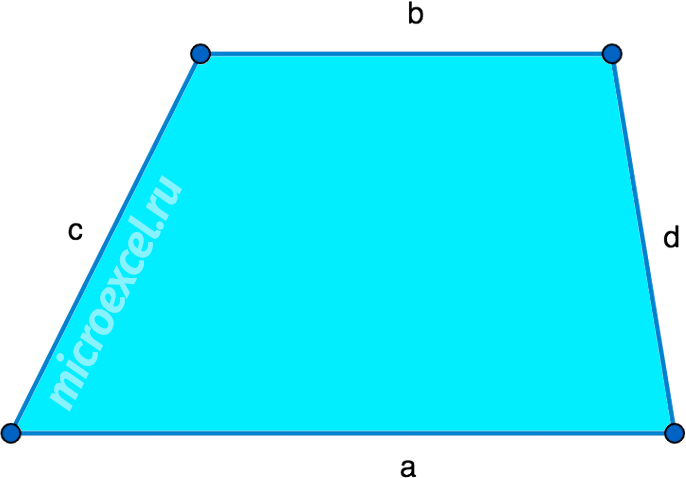
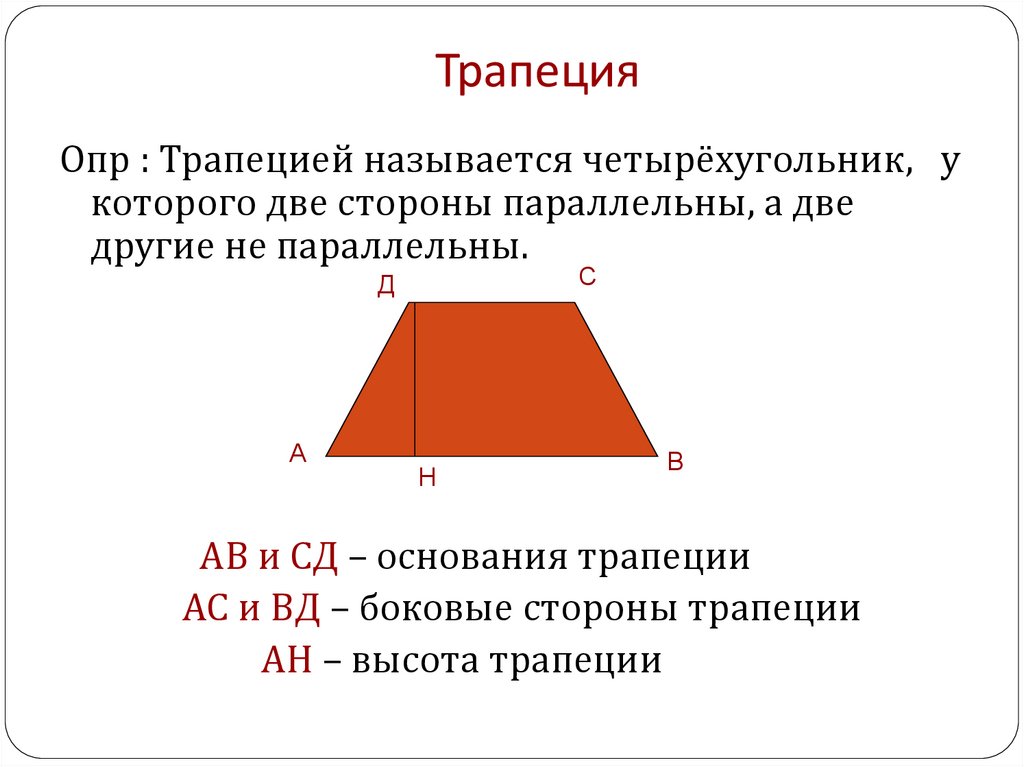
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет.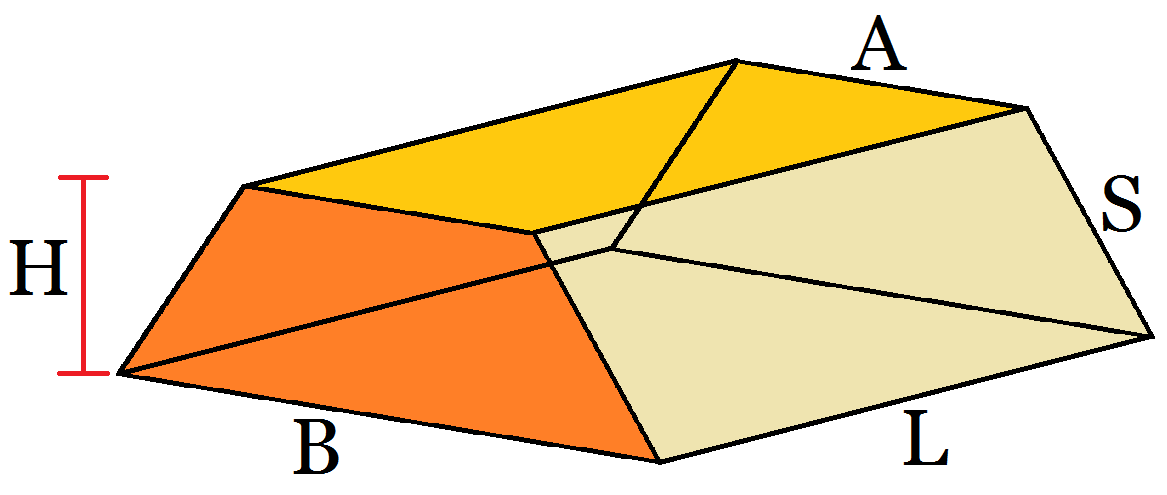 Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.

---

1. Формула высоты трапеции через стороны и углы при основании

 

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

 

Формулы длины высоты, (h ):

 

 

2. Формула высоты трапеции через диагонали и углы между ними

 

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

a , b — основания

h — высота трапеции

m — средняя линия

 

Формулы длины высоты, (h ):

---

 

3. Формула высоты трапеции через площадь

 

S — площадь трапеции

a , b — основания

h — высота трапеции

m — средняя линия

 

Формулы длины высоты, (h ):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Рейтинг:  5 / 5

Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.

---

1. Формула средней линии трапеции через основания

b — верхнее основание

a — нижнее основание

m— средняя линия

 

Формула средней линии, (m ):

 

 

2. Формулы средней линии через основание, высоту и углы при нижнем основании

b — верхнее основание

a — нижнее основание

α, β — углы трапеции

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m):

---

 

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

α, β — углы между диагоналями

d₁ , d₂ — диагонали трапеции

h — высота трапеции

m — средняя линия

 

Формулы средней линии трапеции, (m ):

---

 

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции

h — высота трапеции

m — средняя линия

 

Формула средней линии трапеции, (m):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

---

1. Формула длины основания трапеции через среднюю линию

 

a — нижнее основание

b — верхнее основание

m — средняя линия

 

Формулы длины оснований :

 

 

2. Формулы длины сторон через высоту и углы при нижнем основании

 

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

 

Формулы всех четырех сторон трапеции:

---

 

3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

 

a — нижнее основание

b — верхнее основание

d₁ , d₂ — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

 

Формулы длины сторон трапеции:

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Формула объема трапеции прямоугольной усеченной пирамиды. Формулы объема пирамиды полной и усеченной. Объем пирамиды Хеопса

Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.

Пирамида как объемная фигура

Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.

Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.

Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:

2*n = (n+1) + (n+1) — 2.

Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.

Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды.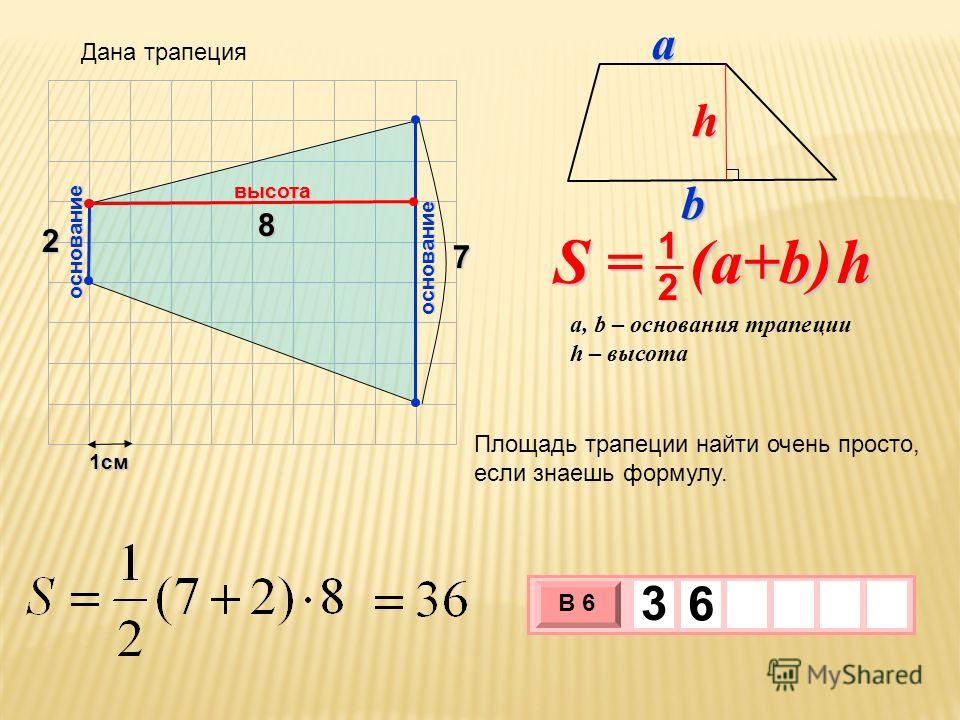 Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.

Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.

Формула объема пирамиды

Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.

Площадь каждого такого слоя можно вычислить по формуле:

A(z) = A 0 *(h-z) 2 /h 2 .

Здесь A 0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0 .

Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:

V = ∫ h 0 (A(z)*dz).

Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:

V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.

Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.

Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.

и ее объем

Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:

A 0 = n/4*L 2 *ctg(pi/n).

Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.

Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:

V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).

Например, для треугольной пирамиды эта формула приводит к следующему выражению:

V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.

Для правильной четырехугольной пирамиды формула объема приобретает вид:

V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.

Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.

Пирамида усеченная

Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.

Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.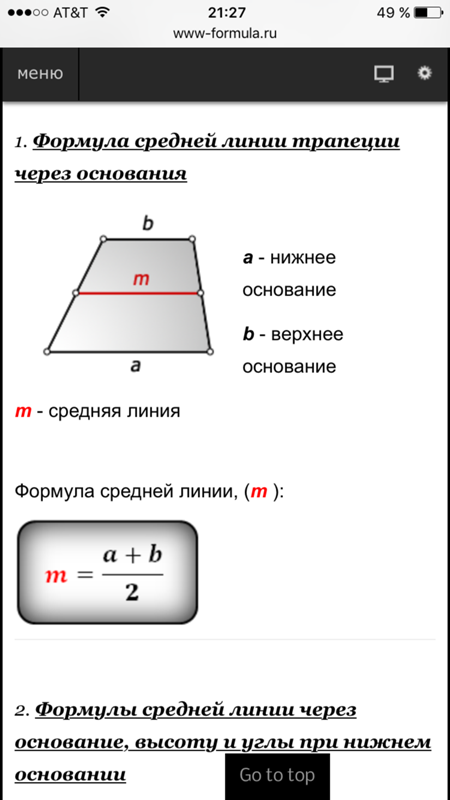

Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:

V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).

Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.

Объем пирамиды Хеопса

Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.

В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.

Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:

Подставляем цифры, получаем:

V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .

Объем пирамиды Хеопса равен практически 2,6 млн м 3 . Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!

• 09.10.2014

  Показанный на рисунке предварительный усилитель предназначен для использования с 4-я видами источников звука, например микрофон, CD-проигрыватель, магнитола и др. При этом у предварительно усилителя один вход, который может менять чувствительность от 50 мВ до 500мВ. выходное напряжение усилителя 1000мВ. Подключая разные источники сигнала при переключении переключателя SA1, мы всегда получим …

• 20.09.2014

  БП рассчитан на нагрузку мощностью 15…20 Вт. Источник выполнен по схеме однотактного импульсного высокочастотного преобразователя. На транзисторе собран автогенератор, работающий на частоте 20…40кГц. Частота настраивается емкостью С5. Элементы VD5,VD6 и С6 образуют цепь запуска автогенератора. Во вторичной цепи после мостового выпрямителя стоит обычный линейный стабилизатор на микросхеме, что позволяет иметь …

• 28.

  09.2014

  На рисунке представлен генератор на микросхеме К174ХА11, частота которого управляется напряжением. При изменении емкости С1 от 560 до 4700пФ можно получить широкий диапазон частот, при этом настройка частоты производится изменением сопротивления R4. Так например автор выяснил что, при С1=560пФ частоту генератора можно изменять при помощи R4 от 600Гц до 200кГц, …

• 03.10.2014

  Блок предназначен для питания мощного УНЧ, он рассчитан на выходное напряжение ±27В и так нагрузки до 3А на каждое плече. БП двух полярный, выполнен на комплектарных составных транзисторах КТ825-КТ827. Оба плеча стабилизатора выполнены по одной схеме, но в другом плече (он не показан) изменена полярность конденсаторов и использованы транзисторы другой …

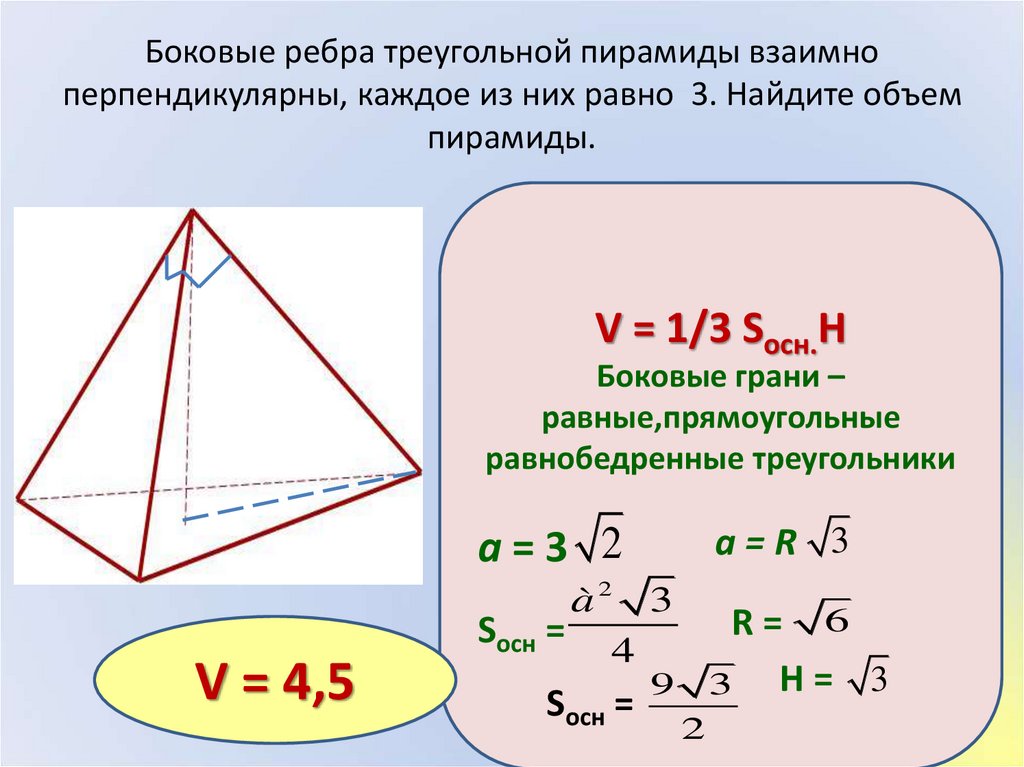
Пирамидой называется многогранник, одна из граней которого многоугольник (основание ), а все остальные грани – треугольники с общей вершиной (боковые грани ) (рис. 15). Пирамида называется правильной , если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .

Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой . Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.

Теоремы

1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.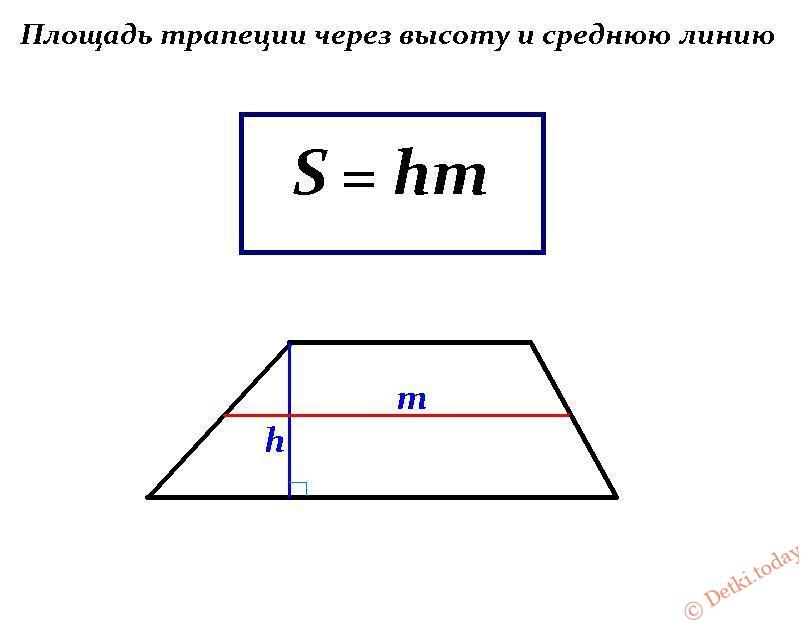

2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.

3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.

Для вычисления объема произвольной пирамиды верна формула:

где V – объем;

S осн – площадь основания;

H – высота пирамиды.

Для правильной пирамиды верны формулы:

где p – периметр основания;

h а – апофема;

H – высота;

S полн

S бок

S осн – площадь основания;

V – объем правильной пирамиды.

Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.

Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Для усеченной пирамиды справедливы формулы:

(4)

где S 1 , S 2 – площади верхнего и нижнего оснований;

S полн – площадь полной поверхности;

S бок – площадь боковой поверхности;

H – высота;

V – объем усеченной пирамиды.

Для правильной усеченной пирамиды верна формула:

где p 1 , p 2 – периметры оснований;

h а – апофема правильной усеченной пирамиды.

Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.

Решение. Сделаем рисунок (рис. 18).

Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС ). Угол наклона бокового ребра (например SB ) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD . Чтобы найти тангенс необходимо знать катеты SO и OB . Пусть длина отрезка BD равна 3а . Точкой О отрезок BD делится на части: и Из находим SO : Из находим:

Ответ:

Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.

Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:

Ответ: 112 см 3 .

Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.

Решение. Сделаем рисунок (рис. 19).

Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС .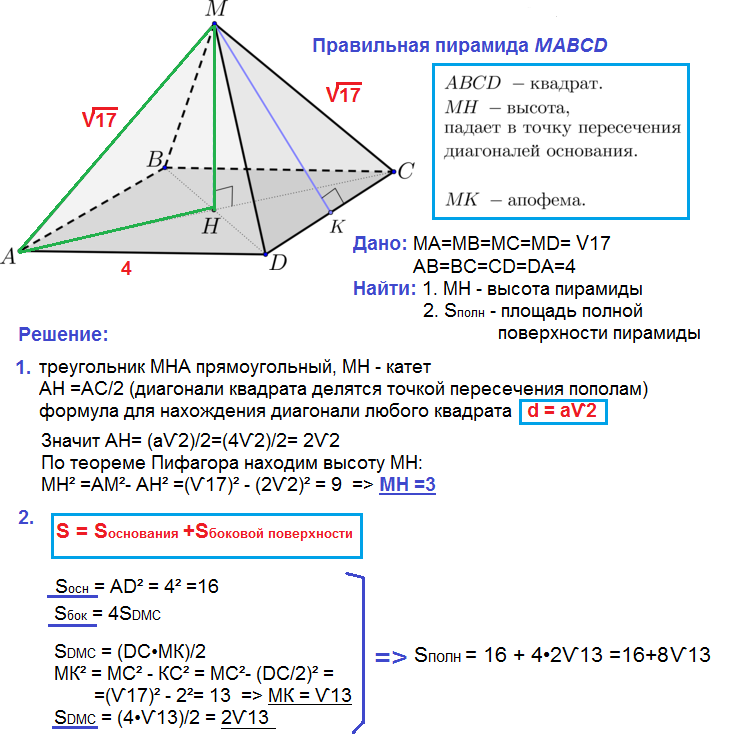 А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:

MK = DE .

По теореме Пифагора из

Площадь боковой грани:

Ответ:

Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b ). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j . Найти площадь полной поверхности пирамиды.

Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .

Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности.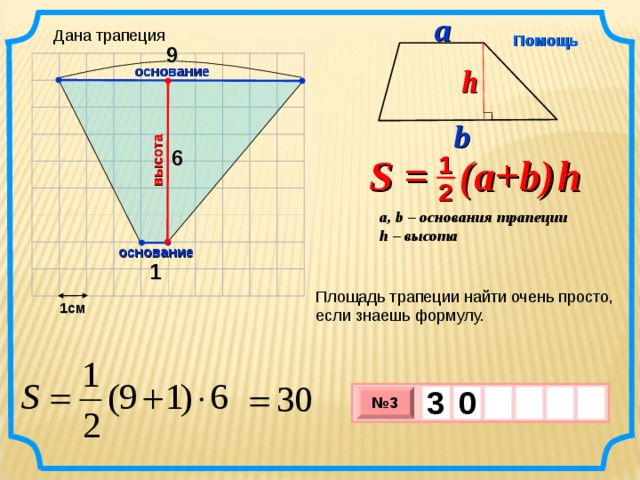 Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:

Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD . Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.

Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем

Сметанный крем с желатином для торта – рецепт

Окунь морской красный рецепты приготовления

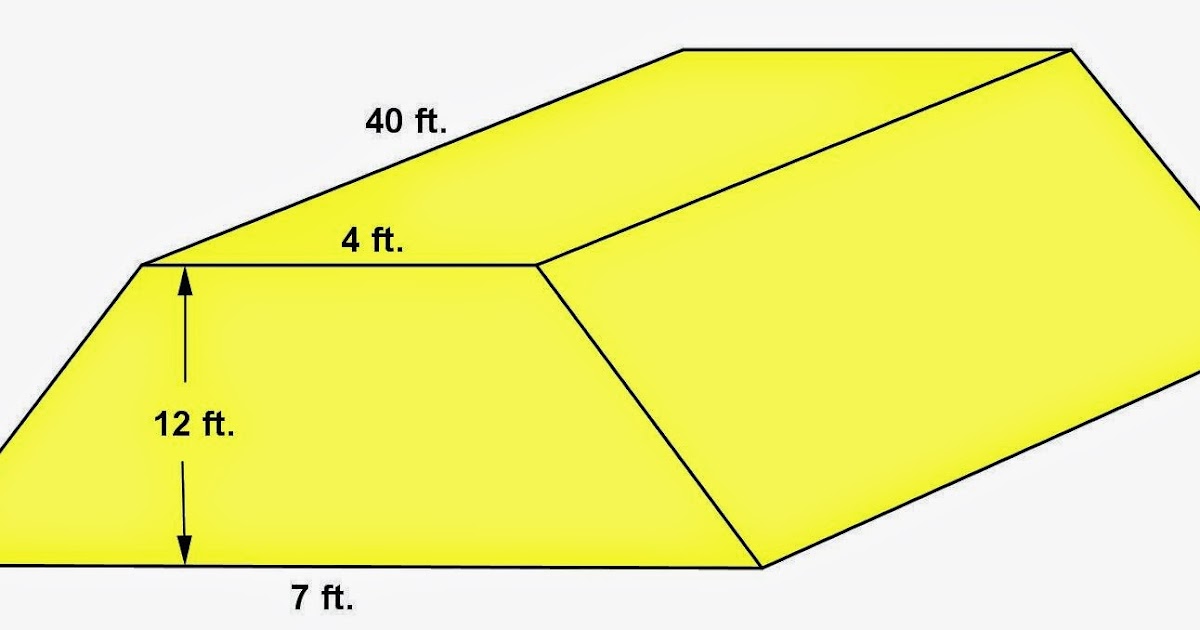
Объем трапециевидной призмы

LearnPracticeDownload

Объем трапециевидной призмы — это емкость призмы. Его также можно определить как пространство внутри трапециевидной призмы. Призма имеет конгруэнтные многоугольники на верхней и нижней гранях, а основания одинаковы. Боковые грани призмы представляют собой параллелограммы, которые называются боковыми гранями.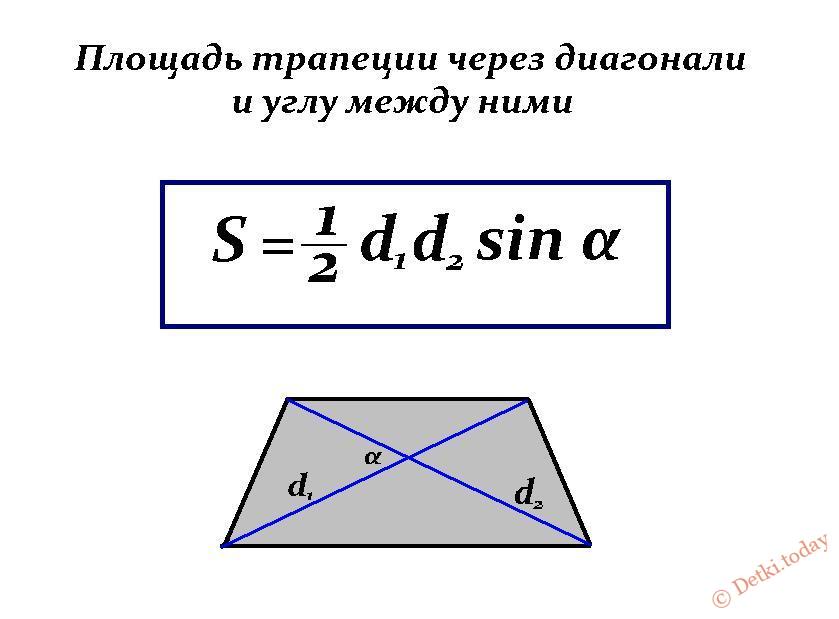 Призму можно назвать по форме двух одинаковых граней на ее конце. Трапециевидная призма представляет собой трехмерное тело, имеющее два основания трапеции/трапеции внизу и вверху. Форма боковых граней/боковых граней трапециевидной призмы – параллелограмм.

1.	Каков объем трапециевидной призмы?
2.	Объем трапециевидной призмы Формула
3.	Как рассчитать объем трапециевидной призмы?
4.	Часто задаваемые вопросы об объеме трапециевидной призмы

Каков объем трапециевидной призмы?

Объем трапециевидной призмы – это пространство внутри нее. Трапециевидная призма представляет собой трехмерную фигуру с двумя трапециевидными основаниями и четырьмя гранями в виде параллелограмма. Призма представляет собой многогранник с равными многоугольниками на верхней и нижней гранях и имеет одинаковые основания.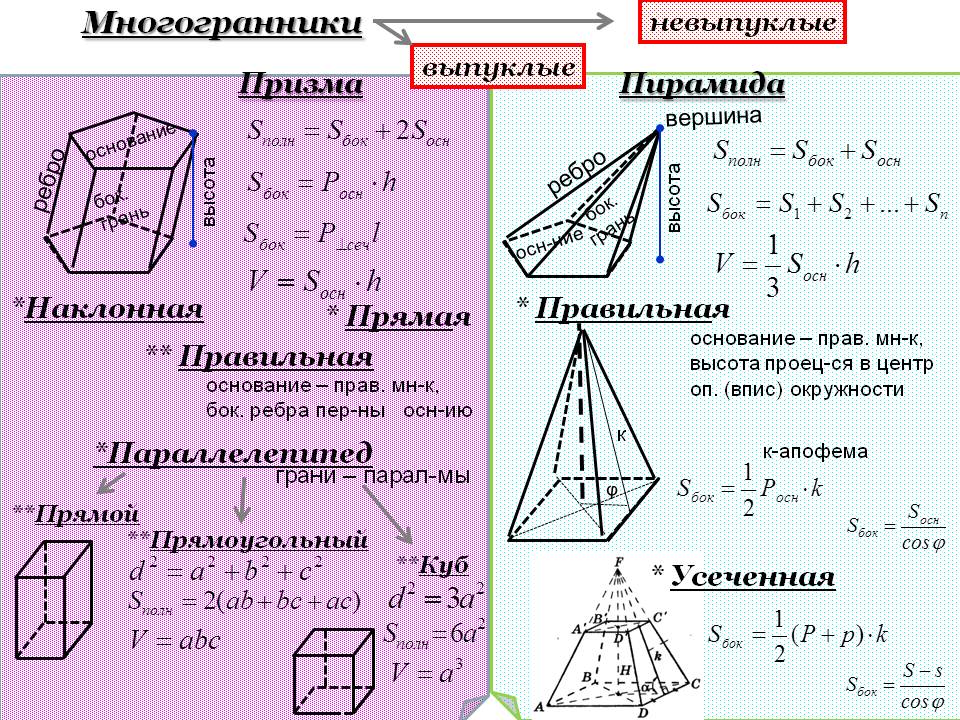 Трапециевидные призмы бывают двух видов: косые и прямые. У косой трапециевидной призмы боковые грани — параллелограммы, а у правильной трапециевидной призмы — прямоугольники. В общем случае трапециевидная призма означает правильную трапециевидную призму. Следовательно, боковые грани прямоугольники. Таким образом, у трапециевидной призмы всего 6 граней, 12 ребер и 8 вершин. Два основания имеют форму трапеции или трапеции, которые конгруэнтны друг другу. Он имеет

• 6 сторон
• 12 кромок
• 8 вершин
• 4 стороны: прямоугольник
• Трапеция/трапеция в качестве основания снизу и сверху

Объем трапециевидной призмы Формула

Объем трапециевидной призмы — вместимость призмы (или) объем трапециевидной призмы — пространство внутри нее. Измеряется в кубических единицах, таких как мм ³ , см ³ , в ³ и т.д. Мы увидим формулы для расчета объема трапециевидной призмы. Объем призмы можно получить, умножив площадь ее основания на общую высоту призмы.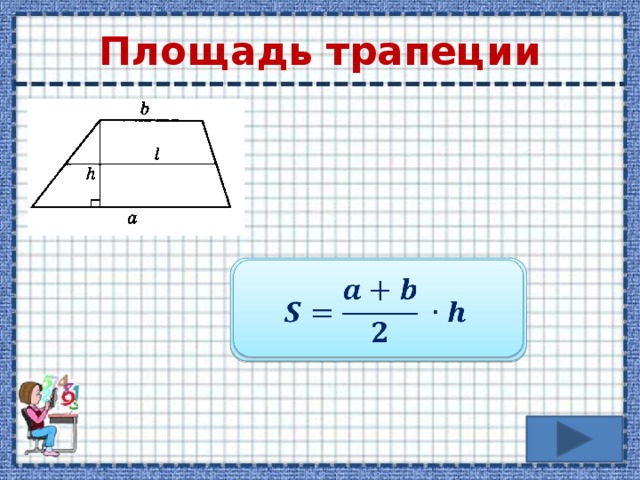 т. е. объем призмы = площадь основания × высота призмы. Мы также будем использовать эту формулу для расчета объема трапециевидной призмы. Рассмотрим трапециевидную призму, две параллельные стороны основания которой равны \(b_1\) и \(b_2\), высота равна ‘h’, а длина призмы равна L. Мы знаем, что основание трапециевидная призма — это трапеция/трапеция. Таким образом,

Площадь основания (площадь трапеции) = \(\dfrac{1}{2}{(b_{1} + b_{2})× h }\)

Теперь, используя объем призмы формула (как указано выше),

Объем трапециевидной призмы = площадь основания × длина = \(\dfrac{1}{2}{(b_{1} + b_{2})×h}×L\)

Как рассчитать объем трапециевидной призмы?

Ниже приведены шаги для расчета объема трапециевидной призмы. Убедитесь, что все измерения выполнены в одних и тех же единицах. Обратитесь к следующему примеру.

• Шаг 1: Определите, что параллельные стороны основания (трапеции) равны \(b_1\) и \(b_2\), а перпендикулярное расстояние между ними равно \(h\), и найдите площадь трапеции, используя формула:
  Площадь трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h}\)
• Шаг 2: Определите его высоту/длину призмы (расстояние по вертикали между двумя основаниями).
• Шаг 3: Умножьте площадь основания, полученную на шаге 1, и высоту, полученную на шаге 2, чтобы найти объем.

 

Примеры объема трапециевидной призмы

1. Пример 1: Найдите объем трапециевидной призмы заданных размеров.

   Решение:

   На рисунке выше, Учитывая, что

   Основание 1 (\(b_1\)) = 6 дюймов, основание (\(b_2\)) = 20 дюймов

   Высота основания трапеции = 12 в

   Длина трапеции = 17 в

   Площадь трапеции/трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h}\)

   ⇒ A = \(\dfrac{1}{2}\) (6 + 20) × 12
   ⇒ А = 13 × 12
   ⇒ a = 156 в ²

   Как мы знаем, объем трапеции. трапецеидальная призма равна 2652 в ³ .

2. Пример 2: Рассчитайте объем трапециевидной призмы, учитывая, что высота основания трапеции 5 см, а длины ее параллельных сторон 14 см и 10 см, длина призмы 6 см.

   Решение:

   На приведенном выше рисунке Учитывая, что

   Основание 1 (\(b_1\)) = 14 см, основание (\(b_2\)) = 10 см

   Высота основания трапеции (h ) = 5 см

   Общая длина трапеции = 6 см

   Площадь трапеции/трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h }\)

   ⇒ А = (1/2) (14 + 10 ) × 5
   ⇒ А = 12 × 5
   ⇒ A = 60 см ²

   Как мы знаем, объем трапециевидной призмы = площадь × длина трапеции

   объем = 60 ^{× 6 = 360 см 3}

   Ответ : Объем трапециевидной призмы равен 360 см ³ .

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Запись на бесплатный пробный урок

Практические вопросы по объему трапециевидной призмы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об объеме трапециевидной призмы

Имеет ли трапециевидная призма объем?

Призма представляет собой трехмерное твердое тело. Трехмерное твердое тело имеет внутри себя пространство. Объем объясняется как пространство внутри объекта. Таким образом, трапециевидная призма имеет объем, поскольку представляет собой трехмерную форму и измеряется в кубических единицах.

Что вы подразумеваете под объемом трапециевидной призмы?

Объем трапециевидной призмы – это вместимость призмы. Формула объема трапециевидной призмы представляет собой площадь основания × высоту призмы в кубических единицах.

Какая формула позволяет найти объем трапециевидной призмы?

Объем трапециевидной призмы равен произведению площади основания на высоту призмы в кубических единицах. Формула объема трапециевидной призмы – это площадь основания × высота призмы.

Как рассчитать объем трапециевидной призмы?

Объем трапециевидной призмы можно рассчитать, умножив площадь ее трапециевидных граней на ее общую длину.

Как найти объем трапециевидной призмы, зная высоту?

Высота призмы — это общее расстояние между двумя конгруэнтными гранями призмы. Зная высоту призмы, ее можно умножить на площадь, чтобы найти объем трапециевидной призмы.

Если единицы измерения трапециевидной призмы различны, то как найти объем трапециевидной призмы?

Если единицы заданных размеров трапециевидной призмы различны, то сначала нужно заменить единицы измерения любых двух измерений на единицу третьего измерения. После этого мы можем найти площадь и объем трапециевидной призмы.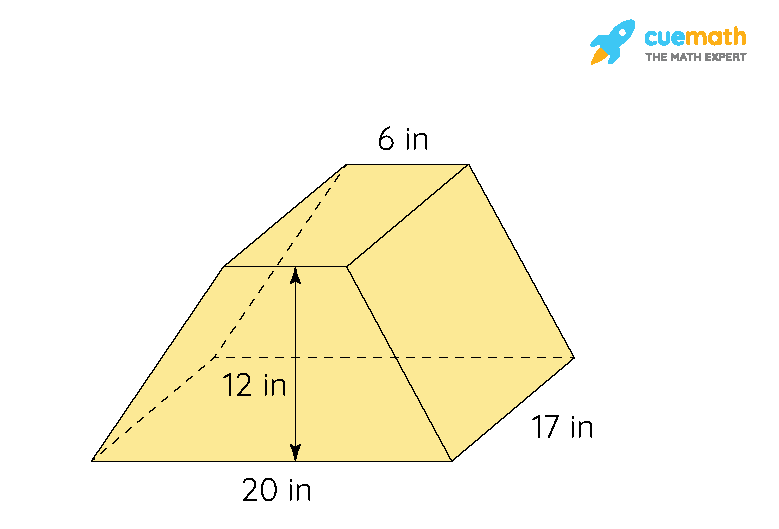

Скачать БЕСПЛАТНЫЕ учебные материалы

Объем призмы. Рабочий лист

Рабочие листы по математике и
наглядный учебный план

Как найти объем \\[3D\\] трапеции?

Совет : Для определения объема трапеции. Сначала нам нужно нарисовать схему трапеции с площадью и длиной. Формулу можно использовать для вычисления площади трапеции, \[A = \dfrac{1}{2}h(a + b)\]. Где h — высота, а \[a\] и \[b \] — длины параллельных сторон. Объем \[3D\] трапеции, рассчитанный по формуле с четырьмя переменными, \[\;V = {\text{}}\dfrac{1}{2}L(a + b)h\] . Где длина равна \[L\], а площадь обозначается как \[A\] .

Полное пошаговое решение:
В этой задаче
Нам нужно найти объем \[3D\] трапеции
Нам нужно найти площадь основания трапеции, чтобы вычислить объем.
Нам нужно найти площадь трапеции, которую можно просто определить как среднюю длину сторон, умноженную на высоту, используя переменные, чтобы нарисовать диаграмму для представления площади трапеции,

Это формула площади трапеции, \[A = \dfrac{1}{2}h(a + b)\]
Пусть \[A\] будет площадью трапеции.
Пусть \[h\] будет высотой трапеции.
Пусть \[a\] — ширина верха, а \[b\] — ширина верха.
Объем не существует в двумерной статистике. Итак, вы можете построить трапециевидную трапецию, которая представляет собой трехмерную фигуру с трапециевидным основанием. Чтобы определить объем чего-либо, нужно сначала определить площадь.
 Чтобы перевести эту концепцию в трехмерную диаграмму, просто умножьте на длину трапеции:
Если длина трапеции равна \[L\] , ширина основания трапеции \[b\] , ширина вершины трапеции \[a\] и высота трапеции \[h\] . Мы можем нарисовать трехмерную фигуру следующим образом.

Объем \[3D\] трапеции вычисляется по формуле с четырьмя переменными:
 \[\;V = \dfrac{1}{2}L \times h(a + b)\] .
Где,
  \[V\] Объем трапеции
 \[h\] — высота трапеции.
 \[a\] Длина верха
 \[b\] Длина низа
 \[L\] — высота трапеции.
Наконец, мы используем эти методы, чтобы найти объем трапеции для любых заданных значений.