Найти область определения функции y=1/cosx-1 — Знания.site
Последние вопросы
Математика
8 минут назад
Помогите с решением данной задачи и вопросаМатематика
8 минут назад
Утро доброе всем) за прошлый урок, кто не выполнил работу — выполняем, присылаем.
По уроку сегодня:
В тетради: число, тема урока «Мюзикл и рок-опера», просмотреть видео по ссылке, заполнить в тетради таблицу на 2 колоночки «Особенности жанров», первая колонка МЮЗИКЛ, вторая РОК-ОПЕРА.
Математика
23 минут назад
В2. Дан треугольник АВС, точка М- середина стороны АВ, точка N середина стороны BC, SAMNC = 60.
Математика
33 минут назад
помогите пж, я не понимаюМатематика
33 минут назад
В1. В прямоугольнике ABCD CD = 9, K — середина ВС, A=10. Найдите AD.Математика
1 час назад
Скільки цілих чисел між числами 34 і 36?Чому дорівнює їх сума?Терміновооо!Математика
1 час назад
помогите пожалуйста срочно!-
Математика
1 час назад
6 солдатів можуть вирити окоп за 21 годину. Скільки знадобиться солдатів щоб виконати цю роботу за 12 год годину? Математика
1 час назад
Как это решать я в ****Математика
1 час назад
1). (-4х-3)-(3х+11)=2). (5у-7)-(4-2у)=БУДЬЛАСКА ДОПОМОЖІТЬ!!!Математика
1 час назад
Математика
1 час назад
СНОВА хелп с матешей.Математика
1 час назад
постав замість * знак >,<,= щоб утворилася правильна рівність ,або нерівність 8+(-7) * -9+(-3)Математика
1 час назад
помогите пожалуйста, нужно с решением- Математика
1 час назад
Дано числа: 3; 0,5; -4; 0,8. Яке із цих чисел є цілим, але не є натуральним?
Скільки знадобиться солдатів щоб виконати цю роботу за 12 год годину?
Все предметы
English
United States
Polski
Polska
Bahasa Indonesia
Indonesia
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Português
Brasil
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Свойства и график функции у= cos x
Функция
y = cos x
её свойства и график
Функция y = cos x определена на всей числовой прямой, и множеством её значений является отрезок [−1;1].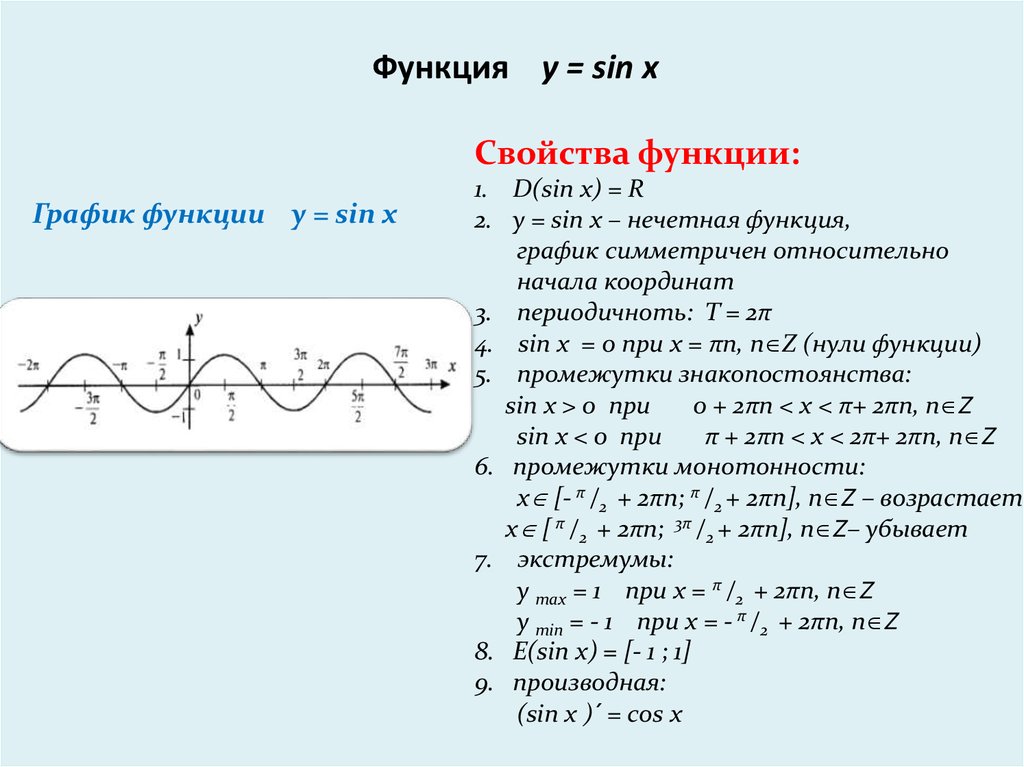
Следовательно, график этой функции расположен в полосе между прямыми y= −1 и y=1.
Так как функция y = cos x периодическая с периодом 2π , то достаточно построить её график на каком-нибудь промежутке длиной 2π , тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, n∈Z, график будет таким же.
Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0; ]
В координатной плоскости
На числовой окружности
Функция y = cos x является чётной. Поэтому её график симметричен относительно оси ОУ
Для построения графика на отрезке — π≤x≤π достаточно построить его для 0≤x≤π , а затем симметрично отразить его относительно оси ОУ
График функции y = cos x
Кривая, являющаяся графиком функции y= cos x, называется косинусоидой .
Свойства функции y = cos x
1. Область определения — множество R всех действительных чисел. D(y) = (-∞ ; + ∞ )
2. Множество значений Е(у) = [−1;1]
3. Функция периодическая с периодом T= 2π .
4. Функция чётная cos(-x) = cos x
(график симметричен относительно оси ОУ ).
5 . Функция ограничена и сверху, и снизу.
6. Функция y= cos x принимает: — значение, равное
7. Промежутки, на которых функция принимает положительные значения при
x ∈ ( -π/2+2π n; π/2+2π n), n ∈ Z
Промежутки, на которых функция принимает отрицательные значения при
x ∈ ( π /2+2 π n; 3 π / 2+2 π n), n ∈ Z
- Функция возрастает на x ∈ [ π + 2 π n; 2 π n ] , n ∈ Z
функция убывает на x ∈ [ 2 π n ; π + 2 π n ] , n ∈ Z
Решение задач
Задача №1
Найти пределы изменения функции y = cos t на данном отрезке [ /6; /2]
Решение
Функция монотонно убывает на указанном промежутке, значит, наибольшее значение принимает на левом конце отрезка у( /6)= 3/2, а наименьшее значение принимает на его правом конце у( /2) = 0
Задача №2
Найти наибольшее и наименьшее значение функции y = cos t на данном отрезке [ / 3 ; 7 / 6 ]
Решение
На данном промежутке функция немонотонна.
Наибольшее значение принимает на левом конце отрезка у( /3)=1/2, а наименьшее значение у( ) = -1
Задача №3
Задача 2. Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы одно решение: 1 + cos t = a
Решение
Построим график функции y =
Уравнение
1 + cos t = a
имеет хотя бы одно решение при a Є [0;2]
В данном случае множество значений параметра совпадает со множеством значений функции.
Ответ: а Є [0; 2]
Задача №4
Решить уравнение
Решение
Построим в одних координатных осях графики функций
Графики имеют только одну общую точку
А(0; 1)
Ответ: х=0
Задача №5
Найти число корней уравнения
Решение
На промежутке [- π ; 0] функция у= cosx монотонно возрастает, функция у=х 2 монотонно убывает.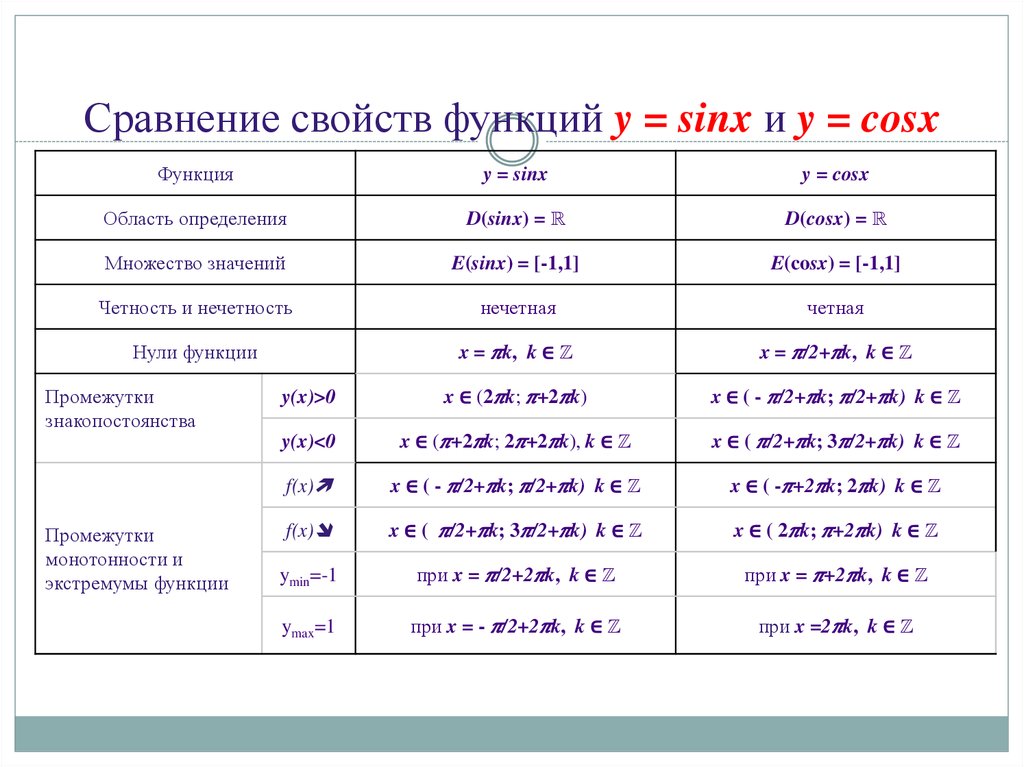
Это значит, что на данном промежутке графики имеют только одну общую точку.
На промежутке [ 0; π ] функция у= cosx монотонно убывает, функция у=х 2 монотонно возрастает. Значит, и на этом промежутке графики имеют только одну общую точку.
Ответ: два корня
Задача №5
Построить график функции y=cos3x
Решение
Косинус – четная функция, строим график на участке
[0; π /3] , затем симметрично отображаем относительно оси y и получаем график на промежутке [- π /3; π /3] длина которого равна периоду. График сжимается к оси Оу в 3 раза.
Задания для самостоятельного решения
1) Постройте графики функций
1) у = cos x + 1;
2) у = cos x – 1;
3) у = cos (x + π /2)
4) у = cos (x – π /3)
2 ) Найти наибольшее и наименьшее значение функции y= cos (x) на отрезке [0; 4π/3]
3) Определить область значений функции y=−8cosx+3.
4) Определить чётность или нечётность функции:
f(x)=x5⋅cos6x.
5) Определить, возрастает или убывает функция y=cosx на отрезке: [−4π;−3π].
6) Найти наибольшее и наименьшее значения функции:
y=cos 4 2x−sin 4 2x+4.
7) Определить наименьшее и наибольшее значения функции y=cosx
на полуинтервале (−4π / 3;−π / 3].
Заключение.
Мы рассмотрели график функции
y = cos x ,
изучили особенности ее поведения, использовали их и свойства функции при решении задач, в том числе и задач с параметром
Как найти домен и диапазон f(x)=cosx+1?
Алгебра
Наука
- Анатомия и физиология
- астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
- Исчисление
- Геометрия
- Преалгебра
- Предварительный расчет
- Статистика
- Тригонометрия
Гуманитарные науки
- Английская грамматика
- История США
- Всемирная история
- Сократическая мета
- Избранные ответы
.
.. и не толькоТемы
Влияние этого вопроса
3517 просмотров по всему миру
Вы можете повторно использовать этот ответ
Лицензия Creative Commons
Область определения функции \[f(x)=\sqrt{\cos x-1}\] равна A) \[R-\{n\pi :n\in Z\}\]B) \[\ {n\pi :n\in Z\}\]C) \[\{2n\pi :n\in Z\}\]D) \[\left( -\infty ,\infty \right)\]
Дата последнего обновления: 23 февраля 2023 г.0066 283,8 тыс.+ просмотров
Подсказка: область определения функции — это множество, из которого берутся все входные значения функции.
Мы знаем, что определенная функция никогда не имеет общего отрицательного члена внутри квадратного корня. Итак, \[\cos x-1\ge 0\] и решаем дальше. Мы знаем, что если \[\cos x=1\], то x=0, \[2\pi ,4\pi ,6\pi ,………….\]
Итак, общее решение \[\cos x=1\] равно \[x=2n\pi \] .
Согласно вопросу у нас есть функция \[f(x)=\sqrt{\cos x-1}\] ……………….(1)
Мы знаем, что определенная функция никогда не имеет общего отрицательного члена внутри квадратного корня. Итак, член внутри квадратного корня должен быть больше нуля.
Из уравнения (1) мы можем получить член внутри квадратного корня и сделать его положительным.
Итак, \[\cos x-1\ge 0\] ……………….(2)
Решая уравнение (2), получаем
\[\cos x-1\ge 0\]
\[ \Rightarrow \cos x\ge 1\]
Мы знаем, что диапазон функции косинуса равен [-1,1]. Максимальное значение функции косинуса может быть равно 1, но не более 1.
Итак, \[\cos x\] не может быть больше 1.
Оно может быть равно только 1.
Итак, \[\cos x=1\]………………….(3)
Мы знайте, что \[\cos 0=1\] . Теперь, используя это в уравнении (3), мы получаем
\[\begin{align}
& \cos x=1 \\
& \Rightarrow \cos x=\cos 0 \\
& \Rightarrow x=0 \\
\end{align}\]
Мы также знаем, что \[\cos 2\pi =1\] . Теперь, используя это в уравнении (3), мы получаем
\[\begin{align}
& \cos x=1 \\
& \Rightarrow \cos x=\cos 2\pi \\
& \Rightarrow x=2\pi \\
\end{align}\]
Мы также знаем, что \[\cos 4\pi =1\] . Теперь, используя это в уравнении (3), мы получаем
\[\begin{align}
& \cos x=1 \\
& \Rightarrow \cos x=\cos 4\pi \\
& \Rightarrow x=4 \pi \\
\end{align}\]
Мы видим, что x может быть 0, \[2\pi \] , \[4\pi \] , \[6\pi \] и т. д.
Мы можем обратите внимание, что x кратно \[2\pi \] ……………….(4)
Теперь, из уравнения (3) и уравнения (4), мы получаем
\[\cos x=1\]
\[\begin{align}
& \Rightarrow \cos x=\cos 2n\pi \\
& \Rightarrow x=2n\pi \\
\end{align}\]
Следовательно, вариант (C) правильный вариант.