Сравнение степеней с одинаковыми основаниями: Сравнить числа 8^80 и 6^90

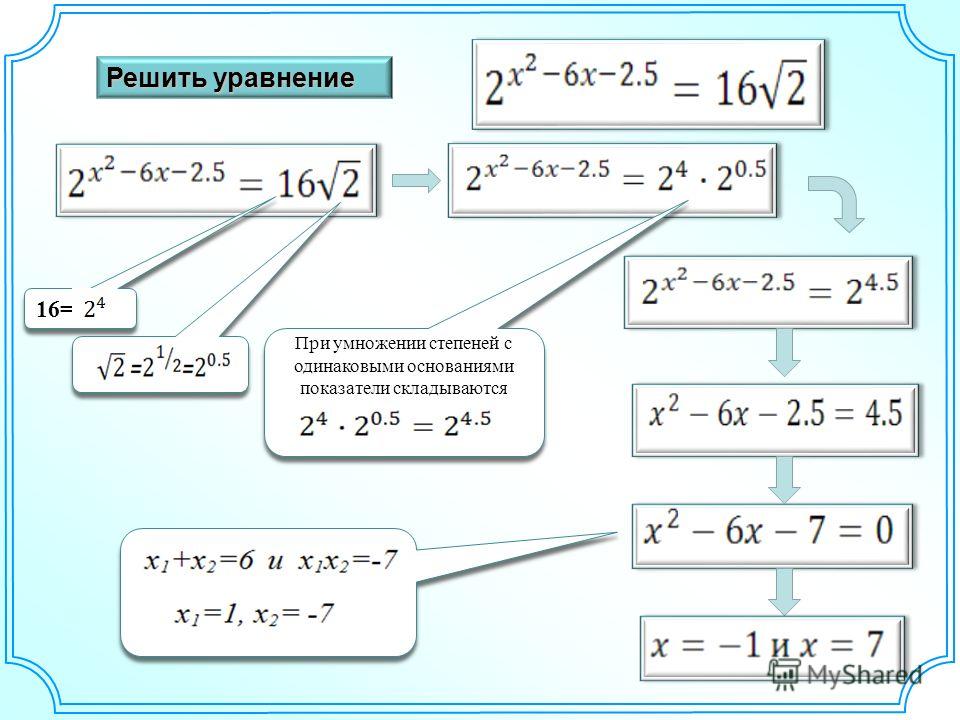
Презентация «Свойства степени с натуральным показателем»

Учитель МКОУ СОШ с.Малиновка

Рыбальченко Т.Н.

Тема урока: «Свойства степени с натуральным показателем»

Цели урока:

Образовательные : изучение свойств степени с натуральным показателем; совершенствование вычислительных навыков.

Развивающие : развитие математического и общего кругозора, мышления и речи, внимания и памяти; формирование умений применять приемы наблюдения, сравнения, анализа.

Воспитательные : воспитание интереса к математике и ее приложениям, активности, общей культуры.

Заполните таблицы буквами, учитывая найденные ответы.

Выполните вычисления.

Вариант 1

Вариант 2

Сравните, не выполняя вычислений.

Найдите верные неравенства. Из соответствующих им букв составьте фамилию архитектора, по проекту которого в 1825 году было построено здание Большого театра в Москве:

Бове По проектам этого известного архитектора также были построены здания Манежа и Триумфальные ворота, создан проект Александровского сада.

Большая часть математических утверждений проходит в своем становлении три этапа.

На первом этапе человек в ряде конкретных случаев подмечает одну и ту же закономерность.

На втором этапе он пытается сформулировать подмеченную закономерность в общем виде, т.е. предполагает, что эта закономерность действует не только в рассмотренных случаях, но и во всех других аналогичных случаях.

На третьем этапе он пытается доказать, что закономерность, сформулированная в общем виде, на самом деле верна.

Свойство первое. Умножение степеней.

Свойство второе. Деление степеней.

Свойство третье. Возведение степени в степень.

Запомните

Правило 1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.

Правило 2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.

Правило 3. При возведении степени в степень

показатели перемножаются, а основание остается неизменным.

Свойства степеней

Заполнить таблицу.

Выполните преобразования. Используя найденные ответы, запишите в таблицах два высказывания:

будь

быть

что

не

им

хочешь

плачем

имеем

потерявши

храним

счастливым

Самопроверка

что имеем не храним потерявши плачем

Что имеем не храним, потерявши плачем.

хочешь быть счастливым будь им

Хочешь быть счастливым — будь им.

Магический квадрат

Заполните свободные клетки квадрата так, чтобы произведение выражений каждого столбца, каждой строки и диагонали равнялось

Такой квадрат называется магическим

12

Значения числовых выражений

Найдите в кружках

значения числовых

выражений,

записанных в овалах.

Соедините их линиями.

Самопроверка

• Сформулируйте определение степени числа с натуральным показателем
• Сформулируйте свойство умножения степеней с одинаковыми основаниями
• Сформулируйте свойство деления степеней с одинаковыми основаниями
• Сформулируйте свойство возведения степени в степень
• Сформулируйте свойство возведения дроби в степень
• Сформулируйте свойство возведения в степень произведения

Устная работа

Вычислительная пауза

Тест

Вариант 1

Вариант 2

Проверь себя!

Вариант 1

1. а)

2. б)

3. а)

Вариант 2

1. б)

2. б)

3. а)

Свойства степени с натуральным показателем. 7 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. 7 класс

Алгебра
Тема: «Свойства степени с натуральным
показателем»
1

2. Сравнение выражений

Сравните, не выполняя вычислений.
Найдите верные неравенства. Из соответствующих им букв
составьте фамилию архитектора, по проекту которого в 1825 году
было построено здание Большого театра в Москве:
Бове. По проектам этого известного архитектора также были
2
построены здания Манежа и Триумфальные ворота, создан проект
Александровского сада.

3. Свойство первое

3

4. Свойство второе

4

5. Свойство третье

5

6. Запомните

Правило 1. При умножении степеней с одинаковыми
основаниями показатели складываются, а основание
остается неизменным.
Правило 2. При делении степеней с одинаковыми
основаниями показатели вычитаются, а основание
остается неизменным.
Правило 3. При возведении степени в степень
показатели перемножаются, а основание остается
неизменным.
6

7. Свойства степеней

n
k
n k
a a a ;
n k
n k
a : a a , где n k , a 0;
a
nk
;
a b ab ;
n
n
an a , где b 0.
b b
n n
7
a
nk
n

8. Выполните преобразования.

Используя найденные ответы, запишите в таблицах два
высказывания Козьмы Пруткова:
будь
быть
что
не
им
хочешь
плачем
имеем
8
5
2
x x
3
x2 x3 4
x x4 x5
x x x
10
8
:
x7 x6
x 😡
12
x 😡
2
3
:
x x
потерявши
храним
счастливым
0
2
3
5
x x 😡
x
3 4 5 14
x x x 😡
5
x x
4
x 😡

9.

Самопроверкачто
имеем
не
храним
потерявши
плачем
Что имеем не храним, потерявши плачем.
хочешь
9
быть
счастливым
Хочешь быть счастливым — будь им.
будь
им

10. Найдите соответствие

Найдите в кружках
значения числовых
выражений,
записанных в овалах.
Соедините их линиями.
10

11. Самопроверка

11

12. Дострой прямоугольник

Заштрихованный квадрат изображает записанное в нем
число. Дочертите прямоугольник, который будет изображать
указанное под ним число:
12

13. Какое число изображает круг?

Узнайте, какое число изображает круг, если заштрихованная
часть изображает указанное число. Ответ запишите в виде
степени.
13
Конец
14

English     Русский Правила

Показатель степени и степень — разница, значение, примеры

LearnPracticeDownload

Показатель степени и степень — термины, используемые, когда число умножается само на себя определенное количество раз.

Разница между показателями и степенью — чрезвычайно незначительное наблюдение, которым большую часть времени пренебрегают. Между показателем степени и степенью существует очень тонкая грань. В этой статье мы будем понимать показатели и степени вместе с их различием.

1.	Что такое экспонента и мощность?
2.	В чем разница между показателем степени и степенью?
3.	Часто задаваемые вопросы о Exponent и Power

Что такое экспонента и мощность?

Когда число умножается само на себя конечное число раз, умножаемое число называется базовым числом, а количество раз, которое оно умножается, называется показатель степени . Предположим, что число умножается само на себя n раз, тогда это выражение называется n ^th степенью данного числа. Итак, подводя итог, мы можем сказать, что показатель степени — это количество раз, которое данное число умножается само на себя, а степень — это значение произведения основного числа, возведенного в степень.

Разница между показателем степени и степенью

Экспоненциальная запись или экспоненциальная форма чисел помогает нам выражать и представлять чрезвычайно большие и малые числа очень удобным способом. Например, 10000000000000 можно представить как 1 × 10 ¹³ , тогда как 0,0000000000000007 можно представить как 7 × 10 ^-16 . Это улучшает читаемость чисел и помогает нам поддерживать точность чисел и экономит наше время. Прежде чем перейти к разнице между показателем степени и степенью, давайте разберемся, что такое показатель степени и степень.

Показатель степени и степень Значение

Давайте рассмотрим пример, чтобы понять определение степени и степени. Рассмотрим 6 × 6 × 6 × 6. Мы знаем, что в экспоненциальной форме 6 × 6 × 6 × 6 можно записать как 6 ⁴ так как число 6 умножается само на себя четыре раза. Показатель степени числа определяется как количество раз, которое число умножается само на себя. Здесь в 6 × 6 × 6 × 6 число 6 умножается само на себя четыре раза, что также представляется как 6 ⁴ . Здесь 6 — основание, а 4 — показатель степени.

Степень определяется как полное выражение повторного умножения, которое включает основание и показатель степени. В данном примере 6 × 6 × 6 × 6 экспоненциальная форма равна 6 ⁴ . Мы можем сказать это как «6 в степени 4», где 6 — основание, а 4 — показатель степени. Другими словами, 6 ⁴ называется степенью 4 ^th числа 6. Следовательно, определение мощности дано для всего выражения экспоненциальной формы.

Показатель степени против степени

Давайте теперь сведем в таблицу разницу между показателем степени и степенью, как показано ниже.

Экспонента	Сила
Показатель степени указывает на то, сколько раз число используется при умножении.	Сила может быть определена как число, умноженное само на себя определенное количество раз.
Показатель степени — это число, до которого возводят число, чтобы определить его степень как целое выражение.	Когда число возводится в определенную степень с использованием показателя степени, число или выражение числа в целом называется степенью.
Показатель степени всегда записывается как верхний индекс числа, в которое возводится степень.	Степень — это целое выражение, включая основание и показатель степени. У него нет конкретной позиции в этом контексте.
Экспонента имеет только одну часть, число в верхнем индексе.	Степень, используемая для описания выражения большого числа, состоит из двух частей: основания и показателя степени.

Важные примечания по экспоненте и мощности

• Показатель степени — это количество раз, которое данное число умножается само на себя.
• Выражение, когда число умножается само на себя n раз, называется n ^-й -й степенью данного числа.

Похожие статьи

• Экспоненциальная форма
• Экспоненты
• Экспонентные правила

 

Примеры степени и степени

1. Пример 1: Напишите показательную форму 16 × 16 × 16. Укажите основание и показатель степени. Какова сила выражения?

   Решение: Из разницы между показателем степени и степенью мы знаем, что показатель степени относится к тому, сколько раз число используется при умножении, а степень определяется для всего выражения повторного умножения, которое включает основание и показатель степени. .

   У нас есть 16 × 16 × 16. Это можно представить как 16 ³ . Основание равно 16, а показатель степени равен 3. Можно сказать, что 16 возводится в степень 3.

2. Пример 2: Найдите значение 2 ⁵ .

   Решение: В заданном выражении 2 ⁵ основание 2, а показатель степени равен 5. Также можно сказать, что 2 возводится в степень 5. Разложим 2 ⁵ . Его можно записать как 2 × 2 × 2 × 2 × 2 = 32. Таким образом, значение 2 ⁵ равно 32,9.0003

3. Пример 3: Определите степень и степень выражения 4 ⁸ .

   Решение: Для выражения 4 ⁸

   , 8 — это показатель степени, 4 — основание числа и 8 ^{-я степень} числа 4. Таким образом, значение 4 ⁸ равно 65, 536.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Экспоненциальные и силовые вопросы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по Exponent и Power

Есть ли разница между показателем степени и степенью?

Да, между показателем степени и степенью существует очень небольшая разница. Показатель степени относится к тому, сколько раз число используется при умножении, тогда как мощность может быть определена как количество раз, когда число умножается само на себя.

В чем основная разница между показателем степени и степенью?

Основное различие между показателем степени и степенью состоит в том, что показатель степени — это число, до которого возводят число, чтобы определить его степень, тогда как степень определяется для всего выражения многократного умножения, которое включает основание и показатель степени.

В чем разница между мощностью и показателем степени?

Степени и степени определены для любого числа, которое многократно умножается само на себя. Показатель степени определяется тем, сколько раз основание умножается само на себя, а мощность определяется для всего выражения, включая основание и показатель степени. Например, в 7 ⁵ , основание равно 7, а показатель степени равен 5. С точки зрения мощности можно сказать, что 7 возводится в степень 5.

Как сравнить показатели степени и степени?

Показатель степени и степени можно сравнивать по равным основаниям. Для равных оснований мы просто проверяем показатели степени, чтобы сравнить результаты. Например, чтобы сравнить 9 ² и 9 ⁵ , мы рассмотрим показатель степени, чтобы сравнить их, поскольку основания равны, то есть 9. Поскольку 2 меньше 5, мы можем сказать, что 9 ² меньше 9 ⁵ .

Почему экспоненты называются степенями?

Экспоненты известны под разными именами, такими как индексы и степени. Показатель степени числа определяется как количество раз, которое число умножается само на себя. Степень определяется для всего выражения многократного умножения, которое включает основание и показатель степени.

Скачать БЕСПЛАТНЫЕ учебные материалы

Разница между степенями и показателями Рабочие листы

Рабочие листы по математике и
наглядная учебная программа

Объяснение урока: Степени и степени над действительными числами

В этом объяснении мы научимся вычислять действительные числа, возведенные в положительные и отрицательные целые и нулевые степени, и решать простые показательные уравнения.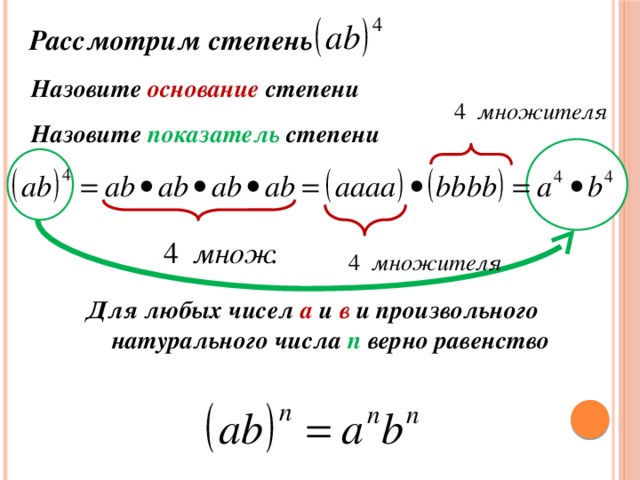

Напомним, что для оценки степени мы умножаем основание на количество раз, указанное в показателе степени. Давайте повторим определение ниже.

Определение: вычисление степени

Для степени с основанием 𝑎, 𝑎∈ℝ−0 и показателем 𝑛, 𝑛∈ℤ, тогда 𝑎=𝑎×𝑎×𝑎×…×𝑎.кратно

Используя это определение, мы можем вычислять степени не только в тех случаях, когда основанием является целое или рациональное число, но также и в тех случаях, когда основание является действительным числом.

Одним из таких типов действительных чисел, которые мы можем вычислить, является квадратный корень. Напомним, что квадратный корень — это число, записанное в форме √𝑎, 𝑎∈ℤ. Мы можем использовать обратную операцию возведения в квадрат, чтобы получить два ключевых результата.

Во-первых, если возвести в квадрат √𝑎, то получится 𝑎, так как возведение в квадрат и извлечение квадратного корня являются обратными операциями. (т. е. √𝑎=𝑎, 𝑎>0).

Во-вторых, если вы извлечете квадратный корень 𝑎, вы получите либо 𝑎, либо −𝑎, в зависимости от того, является ли 𝑎 является отрицательным или положительным. Это потому, что когда мы возводим в квадрат отрицательное число, скажем -3, мы получаем положительное число, 9. Однако, если мы возведем в квадрат аддитивное Обратно к -3, что равно 3, мы также получаем 9. Это означает, что когда мы извлекаем корень из квадрата числа, результат положительный, но исходное число может были отрицательными. Чтобы избежать путаницы, мы говорим, что √𝑎=|𝑎|. Однако, если мы знаем, что 𝑎>0, тогда мы можем сказать √𝑎=𝑎.

Расширяя эти определения и используя определение мощности, мы можем сказать, что √𝑎=√𝑎×√𝑎 и √𝑎=√𝑎×𝑎. Таким образом, мы получаем следующее определение.

Определение: упрощение выражений с помощью квадратов и квадратных корней √𝑎=𝑎.

В нашем первом примере мы применим то, что мы знаем об оценке степеней и вычислении квадратов радикалов, чтобы определить значение неизвестного.

Пример 1: Возведение действительного числа в положительную целую степень

Определите значение 𝑥, учитывая, что 𝑥=8√10.

Ответ

Чтобы найти значение 𝑥, нам нужно подставить 𝑥=8√10 в 𝑥. Это дает нам 𝑥=8√10.

Из определения степени мы знаем, что 8√10 равносильно выражению 8√10×8√10. Таким образом, мы получаем 𝑥=8√10×8√10.

Чтобы вычислить это, нам нужно использовать √𝑎×√𝑎=𝑎, что дает нам 𝑥=8×8×√10×√10=64×10=640.

Следовательно, значение 𝑥 равно 640.

Помимо возведения действительных чисел в степень положительного целого числа, мы также можем возводить их в степень нуля или в степень отрицательного целого числа.

Если мы рассмотрим схему степеней двойки, мы увидим, что, увеличивая степень на 1, мы умножаем на 2 следующим образом: 2,2,2,2,…2,4,8,16,…

Если мы движемся назад по последовательности, мы можем сделать вывод, что 2 должно быть 2, деленным на 2. Тогда это дает нас 2÷2=1. Итак, 2=1.

Точно так же, если мы снова вернемся назад, мы можем сделать вывод, что 2 должно быть 2, деленным на 2. Это дает нам 1÷2=12. Итак, 2=12.

Опять же, если мы продолжим двигаться назад, мы можем сделать вывод, что 2=14 и 2=18 и так далее. Если мы снова выпишем последовательность, то получим следующее: 2,2,2,2,2,2,2,2,…18,14,12,1,2,4,8,16,…

Обратите внимание, что если мы перепишем знаменатели в первых трех членах как степени числа 2, мы получим следующее: 2,2,2,2,2,2,2,2,…12,12,12,1,2,4,8,16,…

Тогда мы можем сказать, что 2=12, 2=12 и 2=12. Продолжая последовательность в отрицательном направлении, мы можем обобщить, что 2=12, 𝑛∈ℤ.

Эти результаты справедливы не только для основания 2, но и для любого действительного числа, кроме нуля. Мы можем обобщить их в следующих законах.

Законы: правила для нулевых и отрицательных степеней

• Закон для нулевых степеней 𝑎=1, где 𝑎∈ℝ−0.
• Закон отрицательных показателей 𝑎=1𝑎, где 𝑎∈ℝ−0 и 𝑛∈ℤ.

В следующем примере мы будем использовать закон для нулевых показателей, чтобы определить значение выражения, включающего степени радикалов.

Пример 2. Возведение действительного числа в нулевую степень

Если 𝑥=√2, найти 𝑥.

Ответ

Чтобы определить значение 𝑥, мы можем заменить 𝑥=√2, что даст нам 𝑥=√2.

Мы знаем, что 𝑎=1, где 𝑎∈ℝ−0; поэтому, 𝑥=1.

Следовательно, значение 𝑥 равно 1.

В следующем примере мы будем использовать закон для отрицательных показателей, чтобы определить значение выражения, включающего степени радикалов.

Пример 3: Возведение действительного числа в отрицательную целую степень

Если 𝑥=√2, найти 𝑥.

Ответ

Чтобы найти значение 𝑥 при 𝑥=√2, нам сначала нужно произвести замену. Это дает нам 𝑥=√2.

Далее, чтобы упростить √2, мы используем закон для отрицательных показателей, который гласит, что 𝑎=1𝑎, где 𝑎∈ℝ−0 и 𝑛∈ℤ. Затем это дает нам √2=1√2.

Мы можем использовать правило √𝑎×√𝑎=𝑎, 𝑎>0, чтобы вычислить знаменатель, расширив степень, что даст нам √2=√2×√2×√2×√2=2×2=4.

Подставляя это в знаменатель, получаем 1√2=14.

Следовательно, значение 𝑥 при 𝑥=√2 равно 14.

В следующем примере мы обсудим, как вычислить выражение с положительными и отрицательными показателями.

Пример 4. Вычисление выражения путем замены сурдов

Если 𝑥=√32, 𝑦=1√2 и 𝑧=√23, затем найдите значение 𝑥+(𝑦+𝑧)−𝑧 в простейшей форме.

Ответ

Чтобы найти значение 𝑥+(𝑦+𝑧)−𝑧, начнем с замены 𝑥=√32, 𝑦=1√2, и 𝑧=√23. Это дает нам 𝑥+(𝑦+𝑧)−𝑧=√32+1√2+√23−√23.

Мы можем упростить это, расширив скобки второго члена, что даст нам 1√2+√23=1√2+2×1√2×√23+√23.

Сокращение общих множителей √2 в 2×1√2×√23 дает нас 1√2+√23=1√2+2×1×13+√23=1√2+23+√23. 

Подставляем обратно в выражение, мы получаем 𝑥+(𝑦+𝑧)−𝑧=√32+1√2+23+√23−√23.

Далее мы можем использовать √𝑎 =𝑎 для оценки квадратов членов, что дает нам для первого, второго и четвертого членов соответственно √32=√32×√32=√32×2=34,1√2=1√2×1√2=1×1√2=12,√23= √23×√23=√23×3=29.

Подставляя обратно в выражение, получаем 𝑥+(𝑦+𝑧)−𝑧=34+12+23+29−√23.

Поскольку √23 равно √23×√23×√23×√23, то мы можем использовать √𝑎×√𝑎=𝑎, чтобы упростить это, давая нам √23×√23×√23×√23=29×29=481.

Подставляя обратно в выражение, получаем 𝑥+(𝑦+𝑧)−𝑧=34+12+23+29−481.

Для дальнейшего упрощения нам нужно найти общий множитель для знаменателей дробей. Для первых четырех членов общий множитель равен 36, что дает нам 𝑥+(𝑦+𝑧)−𝑧=2736+1836+2436+836−481=7736−481.

Наконец, общий делитель 36 и 81 равен 324, что дает нам 𝑥+(𝑦+𝑧)−𝑧=693324−16324=677324. 

Следовательно, ответ равен 677324.

До сих пор мы рассматривали способы упрощения выражений с целыми показателями. Далее мы обсудим, как найти неизвестный показатель степени.

При сравнении двух степеней с одинаковым основанием можно сделать вывод, что если степени равны, то и их показатели должны быть равны. Например, если 3=3, то, поскольку основания одинаковы, показатели степени тоже должны быть одинаковыми, то есть 𝑦=4.

Точно так же, если мы сравним две степени с одинаковым показателем степени, то если они равны и нечетны , основания должны быть равны. Например, если 𝑎=7, тогда, поскольку показатели одинаковы, основания тоже должны быть одинаковыми, то есть 𝑎=7. Однако, если у нас есть показатель степени даже , то возможно что основания не равны, так как одно может быть отрицательным по отношению к другому. Например, (−2)=2, поэтому, если показатели равны, тогда основание может быть -2 или 2, чтобы они были равны. Это означает, что если четные показатели равны, то можно сказать, что модули оснований равны. Например, если 𝑐=3, то |𝑐|=3, поэтому 𝑐=3 или 𝑐=−3. Давайте обобщим эти пункты в правиле ниже.

Правило: приравнивание степеней с одинаковым основанием или показателем степени

• Если 𝑎=𝑎, где 𝑎∈ℝ−[−1,0,1], то 𝑚=𝑛.
• Если 𝑎=𝑏, то 𝑎=𝑏, когда 𝑛∈[1,3,5,…] и |𝑎|=|𝑏| когда 𝑛∈[2,4,6,…].

Мы можем использовать эти правила для решения задач с неизвестными в показателе степени. Давайте обсудим, как это сделать, на следующем примере.

Пример 5. Решение простого экспоненциального уравнения

Найдите значение 𝑥 в уравнении 3=181.

Ответ

Чтобы найти значение 𝑥 в уравнении 3=181, мы можем использовать правило, которое гласит, что если 𝑎=𝑎, где 𝑎∈ℝ−[−1,0,1], то 𝑚=𝑛.

Это правило будет работать только в том случае, если обе части уравнения имеют одинаковое основание. Таким образом, поскольку основание степени в левой части уравнения равно 3, тогда мы также хотим написать правую часть с основанием 3.

Мы знаем, что 81 является степенью числа 3, поскольку 81=3×3×3×3. Следовательно, 81=3. Тогда мы можем сказать, что правая часть 181=13.

Далее мы можем использовать закон отрицательных показателей, который гласит 𝑎=1𝑎, где 𝑎∈ℝ−0 и 𝑛∈ℤ−0, что означает, что для 13 мы получаем 13=3.

Подставляя это в правую часть исходного уравнения, мы получаем 3=3.

Поскольку основания теперь одинаковы, мы можем приравнять показатели, что дает нам 2𝑥−1=−4.

Решая 𝑥, получаем 2𝑥=−3𝑥=−32.

Следовательно, значение 𝑥 равно −32 для уравнения 3=181.

В этом объяснителе мы узнали, как вычислять действительные числа, возведенные в положительную, нулевую и отрицательную степени, и как решать простые показательные уравнения. Напомним ключевые моменты.

Ключевые моменты

• Мы можем использовать свойство √𝑎×√𝑎=√𝑎=𝑎 для упрощения радикалов, возведенных в положительные целые числа.

  No related posts.