Тригонометричні підстановки: 6.7. Тригонометричні підстановки.

6.7. Тригонометричні підстановки.

Інтеграли виду , , приводять до інтегралів від раціональної відносно і функції за допомогою відповідної тригонометричної підстановки.

,

,

.

Подальші обчислення отриманих інтегралів аналогічні обчисленням показаним в прикладах розд. 6.6.

Приклад 6.14. Обчислити невизначений інтеграл:

.

Розв’язок. Зробимо заміну змінної . Тоді

Повертаючись до змінної величини за допомогою підстановки , остаточно одержимо:

.

Л і т е р а т у р а: [4, гл. 6, §2, п. 3; 6, гл. Х, § 13].

Наведені способи обчислення невизначених інтегралів, природно, не вичерпують існуючих методів обчислення інтегралів. Є численна література з цього питання, до якої можна звернутися при необхідності.

Слід мати на увазі, що дуже часто інтеграли від елементарних функцій не виражаються через елементарні функції. До таких інтегралів відносяться, наприклад,

, , , ,

і багато інших. Найбільш важливі з них, що мають застосування у техніці і природознавстві, носять спеціальні назви. Їхні властивості добре вивчені і для них складені таблиці, тому у деяких випадках з ними можна працювати у той же спосіб, що й з елементарними функціями.

Питання для самоперевірки.

1. Що називається первісною функцією?

2. Що називається невизначеним інтегралом?

3. Яка взаємовідповідність існує між операціями диференціювання та інтегрування?

4. Випишіть таблицю основних інтегралів. Зіставте її з таблицею похідних.

5. Які правила інтегрування вам відомі?

6. Виведіть формулу інтегрування частинами.

7. У чому полягає застосування цієї формули? Наведіть приклади.

8. Виведіть формулу заміни змінної у інтегралі. Наведіть приклади.

9. Як інтегрують найпростіші раціональні дроби?

10. Сформулюйте методику обчислення невизначених інтегралів від раціональних функцій. Наведіть приклади.

11. Які інтеграли можна звести до інтегралів від раціональної функції? Які при цьому використовують підстановки?

12. Як обчислюють інтеграли що містять ірраціональні функції? Наведіть приклади.

13. Як обчислюють інтеграли, що містять тригонометричні функції? Наведіть приклади.

14. До яких інтегралів можна застосувати тригонометричні підстановки?

15. Чи всі інтеграли від елементарних функцій виражаються через елементарні функції?

Л і т е р а т у р а: [5, гл. 5, § 5.2; 6, гл. Х, § 14].

93

Інтегрування тригонометричних функцій

Приклади на інтегрування функцій взято з матеріалів контрольної роботи, яку задають студентам 1, 2 курсів математичних факультетів. Для економії Вашого часу самі умови завдань пропущені, всюди потрібно або «Знайти неозначений інтеграл» або «Обчислити інтеграл». Тексту в коментарях до кожного завдання рівно стільки, скільки потрібно Вам для засвоєння матеріалу і вивчення методики та схем інтегрування.

Приклад 20. Для обчислення інтегралу від добутку косинуса та синуса необхідно синус внести під диференціал. В результаті перейдемо до інтегрування показникової функції від косинуса. Через формули це матиме наступний запис

Приклад 21. Спершу слід проаналізувати аргументи під синусом та косинусом та показники. Добуток функцій можемо записати через квадрат синуса подвійного кута, який в свою чергу записуємо через косинус в два рази більшого аргументу. Як тільки дійдемо до функцій в першому степені маємо право застосовувати табличні інтеграли

Приклад 22.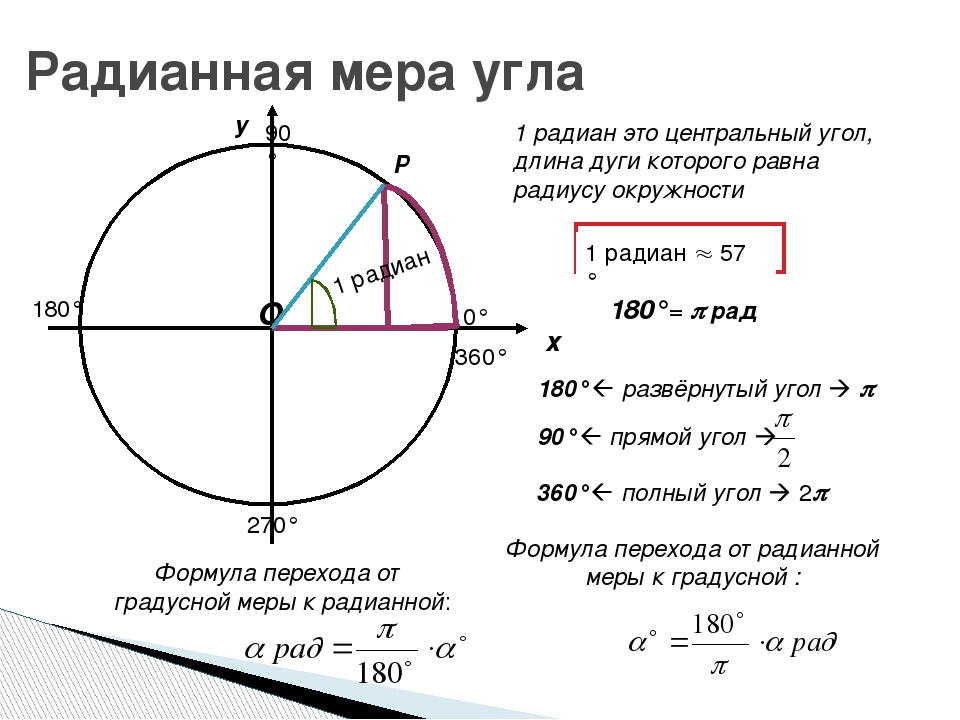 Косинус подвійного кута записуємо згідно тригонометричних формул через косинус 1 кута. Далі, щоб отримати інтеграл від однієї з тригонометричних функцій необхідно синус внести під диференціал. Подальші обчислення зводяться до інтегрування простих функцій

Слід зазначити, що в цьому та попередньому прикладі використовували деякі тригонометричні формули. Для обчислення всіх можливих інтегралів, але для розв’язання базових інтегралів необхідно не більше 10 популярних тригонометричних формул.

Приклад 23. Маємо дробову тригонометричну функцію. Для її обчислення необхідно застосувати універсальну тригонометричну заміну – тангенс половини кута. Синус через тангенс половини кута виражається залежністю

Після підстановки заміни в інтеграл та спрощення, що при таких замінах буває не простим, отримаємо просту дробову функцію. Її інтегрувати повинен вміти кожен студент. Якщо ні, то контрольна чи самостійна на інтеграли покаже «хто є хто».

Приклад 24. Щоб знайти інтеграл можна застосувати універсальну тригонометричну заміну, як один із поширених способів.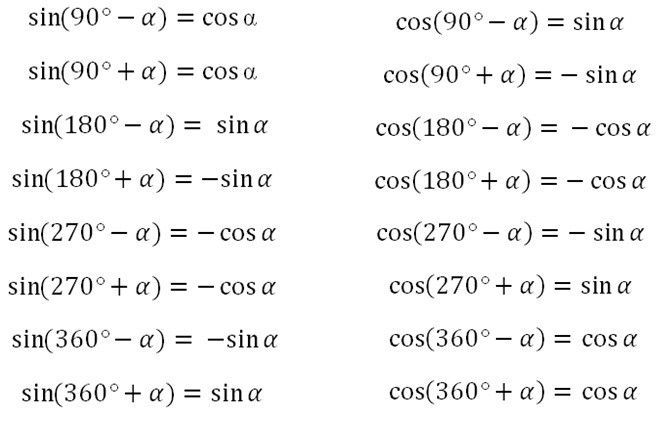

Як альтернативний варіант можна винести квадрат косинуса за дужки, а в дужках додати та відняти одиницю, щоб отримати тангенс. Далі його позначаємо за нову змінну та обчислюємо диференціал (він співпаде з другою частиною підінтегральної функції). Таким способом перейдемо до інтегрування функції, яка зводиться до арктангенса.

Такий підхід дещо спрощує обчислення, але не завжди легко його побачити та застосувати.

Приклад 25. Інтеграл від котангенса в квадраті від потрійного аргументу знаходимо після наведених нижче перетворень

Тут використана проста залежність, що сума квадратів синуса та косинуса рівна одиниці.

 

Приклад 1*. Обчислити невизначені інтеграли від тригонометричних функцій.
а) Уважно проаналізуйте методику інтегрування частинами такого типу прикладів, та як до цього прийти
 

б) Раніше розглядали алгоритмии, як понижувати степінь добутку синусів на косинуси за допомогою тригонометричних формул. Тут маємо приклад з практики, який за кілька перетворень звели до простих табличних інтегралів

Решта готових відповідей з контрольної роботи на інтеграли Ви знайдете за наведеними нижче посиланнями. Завдання та схеми їх обчислень допоможуть розібратися практично з любим інтегралом.

Готові розв’язки контрольної з інтегрування

• < попередні відповіді
• Контрольна робота з інтегрування № 1
• Контрольна робота з інтегрування № 3

2 = 1$. Докажите, что удвоенная площадь этой области равна $t$, как утверждается в раздел 4.11.

Интегрирование с помощью тригонометрической подстановки

Сообщил:

В этом разделе мы узнаем о: Различные типы тригонометрических подстановок.

1. 7
МЕТОДЫ ИНТЕГРАЦИИ

2. МЕТОДЫ ИНТЕГРАЦИИ

7.3
Тригонометрическая замена
В этом разделе мы узнаем о:
Различные виды тригонометрических замен.

3. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА
При нахождении площади круга или эллипса
2 2
возникает интеграл вида  a  x dx,
где a > 0,
2 2
 Если бы было x a 2  x 2 dx , замена u
 a  x
будет эффективной.
 Однако в нынешнем виде
 a 2  x 2 dx сложнее.

4. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА
Если мы изменим переменную с x на θ с помощью
замены x = a sin θ, тождество
1 – sin2θ = cos2θ позволит нам потерять знак корня.
 Это потому, что: a 2  x 2  a 2  a 2 sin 2 
 a 2 (1  sin 2  )
2 2
 a cos 
a cos  5

900 ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА
Обратите внимание на разницу между заменой
u = a2 – x2 и заменой x = a sin θ.

 В первом новая переменная является функцией
старый.
 Во втором случае старая переменная является функцией
новой.

6. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА
В общем, мы можем сделать замену
вида x = g(t)
, используя правило подстановки в обратном порядке.
 Чтобы упростить наши расчеты, предположим, что g
имеет обратную функцию, то есть g взаимно однозначно.

7. ОБРАТНАЯ ПОДСТАВКА
Здесь, если мы заменим u на x и x на t в
Правило подстановки (уравнение 4 в разделе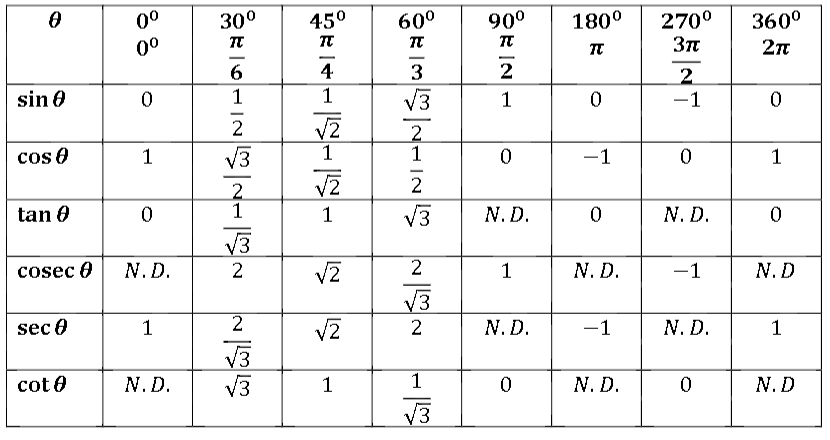 5. 5),
получаем:
f ( x)dx f ( g (t )) g ‘(t )dt
 Такой вид подстановки называется
обратной заменой.

8. ОБРАТНАЯ ПОДСТАВКА
Мы можем сделать обратную замену
x = a sin θ при условии, что она определяет
взаимно однозначную функцию.

 Этого можно добиться, ограничив θ
интервалом [-π/2, π/2].

9. ТАБЛИЦА ТРИГОНОМЕТРИЧЕСКИХ ЗАМЕН
Здесь мы перечисляем тригонометрические замены, которые
эффективны для данного подкоренного выражения
из-за указанного тригонометрического

10. ТАБЛИЦА ТРИГОНОМЕТРИЧЕСКИХ ПОДСТАВОК
В каждом случае ограничение на
накладывается для обеспечения того, чтобы функция, определяющая подстановку
, была взаимно однозначной.
 Это те же самые интервалы, которые использовались в Разделе 1.6
при определении обратных функций.

11. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 1
2
Оценить 9 x
 2
dx
x
 Пусть x = 3 sin θ, где –π/2 ≤ θ ≤ π/2.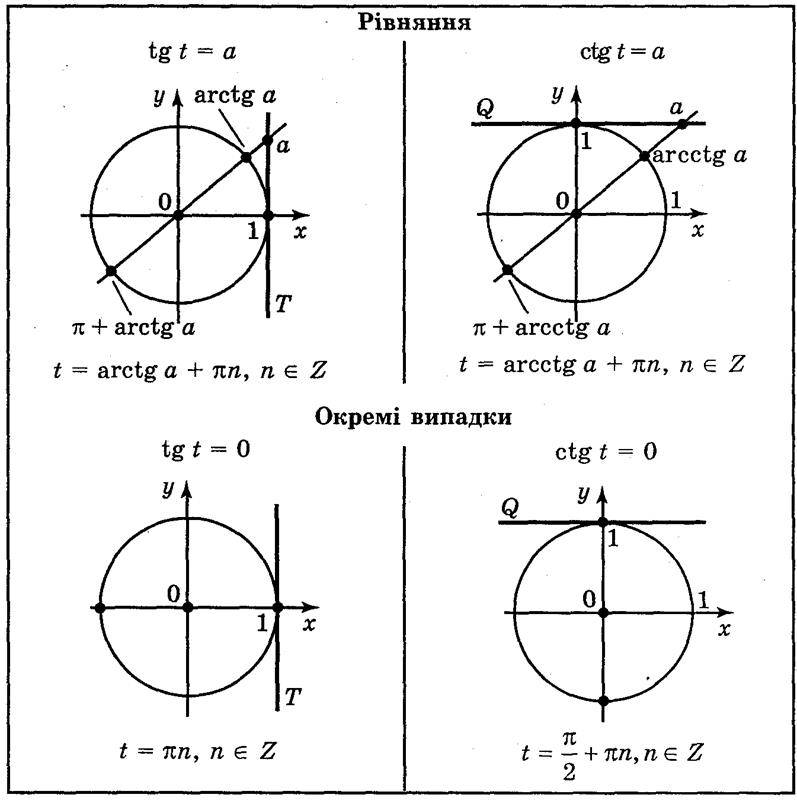
 Тогда dx = 3 cos θ dθ и
9  x 2  9  9sin 2   9 cos 2  3 cos  3cos  π/2.)

12. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 1
Таким образом, правило обратной подстановки
дает:0083 COS 
  2 D
SIN 
COT 2 D
2
 (CSC   1) D
     C

13. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 1
Так как это неопределенный интеграл, мы должны
вернуться к исходной переменной x.
Это можно сделать двумя способами.

14. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 1
Во-первых, мы можем использовать тригонометрические
тождества, чтобы выразить cot θ через
от sin θ = x/3.

15. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 1
Во-вторых, мы можем нарисовать диаграмму, где
θ интерпретируется как прямой угол

16. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 1
Поскольку sin θ = x/3, мы обозначаем противоположную
сторону и гипотенузу как имеющие длины
x и 3.

17. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 1
Тогда теорема Пифагора дает
длину смежной стороны как:
2
9 х

18. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 1
Итак, мы можем просто прочитать значение cot θ
из рисунка:
при θ

19. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 1
Поскольку sin θ = x/3, мы имеем θ = sin-1(x/3).
2 2
9 х 9 х 1 х 
 2
dx  2
 sin    C
x x  3

20. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Найдите площадь, заключенную в
эллипсе x2
y 2
2
 2 1
a b

21. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Решая уравнение эллипса относительно y,
получаем
2 2 2 2
y x a  x
2
1  2  2
b a a
или б 2 2
г  а  х
а

22. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Поскольку эллипс симметричен относительно
относительно обеих осей, общая площадь А в четыре раза больше
площади в первом квадранте.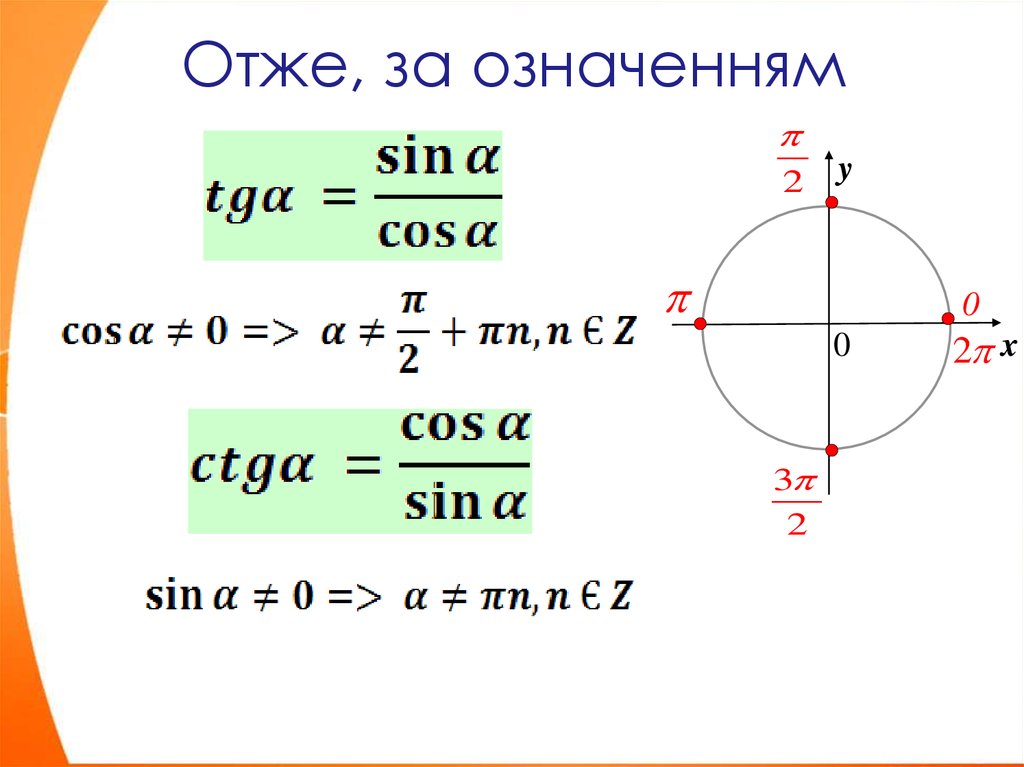

23. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Часть эллипса в первом квадранте
задается функцией
b 2 2
y a  x 0  x a
a
 Следовательно,
ab 2
1
4 A  a  x 2 dx
0 a

24. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Чтобы вычислить этот интеграл,
подставим x = a sin θ.
Тогда dx = a cos θ dθ.

25. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Для изменения пределов интегрирования
заметим, что:
 При x = 0 sin θ = 0; поэтому θ = 0
 Когда x = a, sin θ = 1; поэтому θ = π/2

26. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 2
Кроме того, поскольку 0 ≤ θ ≤ π/2,
2 2 2 2 2
a  x  a  a sin 
2 2
 a cos 
a cos  7 0 9 0 9 0 90 cos 0 . ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
b a 2 2
Следовательно, A 4  a  x dx
a 0
b /2
4   cos 2  d
0
 /2
4ab  1
2 (1  cos 2 ) d
0
 /2
2ab[  ] sin 20083 1
2 0
 
2ab   0  0   ab
2 

28. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 2
Мы показали, что площадь эллипса
с полуосями a и b равна πab.
 В частности, взяв a = b = r, мы доказали
известную формулу о том, что площадь круга с радиусом
r равна πr2.

29. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Примечание
Интеграл в примере 2 был определенным
Итак, мы изменили пределы интегрирования,
и не должны были преобразовывать обратно к
исходную переменную x.

30. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 3
1
Найти x dx
2 2
x 4
 Пусть x = 2 tan θ, –π/2  Тогда dx = 2 sec2 θ dθ и x 2  4  4(tan 2   1)
 4 с 2 
2 с 
2 с 

31. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 3
.

32. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 3
Чтобы вычислить этот тригонометрический интеграл,
мы выражаем все через sin θ и
cos θ: sin 

33. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 3zz
Следовательно, делая замену u = sin θ,
, имеем: dx 1 cos 
x   2 d
2
x 2  4 4 sin 
1 du
 3 2 8
4 1
    C
4 u
1 csc 
  C  C
4sin  4

3

ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 3
Мы используем
цифру, чтобы
определить, что:
2
csc   x  4 / x
dx x2  4
 Следовательно,
x  C
2 2
x 4 4x

35. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 4
x
Найдите  dx
2
x 4
 Можно было бы использовать тригонометрическую
замену x = 2 tan θ (как в примере 3).

36. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 4
 Однако прямая замена u = x2 + 4
проще.
 Это потому, что du = 2x dx
и
x 1 du
 dx  
2
x 4 2 u
 u C
2
 x 4 C

3 7. 002 7. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Примечание
Пример 4 иллюстрирует тот факт, что даже
когда тригонометрические замены возможны,
они могут не дать самого простого решения.
 Сначала следует поискать более простой метод.

38. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 5
Оценить dx
 2
х a 2
, где а > 0.

39. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5 — Решение 1
. Положим x = a sec θ, где 0 π Тогда dx = a sec θ tg θ dθ и
2 2 2 2
x  a  a (sec   1)
2 2
 a загар 
загар  загар 

40. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5—Раствор 1
dx a sec  tan 
  d
2
x a 2 a tan 
сек  d
ln сек   загар   C

41. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5 — Решение 1
Треугольник на рисунке дает:
2 2
tan   x  a / a

42. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E.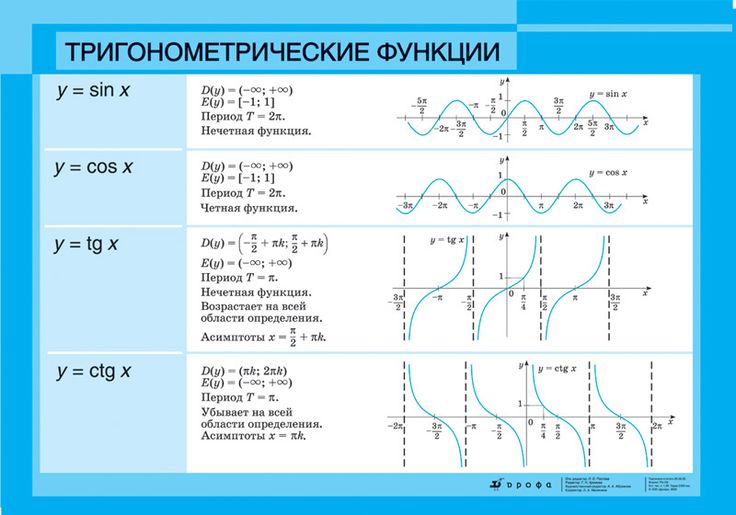 g. 5—Решение 1
Итак, имеем:
2 2
dx x x a
 ln  C
2
x a 2 a a
2 2
ln x 0  8 ln 3 C  a

43. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5 — Сол. 1 (Для 1)
Записав C1 = C – ln a, имеем:
dx 2 2
 ln x  x  a  C1
2 2
x a

44. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5 — Решение 2
Для x > 0 можно также использовать гиперболическую замену
x = a ch t.
 Используя тождество ch3y – sh3y = 1,
, имеем:
x 2  a 2  a 2 (ch 2 t  1)
2 2
 a sh t
 a sh t

4 90. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5—Решение 2
Поскольку dx = a sh t dt,
, получаем:
dx a sh t dt
 
2
x a 2 a sh t
dt
t 9 02 4 C

ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5 — Сол. 2 (For. 2)
Так как ch t = x/a, то t = ch-1(x/a)
dx  x
1
 ch    C
2
x a 2
а

47. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА E. g. 5 — Сол. 2 (For. 2)
Хотя Формулы 1 и 2 выглядят вполне
отличаются, они фактически эквивалентны
Формула 4 в Разделе 3.11

48. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Примечание
Как показывает пример 5, гиперболические
замены могут использоваться вместо
тригонометрических замен, и иногда
они приводят к более простым ответам.
 Однако мы обычно используем тригонометрические замены,
потому что тригонометрические тождества более знакомы
, чем гиперболические тождества.

49. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 6
3
3 3/2 x
 2 3/ 2
dx
0 (4 x  9)
 Во-первых, отметим, что (4 x 2  9)3/ 2 ( 4 x 2  9)3
 Итак, уместна тригонометрическая замена.

50. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 6
2
4 x  9 не совсем одно из
выражений в таблице тригонометрических
 Однако оно становится одним, если мы делаем
предварительная замена u = 2x.

51. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 6
Когда мы комбинируем это с подстановкой касательной
, мы получаем x  32 tan .
2
Это дает dx  с  d и
3
2
2 2
4 x  9  9 tan   9
3 с 

520002 9.000 ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 6
Когда x = 0, tan θ = 0; поэтому θ = 0,
Когда x = 3 3/2, тангенс θ = 3; поэтому θ = π/3.

53. ТРИГОНОМЕТРИЧЕСКАЯ ЗАМЕНА Пример 6
3 3/2
3
x  / 3 27
8 tan 3  3 2
 2 3/ 2
dx  3 2 сек  9  0 (2  d
Sec 
3
ϩ / 3tan 
3
16  D
0 сек. 
3
ϩ / 3 sin 
163  2
DrIIT 
163  2
sin  d
0 cos 

54. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 6
Теперь подставим u = cos θ так, чтобы
du = — sin θ dθ.
 Когда θ = 0, u = 1.
 Когда θ = π/3, u = ½.

55. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 6
3
3 3/2 x
Следовательно, dx
0 2
(4 x  9) 3/ 2
2
1/ 2 1 u
 1 3 160 3

83 DU

U
1/2
 3
16 1  (1  U  2) DU
1/2
 1
 U  
3
16
 U 1
163    12  2   (1 1)   323

56. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 7
x
Вычислить  3  2x  x dx
2
 Подынтегральную функцию можно преобразовать в функцию
, для которой подходит тригонометрическая подстановка,
, сначала заполнив квадрат под знаком корня:
3  2 х  х 2 3  ( х 2  2 х)
3  1  ( х 2  2 х  1)
4  ( х  1) 2

5 7.002 ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 7
Это предлагает сделать замену
u = x + 1.
 Тогда du = dx и x = u – 1.
x u 1
 Итак,
 3 ﲀ 2x  x dx  ду
2
4  у2

58. ТРИГОНОМЕТРИЧЕСКАЯ ПОДСТАВКА Пример 7
Теперь заменим u 2sin  .