Обратная матрица примеры с решением: 1.3.4. Примеры решения задач по теме «Обратная матрица»

1.3.4. Примеры решения задач по теме «Обратная матрица»

Задача 1.

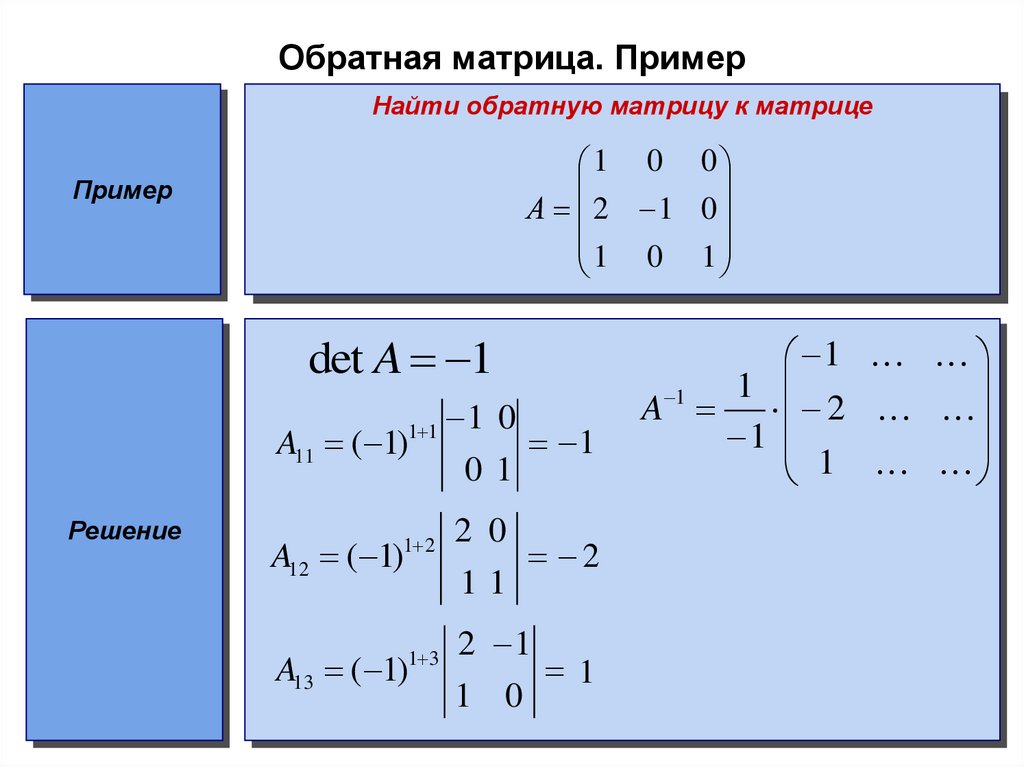
Найти обратную матрицу для матрицы

И проверить выполнение условий ­А А-1 = А-1А = Е.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

Убедимся, что матрица А – невырожденная. ΔА = 1·4 — 2·(-1) ≠ 0, следовательно, А-1 существует.

Вычислим алгебраические дополнения к элементам А:

Применим способ вычисления обратной матрицы:

.

Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы!

Найдем произведения ­А А-1 и А-1А:

Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.

Ответ: .

Задача 2.

Найти обратную матрицу для матрицы

.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

Следовательно, матрица А невырожденная, и обратная матрица существует.

Вычислим алгебраические дополнения к элементам матрицы А:

Обратная матрица имеет вид:

Ответ: .

Задача 3.

Найти обратную матрицу для матрицы

.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

Вычислим определитель матрицы А разложением по первому столбцу:

.

Следовательно, обратная матрица для матрицы А существует.

Найдем алгебраические дополнения к элементам матрицы А:

Значит,

.

Ответ: .

Задача 4.

Найти обратную матрицу для матрицы

.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

.

Ответ:

Задача 5.

При каких X, Y, Z матрица

Является обратной к матрице

Указание

Необходимым условием того, что В = А-1, является требование АВ = Е.

Решение

Проверим невырожденность матрицы А:

Необходимым условием того, что В = А-1, является требование АВ = Е.

Найдем АВ:

Для того, чтобы выполнялось условие АВ = Е, X, Y, Z должны быть решением системы уравнений

Проверим, будет ли равно единичной матрице произведение ВА:

Значит, при найденных значениях X

, Y, Z В = А-1.

Ответ: X = -3, Y = -3, Z = 4.

< Предыдущая		Следующая >

Что такое обратная матрица и как её найти — Журнал «Код»

10. 03.2021

Что такое обратная матрица

Сложная тема из линейной алгебры.

Сложная тема из линейной алгебры.

Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко: 

Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.

С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры. 

Читать ли эту статью?

❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной. 

✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс. 

Обратное — это как? 

В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число: 

Обратные числа при умножении друг на друга всегда дают единицу:

Обратная матрица

В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.

Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:

Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.

Пример квадратной единичной матрицы размером 5×5. Единичная матрица может быть любого размера — состоять из любого количества строк и столбцов

Как рассчитать обратную матрицу

Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:

1. Разделить единицу на матричный определитель. 
2. Найти транспонированную матрицу алгебраических дополнений. 
3. Перемножить полученные значения.

Далее мы по порядку во всём разберёмся.

Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополнений

Определитель — это особое число, которое «определяет» свойства матрицы. 

Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3. 

Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.

Формула для расчёта определителя второго порядка

Пример расчёта определителя второго порядка

Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям. 

Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.

Считаем определитель третьего порядка: 1-й этап — главная диагональ

Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.

Считаем определитель третьего порядка: 2-й этап — первый треугольник

Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.

Считаем определитель третьего порядка: 3-й этап — второй треугольник

Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.

Считаем определитель третьего порядка: 4-й этап — вторая диагональ

Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.

Считаем определитель третьего порядка: 5-й этап — третий треугольник

Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.

Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник

Общий вид формулы для расчёта определителя третьего порядка

Пример расчёта определителя третьего порядка

Транспонированная матрица алгебраических дополнений вычисляется в три шага: 

1. Мы из исходной матрицы находим матрицу миноров. 
2. Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений. 
3. Находим транспонированную матрицу из матрицы алгебраических дополнений. 

Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка. 

Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы: 

• Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.  
• Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров. 
• Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров. 
• Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров. 

Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.

Пример вычисления матрицы миноров из матрицы второго порядка

Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка

Матрица миноров третьего порядка рассчитывается по следующему принципу: 

1. Последовательно вычёркиваем строки и столбцы. 
2. Получаем четыре элемента и считаем определитель.  
3. Записываем результат в матрицу миноров третьего порядка. 

Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему: 

1. Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
2. Найдите этот же элемент в исходной матрице и отметьте его точкой. 
3. Проведите от этой точки две линии: вдоль строки и вдоль столбца. 

После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.

Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы

Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами. 

1-я строка 1-й элемент:  

Δ = 5×1 — 8×6 = -43

1-я строка 2-й элемент: 

Δ = 4×1 — 7×6 = -38

1-я строка 3-й элемент: 

Δ = 4×8 — 7×5 = -3

2-я строка 1-й элемент: 

Δ = 2×1 — 8×3 = -22

2-я строка 2-й элемент: 

Δ = 1×1 — 7×3 = -20

2-я строка 3-й элемент: 

Δ = 1×8 — 7×2 = -6

3-я строка 1-й элемент: 

Δ = 2×6 — 5×3 = -3

3-я строка 2-й элемент: 

Δ = 1×6 — 4×3 = -6

3-я строка 3-й элемент: 

Δ = 1×5 — 4×2 = -3

Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.

Получаем из матрицы третьего порядка матрицу миноров

Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)

Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка

Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:

Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось

Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными

Господи, зачем всё это?

Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь? 

Смотрите: 

• Вам не нужно уметь решать все эти уравнения самостоятельно. Для этого давно есть мощные алгоритмы. 
• Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда. 
• В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
• И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия. 

«Программисты, которые умеют писать алгоритмы, — нишевая профессия»

Спокойствие, всё будет хорошо. 

Текст:

Александр Бабаскин

Редактура:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Мария Дронова

Соцсети:

Олег Вешкурцев

Получите ИТ-профессию

В «Яндекс Практикуме» можно стать разработчиком, тестировщиком, аналитиком и менеджером цифровых продуктов. Первая часть обучения всегда бесплатная, чтобы попробовать и найти то, что вам по душе. Дальше — программы трудоустройства.

Начать карьеру в ИТ

Обратная матрица — Найти, Формула, Примеры

Обратная матрица для матрицы A обозначается A ^-1 . Обратную матрицу 2 × 2 можно вычислить по простой формуле. Далее, чтобы найти обратную матрицу порядка 3 и выше, нам нужно знать определитель и сопряженную матрицу. Обратной матрицей является другая матрица, которая при умножении на данную матрицу дает мультипликативную идентичность.

Обратная матрица используется для нахождения решения линейных уравнений методом обращения матриц. Здесь давайте узнаем о формуле, методах и терминах, связанных с обратной матрицей.

1.	Что такое обратная матрица?
2.	Обратная матричная формула
3.	Как найти обратную матрицу?
4.	Термины, относящиеся к обратной матрице
5.	Методы поиска обратной матрицы
6.	Инверсия матрицы 2 x 2
7.	Обратная матрица 3 x 3
8.	Определитель обратной матрицы
9.	Часто задаваемые вопросы об обратной матрице

Что такое обратная матрица?

, обратная матрице , является другой матрицей, которая при умножении на данную матрицу дает мультипликативную идентичность. Для матрицы A обратной является A ^-1 и A · A ^-1 = A ^-1 · A = I, где I — единичная матрица. Матрица, определитель которой отличен от нуля и для которой можно вычислить обратную матрицу, называется обратимой матрицей. Например, инверсия A = \(\left[\begin{array}{rr}

1&-1\\
0 и 2
\end{массив}\right]\) равно \(\left[\begin{array}{cc}
1&1/2\\
0 и 1/2
\end{массив}\right]\) как

• A · A ^-1 = \(\left[\begin{array}{rr}
  1&-1\\
  0 и 2
  \end{массив}\right]\) \(\left[\begin{массив}{cc}
  1&1/2\\
  0 и 1/2
  \end{массив}\right]\) = \(\left[\begin{массив}{cc}
  1 & 0 \\\
  0 и 1
  \конец{массив}\справа]\) = I
• A ^-1 · A = \(\left[\begin{array}{cc}
  1&1/2\\
  0 и 1 / 2
  \end{массив}\right]\) \(\left[\begin{массив}{rr}
  1&-1\\
  0 и 2
  \end{массив}\right]\) = \(\left[\begin{массив}{cc}
  1 & 0 \\\
  0 и 1
  \конец{массив}\справа]\) = I

Но как найти обратную матрицу? Давайте посмотрим в следующих разделах.

Формула обратной матрицы

В случае действительных чисел, обратное любому вещественному числу a было числом a ^-1 , так что a умножить на a ^-1 равно 1. Мы знали, что для действительного числа обратным числом является обратное число, пока число не равно нулю. Обратной квадратной матрицей A, обозначаемой A ^-1 , является матрица, так что произведение A и A ^-1 является единичной матрицей. Полученная единичная матрица будет того же размера, что и матрица A.

Поскольку |А| находится в знаменателе приведенной выше формулы, обратная матрица существует только в том случае, если определитель матрицы имеет ненулевое значение. т. е. |А| ≠ 0,

Как найти обратную матрицу?

Чтобы найти обратную квадратную матрицу A, мы используем следующую формулу: A ^-1 = adj(A) / |A| ; |А| ≠ 0

, где

• A — квадратная матрица.
• adj(A) — присоединенная матрица матрицы A.
• |А| является определителем A.

Примечание: Для матрицы, обратной которой существует:

• Данная матрица должна быть квадратной матрицей.
• Определитель матрицы не должен быть равен нулю.

Приведенные ниже термины помогают лучше понять и упростить расчет обратной матрицы.

Минор: Минор определяется для каждого элемента матрицы. Минором конкретного элемента называется определитель, полученный после исключения строки и столбца, содержащих этот элемент. Для матрицы A = \(\begin{pmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{ 33}\end{pmatrix}\), минор элемента \(a_{11}\) равен:

Минор от \(a_{11}\) = \(\left|\begin{matrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{matrix}\right|\ )

Кофактор: Кофактор элемента вычисляется путем умножения минора с -1 на показатель степени суммы элементов строки и столбца в порядке представления этого элемента.

Кофактор \(a_{ij}\) = (-1) ^{i + j} × минор \(a_{ij}\).

Определитель: Определитель матрицы — это представление единственного уникального значения матрицы. Определитель матрицы можно вычислить относительно любой строки или столбца данной матрицы. Определитель матрицы равен сумме произведения элементов и его сомножителей определенной строки или столбца матрицы.

Сингулярная матрица: Матрица с нулевым определителем называется сингулярной матрицей. Для сингулярной матрицы A |A| = 0. Обратная сингулярная матрица не существует.

Несингулярная матрица: Матрица, значение определителя которой не равно нулю, называется невырожденной матрицей. Для невырожденной матрицы |A| ≠ 0 и, следовательно, существует обратное ему.

Сопряженная матрица: Сопряженная матрица является транспонированием матрицы элементов кофактора данной матрицы.

Правила для операций со строками и столбцами определителя:

Следующие правила полезны для выполнения операций со строками и столбцами над определителями.

• Значение определителя не изменится, если строки и столбцы поменять местами.
• Знак определителя меняется, если поменять местами любые две строки или (два столбца).
• Если любые две строки или столбца матрицы равны, то значение определителя равно нулю.
• Если каждый элемент определенной строки или столбца умножается на константу, то значение определителя также умножается на константу.
• Если элементы строки или столбца выражены в виде суммы элементов, то определитель может быть выражен в виде суммы определителей.
• Если элементы строки или столбца сложить или вычесть с соответствующими кратными элементам другой строки или столбца, то значение определителя остается неизменным.

Методы поиска обратной матрицы

Обратную матрицу можно найти двумя способами. Обратную матрицу можно вычислить с помощью элементарных операций и с помощью сопряженной матрицы. Элементарные операции над матрицей можно выполнять с помощью преобразований строк или столбцов. Кроме того, обратную матрицу можно вычислить, применяя формулу обратной матрицы с использованием определителя и сопряженной матрицы. Для выполнения обратной матрицы с помощью элементарных операций со столбцами мы используем матрицу X и вторую матрицу B в правой части уравнения.

• Элементарные операции со строками или столбцами
• Обратная формула матрицы (с использованием сопряженного и определителя матрицы)

Проверим каждый из способов, описанных ниже.

Элементарные операции со строками

Чтобы вычислить обратную матрицу A с помощью элементарных преобразований строк, мы сначала берем расширенную матрицу [A | I], где I — единичная матрица, порядок которой такой же, как у A. Затем мы применяем операции со строками, чтобы преобразовать левую часть A в I. Затем матрица преобразуется в [I | А ^-1 ]. Для получения более подробной информации о процессе нажмите здесь.

Элементарные операции со столбцами

Мы можем применить операции со столбцами так же, как это было объяснено для операций со строками, чтобы найти обратную матрицу.

Формула, обратная матрице

Обратная матрица A может быть вычислена с помощью формулы, обратной матрице, путем деления сопряженной матрицы на определитель матрицы. Обратную матрицу можно вычислить, выполнив следующие шаги:

• Шаг 1: Вычислите миноры всех элементов A.
• Шаг 2: Затем вычислите кофакторы всех элементов и напишите матрицу кофакторов, заменив элементы A их соответствующими кофакторами.
• Шаг 3: Найдите примыкание к A (записывается как adj A), взяв транспозицию кофакторной матрицы A.
• Шаг 4: Умножьте adj A на обратную величину определителя.

9{1 + 3} \left|\begin{matrix}a_{21}&a_{22}\\a_{31}&a_{32}\end{matrix}\right|\)

Adj A = Транспонирование матрицы кофакторов

= Транспонирование \(\begin{pmatrix} A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{ 33}\end{pmatrix}\)

=\(\begin{pmatrix} A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13 }&A_{23}&A_{33}\end{pmatrix}\)

A ^-1 = \(\dfrac{1}{|A|}. \begin{pmatrix} A_{11}&A_{21} &A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\end{pmatrix}\)

В этом разделе мы изучили различные методы вычисления обратной матрицы. Давайте лучше поймем это, используя несколько примеров для разных порядков матриц в разделе «Примеры» ниже.

Инверсия матрицы 2 x 2

Обратную матрицу 2 × 2 легче вычислить по сравнению с матрицами более высокого порядка. Мы можем вычислить обратную матрицу 2 × 2, используя общие шаги для вычисления обратной матрицы. Найдем обратную матрицу 2 × 2, приведенную ниже:
A = \(\begin{bmatrix} a & b \\ \\ c & d \end{bmatrix}\)
A ^-1 = (1/|A|) × Adj A
= [1/(ad — bc)] × \(\begin{bmatrix} d & -b \\ \\ -c & a \end{bmatrix}\)

Следовательно, чтобы вычислить обратную 2 × 2, нам нужно сначала поменять местами члены a и d и поставить отрицательные знаки для членов b и c, и, наконец, разделить его на определитель матрицы.

Инверсия матрицы 3 x 3

Мы знаем, что для каждой неособой квадратной матрицы A существует обратная матрица A ^-1 , такая что A × A ^-1 = I. Возьмем любую квадратную матрицу 3 × 3, заданную как

A = \(\begin{bmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{bmatrix}\)

Обратную матрицу 3×3 можно вычислить по формуле обратной матрицы: A ^-1 = (1/|A|) × Adj A

Сначала мы проверим, является ли данная обратим, т. е. |A| ≠ 0. Если существует обратная матрица, мы можем найти сопряженную данную матрицу и разделить ее на определитель матрицы.

Аналогичным методом можно найти обратную любую матрицу размера n × n. Давайте посмотрим, можно ли использовать аналогичные шаги для вычисления обратной матрицы m × n, где m ≠ n.

Обратная матрица 2 × 3

Мы знаем, что первое условие существования обратной матрицы состоит в том, что данная матрица должна быть квадратной матрицей. Кроме того, определитель этой квадратной матрицы не должен быть равен нулю. Это означает, что обратной матрицы порядка m × n не будет, где m ≠ n. Следовательно, мы не можем вычислить обратную матрицу 2 × 3.

Обратная матрица 2 × 1

Как и обратная матрица 2 × 3, обратная матрица 2 × 1 также не существует, поскольку данная матрица не является квадратной матрицей.

Определитель обратной матрицы

Определитель обратной обратимой матрицы является обратным определителем исходной матрицы. т. е. det(A ^-1 ) = 1/det(A). Проверим доказательство предыдущего утверждения.

Мы знаем, что det(A • B) = det (A) × det(B)

Кроме того, A × A ^-1 = I

det(A × A ^-1 ) = det(I)

или det(A) × det(A ^-1 ) = det( I)

Поскольку det(I) = 1

det(A) × det(A ^-1 ) = 1

или det(A ^-1 ) = 1 / det(A)

Значит, доказано.

☛ Статьи по теме:

Следующие ссылки по теме помогут лучше понять обратную матрицу.

• Калькулятор обратной матрицы
• Калькулятор умножения матриц
• Калькулятор определителя

Важные моменты, касающиеся обратной матрицы:

Следующие пункты помогут лучше понять идею обратной матрицы.

• Обратная квадратная матрица (если существует) уникальна.
• Если A и B две обратимые матрицы одного порядка, то (AB) ^-1 = B ^-1 A ^-1 .
• Обратная квадратная матрица A существует, только если ее определитель не равен нулю, |A| ≠ 0,
• Определитель обратной матрицы равен обратной величине определителя исходной матрицы.
• Определитель произведения двух матриц равен произведению определителей двух отдельных матриц. |АВ| = |А|.|В|

Cuemath — одна из ведущих в мире платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Обратные примеры матриц

1. Пример 1: Найдите обратную матрицу A = \(\left(\begin{matrix}-3 & 4\\2 & 5 \end{matrix}\right)\).

   Решение:

   Дана матрица A = \(\left(\begin{matrix}-3 & 4\\ \\2 & 5 \end{matrix}\right)\).

   Формула для вычисления матрицы, обратной A = \(\left(\begin{matrix}a&b\\\\c&d\end{matrix}\right)\) A ^-1 = \(\dfrac{ 1}{ad — bc}\left(\begin{matrix}d&-b\\\\-c&a\end{matrix}\right)\).

   Используя эту формулу, мы можем вычислить A ^-1 следующим образом.

   A ^-1 = \(\dfrac{1}{(-3)× 5 — 4 × 2}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix }\right)\)

   = \(\dfrac{1}{-15 — 8}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix}\right)\ )

   = \(\dfrac{-1}{23}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix}\right)\)

   Ответ: Следовательно, A ^-1 = \(\dfrac{-1}{23}\left(\begin{matrix}5&-4\\\\-2&-3\end{matrix}\right)\)

2. Пример 2: Найдите матрицу, обратную матрице A = \(\left(\begin{matrix}4 & -2 & 1\\5&0&3\\-1&2 & 6\end{matrix}\right)\) .

   Решение:

   Дана матрица A = \(\left(\begin{matrix}4 & -2 & 1\\5&0&3\\-1&2 & 6\end{matrix}\right)\)

   Шаг — 1: Найдем определитель данной матрицы, используя Строку — 1 вышеприведенной матрицы.

   |А| = \(4\left|\begin{matrix}0&3\\2 & 6\end{matrix}\right| -(-2)\left|\begin{matrix}5&3\\-1 & 6\end{matrix }\right|+1\left|\begin{matrix}5&0\\-1& 2\end{matrix}\right|\)

   = 4(0 х 6 — 3 х 2) + 2(5 х 6 — (-1) х 3) +1(5 х 2 — 0 х (-1))

   = 4(0 — 6) + 2(30 + 3) + 1(10 — 0)

   = -24 + 66 + 10

   = 52

   Теперь определим сопряженную матрицу A, вычислив кофакторы каждого элемента, а затем взяв транспонирование кофакторной матрицы.

   Adj A = \(\left(\begin{matrix}-6 & 14 & -6\\-33&25&-7\\10&-6 & 10\end{matrix}\right)\)

   Инверсия матрица A задается формулой A ^-1 = \(\dfrac{1}{|A|}\).Adj A

   A ^-1 = \(\dfrac{1}{52}\).\(\left(\begin {матрица}-6 и 14 и -6\\-33&25&-7\\10&-6 и 10\конец{матрица}\справа)\)

   = \(\слева(\начало{матрица}-3/26 & 7/26 & -3/26\\-33/52&25/52&-7/52\\5/26&-3/26 & 5/26\end{matrix}\right)\)

   Ответ: A ^-1 = \(\left(\begin{matrix}-3/26 & 7/26 & -3/26\\-33/52&25/52&-7/52\\5/26&-3/26 & 5/26\конец{матрица}\справа)\) 9{-1} = \dfrac{1}{22} \begin{pmatrix}5 & -2 \\\\ 1 & 4 \end{pmatrix} = \begin{pmatrix} 5/22 & -2/22 \\ \\ 1/22 & 4/22 \end{pmatrix} \)

   Ответ: Обратная заданной матрицы \( = \begin{bmatrix} 5/22 & -1/11 \\\\ 1/22 & 2/11 \end{bmatrix}\)

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по обратной матрице

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об обратной матрице

Что означает обратная матрица?

, обратная матрице , является другой матрицей, которая умножается на данную матрицу и дает мультипликативную идентичность. Для матрицы A обратная ей равна A ^-1 , а A · A ^-1 = I. Общая формула обратной матрицы равна присоединенной матрице, деленной на определитель матрицы. т. е. А ^-1 = \(\dfrac{1}{|A|}\) · Adj A. Обратная матрица существует только в том случае, если определитель матрицы имеет ненулевое значение.

Как найти обратную матрицу?

Обратная квадратная матрица находится в два простых шага. Сначала вычисляются определитель и сопряженный к данной квадратной матрице. Далее сопряженная матрица делится на определитель, чтобы найти обратную матрицу. Обратная матрица A равна \(\dfrac{1}{|A|}\).Adj A.

Как найти обратную матрицу 2 × 2?

Обратная матрица 2 × 2 равна сопряженной матрице, деленной на определитель матрицы. Для матрицы A = \(\left(\begin{matrix}a&b\\ \\c&d\end{matrix}\right)\) ее сопряженный равен перестановке элементов первой диагонали и смене знака элементов второй диагонали. Формула обратной матрицы выглядит следующим образом.

A ^-1 = \(\dfrac{1}{ad — bc}\left(\begin{matrix}d&-b\\\\-c&a\end{matrix}\right)\)

Как использовать обратную матрицу?

Обратная матрица полезна при решении уравнений методом обращения матриц. Метод обращения матриц с использованием формулы X = A ^-1 B, где X — переменная матрица, A — матрица коэффициентов, а B — постоянная матрица.

Можно ли вычислить обратную матрицу для обратимой матрицы?

Да, для обратимой матрицы можно вычислить обратную матрицу. Матрица, определитель которой не равен нулю, является невырожденной матрицей. А для невырожденной матрицы мы можем найти определитель и обратную матрицу.

Когда обратная матрица не существует в некоторых случаях?

Матрица, обратная матрице, существует только в том случае, если значение ее определителя не равно нулю и данная матрица является квадратной матрицей. Поскольку сопряженная матрица делится на определитель матрицы, чтобы получить обратную матрицу. Матрица, определитель которой не равен нулю, называется невырожденной матрицей. Обратная матрица не определена для прямоугольных матриц.

Какова формула обратной матрицы?

Формула обратной матрицы используется для определения обратной матрицы для любой заданной матрицы. Обратная квадратная матрица A равна A ^-1 только тогда, когда: A × A ^-1 = A ^-1 × A = I . Формула обратной матрицы может быть представлена ​​как A ^-1 = adj(A)/|A|; |А| ≠ 0, где A — квадратная матрица.

Для данной матрицы 2 × 2. Какова формула для нахождения обратной матрицы?

Для заданной матрицы 2×2 A = \(\left(\begin{matrix}a&b\\ \\c&d\end{matrix}\right)\) , обратная дается A ^-1 = \(\dfrac{1}{ad — bc}\left(\begin{matrix}d&-b\\\\-c&a\end{matrix}\right)\). Здесь A ^-1 является инверсией A.

Что такое инверсия матрицы идентичности?

Обратная единичная матрица сама по себе. Это связано с тем, что для любой единичной матрицы порядка I мы имеем I × I = I × I = I. Для получения дополнительной информации нажмите здесь.

Как использовать формулу обратной матрицы?

Формулу обратной матрицы можно использовать, выполнив указанные шаги:

• Шаг 1: Найдите матрицу миноров для данной матрицы.
• Шаг 2: Затем найдите матрицу кофакторов.
• Шаг 3: Найдите сопряженное, транспонировав матрицу кофакторов.
• Шаг 4: Разделите на определитель.

Что такое формула обратной матрицы 3 × 3?

Формула обратной матрицы для матрицы 3 × 3: A ^-1 = adj(A)/|A|; |А| ≠ 0, где A = квадратная матрица, adj(A) = сопряженная квадратная матрица, A ^-1 = обратная матрица.

Что является обратной диагональной матрицей?

Обратная диагональная матрица снова является диагональной матрицей, в которой элементы главной диагонали обратной матрицы являются обратными величинами соответствующих элементов исходной матрицы. Чтобы узнать, как это доказать, нажмите здесь.

Обратная матрица

Сначала прочтите наше введение в матрицы.

Что такое обратная матрица?

Так же, как номер имеет ответную…

Обратное число (примечание: 1 8 также можно записать как 8 ^-1 )

… матрица имеет обратную :

Обратная матрица

Мы пишем A ^-1 вместо 1 A , потому что мы не делим на матрицу!

Есть и другие сходства:

Когда мы умножаем число на его обратное Мы получаем 1 :

8 × 1 8 = 1

, когда мы Multiply A Matrix Matrix Idity , что мы получаем 9059 и идентификатор , что я получаем 98. матрицы):

А × А ^-1 = I

То же самое, когда сначала идет обратное:

1 8 × 8 = 1

A ^-1 × A = I

Идентификационная матрица

Мы только что упомянули «Матрицу личности». Это матричный эквивалент числа «1»:

.

I =

100 010 001

Идентификационная матрица 3×3

• Это «квадрат» (имеет такое же количество строк, как и столбцов),
• У него 1 с по диагонали и 0 с везде.
• Его символ — заглавная буква I .

Матрица идентичности может быть размером 2×2 или 3×3, 4×4 и т. д.

Определение

Вот определение:

Обратное к A равно A ^-1 только тогда, когда:

AA ^-1 = A ^-1 A = I

Иногда обратного нет вообще.

(Примечание: запись AA ^-1 означает A, умноженное на A ^-1 )

Матрица 2×2

Хорошо, а как вычислить обратное?

Ну, для матрицы 2×2 обратное:

−1 = 1 ad-bc

д-б −ок

Другими словами: поменять местами a и d, поставить отрицательных чисел перед b и c, и разделить всего на ad-bc .

Примечание: ad-bc называется определителем.

Давайте попробуем пример:

−1 = 1 4×6−7×2

6−7 −24

= 1 10

6−7 −24

=

0,6−0,7 −0,20,4

Откуда мы знаем, что это правильный ответ?

Помните, должно быть верно, что: AA ^-1 = I

Итак, давайте проверим, что произойдет, если мы умножим матрицу на обратную:

0,6−0,7 −0,20,4

=

4×0,6+7×−0,24×−0,7+7×0,4 2×0,6+6×−0,22×−0,7+6×0,4

=

2,4−1,4−2,8+2,8 1,2−1,2−1,4+2,4

И, эй!, мы получаем Матрицу Личности!
Значит, это правильно.

Должно быть и верным, что: A ^-1 A = I

Почему бы тебе не попробовать их умножить? Посмотрите, получите ли вы также матрицу идентичности:

0,6−0,7 −0,20,4

=

Зачем нужна инверсия?

Потому что с матрицами мы не делим ! Серьезно, нет понятия деления на матрицу.

Но мы можем умножить на обратное , который делает то же самое.

Представьте, что мы не можем делить на числа…

… и кто-то спрашивает: «Как мне разделить 10 яблок с двумя людьми?»

Но мы можем взять , обратное от 2 (что равно 0,5), поэтому мы ответим:

10 × 0,5 = 5

Каждый получил по 5 яблок.

То же самое можно сделать с матрицами:

Допустим, мы хотим найти матрицу X, и мы знаем матрицы A и B:

XA = B

Было бы неплохо разделить обе части на A (чтобы получить X=B/A), но помните нельзя разделить на .

 

Но что, если мы умножим обе части на A ^-1 ?

XAA ^-1 = BA ^-1

И мы знаем, что AA ^-1 = I, поэтому:

XI = BA ^-1

Мы можем удалить I (по той же причине мы можем удалить I можно удалить «1» из 1x = ab для чисел):

X = BA ^-1

И у нас есть ответ (при условии, что мы можем вычислить A ^-1 )

В этом примере мы очень внимательно следили за правильным умножением, потому что в случае с матрицами важен порядок умножения. AB почти никогда не равен BA.

Пример из жизни: автобус и поезд

Группа совершила поездку на автобусе по цене 3 доллара США за ребенка и 3,20 доллара США за взрослого на общую сумму 118,40 долларов США.

Они сели на поезд обратно по цене 3,50 доллара за ребенка и 3,60 доллара за взрослого, всего 135,20 доллара.

Сколько детей и сколько взрослых?

Во-первых, давайте настроим матрицы (будьте внимательны, чтобы строки и столбцы были правильными!):

Это как в примере выше:

ХА = В

Итак, чтобы решить это, нам нужно обратное «А»:

33,5 3.23.6

−1 = 1 3×3,6−3,5×3,2

3,6−3,5 −3,23

=

−98,75 8−7,5

 

Теперь у нас есть обратное, которое мы можем решить, используя:

Х = БА ^-1

=

118,4 135,2

−98,75 8−7,5

=

118,4×−9 + 135,2×8118,4×8,75 + 135,2×−7,5

Было 16 детей и 22 взрослых!

Ответ появляется почти как по волшебству. Но он основан на хорошей математике.

Подобные расчеты (но с использованием гораздо более крупных матриц) помогают инженерам проектировать здания, используются в видеоиграх и компьютерной анимации, чтобы вещи выглядели трехмерными, и во многих других местах.

Это также способ решения систем линейных уравнений.

Расчеты выполняются компьютером, но люди должны понимать формулы.

 

Заказ важен

Предположим, что мы пытаемся найти «X» в этом случае:

AX = B

Это отличается от приведенного выше примера! X теперь после A.

С матрицами порядок умножения обычно меняет ответ. Не думайте, что AB = BA, это почти никогда не верно.

 

Итак, как решить эту задачу? Используя тот же метод, но поместите A ^-1 впереди:

A ^-1 AX = A ^-1 B

И мы знаем, что A ^-1 A= I, поэтому:

IX = A ^-1 B

Мы можем удалить I:

X0 = A

1 B

И у нас есть ответ (при условии, что мы можем вычислить A ^-1 )

Почему бы нам не попробовать наш пример с автобусом и поездом, но с данными, настроенными таким образом.

Это можно сделать и так, но мы должны быть осторожны при настройке.

Вот как это выглядит, когда AX = B:

33,2 3.53.6

=

118,4 135,2

Выглядит так аккуратно! Я думаю, что предпочитаю это так.

Также обратите внимание, как строки и столбцы меняются местами в
(«Транспонированные») по сравнению с предыдущим примером.

Чтобы решить это, нам нужно обратное «А»:

33,2 3.53.6

−1 = 1 3×3,6−3,2×3,5

3,6−3,2 −3,53

=

−98 8,75−7,5

Это похоже на инверсию, которую мы получили раньше, но
Transposed (строки и столбцы меняются местами).

Теперь мы можем решить, используя:

Х = А ^-1 В

=

−98 8,75−7,5

118,4 135,2

=

−9×118,4 + 8×135,2 8,75×118,4 − 7,5×135,2

Тот же ответ: 16 детей и 22 взрослых.

Итак, матрицы — мощная штука, но их нужно правильно настроить!

 

Обратное может не существовать

Прежде всего, чтобы получить обратную матрицу, она должна быть «квадратной» (одинаковое количество строк и столбцов).

Но также и определитель не может быть равен нулю (иначе мы закончим делением на ноль). Как насчет этого:

−1 = 1 3×8−4×6

8−4 −63

= 1 24−24

8−4 −63

24−24? Это равно 0, а 1/0 не определено .
Дальше идти нельзя! Эта матрица не имеет обратной.

Такая матрица называется «Singular»,
что происходит только тогда, когда определитель равен нулю.

И в этом есть смысл… посмотрите на числа: вторая строка просто удваивает первую строку, и не добавляет никакой новой информации .

И определитель 24−24 позволяет нам узнать об этом факте.

No related posts.