Округлить сомнительные цифры числа оставив верные цифры: Округлить сомнительные цифры числа, оставив верные знаки: 0,34484 б=0,4%

alexxlab / / Разное

Содержание

Последовательность выполнения работы — МегаЛекции

Главная | Обратная связь | Поможем написать вашу работу!
  • Архитектура
  • Биология
  • География
  • Искусство
  • История
  • Информатика
  • Маркетинг
  • Математика
  • Медицина
  • Менеджмент
  • Охрана труда
  • Политика
  • Правоотношение
  • Разное
  • Социология
  • Строительство
  • Физика
  • Философия
  • Финансы
  • Химия
  • Экология
  • Экономика
  • Электроника

ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ

Теоретические сведения

Абсолютная и относительная погрешности. Знак равенства в приближенных вычислениях имеет не тот смысл, как в алгебре.

Равенство означает не совпадение значений, а лишь близость значений. Точность приближенного равенства, т.е. степень близости точного значения и приближенного , характеризует абсолютная погрешность,

.

На практике вместо абсолютной погрешности, которая обычно неизвестна, используют предельную абсолютную погрешность,

причем слово предельная для краткости опускают. Если интересует точность уже проведенного расчета, то за берут число, которое возможно ближе к “истинной” погрешности. Называют это оценкой погрешности. Оценка погрешности может быть грубой или более точной. Погрешность может быть задана заранее, тогда вычисление проводится так, чтобы это неравенство выполнялось.

Для того чтобы записать, что является приближенным значением с абсолютной погрешностью , пишут:

Относительной погрешностью, часто выражаемой в процентах, называют величину такую, что

Относительная погрешность более полно характеризует степень точности приближенного числа, поскольку можно сравнивать точность задания величин, как существенно различающихся по порядку, так и выраженных в разных единицах измерения.

Верные и сомнительные цифры. Значащую цифру называют верной в узком смысле, если абсолютная погрешность числа не превышает 1/2 единицы разряда, соответствующего этой цифре.

Например, ; ;

.

Имеем ; также . Следовательно, верные цифры в узком смысле 9 и 3. Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превышает единицы разряда, соответствующего этой цифре (В примере 9, 3 и 4). Цифры, стоящие в более младших разрядах, называют сомнительными.

Последовательность выполнения работы

Пример 1. Заданы точное и приближенное значения числа. Найти абсолютную и относительную погрешности (решение приведено на рис. 2.1)

;

;

Рис. 2.1 – Решение примера 1

Пример 2. Найти предельные абсолютные и относительные погрешности чисел и , если они имеют только верные цифры: а) в узком смысле, б) в широком смысле.

Решение задания приведено на рис. 2.2

Рис. 2.2 – Решение примера 2

Пример 3. Задано число и относительная погрешность . Определить количество верных цифр числа по его относительной погрешности.

Решение: так как и , то число имеет, по крайней мере, две цифры, верных в узком смысле. Определим абсолютную погрешность:

Значит, в узком смысле верными являются цифры 2 и 3.

Пример 4. Пусть , . Определить количество верных цифр в числе .

Решение: так как и , то число имеет, по крайней мере, одну цифру, верную в узком смысле (цифра 9). Проверим этот результат, используя определение цифры, верной в узком смысле.

Для этого определим абсолютную погрешность:

Полученная абсолютная погрешность не превышает половину единицы разряда сотен. Следовательно, цифра 9 верна в узком смысле, как по относительной погрешности, так и по абсолютной.

Пример 5. Пусть , . Определить все верные цифры числа.

Решение: так как , то число имеет, по крайней мере, четыре цифры, верных в узком смысле (цифры 2, 4, 3, 0). Вычислим

Пример 6. При взвешивании двух грузов получили следующие значения их масс кг и кг. Считая абсолютную погрешность взвешивания равной 1 г, определить относительную погрешность измерения масс тел . Какое из тел взвешено более точно?

Решение примера на рис. 2.3.

Рис. 2.3 – Решение примера 6

Пример 7. Определить, какое равенство точнее или

Решение: найдем значения данных выражений с бóльшим числом десятичных знаков: , . Вычислим предельные абсолютные погрешности, округляя их с избытком:

Предельные относительные погрешности составляют:

Так как , то равенство является более точным.

Пример 8.Округлить сомнительные цифры числа, оставив верные знаки:

а) в узком смысле ;

б) в широком смысле .

Определить абсолютную погрешность результата.

Решение:

а) пусть . Согласно условию, погрешность ; это означает, что в числе верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдём приближенное значение числа, сохранив десятые доли:

Полученная погрешность больше 0,05; значит, нужно уменьшить число цифр в приближенном числе до двух:

Поэтому обе оставшиеся цифры верны в узком смысле.

б) ; тогда . В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:

Значит, и в округлённом числе все три цифры верны в широком смысле.

Пример 9. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры:

а) в узком смысле ;

б) в широком смысле

Решение: а) так как все четыре цифры верны в узком смысле, то абсолютная погрешность , а относительная погрешность

б) так как все пять цифр числа верны в широком смысле, то: ;

da=1/(1∙104)=0,0001= 0,01%.

Пример 10. Вычислить и определить погрешности результата.

где

Решение. Находим

Далее имеем

откуда

4.

Контрольные вопросы:

1. Что такое абсолютная и относительная погрешности?

2. Что значит цифра, верная в широком и узком смыслах?

3. Как определить количество верных цифр по относительной погрешности приближенного числа?

4. Как определяются абсолютная и относительная погрешности в арифметических действиях?

Варианты заданий к лабораторной работе 2

Задание 1

1) Определить, какое равенство точнее.

2) Округлить сомнительные цифры числа, оставив верные знаки:

а) в узком смысле; б) в широком смысле.

Определить абсолютную погрешность результата.

3) Найти предельные абсолютные и относительные погрешности

чисел, если они имеют только верные цифры:

а) в узком смысле; б) в широком смысле.

Варианты заданий приведены в табл. 1.1.

№ вар. Задание 1 Задание 2 Задание 3
а) б) а) б)
19/41=0,463 =6,630 22,55300 (±0,01600) 2,85460; d=0,30% 0,2387 42,8840
7,15=0,467 =5,480 17,28340; d=0,30% 6,42570 (±0,00240) 3,7510 0,5370
=3,240 4/17=0,253 2,34850 (±0,00420) 0,34484; d=0,40% 11,4450 2,0430
15/7=2,140 =3,160 34,83400; d=0,10% 0,57480 ( ±0,00340) 2,3445 0,7450
6/7=0,857 =2,190 5,43500 (±0,00280) 10,84410; d=0,50% 8,3450 0,2880
12/11=1,091 =2,610 8,24163; d=0,20% 0,12356 (±0,00036) 12,4500 3,4453
2/21=0,095 =4,690 2,45430 (±0,00320) 24,56430; d=0,10% 0,3740 4,3480
23/15=1,530 =3,130 23,57400; d=0,20% 8,34450 (±0,00220) 20,4300 0,5760
6/11=0,545 =9,110 3,78340 (±0,00410) 7,52100; d=0,12% 5,6340 0,0748
17/19=0,895 =7,210 21,68563; d=0,30% 13,53700 (±0,00260) 41,7200 0,6780
21/29=0,723 =6,630 0,35670; d=0,042% 13,62530 (±0,00210) 0,5746 236,5800
50/19=2,630 =5,190 1,78400 (±0,00630) 0,85637; d=0,21% 18,3570 2,1600
13/17=0,764 =5,560 3,68780 (±0,00130) 15,87300; d=0,42% 0,3648 21,7000
7/22=0,318 =3,600 27,15480 (±0,00160) 0,39450; d=0,16% 8,7300 14,8620
17/11=1,545 =4,240 0,86470 (±0,00130) 24,36180; d=0,22% 2,4516 0,8630
5/3=1,667 =6,160 3,75420; d=0,32% 0,98351 (±0,00042) 62,7400 0,3890
49/13=3,770 =3,740 83,73600; d=0,085% 5,64830 (±0,00170) 5,6432 0,0085
13/7=1,857 =2,640 2,88670; d=0,43% 32,74860 (±0,00120) 0,0384 63,7450
19/12=1,580 =3,460 4,88445 (±0,000520) 0,096835; d=0,32% 12,6880 4,6360
51/11=4,640 =5,910 38,42580 (±0,00140) 0,66385; d=0,34% 6,7430 0,5430

 

Задание 2

Задание. Вычислить и определить погрешности результата.

Варианты заданий приведены в табл. 1.2

Вариант
a 3,8500 (±0,0001)
b 2,0435 (±0,0004)
c 62,6000 (±0,0001)
Вариант
a 4,300 (±0,050)
b 17,210 (±0,020)
c 8,200 (±0,050)
m 12,417 (±0,003)
n 8,370 (±0,005)
Вариант
: a 1,141(±0,002)
b 3,156 (±0,001)
h 1,140 (±0,030)
Вариант
a 228,600 (±0,060)
b 86,400 (±0,020)
c 68,700 (±0,050)
Вариант
a 13,500 (±0,020)
b 3,700 (±0,020)
m 4,220 (±0,004)
c 34,500 (±0,020)
d 23,725 (±0,005)

 

Вариант
a 8,530 (±0,050)
b 6,271 (±0,002)
h 12,480 (±0,002)
Вариант
a 3,850 (±0,004)
b 16,200 (±0,050)
c 10,800 (±0,100)
Вариант
a 2,754 (±0,001)
b 11,700 (±0,040)
m 0,560 (±0,005)
c 10,536 (±0,002)
d 6,320 (±0,008)
Вариант
a 0,5620 (±0,0010)
b 0,2518 (±0,0025)
h 0,6800 (±0,0030)
Вариант
a 3,4560 (±0,0020)
b 0,6420 (±0,0005)
c 7,1200 (±0,0040)
Вариант
a 23,160 (±0,020)
b 8,230 (±0,005)
c 145,500 (±0,080)
d 28,600 (±0,100)
m 0,280 (±0,006)
Вариант
a 8,51 (±0,020)
A 23,42 (±0,005)
S 45,80 (±0,100)
h 3,81 (±0,004)
Вариант
a 0,6430 (±0,0005)
b 2,1700(±0,0020)
c 5,8430 (±0,0010)
Вариант
h 21,10 (±0,040)
a 22,08 (±0,020)
b 31,11 (±0,002)
Вариант
a 27,160 (±0,006)
b 5,030(±0,010)
c 3,600 (±0,020)
m 12,375 (±0,004)
n 86,200 (±0,050)
Вариант
a 0,3575 (±0,0002)
b 2,6300 (±0,0100)
c 0,8540 (±0,0005)
Вариант
a 16,342 (±0,001)
b 2,500 (±0,030)
c 38,170 (±0,002)
d 9,140 (±0,005)
m 3,600 (±0,040)
Вариант
a 2,456 (±0,0015)
h 1,760 (±0,0020)
Вариант
D 54,000 (±0,500)
d 8,235 (±0,001)
Вариант
D 36,500 (±0,100)
d 26,350 (±0,005)

 

Воспользуйтесь поиском по сайту:

©2015- 2022 megalektsii. ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.

Теория погрешностей — презентация онлайн

Похожие презентации:

Элементы теории погрешностей

Математические методы в инженерии

Основные понятия вычислительной математики. Элементы теории погрешностей

Теория погрешностей, случайные и систематические погрешности

Приближенные числа. Учет погрешностей результатов операций над приближенными числами

Погрешности измерений

Основные понятия теории погрешностей. Классификация погрешностей

Общие вопросы теории погрешностей и приборов и измерений

Теория погрешностей

Математическое моделирование. Форма и принципы представления математических моделей

1. Лабораторная работа №1

Тема:
Теория погрешностей

2. 1. Источники и классификация погрешности

Под погрешностью понимается некоторая величина, характеризующая
точность результата.
Выделяют три вида погрешностей:
1. Неустранимая погрешность – эта погрешность связана с ошибками
в исходной информации. Причинами этих ошибок могут быть,
например, неточность измерений, невозможность представления
некоторой величины конечной дробью.
2. Погрешность метода связана с тем, что точные операторы и
исходные данные заменяются приближенными. Например, заменяют
интеграл суммой, производную – разностью, функцию – многочленом
или строят бесконечный итерационный процесс, который обрывают
после конечного числа итераций.
3. Погрешность вычислений возникает при округлении
промежуточных и конечных результатов.
2

3. 2. Абсолютная и относительная погрешности

Пусть – точное значение величины, а
– ее приближенное значение.
Абсолютной погрешностью числа
называется наименьшая
величина , удовлетворяющая условию
, т.е. точное
значение величины лежит в интервале
.
Относительной погрешностью называется величина
удовлетворяющая условию
или
,
.
Относительную погрешность часто выражают в процентах. Для этого
необходимо величину
умножить на 100%.
3

4. 3. Верные значащие цифры

Значащими цифрами числа называются все цифры в его записи,
начиная с первой ненулевой слева, например:
1)
— все цифры значащие;
2)
– значащие только
; первые три нуля
незначащие, т.к. они служат вспомогательной цели – определению
положения цифр
, поэтому может быть принята запись
;
3)
и
. В первой записи все семь цифр (и
последние четыре нуля) значащие, во второй – значащие только
.
Верные значащие цифры. Значащая цифра называется верной, если
абсолютная погрешность числа не превосходит
единицы разряда,
соответствующего этой цифре.
4
Пример 1. Пусть
и известно, что
число верных значащих цифр у числа .
Имеем:
Значит, у числа
;
. Определить
и
верные знаки
.
а
и
– сомнительные.
Пример 2. Определить число верных значащих цифр у числа
Пусть
и
.
Так как
верные.
, то у числа
.
три знака после запятой
5

6. Правила округления

При записи чисел руководствуются следующим правилом: все
значащие цифры должны быть верными. Поэтому округление чисел,
записанных в десятичной системе, производится по правилу первой
отбрасываемой цифры:
если первая из отбрасываемых цифр меньше 5, то оставляемые
десятичные знаки сохраняются без изменения;
если первая из отбрасываемых цифр больше или равна 5, то
последняя оставляемая цифра увеличивается на единицу;
Примеры. Округлить числа:
1) 1,2537≈1,25, m=3 – количество верных значащих цифр;
2) 1,2563≈1,26, m=3;
3) 2,36566≈2,37, m=3;
6

7. 4. Прямая задача теории погрешностей:

Оценить погрешность вычисления значений функции по заданной
погрешности аргументов.
Пусть
— непрерывно дифференцируемая функция,
где
;
— приближенные значения аргументов,
;
— абсолютные погрешности аргументов.
Тогда абсолютная погрешность вычисления значения функции в точке
равна
(1.1)
Относительная погрешность значения
в точке
равна
(1.2)
7

8. Погрешность результатов арифметических операций

Погрешность суммы. Абсолютная погрешность алгебраической
суммы приближенных чисел равна сумме абсолютных погрешностей
этих чисел.
Пусть
, тогда
(1.3)
Погрешность разности. Абсолютная погрешность разности
приближенных чисел равна сумме абсолютных погрешностей
уменьшаемого
и вычитаемого .
Пусть
, тогда
(1.4)
Погрешность произведения. Пусть
, известны
и ,
, тогда абсолютная погрешность произведения вычисляется по
формуле
(1.5)
8
Погрешность частного. Пусть
.
Очевидно, что
(1.6)
Из формул (1.3) – (1.6) выводятся формулы для соответствующих
относительных погрешностей:
9

10. Пример (прямая задача)

а) Записать порядок выполняемых операций, оценить погрешности их
результатов, вычислить и оценить погрешность искомого значения .
б) Определить число верных знаков в результате.
0
Решение. а) приближенные значения исходных данных:
,
0,
.
Абсолютные погрешности исходных данных:
,
.
Относительные погрешности исходных данных:
0
10
Порядок выполняемых операций:
11
0
12

13. 5. Обратная задача теории погрешностей

Необходимо определить допустимую погрешность аргументов по
допустимой погрешности функции.
Для функции
одной переменной абсолютную погрешность
можно приближенно вычислить по формуле
Для функции нескольких переменных
:
если значения всех аргументов можно одинаково легко определить с
любой точностью, то применяют принцип равных влияний, т.е.
считают, что все слагаемые
, равны между собой.
Тогда абсолютные погрешности всех аргументов определяются
формулой
13

14. Пример (обратная задача)

Выяснить погрешность задания исходных данных, необходимую для
получения результата с
верными значащими цифрами.
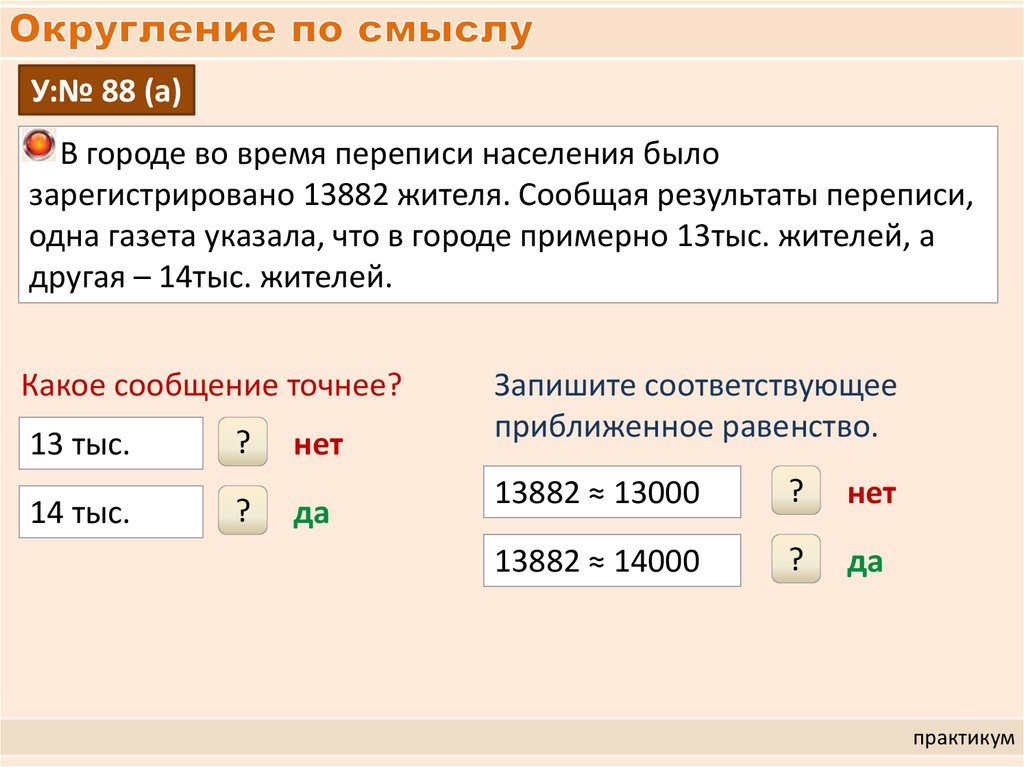
Решение. Находим
(полагаем первые
Согласно определению
цифр верными).
-верного знака, абсолютная погрешность
14
Исходим из того, что
Для использования принципа равных влияний считаем, что все
слагаемые
, равны между собой. Тогда абсолютные
погрешности всех аргументов определяются формулой:
Находим
15

16. Задание №1

Тема: Погрешность
1. Определить, какое равенство точнее.
2. Округлить сомнительные цифры числа, оставив верные знаки.
3. Найти абсолютные и относительные погрешности чисел, если они
имеют только верные цифры.
4. а) Записать порядок выполняемых операций, оценить погрешности
их результатов, вычислить и оценить погрешность искомого значения
(прямая задача).
б) Определить число верных знаков в результате.
5. Выяснить погрешность задания исходных данных, необходимую для
получения результата с
верными значащими цифрами (обратная
задача).
16

English     Русский Правила

Контрольная работа по «Вычислительной математике»

 

 

Оглавление

 

 

 

Элементарная теория погрешностей

Задание 1 (переделано):

Вариант №21.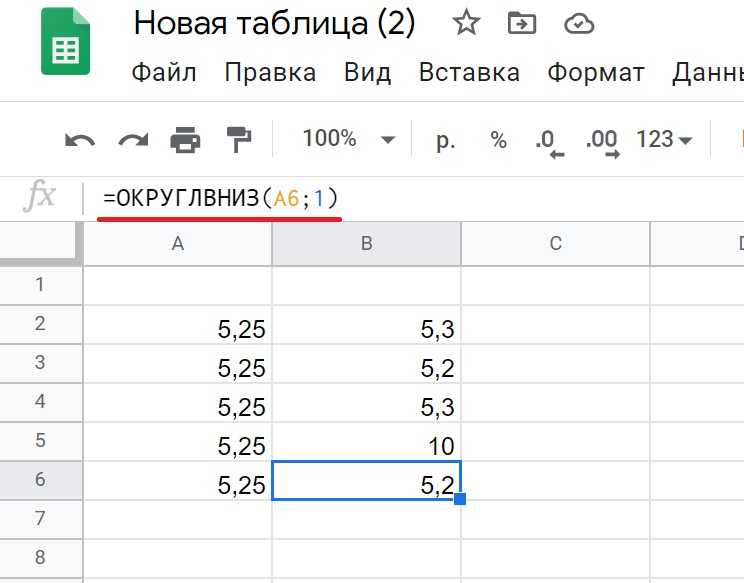

 

  1. Определить, какое равенство точнее.

; 
.

 

РЕШЕНИЕ:

 

1,88888889-2,11= — 0,22111111

– отрицательное, поэтому возьмем 

2,11-1,88888889=0,104791996=

Далее:

 

4,123105626-4,12=0,003105626=

Теперь найдет относительные погрешности:

 

 

поскольку d(L) >d( d ) то второе равенство является более точным.

 

ОТВЕТ:

второе равенство является более  точным

 

 

  1. Округлить сомнительные цифры числа, оставив верные знаки:

 

а) в  узком смысле;

б) в  широком смысле.

Определить  абсолютную погрешность результата.

а) 5.8425; d=0.23%

б) 0.66385±0.00042

РЕШЕНИЕ:

а) 5.8425; d=0.23%

а) в узком смысле

Абсолютная  погрешность числа: = 5,8425*0,0023= 0,013438

Говорят, что n  первых значащих цифр приближенного  числа являются верными в узком  смысле, если абсолютная погрешность этого числа не превышает половины единица разряда выражаемого n–ой значащей цифрой, считая слева направо. Остальные значащие цифры числа называются сомнительными.

Таким образом, если

,

то по определению, первые n цифр этого числа являются верными.

Для числа A = 5.8425, a=5.8425+0,013438=5,855938

 число a = 5,9 является приближением с двумя верными знаками.

б) в широком смысле:

Абсолютная  погрешность числа: = 5,8425*0,0023= 0,013438

Число a является приближением точного числа A с n верными знаками в широком смысле, если его абсолютная погрешность D не превышает единицы десятичного разряда, выражаемого n-ой значащей цифрой, считая слева направо, т.е.

то по определению, первые n цифр этого числа являются верными.

Для числа A = 5.8425, a=5.8425+0,013438=5,855938

 число a = 5,9 является приближением с двумя верными знаками.

 

Определить  абсолютную погрешность результата

Абсолютная  погрешность числа: = 0,0575

б) 0.66385±0.00042

 

а) в  узком смысле

Абсолютная  погрешность числа: = 0,00042

Говорят, что n  первых значащих цифр приближенного  числа являются верными в узком  смысле, если абсолютная погрешность этого числа не превышает половины единица разряда выражаемого n–ой значащей цифрой, считая слева направо. Остальные значащие цифры числа называются сомнительными.

Таким образом, если

,

то по определению, первые n цифр этого числа являются верными.

Для числа A = 0.66385, a=0.66385+0.00042=0,66427

 число a = 0,664 является приближением стремя верными знаками.

б) в широком смысле:

Абсолютная  погрешность числа: = 0,00042

Число a является приближением точного числа A с n верными знаками в широком смысле, если его абсолютная погрешность D не превышает единицы десятичного разряда, выражаемого n-ой значащей цифрой, считая слева направо, т.е.

то по определению, первые n цифр этого числа являются верными.

Для числа A = 0.66385, a=0.66385+0.00042=0,66427

 число a = 0.664 является приближением с тремя верными знаками.

Определить абсолютную погрешность  результата

Абсолютная  погрешность числа: 0,664-0,66358=0,00042

ОТВЕТ:

а) а1 = 5,9; а1 = 5,9; 0,0575;

b) а1 = 0,664; а1 = 0,664; 0,00042

 

  1. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры:

а) в  узком смысле;

б) в  широком смысле.

а) 0.3825; б) 24.6

 

РЕШЕНИЕ:

а) 0.3825;

а) в  узком смысле;

Значит предельная абсолютная погрешность – 0,00005 (половина разряда значащей цифры). Т.е

Предельная  относительная погрешность в  этом случае равна:

 

б) в  широком смысле.

Значит предельная абсолютная погрешность – 0,0001 (единица разряда значащей цифры). Т.е

Предельная  относительная погрешность в  этом случае равна:

 

 

б) 24.6

а) в  узком смысле;

Значит предельная абсолютная погрешность – 0,05 (половина разряда значащей цифры). Т.е

Предельная относительная  погрешность в этом случае равна:

 

б) в  широком смысле.

Значит предельная абсолютная погрешность – 0, 1 (единица разряда значащей цифры). Т.е

Предельная относительная  погрешность в этом случае равна:

ОТВЕТ:

а)

;
;
;

b) ;

 

Задание 2 (переделано):

Вычислить и определить погрешность результата.

21

p=3.14    D=72±0.3

d=3.274±0.002

p=3.14     D=52.6±0.01    d=48.39±0.001

 

РЕШЕНИЕ:

  1. Соответственно:

Найдем погрешность  результата:

 

 

Предельная  относительная погрешность m-ой степени числа в m раз больше предельной относительной погрешности самого числа, т.е. если , то

 (23)

Зная предельную относительную погрешность du степени u, можно определить предельную абсолютную погрешность Du по формуле

 (24)

Тогда:

 

 

Предельная  относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя, т.е., если  , то

 (21)

Зная предельную относительную погрешность du частного u, можно определить предельную абсолютную погрешность Du по формуле

 (22)

 

 

Предельная  относительная погрешность 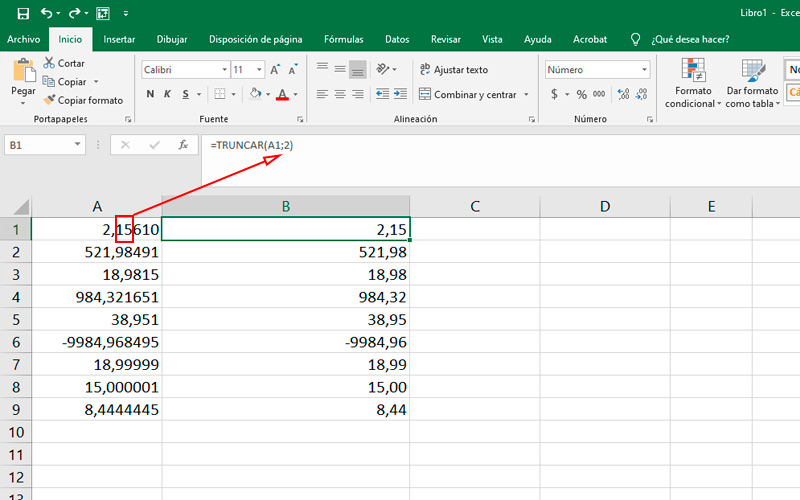произведения равна сумме предельных относительных  погрешностей множителей, т. е.

 (19′)

Зная предельную относительную погрешность du произведения u, можно определить предельную абсолютную погрешность Du по формуле

Т.о.

 

  1. Соответственно:

72,30533125

 

Найдем погрешность  результата:

 

 

Предельная  относительная погрешность m-ой степени числа в m раз больше предельной относительной погрешности самого числа, т.е. если , то

 (23)

Зная предельную относительную погрешность du степени u, можно определить предельную абсолютную погрешность Du по формуле

 (24)

Тогда:

 

 

Тогда:

Предельная  абсолютная погрешность разности равна  сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого, т.е. если , тогда

 (17)

Предельная  относительная погрешность разности определяется формулой

 (18)

 

Предельная  относительная погрешность коня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа, т. е. если , то

 (25)

Предельная  относительная погрешность произведения равна сумме предельных относительных  погрешностей множителей, т.е.

 (19′)

Зная предельную относительную погрешность du произведения u, можно определить предельную абсолютную погрешность Du по формуле

Т.о.

 

 

ОТВЕТ:

 

 

Задание №3 (переделано)

 

Задание: Решить уравнение f(x)=0 с точностью e=10-3 следующими методами:

Вариант 1, 5, 9, 13, 17, 21, 25, 29 — Метод хорд

 

 

РЕШЕНИЕ:

 

 

 

 

 

 

Уравнение хорды AB будет иметь вид

Для точки пересечения хорды  с осью Ox получаем

Поэтому в качестве начального приближения  в методе хорд берется конец отрезка противоположный закрепленному, т.е.

если , тогда и последовательные приближения вычисляются по правилу

, (16.1)

 

Тогда

 

x

f(x)

ͤ

0

2,000

1,525440854

 

1

1,708

0,808165881

0,292

2

1,566

0,438301075

0,142

4

1,492

0,243696058

0,073

5

1,453

0,137684112

0,040

6

1,431

0,078532762

0,022

7

1,418

0,045042564

0,012

8

1,411

0,025917196

0,007

9

1,407

0,014940259

0,004

10

1,405

0,008621713

0,002

11

1,403

0,004978494

0,001

12

1,402

0,002875794

0,001

13

1,402

0,001661527

0,000

 

Т. о.

При f(x)=0

ОТВЕТ:

 

Задание №4 (переделано).

Задание:

Найти решение системы  Ax=b методом Гаусса (вычисления вести с тремя знаками после запятой).

Найти приближенное решение системы итерационным методом c точностью e=10-3.

Метод

Вариант

Итерационный  параметр

метод Якоби 

1, 9, 7, 25, 5, 13, 21, 29

 

 

Матрица системы  определяется формулой

A=D+kC, где k – номер варианта=21,

 

, ,

k=21.

РЕШЕНИЕ:

  1. Найти решение системы  Ax=b методом Гаусса (вычисления вести с тремя знаками после запятой).

Найдем матрицы, с которыми будем работать:

 

1,552

0,432

-0,599

0,202

0,202

1,552

0,432

-0,599

-0,599

0,202

1,552

0,432

0,432

-0,599

0,202

1,552

 

 

 

Далее используем метод Гаусса:

A

b

1,552

0,432

-0,599

0,202

1,941

0,202

1,552

0,432

-0,599

-0,230

-0,599

0,202

1,552

0,432

-1,941

0,432

-0,599

0,202

1,552

0,230

сложением уравнений с первым, умноженным соответственно на

1,552

0,432

-0,599

0,202

1,941

0,000

1,496

0,510

-0,625

-0,483

0,000

0,369

1,321

0,510

-1,192

0,000

-0,719

0,369

1,496

-0,310

Лабораторная работа № 1 Тема:

Лабораторная работа № 1 Тема: Теория погрешностей

1. Источники и классификация погрешности Под погрешностью понимается некоторая величина, характеризующая точность результата. Выделяют три вида погрешностей: 1. Неустранимая погрешность – эта погрешность связана с ошибками в исходной информации. Причинами этих ошибок могут быть, например, неточность измерений, невозможность представления некоторой величины конечной дробью. 2. Погрешность метода связана с тем, что точные операторы и исходные данные заменяются приближенными. Например, заменяют интеграл суммой, производную – разностью, функцию – многочленом или строят бесконечный итерационный процесс, который обрывают после конечного числа итераций. 3. Погрешность вычислений возникает при округлении промежуточных и конечных результатов. 2

2. Абсолютная и относительная погрешности Пусть – точное значение величины, а – ее приближенное значение. Абсолютной погрешностью числа называется наименьшая величина , удовлетворяющая условию , (1) т. е. точное значение величины лежит в интервале (2) Относительной погрешностью называется величина , удовлетворяющая условию (3) или (4) Относительную погрешность часто выражают в процентах. Для этого необходимо величину умножить на 100%. 3

3. Верные значащие цифры Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева, например: 1) — все цифры значащие; 2) – значащие только ; первые три нуля незначащие, т. к. они служат вспомогательной цели – определению положения цифр , поэтому может быть принята запись ; 3) и . В первой записи все семь цифр (и последние четыре нуля) значащие, во второй – значащие только . 4

Верные значащие цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре. Пример 1. Пусть и известно, что . Определить число верных значащих цифр у числа. Имеем: ; и . Значит, у числа верные знаки а и – сомнительные. Пример 2. Определить число верных значащих цифр у числа . Пусть и . Так как , то у числа три знака после запятой верные. 5

Правила округления При записи чисел руководствуются следующим правилом: все значащие цифры должны быть верными. Поэтому округление чисел, записанных в десятичной системе, производится по правилу первой отбрасываемой цифры: если первая из отбрасываемых цифр меньше 5, то оставляемые десятичные знаки сохраняются без изменения; если первая из отбрасываемых цифр больше 5, то последняя оставляемая цифра увеличивается на единицу; если первая из отбрасываемых цифр равна 5, а за ней идут не нули, то последняя оставляемая цифра увеличивается на единицу; если первая из отбрасываемых цифр равна 5 и все значащие цифры, идущие за ней, – нули, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если – четная. Примеры. Округлить числа: 1) 1, 2537≈1, 25, m=3 – количество верных значащих цифр; 2) 1, 2563≈1, 26, m=3; 3) 2, 36566≈2, 37, m=3; 4) 2, 665≈2, 66, m=3, 6 -четная; 2, 635≈2, 64, m=3, 3 -нечетная. 6

4. Прямая задача теории погрешностей: Оценить погрешность вычисления значений функции по заданной погрешности аргументов. Пусть — непрерывно дифференцируемая функция, где ; — приближенные значения аргументов, ; — абсолютные погрешности аргументов. Тогда абсолютная погрешность вычисления значения функции в точке равна (5) Относительная погрешность значения в точке равна (6) 7

Погрешность результатов арифметических операций Погрешность суммы. Абсолютная погрешность алгебраической суммы приближенных чисел равна сумме абсолютных погрешностей этих чисел. Пусть , тогда (7) Погрешность разности. Абсолютная погрешность разности приближенных чисел равна сумме абсолютных погрешностей уменьшаемого и вычитаемого . Пусть , тогда (8) Погрешность произведения. Пусть , известны и , , тогда абсолютная погрешность произведения вычисляется по формуле (9) 8

Погрешность частного. Пусть . Тогда, (10) Из формул (1. 3) – (1. 6) выводятся формулы для соответствующих относительных погрешностей: (11) (12) (13) 9

Пример (прямая задача) а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого значения. б) Определить число верных знаков в результате. Решение. а) приближенные значения исходных данных: , , . Абсолютные погрешности исходных данных: , . Относительные погрешности исходных данных: 10

Порядок выполняемых операций: 11

б) Для определения числа верных знаков воспользуемся определением и оценкой (5) для абсолютной погрешности функции. Таким образом, По определению числа верных знаков, Ответ: число верных знаков и 12

5. Обратная задача теории погрешностей Необходимо определить допустимую погрешность аргументов по допустимой погрешности функции. Для функции одной переменной абсолютную погрешность можно приближенно вычислить по формуле (14) Для функции нескольких переменных : применяют принцип равных влияний, т. е. считают, что все слагаемые , равны между собой. Тогда абсолютные погрешности всех аргументов определяются формулой (15) 13

Пример (обратная задача) Выяснить погрешность задания исходных данных, необходимую для получения результата с верными значащими цифрами. Решение. Находим (полагаем первые цифр верными). Согласно определению -верного знака, абсолютная погрешность 14

Исходим из того, что Для использования принципа равных влияний считаем, что все слагаемые , равны между собой. Тогда абсолютные погрешности всех аргументов определяются формулой: Находим 15

Задание № 1 Тема: Погрешность 1. Определить, какое равенство точнее. 2. Округлить сомнительные цифры числа, оставив верные знаки. 3. Найти абсолютные и относительные погрешности чисел, если они имеют только верные цифры. 4. а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого значения (прямая задача). б) Определить число верных знаков в результате. 5. Выяснить погрешность задания исходных данных, необходимую для получения результата с верными значащими цифрами (обратная задача). 16

Страница не найдена | АКВТ

Запрошенную информацию найти не удалось. Возможно, будет полезен поиск по сайту или приведённые ниже ссылки.

Не нашли то, что искали?

Search

Страницы

  • QR код для оказания благотворительной помощи колледжу
  • Безопасный Интернет
  • Виртуальный тур
    • Фотогалерея
      • «Мы — Добровольцы!»
      • АКВТ на Дне Победы!
      • АКВТ на митинг-концерте, посвященном Крымской весне
      • Вручение дипломов 2016
      • Встречаем Олимпийский огонь
      • День народного единства 2015
      • День народного единства 2017
      • День Открытых дверей 2015
      • День Открытых Дверей 2016
      • День открытых дверей в АКВТ 2017
      • КРЫМ! Мы с тобой!
      • Мы — добровольцы 2016!
      • Награждение победителей фестиваля «Мисс Зимнее Очарование»
      • Новогодний концерт «АКВТ в Джунглях»
      • Празднование Масленицы 2016
      • Прогноз безопасности в АКВТ!
      • Студенты АКВТ и члены военно-патриотического клуба «Покров» на масленичных забавах
      • Торжественное открытие мемориала «Журавли»
      • Торжественный митинг (Хулхута)
      • Фестиваль «Мисс Зимнее Очарование»
      • Фестиваль студенческой науки 2016
      • Шарик Радости
      • Ярмарка вакансий 2016
  • Все новости
  • Дистанционное обучение
  • Информационная безопасность
  • Курс «Основы web-дизайна»
  • Курс «Основы компьютерной грамотности. Комплексная программа»
  • Курс «Основы разработки web-сайта»
  • Министерство образования и науки Российской Федерации
  • Обратная связь
  • Обращения граждан
  • Партнеры
    • Служба содействия трудоустройству выпускников
  • Политика в отношении обработки персональных данных
  • Поступающим
    • Приемная кампания 2022
      • Подача документов онлайн
      • Подача документов через операторов почтовой связи
    • Обращение директора
    • Реализуемые специальности
    • Правила приёма
    • Контрольные цифры приема на 2022 год
    • Количество поданных заявлений
    • Информирование поступающих
    • Заявление
    • Информация о результатах приема по каждой профессии, специальности среднего профессионального образования
    • Приказы о зачислении
    • Информация о дополнительном наборе
    • Платное обучение
    • Общежитие
    • Подготовительные курсы
      • Заявка на поступление на подготовительные курсы
    • Схема проезда
    • Горячая линия по вопросам приема, в том числе для лиц с ОВЗ и инвалидов
    • Горячая линия Минобрнауки
    • Information for Foreign Citizens (Training of foreign citizens)
    • Обучение иностранных граждан
  • Предупреждение распространения коронавирусной инфекции
    • Профилактика новой коронавирусной инфекции COVID-19
  • Преподавателям
    • График учебного процесса
    • Расписание занятий
      • График консультаций для студентов заочного отделения 2 семестр 2018-2019 учебного года
      • Расписание занятий для студентов заочного отделения
    • Оформление документации
      • Преподавателю
      • Заведующему кабинетом/лабораторией
      • Куратору
      • Руководителю курсового/дипломного проектирования
    • Аттестация преподавателей
    • Нормативные документы, регламентирующие деятельность преподавателей
    • Конкурсы
      • Всероссийский конкурс социально рекламы в области формирования культуры здорового и безопасного образа жизни «СТИЛЬ ЖИЗНИ — ЗДОРОВЬЕ! 2020»
    • Полезные вкладки
  • Родителям
    • Методические материалы для родителей и классных руководителей по здоровому образу жизни
    • О чем молчит подросток
    • Отцовство — твой главный жизненный проект
  • Сведения об образовательной организации
    • Герои Великой Победы в миниатюре
      • Диорама 1 «Полундра!»
      • Диорама 2 «Полигон»
      • Диорама 3 «Операция «Уран»
      • Диорама 4 «Тигры перед боем»
      • Диорама 5 «Герои Белостока»
      • Диорама 6 «Школьник Свердловска»
    • Международное сотрудничество
    • Наставничество
    • Основные сведения
    • Студенческий спортивный клуб СПО
    • Федеральный проект «Молодые профессионалы»
      • Аттестаты о присвоении статуса центра проведения демонстрационного экзамена
      • Банк фотоматериалов
      • Графики работы мастерских
      • Дизайн-проект мастерских
      • Дополнительное профессиональное образование
      • Дополнительные образовательные программы
      • Локальные акты по проекту
      • Программы повышения квалификации
      • Программы профессиональной переподготовки
      • Профессиональное обучение
      • Ссылки на репортажи, публикации в СМИ
    • Часто задаваемые вопросы
    • Структура и органы управления колледжем
    • Документы
      • Антимонопольный комплаенс
      • Нормативные акты Министерства образования и науки Астраханской области
      • Устав колледжа
      • Лицензия на осуществление образовательной деятельности
      • Cвидетельство о государственной аккредитации
      • Локальные нормативные акты
        • Документы, регламентирующие деятельность колледжа в целом
        • Документы, регламентирующие образовательную и воспитательную деятельность
        • Проекты документов
        • Единый план работы колледжа
      • Отчет о результатах самообследования
      • Документ о порядке оказания платных образовательных услуг
      • Предписания органов, осуществляющих государственный контроль в сфере образования
      • Установление размера платы, взимаемой с родителей за присмотр и уход за детьми
    • Руководство. Педагогический (научно-педагогический) состав
    • Образование
      • Информация о реализуемых образовательных программах
      • Основные профессиональные образовательные программы
      • Календарный учебный график
      • Численность обучающихся по реализуемым образовательным программам
      • Язык, на котором осуществляется образование
      • Информация о результатах приема, перевода, восстановления и отчисления студентов
      • Направления и результаты научно-исследовательской деятельности
    • Образовательные стандарты
    • Материально-техническое обеспечение и оснащенность образовательного процесса
    • Стипендии и меры поддержки обучающихся
    • Платные образовательные услуги
    • Финансово-хозяйственная деятельность
    • Вакантные места для приема (перевода) обучающихся
    • Противодействие коррупции
    • Доступная среда. Организация получения образования студентами с ОВЗ
    • Информация по защите прав обучающихся
  • Студентам
    • Кружки, секции и студии АКВТ
    • Студенческое самоуправление
      • Волонтерское движение АКВТ
      • Студенческая газета «Студ&ты»
    • График учебного процесса
    • Расписание занятий
      • График консультаций для студентов заочного отделения 2 семестр 2018-2019 учебного года
      • Расписание занятий для студентов заочного отделения
    • Учебно-методические материалы
      • Компьютерные системы и комплексы
      • Программирование в компьютерных системах
      • Сетевое и системное администрирование
      • Информационные системы и программирование
      • Информационная безопасность автоматизированных систем
      • Обеспечение информационной безопасности автоматизированных систем
      • Техническая эксплуатация и обслуживание электрического и электромеханического оборудования
      • Автоматизация технологических процессов и производств
      • Оснащение средствами автоматизации технологических процессов и производств
      • Специальности НПО
      • Заочное
    • Государственная Итоговая Аттестация
    • Трудоустройство
    • Сдать ЕГЭ
    • Библиотека
      • Библиотека сегодня
      • Информационные ресурсы свободного доступа
      • Электронно-библиотечная система
      • Доска объявлений библиотеки
    • Полезные вкладки
      • 8 мифов о наркотиках
      • «Народная дружина города Астрахани»
      • Ловушки для пешеходов
      • Противодействие терроризму

Записи

  • Анонс
    • АНОНС. Международная акция «Тест по истории Великой Отечественной войны»
    • АНОНС. О проведении VI Международной просветительской акции «Большой этнографический диктант-2021»
    • Профессионально-техническому образованию посвящается…
    • Объявление по собраниям для студентов нового набора
  • Новости
    • Всероссийский день ходьбы
    • Презентация проектов РСМ
    • Профилактика ПАВ
    • Преподаватель Астраханского колледжа вычислительной техники представит Астраханскую область на всероссийском конкурсе «Мастер года — 2022»
    • Профилактика преступлений в сфере незаконного оборота наркотиков
    • День среднего профессионального образования
    • Подготовительный этап VIII Национального чемпионата профессионального мастерства «Абилимпикс»
    • Профилактика употребления ПАВ
    • Легкоатлетическая эстафета посвященная «Дню города»
    • Торжественное мероприятие, в поддержку референдумов о присоединении Донбасса к России
    • Всероссийская Неделя безопасности дорожного движения
    • 2 октября в России отмечают День профессионально-технического образования
    • Митинг-возложение памяти героям 28 Армии
    • Полуфинал Всероссийского конкурса «Большая перемена»
    • Соревнования по легкой атлетике «Кросс наций»
    • Студент АКВТ принял участие в федеральном Просветительском марафоне «Знание»
    • Региональная научно-практическая конференция «МЕДИАЦИЯ КАК АЛЬТЕРНАТИВА КОНФРОНТАЦИИ»
    • Разговоры о важном
    • ГБПОУ АО «АКВТ» проводит дополнительный набор
    • Каспийский молодёжный образовательный форум «СЕЛИАС»
    • «Поделись своим знанием»
    • Мастер года 2022
    • Всероссийская акция «Поделись своим знанием»
    • День знаний 2022!
    • Лекция-беседа на тему «Профилактика терроризма и экстремизма в молодёжной среде»
    • Праздничные мероприятия 1 сентября 2022 года
    • Федеральный марафон «Знание»
    • Объявление по собраниям для студентов нового набора
    • День Государственного флага Российской Федерации
    • Запущена регистрация на Всероссийскую медиашколу «Без срока давности 3. 0» для студентов педагогических вузов и педагогических работников сферы гражданско-патриотического воспитания
    • Курсы для школьников «Погружение в специальность»
    • Вручение дипломов выпускникам 2022 года!
    • Демонстрационный экзамен в соответствии со стандартами Worldskills Russia
    • Великий государь великого государства: 350-летие со дня рождения Петра I
    • Вместе — ЗА здоровье нации!
    • Линейка памяти и скорби
    • Открытие мемориальной доски генерал-полковнику Тутаринову Ивану Васильевичу
    • XV Международный конкурс ВКР с использованием программных продуктов 1С
    • Студент 1 курса АКВТ в составе археологической экспедиции принял участие в «Вахте памяти»
    • День России!
    • Студенты АКВТ на областной конференции «IT-технологии XXI века: вызовы, становление, развитие»
    • Студенты АКВТ на финале Всероссийских просветительских игр
    • «Цени своё здоровье»
    • Стань Студентом года — 2022!
    • Памятка «Безопасность детства»
    • V Региональный чемпионат профессионального мастерства «Абилимпикс»
    • Итоги областной олимпиады по информатике!
    • Городская легкоатлетическая эстафета посвящённая Дню победы
    • Военная академия воздушно-космической обороны
    • День Победы!
    • Праздничный концерт «День Победы»
    • ГОРЯЧАЯ ЛИНИЯ В СИСТЕМЕ СПО НА БАЗЕ МИНИСТЕРСТВА ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ
    • Как провести майские праздники вместе с Пушкинской картой
    • Праздник Весны и Труда
    • Субботник в АКВТ
    • Финал по подтягиваниям «Я-Чемпион»
    • Спартакиада ПОО среди учащихся по стритболу
    • Областная практическая конференция по дисциплинам ОБЖ, БЖ «Астраханская область территория безопасности»
    • Акция «Чистые игры»
    • Полуфинальный этап соревнований по подтягиваниям «Я-Чемпион»
    • Товарищеская игра по мини-футболу
    • Интерактивная лекция «Здоровый образ жизни»
    • Марафон «Новые горизонты»
    • День открытых дверей!
    • Турнир по мини-футболу на кубок «Дружбы народов»
    • День открытых дверей в АКВТ
    • День здоровья в стенах АКВТ!
    • Патриотическая акция, посвященная восьмилетию со дня провозглашения Донецкой Народной Республики
    • Родительские собрания в группах 1-3 курсов
    • Итоги отборочного тура олимпиады по информатике!
    • Первенство студенческой лиги по пулевой стрельбе из пневматического оружия
    • Агрегатор профориентационных возможностей
    • «Всероссийский урок добровольчества»
    • Встреча с ветеранами боевых действий
    • День открытых дверей
    • Профориентационный проект «Загляни за горизонт»
    • Акция «Сообщи, где торгуют смертью»
    • Областной профориентационный форум «Топ профессий на селе»
    • Без срока давности
    • Профилактика заболевания туберкулезом
    • День открытых дверей в АКВТ 2022
    • Методическое объединение преподавателей ССУзов Астраханской области
    • Праздничный концерт под девизом «Zа Мир! Zа Россию! Zа Президента!»
    • Встреча с представителем Областного центра крови
    • Начни свой путь из кандидата в бойцы студенческих отрядов!
    • Встреча студентов с медицинским психологом
    • Реализация программы «Пушкинская карта»
    • С праздником прекрасная половина Астраханского колледжа вычислительной техники!
    • С Международным женским днем!
    • #МЫВМЕСТЕ
    • Соревнования по стрельбе из пневматической винтовки
    • «В Питере — учиться»
    • Осторожно мошенники!!!
    • Спартакиада учащихся ПОО по настольному теннису
    • Школа бизнеса «Точка роста»
    • Поздравляем с 23 февраля! С Днем защитника Отечества!
    • Студент АКВТ награжден дипломом победителя Кубка России по судомодельному спорту
    • Презентация РСМ
    • С Днем защитника Отечества!
    • Турнир по DOTA2
    • Международной конкурс-премии уличной культуры и спорта «КАРДО»
    • Набор студентов в Корпус общественных наблюдателей
    • День снятия блокады Ленинграда
    • С Днём студента!
    • Региональный этап Всероссийских соревнований по мини-футболу
    • Совещание органов студенческого самоуправления
    • VI Открытый Региональный Чемпионат «Молодые профессионалы России»: финальный день
    • VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 4
    • VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 2
    • VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 1
    • Поздравляем победителей международных конкурсов
    • Курсы для школьников
    • Конкурс на лучшее видео – поздравление «С Новым годом!»
    • Конкурс на лучшее видео – поздравление «С Новым годом!»
    • Студенты АКВТ приняли участие в открытии памятника легендарному командарму
    • Поздравления от Деда Мороза и Снегурочки
    • Поздравляем с началом сессии!
    • Проведение независимой оценки качества условий осуществления образовательной деятельности ГБПОУ АО «Астраханский колледж вычислительной техники»
    • В АКВТ прошла акция Всероссийский тест на знание Конституции РФ
    • I заседание МК СПО АО преподавателей информатики 10 декабря 2021 г.
    • Конкурс на лучшее видео-поздравление с Новым годом
    • Телеканал «Астрахань 24» о выставке студентов АКВТ — участников проекта «Герои Великой Победы в миниатюре» в Музее боевой славы
    • Анонс! Массовая просветительская акция Всероссийский тест на знание Конституции РФ
    • Интерактивная игра «Я, мои права и обязанности»
    • Всероссийский конкурс «Флагманы образования. Студенты»
    • Команда АКВТ на фестивале студенческой лиги КВН
    • Выставка студентов АКВТ в Музее боевой славы
    • Студенты и преподаватели АКВТ прошли исторический тест в День Неизвестного солдата
    • В Музее боевой славы пройдёт 2-ая выставка работ студентов АКВТ
    • Астраханский колледж вычислительной техники стал площадкой федерального проекта «Билет в будущее»
    • С днём матери!
    • Акция «Призывник»
    • Проведение родительских собраний
    • АКВТ посетили участники клуба моделистов «Сталинградский фронт»
    • Студент Астраханского колледжа вычислительной техники – победитель Всероссийского конкурса «Большая перемена»
    • В АКВТ состоялась встреча, посвящённая сохранению исторической памяти и защите Отечества
    • Об организации межведомственного штаба по организации волонтерской деятельности
    • О программе «Пушкинская карта»
    • Семинар, посвященный всероссийскому конкурсу «Soft Skills Russia»
    • VI Международная просветительская акция «Большой этнографический диктант-2021»
    • Студенты Астраханского колледжа вычислительной техники – финалисты Всероссийского конкурса «Большая перемена»
    • Студенты АКВТ в финале Международной олимпиады в сфере информационных технологий «IT-Планета 2020/21»
    • Пушкинская карта
    • Анкетирование в рамках проекта «Без срока давности»
    • Акция «Сообщи, где торгуют смертью»
    • День учителя в стенах АКВТ
    • С днем учителя!
    • Расписание спортивных секций
    • Выставка посвящённая Дню профтехобразования
    • «Полетели поздравительные телеграммы…»
    • Марафон танцевальных поздравлений
    • Студенты АКВТ провели выставку военных диорам на Кубке Прикаспийских государств по рукопашному бою
    • В АКВТ прошли первые занятия в рамках проекта «Герои Великой Победы в миниатюре»
    • Посвящение в студенты в стенах АКВТ
    • АКВТ в полуфинале Всероссийского конкурса «Большая перемена»
    • Совещание органов студенческого самоуправления
    • Студент нашего колледжа рассказывает о своём незабываемом опыте работы вожатым в детском лагере
    • Студенты АКВТ приняли участие в акции по сбору подписей для получения Астрахани звания «Город трудовой доблести»
    • АКВТ во Всероссийском историческом квесте «Наша победа»
    • Студенты АКВТ приняли участие в областном уроке мужества «Славы героев достойны»
    • День знаний в стенах АКВТ!
    • Группы 1 курса
    • Объявление по собраниям для студентов нового набора
    • АКВТ примет участие во Всероссийском конкурсе на лучшую выставку
    • Итоги заседания комиссии по переводу с коммерческого обучения на бюджет
    • Выпускники АКВТ — 2021
    • V Открытый Региональный Чемпионат «Молодые профессионалы России»: 1 день
    • Наши студенты на субботнике
    • «Молодежный кадровый резерв»
    • Информация для участников ЕГЭ 2014 года
    • «Проблема сиротства» — проблема нашего будущего»
    • Центр гражданского воспитания «Прометей»
    • Подготовка студентов по программе прикладного бакалавриата по специальности Компьютерные системы и комплексы
Версия для слабовидящих

X Выбор шрифта:

Как найти квадратный корень числа вручную.

Нахождение приближенных значений квадратного корня

ГУ « Средняя общеобразовательная школа №5 им. Бауыржана Момышулы»

отдела образования акимата г. Костаная

ПЛАН-КОСПЕКТ УРОКА

ФИО (полностью) Пластун Сергей Владимирович

Предмет алгебра

Класс 8А-8б-1

Дата 23.09.17

Источники Алматы «Мектеп-2016»

Базовый учебник

Дополнительная литература

Нахождение приближенных значений квадратного корня.

1. Цель урока: познакомить учащихся с понятием « приближенное значение квадратного корня» и научить применять это понятие на практике.

Задачи:

Образовательные:

-научить находить приближенные значения квадратного корня;

-выработка умений рассуждать, четко формулировать правила, приводить примеры, применять свои знания и умения на практике.

корень, приводить и находить значения арифметического квадратного корня.

Развивающие:

-развивать у учащихся навык решения заданий на данную тему;

-развивать мыслительную деятельность учащихся.

Воспитательные:

— воспитывать внимательность, активность, ответственность.

2. Тип урока: комбинированный .

3. Формы работы с учащимися: фронтальная, индивидуальная.

4. Необходимое техническое оборудование.

5. Наглядные пособия, дидактические материалы, используемые на уроке.

6. Структура и ход урока.

СТРУКТУРА И ХОД УРОКА

Ход урока

1. Организационный момент .

Проверка готовности класса к уроку. Приветствие.

2. Проверка домашнего задания.

3. Повторение ранее изученного материала.

Начнем с повторения. Устная работа

Давайте вспомним, что такое квадратный корень (Квадратным корнем из неотрицательного числа а называется число, квадрат которого равен а).

(Арифметический квадратный корень) Арифметическим квадратным корнем из неотрицательного числа а называется такое неотрицательное число b , квадрат которого равен а.

Арифметический квадратный корень из числа а обозначается так:. Знак называется знаком арифметического квадратного корня, или радикалом, а –подкоренным выражением. Выражение читается так: «Арифметический квадратный корень из числа а».

По определению арифметического корня равенство
выполняется при условии, когда
.

4. Изучение нового материала.

1. Вычислите: 25 , 16, 9, 81,

Найдите значение выражения √2

— Что вам необходимо было сделать?

Что у вас получилось? (Учащиеся показывают свои варианты:)

В чём возникло затруднение?

Извлекается √2 нацело?

Как будем находить?

Какие знаем способы нахождения корней?

Ребята, видите, не всегда мы имеем дело с числами, легко представимыми в виде квадрата числа, которые извлекаются из- под корня нацело

1 МЕТОД вычислить √2 с точностью до двух знаков после запятой Будем рассуждать следующим образом.

Число √2 больше 1, так как 1 2 десятичная запись числа будет начинаться следующим образом: 1,… То есть корень из двух, это единица с чем-то.

1

Теперь попытаемся отыскать цифру десятых.

Для этого будем дроби от единицы до двойки возводить в квадрат, пока не получим число большее двух.

Шаг деления возьмем 0,1, так как мы ищем число десятых.

Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9

1,1 2 =1,21; 1,2 2 =1,44; 1,3 2 =1,69; 1,4 2 =1,96; 1,5 2 =2,25.

Получили число превышающее двойку, остальные числа уже не надо возводить в квадрат. Число 1,4 2 меньше 2, а 1,5 2 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 . Следовательно, десятичная запись числа √2 в разряде десятых должна содержать 4. √2=1,4… .

1,41 2 =1,9881, 1,42 2 =2,0164.

Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.

Из этого получаем, что число √2 будет принадлежать промежутку от 1,41 до 1,42 (1,41

Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.

√2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.

Задание

Вычислите с точностью до двух знаков после запятой

√3 = , √5 = , √6 = , √7 =, √8 =

Вывод Данный прием позволяет извлекать корень с любой заданной наперед точностью.

2 МЕТОД Чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.

Например, найдем √16 так:

Выполнено 4 действия, значит, √16 = 4

Задание. Вычислите

√1 √6

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www. allbest.ru/

Тема приближенного вычисления корней актуальна всегда, так как задания с квадратными корнями есть в каждом курсе предметов естественнонаучного цикла. В ходе решения многих математических задач, а так же задач по геометрии, по физике, по химии и т.д. приходится сталкиваться с квадратными корнями. Для извлечения квадратного корня существуют таблицы квадратов для двухзначных чисел, но ее бывает недостаточно. Извлечение корня разложением на множители тоже непростая задача, которая не всегда приводит к желаемому результату, и я решила изучить различные способы извлечения квадратных корней с целью их практического применения.

Поэтому цель работы направлена на сопоставление различных способов приближенного извлечения квадратных корней, при этом ставятся задачи: изучение материала, выявление наиболее эффективного способа в зависимости от поставленной задачи.

Решим графически уравнение. Для этого в одной системе координат построим параболу и прямую. Абсциссы точек A и B являются корнями уравнения. Решим уравнение. Ясно, что это уравнение имеет два корня и, причем эти числа, как и в двух предыдущих случаях, равны по абсолютной величине и противоположны по знаку (). По чертежу мы не можем указать точные значения корней. Интересующее нас число x1 расположено между числами 1 и 2, но между числами 1 и 2 находится бесконечное множество рациональных чисел, например и т.д. В работе доказано, что располагая только рациональными числами, уравнение мы решить не сможем.

Математики ввели в рассмотрение новый символ, который назвали квадратным корнем, и с помощью этого символа корни уравнения записали так: и. Читается: «арифметический квадратный корень из двух». Теперь для любого уравнения вида, где, можно найти корни — ими являются числа и.

Квадратным корнем из неотрицательного числа называют такое неотрицательное число, квадрат которого равен. Это число обозначают. Если, то уравнение не имеет корней.

Операцию нахождения квадратного корня из неотрицательного числа называют извлечением квадратного корня.

В ходе исследования методов вычисления квадратного корня были найдены несколько методов, такие как: арифметический способ; метод грубой оценки; столбиком; Вавилонский способ; метод Герона и метод Ньютона; геометрический метод. В данной работе рассмотрены лишь некоторые из них.

квадратный корень извлечение приближенное

Для квадратов натуральных чисел верны следующие равенства:

То есть, чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.

Например, найдем квадратный корень числа 16 так:

Выполнено 4 действия, значит, квадратный корень числа 16 равен 4. Аналогично найдем квадратный корень числа 12:

Выполнено 3 действия, квадратный корень числа 12 равен 3 целым.

Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне пригоден для грубой оценки, для учащихся, решающих простейшие математические задачи, требующие извлечения квадратного корня.

Доказательство теоремы рассмотрено в работе. Поскольку и являются приближенными значениями для по избытку и по недостатку, и является средним геометрическим чисел и, то в качестве лучшего приближения для естественно выбрать среднее арифметическое этих чисел, т.е. число. А чтобы получить ещё более точное значение для, надо взять среднее арифметическое чисел и, т.е. число. Так вычисляются одно за другим все более точные приближенные значения для. Приближения ведут до тех пор, пока два полученных значения и не совпадут в пределах заданной точности. Тогда мы имеем формулу:

Таким образом, для получилось квадратное уравнение. Если его решить, то. Мы, получается, ходим по кругу: чтобы найти, нужно сосчитать, а чтобы найти, надо вычислить. На помощь приходит следующее соображение. Погрешность приближенного значения невелика, она меньше единицы, значит число еще меньше, поэтому в равенстве (2) его можно отбросить. При этом для получается приближенное уравнение, значит. Итак, приближенное значение поправки найдено.

Работа над данным исследованием показала, что изучение квадратных корней — объективная необходимость: в реальной жизни случаются ситуации, математические модели которых содержат операцию извлечения квадратного корня. Но не всегда под рукой мы имеем калькулятор. Помимо того, бывают ситуации, когда использование калькулятора недопустимо, например, ЕГЭ.

Хотелось бы выбрать оптимально рациональный способ извлечения квадратных корней. Конечно же, арифметический способ и особенно способ грубой оценки, просты в использовании, но не точны, хотя вполне пригодны для первого приближения. К тому же при применении этих способов извлечения квадратных корней любая ошибка, допущенная в каком-то месте, полностью обесценивает дальнейшие вычисления. Иначе состоит дело при применении Вавилонского способа или способа последовательных приближений. Хоть он и трудоемкий, однако можно верно вычислить значение корня с заданной точностью.

Размещено на Allbest.ru

Подобные документы

    Понятие и математическая сущность квадратного корня, его назначение и методика вычисления. Теоремы, отображающие свойства квадратного коря, их обоснование и доказательство. Применение характеристик квадратных корней в решении геометрических задач.

    реферат , добавлен 05.01.2010

    Выведение формулы решения квадратного уравнения в истории математики. Сравнительный анализ технологий различных способов решения уравнений второй степени, примеры их применения. Краткая теория решения квадратных уравнений, составление задачника.

    реферат , добавлен 18.12.2012

    Изучение способов приближенного решения уравнений с помощью графического изображения функций. Исследование метода определения действительных корней квадратного уравнения с помощью циркуля и линейки для приведенных семи уравнений, построение их графиков.

    творческая работа , добавлен 04.09.2010

    Метод Гаусса, LU-разложение. Прогонка для решения линейных систем с трехдиагональными матрицами коэффициентов. Метод квадратного корня для решения систем: краткая характеристика, теоретическая основа, реализация, тестирование и листинг программы.

    курсовая работа , добавлен 15.01.2013

    Система линейных алгебраических уравнений. Основные формулы Крамера. Точные, приближенные методы решения линейных систем. Алгоритм реализации метода квадратных корней на языке программирования в среде Matlab 6.5. Влияние мерности, обусловленности матрицы.

    контрольная работа , добавлен 27.04.2011

    Исследование метода квадратных корней для симметричной матрицы как одного из методов решения систем линейных алгебраических уравнений. Анализ различных параметров матрицы и их влияния на точность решения: мерность, обусловленность и разряженность.

    курсовая работа , добавлен 27.03.2011

    История развития формул корней квадратных уравнений. Квадратные уравнения в Древнем Вавилоне. Решение квадратных уравнений Диофантом. Квадратные уравнения в Индии, в Хорезмии и в Европе XIII — XVII вв. Теорема Виета, современная алгебраическая запись.

    контрольная работа , добавлен 27.11.2010

    Нахождение корней уравнений (Equation Section 1) методом: Ньютона, Риддера, Брента, Лобачевского и Лагерра. Вычисление корней многочленов по схеме Горнера. Функции произвольного вида (при использовании пакета Mathcad). Нахождение корней полиномов.

    контрольная работа , добавлен 14.08.2010

    Изучение истории квадратных уравнений. Анализ общего правила решения квадратных уравнений, изложенного итальянским математиком Леонардо Фибоначчи. Решение квадратных уравнений с помощью циркуля и линейки, с помощью номограммы, способом «переброски».


ДИПЛОМНЫЕ РАБОТЫ

Многое уже позади и теперь ты — выпускник, если, конечно, вовремя напишешь дипломную работу. Но жизнь — такая штука, что только сейчас тебе становится понятно, что, перестав быть студентом, ты потеряешь все студенческие радости, многие из которых, ты так и не попробовал, всё откладывая и откладывая на потом. И теперь, вместо того, чтобы навёрстывать упущенное, ты корпишь над дипломной работой? Есть отличный выход: скачать нужную тебе дипломную работу с нашего сайта — и у тебя мигом появится масса свободного времени!
Дипломные работы успешно защищены в ведущих Университетах РК.
Стоимость работы от 20 000 тенге

КУРСОВЫЕ РАБОТЫ

Курсовой проект — это первая серьезная практическая работа. Именно с написания курсовой начинается подготовка к разработке дипломных проектов. Если студент научиться правильно излагать содержание темы в курсовом проекте и грамотно его оформлять, то в последующем у него не возникнет проблем ни с написанием отчетов, ни с составлением дипломных работ, ни с выполнением других практических заданий. Чтобы оказать помощь студентам в написании этого типа студенческой работы и разъяснить возникающие по ходу ее составления вопросы, собственно говоря, и был создан данный информационный раздел.
Стоимость работы от 2 500 тенге

МАГИСТЕРСКИЕ ДИССЕРТАЦИИ

В настоящее время в высших учебных заведениях Казахстана и стран СНГ очень распространена ступень высшего профессионального образования, которая следует после бакалавриата — магистратура. В магистратуре обучаются с целью получения диплома магистра, признаваемого в большинстве стран мира больше, чем диплом бакалавра, а также признаётся зарубежными работодателями. Итогом обучения в магистратуре является защита магистерской диссертации.
Мы предоставим Вам актуальный аналитический и текстовый материал, в стоимость включены 2 научные статьи и автореферат.
Стоимость работы от 35 000 тенге

ОТЧЕТЫ ПО ПРАКТИКЕ

После прохождения любого типа студенческой практики (учебной, производственной, преддипломной) требуется составить отчёт. Этот документ будет подтверждением практической работы студента и основой формирования оценки за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный план и описать свою практическую деятельность.
Мы поможет написать отчёт о прохождении практики с учетом специфики деятельности конкретного предприятия.

При решение задач, связанных с вычислениями, получаются числовые результаты, которые часто не являются точными, т.к. при постановке задачи и в ходе вычислений возникают погрешности.

Источниками погрешностей являются:

1) погрешности исходных данных;

2) погрешности округления промежуточных и окончательных результатов;

3) погрешности приближенного метода решения задачи.

При выполнении действий над приближенными числами надо:

1) зная точность исходных данных, уметь оценивать точность результата;

2) брать исходные данные с такой точностью, чтобы обеспечить заданную точность результата.

2.1 Погрешности приближенных чисел

Пусть число х является точным значением, а число а — приближенным значением некоторой величины.

Определение. Разность между числом x и его приближенным значением а называется погрешностью приближенного числа а: Δ = |х-а |.

Пусть х=10,5, а=10, тогда Δ=10,5-10=0,5.

Пусть х=9,5, а=10, тогда Δ=9,5-10=-0,5.

Определение. Абсолютная величина разности между числом x и его приближенным значением а называется абсолютной погрешностью приближенного числа а: Δа = |х-а|

Пусть х=10,5, а=10, тогда Δа =|10,5-10|=0,5.

Пусть х=9,5, а=10, тогда Δa=|9,5-10|=0,5.

Часто точное число х неизвестно. Тогда нельзя найти Δа = |х-а|, поэтому используют оценку абсолютной погрешности — предельную абсолютную погрешность Δ а ≥ Δа =x-а|. При этом число х заключено в границах:

а — Δ а  х  а + Δ а или кратко: х = а ± Δ а.

Читают: х равно а с точностью Δ а.

Для того, чтобы определить качество производимых вычислений, надо определить, какую долю составляет абсолютная погрешность от измеряемой величины. Для этого используют относительную погрешность.

Определение. Относительной погрешностью δа приближенного числа а называется отношение абсолютной погрешности Δа к модулю числа х:

или
.

Оценкой относительной погрешности ба является предельная относительная погрешность:

Пример. Дано число х=0,4287 и его приближенное значение а=0,4264. Найти абсолютную и относительную погрешности числа а.

Решение. Вычислим абсолютную погрешность числа а:

Δа=|0,4287- 0,4264| = 0,0023.

Вычислим относительную погрешность числа а:

или 5,4%.

Замечания. 1. При записи погрешности принято оставлять 1-2 значащих цифры. Погрешности всегда округляют в сторону увеличения. При этом границы точного числа х расширяются.

2. Если число х неизвестно, то при нахождении относительной погрешности используют число а.

3. Относительную погрешность часто выражают в процентах, домножая ее на 100%.

2.2. Значащие и верные цифры приближенного числа

Для оценки точности приближенного числа а принято записывать его в виде десятичной дроби. Точность вычислений определяется не числом десятичных знаков (цифр после запятой), а числом верных значащих цифр результата.

Определение. Значащими цифрами числа а называются все его цифры, кроме нулей, записанных перед первой цифрой, отличной от нуля, и нули в конце записи, если они служат для сохранения разряда или точности числа.

Пример. Определить значащие цифры числа а.

а = 0,02701 => значащие цифры: 2,7,0,1.

а = 0,0270 => значащие цифры: 2,7,0.

а = 2700 => значащие цифры: 2,7,0,0.

Определение. Цифра α i приближенного числа а называется верной значащей цифрой в широком смысле (в строгом смысле), если предельная абсолютная погрешность числа а не превышает единицы (половины единицы) разряда, в котором записана цифра α i: Δ а 10 i (Δ а 0,5∙10 i).

Пример. Определить верные цифры приближенного числа а=0,7264, если абсолютная погрешность Δ а =0,0023.

Решение. Абсолютная погрешность Δ а =0,0023  0,005 = 0,5∙10 -2 . Следовательно, цифры 7 и 2 — верные в строгом смысле, цифры 6 и 4 – неверные (сомнительные). Так как Δ а  = 0,0023

Замечания. 1. В математических таблицах все значащие цифры являются верными в строгом смысле.

2. В окончательном результате принято оставлять только верные цифры. Тогда предельная абсолютная погрешность числа а определяется по единице младшего разряда.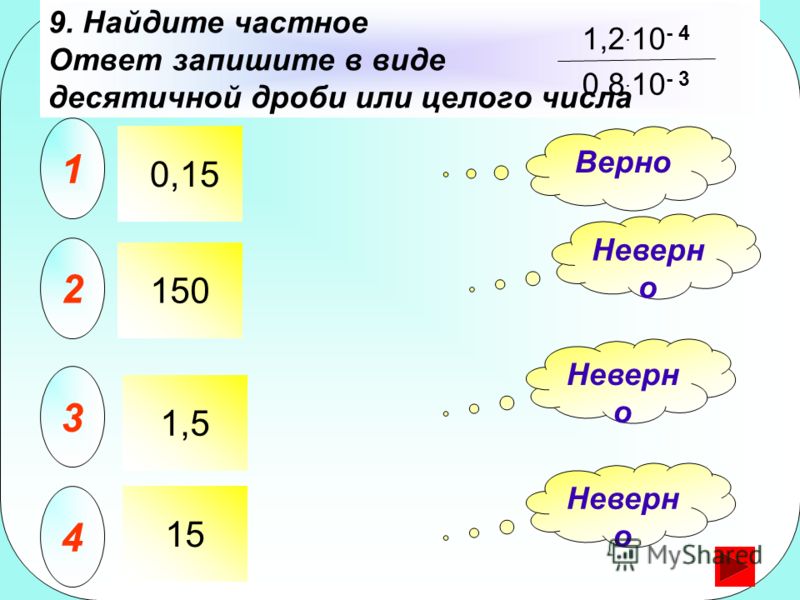 Например, пусть а=127,38, тогда Δ а =0,01, если все цифры являются верными в строгом смысле, и Δ а = 0,5∙ 0,01 = 0,005, если все цифры являются верными в широком смысле.

Пример. Определить, какое равенство точнее 13/19=0,684 или
=7,21?

Решение. Обозначим а =0,684, в =7,21. Найдем абсолютные погрешности этих чисел. Для этого возьмем 13/19 и
с большим числом десятичных знаков: 13/39=0,68421…,
=7,2111…

Тогда Δ а =|0,68421…-0,684|

Найдем относительные погрешности:

или 0,033%.

или 0,017%.

Второе равенство более точное, так как
.

2.3. Округление чисел

В приближенных вычислениях часто приходится округлять числа как приближенные, так и точные, т. е. отбрасывать одну или несколько последних цифр. При округ­лении числа мы заменяем его приближенным числом с меньшим коли­чеством значащих цифр, в результате чего возникает погрешность ок­ругления. Чтобы эта погрешность была минимальной, нужно придер­живаться некоторых правил округления.

Правило I . Если первая слева из отбрасываемых цифр больше 5, то последняя из сохраняемых цифр усиливается, т.е. увеличивается на единицу. Усиление производится и тогда, когда первая слева из от­брасываемых цифр равна 5, а за ней следуют отличные от нуля цифры.

Пример. Округляя до десятых долей число 73,473, получим 73,5. Послед­няя из оставшихся цифр усилена, так как 7 > 5.

Правило II . Если первая из отброшенных цифр меньше 5, то последняя из оставшихся цифр не усиливается, т. е. остается без изменения.

Пример. Округляя до сотых долей число 73,473, получим 73,47.

Правило III . Если первая слева из отброшенных цифр равна 5 и за ней не следуют отличные от нуля цифры, то последняя остав­шаяся цифра усиливается, если она нечетная, и остается без изменения, если она четная (правило четной цифры).

Пример. Округляя число 5,785 до сотых долей, получаем 5,78. Усиления не делаем, так как последняя сохраняемая цифра 8 — четная. Округляя число 5,775 до второго десятичного знака, имеем 5,78. Последняя сохраняемая цифра 7 увеличивается на единицу, поскольку она нечетная.

При применении правила III к округлению одного числа мы фак­тически не увеличиваем точность вычислений, однако при многочис­ленных округлениях избыточные числа встречаются примерно так же часто, как и недостаточные. Происходит взаимная компенсация погреш­ностей, результат оказывается более точным.

Таким образом, при применении выше рассмотренных правил ок­ругления абсолютная погрешность округления не превосходит полови­ны единицы разряда, определяемого последней оставленной значащей цифрой.

Если точное число х округляется до n значащих цифр, то получаемое приближенное число а имеет абсолютную погрешность, равную погрешности округления. В этом случае прибли­женное число а имеет n верных значащих цифр в узком смысле.

Пример. Округляя число х=26,837 до трех значащих цифр, получим а =26,8, откуда Δ а = |х-а | = | 26,837-26,8 |=0,037

При округлении приближенного числа a получаем новое прибли­женное число а 1 .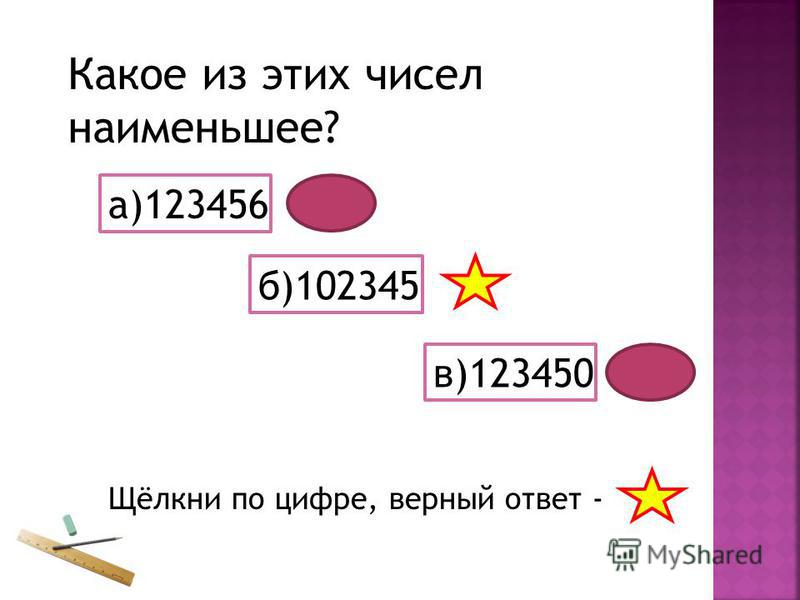

Определение. Число Δ а1 = Δ а +Δ окр называется погрешностью округления.

Абсолютная погрешность числа a 1 складывается из абсолютной погрешности первоначального числа Δ а и погрешности округления Δ окр, т. е.

Δ а1 = Δ а +Δ окр.

Пример. Округлить сомнительные цифры числа х=34,124 ± 0,021. Определить абсолютную погрешность результата.

Решение. Приближенное число a=34,124 имеет три верные цифры в узком смыс­ле: 3, 4, 1, так как Δ а =0,021

Таким образом, все значащие цифры числа а 2 верные (в узком смысле).

Итак, х=34,1 ±0,045.

Однако при округлении приближенного числа а, имеющего n вер­ных значащих цифр (в узком смысле), до n значащих цифр может ока­заться, что округленное число а 1 будет иметь n верных значащих цифр в широком смысле.

Пример. Приближенное число a=15,3654 (± 0,0018) имеет четыре верные значащие цифры в узком смысле (1, 5, 3, 6), так как Δ а =0,0018

Очевидно, что 0,005 ± 0,0064) имеет четыре верные цифры в широком смысле.

Итак, х=15,37 ±0,0064.

Пример. Округлить сомнительные цифры числа а=26,7245 (± 0,0026), оставив верные знаки в узком смысле. Определить абсолютную погрешность ре­зультата.

Решение. По условию Δ а = 0,0026

Полученная погрешность больше 0,005 (0,005 = 26,7. Находим Δ а2 = =Δ а +Δ окр =0,0026+|26,7245-26,7|=0,0271

Итак, х=26,7 ±0,0271 => х=26,7 ±0,03, округляя погрешность до двух знаков.

Пример. Округлить сомнительные цифры числа а=22,7314, оставив верные знаки в узком смысле. Определить абсолютную погрешность числа, если δ а = 0,2%.

Решение. Запишем δ а в виде десятичной дроби: δа=0,002 и опреде­лим абсолютную погрешность . Так какΔ а = =0,0455 = 22,73. Тогда Δ а1 = =Δ а +Δ окр =0,0455+|22,7314-22,73|=0,0769>0,05, поэтому уменьшим чис­ло цифр в приближенном числе до двух: а 2 =23. Находим Δ а2 = =Δ а +Δ окр =0,0455+|22,7314-23|=0,3141

Итак, х=23 ±0,3141 => х=23 ±0,32.

2.3. Правила действий над приближенными числами

Правило 1. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей этих чисел:

Δ а±в =Δ а + Δ в

Правило 2. Относительная погрешность произведения нескольких приближенных чисел равна сумме относительных погрешностей этих чисел:

δ ав = δ а +δ в.

Правило 3. Относительная погрешность частного приближенных чисел равна сумме относительных этих чисел: δ а/в = δ а +δ в.

Правило 4. Относительная погрешность степени приближенного числа а равна: δa n = nδ а.

Правило 5. Относительная погрешность корня из приближенного числа а равна:
.

Правило 6. При вычислениях, если не проводится строгий подсчет погрешностей, рекомендуется пользоваться правилами подсчета цифр. Эти правила указывают, как следует проводить округление результатов, чтобы обеспечить заданную точность результата и при этом не производить вычислений с лишними знаками.

Правила предполагают, что числа, над которыми производятся действия, содержат только верные цифры, и число действий невелико.

I. При сложении и вычитании приближенных чисел в результате следует сохранить столько десятичных знаков, сколько их в числе, имеющем наименьшее число десятичных знаков.

II. При умножении и делении в результате следует сохранить столько значащих цифр, сколько их в числе с наименьшим числом значащих цифр.

III. При возведении приближенного числа в степень в результате следует сохранить столько значащих цифр, сколько их в основании степени.

IV. При извлечении корня из приближенного числа следует сохранить столько значащих цифр, сколько их в подкоренном числе.

V. В промежуточных результатах следует сохранять на 1-2 цифры больше, чем рекомендуют правилах I-IV. В окончательном результате «запасные цифры» отбрасываются с округлением числа.

VI. Если некоторые исходные данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при других действиях), чем другие, то их предварительно следует округлить, сохраняя лишь одну «эапасную цифру».

VII. Для получения результата с N верными цифрами исходные данные следует брать с таким числом цифр, которые согласно предыдущим правилам обеспечивают N+1 цифру в результате.

Пример. Найдем s=2,35+11,8 без учета погрешностей. Применяя правило I, получим s=14,15. Результат округлим по числу 11,8 с наименьшим количеством десятичных знаков. Получим: s =14,2.

Решим задачу с учетом погрешностей. В числе s=14,15 надо оставить только верные цифры. Для этого найдем предельную абсолютную погрешность суммы s, используя правило 1. Учитывая, что все цифры в числах 2,35 и 11,8 являются верными, получим: Δ 14,15 =Δ 2,35 +Δ 11,8 =0,01+0,1=0,11

Аналогично решаются задачи при выполнении других действий над приближенными числами.

Тема: «Нахождение
приближенных значений квадратного корня»

Тип урока : ОНЗ, Р

Основные цели:

  • научиться находить приближенные значения квадратного корня,
  • познакомиться с методами для вычисления корней.

1. Самоопределение к учебной деятельности

Цель этапа: 1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урока: продолжаем работать над квадратными корнями

Организация учебного процесса на этапе 1:

Что сейчас изучаем на уроках алгебры? (Квадратные корни)

А что такое квадратные корни?

– Молодцы! Для успешной работы выполним следующие задания.

2. Актуализация знаний и фиксация затруднения в деятельности

Цель этапа: 1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: нахождение значений квадратного корня;

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;

4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: найти значение выражения .

Организация учебного процесса на этапе 2:

1. Вычислите: , , , ,

4. Индивидуальное задание .

Найдите значение выражения ..

3. Выявление причины затруднения и постановка цели деятельности

Цель этапа: 1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности: возможность найти значение квадратного корня;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

– что вам необходимо было сделать?

– Что у вас получилось? (Учащиеся показывают свои варианты:)

– В чём возникло затруднение?

Извлекается √2 нацело?

Нет.

Как будем находить?

Какие знаем способы нахождения корней?

Ребята, видите, не всегда мы имеем дело с числами, легко представимыми в виде квадрата числа, которые извлекаются из- под корня нацело.

– Какую цель мы поставим перед собой?

– Сформулируйте тему урока.

– Запишите тему в тетрадь.

4. Построение проекта выхода из затруднения

Цель этапа: 1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме.

Организация учебного процесса на этапе 4:

1 МЕТОД в ычислить √2 с точностью до двух знаков после запятой Будем рассуждать следующим образом.

Число √2 больше 1, так как 1 2 2 больше 2. Следовательно, десятичная запись числа будет начинаться следующим образом: 1,… То есть корень из двух, это единица с чем-то.

Теперь попытаемся отыскать цифру десятых.

Для этого будем дроби от единицы до двойки возводить в квадрат, пока не получим число большее двух.

Шаг деления возьмем 0,1, так как мы ищем число десятых.

Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9

1,1 2 =1,21; 1,2 2 =1,44; 1,3 2 =1,69; 1,4 2 =1,96; 1,5 2 =2,25.

Получили число превышающее двойку, остальные числа уже не надо возводить в квадрат. Число 1,4 2 меньше 2, а 1,5 2 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 . Следовательно, десятичная запись числа √2 в разряде десятых должна содержать 4. √2=1,4… .

Иначе говоря, 1,4

1,41 2 =1,9881, 1,42 2 =2,0164.

Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.

Из этого получаем, что число √2 будет принадлежать промежутку от 1,41 до 1,42 (1,41

Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.

√2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.

Задание

Вычислите с точностью до двух знаков после запятой

√3 = , √5 = , √6 = , √7 =, √8 =

Вывод Данный прием позволяет извлекать корень с любой заданной наперед точностью.

2 МЕТОД Чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.

Например, найдем √16 так:

  1. 16 — 1 = 15
  2. 15 — 3 = 12
  3. 12 — 5 = 7
  4. 7 — 7 =0
  • Выполнено 4 действия, значит, √16 = 4

Задание Вычислите

√1 = √6 =

√2 = √7 =

√3 = √8 =

√4 = √9 =

√5 = √10 =

Вывод Данный прием удобен тогда, когда корень извлекается нацело

3 МЕТОД Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а 2 +b,

где а 2 — ближайший к числу х точный квадрат натурального числа а, и пользовались формулой.

Извлечем с помощью формулы квадратный корень,

Например из числа 28:

Вывод Способ вавилонян дает хорошее приближение к точному значению корня.

5. Первичное закрепление во внешней речи

Цель этапа: зафиксировать изученное учебное содержание во внешней речи.

Организация учебного процесса на этапе 5:

из учебника: №№ 336, 337, 338,339, 343,345

6. Самостоятельная работа с самопроверкой по эталону.

Цель этапа: проверить своё умение применять алгоритм сложения и вычитания в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.

Организация учебного процесса на этапе 6:

№№ 338 (а), 339 (в, г)

После проверки по эталону анализируются и исправляются ошибки.

7. Включение в систему знаний и повторение

Цель этапа: 1) тренировать навыки использования нового содержания совместно с ранее изученным;

Организация учебного процесса на этапе 7:

1 группа (средн) «№№ ______________

2 группа (высок) №№ _________________

8. Рефлексия деятельности на уроке

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 8:

– С чем мы познакомились сегодня на уроке?

– Что мы научились сегодня выполнять?

– Проанализируйте свою деятельность на уроке и дайте своей работе оценку.

Домашнее задание №№ 344 , 346, 351


4.6: Значащие цифры и округление

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    3555
    • Стивен Лоуэр
    • Университет Саймона Фрейзера
    Цели обучения
    • Приведите пример измерения, в котором количество значащих цифр явно слишком велико, и объясните, почему.
    • Укажите цель округления и опишите информацию, которую необходимо знать, чтобы сделать это правильно.
    • Округление числа до указанного количества значащих цифр.
    • Объясните, как округлить число, у которого вторая по значимости цифра равна 9.
    • Выполните простой расчет, включающий две или более наблюдаемых величин, и выразите результат в соответствующем количестве значащих цифр.

    Числовые значения, с которыми мы имеем дело в науке (и во многих других аспектах жизни), представляют собой измерения, значения которых никогда точно не известны. Наши карманные калькуляторы или компьютеры этого не знают; они рассматривают числа, которые мы в них вводим, как «чистые» математические объекты, в результате чего арифметические операции часто дают ответы, которые физически нелепы, хотя и математически правильны. Цель этого раздела — помочь вам понять, почему это происходит, и показать, что с этим делать.

    Цифры: значащие и прочие

    Рассмотрим два утверждения, показанные ниже:

    • «Население нашего города составляет 157 872 человека».
    • «Количество зарегистрированных избирателей на 1 января составило 27 833 человека.

    Какие из них вы бы немедленно уволили? Конечно, не второй, потому что он, вероятно, исходит из базы данных, которая содержит одну запись для каждого избирателя, поэтому число находится просто путем подсчета количества записей. Первое утверждение не может быть правильным. Даже если бы население города можно было точно определить (постоянные жители? теплые тела?), как мы можем объяснить ежеминутные изменения, происходящие по мере того, как люди рождаются и умирают, въезжают и уезжают?

    В чем разница между двумя цифрами населения, указанными выше? Первый выражает величину, которую нельзя точно знать, т. е. несет в себе некоторую степень неопределенности. Вполне возможно, что последняя перепись дала именно 157 872 записи, и это может быть «население города» для юридических целей, но это, конечно, не «настоящее» население. Чтобы лучше отразить этот факт, можно указать население (например, в атласе) как 157 900 или даже 158 000 . Эти две величины были округлены до четырех и трех значащих цифр, соответственно, и имеют следующие значения: в пределах от примерно 1578 50 до примерно 1579 50. Другими словами, население составляет 1579 00±50. Добавление «плюс-минус 50» к этому числу означает, что мы считаем абсолютную неопределенность измерения населения равной 50 – (–50) = 100. Мы также можем сказать, что относительная неопределенность составляет 100/1579.00, что мы также можем выразить как 1 часть на 1579, или 1/1579 = 0,000633, или около 0,06 процента.

  • Значение 158 000 означает, что численность населения, вероятно, находится между 157 500 и 158 500, или 158 000±500,000. Абсолютная неопределенность 1000 переводится в относительную неопределенность 1000/158000, или 1 часть на 158, или около 0,6 процента.

    • Какое из этих двух значений мы будем указывать как «население», будет зависеть от степени нашей уверенности в исходных данных переписи; если перепись была завершена на прошлой неделе, мы могли бы округлить до четырех значащих цифр, но если это было год или около того назад, округление до трех знаков могло бы быть более разумным выбором. В таком случае нет действительно объективного способа выбора между двумя альтернативами.

    Это иллюстрирует важный момент: концепция значащих цифр имеет меньше общего с математикой, чем с нашей уверенностью в измерении. Эта уверенность часто может быть выражена численно (например, высота жидкости в измерительной трубке может быть определена с точностью до ±0,05 см), но когда это невозможно, как в примере с нашей популяцией, мы должны полагаться на наш личный опыт и суждения.

    Итак, что такое значащая цифра? Согласно обычному определению, это все числительные в измеряемой величине (считая слева), значения которых считаются точно известными, плюс еще одно, значение которого может быть на единицу больше или меньше:

    • В « 1579 00» (четыре значащие цифры) точно известны три крайние левые цифры, но четвертая цифра, «9», вполне может быть «8», если «истинное значение» находится в подразумеваемом диапазоне. от 1578 50 до 1579 50.
    • В « 158 000» (три значащие цифры) две крайние левые цифры известны точно, а третья цифра может быть либо «7», либо «8», если истинное значение находится в подразумеваемом диапазоне 157 . от 500 до 158 500.

    Хотя округление всегда приводит к потере числовой информации, то, от чего мы избавляемся, можно считать «числовым шумом», который не способствует качеству измерения. Цель округления состоит в том, чтобы избежать выражения значения с большей степенью точности, чем это согласуется с неопределенностью измерения.

    Подразумеваемая погрешность

    Если вы знаете, что точность весов составляет, скажем, 0,1 мг, то погрешность любого измерения массы, выполненного на этих весах, составит ±0,1 мг. Предположим, однако, что вам просто сказали, что объект имеет длину 0,42 см, без указания его точности. В этом случае все, что вам нужно сделать, это количество цифр, содержащихся в данных. Таким образом, количество «0,42 см» указано до 0,01 единицы в 0 42 или одной части в 42 . Подразумеваемая относительная неопределенность этой цифры составляет 1/42, или около 2%. Таким образом, точность любого числового ответа, рассчитанного на основе этого значения, ограничена примерно такой же величиной.

    Ошибка округления

    Важно понимать, что количество значащих цифр в значении дает лишь приблизительное представление о его точности, и что при округлении информация теряется. Предположим, например, что мы измеряем вес объекта как 3,28 г на весах, которые, как полагают, имеют точность в пределах ±0,05 грамма. Полученное значение 3,28 ± 0,05 грамма говорит нам о том, что истинный вес объекта может быть где-то между 3,23 г и 3,33 г. Абсолютная неопределенность здесь составляет 0,1 г (±0,05 г), а относительная неопределенность составляет 1 часть на 32,8, или около 3 процентов.

    Сколько значащих цифр должно быть в сообщаемом измерении? Так как только крайняя левая «3» в «3,28» определена, вы, вероятно, предпочтете округлить значение до 3,3 г. Все идет нормально. Но что кто-то другой должен думать об этой цифре, когда увидит ее в вашем отчете? Значение «3,3 г» предполагает подразумеваемую неопределенность , равную 3,3±0,05 г, что означает, что истинное значение, вероятно, находится между 3,25 г и 3,35 г. Этот диапазон на 0,02 г ниже, чем связанный с первоначальным измерением, поэтому округление внесло погрешность в результат на эту величину. Поскольку это составляет менее половины погрешности взвешивания ±0,05 г, само по себе это не очень серьезно. Однако, если в расчете объединяются несколько значений, округленных таким образом, ошибки округления могут стать значительными.

    Правила округления

    Стандартные правила округления хорошо известны. Прежде чем мы их изложим, давайте договоримся, как называть различные компоненты числового значения.

    • Самая значащая цифра — самая левая цифра (не считая начальных нулей, которые служат только заполнителями и никогда не являются значащими цифрами).
    • Если округлить до n значащих цифр, то младшая значащая цифра — это n -я цифра от старшего разряда. Младшая значащая цифра может быть нулем.
    • Первая незначащая цифра — это n +1-я цифра.

    Правила округления

    • Если первая незначащая цифра меньше 5, то младшая значащая цифра остается неизменной.
    • Если первая незначащая цифра больше 5, младшая значащая цифра увеличивается на 1.
    • Если первая незначащая цифра равна 5, младшая значащая цифра может быть либо увеличена, либо оставлена ​​без изменений ( см. ниже! )
    • Все незначащие цифры удаляются.

    Фантазии о пятерках

    Иногда учащимся предлагается увеличить младшую значащую цифру на 1, если она нечетная, и оставить ее без изменений, если она четная. Интересно, отражает ли это какую-то идею о том, что четные числа как-то «лучше» нечетных! (Древнее суеверие как раз противоположное, что только нечетные числа являются «счастливыми».)

    На самом деле, вы могли бы сделать то же самое и наоборот, увеличивая только четные числа. Если вы округляете только одно число, на самом деле не имеет значения, что вы делаете. Однако при округлении ряда чисел, которые будут использоваться в расчетах, если вы одинаково обрабатываете каждую первую незначащую 5, вы завышаете или занижаете значение округленного числа, тем самым накапливая ошибку округления. . Поскольку существует одинаковое количество четных и нечетных цифр, увеличение только одного из них предотвратит возникновение ошибки такого рода. Конечно, вы могли бы сделать то же самое, подбросив монетку!

    Таблица \(\PageIndex{1}\): Примеры округления

    число округлить до

    		 количество значащих цифр

    результат

    комментарий

    34,216 3 34,2 Первая незначащая цифра (1) меньше 5, поэтому число просто усекается.
    2,252 2 2,2 или 2,3 Первая незначащая цифра — 5, поэтому наименьший знак. цифра может либо оставаться неизменной, либо увеличиваться.
    39,99 3 40,0 Пересечение «десятичной границы», поэтому все числа меняются.
    85 381 3 85,4 00 Два нуля — это просто заполнители
    0,04597 3 0,0460 Два начальных нуля не являются значащими цифрами.

    Округление девяток

    Предположим, что вес объекта составляет 3,98 ± 0,05 г. Это поместит его истинный вес где-то в диапазоне от 3,93 г до 4,03 г. Решая, как округлить это число, вы подсчитываете количество цифр в «3,98», которые точно известны, и не находите ни одной! Поскольку «4» — это самая левая цифра, значение которой является неопределенным, это будет означать, что результат следует округлить до одной значащей цифры и указать просто как 4g. Альтернативой может быть изменение правила и округление до двух значащих цифр, что дает 4,0 г. Как вы можете решить, что делать? В таком случае вы должны посмотреть на подразумеваемые неопределенности в двух значениях и сравнить их с неопределенностью, связанной с исходным измерением.

    Таблица \(\PageIndex{2}\)

    округленное значение

    подразумеваемый максимум

    подразумеваемый минимум

    абсолютная неопределенность

    относительная неопределенность

    3,98 г 3,985 г 3,975 г ±0,005 г или 0,01 г 1 из 400, или 0,25%
    4 г 4,5 г 3,5 г ±0,5 г или 1 г 1 из 4, 25%
    4,0 г 4,05 г 3,95 г ±0,05 г или 0,1 г 1 из 40, 2,5%

    Ясно, что округление до двух цифр является единственным разумным вариантом в этом примере. Наблюдаемые значения следует округлить до числа цифр, наиболее точно отражающего неопределенность измерения.

    • Обычно это означает округление до количества значащих цифр в количестве; то есть количество цифр (считая слева), которые точно известны, плюс еще одна.
    • Если это неприменимо (как в приведенном выше примере, когда добавление вычитания абсолютной неопределенности связывает десятую степень), то мы округляем таким образом, чтобы относительная подразумеваемая неопределенность результата была как можно ближе к неопределенности наблюдаемое значение.

    Округление результатов вычислений

    При выполнении вычислений, состоящих из нескольких шагов, следует избегать округления до получения окончательного результата. Предположим, вы используете свой калькулятор для расчета площади прямоугольника:

    округленное значение

    относительная подразумеваемая неопределенность

    1,58 1 часть на 158 или 0,6%
    1,6 1 часть на 16, или 6 %
    Примечание

    Ваш калькулятор, конечно, верен в чистом виде, но вы ошибетесь, записав «1,57676 см 9». 0404 2 «. Справа показаны два возможных варианта округления ответа калькулятора.

    Понятно, что ни один из вариантов не является полностью удовлетворительным; правило, и округление до двух цифр в «.42» приводит к потере некоторой точности. В этом случае можно утверждать, что округление до трех цифр оправдано, поскольку подразумеваемая относительная неопределенность в ответе, 0,6%, больше в соответствии с двумя факторами.

    «Правила» округления, как правило, полезны и удобны, но они не всегда приводят к желаемому результату. В случае сомнений лучше полагаться на относительную подразумеваемую неопределенность.

    Сложение и вычитание

    В операциях со значащими цифрами ответ сообщается таким образом, чтобы он отражал надежность наименее точной операции. Ответ не более точен, чем наименее точное число, использованное для получения ответа. При сложении или вычитании мы идем по числу десятичных знаков (т. е. количество цифр справа от десятичной точки), а не по количеству значащих цифр. Определите количество, имеющее наименьшее количество знаков после запятой, и используйте это число, чтобы задать количество знаков после запятой в ответе.

    Умножение и деление

    Результат должен содержать такое же количество значащих цифр, как и значение с наименьшим количеством значащих цифр.

    Логарифмы и антилогарифмы

    Если число выражено в виде а × 10 Ь («научная запись») с дополнительным ограничением, что коэффициент а не меньше 1 и меньше 10, число находится в его нормализованная форма . Выразите логарифм по основанию 10 значения, используя то же количество значащих цифр, которое присутствует в нормализованной форме этого значения. Точно так же для антилогарифмов (числа, выраженные в степени 10) используйте то же количество значащих цифр, что и в этой степени.

    Примеры \(\PageIndex{1}\)

    Следующие примеры иллюстрируют наиболее распространенные проблемы, с которыми вы, вероятно, столкнетесь при округлении результатов вычислений. Они заслуживают вашего внимательного изучения!

    результат калькулятора

    		закругленный замечания
    1,6 Округление до двух значащих цифр дает подразумеваемую неопределенность 1/16 или 6 %, что в три раза больше, чем у наименее точно известного коэффициента. Это хорошая иллюстрация того, как округление может привести к потере информации.
    1.9E6 Фактор «3.1» указан как 1 часть из 31, или 3%. В ответе 1. 9 значение выражено в 1 части 19, или 5%. Эти точности сопоставимы, поэтому правило округления дало нам разумный результат.

    Некая книга имеет толщину 117 мм; найдите высоту стопки из 24 одинаковых книг:

    		 281 0 мм «24» и «1» являются точными, поэтому единственным неопределенным значением является толщина каждой книги, представленная 3 значащими цифрами. Конечный ноль в ответе — это только заполнитель.
    10,4 При сложении или вычитании найдите термин с наименьшим числом знаков после запятой и округлите ответ до такого же числа знаков.
       
      23 см см. ниже

    Последний из показанных выше примеров представляет очень распространенную операцию преобразования одной единицы в другую. Здесь есть некоторая двусмысленность; если мы возьмем «9дюймов» означает расстояние в диапазоне от 8,5 до 9,5 дюймов, то подразумеваемая неопределенность составляет ±0,5 дюйма, что составляет 1 часть на 18, или примерно ± 6%. Относительная неопределенность ответа должна быть одинаковой, поскольку все значения умножаются на один и тот же коэффициент 2,54 см/дюйм. В этом случае мы вправе записывать ответ с двумя значащими цифрами, что дает погрешность около ±1 см. Если бы мы использовали ответ «20 см» (один значащий цифра), его подразумеваемая неопределенность будет ±5 см, или ±25%.

    Если возникает вопрос о подходящем количестве значащих цифр, расчет относительной неопределенности может помочь вам принять решение.

    Эта страница под названием 4.6: Значимые цифры и округление распространяется под лицензией CC BY 3. 0 и была создана, изменена и/или курирована Стивеном Лоуэром с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Стивен Лоуэр
        Лицензия
        СС BY
        Версия лицензии
        3,0
        Показать страницу TOC
        № на стр.
      2. Теги
        1. источник@http://www.chem1.com/acad/webtext/virtualtextbook.html

      Округление чисел — GeeksforGeeks

      Оценка является формой округления . Оценка используется в повседневной жизни, а также в таких темах, как математика и физика. Многие физические величины, такие как количество денег, пройденное расстояние, измеренная длина и т. д., рассчитываются путем округления фактической цифры до ближайшего целого числа.

      Каждое измерение имеет погрешность. Точность и достоверность — два элемента, влияющие на измерение. Эти два критерия помогают выявить наличие физических величин, а также их сравнение и измерение. Давайте опишем Точность и Точность как:

      • Точность: Близость измеренного значения к стандартному значению определяется как точность . например Если вы взвешиваете коробку и отмечаете 5 кг, но ее известный вес составляет 6 кг, ваши измерения неточны.
      • Точность: Точность определяется как близость двух или более измеренных значений друг к другу. Если вы взвесите одну и ту же коробку пять раз и получите близкие значения, такие как 4,11, 4,2, 4,22, 4,4 и 40, ваши измерения точны.

      Точность и аккуратность — это два разных понятия. Вы можете быть предельно точны, но неточны, или наоборот. Единичные измерения — это точность и аккуратность. Результат измерения должен быть точным. Физическая сумма измеряется двумя цифрами. Цифры делятся на два типа: надежный и неопределенный . Теперь пришло время понять, что такое значащие цифры.

      Что такое значимые цифры?

      Измерения физических товаров представляют собой комбинацию набора надежных и ненадежных, то есть неопределенного количества цифр. Значимые биты числа включали первую неуверенную цифру и все достоверные цифры. Их также называют значащими цифрами . Количество цифр, которые известны с некоторой степенью достоверности, называется значащими цифрами.

      Например, вес человека составляет 90,46 кг. В этом случае цифры 9,0 и 4 составляют значащие цифры, а 6 – незначащие.

      Правила учета значащих цифр:

      • Ненулевые цифры всегда значащие.
      • Последние нули в правой части десятичной дроби считаются значащими.
      • Нули, записанные в качестве заполнителей, не имеют значения.
      • Нули между двумя значащими цифрами являются значащими. Например, 0,00065 имеет две значащие цифры.
      • Нули слева от первой ненулевой цифры не имеют значения. Например, 0,0000466 имеет три значащих цифры.
      • Для недесятичных чисел нули в конце не имеют значения. Например, 63000 имеет две значащие цифры.

      Значащие цифры являются показателем точности измерения величины. Это зависит от наименьшего количества измерительных приборов.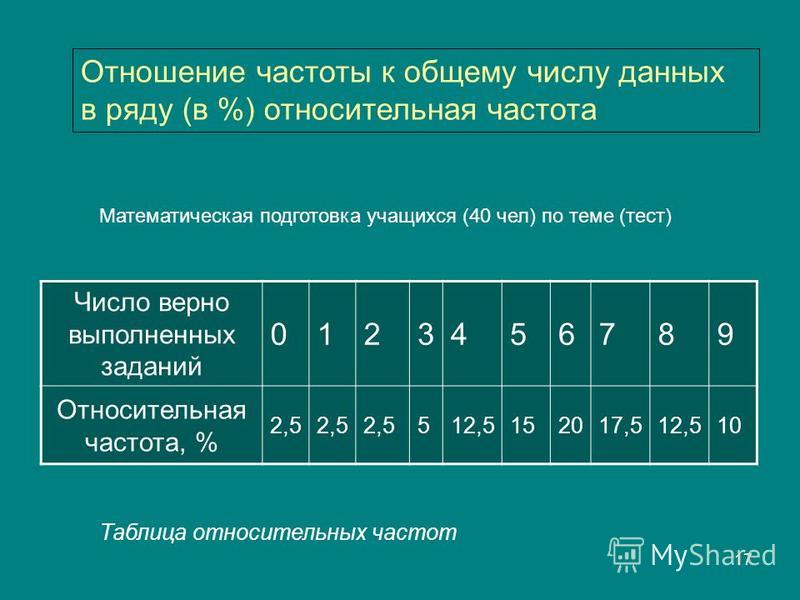 В случае сохранения количества значащих цифр при взаимопересчете между единицами одного и того же товара количество обозначается в научной записи вида Х × 10 Y , где X — число от 1 до 10, обозначающее количество значащих цифр.

      Округление цифр

      Округление цифр — это явление, используемое для оценки. Оценка формирует важный аспект для точного и точного измерения объектов и товаров в повседневной жизни. Это также снижает неопределенность при работе с количествами. Необходимо уменьшить количество незначащих цифр, необходимых для соблюдения правил арифметических действий со значащими цифрами.

      Округление подразумевает упрощение числа путем сохранения его значения, но приближения его к следующему числу. Он выполняется для целых чисел, а также для десятичных знаков в различных точках, таких как сотни, десятки, десятые и так далее.

      Числа округлены, чтобы сохранить важные цифры. Количество важных цифр в результате просто относится к количеству цифр, которые понятны с некоторой степенью уверенности.

      В числе 21.3 три значащих цифры. Ненулевые цифры всегда имеют смысл. Номер 21.3149имеет шесть значащих цифр (все числа дают вам полезную информацию). В результате число 76 имеет две значащие цифры, а число 76,3 — три значащие цифры.

      Правила округления цифр

      При округлении цифр соблюдаются стандартные правила: неизмененный.

                9,81 округляется до 9,8, так как отбрасываемая цифра меньше 5, а предыдущая цифра остается неизменной.

      • Если округляемая цифра в указанном числе больше 5, то предыдущая цифра изменяется и увеличивается на единицу.

                 9,88 округляется до 9,9, поскольку отбрасываемая цифра больше 5, а предыдущая цифра увеличивается на единицу.

      • Если отбрасываемая цифра эквивалентна 5 и если за ней следуют другие ненулевые цифры, то предыдущая цифра указанного числа увеличивается на единицу.

                напр.  число 9,755 необходимо округлить с учетом десятков цифр, затем оно округляется до 9,8, так как за ним следуют другие ненулевые цифры.

      • Если отбрасываемая цифра эквивалентна 5 или если за 5 следуют другие нулевые цифры, то предыдущая цифра указанного числа остается неизменной, если оно четное.

                 число 9.850 нужно округлить с учетом десятков цифр, тогда оно округляется до 9.8, так как за ним следуют другие нули.

      • Если отбрасываемая цифра эквивалентна 5 или если за 5 следуют другие нулевые цифры, то предыдущая цифра указанного числа увеличивается на единицу, если оно нечетное.

                 число 9,750 необходимо округлить с учетом десятков цифр, затем оно округляется до 9,8, так как за ним следуют другие нули.

      Первая незначащая цифра находится на (n+1)-й позиции с крайнего левого места.

      Правила устранения неоднозначностей при определении количества значащих цифр

      Некоторые из важных правил устранения неоднозначностей при определении количества значащих цифр:

      • Изменение единиц измерения не должно влиять на число значащих цифр числа.

                напр.  5,900 м = 590,0 см = 5900 мм. Первые два числа являются 4 значащими цифрами, а последнее имеет 2 цифры соответственно.

      • Экспоненциальная запись может использоваться для сообщения об измерениях чисел.
      • Умножение или деление точных чисел может иметь бесконечное количество значащих цифр.

      Правила округления целых чисел
      • Выбирается меньшее значение разряда для указанного целого числа.
      • Используйте следующий меньший разряд справа от округляемого числа. При округлении цифр от разряда десятков ищется цифра в разряде единиц.
      • Найдите величину цифры. Если наименьший разряд меньше 5, то цифра остается нетронутой. Любое количество цифр после этого числа становится нулем, что называется округлением цифры в меньшую сторону. Однако, если наименьший разряд больше или равен 5, то к цифре добавляется +1. Любые цифры после этого числа становятся нулем и называются округлением цифры в большую сторону.

      Правила округления десятичных чисел
      • Определите цифры округления и оцените правую часть.
      • Если цифры в правой части меньше 5, они считаются равными нулю. Если больше или равно 5, то добавьте +1 к этой цифре и считайте все остальные цифры равными нулю.

      Во многих случаях получение оценки проще, дешевле и занимает меньше времени, чем выполнение фактического подсчета. Если сценарий не требует точного подсчета, будет достаточно оценки. Рассмотрим несколько методов оценки.

      1. Округление до ближайших десятков: Рассмотрим следующие три числа: 24, 25 и 26. Эти числа необходимо округлить до ближайших десятков. Попробуйте положить эти числа на весы. 24 ближе к двадцати или к тридцати? Это ближе к двадцати, поэтому мы округлим до двадцати. Точно так же 26 близко к 30, поэтому мы можем округлить его до 30. 25 — это то же расстояние, что и 20 и 30. Округление в большую сторону является обычной практикой, поэтому 25 также будет округлено до 30. Наконец, числа, оканчивающиеся на 1, 2, 3 и 4, округляются в меньшую сторону, а числа, оканчивающиеся на 5, 6, 7, 8 и 9,округляются до ближайших десятков.
      2. Округление до сотен: Здесь применима та же идея. Мы смотрим на числовую прямую, чтобы определить, ближе ли она к нижней сотне или к верхней. С примерами у нас будет более глубокое понимание. Завершение чисел 527 и 582. 527 явно ближе к 500 в этом случае, поэтому мы округлим его до 500. А 582 будет округлено до ближайшей сотни, в результате чего получится 600. Следует иметь в виду, что 450, которое составляет примерно от 400 до 500, обычно округляется до 500. Например, округляем 43 до ближайшей сотни. Поскольку 43 ближе к 0, чем к 100, мы округлим его до 0,9.0010
      3. Округление до тысяч: Все значения от 0 до 499, которые ближе к 0 на числовой прямой, будут округлены до 0. Числа от 500 до 999 будут округлены до 1000. Та же идея применима ко всем большие целые числа. Числа ближе к меньшей тысяче будут округлены в меньшую сторону, а числа более 500 будут округлены в большую сторону.

      Примеры задач

      Задача 1. Объясните количество значащих цифр в числе 0,000650.

      Решение:

      Так как ведущие нули не нужны для значащих цифр.

      Следовательно, есть три значащих цифры 650. 

      Задача 2. Округлите эти числа до трех значащих цифр каждое: (a) 9,845 и (b) 6,735.

      Решение: 

      (a) Округляемое число эквивалентно 5, поэтому в первом случае предшествующие цифры четные, поэтому остаются без изменений. Следовательно, полученное число 90,84.

      (b) Округляемое число равно 5, поэтому в первом случае предшествующие цифры нечетные, поэтому увеличиваются на единицу. Следовательно, полученное число 9,83.

      Задача 3: Меняются ли значащие цифры при изменении единиц измерения?

      Решение: 

      Изменение единиц не меняет значащие цифры. Например, с точки зрения длины 12 м = 1,2 × 10 м = 1,2 × 10 3 см, где значащие цифры эквивалентны 1, 

      Задача 4: Запишите количество значащих цифр в числе 0,410 м.

      Решение:

      Нули слева от значащего числа, не ограниченные слева другой значащей цифрой, не являются значащими, согласно общему критерию определения значащих цифр. Значимыми считаются нули, которые ставятся после других чисел, но перед запятой. В результате для предоставленного значения 0,410 последние три цифры будут значащими числами. В результате у него есть три важные фигуры.

      Задача 5: Чему равны числа 4,845 и 4,835 при округлении до 3-х значащих цифр?

      Решение:

      Поскольку предыдущая цифра четная, число 4,845, округленное до трех значащих цифр, дает 4,84. С другой стороны, число 4,835, округленное до трех значащих цифр, становится 4,84, поскольку предыдущая цифра нечетная.


      Что такое округление и значащие цифры? + Пример

      ПРЕДУПРЕЖДЕНИЕ: Это длинный ответ. Там даны все правила и множество примеров.

      Значащие цифры — это цифры, используемые для представления измеренного числа. Только крайняя справа цифра является неопределенной. Самая дальняя справа цифра имеет некоторую ошибку в своем значении, но все же является значимой.

      Точные числа имеют точно известное значение. Нет ошибки или неопределенности в значении точного числа. Вы можете думать о точных числах как о бесконечном числе значащих цифр.

      Примерами являются числа, полученные путем подсчета отдельных объектов, и определенные числа (например, в 1 м 10 см) являются точными.

      Измеренные числа имеют значение, которое НЕ известно точно из-за процесса измерения. Величина неопределенности зависит от точности измерительного устройства.

      Примерами являются числа, полученные путем измерения объекта каким-либо измерительным устройством.

      ПРАВИЛА ПОДСЧЕТА ЗНАЧИМЫХ ЦИФР :

      1. Ненулевые цифры всегда являются значащими.
      2. Все нули между другими значащими цифрами являются значащими.
      3. Начальные нули не имеют значения.
      4. Нули в конце имеют значение только в том случае, если они идут после десятичной точки и имеют значащие цифры слева.

      Примеры :

      1. Сколько значащих цифр в числе 0,077?
        Ответ : Два. Ведущие нули не имеют значения.
      2. Сколько значащих цифр в длине 206 см? Ответ : Три. Ноль значащий, потому что он находится между двумя значащими цифрами. Замыкающие нули имеют значение только в том случае, если они идут после десятичной точки и имеют значащие цифры слева.
      3. Сколько значащих цифр в значении 206,0 °C? Ответ : Четыре. Первый ноль значащий, потому что он находится между двумя значащими цифрами. Конечный нуль является значащим, поскольку он идет после десятичной точки и имеет значащие цифры слева от него.

      Округление означает уменьшение количества цифр в числе по определенным правилам.

      ПРАВИЛА ОКРУГЛЕНИЯ :

      1. При сложении или вычитании чисел найдите число, известное с наименьшим десятичным знаком. Затем округлить результат до этого десятичного знака.
      2. При умножении или делении чисел найдите число с наименьшим числом значащих цифр. Затем округлить результат до указанного количества значащих цифр.
      3. Если неокругленный результат или результат, округленный в соответствии с правилом 2, имеет 1 в качестве старшей значащей цифры, и ни один из операндов не имеет 1 в качестве ведущей значащей цифры, оставьте в результате дополнительную значащую цифру, убедившись, что ведущая цифра остается 1.
      4. При возведении числа в квадрат или извлечении из него квадратного корня считайте значащие цифры числа. Затем округляем результат до указанного количества значащих цифр.
      5. Если либо неокругленный результат, либо результат, округленный в соответствии с правилом 4, имеет 1 в качестве старшей значащей цифры, а ведущая значащая цифра операнда не равна 1, оставьте в результате дополнительную значащую цифру.
      6. Числа, полученные путем счета, и определенные числа имеют бесконечное количество значащих цифр.
      7. Во избежание «ошибки округления» при многошаговых вычислениях сохраняйте дополнительную значащую цифру для промежуточных результатов. Затем округлить должным образом, когда вы достигнете окончательного результата.

      ПРИМЕРЫ :

      Ответы округлить до нужного количества значащих цифр:

      1. 21,398 + 405 — 2,9; Ответ = #423#. Число 405 известно лишь избранным. Правило 1 говорит, что результат должен быть округлен до единиц.
      2. # (0,0496 × 32,0) / 478,8 #. Ответ = #0.003 32#. И 0,0496, и 32,0 известны только до трех значащих цифр. Правило 2 говорит, что результат должен быть округлен до трех значащих цифр.
      3. 3,7 × 2,8; Ответ = #10.4#. Следуя правилу 2, мы получим 10. в качестве результата. Это с точностью до 1 части из 10. Это существенно менее точно, чем любой из двух операндов. Вместо этого мы ошибаемся в пользу дополнительной точности и пишем 10.4.
      4. 3,7×2,8×1,6; Ответ = #17#. На этот раз число 1,6 известно только с точностью до 1 части из 16, поэтому результат следует округлить до 17, а не до 16,6.
      5. 38 × 5,22; Ответ = #198#. Правило 2 дало бы нам 2,0 x 10², но, поскольку неокругленный результат равен 198,36, Правило 3 говорит о сохранении дополнительной значащей цифры.
      6. #7.81/80#. Ответ = #0.10#. Число 80 имеет одну значащую цифру. Правило 2 говорит округлить 0,097 625 до 0,1, после чего Правило 3 говорит нам сохранить вторую значащую цифру.
        Запись 0,098 означала бы неопределенность в 1 часть из 98. Это слишком оптимистично, поскольку неопределенность числа 80 составляет 1 часть из 8. Поэтому мы оставляем 1 в качестве старшей цифры и пишем 0,10.
      7. (5,8)²; Ответ = #34#. Число 5,8 известно до двух значащих цифр, поэтому Правило 4 говорит, что результат должен быть округлен до двух значащих цифр.
      8. (3,9)²; Ответ = #15.2#. Правило 4 предсказывает ответ 15. Старшая цифра 15 равна 1, но первая цифра 3,9 не равна 1. Правило 5 говорит, что мы должны оставить в результате дополнительную значащую цифру.
      9. #√0.0144#; Ответ = #0.120#. Число 0,0144 состоит из трех значащих цифр. Правило 4 гласит, что в ответе должно быть одинаковое количество значащих цифр.
      10. (40)²; Ответ = #1,6 × 10³#. Число 40 имеет одну значащую цифру. Правило 4 дало бы 2 x 10³, но неокругленный результат имеет 1 в качестве первой цифры, поэтому Правило 5 говорит о сохранении дополнительной значащей цифры.
      11. Если десять шариков вместе имеют массу 265,7 г, какова средняя масса одного шарика? Ответ = #(265,7 г)/10# = 26,57 г. Число 10 имеет бесконечное число значащих цифр, поэтому Правило 6 говорит, что в ответе четыре значащих цифры.
      12. Вычислите длину окружности с измеренным радиусом 2,86 м. Ответ : #C = 2πr# = 2 × π × 2,86 м = 17,97 м. Число 2 точное, а ваш калькулятор хранит значение π до многих значащих цифр, поэтому мы используем правило 3, чтобы получить результат с четырьмя значащими цифрами.

      Анализ данных

      Анализ данных
      Анализ данных
      Ульриха де ла Кампа и Оливера Сили

      ЗНАЧИМЫЕ ЦИФРЫ ИЛИ ЦИФРЫ

      Любое количественное измерение свойства требует размещения числового значения на этом свойство, а также указание единиц измерения (см, г, мл и т. д.). количество цифр, используемых для обозначения числового значения, называется числом значащих числа или цифры, и они зависят от точности измерительного прибора. Ценный информация может быть потеряна, если опущены значащие цифры. Так же неправильно записывать слишком много цифр, так как это подразумевает большую точность, чем существует на самом деле.

      Таким образом, значащие цифры — это те цифры, которые дают смысл, но не вводят в заблуждение. Информация. Только последняя цифра содержит погрешность, связанную с точностью измерения. Поэтому, когда производится измерение и учитывается точность измерения, все цифры, считающиеся достаточно надежными, являются значительными. Например:

      2.05 имеет три значащие цифры

      64,472 имеет пять значащих цифр

      0,74 имеет две значащие цифры

      Нули могут быть или не быть значащими. Следующие правила должны быть полезными:

      1. Ноль между двумя цифрами является значащим. 107,8 имеет четыре значащие цифры

      2. Конечные нули после запятой всегда имеют значение. 1.5000 имеет пять значащих цифры

      3. Нули не имеют значения, если они используются для фиксации положения десятичной точки. 0,0031 имеет две значащие цифры

      4. Некоторые обозначения неоднозначны, и их следует избегать, например, для таких чисел, как 700 непонятно, сколько цифр значащих. Этой двусмысленности можно избежать, если использовать научная нотация.

      7 x 10 2 указывает одну значащую цифру
      7,0 x 10 2 указывает две значащие цифры
      7,00 х 10 2 указывает три значащие цифры

      Важно понимать, что значащими цифрами считаются все цифры, которые являются определенными плюс один цифра, а именно последняя, ​​которая имеет неопределенность плюс-минус один в этом месте. самая левая цифра в числе называется самой значащей цифрой (msd), а самая правая цифра — наименее значащая цифра (lsd). Для другого обсуждения этой темы см. страницы 39-40 в SHW.

      ЗНАЧИМЫЕ ЦИФРЫ СУММЫ ИЛИ РАЗНОСТИ

      При добавлении или вычитании значащих цифр ответ выражается только до последней полный столбец цифр.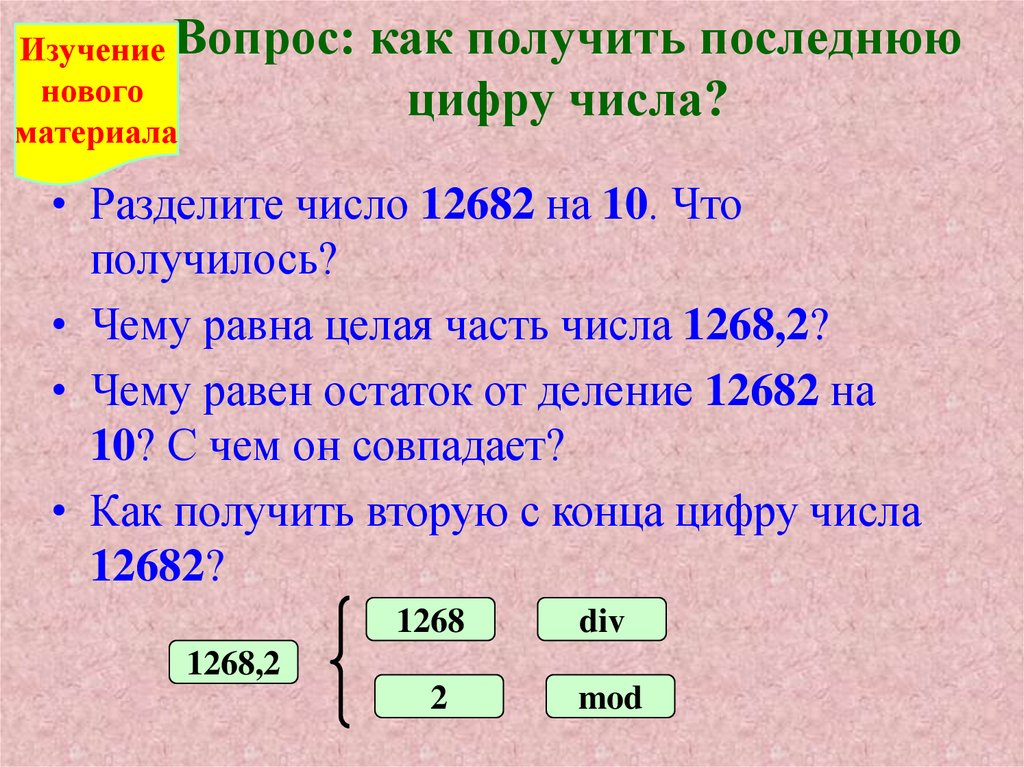 Вот некоторые примеры:

      15,42+0,307=15,73

      3,43+8,6=12,0

      27,0-0,364=26,6

      ЗНАЧИТЕЛЬНЫЕ ЦИФРЫ ДЛЯ ПРОДУКТА ИЛИ ЧАСТНОГО

      Часто говорят, что количество значащих цифр в ответе должно быть таким же, как в количество значащих цифр в данных, которое имеет наименьшее количество значащих цифр. За пример для результата следующего деления 90,8/9,41 = 1,0414 результат, согласно вышеприведенное правило должно быть округлено до двух значащих цифр, поскольку данные с наименьшим значащим цифр, а именно 9,8 имеет только две цифры. Это правило, которое часто цитируют и которое многие ученики найти знакомых и простых страдает от серьезного дефекта. Относительная неопределенность двух частей данных совсем другое. Для 9,8 это 1/98 0,01, а для 9,41 это 1/941 0,001. Очевидно, ответ не должен показывать относительную неопределенность меньше, чем наибольшая относительная неопределенность в данные. И наоборот, ответ не должен даваться таким образом, чтобы его относительная неопределенность больше, чем следует из данных. В примере приведено применение общего правила бы указать, что ответ должен состоять из двух значащих цифр, т. е. должен быть равен 1,0. Относительная неопределенность тогда будет 1/10 = 0,1, что намного больше, чем 0,01. По этой причине представляется, что более сложное правило, учитывающее относительную неопределенность как данных, так и ответа, нужный. Относительно простое правило, которое делает это, может быть получено из следующего соображения. Для одиночных и цепных умножений и в хорошем приближении для делений неопределенность в A связано с неопределенностью в D соотношением:

      Относительная неопределенность D равна относительной неопределенности A.

      Усовершенствованное правило произведения-частного, основанное на предыдущем анализе, приведено ниже.

      1. Определите данные с наименьшим количеством цифр или, если два или более данных заданы для одинаковое количество цифр, то есть наименьшее число, если десятичная точка игнорируется. Запишите цифры данных, определенных таким образом, как целое число, игнорируя десятичную дробь. точка.

      2. Разделите это целое число на ответ и обратите внимание на старший разряд результата. позиция этой цифры — позиция последней цифры, которую следует сохранить в ответе.

      В приведенном выше примере 9.8 явно является элементом данных с наименьшим количеством цифр. Один следовательно делит 1,0414 на 98, получая 0,01063. Самая значащая цифра в этом ответе находится в сотое место. Результат деления 9,8 на 9,41 должен быть выражен с наименьшим значительный цифра в сотых, т.е. 1,04. Обратите внимание, что относительная неопределенность этого результата составляет 1/104. 0,01, что как раз и является относительной неопределенностью в 9.8.

      ЗНАЧИТЕЛЬНЫЕ ЦИФРЫ ДЛЯ СТЕПЕНЕЙ И КОРНЕЙ

      Пусть A = KD a , где K — константа, а «a» — постоянный показатель степени, либо целое или дробное. Это можно показать, что относительная неопределенность A равна относительной неопределенности D, умноженной на через «а», т.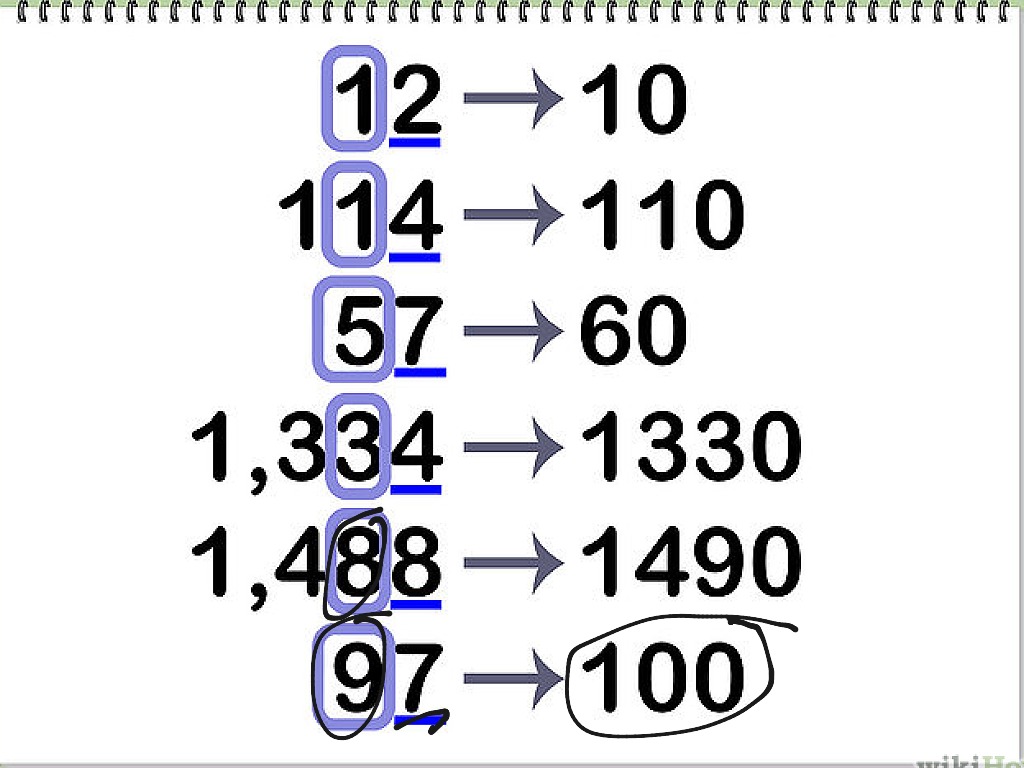 е.

      Например, пусть A = (0,0768) 1/4 = 0,52643…. Тогда

      Поскольку старшая цифра в последнем ответе стоит в четвертом десятичном разряде, правильный число значащих цифр в A равно четырем, т. е. A = 0,5264.

      ЗНАЧИМЫЕ ЦИФРЫ ДЛЯ ЛОГАРИФМОВ И АНТИЛОГАРИФМОВ

      Учитывая [H + ] = 1,8 x 10 -4 , мы можем рассчитать pH из определение количества, т.е.

      pH = -log[H + ]. Сколько значащих должно показывать значение pH?

      Логарифм состоит из двух частей. Цифры слева от запятой, эти цифры известен как характеристика. Характеристика не является значащей цифрой, поскольку она указывает только величина числа. Цифры справа от запятой — это мантисса, и они представляют точность, с которой известен результат. Отсюда вытекают следующие правила:

      1. При вычислении логарифма сохранять в мантиссе одинаковое количество значащих цифры как присутствовали в исходных данных.

      2. При вычислении антилогарифма сохраняйте то же количество значащих цифр, что и мы присутствует в мантиссе логарифма.

      3. Обратите внимание, что все нули в мантиссе значимы независимо от позиции.

      ОКРУГЛЕНИЕ ЧИСЕЛ

      Когда мы используем значащие цифры в числовых операциях, мы часто получаем ответы с более цифры чем оправданы. Затем мы должны округлить ответы до правильного количества значащих цифр на отбрасывая лишние цифры. Используйте следующие правила для округления:

      1. Если отбрасываемая цифра 0, 1, 2, 3 или 4, отбросьте ее и оставьте последнюю оставшуюся цифру без изменений. является.

      473,4 округляется до 473

      2. Если отбрасывается цифра 5, 6, 7, 8 или 9увеличить последнюю оставшуюся цифру на 1.

      27,8 округляется до 28

      Приведенные выше правила можно резюмировать следующим образом: «Если первая (крайняя левая) цифра, которую нужно отбросить, значителен и округляется до 5-9, в противном случае обрезается. Важно понимать, что округление должно отложить до завершения расчета, т.е. не округлять промежуточные результаты.

      ТОЧНОСТЬ ПРОТИВ. ТОЧНОСТЬ

      Экспериментальное определение любой величины может быть ошибочным, поскольку невозможно нести вне любое измерение с абсолютной достоверностью. Степень ошибки в любом определении является функцией из качество инструмента или измерительного устройства, навыки и опыт экспериментатор. Таким образом, обсуждение ошибок является неотъемлемой частью экспериментальной работы в любой количественной науке.

      Типы ошибок, возникающих при проведении измерений, подразделяются на три группы:

      1. Грубые, небрежные ошибки — ошибки, которые вряд ли будут повторный в подобном определения. К ним относятся проливание образца, неправильное считывание веса, считывание объем бюретки неправильный и т.д..

      2. Случайные ошибки. также называется неопределенной ошибкой. связаны с присущий ограничения оборудование или виды проводимых наблюдений. Ошибки такого типа также могут быть связаны с отсутствием внимание экспериментатора. Как правило, их можно свести к минимуму, используя высококачественное оборудование и тщательной работой с этим оборудованием, но никогда не может быть полностью устранена. принято проводить измерения повторно, чтобы уменьшить влияние случайных ошибок на решимость.

      3. Систематические ошибки , также называемые детерминированными ошибками каждый человек результат повторных определений точно таким же образом. Это могут быть ошибки измерения инструмента, наблюдателя или самого метода. Примеры ошибок в химических анализах включают такие вещи, как использование нечистых материалов для стандартизации растворов, калиброванная мерная посуда, такая как пипетки, бюретки и мерные колбы.

      Учащиеся могут распознать возникновение небрежных или случайных ошибок по отклонениям отдельный определения друг от друга. Это называется точностью измерения . существование систематических ошибок реализуется при сравнении экспериментальных результатов с истинным значением. Это точность результата. Дальнейшее обсуждение этих условий приведено ниже:

      Точность измерения относится к близости числового значения к правильному или принято ценность. Его часто выражают через относительную процентную ошибку:

      экспериментально — верно x 100 = отн. процент ошибки правда

      Оценивается только при наличии независимого определения, которое принимается за истинное ценность. В тех случаях, когда истинное значение неизвестно, можно заменить «истинное» значение в среднее значение повторных определений для расчета относительной процентной ошибки.

      Точность измерения относится к воспроизводимости результатов, т.е. соглашение между значения в повторных испытаниях. Химические анализы обычно проводят в трехкратной повторности. Небезопасно использовать только два испытания, потому что в случае отклонения никто не знает, какое из двух значений больше надежный. Как правило, слишком трудоемко использовать более трех образцов.

      СРЕДНЕЕ ОТКЛОНЕНИЕ

      Прецизионность набора измерений обычно выражается в стандарте отклонение. А несколько проще для понимания и для небольших наборов данных, так же как и значимая мера точности. в среднее отклонение. Шаги, необходимые для вычисления этого среднего отклонения, следующие: кратко изложены ниже.

      1. Вычислите среднее арифметическое (среднее) набора данных.

      2. Рассчитайте отклонение каждого определения от среднего.

      3. Теперь вычислите сумму абсолютных значений отклонений, найденных в 2. выше. затем разделить эту сумму на количество определений.

      Результат анализа может быть выражен как «среднее + среднее отклонение».

      Эту процедуру можно проиллюстрировать следующими данными. Предположим, что вы хотели рассчитать средний пробег на галлон бензина вашего автомобиля. Результаты трех различных испытаний, проведенных под аналогичные условия вождения дали следующие мили на галлон:

      20. 8, 20.4 и 21.2

      Среднее арифметическое можно рассчитать как (20,8 + 20,4 + 21,2)/3=20,8

      Отклонение от среднего в каждом случае составляет
      |20,8-20,8|=0,0
      |20,4-20,8|=0,4
      |21,2-20,8|=0,4
      Среднее отклонение от среднего затем рассчитывается как
      (0,0+0,4+0,4)/3=0,3, к одному. значащая фигура

      Таким образом, экспериментальное значение должно быть указано как:

      20,8 ± 0,3 мили на галлон

      ОТКАЗ ДАННЫХ

      Когда набор данных содержит выпадающий результат, который кажется чрезмерно отклоняющимся от средний или медиана, необходимо принять решение либо сохранить, либо отклонить это конкретное измерение. отклонение части данных является серьезным вопросом, который никогда не должен касаться чего-либо, кроме самый доступные объективные критерии, и уж точно никогда не основанные на догадках или личных предубеждениях. Даже выбор критериев для отклонения предполагаемого результата имеет свои риски. Если кто-то требует подавляющий шансы в пользу отказа и тем самым затрудняет отказ от сомнительного измерение, вы рискуете сохранить ложные результаты. С другой стороны, если нереально высокая оценка точности набора измерений предполагается, что ценный результат может быть отброшен. К сожалению, нет простого правила, которое могло бы дать одно руководство. Q-Test имеет некоторые полезность, если есть одно измерение, которое, как можно подозревать, может чрезмерно отклоняться от остальных измерения:

      В наборе n измерения, если наблюдается сомнительное значение (выброс), x q , абсолютное ценность разница между этим значением и его ближайшим соседом, x nn , деленная на абсолютное значение разница между самым высоким и самым низким значением в наборе является экспериментальным коэффициентом Q, или Вопрос опыта . Если Q exp превышает заданный «критический» Q (Q crit ) для данного уровня уверенность, то можно решить отказаться это значение при заданном уровне достоверности. Стол (1)г значения Q crit приведены ниже:

      нет (наблюдения) 90% конф. 95% конф. 99% конф.
      3 .941 .970 .994
      4 .765 .829 .926
      5 .642 .710 .821
      6 .560 .625 .740
      7 .507 .568 .680
      8 .468 . 526 .634
      9 .437 .493 .598
      10 .412 .466 .568

      ОБЩИЕ ЗАМЕЧАНИЯ ПО ОТКЛОНЯЕМЫМ РЕЗУЛЬТАТАМ

      В свете вышеизложенного ряд рекомендаций по обработке наборов данных содержащий подозрительный результат, можно сделать.

      1. Оцените точность, которую можно разумно ожидать от метода. Быть уверенным что в внешний результат действительно сомнительный.

      2. Тщательно перепроверьте все данные, относящиеся к сомнительному результату, чтобы исключить вероятность того, что грубая ошибка повлияла на его значение. Помните, что единственное надежное оправдание отвержение есть знание грубой ошибки.

      3. Повторите анализ, если это вообще возможно. Согласование вновь приобретенной стоимости с те что кажутся действительными, будет поддерживать утверждение о том, что посторонний результат следует отклонить.

      4. Если невозможно получить дополнительные данные, примените Q-Test. Также уделите внимание составление отчетов в медиана, а не среднее значение множества. Медиана является центральным значением множества и будут свести к минимуму влияние постороннего результата.

      Отказ от ответственности: взгляды и мнения, выраженные на неофициальных страницах штата Калифорния Университет, преподаватели, сотрудники или студенты Домингес-Хиллз строго принадлежат авторы страницы. Содержание этих страниц не было проверено или одобрен Калифорнийским государственным университетом, Домингес-Хиллз.

      Выражение чисел: значащие цифры

      Это «Выражение чисел: значащие цифры», раздел 1.5 из книги «Введение в химию: общая, органическая и биологическая» (v. 1.0). Для получения подробной информации об этом (включая лицензирование) нажмите здесь.

      Для получения дополнительной информации об источнике этой книги или о том, почему она доступна бесплатно, посетите домашнюю страницу проекта. Там вы можете просматривать или скачивать дополнительные книги. Чтобы загрузить ZIP-файл с этой книгой для использования в автономном режиме, просто нажмите здесь.

      Помогла ли вам эта книга? Рассмотрите возможность передачи:

      Помощь Creative Commons

      Creative Commons поддерживает свободную культуру от музыки до образования. Их лицензии помогли сделать эту книгу доступной для вас.

      Помогите государственной школе

      DonorsChoose.org помогает таким людям, как вы, помогать учителям финансировать их классные проекты, от художественных принадлежностей до книг и калькуляторов.

      Предыдущий раздел

      Содержание

      Следующий раздел

      1.5 Выражение чисел: значащие цифры

      Цели обучения

      1. Определение количества значащих цифр в сообщаемом значении.
      2. Правильно используйте значащие цифры в арифметических операциях.

      Ученые установили определенные правила для обозначения степени точности измерения. Представьте, например, что вы используете линейку для измерения ширины стола. Сантиметры (см) отмечены, говоря вам, сколько сантиметров ширина стола. На многих измерительных линейках также отмечены миллиметры (мм), поэтому мы можем измерить стол с точностью до миллиметра. Но на большинстве измерительных стержней не указаны более точные измерения, поэтому вы не можете указать ширину стола с точностью до ближайшего миллиметра. Все, что вы можете сделать, это оценить следующий десятичный разряд в измерении (рис. 1.7 «Измерение объекта до правильного числа цифр»).

      Рисунок 1.7 Измерение объекта до правильного количества цифр

      Сколько цифр должно быть указано для длины этого объекта?

      Концепция значащих цифр учитывает это ограничение. Значащие цифрыВсе цифры измеренной величины, известные с уверенностью, и первая неопределенная или предполагаемая цифра. измеряемой величины определяются как все цифры, известные с уверенностью, и первая неопределенная или предполагаемая цифра. Нет смысла сообщать какие-либо цифры после первой неопределенной, поэтому это последняя цифра, сообщаемая в измерении. Нули используются, когда необходимо разместить значащие цифры на их правильных позициях. Таким образом, нули не могут быть значащими цифрами.

      Примечание

      «Сиг инжир» — общепринятое сокращение для значащих цифр.

      Например, если стол измерен и имеет ширину 1357 мм, число 1357 имеет четыре значащих цифры. 1 (тысячи), 3 (сотни) и 5 ​​(десятки) точны; предполагается, что 7 (единиц) были оценены. Было бы бессмысленно сообщать о таких измерениях как 1 357,0 или 1 357,00, потому что это означало бы, что измерительный прибор способен определять ширину с точностью до десятых или сотых долей миллиметра, хотя на самом деле он показывает только десятки миллиметров, а единицы измерения не совпадают. быть оцененным.

      С другой стороны, если размер сообщается как 150 мм, известно, что 1 (сотни) и 5 ​​(десятки) значимы, но как мы узнаем, значим ли ноль или нет? На измерительном приборе могли быть отметки, указывающие каждые 10 мм, или отметки, обозначающие каждый 1 мм. Является ли ноль оценкой или 5 — оценкой, а ноль — заполнителем?

      Правила определения того, какие цифры в измерении являются значащими, следующие:

      1. Все ненулевые цифры являются значимыми. В числе 1357 все цифры значащие.
      2. Закрытые (или встроенные) нули , которые представляют собой нули между значащими цифрами, являются значащими. В 405 все цифры значащие.
      3. Начальные нули , которые являются нулями в начале десятичного числа меньше 1, не являются значащими. В 0,000458 первые четыре цифры являются ведущими нулями и не являются значащими. Нули служат только для того, чтобы поставить цифры 4, 5 и 8 на правильные позиции. Это число имеет три значащие цифры.
      4. Нули в конце , которые являются нулями в конце числа, имеют значение, только если число имеет десятичную точку. Таким образом, в числе 1500 два завершающих нуля не имеют значения, поскольку число записывается без десятичной точки; число имеет две значащие цифры. Однако в числе 1 500,00 все шесть цифр являются значащими, поскольку число имеет десятичную точку.

      Пример 8

      Сколько значащих цифр имеет каждое число?

      1. 6 798 000
      2. 6 000 798
      3. 6 000 798,00
      4. 0,0006798

      Раствор

      1. четыре (по правилам 1 и 4)
      2. семь (по правилам 1 и 2)
      3. девять (по правилам 1, 2 и 4)
      4. четыре (по правилам 1 и 3)

      Упражнение для развития навыков

        Сколько значащих цифр имеет каждое число?

      1. 2,1828

      2. 0,005505

      3. 55 050

      4. 5

      5. 500

      Объединение чисел

      При математических операциях с числами важно помнить о значащих цифрах. Например, деление 125 на 307 на калькуляторе дает 0,4071661238… с бесконечным числом цифр. Но имеют ли цифры в этом ответе какое-либо практическое значение, особенно когда вы начинаете с чисел, каждое из которых имеет только три значащих цифры? При выполнении математических операций существует два правила ограничения количества значащих цифр в ответе: одно правило для сложения и вычитания, а другое правило для умножения и деления.

      Для сложения или вычитания правило состоит в том, чтобы сложить все числа так, чтобы их десятичные точки были выровнены, а затем ограничить значащие цифры ответа крайним правым столбцом, для которого все числа имеют значащие цифры. Рассмотрим следующее:

      Стрелка указывает на крайний правый столбец, в котором все числа имеют значащие цифры — в данном случае десятые разряды. Поэтому ограничим наш окончательный ответ десятым местом. Таким образом, является ли наш окончательный ответ 1459,0? Нет, потому что, когда мы опускаем цифры с конца числа, мы также должны округлить процесс оценки конечной значащей цифры количества, чтобы определить, следует ли ее оставить или поднять выше. число. Обратите внимание, что вторая пропущенная цифра в сотом разряде — 8. Это говорит о том, что ответ на самом деле ближе к 1459..1, чем до 1459,0, поэтому нам нужно округлить до 1459,1. Правила округления просты: если первая пропущенная цифра равна 5 или больше, округляйте в большую сторону. Если первая выпавшая цифра меньше 5, не округляйте.

      Для умножения или деления правило состоит в том, чтобы подсчитать количество значащих цифр в каждом умножаемом или делимом числе, а затем ограничить значащие цифры в ответе наименьшим числом. Пример:

      Окончательный ответ, ограниченный четырьмя значащими цифрами, равен 4,09.4. Первая выпавшая цифра — 1, поэтому мы не округляем.

      Экспоненциальная запись обеспечивает способ передачи значащих цифр без двусмысленности. Вы просто включаете все значащие цифры в начальное число. Например, число 450 имеет две значащие цифры и будет записано в научной записи как 4,5 × 10 2 , тогда как число 450,0 имеет четыре значащих цифры и будет записано как 4,500 × 10 2 . В экспоненциальном представлении все значащие цифры указаны явно.

      Пример 9

      Напишите ответ для каждого выражения, используя экспоненциальную запись с соответствующим количеством значащих цифр.

      1. 23,096 × 90,300
      2. 125 × 9.000
      3. 1027 + 610 + 363,06

      Решение

      1. Ответ калькулятора: 2 085,5688, но нам нужно округлить его до пяти значащих цифр. Поскольку первая отбрасываемая цифра (в сотых) больше 5, мы округляем до 2085,6, что в экспоненциальном представлении равно 2,0856 × 10 3 .
      2. Калькулятор дает в качестве ответа 1,125, но мы ограничиваем его тремя значащими цифрами и переводим в экспоненциальное представление: 1,13 × 10 3 .
      3. Калькулятор дает в качестве ответа 2000,06, но поскольку 610 имеет крайнюю правую значащую цифру в столбце десятков, наш ответ должен быть ограничен разрядом десятков: 2,0 × 10 3 .

      Упражнение для развития навыков

        Напишите ответ для каждого выражения в экспоненциальном представлении с соответствующим количеством значащих цифр.

      1. 217 ÷ 903

      2. 13,77 + 908,226 + 515

      3. 255,0 − 99

      4. 0,00666 × 321

      Помните, что калькуляторы не понимают значащие цифры. Вы тот, кто должен применить правила значащих цифр к результату вашего калькулятора.

      Упражнения по обзору концепции

      1. Объясните, почему понятие значащих цифр важно в числовых вычислениях.

      2. Укажите правила определения значащих цифр измерения.

      3. Когда вы округляете число в большую сторону, а когда , а не округляете число в большую сторону?

      Ответы

      1. Значащие цифры представляют собой все известные цифры измерения плюс первая расчетная цифра.

      2. Все ненулевые цифры являются значащими; нули между ненулевыми цифрами являются значащими; нули в конце недесятичного числа или в начале десятичного числа не имеют значения; нули в конце десятичного числа являются значащими.

      3. Округлять в большую сторону только в том случае, если первая пропущенная цифра равна 5 или больше.

      Ключевые выводы

      • Значащие цифры правильно отражают количество измеренных и оцененных цифр в измерении.
      • Существуют правила применения значащих цифр в расчетах.

      Упражнения

      1. Определить значащих цифр . Почему они важны?

      2. Определите различные типы нулей, встречающихся в числе, и объясните, являются ли они значащими.

      3. Сколько значащих цифр в каждом числе?

        1. 140
        2. 0,009830
        3. 15 050
        4. 221 560 000
        5. 5,67 × 10 3
        6. 2,9600 × 10 −5

      4. Сколько значащих цифр в каждом числе?

        1. 1,05
        2. 9 500
        3. 0,0004505
        4. 0,00045050
        5. 7,210 × 10 6
        6. 5,00 × 10 −6

      5. Каждое число округлить до трех значащих цифр.

        1. 34 705
        2. 34 750
        3. 34 570

      6. Округлите каждое число до четырех значащих цифр.

        1. 34 705
        2. 0,0054109
        3. 8, × 10 8

      7. Выполните каждую операцию и выразите ответ правильным количеством значащих цифр.

        1. 467,88 + 23,0 + 1306 = ?
        2. 10 075 + 5 822,09 — 34,0 = ?
        3. 0,00565 + 0,002333 + 0,0991 = ?

      8. Выполните каждую операцию и выразите ответ правильным количеством значащих цифр.

        1. 0,9812 + 1,660 + 8,6502 = ?
        2. 189 + 3 201,8 — 1 100 = ?
        3. 675,0 — 24 + 1190 = ?

      9. Выполните каждую операцию и выразите ответ правильным количеством значащих цифр.

        1. 439 × 8767 = ?
        2. 23.09 ÷ 13.009 = ?
        3. 1,009 × 876 = ?

      10. Выполните каждую операцию и выразите ответ правильным количеством значащих цифр.

        1. 3,00 ÷ 1,9979 = ?
        2. 2300 × 185 = ?
        3. 16,00 × 4,0 = ?

      11. Используйте свой калькулятор, чтобы решить каждое уравнение. Выразите каждый ответ в правильном экспоненциальном представлении и с надлежащим количеством значащих цифр. Если вы не получили правильных ответов, возможно, вы неправильно вводите экспоненциальную запись в свой калькулятор, поэтому обратитесь за помощью к инструктору.

        1. (5,6 × 10 3 ) × (9,04 × 10 −7 ) = ?
        2. (8,331 × 10 −2 ) × (2,45 × 10 5 ) = ?
        3. 983,09 ÷ (5,390 × 10 5 ) = ?
        4. 0,00432 ÷ (3,9001 × 10 3 ) = ?

      12. Используйте свой калькулятор, чтобы решить каждое уравнение. Выразите каждый ответ в правильном экспоненциальном представлении и с надлежащим количеством значащих цифр. Если вы не получили правильных ответов, возможно, вы неправильно вводите экспоненциальную запись в свой калькулятор, поэтому обратитесь за помощью к инструктору.

        1. (5,2 × 10 6 ) × (3,33 × 10 −2 ) = ?
        2. (7,108 × 10 3 ) × (9,994 × 10 −5 ) = ?
        3. (6,022 × 10 7 ) ÷ (1,381 × 10 −8 ) = ?
        4. (2,997 × 10 8 ) ÷ (1,58 × 10 34 ) = ?

      Ответы

      1. Значащие цифры представляют все известные цифры плюс первую расчетную цифру измерения; это единственные значения, о которых стоит сообщать в измерении.

        1. два
        2. четыре
        3. четыре
        4. пять
        5. три
        6. пять
        1. 34 700
        2. 34 800
        3. 34 600
        1. 1 797
        2. 15 863
        3. 0,1071
        1. 3 850 000
        2. 1,775
        3. 884
        1. 5,1 × 10 −3
        2. 2,04 × 10 4
        3. 1,824 × 10 −3
        4. 1,11 × 10 −6

      Значимые цифры Учебное пособие по химии

      Значимые цифры Учебное пособие по химии

      Ключевые понятия

      • Значащие цифры или значащие цифры определяют значение числа.
      • Нули, показанные только для определения десятичной точки, НЕ являются значащими цифрами.

        НЕ ВАЖНО  
          0,00 148  
          3 значащие цифры

      • Нули, расположенные справа от другого числа после запятой, являются значащими

        НЕ ВАЖНО  
          0,00 1480000  
          7 значащих цифр

      • Последняя значащая цифра справа несколько неопределенна (даже если она равна 0)

        определенный  
          0,0014 8  
          неопределенный

      • Можно считать, что точное число, такое как количество подсчитанных объектов, имеет бесконечное количество нулей после запятой, все из которых являются значимыми.

        3 атома = 3,0 атома = 3,00 атома = 3000 атомов и т. д.

      • Невозможно сказать, сколько значащих цифр в большом числе с нулями слева от десятичной точки, не выражая число в экспоненциальной записи

        1250 можно выразить как:

        1,25 × 10 3 (3 значащие цифры, «5» не определено)

        или как

        1,250 × 10 3 (4 значащие цифры, «0» не определен)

      • Чтобы найти количество значащих цифр в заданном числе:

        ⚛ подсчитать все цифры, начиная с первой ненулевой цифры слева

        ⚛ для числа, записанного в экспоненциальном представлении, считать только цифры в коэффициенте

      • При сложении или вычитании чисел количество цифр справа от запятой в результате должно совпадать с количеством цифр справа от запятой в числе с наименьшим количеством цифр справа от запятой точка

        1. 23 + 0. 123 = 1. 35
        (2 цифры)   (3 цифры)   (2 цифры)
        1. 23 — 0. 123 = 1. 11

      • При умножении или делении чисел количество значащих цифр в результате совпадает с наименьшим количеством значащих цифр в любом из умножаемых или делимых членов

        1,234 × 0,123 = 0,152
        (4 знака рис.)   (3 знака рис.)   (3 знака рис.)
        1,234 ÷ 0,123 = 10,0

      • При выполнении вычислений используйте как минимум на одну значащую цифру больше, чем требуется, пока не будет получен окончательный ответ, затем округляйте ответ в большую или меньшую сторону, чтобы получить правильное количество значащих цифр.

        Округление до последней значащей цифры на каждом шаге многоэтапного вычисления может привести к ошибкам округления в окончательном вычислении.

      Пожалуйста, не блокируйте рекламу на этом сайте.
      Нет рекламы = нет денег для нас = нет бесплатных вещей для вас!

      Нахождение количества значащих цифр в заданном числе

      Количество значащих цифр в заданном числе — это сокращение, используемое для того, чтобы сообщить читателю, с какой точностью вы знаете это число.
      Если вы используете линейку с градациями в миллиметрах для измерения длины чего-либо длиной чуть более 3 мм, то вы уверены в «3», но вы можете только угадать доли миллиметра после этого, скажем, 3,2 мм . «2» несколько неуверенно, ваш друг может возразить, что измерение действительно составляет 3,1 мм, а кто-то другой может измерить его как 3,3 мм. Мы включаем это неопределенное число в число значащих цифр, но наши читатели знают, что оно неопределенное. Если бы наша линейка имела еще более мелкие деления, скажем, десятые доли миллиметра, то мы могли бы быть уверены, что наш объект имеет длину чуть больше 3,2 мм, поэтому мы угадываем следующее число, 3,27, и «7» становится неопределенным числом в число, выраженное до 3-х значащих цифр.

      Общие правила определения количества значащих цифр в данном числе следующие:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.
      2. Для неточного числа, например измерения:

      Определение количества значащих цифр Примеры работы

      Определить количество значащих цифр в 5 мл

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение объема

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей значащей цифрой.

        5  
        самый значимый  

      • Если в числе , а не есть десятичная точка, то самая правая цифра является младшей значащей цифрой, если только она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        5  
        наиболее значимый
        наименее значимый        		  

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.

        Неприменимо: без десятичной точки

      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

        1 значащая цифра

      Определить количество значащих цифр в 5,2 г

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение массы

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей значащей цифрой.

        5 .2
        самый значимый  

      • Если в числе , а не есть десятичная точка, то самая правая цифра является младшей значащей цифрой, если только она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        Неприменимо: присутствует десятичная точка

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.

            младший значащий
        5 . 2
        наиболее значащие    

      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

        2 значащие цифры

      Определить количество значащих цифр в 5,0 кг

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение массы

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей значащей цифрой.

        5 .0
        самый значимый  

      • Если число равно , а не имеют десятичную точку, тогда самая правая цифра является младшей значащей цифрой, если она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        Неприменимо: присутствует десятичная точка

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.

            младший значащий
        5 . 0
        самый значимый    

      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

        2 значащие цифры

      Определить количество значащих цифр в 5.000 л

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение объема

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей цифрой.

        5 .000
        самый значимый  

      • Если в числе , а не есть десятичная точка, то самая правая цифра является младшей значащей цифрой, если только она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        Неприменимо: присутствует десятичная точка

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.

            младший значащий
        5 .00 0
        наиболее значащие    

      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

        самый значимый   младший значащий
        5 .00 0
        1, 2,3 ,4

        4 значащие цифры

      Определить количество значащих цифр в 0,005 м

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение длины

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей значащей цифрой.

        0,00 5
          самый значимый

      • Если в числе , а не есть десятичная точка, то самая правая цифра является младшей значащей цифрой, если только она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        Неприменимо: присутствует десятичная точка

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.

        0,00 5
          наиболее значимый
        наименее значимый

      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

        1 значащая цифра

      Определить количество значащих цифр у 5 футболистов

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Это подсчитанное количество людей, поэтому это точное число.

        Бесконечное количество значащих цифр

      2. Для неточного числа, например измерения:

        Неприменимо: это точное число

      Определить количество значащих цифр в 500 мм

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение длины

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей значащей цифрой.

        5 00
        самый значимый  

      • Если в числе , а не есть десятичная точка, то самая правая цифра является младшей значащей цифрой, если только она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        Крайнее правое число равно нулю, поэтому мы не можем определить количество значащих цифр.

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.
      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

      Определить количество значащих цифр в 5,00 × 10 3 г

      Решение:

      1. Считается, что точное число (подсчитанное количество элементов) имеет бесконечное число значащих цифр.

        Неприменимо: это измерение массы

      2. Для неточного числа, например измерения:
      • Самая левая цифра, не являющаяся нулем, является старшей значащей цифрой.

        5 .00 × 10 3
        самый значимый    

      • Если в числе , а не есть десятичная точка, то самая правая цифра является младшей значащей цифрой, если только она не является нулем.

        Если самое правое число равно нулю, невозможно определить количество значащих цифр, и число должно быть выражено в экспоненциальном представлении.

        Неприменимо: присутствует десятичная точка

      • Если в числе есть десятичная точка, самая правая цифра является младшей значащей цифрой, даже если это ноль.

        самый значимый   младший значащий
        5 .0 0 × 10 3  

      • Каждая цифра между младшей и старшей значащей цифрой должна считаться значащей цифрой.

        самый значимый   младший значащий
        5 .0 0 × 10 3  
        1 ,2 ,3    

        3 значащие цифры

      Определение количества значащих цифр в результате вычисления сложения или вычитания

      Когда вы складываете два числа вместе, вы также суммируете их неопределенность.
      Рассмотрим следующее дополнение
      1234,5 + 0,0006
      Большее число имеет 5 значащих цифр, причем последняя цифра не определена.
      Меньшее число имеет только 1 значащую цифру, что само по себе несколько неопределенно.
      Если я напишу ответ как 1234,5006, то единственной достоверной частью числа будет 1234. «5» уже является неопределенным, поэтому «6» не влияет на уровень уверенности и неопределенности в конечном результате, поэтому ответ должно быть выражено как 1234,5
      Аналогичный результат будет получен при вычитании двух чисел.
      Таким образом, при сложении или вычитании чисел количество значащих цифр в окончательном ответе зависит от числа в вычислении, которое имеет наименьшее количество цифр после запятой.

      Чтобы определить количество значащих цифр после сложения или вычитания:

      • Определите количество цифр после запятой в каждом числе, которое нужно добавить или вычесть.
      • Выберите наименьшее количество цифр после запятой, чтобы применить к конечному результату.
      • Выполнить расчет
      • Округлите результат в большую или меньшую сторону, чтобы получить правильное количество знаков после запятой.

      Рабочий пример значащих цифр после дополнительных расчетов

      Вопрос 1: 12,47 г + 7 г = ? грамм

      Решение:

      • Определите количество цифр после запятой в каждом числе, которое нужно добавить или вычесть.

        12.47 имеет 2 цифры после запятой

        7 не имеет цифр после запятой

      • Выберите наименьшее количество цифр после запятой, чтобы применить к конечному результату.

        Окончательный результат не будет содержать знаков после запятой

      • Выполнить расчет

        12,47 + 7 = 19,47

      • Округлите результат в большую или меньшую сторону, чтобы получить правильное количество знаков после запятой.

        19,47 округляется до 19 (без знаков после запятой)

      Ответ: 19 г

      Вопрос 2: 12300 г + 1,23 г = ? грамм

      Решение:

      • Определите количество цифр после запятой в каждом числе, которое нужно добавить или вычесть.

        12300 имеет 0 цифр после запятой, но мы не знаем, насколько точны 3 или нули!

        1.23 имеет 2 цифры после запятой

      • Выберите наименьшее количество цифр после запятой, чтобы применить к конечному результату.

        Окончательный результат не будет содержать знаков после запятой

      • Выполнить расчет

        12300 + 1,23 = 12301,23

      • Округлите результат в большую или меньшую сторону, чтобы получить правильное количество знаков после запятой.

        Предполагая, что нули значимы: 12301,23 округлить до 12301 (без знаков после запятой)

        Предполагая, что нули НЕ значимы: 12301,23 округлить до 12300 (без знаков после запятой)

      Лучший ответ: 12300 г (при условии, что нули НЕ значимы)

      Рабочий пример значащих цифр после вычисления вычитания

      Вопрос 1: 32,56 мм — 4,9 мм = ? мм

      Решение:

      • Определите количество цифр после запятой в каждом числе, которое нужно добавить или вычесть.

        32,56 имеет 2 цифры после запятой

        4.9 имеет 1 цифру после запятой

      • Выберите наименьшее количество цифр после запятой, чтобы применить к конечному результату.

        Окончательный результат будет иметь 1 цифру после запятой

      • Выполнить расчет

        32,56 — 4,9 = 27,66

      • Округлите результат в большую или меньшую сторону, чтобы получить правильное количество знаков после запятой.

        27,66 округляется до 27,7 (1 цифра после запятой)

      Ответ: 27,7 мм

      Вопрос 2: 13,7 мл — 1,3 мл = ? мл

      Решение:

      • Определите количество цифр после запятой в каждом числе, которое нужно добавить или вычесть.

        13.7 имеет 1 цифру после запятой

        1.3 имеет 1 цифру после запятой

      • Выберите наименьшее количество цифр после запятой, чтобы применить к конечному результату.

        Окончательный результат будет иметь 1 цифру после запятой

      • Выполнить расчет

        13,7 — 1,3 = 12,4

      • Округлите результат в большую или меньшую сторону, чтобы получить правильное количество знаков после запятой.

        12,4 (не требует округления в большую или меньшую сторону, так как содержит 1 цифру после запятой)

      Ответ: 12,4 мл

      Определение количества значащих цифр в результате вычисления умножения или деления

      Когда вы умножаете два числа, вы также умножаете их неопределенность.

      Рассмотрим обычный расчет в химии, когда вы умножаете объем в литрах на концентрацию раствора в молях на литр:
      0,02518 л × 1,03 моль л -1
      Неопределенность в «8» числа 0,02518 л (может ли это быть 0,02517 или 0,02519?)
      Неопределенность в «3» 1,03 моль л -1 (может быть 1,02 или 1,04?)
      Давайте умножим 4 комбинации «высоких» и «низких» значений, чтобы увидеть, что мы получим

      0,02517 × 1,02 = 0,0256734 наименьшее значение
      0,02517 × 1,04 = 0,0261768  
      0,02519 × 1,02 = 0,0256938  
      0,02519× 1,04 = 0,0261976 наибольшее значение

      Сколько значащих цифр следует использовать?
      В приведенных выше расчетах кажется, что верно только первое ненулевое число!
      Но насколько неопределенна следующая цифра после этой? Это должно быть «5» или «6»?
      Если бы мы округлили все четыре числа, то все они округлились бы до 0,026, так что, возможно, эта вторая цифра тоже вполне достоверна.
      Это означает, что третья цифра определяет значение второй цифры и, следовательно, является наименее достоверной и наименее значащей цифрой, поэтому мы будем использовать 3 значащих числа в нашем окончательном расчете:

      0,02518 × 1,03 = 0,0259

      Вы заметите, что мы использовали то же количество значащих цифр, что и число с наименьшим количеством значащих цифр, то есть 1,03 имеет 3 значащих цифры по сравнению с 0,02518, у которого 4 значащих цифры.

      В общем, когда мы умножаем или делим числа, мы используем в результате такое же количество значащих цифр, какое было в числе с наименьшим количеством значащих цифр.

      Чтобы определить количество значащих цифр в результате вычисления умножения или деления:

      • Подсчитайте количество значащих цифр в каждом числе.
      • Выберите наименьшее количество значащих цифр для применения к результату вычисления.
      • Выполнить расчет.
      • Округлите результат в большую или меньшую сторону до нужного количества значащих цифр.

      Рабочие примеры количества значащих цифр после вычисления умножения

      Вопрос 1: 4,1 × 10 3 г моль -1 × 8,635 × 10 2 моль = ? грамм

      Решение:

      • Подсчитайте количество значащих цифр в каждом числе.

        4,1 × 10 3 имеет 2 значащих цифры

        8,635 × 10 2 имеет 4 значащих цифры

      • Выберите наименьшее количество значащих цифр для применения к результату вычисления.

        2 значащие цифры

      • Выполнить расчет.

        4,1 × 10 3 × 8,635 × 10 2 = 3540350 = 3,540350 × 10 6

      • Округлите результат в большую или меньшую сторону до нужного количества значащих цифр.

        3,540350 × 10 6 округлить до 2 значащих цифр будет 3,5 × 10 6

      Ответ: 3,5 × 10 6 г

      Вопрос 2: 2,00 моль л -1 × 10,14 л = ? моль

      Решение:

      • Подсчитайте количество значащих цифр в каждом числе.

        2.00 имеет 3 значащие цифры

        10.14 имеет 4 значащих цифры

      • Выберите наименьшее количество значащих цифр для применения к результату вычисления.

        3 значащие цифры

      • Выполнить расчет.

        2,00 × 10,14 = 20,28

      • Округлите результат в большую или меньшую сторону до нужного количества значащих цифр.

        20,28 округляется до 20,3, так что ответ имеет 3 значащие цифры.

      Ответ: 20,3 моль

      Рабочие примеры количества значащих цифр после вычисления деления

      Вопрос 1: 1,473 г ÷ 2,6 г моль -1 = ? моль

      Решение:

      • Подсчитайте количество значащих цифр в каждом числе.

        1.473 имеет 4 значащих цифры

        2.6 имеет 2 значащие цифры

      • Выберите наименьшее количество значащих цифр для применения к результату вычисления.

        2 значащие цифры

      • Выполнить расчет.

        1,473 ÷ 2,6 = 0,566538461 = 5,66538461 × 10 -1

      • Округлите результат в большую или меньшую сторону до нужного количества значащих цифр.

        No related posts.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *