X0 формула физика: Формулы кинематики с пояснениями по физике / Блог / Справочник :: Бингоскул

Содержание

Формулы кинематики с пояснениями по физике / Блог / Справочник :: Бингоскул

добавить в закладки удалить из закладок

Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.

Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.

Путь, время, скорость

S=v *t

S — путь
v — скорость
t — время

Равномерное движение

x=x_0 + v*t

x — координата
x₀ — начальная координата
v — скорость
t — время

Равномерно ускоренное движение:

ускорение

a=\frac { v — v_0 } { t }

a — ускорение
v — скорость
v₀ — начальная скорость
t — время

Равномерно ускоренное движение:

скорость

v=v_0 + at

v — скорость
v₀ — начальная скорость
a — ускорение
t — время

Равномерно ускоренное движение:

путь

S=vt + \frac { at^2 } { 2 }

s — путь
v — скорость
t — время
a — ускорение

Равномерно ускоренное движение:

координата

x=x_0 + vt + \frac { at^2 } { 2 }

x — координата
x₀ — начальная координата
v — скорость
t — время
a — ускорение

Высота тела, брошенного вертикально вверх (вниз)

h=h_0 + v_ { 0 } t — \frac { gt^2 } { 2 }

h — высота
h₀ — начальная высота
v₀ — начальная скорость
t — время
g — ускорение свободного падения

Скорость тела, брошенного вертикально вверх (вниз)

v=v_0 — gt

v — скорость
v₀ — начальная скорость
g — ускорение свободного падения
t — время

Скорость, ускорение, время

v=at

v — скорость
a — ускорение
t — время

Скорость свободно падающего тела

v=gt

v — скорость
g — ускорение свободного падения
t — время

Центростремительное ускорение

a=\frac { v^2 } { R }

a — центростремительное ускорение
v — скорость
R — радиус

Угловая скорость

\omega=\frac { \phi } { t }

ω — угловая скорость
φ — угол
t — время

Равномерное круговое движение

l=R\phi

l — длина дуги окружности
R — радиус
φ — угол

Равномерное круговое движение: линейная скорость

v=R \omega

v — линейная скорость
R — радиус
ω — угловая скорость

Период вращения

T=\frac { t } { N }

T — период
t — время
N — число вращений

T=\frac { 2 \pi R } { v }

T — период
R — радиус
v — линейная скорость

T=\frac { 2 \pi } { \omega }

T — период
ω — угловая скорость

Центростремительное ускорение

a=\frac { 4 \pi^ { 2 } R } { T^2 }

a — центростремительное ускорение
R — радиус
T — период вращения

a=4 \pi^ { 2 } Rn^2

a — центростремительное ускорение
R — радиус
n — частота вращения

Частота вращения

n=\frac { 1 } { T }

n — частота вращения
T — период вращения

Центростремительное ускорение

a=\omega ^ { 2 } R

a — центростремительное ускорение
ω — угловая скорость
R — радиус

Дальность броска тела, брошенного под углом к горизонту

x=v_0t \cos(\alpha)

x — координата (дальность)
v₀ — начальная скорость
t — время
α — угол

Высота подъема тела, брошенного под углом к горизонту

y=v_0t \sin (\alpha) — \frac { gt^2 } { 2 }

y — координата (высота подъема )
v₀ — начальная скорость
t — время
g — ускорение свободного падения
α — угол

Вертикальная скорость тела, брошенного под углом к горизонту

v_y=v_0* \sin (\alpha) — gt

v_y — вертикальная скорость
v₀ — начальная скорость
α — угол
g — ускорение свободного падения
t — время

Максимальная высота подъема тела, брошенного под углом к горизонту

h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }

h_макс— максимальная высота
v₀ — начальная скорость
α — угол
g — ускорение свободного падения

Общее время движения тела, брошенного под углом к горизонту

t=\frac { 2v_0 * \sin (\alpha) } { g }

t — время
v₀ — начальная скорость
α — угол
g — ускорение свободного падения

Дальность броска тела, брошенного горизонтально

x=x_0 + vt

x — координата (дальность)
x₀ — начальная координата
v — скорость
t — время

Высота подъема тела, брошенного горизонтально

y=y_0 — \frac { gt^2 } { 2 }

y — координата (высота подъема)
y₀ — начальная координата (высота)
g — ускорение свободного падения
t — время

Общее время движения тела, брошенного горизонтально

t_max=\sqrt { \frac { 2h } { g } }

t_макс — максимальное время
h — высота
g — ускорение свободного падения

Смотри также:

Формулы МКТ
Справочные материалы по физике
Физические величины и единицы их измерения

Поделитесь в социальных сетях:

16 октября 2018, 17:33

Could not load xLike class!

Механическое движение — определение, формулы, примеры

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

тело отсчета
система координат
часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным.

Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

Время — в международной системе единиц СИ измеряется в секундах [с].
Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср. путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]

S — путь [м]
t — время [с]

В чем разница между перемещением и путем?

Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) = x₀ + v_xt

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

Уравнение движения при движении против оси

x(t) = x₀ − v_xt

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) = x₀ + v_0xt + a_xt²/2

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с²]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с²]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч²
Теперь возьмем уравнение движения.
x(t) = x₀ + v

0xt + a_xt²/2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с², а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с². В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с

И кому же верить?

Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с².

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Равноускоренное движение — формулы, законы и примеры

Основные определения

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.

Несколько примеров равноускоренного движения:

разгон самолета перед взлетом;
торможение лыжника на горном склоне;
свободное падение в результате прыжка с парашютом;
велосипедист, спускающийся с горки;
мальчишки, играющие в догонялки.

Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Формула ускорения при равноускоренном движении

где a — ускорение тела [м/с²],
V — мгновенная скорость [м/с],
V₀ — начальная скорость [м/с],
t — время [с].

Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:

При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.

Если из формулы ускорения выразить мгновенную скорость, т. е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:

V(t) = V₀ + at,
где V(t) — скорость в момент времени t [м/с],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с²],
t — время [с].

Задача 1

Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с²?

Решение.

По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:

V(10) = 6 + 0,5 · 10 = 11 м/с.

Ответ: за 10 с Арсений разгонится до скорости 11 м/с.

Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.

Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.

Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.

Практикующий детский психолог Екатерина Мурашова

График зависимости скорости от времени при равноускоренном движении

Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.

На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V₀).

При равнозамедленном движении прямая на графике будет убывать.

С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:

Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V₀t и треугольника .

Формула пути при равноускоренном движении

,
где S — путь, пройденный за время t [м],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с²],
t — время [с].

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

,
где S — путь, пройденный за время t [м],
V₀ — начальная скорость [м/с],
V — скорость в момент времени t [м/с],
a — ускорение тела [м/с²].

Задача 2

Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с² после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?

Решение.

По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
Поскольку время движения неизвестно, то определим путь по второй формуле:
Подставим числа и выполним расчет:
м.

Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.

Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.

Например, на этом графике путь тела равен S₁ + S₂, а перемещение — S₁ − S₂.

Уравнение перемещения при равноускоренном движении

,
где S — перемещение за время t [м],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с²],
t — время [с].

Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.

Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени.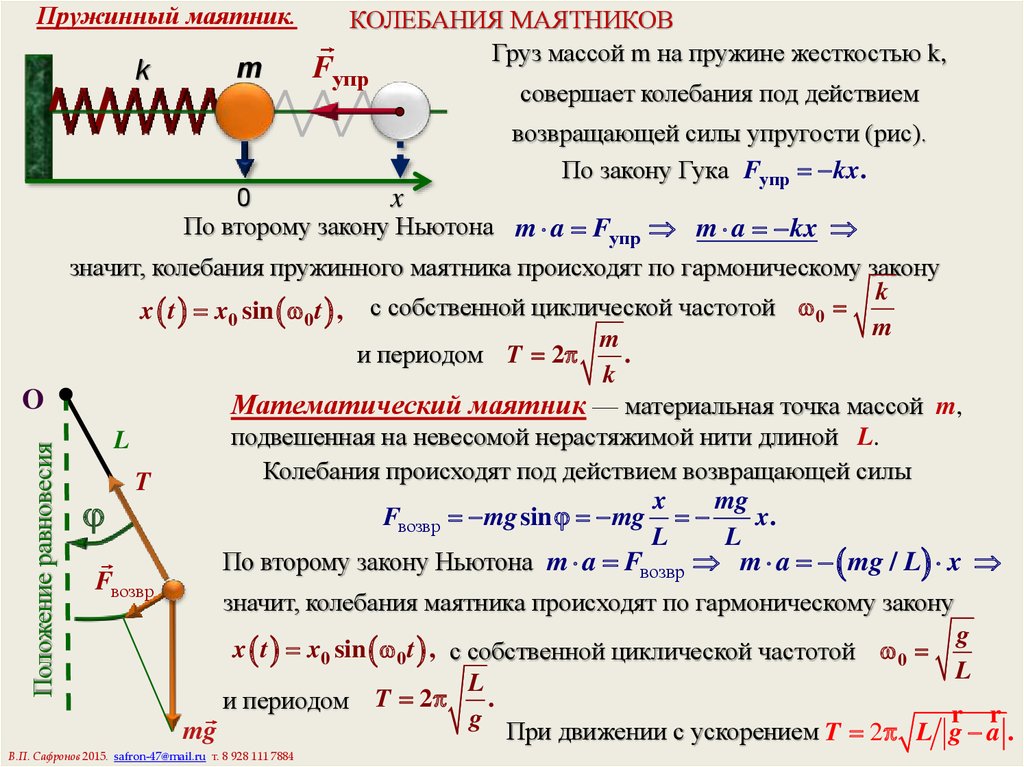 Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).

Уравнение равноускоренного движения

,
где x(t) — координата в момент времени t [м],
x₀ — начальная координата [м],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с²],
t — время [с].

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.

Решение.

Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V₀ = 3 м/с. Начальная координата равна нулю.
Найдем ускорение из формулы пути при равноускоренном движении:
м/с².
Составим уравнение движения лыжника:
.
По уравнению определим координату лыжника в момент времени t = 2 с:
м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Учёба без слёз (бесплатный гайд для родителей)

Графики равноускоренного движения

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.

Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!

Колебания — Физика — Теория, тесты, формулы и задачи

Основные теоретические сведения
- Гармонические колебания
- Математический маятник
- Пружинный маятник
- Механические волны
- Электрический контур
- Переменный ток. Трансформатор
- Электромагнитные волны

Гармонические колебания

К оглавлению…

В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями. Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия, A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ₀, поэтому φ₀ называют начальной фазой (то есть той стадией, из которой начиналось колебание).

Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях. Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

физические свойства колебательной системы определяют только собственную частоту колебаний ω₀ или период T.
Такие параметры процесса колебаний, как амплитуда A = x_m и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т. е. начальными условиями.
При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.
Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.
Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.
Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

Математический маятник

К оглавлению…

Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:

Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.
Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.

Пружинный маятник

К оглавлению…

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.

Циклическая частота колебаний пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную:

А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.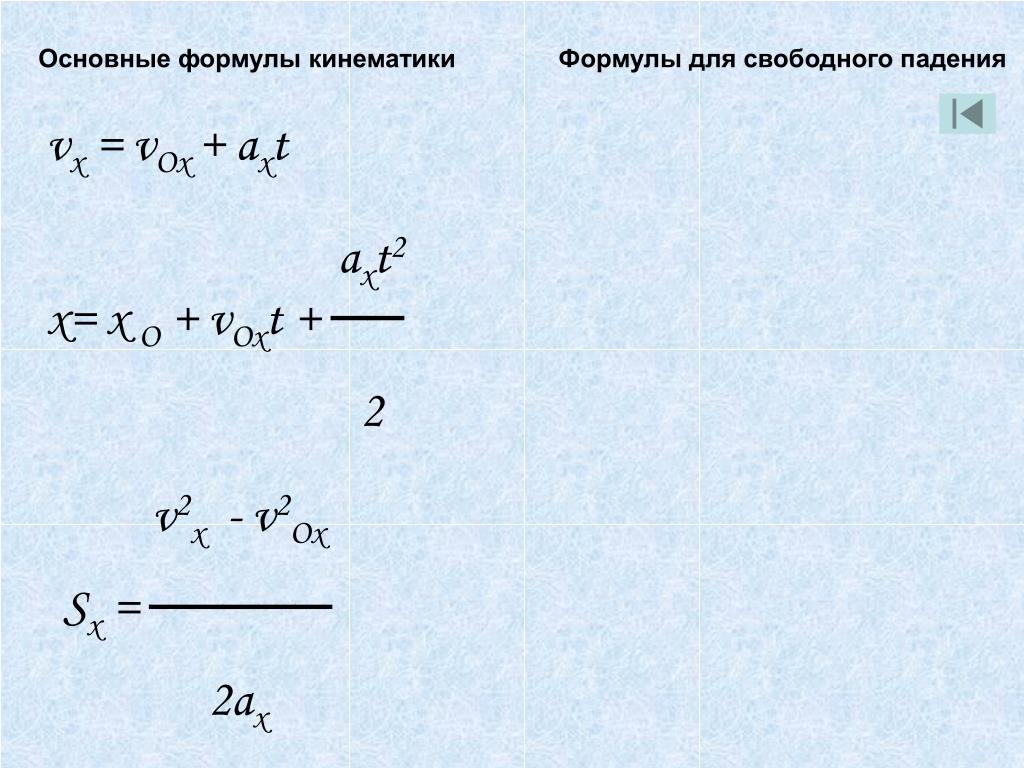 Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):

Механические волны

К оглавлению…

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).

Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:

где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.

Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:

Электрический контур

К оглавлению. ..

В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Все реальные контура содержат электрическое сопротивление R.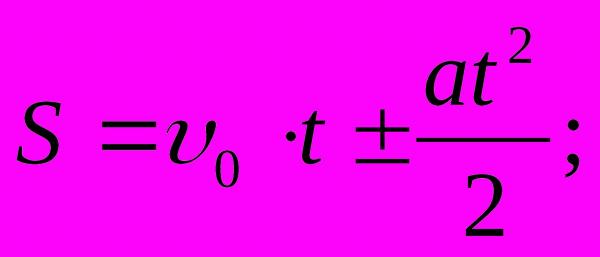 Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.

Переменный ток. Трансформатор

К оглавлению…

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Они позволяют наиболее просто и экономно осуществлять передачу, распределение и использование электрической энергии.

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. Он характеризуется переменным напряжением U(t) (индуцированной ЭДС) на его клеммах. В основу работы генератора переменного тока положено явление электромагнитной индукции.

Переменным током называется электрический ток, который изменяется с течением времени по гармоническому закону. Величины U₀, I₀ = U₀/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.

Переменный ток характеризуется действующими значениями силы тока и напряжения. Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток. Для переменного тока действующее значение силы тока может быть рассчитано по формуле:

Аналогично можно ввести действующее (эффективное) значение и для напряжения, рассчитываемое по формуле:

Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

Обратите внимание, что если идет речь о напряжении или силе переменного тока, то (если не сказано иного) имеется в виду именно действующее значение. Так, 220В – это действующее напряжение в домашней электросети.

Конденсатор в цепи переменного тока

Строго говоря, конденсатор ток не проводит (в том смысле, что носители заряда через него не протекают). Поэтому, если конденсатор подключен в цепь постоянного тока, то сила тока в любой момент времени в любой точке цепи равна нулю. При подключении в цепь переменного тока из-за постоянного изменения ЭДС конденсатор перезаряжается. Ток через него по-прежнему не течет, но ток в цепи существует. Поэтому условно говорят, что конденсатор проводит переменный ток. В этом случае вводится понятие сопротивления конденсатора в цепи переменного тока (или емкостного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Оно в корне отличается от привычного нам сопротивления R. Так, на сопротивлении R выделяется теплота (поэтому его часто называют активным), а на емкостном сопротивлении теплота не выделяется. Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.

Катушка индуктивности в цепи переменного тока

При протекании переменного тока в катушке возникает явление самоиндукции, и, следовательно, ЭДС. Из-за этого напряжение и сила тока в катушке не совпадают по фазе (когда сила тока равна нулю, напряжение имеет максимальное значение и наоборот). Из-за такого несовпадения средняя тепловая мощность, выделяющаяся в катушке, равна нулю. В этом случае вводится понятие сопротивления катушки в цепи переменного тока (или индуктивного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и на емкостном сопротивлении, на индуктивном сопротивлении теплота не выделяется. Индуктивное сопротивление связано с явлением самоиндукции в катушке.

Трансформаторы

Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы, на который намотаны две обмотки: первичная и вторичная. Первичная обмотка подсоединяется к источнику переменного тока с некоторым напряжением U₁, а вторичная обмотка подключается к нагрузке, на которой появляется напряжение U₂. При этом, если число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

Электромагнитные волны

К оглавлению. ..

Электромагнитные волны – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:

где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:

где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии.
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. А вот цепи, в которых протекает переменный ток, т.е. такие цепи в которых носители заряда постоянно меняют направление своего движения, т.е. двигаются с ускорением – являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

Основные формулы по физике по 9 класс. Все, что нужно знать

Формулы за 9 класс по физике

Физика — строгая техническая наука. Порой не у всех получается успевать в этой дисциплине в школьные годы. Тем более, что не каждый школьник обладает логическим и техническим складом ума, а физику в школе принуждают учить абсолютно каждого. Формулы из учебника могут не укладываться в голове. В данной статье мы рассмотрим основные формулы по физике по 9 класс по механике.

Механика

Начать стоит с самых основных и простейших законов в физике. Как известно, такая обширная тема, как механика состоит из трех параграфов:

Статика. Динамика. Кинематика.

Кинематика изучается в 10 классе, поэтому рассматривать ее в рамках данной статьи мы не будем.

Статика

Ее следует изучать последовательно, начиная с простых формул статики. А именно с формул давления, момента инерции тел вращения и момента силы. Формулы по физике 9 класса с пояснениями будут наглядно представлены ниже.

Давление — мера силы, действующая на площадь поверхности тела, измеряется в Паскалях. Давление рассчитывается отношением силы к площади, поэтому формула будет выглядеть максимально просто:

Момент инерции тел вращения — это мера инертности во вращательном движении тела вокруг себя самого, или, строго говоря, произведение массы тела на его радиус, возведенный в квадрат. Соответствующая формула:

Моментом силы (или как многие называют — вращательным моментом) называют силу, приложенную к твердому телу и создающую вращение. Это векторная величина, которая также может иметь отрицательный знак, измеряется в метрах умноженных на Ньютон. В каноничном представлении формула подразумевает собой произведение силы, приложенной к телу и расстояния (плечо силы), формула:

Динамика

Формулы по физике 7-9 класса с пояснениями по динамике — наш следующий этап. Собственно, это самый большой и самый значимый раздел механики. Все тела подвержены движению, даже находясь в состоянии покоя на них действуют некоторые силы, провоцируя на движение. Важные понятия, которые следует изучить перед вниканием в динамику — путь, скорость, ускорение и масса.

Первым делом, конечно же, стоит изучить законы Ньютона.

Первый закон Ньютона — это определение, не имеющее формулы. Он гласит, что тело либо находится в состоянии покоя, либо же движется, но только лишь после того, как все силы, сконцентрированные на нем, будут сбалансированы.

Второй и самый известный закон Ньютона гласит об ускорении тела в зависимости от приложенной к нему силе. В формуле также фигурирует масса объекта, к которому приложена сила.

Обратите внимание, что формула выше записана в скалярном виде — сила и ускорение в векторном могут иметь отрицательный знак, это нужно учитывать.

Третий закон Ньютона: сила действия равна силе противодействия. Все, что нужно знать из этого закона, это то, что каждая сила имеет в противовес такую же силу, только направленную в обратную сторону, таким образом соблюдается баланс на нашей планете.

Теперь же рассмотрим другие силы, действующие в рамках динамики, а это сила тяжести, упругости, трения и сила трения качения. Все они являются векторными и могут быть направлены в любые стороны, также в совокупности способны образовывать системы: складываться и вычитаться, умножаться или делиться. Если силы, направленные не параллельно друг другу, то в вычисления нужно будет использовать косинус угла между ними.

Формулы по физике 9 класса включают в свою программу также закон всемирного тяготения и космические скорости, которые каждый школьник должен знать.

Закон всемирного тяготения — это закон уже небезызвестного нам Исаака Ньютона, фигурирующий в его классической теории. По сути, он оказался революционным: закон утверждает, что любое тело, находящееся в гравитационном поле Земли, притягивается к его ядру. И это действительно так.

Космические скорости

Первая космическая скорость необходима для выхода на орбиту Земли (численно равна 7,9 км/с), а вторая космическая скорость нужна для преодоления гравитационного притяжения, чтобы выйти не только за орбиту, но и позволить объекту двигаться не по круговой траектории. Она равна 11,2 км/с соответственно. Важно, что обе космические скорости были преодолены человечеством, и благодаря им сегодня возможны полеты в космос. Формулы по физике по 9 класс не предполагают третью и четвертую космические скорости, однако они также существуют.

Вывод

В этой статье были рассмотрены основные формулы по физике по 9 класс. Их изучение открывает возможности школьнику познавать более сложные разделы физики, такие как электричество, магнетизм, звук или молекулярную теорию. Не зная механику, невозможно понять остальную физику, механика является основополагающей частью этой науки на сегодняшний день. Формулы по физике по 9 класс также необходимы для прохождения государственного экзамена ОГЭ по физике, их краткое содержание и написание обязан знать каждый выпускник 9-го класса, поступающий в технический колледж. Запомнить их не составляет труда.

Все, что нужно знать.

Www. syl. ru

03.03.2017 11:12:02

2017-03-03 11:12:02

Источники:

Https://www. syl. ru/article/391425/osnovnyie-formulyi-po-fizike-po-klass-vse-chto-nujno-znat

Все ⚠️ формулы по физике за 9 класс: определения, пояснения » /> » /> .keyword { color: red; }

Формулы за 9 класс по физике

Программа обучения по предмету физика в 9 классе включает в себя несколько разделов: кинематика и динамика, которые в свою очередь состоят из подразделов. Таким образом ученики старшей школы изучают механические колебания и волны, законы взаимодействия и движения тел, электромагнитные явления, строение атомов и их ядер, основные законы механики. В школьную программу девятого года обучения также входят основные свойства света: интерференция, преломление и дисперсия.

Кинематика

Кинематика — один из разделов механики. Кинематика изучает механическое движение тел и способы его описания, независимо от причин этого движения. В данном случае под механическим движением подразумевается любое изменение положения какого-либо тела полностью или частично относительно других тел, случившееся с течением времени.

В Кинематике изучают простые виды движения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равномерное прямолинейное движение

Понятие равномерного прямолинейного движения заключается в том, что тело движется по прямой с одинаковой скоростью, то есть за равные промежутки времени тело перемещается на одинаковое расстояние. В таком случае скорость тела остается постоянной, однако является векторной величиной.

Скорость может быть как положительной, так и отрицательной. Все зависит от того, в каком направлении оси X (положительном или отрицательно) направлен вектор скорости. Если тело находится в покое, то его скорость равняется нулю, а координата не меняется в течение времени.

При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:

В этой формуле x0 – начальная координата, x – конечная координата, v – скорость, t – время.

Если начальная координата — это начало движения и x0 = 0, то формулу можно сократить до x1 = v · t.

Если x0 = 0, то пройденный путь S будет равен координате x. Из этого утверждения можно получить формулу прямолинейного равномерного движения относительно пройденного телом расстояния:

Из этого можно вывести формулы относительно скорости и времени:

Скорость и время также можно выразить из полной формулы для тех случаев, когда x0 не равно 0:

Равноускоренное прямолинейное движение

В случае равноускоренного прямолинейного движения тело изменяет скорость своего движения на одинаковую величину за любые равные промежутки времени. Под ускорением в контексте данного определения понимается изменение значения скорости за единицу времени.

Скорость тела вычисляется по формуле:

В данной формуле v – конечная скорость, v0 – начальная скорость, a – ускорение, t – время.

В равноускоренном прямолинейном движении постоянной величиной является ускорение, а не скорость. Ускорение может быть больше или меньше нуля. В случае увеличения скорость, значение ускорения будет больше нуля, а в случае уменьшения — меньше.

Рассмотрим случай, если начальная скорость тела равно 0. Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:

Допустим, что нам известны текущая скорость тела и время, за которое тело развило указанную скорость из состояния покоя. Тогда мы можем определить ускорение:

В том случае, если начальная скорость тела не равна нулю, мы можем рассчитать конечную скорость тела по следующей формуле:

Взглянем на случаи, когда вектор скорости направлен в противоположном направлении (например, подброшенный камень, его скорость направлена в противоположную сторону от ускорения свободного падения) или в случае торможения. Тогда формула будет выглядеть следующим образом:

В случае свободного ускорения остальные формулы будут записываться так:

At = v – v0, a = (v – v)/t

А говоря о торможении, мы используем эти формулы:

Если тело останавливается, то нам следует использовать эту формулу:

А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:

Обратимся к формуле, которая поможет найти путь, которое тело проходит при прямолинейном ускорении. Если при равномерном движении, оси времени и расстояния параллельны, то в случае равноускоренного движения ось движения либо возрастает, либо убывает. Тогда вместо прямоугольника, чью площадь мы вычисляли при равномерном движении, необходимо вычислить площадь трапеции.

Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:

Пройденный путь определяется по формуле:

Путь торможения рассчитывается с помощью этой формулы:

Равномерное движение по окружности

Говоря о равномерном движении по окружности, нужно понимать, что в этом случае вектор скорости тела изменяется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным.

Предположим, что необходимо вычислить модуль скорости за один оборот тела по окружности. Обозначим оборот как S, а время, за которое тело его совершило, как t. Тогда формула будет записываться следующим образом: v = s/t.

Однако, если мы говорим об одном обороте, то это называется период. То есть время, за которое тело совершает один оборот вокруг окружности. Он обозначается как T. И тогда формула одного оборота будет выглядеть так: v = s/T

Если S в данном случае это длина окружности (l), то формула принимает вид v = 2πR/T, в соответствии с формулой окружности l = 2\piR

Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2\piR/v

Аналогично радиус можно найти через формулу R = ½ vT/\pi

Динамика

Динамика — раздел механики, изучающий предпосылки изменения в характере движения. Например, возникновение движения. Именно этот раздел изучает три закона Ньютона. В задачах динамики содержится решение таких вопросов как определение действующих на тело сил по характеру его движения и наоборот.

Законы Ньютона

Первый закон Ньютона гласит, что существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действуют другие тела или их действия скомпенсированы.

Введем основные величины:

Инерциальными называются системы отсчета, которые движутся равномерно прямолинейно относительно Земли. Все системы отсчета, которые движутся прямолинейно и равномерно относительно инерциальной, также являются таковыми. Если система отсчета движется с ускорением, то она — неинерциальная.

Сила — это физическая величина, которая характеризует действие одного тела на второе. В результате этого действия второе тело получает ускорение в инерциальной системе отсчета. Измеряется в ньютонах.

Масса — это физическая величина, которая количественно характеризует инертность тела. Измеряется в килограммах.

Взглянем на тело, на которое действует сила с модулем равным 1 Н. Так как изначально тело массой 1 кг находилось в покое в инерциальной системе, модуль его ускорения будет равен 1 м/с 2 .

В соответствии со вторым законом Ньютона сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Это основной закон динамики.

Для выведения второго закона Ньютона и формулы, где F = ma, необходимо обобщить два факта:

если на два тела, масса которых различна, подействовать равной силой, то ускорения, которые приобретут тела, будут обратно пропорциональны массам; если на одно и то же тело действуют силы разной величины, то ускорения тела будут прямо пропорциональны приложенным силам.

Благодаря этому закону, возможно вычислить не только силу, действующую на тело, но и ускорение. Для этого нужно использовать формулу \[w = \frac\]

В векторной форме второй закон Ньютона записывается как ma = mg + N + Fтр

Третий закон Ньютона гласит, что силы, с которыми две материальные точки воздействуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.

Выразить закон формулой можно следующим образом F1 = — F2

В случае взаимодействия тел силы имеют одинаковую природу, однако, они приложены к разным телам. Таким образом эти силы не могут уравновешивать друг друга, а складывать можно только силы, приложенные к одному телу.

Силы в природе

В соответствии с законом Гука, при деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Природа этой силы состоит в электромагнитном взаимодействии между атомами и молекулами вещества. Эта сила называется упругость.

В данном случае коэффициент k — жесткость тела, она измеряется в ньютонах на метр (Н/м).

Физике свойственен другой способ записи закона Гука. В его записи используются понятия относительной деформации и напряжения. Относительная деформация ε = x / l, а напряжение — это отношение силы к площади поперечного сечения деформированного тела δ = F / S = — Fупр / S.

Исходя из этого, закон Гука можно сформулировать так \[ε = \frac\]

Коэффициент Е — это модуль Юнга. Он зависит исключительно от свойств материала. Размеры и форма не имеют значения.

Если говорить о случаях сложных деформациях, например в случае деформации изгиба, в формуле появляется сила N — сила реакции опоры. Эта сила направлена перпендикулярно поверхности соприкосновения. N = — mg

Сила всемирного тяготения

Закон всемирного тяготения говорит, что все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональна квадрату расстояния между ними.

Эту силу можно вычислить по формуле F = G\fracMR3 2 m = mg

G в данном случае — ускорение свободного падения, о котором говорилось выше. В данном случае g = G\fracMR3 2 . Среднее значение ускорения свободного падения равно 9,81 м/с 2 .

R3 — это радиус Земли. Он равен 6,38·10 6 м.

G в формуле обозначает гравитационную постоянную. Она равна 6,67·10 –11 Н·м 2 /кг 2 .

Движение тела под действием силы тяжести

Ускорение свободного падение является частным случаем равноускоренного прямолинейного движения. В этом случае ускорение всегда будет равно 9,8 м/с 2 и обозначается буквой g. Таким образом g — это ускорение свободного падения.

Ускорение свободного падения можно вычислить по следующей формуле: g = GM3/(R3+H) 2

В данном случае H — это гравитационная постоянная, M — масса земли, R — радиус земли, а H — высота падения тела.

Скорость тела под действием силы тяжести можно вычислить по формуле: v = gt

Высоту, с которой падает тело, можно вычислить по формуле H=gt 2 /2

Силы трения

Силой трения называют силу, характеризующую взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению. Сила трения имеет электромагнитную природу.

Трение можно разделить на три вида: трение покоя, трение скольжения и трение качения.

Трение покоя — это трение, которое возникает при отсутствии перемещения соприкасающихся тел относительно друг друга.

Можно сказать, что эта сила не позволяет одному телу двигаться относительно другого. Эта сила направлена противоположно силе, приложенной извне параллельно поверхности соприкосновения. Сила трения покоя возрастает вместе с силой, которая стремится сдвинуть тело с места.

Трение скольжения возникает при действии на тело силе, превышающей максимальную силу трения покоя.

Это тело сдвигается с места и начинает дальнейшее движение. Сила трения скольжения всегда направлена в противоположную сторону от относительной скорости соприкасающихся тел.

Трение качения возникает в случае, если тело не скользит по другому телу, а катится наподобие колеса или цилиндра. Трение качения — это трение, которое возникает на месте их соприкосновения.

В виде формулы сила трения выглядит следующим образом: Fтр = μmg

В данном случае μ – коэффициент трения, m – масса тела, а g — ускорение свободного падения (постоянная величина 9,81 м/с 2 ).

Движение тела под действием нескольких сил

Если на тело действуют несколько сил одновременно, то необходимо найти равнодействующую всех сил по формуле F = F1 + F2 + F3

Равнодействующая сила может быть равна нулю. В таком случае тело находится в состоянии покоя.

Закон сохранения в механике

Закон сохранения импульса гласит, что геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.

В виде формулы закон сохранения импульса выглядит следующим образом: p1 + p2 = p1’ + p2’ m1v + m2u = m1v’ + m2u’

В свою очередь импульсом тела называют величину, которая равна произведению массы тела на его скорость: p = mv.

Изменение импульса тела равно импульсу силы, который в свою очередь вычисляется по формуле P = Ft

Кинетическая энергия равна половине произведения массы тела и квадрата его скорости: Ek = mv2/2

Кинетическая энергия — это физическая величина, которая характеризует движущиеся тела. Выражается в Дж.

Закон сохранения энергии состоит в том, что полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.

Мощность — это величина, которая равна отношению совершенной работы к промежутку времени, за который она совершена. Выражается в Вт.

Вычисляется по формуле N = A/t

Коэффициент полезного действия (КПД) — это название величины, равной отношению полезной работы ко всей совершенной работе. Выражается в Дж.

КПД демонстрирует эффективность использования затраченной энергии. Коэффициент не может быть больше единицы, однако его можно выразить в процентах.

Вычисляется КПД по формуле η = Aп/Aз

Для выражения в процентах применяется формула η = Aп/Aз ∙ 100%

Движение жидкостей и газов по трубам

Закон Бернулли гласит, что давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость ее движения меньше, и наоборот, в тех частях трубы, где скорость больше, давление меньше.

Уравнение Бернулли для горизонтальной трубы выглядит следующим образом \(\[p_ + \frac = p_ +\frac\]\)

В этом уравнении p1 и p2 — статические давления, а \rho — плотность жидкости. В данном случае статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю.

Если труба не горизонтальная, то уравнение Бернулли примет следующую форму:

Примеры задач

На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?

На рисунке показаны графики равномерного движения тел.

В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0. Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени. Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.

Тогда для первого, второго тела соответственно:

Определим скорости первого и второго тела:

Шар подвешен на невесомой нерастяжимой нити длиной l = 0,5 м. Какую минимальную горизонтально направленную скорость vo надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости?

Воспользуемся законом сохранения механической энергии при переходе шарика из нижнего положения в верхнее:

В верхней точке на шарик будут действовать 2 силы: сила тяжести mg (направлена вниз) и сила натяжения нити T (также направлена вниз). Эти силы сообщают шарику центростремительное ускорение, направленное вниз — к точке подвеса, где l — длина подвеса или нерастяжимой нити.

Поскольку шарик достиг верхней точки (T = 0, условие задачи), то \(\[ \frac = mg \]\) , отсюда v 2 = gl

Сделаем подстановку и получим \(\[ \frac = 2mgl + \frac\]\)

Vo 2 = g4l + gl = 5gl

Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).

Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.

Экваториальный радиус Земли равен 6370 км. Определить линейную и угловую скорости движения точек экватора при вращении Земли вокруг оси.

В Кинематике изучают простые виды движения.

Равномерное прямолинейное движение

При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:

В этой формуле x0 – начальная координата, x – конечная координата, v – скорость, t – время.

Если начальная координата — это начало движения и x0 = 0, то формулу можно сократить до x1 = v · t.

Из этого можно вывести формулы относительно скорости и времени:

Скорость и время также можно выразить из полной формулы для тех случаев, когда x0 не равно 0:

Равноускоренное прямолинейное движение

Скорость тела вычисляется по формуле:

В данной формуле v – конечная скорость, v0 – начальная скорость, a – ускорение, t – время.

В случае свободного ускорения остальные формулы будут записываться так:

At = v – v0, a = (v – v)/t

А говоря о торможении, мы используем эти формулы:

Если тело останавливается, то нам следует использовать эту формулу:

А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:

Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:

Пройденный путь определяется по формуле:

Путь торможения рассчитывается с помощью этой формулы:

Равномерное движение по окружности

Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2\piR/v

Аналогично радиус можно найти через формулу R = ½ vT/\pi

Равномерное движение по окружности.

Wiki. fenix. help

25.06.2019 20:03:39

2019-06-25 20:03:39

Источники:

Https://wiki. fenix. help/fizika/vse-formuly-po-fizike-za-9-klass

Физика 9 класс. Все формулы и определения. Скачать в PDF и JPEG » /> » /> .keyword { color: red; }

Формулы за 9 класс по физике

Физика 9 класс. Все формулы и определения

«Физика 9 класс. Все формулы и определения» — это Справочник по физике в 9 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 7-ми страницах) и МЕЛКО (формат JPG, на 2-х страницах). Смотрите также справочные материалы по физике за другие классы:

Физика 9 Все формулы КРУПНО

Физика 9. Все формулы МЕЛКО. Стр 1

Физика 9. Все формулы МЕЛКО. Стр 2

В пособии «Физика 9 класс. Все формулы и определения» представлено 45 формул :

Физика 9 класс. Все формулы и определения в разделе «КИНЕМАТИКА»

I. Равномерное прямолинейное движение

1. Скорость
2. Проекция скорости на координатную ось
3. Перемещение
4. Проекция перемещения на координатную ось

II. Равноускоренное прямолинейное движение

5. Средняя скорость при неравномерном прямолинейном движении
6. Ускорение
7. Скорость
8. Перемещение
9. Координата тела
10. Ускорение свободного падения

III. Равномерное движение по окружности

11. Угловая скорость
12. Частота обращения
13. Период обращения
14. Линейная скорость
15. Центростремительное ускорение

Физика 9 класс. Все формулы и определения в разделе «ДИНАМИКА»

IV Законы Ньютона

16. Первый закон Ньютона
17. Второй закон Ньютона
18. Третий закон Ньютона

V Силы в природе

19. Закон Гука
20. Закон всемирного тяготения
21. Гравитационная постоянная
22. Сила тяжести
23. Ускорение свободного падения
24. Вес покоящихся и движущихся тел.

VI. Движение тела под действием силы тяжести

25. Движение тела под углом к горизонту.
26. Горизонтально брошенное тело.
27. Скорость искусственного спутника Земли.

VII. Силы трения

28. Трение покоя.
29. Трение скольжения.
30. Коэффициент трения.
31. Движение тела под действием силы трения.

VIII. Движение тела под действием нескольких сил

32. Условие равновесия тела (как материальной точки)
33. Движение тела по наклонной плоскости.
34. Движение связанных тел через неподвижный блок.

IX. Законы сохранения в механике

36. Импульс тела
37. Импульс силы
38. Закон сохранения импульса
39. Механическая работа силы
40. Теорема о кинетической энергии
41. Потенциальная энергия поднятого тела
42. Работа силы тяжести
43. Потенциальная энергия деформированного тела
44. Закон сохранения полной механической энергии

X. Движение жидкостей и газов по трубам

45. Закон Бернулли

Дополнительные материалы

Девять самых необходимых (самых востребованных) формул по физике в 9 классе.

Таблицы физических величин

Вы смотрели «Физика 9 класс. Все формулы». Смотрите также справочные материалы по физике за другие классы:

Закон Бернулли.

Uchitel. pro

04.09.2020 23:58:12

2020-09-04 23:58:12

Источники:

Https://uchitel. pro/%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0-9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%B2%D1%81%D0%B5-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B/

Теория к заданию 1 из ЕГЭ по физике

Архитектор, инженер, программист, технолог — это далеко не полный список специальностей, для которых нужно сдавать экзамен по физике. Задание 1 из ЕГЭ по этому предмету кажется школьникам простым, однако для его решения нужно выучить большой блок теории. Все задачи из первого номера относятся к теме «Движение». Выпускник должен разбираться в видах движения, уметь анализировать графики и знать принцип относительности. Если вы понимаете эту тему и хотите освежить знания перед ЕГЭ, наша статья напомнит вам основные формулы и правила. Также стоит обратить внимание на курсы подготовки к ЕГЭ: там преподаватель объяснит все подробно, с нуля. А чтобы быть уверенным в высоких баллах, можно выбрать комплексную программу, включающую также занятия по русскому языку и профильной математике.

Кинематика

Путь, траектория, перемещение — понятия, без знания которых не решить задание 1 на ЕГЭ по физике. Подготовка должна начинаться с теории. Когда вы будете хорошо ориентироваться в ней, можно переходить к практике. Наука кинематика, о которой идет речь в первом вопросе, изучает механическое движение тел без описания причин этого движения. А механическим движением называют изменение взаимного расположения тел или их частей в пространстве с течением времени. Для его изучения пользуются системами отсчета. В кинематике это система координат (X, Y, Z), тело отсчета (тело, относительно которого двигаются другие тела) и часы для измерения времени. Форма тел значения не имеет, поэтому в задачах их обозначают материальными точками — объектами, у которых есть масса, а размеры пренебрежимо малые. Не каждое тело может считаться материальной точкой, главное правило — расстояние, которое оно проходит, должно быть намного больше размера. Если мы исследуем скорость самолета на пути из одного города в другой, он является материальной точкой. Если мы определяем сопротивление воздуха в момент полета, нам важна форма, и представить самолет точкой уже нельзя.

Если материальная точка перемещается в пространстве, у нее есть траектория — это условная линия, описывающая движение. Форма траектории зависит от выбранной системы отсчета, в задачах ЕГЭ траектории обычно рассматривают относительно Земли. Если мы свяжем траекторию с часами, то получим путь — то, что прошло тело за определенный временной промежуток. Путь, как и траектория, может иметь любую форму, но у него есть начальная и конечная точка. Соединив их прямой линией, мы нарисуем вектор перемещения. Он не может быть больше пути, а иногда вовсе равняется нулю (в том случае, когда тело двигалось по замкнутой линии). Теория к заданию 1 из ЕГЭ по физике не будет полной без описания принципа относительности движения. Для этого представим, что мы сидим в поезде и видим еще один на соседнем пути. Сначала наш поезд стоит неподвижно, а потом трогается. Если посмотреть на ситуацию относительно Земли, мы двигаемся: были на станции, а теперь отъехали от нее. Относительно самого поезда мы стоим на месте — как сидели у окна, так и сидим. А если взглянуть на соседний состав? Он постепенно удаляется от нас. Несмотря на то, что он по-прежнему стоит на станции, нам кажется, что он перемещается. Вывод: движение зависит от того, в какой системе координат его изучают.

Виды движения

От теории мы переходим к решению задач. Чаще всего в них фигурируют два понятия: скорость и ускорение. Скорость — это быстрота и направление перемещения. Средняя скорость перемещения находится по формуле u = s / t, средняя путевая — u = l / t. Здесь u — скорость, l — путь, s — перемещение. Первая величина будет векторной, вторая — скалярной. Существует также мгновенная скорость, то есть скорость в определенной точке. Ее можно найти по графику или из уравнения u = u0 + at. a — ускорение, то есть изменение скорости за единицу времени. Это векторная величина, она рассчитывается следующим образом: a = u / t. При ускоренном движении она направлена так же, как и скорость, при замедленном — противоположно ей. В случае с движением по окружности эти величины перпендикулярны. Перечислим несколько формул для задания 1 ЕГЭ по физике, связанных с видами движения:

равномерное прямолинейное:

x = x0 + ut (x — координата точки в данный момент времени).
s = ut.
u = const.
a = 0.

прямолинейное равноускоренное:

x = x0 + u0t + аt2 / 2.
s = u0t + аt2 / 2.
u= uox+ at.
a = const.

движение по окружности (u = const):

T = t / N = 1 / v — период.
v = N / t = 1 / T — частота.
u = l / t = 2πR / T = 2πRv — линейная скорость.
ω = ϕ / t = 2π / T = 2πv — угловая скорость.
a = u2 / R = ω2R = ωu — ускорение.

движение по параболе с ускорением свободного падения:

x = xo + uoxt + gt2 / 2.
y = yo + uoyt +gt2 / 2.
ux= uox+ gt.
uy= uoy+ gt.
uоx = u0 cosα.
uоy = u0 sinα.

Частные случаи равноускоренного движения под действием силы тяжести

В рамках теории к заданию 1 ЕГЭ по физике нужно знать два частных случая:

движение по вертикали:

при u0 = 0 высота h = gt2 / 2 и u = gt.
при u0↑ и движении вверх h = u0t — gt2 / 2 и u = u0 – gt.
при u0↑ и движении вниз h = -u0t + gt2 / 2 и u = -u0 + gt.
при υ0↓ h = u0t + gt2 / 2 и υ = υ0 + gt.

движение тела, брошенного горизонтально:

h = gt2 / 2 — высота полета.
s = uоt — дальность полета.
υy= gt — скорость относительно оси OY.

Дополнительная информация для частных случаев решения задач

Еще несколько формул для задания 1 ЕГЭ по физике:

модуль вектора: S=sx2+sy2.
средняя скорость: uср = (s1 + s2 + … + sn ) / (t1 + t2 + … + tn) = 2u1u2 / (u1 + u2).
площадь фигуры равна пройденному пути: S = S1 — S2.
физический смысл производной: ux = x΄ и uy = y΄, ах = u΄x = x΄΄ и аy = u΄y = y΄΄.
движение колеса без проскальзывания: uпост = uвращ и u = uпост + uвращ.

Пример решения задач

Задача 1: Велосипедисты движутся по уравнениям x1 = 3t и x2 = 12 — t. Найти координату их встречи.

Решение: В момент встречи велосипедистов их координаты совпадут: x1 = x2, следовательно, 3t = 12 — t. Решив уравнение, найдем, что t = 3 с. Чтобы найти координату, подставим значение в любое из уравнений (для самопроверки лучше подставить в оба): x1 = 3 • 3 = 9.

Ответ: 9.

Задача 2: Первую половину пути супермен пролетел со скоростью 30 км/ч, вторую — со скоростью 50 км/ч. Найти среднюю скорость супермена.

Решение: Нам известны две скорости: u1 и u2, поэтому мы можем воспользоваться формулой uср = 2u1u2 / u1 + u2 = 2 • 30 • 50 / (30 + 50) = 37,5 км/ч.

Ответ: 37,5.

Теперь вы знаете больше теории для ЕГЭ по физике в 2020 году. Задание 1 только кажется очень простым, в нем бывают нетипичные задачи, поэтому стоит уделить внимание его разбору. Грамотно подготовиться к ЕГЭ вам помогут курсы ЦМДО «Уникум» . На них вы разберете каждую тему из экзамена, переходя от простого к сложному. Много времени преподаватели уделяют решению задач, объяснению сложных моментов. Но независимо от того, какой способ подготовки вы выберете, мы желаем вам удачи, высоких баллов и поступления в вуз мечты.

Уравнения кинематики и постоянное ускорение

В своих «Диалогах двух новых наук» Галилей вывел связь между пройденным расстоянием и временем, когда шары катятся по наклонной плоскости. Это часто называют законом падающих тел. Интересно, что доказательство Галилея использовало классическую евклидову геометрию (которая была бы незнакома современному изучающему геометрию из учебников) вместо алгебры, которую мы представим здесь. Продвинутые учащиеся могут вывести эти же уравнения с помощью исчисления.

В основе закона падающих тел лежит то, что когда мяч катится по пандусу, он ускоряется. По мере того, как его скорость увеличивается, расстояние, которое он проходит в каждую единицу времени, увеличивается. Галилей определил это по тому, что катящийся шар срабатывает при вращении.

Процитировать Галилея в переводе:

По сути, Галилей представил, что не только ускорение вниз по рампе из-за гравитации постоянно, но и что скорость увеличивается линейно с время . Он представил, что положение увеличивается с квадратом времени, что часто называют Законом Падающих Тел. Последний момент в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.

Основываясь на том, что вы уже узнали, и на том, что представил Галилей, у нас есть то, что мой учитель физики Гленн Глейзер любил называть пятью священными уравнениями кинематики для постоянного ускорения. В этих уравнениях v — скорость, x — положение, t — время, и — ускорение. Помните, Δ означает изменение в.

1. или Δx = V _AVG ΔT

2. или V _F = V _O + AΔT или ΔV = AΔT

4. Δx = V _o Δt + ½ a Δt ²

5. v _f ² =v _o ² Первые два уравнения, которые мы видели до 90. Важно отметить, что в первом уравнении используется средняя скорость , тогда как второе уравнение использует изменение между исходной скоростью и конечной скоростью . Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел. Средняя скорость – это среднее значение начальной и конечной скоростей.

Из этих трех основных определений мы можем вывести следующие два уравнения, используя либо геометрию, либо алгебру (или исчисление).

Используя алгебру, мы можем вывести уравнение №4.

Начиная с уравнения №1

Δx = v _avg Δt

Затем мы подставляем в определение среднюю скорость из уравнения №3.

Отсюда мы подставляем конечную скорость, полученную в уравнении № 2

Затем мы распределяем член Δt и упрощаем, комбинируя члены v _o.

Упростим оставшиеся два условия, чтобы получить

Стоит отметить, что происходит, когда исходная скорость v _o, равно нулю. Это уравнение еще больше упрощается и становится равным

. Если мы предположим, что исходное положение и время равны нулю, мы можем дополнительно уменьшить это до

Используя геометрию, мы можем исследовать площадь под кривой графика зависимости скорости от времени. для постоянного ускоренного движения.

Если мы посмотрим на область под кривой, мы можем разбить ее на прямоугольник и треугольник. Красный прямоугольник — вклад исходной скорости объекта. Смещение из-за ускорения представлено зеленым треугольником. Треугольник имеет ширину Δt и высоту aΔt, которые мы знаем из уравнения № 2. Член ½ происходит от формулы площади треугольника.

Мы также можем использовать вычисления, чтобы вывести это уравнение, интегрируя удвоенное ускорение по времени.

Пятое священное уравнение может быть получено аналогичными заменами и останется в качестве домашнего задания.

Теперь давайте рассмотрим несколько примеров задач: Численное решение задач.

Пример 1

Согласно легенде, Галилей уронил мяч с Пизанской башни. Если башня имеет высоту 55,9 м , и пренебрегая сопротивлением воздуха, сколько времени потребуется свинцовому шару, чтобы достичь земли?

Дано: a = g ≈ 10 м/с ²

Δx = 55,9 м

Неизвестно: t = ???

Уравнение, которое связывает эти переменные, называется священным уравнением 4 ^th.

Δx = v _o Δt + ½ a Δt ²

Как упоминалось ранее, поскольку начальная скорость равна нулю, уравнение упрощается.

Δx = v _o Δt + ½ a Δt ² = ½ a Δt ²

Поскольку мы хотим изолировать переменную для времени, мы пересекаем умножение, чтобы сдвинуть ½ и ускорение в другую сторону .

Затем мы извлекаем квадратный корень из обеих частей.

В результате получается выражение для времени. Обратите внимание, что я вставил несколько дополнительных наборов скобок, которые вам могут показаться ненужными.

При подключении номеров довольно просто то, что мы называем «подключи и пыхти». Однако с юнитами нужно быть осторожным. Вы, наверное, догадались, что время будет измеряться в секундах. Тем не менее, вы должны иметь возможность отменить фактические единицы, чтобы получить секунды для времени.

Пример 2

Койот падает со скалы высотой 25 метров. С какой скоростью падает койот, когда ударяется о землю? Если задача о койоте

Дано x = 25 м

a = g ≈ 10 м/с ²

Неизвестно: v = ???

Существует несколько способов решения этой проблемы. Можно было бы использовать комбинацию или Священные уравнения № 2 и № 4. Или вы можете напрямую использовать уравнение № 5.

Использование версии _f ² =v _o ² + 2a∆x

Это упрощает, поскольку исходная скорость v _o, равна нулю.

Если мы возьмем квадратный корень из обеих частей уравнения

Обратите внимание, как вы извлекаете квадратный корень из единиц, чтобы получить м/с .

Мы оставим решение этой задачи с двумя уравнениями для домашнего задания.

Резюме задач построения графиков и наклона и площади под кривыми

Изучив графики положения, скорости и ускорения, вы сможете нарисовать их взаимозаменяемо.

Вчера в классе вы видели, что график объекта, ускоряющегося при спуске с холма, выглядит следующим образом:

В этом примере мы используем программное обеспечение для анализа изображений. Это пример с катящимся с горки мячом. Следует отметить, что график ускорения не говорит вам о фактической скорости, а только о том, как она меняется. Точно так же график скорости не показывает фактическое положение объекта, а только то, как оно меняется. Щелкнув по мячу и нажав кнопку отслеживания, вы увидите сгенерированный график положения и скорости.

Здесь вы можете увидеть результаты построения графика движения. График положения представляет собой параболу, а график скорости — линейный.

Вывод уравнения кинематики

Курсы физики в средней школе обычно начинаются с изучения классической механики. В начале курса студенты знакомятся с уравнениями движения, уравнениями кинематики.

Кинематика

Кинематика — это изучение движения объектов без учета сил, вызывающих движение. Эти знакомые уравнения позволяют учащимся анализировать и предсказывать движение объектов, и учащиеся будут продолжать использовать эти уравнения при изучении физики. Четкое понимание этих уравнений и того, как их использовать для решения задач, необходимо для успеха в физике. Эта статья представляет собой чисто математическое упражнение, предназначенное для быстрого обзора того, как уравнения кинематики выводятся с помощью алгебры.

Рисунок 1

В этом упражнении используется ссылка на диаграмму на рис. 1, на которой ось x представляет время, а ось y представляет скорость. Диагональная линия представляет движение объекта, скорость которого изменяется с постоянной скоростью. Заштрихованная область (A ₁ + A ₂ ) представляет собой смещение объекта за интервал времени между t ₁ и t ₂ , в течение которого скорость объекта увеличилась с v ₁ до v ₂ .

В этом документе будут использоваться следующие переменные:

v = модуль скорости объекта (метры в секунду, м/с)

v ₁ = модуль начальной скорости (метры в секунду, м/с) (в некоторых в текстах это vi или v ₀ )

v ₂ = величина конечной скорости (метры в секунду, м/с) (в некоторых текстах это v _f )

a = величина ускорения (в метрах в секунду в квадрате, м/с ² )

с = вектор смещения, модуль смещения — расстояние,

с = │ с │ = d (векторы выделены жирным шрифтом; тот же символ, не выделенный жирным шрифтом, представляет собой модуль вектор)

Δ Указывает изменение, например, ΔV = (V ₂ –V ₁)

T = время

T ₁ = начальное время

T ₁ = начальное время
₁ = начальное время
₁ = исходное время
₁ = начальное время
₁ = начальное время
₂ = последний раз
Как вывести уравнения
Первым шагом будет вычисление наклона диагональной линии. В этом случае, поскольку наклон будет представлять собой изменение скорости (подъем), деленное на изменение времени (бег), наклон будет равен ускорению.
Для простоты перепишите t ₂ – t ₁ как Δt.
Это Уравнение 1 . Переставьте в уравнении 1 , чтобы получить v ₂ в левой части уравнения. Это выражает уравнение в форме пересечения наклона линии, y = mx + b.
Чтобы получить следующее уравнение, выведите выражение для смещения объекта за интервал времени Δt. Смещение объекта, движущегося с постоянной скоростью, можно найти, умножив скорость объекта на время, в течение которого объект движется с этой скоростью.
Объект в этом упражнении, однако, не движется с постоянной скоростью. Как можно рассчитать расстояние до объекта, который не движется с постоянной скоростью?
Рассмотрим объект, движущийся с постоянной скоростью v ₁ , с момента времени t ₁ до t ₂ . Смещение объекта представлено как s . Абсолютная величина смещения есть пройденное расстояние. Перемещение можно рассчитать по формуле:
Где Δt – временной интервал t ₂ – t ₁ . Рассмотрим график движения этого объекта, как на рис. 2. рисунок 2
Перемещение объекта на рис. 2 равно v ₁ Δt. Произведение v ₁ Δt также равно площади A ₁ . Точно так же полное перемещение объекта на рис. 1, движущегося с изменяющейся скоростью, можно найти, вычислив площадь под линией за временной интервал Δt. Для некоторых объектов это вычисление может быть немного сложным, но для объекта, изображенного на рис. 1, вычисление площади под линией просто означает вычисление площади прямоугольника A ₁ и треугольника A ₂ и сложение значений .
Площадь A ₁ представляет собой прямоугольник. Длина l равна v ₁ . Ширина w равна t ₂ – t ₁ , (Δt).
Площадь прямоугольника A ₁ = l x w
Площадь A ₂ представляет собой треугольник с основанием Δt и высотой v ₂ – v ₁ .
Площадь треугольника A ₂ = ½ b x h
Сложение площадей A ₂ и A ₁ дает полное перемещение объекта за интервал времени.
Замена A ₂ и A ₁ дает:
Упрощение:
Это Уравнение 2.
Уравнение 1 не включает переменную s. Уравнение 2 не включает переменную a. Остальные уравнения кинематики можно найти, исключив переменные v ₂ и Δt. Начальная скорость v ₁ по-прежнему присутствует в каждом уравнении, но v ₁ часто можно установить равным нулю, если объект начинает движение из состояния покоя.
Написание набора уравнений, в каждом из которых исключена одна или несколько переменных, позволит получить набор уравнений, которые можно использовать в самых разных задачах, в зависимости от предоставленной информации.
Уравнение 3 получается путем исключения v ₂ .
Начните с Уравнение 1 .
Применив некоторую алгебру, левую часть этого уравнения можно сделать похожей на правую часть уравнения 2 .Все, что делается с одной частью уравнения, должно быть сделано с другой частью уравнения.
Добавьте v ₁ с обеих сторон.
Теперь умножьте обе части на (1/2)Δt.
Подстановка левой части уравнения вместо s исключает v ₂ и дает:
Уравнение 3.
Уравнение 4 находится путем исключения переменной времени или Δt.
Начните с Уравнение 1 переставьте ускорение слева от знака равенства:
Уравнение 1.
Умножьте левую часть Уравнение 2 на левую часть 901 19 Умножьте 4, 001 правая часть уравнения 2 правая часть уравнения 1.
Это означает умножение обеих частей на ускорение, но это позволит сократить Δt в правой части уравнения.
Уравнение 2.
ΔT Отмена, а уравнение упрощает:
Это уравнение часто записывается как:
Уравнение 4.
Вот все четыре стандартных уравнения Kinematics:
.
Уравнение 1.
Уравнение 2.
Уравнение 3.
Уравнение 4.
Используя уравнения кинематики в этих четырех знакомых схемах, студенты-физики могут практиковать свое критическое мышление и навыки решения задач по широкому кругу вопросов физики. Вывод уравнений полезен для развития математических навыков, показывая учащимся, как разрабатываются уравнения и формулы, и знакомит их с этими уравнениями, которые будут использоваться на протяжении всего курса. Студенты будут повторно обращаться к уравнениям кинематики, когда будут изучать круговое и вращательное движение, движение снаряда, энергию и импульс.
Ресурсы
Учащиеся могут применять уравнения кинематики при проведении исследований с помощью следующих продуктов:
Магазин Наклонная плоскость НаборМагазин Наклонная плоскость с кольцом и диском PullyShop Экономичный цифровой таймер и фотодатчикМагазин Снарядная пусковая установкаМагазин Столкновение в 2-D аппаратеМагазин Линейная воздушная дорожка, 1,5 мМагазин Алюминиевая тележка для ускорения
Shop Force, Energy, & Motion
Учебные пособия и практические занятия доктора Юэ-Линг Вонг по естественнонаучному образованию
Учебные пособия и практические занятия по научному образованию доктора Юэ-Линг Вонг
Учебники и практические упражнения для естественнонаучного образования
Общая химия

Органическая химия

Общая физика
Общая математика

Домашняя страница доктора Юэ-Линг Вонг

Общая физика :: Движение снаряда :: Как рассчитать #1
Задача №1: найти где приземлится пушечное ядро, учитывая начальную скорость ( v ₀ ) и угол выстрела ( θ ₀ )
(Параметры, значения которых известны, выделены красным цветом. Основное направление решения задачи: попытаться вывести уравнения которые используют эти параметры с известными значениями.)
Решение Пошаговое руководство:
Разложите вектор начальной скорости на компоненты x и y.
Начальная скорость:
x-компонента: v _x0 = v ₀ × cos θ ₀
Y-компонента: v _y0 = v ₀ × sin θ ₀

Этап 1
Рассчитать:
v _x0 и v _у0
От:
v ₀ и θ ₀
Попробуйте:
Измените значения для v ₀ и θ ₀ в приведенные ниже уравнения, а затем нажмите кнопку «Рассчитать», чтобы рассчитать v _x0 и v _у0 :
v _x0 = v ₀ × cos θ ₀
v _x0 = м/сек. × потому что (градус) = 6,928 м/сек.
v _y0 = v ₀ × sin θ ₀
v _y0 = м/сек. × грех (градус) = 4 м/сек.

Независимый анализ горизонтального и вертикального движения:
Вертикальное движение: использовать постоянную ускорение (g)
v _y = v _y0 — g × t
, где g — сила тяжести (9,8 м/с) или свободное падение ускорение, t — время, прошедшее.
Когда объект достигает вершины его траектория движения по параболе, v _г = 0 .
т. е. v _y0 — g × t _макс. = 0
Þ t _макс. = v _y0 / g

где t _max — время, необходимое объекту для достижения максимума высота.
Этап 2
Рассчитать:
т _макс.
От:
v _у0
Попробуйте:
Используйте значения v _y0 , полученные выше для расчета времени (t _max), когда объект достигает своего максимума высота:
т _макс = v _y0 / g
t _макс = м/сек. / 9,8 м/сек. = 0,408 сек.

Итак, теперь вы знаете, сколько времени требуется объекту, чтобы достичь вершины его траектория движения по параболе. После этого момента он начнет падать.
Что делать, чтобы выяснить это время, чтобы узнать, где пушечное ядро приземлится и горизонтальное положение, когда оно достигнет самая высокая точка?
Из-за симметрии вертикального движения требуется столько же времени, чтобы пушечное ядро вернулось на землю (предположим, что пушечное мяч был выпущен на уровне земли). Таким образом, весь путь пушки мяч, от выстрела до возвращения на землю, занимает:
t _всего = 2 × t _макс.

Этап 3
Рассчитать:
т _всего
От кого:
т _макс.
Попробуйте:
Используйте t _max полученный выше вычислить общее время (t _всего ) для
t _всего = 2 × t _max
t _всего = 2 × сек. = 0,816 сек.
Например, если пушечному ядру требуется 3 секунды, чтобы достичь максимальной точки на траектории его движения по параболе, то требуется еще 3 секунды для это вернуться с самой высокой точки. Общее время для пушки мяч, чтобы вернуться на землю после выстрела составляет 6 секунд.
Эта временная информация может быть использована для расчета, где находится пушечное ядро. приземлится. (См. анализ горизонтального движения ниже)
Горизонтальное движение: используйте постоянную скорость (v _x )
v _x = v _x0
горизонтальное расстояние (d _x ), которое пролетело пушечное ядро когда он приземлится на землю:
d _x = v _x0 × t _всего
Этап 4
Рассчитать:
д _х
От кого:
v _x0 и т _всего
Попробуйте:
Используйте т _всего полученное выше рассчитать d _x :
d _x = v _x0 × t _всего
d _x = м/сек. × сек. = 5,653 м
[произошла ошибка при обработке этой директивы]

Что такое кинематические уравнения?
Похожие материалы
сообщите об этом объявлении
Lesson Contents
The Four Kinematic Equations
Equation 1: v = v ₀ + at
Equation 2: v ² = v ₀ ² + 2a(Δx)
Уравнение 3: x = x ₀ + v ₀ t
Уравнение 4: x = x ₀ + V ₀ T + ¹ /₂ на ²
Кинематические переменные
x — Дисвязание 9052 V — VELOCITY 9040
x — 9052 V — VELOCITY 9052. четыре переменные в игре с кинематическими уравнениями. Уравнения описывают движение объекта с постоянным ускорением. Используя уравнения, мы можем найти начальное и конечное значения этих переменных.
Важно: Направленность переменных
Перемещение, скорость и ускорение являются направленными, тогда как время не направлено. Направленные переменные будут иметь положительное значение, если их вектор указывает в положительном направлении, и отрицательное значение, если их вектор указывает в отрицательном направлении. Поскольку время не имеет направления, оно всегда будет иметь положительное значение.
При использовании кинематических уравнений для решения задач полезно выбрать направление для положительного x , v и a . Иногда это направление дается в условии задачи. Противоположным положительному направлению будет отрицательное направление.
Когда использовать кинематические уравнения
Кинематика — это изучение движения объекта без учета сил, вызывающих движение. Кинематические уравнения представляют собой упрощение движения объекта. Три уравнения предполагают постоянное ускорение (уравнения 1, 2 и 4), а другое уравнение предполагает нулевое ускорение и постоянную скорость (уравнение 3).
Когда задача движения объекта попадает в эти категории, мы можем использовать кинематические уравнения для ее решения. Например, мы можем использовать их, чтобы выяснить, как далеко летит снаряд, пока снаряд испытывает постоянное ускорение во время полета. Еще одним примером простого и эффективного использования кинематических уравнений является движение автомобиля с постоянной скоростью. Поскольку он имеет нулевое ускорение, мы можем использовать уравнение, в котором нет условий ускорения (уравнение 3).
Как выбрать кинематическое уравнение
Мы должны решить, какое кинематическое уравнение лучше всего подходит для того, что мы решаем. Как правило, задачи кинематики включают решение для некоторых неизвестных. Неизвестным может быть начальное перемещение, конечное перемещение, изменение смещения, начальная скорость, конечная скорость, ускорение или время.
Мы выбираем уравнение, исходя из того, что известно и что неизвестно. В некоторых случаях мы должны использовать несколько уравнений последовательно, чтобы найти значение нашего неизвестного. Приведенные ниже примеры задач дают больше понимания процесса выбора уравнения.
Примеры задач
Кинематическое уравнение 1 Пример
Снаряд вылетает из патронника пушки и разгоняется до скорости 1500 м/с ² за 0,75 секунды до вылета из ствола. Какова скорость снаряда в момент вылета из ствола пушки?
Решение:
1. Поскольку снаряд не движется до момента выстрела, наша начальная скорость будет равна нулю. Нам даны значения ускорения (1500 м/с ² ) и время (0,75 секунды), поэтому мы будем использовать уравнение v = v ₀ + at .
2. Поскольку мы знаем значения всех переменных, кроме конечной скорости, мы можем подставить наши известные значения, чтобы найти v, что дает нам v = (0 м/с) + (1500 м/с ² )(0,75 секунд) = 1125 м/с .
3. Скорость снаряда составляет 1125 м/с при выходе из ствола.
Кинематическое уравнение 2 Пример
Спринтер движется со скоростью 5 м/с, когда он достигает 20 метров в своем забеге. Они сохраняют постоянное ускорение 2 м/с ² через 40 метров в гонку. Какова скорость спринтера на 40-метровой дистанции?
Решение:
1. Нам известны значения начальной скорости (5 м/с), ускорения (2 м/с ² ) и изменения смещения (40 – 20 = 20 метров). Уравнение, которое мы будем использовать: v ² = v ₀ ² + 2a(Δx) .
2. Поскольку мы знаем значения всех переменных, кроме конечной скорости, мы можем подставить наши известные значения и найти v.
v ² = (5 м/с) ² + 2(2 м/с ² )(20 метров)
v ² = 105
3 v = 4 с 3,05 Скорость спринтера составляет 10,25 м/с на 40-метровой дистанции.
Кинематическое уравнение 3 Пример
Автомобиль находится в 200 метрах от здания и начинает отъезжать от здания со скоростью 20 м/с. На каком расстоянии от здания находится автомобиль после движения в течение 6 секунд?
Решение:
1. Известны значения начального перемещения (200 метров), начальной скорости (20 м/с) и времени в движении (6 секунд). Мы должны найти конечное перемещение. Кинематическое уравнение, которое мы будем использовать: x = x ₀ + v ₀ t .
2. Поскольку мы знаем значения всех переменных, кроме одной, мы можем подставить известные значения, чтобы найти неизвестное значение x.
x = (200 метров) + (20 м/с)(6 секунд) = 320 метров
3. Через 6 секунд автомобиль проедет 320 метров подальше от здания.
Кинематическое уравнение 4 Пример
Человек стоит в 6 метрах позади вас. Они бросают мяч над головой с горизонтальной скоростью 20 м/с. Мяч испытывает постоянное горизонтальное замедление со скоростью 4 м/с ² во время полета, и ему требуется 2 секунды, чтобы приземлиться. На каком расстоянии перед вами приземлится мяч?
Решение:
1. Нам известны значения начального перемещения (-6 метров), начальной скорости (20 м/с), ускорения (-4 м/с ² ) и время (2 секунды). Уравнение, которое мы будем использовать: x = x ₀ + v ₀ t + ¹ / ₂ at ² .
2. Поскольку мы знаем значения всех переменных, кроме конечного смещения, мы можем подставить известные значения и найти x.
x = (-6 метров) + (20 м/с)(2 секунды) + ¹ / ₂ (-4 м/с ² )(2 секунды) ²
x = -6 + 40 – 8
х = 26 метров
3. Мяч приземляется 26 метров перед вами.
Дополнительный урок кинематики
Что такое движение снаряда?
Ранее мы упоминали, что задачи движения снаряда можно решить с помощью кинематических уравнений. Хотя движение снаряда — это лишь одна из многих проблем, с которыми мы сталкиваемся в кинематике, очень полезно точно понимать, что это такое.
Движение снаряда по определению — это движение объекта или частицы, на которое действует только сила тяжести. Снаряд движется по параболической траектории, аналогичной траектории броска мяча. Эта параболическая траектория также называется баллистической траекторией.
Как решить движение снаряда
Поскольку мы пренебрегаем силой сопротивления воздуха при движении снаряда, мы можем вычислить, как далеко улетит снаряд, разложив его скорость на вертикальную и горизонтальную составляющие. Горизонтальная составляющая скорости во время полета будет постоянной. Вертикальная составляющая скорости будет влиять на время полета снаряда или время зависания.
Вот уравнения для горизонтального и вертикального движения снаряда. Они выводятся из кинематических уравнений.
A _x = 0
V _x = V ₀ COS (α)
x = V ₀ COS (α) T + X ₀ ₀ COS (α) T + x ₀ 212222. _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{2 _{. = -g}}}}}}}}}}}
V _Y = V ₀ SIN (α)
T = ^{2V _Y} /_G
ПРИМЕР ДОСТОЯНИЕ ПРИМЕЧАНИЕ

ПРИМЕР ДОСТИНЕ ПРИМЕЧАНИЕ

ПРИМЕЧАНИЕ ПРИМЕЧАНИЕ

ПРИМЕР.1040
Мяч брошен с поверхности Земли со скоростью 25 м/с под углом 30° над горизонтом. Пренебрегая сопротивлением воздуха, какое расстояние пролетит мяч по горизонтали, прежде чем упадет на землю?
Решение:
1. Сначала установим известные нам переменные.
v ₀ = 25 м/с
α = 30°
g = 9,81 м/с ² .
2. Найдем компоненты скорости.
v _x = v ₀ cos(α) = 25cos(30°) = 21,65 м/с
v _y = v ₀ sin(α) = 25sin(30°) = 12,5 м/с
3. Теперь мы можем найти время зависания и использовать его для расчета пройденного горизонтального расстояния.
T = ^{2V _Y} /_G = ^{2 (12,5)} /_9,81 = 2,55
x = V ₀ Cos (α) T + X = V ₀ Cos (α) T + X _{00031 = V ₀ COS (α) T + X _{00031 0_{313 = x = v ₀ Cos (α) T + X = x = v ₀ Cos (α) T + X _{. °)(2,55) + 0 = (21,65)(2,55) = 55,21}
4. Мяч проходит горизонтально 55,21 м , прежде чем коснуться земли.}}}
Copyright © 2022 ООО «Вооверс». Все права защищены.
3.6 Определение скорости и смещения по ускорению
Цели обучения
К концу этого раздела вы сможете:
Выводить кинематические уравнения для постоянного ускорения с помощью интегрального исчисления.
Использовать интегральную формулировку кинематических уравнений при анализе движения.
Найдите функциональную форму зависимости скорости от времени по заданной функции ускорения. 907:10
Найдите функциональную форму зависимости положения от времени по заданной функции скорости.
В этом разделе предполагается, что у вас достаточно знаний в области исчисления, чтобы быть знакомым с интеграцией. В разделах «Мгновенная скорость и скорость» и «Среднее и мгновенное ускорение» мы ввели кинематические функции скорости и ускорения с помощью производной. Взяв производную от функции положения, мы нашли функцию скорости, и точно так же, взяв производную от функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.
Кинематические уравнения интегрального исчисления
Начнем с частицы с ускорением a (t) — известная функция времени. Поскольку производная по времени от функции скорости есть ускорение,
[латекс] \фрак{д}{дт}в(т)=а(т), [/латекс]
, мы можем взять неопределенный интеграл от обеих сторон, нахождение
[латекс] \int \frac{d}{dt}v(t)dt=\int a(t)dt+{C}_{1}, [/latex]
, где C ₁ есть постоянная интегрирования. Поскольку [латекс] \int \frac{d}{dt}v(t)dt=v(t) [/latex], скорость определяется как
[латекс] v(t)=\int a(t)dt+{C}_{1}. [/latex]
Точно так же производная по времени от функции положения является функцией скорости,
[latex] \frac{d}{dt}x(t)=v(t). [/latex]
Таким образом, мы можем использовать те же математические манипуляции, которые мы только что использовали, и найти
[latex] x(t)=\int v(t)dt+{C}_{2}, [/latex]
, где C ₂ — вторая постоянная интегрирования.
Мы можем вывести кинематические уравнения для постоянного ускорения, используя эти интегралы. С a ( t ) = a константа, и, выполняя интегрирование на (рис.), находим
[латекс] v(t)=\int adt+{C}_{1}=at+{C }_{1}. [/latex]
Если начальная скорость равна v (0) = v ₀ , тогда
[латекс] {v}_{0}=0+{C}_{1}. [/latex]
Затем C ₁ = v ₀ и
[латекс] v(t)={v}_{0}+at, [/latex]
, что (Уравнение). Подстановка этого выражения в (Рисунок) дает 9{2} [/латекс]. а) Какова функция скорости моторной лодки? б) В какой момент времени скорость достигает нуля? в) Какова функция положения моторной лодки? г) Каково водоизмещение моторной лодки с момента начала торможения до момента, когда скорость равна нулю? (e) Нарисуйте график функций скорости и положения.
Стратегия
(a) Чтобы получить функцию скорости, мы должны проинтегрировать и использовать начальные условия, чтобы найти константу интегрирования. (b) Приравняем функцию скорости к нулю и решим для т . (c) Точно так же мы должны проинтегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти константу интегрирования. (d) Поскольку начальная позиция принимается равной нулю, нам нужно только оценить функцию позиции в [латекс] t=0 [/латекс].
Решение
Примем t = 0 за время, когда лодка начинает замедляться.
Из функциональной формы ускорения мы можем решить (Рисунок), чтобы получить v ( t ):
Показать ответ
Показать ответ
Решите (рисунок):
Показать ответ
Показать ответ
Рис. 3.30 (a) Скорость моторной лодки как функция времени. Моторная лодка уменьшает скорость до нуля за 6,3 с. В моменты времени, превышающие это значение, скорость становится отрицательной, то есть лодка меняет направление. (b) Положение моторной лодки в зависимости от времени. В момент времени t = 6,3 с скорость равна нулю, и лодка остановилась. В моменты времени, превышающие это, скорость становится отрицательной — это означает, что если лодка продолжает двигаться с тем же ускорением, она меняет направление и направляется обратно к тому месту, где она возникла.
Значение
Функция ускорения линейна во времени, поэтому при интегрировании используются простые полиномы. На (рисунке) мы видим, что если мы расширим решение за точку, где скорость равна нулю, скорость станет отрицательной, и лодка изменит направление. Это говорит нам о том, что решения могут дать нам информацию, выходящую за рамки нашего непосредственного интереса, и мы должны быть осторожны при их интерпретации. {2} [/латекс]. а) Что такое функция скорости? б) Что такое функция положения? в) Когда скорость равна нулю?
Показать решение
Резюме
Интегральное исчисление дает нам более полную формулировку кинематики.
Если ускорение a ( t ) известно, мы можем использовать интегральное исчисление, чтобы получить выражения для скорости v ( t ) и положения x ( t ).
Если ускорение постоянно, интегральные уравнения сводятся к (Рисунок) и (Рисунок) для движения с постоянным ускорением.
Ключевые уравнения
«> 9{2}-2g(y-{y}_{0}) [/латекс]
Рабочий объем [латекс] \text{Δ}x={x}_{\text{f}}-{x}_{\text{i}} [/latex]
Полный водоизмещение [латекс] \text{Δ}{x}_{\text{Всего}}=\sum \text{Δ}{x}_{\text{i}} [/latex]
Средняя скорость [латекс] \overset{\text{–}}{v}=\frac{\text{Δ}x}{\text{Δ}t}=\frac{{x}_{2}-{x} _{1}}{{t}_{2}-{t}_{1}} [/латекс]
Мгновенная скорость [латекс] v(t)=\frac{dx(t)}{dt} [/латекс]
Средняя скорость [латекс] \text{Средняя скорость}=\overset{\text{–}}{s}=\frac{\text{Общее расстояние}}{\text{Прошедшее время}} [/latex]
Мгновенная скорость [латекс] \text{Мгновенная скорость}=|v(t)| [/латекс]
Среднее ускорение [латекс] \overset{\text{–}}{a}=\frac{\text{Δ}v}{\text{Δ}t}=\frac{{v}_{f}-{v} _{0}}{{t}_{f}-{t}_{0}} [/латекс]
Мгновенное ускорение [латекс] a(t)=\frac{dv(t)}{dt} [/латекс]
Положение по средней скорости [латекс] x={x}_{0}+\overset{\text{–}}{v}t [/латекс]
Средняя скорость [латекс] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex]
Скорость от ускорения [латекс] v={v}_{0}+at\enspace(\text{константа}\,a\text{)} [/латекс]
Скорость от ускорения [латекс] v(t)=\int a(t)dt+{C}_{1} [/латекс]
Положение по скорости [латекс] x(t)=\int v(t)dt+{C}_{2} [/латекс]
Концептуальные вопросы
Какая дополнительная информация необходима для определения функции скорости и функции положения при наличии функции ускорения?
Задачи
Ускорение частицы изменяется со временем согласно уравнению [латекс] a(t)=p{t}^{2}-q{t}^{3} [/latex]. Первоначально скорость и положение равны нулю. а) Как зависит скорость от времени? б) Что такое положение как функция времени? 9{1\,\text{/}2} [/latex], где A и B — константы. (a) Если x в метрах, а t в секундах, каковы единицы A и B ? (b) Если ракета стартует из состояния покоя, как изменится скорость между t = 0 и t = t ₀ ? в) Если ее начальное положение равно нулю, каково положение ракеты в зависимости от времени в течение этого же интервала времени?
Показать решение 9{-1} [/латекс], где A = 2 м/с, B = 0,25 м и [латекс] 1,0\,\text{s}\le t\le 8,0\,\text{s } [/латекс]. Определить ускорение и положение частицы при t = 2,0 с и t = 5,0 с. Предположим, что [латекс] x(t=1\,\text{s})=0 [/латекс].
Частица, находящаяся в состоянии покоя, покидает точку отсчета, ее скорость увеличивается со временем по формуле v ( t ) = 3,2 t м/с. Через 5,0 с скорость частицы начинает уменьшаться согласно [16,0 – 1,5( t – 5,0)] м/с. Это уменьшение продолжается до t = 11,0 с, после чего скорость частицы остается постоянной и равной 7,0 м/с. а) Как зависит ускорение частицы от времени? б) Каково положение частицы в момент времени t = 2,0 с, t = 7,0 с и t = 12,0 с?
Показать решение
Дополнительные задачи
Профессиональный игрок в бейсбол Нолан Райан мог подать бейсбольный мяч со скоростью примерно 160,0 км/ч. При такой средней скорости сколько времени потребовалось мячу, брошенному Райаном, чтобы достичь домашней площадки, которая находится в 18,4 м от насыпи питчера? Сравните это со средним временем реакции человека на зрительный стимул, которое составляет 0,25 с.
Самолет вылетает из Чикаго и пролетает 3000 км до Лос-Анджелеса за 5 часов. Второй самолет вылетает из Чикаго на полчаса позже и прибывает в Лос-Анджелес в то же время. Сравните средние скорости двух самолетов. Не обращайте внимания на кривизну Земли и разницу в высоте между двумя городами.
Показать решение
Необоснованные результаты Велосипедист проезжает 16,0 км на восток, затем 8,0 км на запад, затем 8,0 км на восток, затем 32,0 км на запад и, наконец, 11,2 км на восток. Если его средняя скорость равна 24 км/ч, то за какое время он проделал путь? Это разумный срок? 9{2} [/латекс] м. Каковы скорость и ускорение при [латексе] t=2,0 [/латекс] с и [латекс] t=5,0 [/латекс] с?
Частица, движущаяся с постоянным ускорением, имеет скорости [латекс] 2,0\,\text{м/с} [/латекс] при [латекс] t=2,0 [/латекс] с и [латекс] -7,6\,\текст {м/с} [/латекс] при [латекс] t=5,2 [/латекс] с. Чему равно ускорение частицы?
Показать решение
Поезд движется вверх по крутому склону с постоянной скоростью (см. следующий рисунок), когда его камбуз отрывается и начинает свободно катиться по рельсам. Через 5,0 с камбуз отстает от поезда на 30 м. Каково ускорение камбуза? 9{2} [/latex] по той же прямой. а) Какова скорость электрона, когда он вылетает из этой области? б) Сколько времени требуется электрону, чтобы пересечь область?
Показать решение
Водитель скорой помощи везет пациента в больницу. Двигаясь со скоростью 72 км/ч, она замечает, что светофор на предстоящем перекрестке загорелся желтым. Чтобы добраться до перекрестка до того, как загорится красный свет, она должна проехать 50 м за 2,0 с. а) Какое минимальное ускорение должна иметь машина скорой помощи, чтобы добраться до перекрестка до того, как загорится красный сигнал светофора? б) С какой скоростью машина скорой помощи доедет до перекрестка? 9{2} [/латекс]. Затем она движется с постоянной скоростью в течение следующих 5,0 мин. Затем она замедляется с постоянной скоростью так, что через 3,0 мин останавливается в точке B. а) Нарисуйте график зависимости скорости от времени для поездки. б) Чему равно ускорение за последние 3 мин? в) Какое расстояние проехал велосипедист?
Два поезда движутся со скоростью 30 м/с в противоположных направлениях по одному и тому же пути. Инженеры одновременно видят, что они находятся на встречном курсе, и включают тормоза, когда расстояние между ними составляет 1000 м. Предполагая, что оба поезда имеют одинаковое ускорение, каким должно быть это ускорение, чтобы поезда остановились перед столкновением?
Показать решение
Грузовой автомобиль длиной 10,0 м, движущийся с постоянной скоростью 97,0 км/ч, проезжает автомобиль длиной 3,0 м, движущийся с постоянной скоростью 80,0 км/ч. Сколько времени проходит между моментом, когда передняя часть грузовика окажется на одном уровне с задней частью автомобиля, и моментом, когда задняя часть грузовика окажется на одном уровне с передней частью автомобиля?
Полицейская машина спряталась немного в стороне от шоссе. Полицейская машина замечает мчащуюся машину, которая движется со скоростью 40 м/с. В момент, когда мчащаяся машина проезжает мимо полицейской машины, полицейская машина ускоряется из состояния покоя со скоростью 4 м/с ², чтобы поймать мчащуюся машину. Сколько времени потребуется полицейской машине, чтобы догнать мчащуюся машину?
Показать решение
Пабло бежит полумарафон со скоростью 3 м/с. Другой бегун, Джейкоб, с такой же скоростью отстает от Пабло на 50 метров. Джейкоб начинает ускоряться со скоростью 0,05 м/с ² . а) Сколько времени потребуется Джейкобу, чтобы поймать Пабло? б) Какое расстояние преодолел Иаков? в) Какова конечная скорость Якова?
Необоснованные результаты Бегун приближается к финишу и находится на расстоянии 75 м; ее средняя скорость в этом положении 8 м/с. В этот момент она замедляется со скоростью 0,5 м/с ² . За какое время она пересечет финишную черту с расстояния 75 м? Это разумно?
Показать решение
Самолет разгоняется до 5,0 м/с ² в течение 30,0 с. За это время он преодолевает расстояние 10,0 км. Каковы начальная и конечная скорости самолета?
Сравните расстояние, пройденное объектом, скорость которого изменилась в два раза по сравнению с начальной скоростью, с объектом, скорость которого изменилась в четыре раза по сравнению с начальной скоростью за тот же период времени. Ускорения обоих тел постоянны.
Показать решение
Объект движется на восток с постоянной скоростью и находится в позиции [латекс] {x}_{0}\,\text{at}\,\text{time}\,{t}_{0}=0 [/латекс]. а) Какое ускорение должен иметь объект, чтобы его полное перемещение стало равным нулю в более позднее время t ? (b) Какова физическая интерпретация решения для случая [латекс] t\to \infty [/латекс]?
Мяч брошен прямо вверх. На своем пути вверх он проходит окно высотой 2,00 м на высоте 7,50 м от земли, и ему требуется 1,30 с, чтобы пройти мимо окна. Какова была начальная скорость мяча?
Показать решение
Монета сбрасывается с воздушного шара, находящегося на высоте 300 м над землей и поднимающегося вверх со скоростью 10,0 м/с. {-3}\,\text{s}) [/латекс] (d) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?
Показать решение
Необоснованные результаты . Капля дождя падает из облака на высоте 100 м над землей. Сопротивлением воздуха пренебречь. Какова скорость капли дождя в момент удара о землю? Это разумное число?
Сравните время нахождения в воздухе баскетболиста, прыгнувшего с пола на 1,0 м вертикально, со временем игрока, прыгнувшего на 0,3 м вертикально.
Показать решение
Предположим, что человеку требуется 0,5 с, чтобы среагировать и двинуть рукой, чтобы поймать предмет, который он уронил. (а) Как далеко объект падает на Землю, где [латекс] g = 9{2}? [/latex] (b) Как далеко падает объект на Луне, где ускорение свободного падения составляет 1/6 от земного?
Воздушный шар поднимается над землей с постоянной скоростью 3,0 м/с. Через минуту после старта с воздушного шара случайно сбрасывается мешок с песком. Вычислите: а) время, за которое мешок с песком достигает земли, и б) скорость мешка с песком в момент удара о землю.
Показать решение
(a) Мировой рекорд был установлен в беге на 100 м среди мужчин на Олимпийских играх 2008 года в Пекине Усэйном Болтом с Ямайки. Болт пересек финишную черту со временем 9.0,69 с. Если мы предположим, что Болт ускорялся в течение 3,00 с, чтобы достичь своей максимальной скорости, и поддерживал эту скорость до конца гонки, рассчитайте его максимальную скорость и его ускорение. (b) Во время той же Олимпиады Болт также установил мировой рекорд в беге на 200 м со временем 19,30 с. Используя те же предположения, что и для бега на 100 м, какова была его максимальная скорость в этом забеге?
Предмет падает с высоты 75,0 м над уровнем земли. а) Определите путь, пройденный за первую секунду. б) Определить конечную скорость, с которой тело упадет на землю. в) Определите расстояние, пройденное за последнюю секунду движения до удара о землю. 9{-5}\,\text{s}) [/latex] (d) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?
Предмет падает с крыши здания высотой ч . За последнюю секунду спуска он проходит расстояние ч /3. Рассчитайте высоту здания.
Показать решение
Задачи-вызовы
В забеге на 100 м победитель показывает время 11,2 с. Время второго места – 11,6 с. Как далеко занявшая второе место отстаёт от победительницы, когда она пересекает финишную черту? Предположим, что скорость каждого бегуна постоянна на протяжении всего забега. 9{3} [/латекс] м. Найти: а) скорость и ускорение частицы как функции времени, б) скорость и ускорение в момент времени t = 2,0 с, в) время, когда положение максимально, скорость которого равна нулю, и (e) максимальное положение.
Показать решение
Велосипедист мчится в конце гонки, чтобы одержать победу. Она имеет начальную скорость 11,5 м/с и ускоряется со скоростью 0,500 м/с ² за 7,00 с. а) Какова его конечная скорость? (b) Велосипедист продолжает движение с этой скоростью до финиша. Если она находится в 300 м от финиша, когда начинает разгоняться, сколько времени она сэкономила? (c) Победитель, занявший второе место, был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и двигался со скоростью 11,8 м/с до финиша. Какая разница во времени финиша в секундах между победителем и призером? Как далеко от финиша финишировал занявший второе место?
В 1967 году новозеландец Берт Манро установил мировой рекорд для индийского мотоцикла на соляных равнинах Бонневиль в штате Юта, со скоростью 295,38 км/ч. Длина трассы в один конец составила 8,00 км. Темпы ускорения часто описываются временем, которое требуется для достижения 96,0 км/ч из состояния покоя. Если это время составило 4,00 с, и Берт разогнался с такой скоростью, пока не достиг своей максимальной скорости, сколько времени потребовалось Берту, чтобы пройти этот путь?
Показать решение
3.
4 Движение с постоянным ускорением — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
Определите, какие уравнения движения следует использовать для решения неизвестных.
Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Можно догадаться, что чем больше ускорение, скажем, автомобиля, удаляющегося от знака остановки, тем больше перемещение автомобиля за заданное время. Но мы не разработали конкретное уравнение, связывающее ускорение и перемещение. В этом разделе мы рассмотрим некоторые удобные уравнения для кинематических отношений, начиная с определений перемещения, скорости и ускорения. Сначала мы исследуем один объект в движении, называемое движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Сначала сделаем некоторые упрощения в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно Δt=tf−t0Δt=tf−t0, принятие t0=0t0=0 означает, что Δt=tfΔt=tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем нижний индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость 9.0122 . Мы не помещаем нижние индексы в окончательные значения. То есть t — конечное время , x — конечное положение , а v — конечная скорость . Это дает более простое выражение для прошедшего времени Δt=tΔt=t. Это также упрощает выражение для смещения x , которое теперь равно Δx=x−x0Δx=x−x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv=v−v0Δv=v−v0. Подводя итог, используя упрощенную запись, с начальным временем, принятым равным нулю,
Δt=tΔx=x−x0Δv=v−v0, Δt=tΔx=x−x0Δv=v−v0,
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса обозначает конечное значение любого рассматриваемого движения.
Теперь мы делаем важное предположение, что ускорение является постоянным . Это предположение позволяет нам избежать использования исчисления для нахождения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, т. е.
.
а–=а=константа.а–=а=константа.
Таким образом, мы всегда можем использовать символы и для ускорения. Предположение, что ускорение является постоянным, серьезно не ограничивает ситуации, которые мы можем изучать, и не снижает точность нашего лечения. Во-первых, ускорение является постоянным в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, предполагая постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, при котором ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до полной остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет свое постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
v–=ΔxΔt.v–=ΔxΔt.
Подстановка упрощенных обозначений для ΔxΔx и ΔtΔt дает
v–=x−x0t.v–=x−x0t.
Решение для x дает нам
х=x0+v–t,x=x0+v–t,
3,10
где средняя скорость
v–=v0+v2.v–=v0+v2.
3.11
Уравнение v–=v0+v2v–=v0+v2 отражает тот факт, что при постоянном ускорении v–v– представляет собой простое среднее значение начальной и конечной скоростей. Рисунок 3.18 иллюстрирует эту концепцию графически. В части (а) рисунка ускорение постоянно, а скорость увеличивается с постоянной скоростью. Средняя скорость на часовом интервале от 40 км/ч до 80 км/ч составляет 60 км/ч:
v–=v0+v2=40км/ч+80км/ч3=60км/ч.v–=v0+v2=40км/ч+80км/ч3=60км/ч.
В части (b) ускорение непостоянно. В течение 1-часового интервала скорость ближе к 80 км/ч, чем к 40 км/ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (а) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0 и vv0 и v. Средняя скорость 12(v0+v)=60 км/ч22(v0+v)=60 км/ч. (b) График зависимости скорости от времени с ускорением, изменяющимся со временем. Средняя скорость не равна 12(v0+v)12(v0+v), но больше 60 км/ч.
Расчет конечной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
а=ΔvΔt.a=ΔvΔt.
Подставляя упрощенные обозначения для ΔvΔv и ΔtΔt, мы получаем
a=v−v0t(константа). a=v−v0t(константа).
Решение для v дает
v=v0+at(константа).v=v0+at(константа).
3.12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70,0 м/с и затем разгоняется против движения со скоростью 1,50 м/с ² за 40,0 с. Какова его конечная скорость?
Стратегия
Сначала выделим известные: v0=70 м/с, a=-1,50 м/с2, t=40sv0=70 м/с, a=-1,50 м/с2, t=40 с.
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого выясняем, какое кинематическое уравнение дает неизвестное через известные. Мы рассчитываем конечную скорость, используя уравнение 3.12, v=v0+atv=v0+at.
Решение
Подставляем известные значения и решаем:
v=v0+at=70,0 м/с+(−1,50 м/с2)(40,0 с)=10,0 м/с. v=v0+at=70,0 м/с+(−1,50 м/с2)(40,0 с)=10,0 РС.
На рис. 3.19 показан эскиз, показывающий векторы ускорения и скорости.
Рисунок 3.19 Самолет приземляется с начальной скоростью 70,0 м/с и замедляется до конечной скорости 10,0 м/с перед тем, как взять курс на аэродром. Обратите внимание, что ускорение отрицательно, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, как и требуется при замедлении, но все же положительна (см. рисунок). С реактивными двигателями реверсивная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение его назад, на что указывает отрицательная конечная скорость, но здесь это не так.
Уравнение v=v0+atv=v0+at не только полезно при решении задач, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что
Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀ ), как и ожидалось (другими словами, скорость постоянна)
Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Нахождение конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволит нам вычислить конечное положение объекта, испытывающего постоянное ускорение. Начнем с
v=v0+at.v=v0+at.
Если добавить v0v0 к каждой части этого уравнения и разделить на 2, получится
.
v0+v2=v0+12at.v0+v2=v0+12at.
Поскольку v0+v2=v–v0+v2=v– для постоянного ускорения, мы имеем
v–=v0+12at.v–=v0+12at.
Теперь мы подставляем это выражение для v–v– в уравнение для смещения x=x0+v–tx=x0+v–t, что дает
x=x0+v0t+12at2(константа).x=x0+v0t+12at2(константа).
3.13
Пример 3,8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м/с ² . Предположим, что драгстер разгоняется с такой скоростью за 5,56 с. Рисунок 3.20. Какое расстояние он проходит за это время?
Рисунок 3.20 Пилот Top Fuel армии США Тони «Сержант» Шумахер начинает гонку с контролируемым выгоранием. (Источник: подполковник Уильям Турмонд. Фото предоставлено армией США.)
Стратегия
Сначала нарисуем эскиз Рисунок 3.21. Нас просят найти смещение, которое равно x , если мы принимаем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулем и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x=x0+v0t+12at2x=x0+v0t+12at2 когда мы идентифицируем v0v0, aa и т из условия задачи.
Рисунок 3.21 Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно идентифицировать известные. Запуск из состояния покоя означает, что v0=0v0=0, a задается как 26,0 м/с ² и t задается как 5,56 с.
Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x=x0+v0t+12at2.x=x0+v0t+12at2.
Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
х=12ат2.х=12ат2.
Замена идентифицированных значений a и t дает
x=12(26,0 м/с2)(5,56 с)2=402 м.x=12(26,0 м/с2)(5,56 с)2=402 м .
Значение
Если мы преобразуем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартной дистанции для дрэг-рейсинга. Итак, наш ответ разумен. Это впечатляющее смещение, которое можно преодолеть всего за 5,56 с, но первоклассные драгстеры могут проехать четверть мили за еще меньшее время. Если бы драгстеру была задана начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении используются те же ускорение и время, то пройденное расстояние будет намного больше.
Что еще мы можем узнать, исследуя уравнение x=x0+v0t+12at2?x=x0+v0t+12at2? Мы можем видеть следующие отношения:
Смещение зависит от квадрата прошедшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину истекшего времени.
Если ускорение равно нулю, то начальная скорость равна средней скорости (v0=v–)(v0=v–), и x=x0+v0t+12at2 становится x=x0+v0t.x=x0+v0t+12at2 становится x=x0+v0t. 907:10
Нахождение конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено из другой алгебраической манипуляции с предыдущими уравнениями. Если мы решим v=v0+atv=v0+at для t , мы получим
t=v−v0a. t=v−v0a.
Подставив это и v–=v0+v2v–=v0+v2 в x=x0+v–tx=x0+v–t, мы получим
v2=v02+2a(x−x0)(константа).v2=v02+2a(x−x0)(константа).
3.14
Пример 3,9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в примере 3.8 без использования информации о времени.
Стратегия
Уравнение v2=v02+2a(x−x0)v2=v02+2a(x−x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорения и перемещения и не требует информации о времени.
Решение
Во-первых, мы идентифицируем известные значения. Мы знаем, что v ₀ = 0, так как драгстер трогается с места. Мы также знаем, что x − x ₀ = 402 м (это был ответ в примере 3. 8). Среднее ускорение было равно a = 26,0 м/с ² .
Во-вторых, мы подставляем известные значения в уравнение v2=v02+2a(x−x0)v2=v02+2a(x−x0) и находим v :
v2=0+2(26,0 м/с2 )(402м).v2=0+2(26.0м/с2)(402м).
Таким образом,
v2=2,09×104м2/с2v=2,09×104м2/с2=145м/с.v2=2,09×104м2/с2v=2,09×104м2/с2=145м/с.
Значение
Скорость 145 м/с составляет около 522 км/ч, или около 324 миль/ч, но даже эта головокружительная скорость не соответствует рекорду на четверть мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.
Изучение уравнения v2=v02+2a(x−x0)v2=v02+2a(x−x0) может дать дополнительные сведения об общих соотношениях между физическими величинами:
Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует. 907:10
При фиксированном ускорении автомобиль, который движется в два раза быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо больше. (Поэтому у нас есть зоны пониженной скорости возле школ.)
Составление уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного более алгебраических манипуляций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для удобства обращения к необходимым уравнениям. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных и нужно два уравнения из набора для решения неизвестных. Нам нужно столько уравнений, сколько неизвестных, чтобы решить данную ситуацию.
Сводка кинематических уравнений (константа
a )
x=x0+v–tx=x0+v–t
v–=v0+v2v–=v0+v2
v=v0+atv=v0+at
x=x0+v0t+12at2x=x0 +v0t+12at2
v2=v02+2a(x−x0)v2=v02+2a(x−x0)
Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Преобразовывая уравнение 3.12, мы имеем
а=v-v0t.a=v-v0t.
Отсюда мы видим, что для конечного времени, если разность между начальной и конечной скоростями мала, ускорение мало, стремясь к нулю в пределе, когда начальная и конечная скорости равны. Наоборот, в пределе t→0t→0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переформулировав уравнение 3.14, мы можем выразить ускорение через скорость и перемещение:
а=v2-v022(x-x0).a=v2-v022(x-x0).
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе перемещение стремится к нулю. Ускорение стремится к нулю в пределе, когда разность начальной и конечной скоростей стремится к нулю при конечном перемещении.
Пример 3.10
Как далеко едет машина?
На сухом бетоне автомобиль может ускоряться против движения со скоростью 7,00 м/с ² , тогда как на мокром бетоне он может ускоряться против движения только со скоростью 5,00 м/с ² . Найдите расстояние, необходимое для остановки автомобиля, движущегося со скоростью 30,0 м/с (около 110 км/ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите перемещение от точки, в которой водитель видит красный сигнал светофора, учитывая время его реакции 0,500 с, чтобы нажать на педаль тормоза.
Стратегия
Сначала нам нужно нарисовать эскиз рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рисунок 3,22 Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v ₀ = 30,0 м/с, v = 0, а a = −7,00 м/с ² ( a отрицательно, потому что оно находится в направлении, противоположном скорости). Мы принимаем x ₀ за ноль. Ищем смещение ΔxΔx, или x − x ₀ .
Во-вторых, мы определяем уравнение, которое поможет нам решить задачу. Лучше всего использовать уравнение
v2=v02+2a(x−x0).v2=v02+2a(x−x0).
Это уравнение лучше всего, потому что оно включает только одно неизвестное, х . Мы знаем значения всех остальных переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которого мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)
В-третьих, мы переставьте уравнение для решения x :
х-х0=v2-v022ax-x0=v2-v022a
и подставляем известные значения:
x−0=02−(30,0 м/с)22(−7,00 м/с2).x−0=02−(30,0 м/с)22(−7,00 м/с2).
Таким образом,
x=64,3 м на сухом бетоне.x=64,3 м на сухом бетоне.
Эту часть можно решить точно так же, как (а). Единственное отличие состоит в том, что ускорение равно −5,00 м/с ² . Результат
xwet=90,0 м на мокром бетоне.xwet=90,0 м на мокром бетоне.
Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и мокрого бетона. Итак, чтобы ответить на этот вопрос, нам нужно рассчитать, какое расстояние автомобиль проедет за время реакции, а затем добавить это ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы снова идентифицируем известные вещи и то, что мы хотим решить. Мы знаем, что v–=30,0 м/сv–=30,0 м/с, treaction=0,500streaction=0,500 с и areaaction=0areaction=0. Примем x0-реакциюx0-реакцию равной нулю. Мы ищем xreactionxreaction.
Во-вторых, как и прежде, мы определяем наилучшее уравнение для использования. В этом случае x=x0+v–tx=x0+v–t работает хорошо, потому что единственным неизвестным значением является x , что мы и хотим найти.
В-третьих, подставляем известные значения для решения уравнения:
x=0+(30,0 м/с)(0,500 с)=15,0 м.x=0+(30,0 м/с)(0,500 с)=15,0 м.
Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее перемещение в двух случаях с сухим и влажным бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем перемещение за время реакции к перемещению при торможении (рис. 3.23),
xbraking+xreaction=xtotal,xbraking+xreaction=xtotal,
и найдите (a) 64,3 м + 15,0 м = 79,3 м в сухом состоянии и (b) 90,0 м + 15,0 м = 105 м во влажном состоянии. 907:10
Рисунок 3,23 Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны тормозные пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося изначально со скоростью 30,0 м/с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит красный свет, при условии времени реакции 0,500 с.
Значение
Перемещения, найденные в этом примере, кажутся приемлемыми для остановки быстро движущегося автомобиля. На мокром асфальте машина останавливается дольше, чем на сухом. Интересно, что к перемещениям существенно добавляет время реакции, но важнее общий подход к решению задач. Мы идентифицируем известные и определяемые величины, затем находим соответствующее уравнение. Если имеется более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных для решения. Часто существует более одного способа решения проблемы. Различные части этого примера на самом деле могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример 3.11
Расчет времени
Предположим, что автомобиль въезжает в полосу движения автострады по съезду длиной 200 м. Если его начальная скорость равна 10,0 м/с, а ускорение составляет 2,00 м/с ² , за какое время автомобиль проедет 200 м вверх по пандусу? (Такая информация может быть полезна инженеру по дорожному движению. )
Стратегия
Сначала рисуем эскиз Рисунок 3.24. Нас просят решить за время t . Как и раньше, мы отождествляем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, т .)
Рисунок 3,24 Эскиз автомобиля, ускоряющегося на съезде автострады.
Решение
Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0=0,x0=0,
v0=10 м/с, a=2,00 м/с2v0=10 м/с, a=2,00 м/с2 и x = 200 м.
Нам нужно решить для t . Уравнение x=x0+v0t+12at2x=x0+v0t+12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , для которой нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , а затем подставить известные значения в уравнение: м/с)t+12(2,00 м/с2)t2.
Затем упростим уравнение. Единицы метров сокращаются, потому что они находятся в каждом члене. Мы можем получить единицы измерения секунд для сокращения, взяв t = t с, где t — величина времени, а с — единица измерения. При этом остается
200=10t+t2.200=10t+t2.
Затем с помощью квадратичной формулы находим t ,
t2+10t−200=0t=−b±b2−4ac2a,t2+10t−200=0t=−b±b2−4ac2a,
, которые дает два решения: t = 10,0 и t = −20,0. Отрицательное значение времени неразумно, так как это означало бы, что событие произошло за 20 с до начала движения. Мы можем отказаться от этого решения. Таким образом,
t=10. 0s.t=10.0s.
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых задачах оба решения имеют смысл; в других разумно только одно решение. Ответ 10,0 с кажется разумным для типичного съезда с автострады.
Проверьте свое понимание 3,5
Ракета разгоняется со скоростью 20 м/с ² во время запуска. За какое время ракета достигнет скорости 400 м/с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Он разгоняется со скоростью 20 м/с ² за 2 мин и преодолевает расстояние 1000 км. Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не даст ответа. Мы должны использовать одно кинематическое уравнение, чтобы найти одну из скоростей, и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.
Решение
Сначала мы решаем для v0v0, используя x=x0+v0t+12at2:x=x0+v0t+12at2:
x−x0=v0t+12at2x−x0=v0t+12at2
1,0×106m=v0(120,0 с)+12(20,0 м/с2)(120,0 с)21,0×106m=v0(120,0 с)+12( 20,0 м/с2)(120,0 с)2
v0=7133,3 м/с. v0=7133,3 м/с.
Затем мы подставляем v0v0 в v=v0+atv=v0+at, чтобы найти конечную скорость: =v0+at=7133,3 м/с+(20,0 м/с2)(120,0 с)=9533,3 м/с.
Значение
В смещении, времени, скорости и ускорении есть шесть переменных, описывающих движение в одном измерении. Начальными условиями данной задачи может быть множество комбинаций этих переменных. Из-за этого разнообразия решения могут быть не такими простыми, как простые подстановки в одно из уравнений. Этот пример показывает, что для решения кинематики может потребоваться решение двух одновременных кинематических уравнений.
Познакомившись с основами кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также заметили общий подход к решению задач, который дает как правильные ответы, так и понимание физических взаимосвязей. Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До сих пор мы рассматривали примеры движения одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти задачи, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рис. 3.25.
Рисунок 3,25 Сценарий преследования двух тел, в котором автомобиль 2 движется с постоянной скоростью, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догоняет автомобиль 2 позже.
Время и расстояние, необходимые для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния между автомобилем 1 и автомобилем 2, а также от скоростей обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард ждет, прячась за кустом. Гепард замечает газель, пробегающую мимо со скоростью 10 м/с. В тот момент, когда газель проходит мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м/с ², чтобы догнать газель. а) Сколько времени потребуется гепарду, чтобы поймать газель? б) Каково водоизмещение газели и гепарда?
Стратегия
Для решения этой задачи воспользуемся системой уравнений для постоянного ускорения. Поскольку движутся два объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но что связывает уравнения, так это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, то станет ясно, что общим параметром для каждого животного является их позиция 9.1884 x позже t . Поскольку они оба начинаются в точке x0=0x0=0, их перемещения будут одинаковыми в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое определяет смещение для каждого животного, мы можем тогда установить уравнения равными друг другу и найти неизвестное, то есть время.
Решение
Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется. Поэтому мы используем уравнение 3.10 с x0=0x0=0:
x=x0+v–t=v–t.x=x0+v–t=v–t.
Уравнение для гепарда: Гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0=0x0=0 и v0=0v0=0:
x=x0+v0t+12at2=12at2.x=x0+v0t+12at2=12at2 .
Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае для t :
решаем x=v–t=12at2t=2v–a.x=v–t=12at2t=2v–a.
Газель имеет постоянную скорость 10 м/с, что является ее средней скоростью. Ускорение гепарда 4 м/с ² . Оценивая t , время, за которое гепард достигнет газели, мы имеем
t=2v–a=2(10 м/с)4м/с2=5с.t=2v–a=2(10 м/с)4м/с2=5с.
Чтобы получить перемещение, мы используем либо уравнение движения гепарда, либо газели, так как они оба должны давать один и тот же ответ.
Водоизмещение гепарда:
x=12at2=12(4м/с2)(5)2=50м.x=12at2=12(4м/с2)(5)2=50м.
Водоизмещение газели:
x=v–t=10 м/с(5)=50м.x=v–t=10 м/с(5)=50м.
Мы видим, что оба смещения равны, как и ожидалось.
No related posts.

Формулы кинематики с пояснениями по физике / Блог / Справочник :: Бингоскул

Путь, время, скорость

Равномерно ускоренное движение:

Равномерно ускоренное движение:

Равномерно ускоренное движение:

Равномерно ускоренное движение:

Равномерное круговое движение: линейная скорость

Период вращения

Высота подъема тела, брошенного под углом к горизонту

Механическое движение — определение, формулы, примеры

Механическое движение

Прямолинейное равномерное движение

Скалярные величины (определяются только значением)

Векторные величины (определяются значением и направлением)

Проецирование векторов

Уравнение движения

Прямолинейное равноускоренное движение

Уравнение движения и формула конечной скорости

Движение по вертикали

Равноускоренное движение — формулы, законы и примеры

Основные определения

Задача 1

График зависимости скорости от времени при равноускоренном движении

Задача 2

Перемещение при равноускоренном движении

Задача 3

Графики равноускоренного движения

Колебания — Физика — Теория, тесты, формулы и задачи

Оглавление:

Гармонические колебания

Математический маятник

Пружинный маятник

Механические волны

Электрический контур

Переменный ток. Трансформатор

Конденсатор в цепи переменного тока

Катушка индуктивности в цепи переменного тока

Трансформаторы

Электромагнитные волны

Основные формулы по физике по 9 класс. Все, что нужно знать

Механика

Статика

Динамика

Космические скорости

Вывод

Источники:

Кинематика

Равномерное прямолинейное движение

Равноускоренное прямолинейное движение

Равномерное движение по окружности

Динамика

Законы Ньютона

Силы в природе

Сила всемирного тяготения

Движение тела под действием силы тяжести

Силы трения

Движение тела под действием нескольких сил

Закон сохранения в механике

Движение жидкостей и газов по трубам

Примеры задач

Равномерное прямолинейное движение

Равноускоренное прямолинейное движение

Равномерное движение по окружности

Источники:

Физика 9 класс. Все формулы и определения

Физика 9 Все формулы КРУПНО

Физика 9. Все формулы МЕЛКО. Стр 1

Физика 9. Все формулы МЕЛКО. Стр 2

Физика 9 класс. Все формулы и определения в разделе «КИНЕМАТИКА»

Физика 9 класс. Все формулы и определения в разделе «ДИНАМИКА»

Источники:

Теория к заданию 1 из ЕГЭ по физике

Кинематика

Виды движения

Частные случаи равноускоренного движения под действием силы тяжести

Дополнительная информация для частных случаев решения задач

Пример решения задач

Уравнения кинематики и постоянное ускорение

Пример 1

Пример 2