Онлайн аргумент комплексного числа: Комплексные числа онлайн

Комплексные числа. Модуль и аргумент комплексного числа

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Комплексные
числа
Множество комплексных чисел обозначается С
C
R
Q
Z
N
I
Термин “мнимые числа” ввел в 1637 году
французский математик и философ Р. Декарт,
а в 1777 году один из крупнейших
математиков XVIII века — Л. Эйлер предложил
использовать первую букву французского
слова imaginaire (мнимый) для обозначения

числа i(мнимой единицы). Этот символ
вошел во всеобщее употребление благодаря
К. Гауссу . Термин “комплексные числа” так
же был введен Гауссом в 1831 году. Слово
«комплекс» (от латинского complexus)
означает связь, сочетание, совокупность
понятий, предметов, явлений и т. д.
образующих единое целое.
Большой вклад в развитие теории функций комплексного
переменного внесли русские и советские ученые:
Н. И. Мусхелишвили занимался ее
применениями к теории упругости;
М. В. Келдыш и
М. А. Лаврентьев — к
аэро- и гидродинамике;
Н. Н. Богомолов и В. С. Владимиров
— к проблемам квантовой теории
поля.
ОпределениеКомплексным
:
числом
называется число вида a+bi ,
где a, b − некоторые
действительные числа, а i−
мнимая единица, причем:
i 1, i 1 .
2
Обозначение:
z a b i
алгебраическая форма записи
комплексного числа
z a b i
a — действительная часть
b -мнимая часть
комплексного числа z.
Обозначается a=Re z.
комплексного числа z.
Обозначается b=Im z.
Геометрическое изображение
комплексных чисел
Мнимая ось
b
M(a; b)
1
0
Действительная
ось
1
a
2) Запишите комплексные числа, изображенные на координатной
плоскости, в алгебраической форме.
z6
3
z5
1
z4
-4
z1
-2
0
1
2
4
z2
-3
z3
-5
Примеры:
1) Изобразите комплексные числа на плоскости
z1 1 5i;
z 2 7 3i;
z3 1,5 5i;
z 4 3,5 2i
z5 3
z6 6i
z 7 2 i;
3) На какой из координатных плоскостей изображено число
z 2 3i
1.
2.
0
3.
0
4.
0
0
Определени е :Комплексное число z a b i
называется противоположным
комплексному числу z=a+bi
Определени е :Комплексное число z a b i
называется сопряженным комплексному
числу z=a+bi
b
-a
-z
0
-b
z=a+bi
a
z
Примеры:
1. Запишите числа, противоположные и сопряженные
данным:
z1 7 3i
z 2 1 5i
z3 i 1
z 4 5i
z5 6
2. Какие из данных чисел являются сопряженным и
противоположным для числа
z 3 2i
а) z 3 2i
б ) z 3 2i
в) z 3 2i
г ) z 3i 2.
Модуль и аргумент
комплексного
числа
Определени е: Модулем комплексного числа z a b i
называется действительное число
r z a b 0.
2
Примеры:
Найти модуль комплексных чисел:
z1 3 4i r1 z1
z 2 12 5i
z3 1 3i
z 4 3
z5 2i
2
Определени е: Аргументом комплексного числа z
называется угол α, между положительным
направлением действительной оси и
вектором OM
Обозначение:
arg z α
b
tg
a
b
arctg
a
M
b
0
α
a
Частные случаи
z bi
z a
argbi
z a
z bi
,
2
3
arg(-bi)
,
2
arga 0 ,
arg(-a) .
Примеры:
z 3i
z 2
arg3i
2
3
arg(-4i)
2
z 7
z 4i
arg7 0
arg(-2) π

English     Русский Правила

Решение высшей математики онлайн

‹— Назад

Рассмотрим на плоскости декартову прямоугольную систему координат . Каждому комплексному числу можно сопоставить точку с координатами , и наоборот, каждой точке с координатами можно сопоставить комплексное число . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплекные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

        Пример 17.3   Изобразим на комплексной плоскости числа , , , , :

Рис.17.1.Изображение комплексных чисел точками плоскости

        

Однако чаще комплексные числа изображают в виде вектора с началом в точке , а именно, комплексное число изображается радиус-вектором точки с координатами . В этом случае изображение комплексных чисел из предыдущего примера будет таким:

Рис.17.2.Изображение комплексных чисел векторами

Отметим, что изображением суммы двух комплексных чисел , является вектор, равный сумме векторов, изображающих числа и . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 17.3).

Рис.17.3.Изображение суммы комплексных чисел

Пусть комплексное число изображается радиус-вектором. Тогда длина этого вектора называется модулем числа и обозначается . Из рисунка 17.4 очевидно, что

(17.6)

Рис.17.4.Модуль и аргумент

Угол, образованный радиус-вектором числа с осью , называется аргументом числа и обозначается . Аргумент числа определяется не однозначно, а с точностью до числа, кратного . Однако, обычно аргумент указывают в диапазоне от 0 до или в диапазоне от до . Кроме того у числа аргумент не определен.

На рис. 17.4 равен углу . Из того же рисунка очевидно, что

С помощью этого соотношения можно находить аргумент комплексного числа:

или

(17. 7)

причем первая формула действует, если изображение числа находится в первой или четвертой четверти, а вторая, если — во второй или третьей. Если , то комплексное число изображается вектором на оси и его аргумент равен или .

Получим еще одну полезную формулу. Пусть . Тогда ,

С учетом формулы (17.6) получим

или

        Пример 17.4   Найдите модуль и аргумент комплексных чисел: , , , , .

Решение. Запишем числа со строгим указанием действительной и мнимой части:

Тогда по формулам (17.6) и (17.7) находим:

В последнем случае можно вычислить с помощью калькулятора и записать .         

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Как найти модуль и аргумент комплексного числа – mathsathome.

com

Видеоурок: Как найти модуль и аргумент комплексного числа

Что такое модуль комплексного числа?

Модуль — это расстояние комплексного числа от начала координат на диаграмме Аргана. Для любого комплексного числа z = a + bi модуль вычисляется по теореме Пифагора по формуле |z| = √ (а ² + b ² ).

Комплексное число образует прямоугольный треугольник на комплексной плоскости, как показано ниже.

Модуль равен длине вектора от начала координат до точки комплексного числа. То есть он образует гипотенузу прямоугольного треугольника с ‘a’ и ‘b’ , образующими две более короткие стороны.

Модуль (также известный как величина или абсолютное значение) комплексного числа — это скалярное значение, представляющее расстояние комплексного числа от начала координат на комплексной плоскости. Это неотрицательное действительное число, поскольку оно представляет собой расстояние.

Формула модуля комплексного числа

Как найти модуль комплексного числа

Чтобы вычислить модуль комплексного числа, z = a + bi, используйте формулу |z| = √ (а ² + b ² ). Например, модуль z = 3 + 4i равен |z| = √ (3 ² + 4 ² ) . Упрощая это, модуль оказывается |z| = √ 25, что можно вычислить как |z| = 5.  

Пример: Найдите модуль .

• ‘а’ — размер действительной части числа. Следовательно, a = 3.
• ‘b’ — это размер мнимой части числа. Поэтому b = 4.

становится .

Оценка этого и т. д. .

Размер модуля .

---

Чтобы пошагово вычислить модуль комплексного числа:

1. Возведите в квадрат размер действительной части комплексного числа.
2. Квадрат размера мнимой части комплексного числа.
3. Сложите два результата вместе.
4. Квадратный корень этого результата.

Например: Найдите модуль z = √ 3 + i.

Шаг 1. Возведите в квадрат размер действительной части комплексного числа

Действительная часть   — это часть без i .

То есть действительная часть равна √ 3.

Возведение этого в квадрат, .

Шаг 2. Возведение в квадрат размера мнимой части комплексного числа

Мнимая часть — это часть с i .

То есть мнимая часть — это просто i , что равно 1 i .

 Размер мнимой части равен 1.

Возведение этого в квадрат, .

Шаг 3. Сложите два результата вместе

3 + 1 = 4

Шаг 4. Извлеките квадратный корень из этого результата

и, таким образом, модуль равен .

---

В следующей таблице приведены некоторые примеры вычисления модуля комплексного числа:

9015 1 z = -1 + 5i

Комплексный номер	Расчет модуля	Модуль
z = 1 + 3i	√ 90 009 (1 2 + 3 2 )	√ 10
z = 1 + i	√ (1 2 + 1 2 )	√ 2
√ ( (-1) 2 + 5 2 )	√
z = i	√ (1 2 )	√ 1
z = -2i	√ ( (-2) 2 )	√ 2

Как используется модуль комплексного числа?

Некоторые из наиболее распространенных применений модуля в математике, физике и технике включают:

1. Вычисление расстояния от начала координат: Модуль комплексного числа — это расстояние числа от начала координат на комплексной плоскости. Его можно использовать для вычисления расстояния между двумя комплексными числами.
2. Запись комплексного числа в полярной форме: модуль комплексного числа используется для выражения числа в полярной форме, где модуль представляет собой величину или радиус, а аргумент представляет собой угол, который комплексное число образует с положительной x- ось.
3. Запись комплексного числа в форме модуль-аргумент: Модуль и аргумент комплексного числа можно использовать для представления комплексного числа в форме модуль-аргумент.
4. Комплексная амплитуда: В обработке сигналов и физике модуль комплексного числа может использоваться для представления амплитуды сигнала.
5. Обратные тригонометрические функции: Модуль комплексного числа используется при нахождении обратных тригонометрических функций комплексных чисел, что полезно в физике и технике.
6. Определение устойчивости системы: В системах управления модуль комплексного числа может использоваться для определения устойчивости системы.

Свойства модуля комплексного числа

Ниже приведены некоторые ключевые свойства модуля комплексного числа:

1. Модуль комплексного числа представляет собой неотрицательное действительное число. Это означает, что модуль всегда будет больше или равен нулю. То есть, .
2. Если модуль комплексного числа равен нулю, то комплексное число равно z = 0.
3. Модуль коммутативен для умножения и деления. То есть и .
4. Модуль комплексного числа не изменяется относительно вращения комплексной плоскости. Это означает, что модуль не меняется при вращении комплексного числа в комплексной плоскости.
5. Модуль комплексного числа равен модулю сопряженного ему числа. Это означает, что модуль a + bi такой же, как модуль a – bi. То есть и .
6. Неравенство треугольника: модуль комплексного числа удовлетворяет неравенству треугольника, которое гласит, что сумма абсолютных значений любых двух комплексных чисел должна быть больше или равна абсолютному значению их суммы. То есть, .
7. Модуль комплексного числа, возведенного в степень, равен модулю комплексного числа, возведенного в эту степень. То есть, .
8. Квадрат модуля комплексного числа равен разности между комплексным числом и сопряженным комплексным числом. То есть, .
9. Если модуль комплексного числа равен 1, то есть |z|=1, то оно называется унимодулярным.

Что такое аргумент комплексного числа?

Аргумент ( также известный как фаза или амплитуда ) комплексного числа представляет собой угол, который вектор, представляющий число, составляет с положительной действительной осью в комплексной плоскости. Обычно его обозначают греческой буквой «фи» (φ), измеряемой в радианах между интервалом – π и π .

Аргумент комплексного числа может быть записан как arg(z) для краткости.

Аргумент всегда отсчитывается от положительной действительной оси, которая является направлением вправо.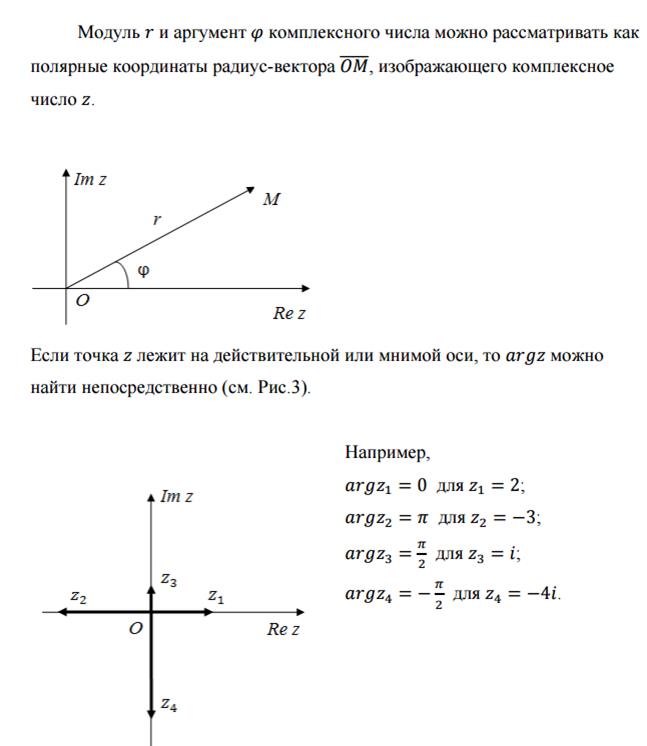

Аргумент комплексного числа является периодическим с периодом 2 π . Поэтому общий аргумент комплексного числа представлен как θ + 2 π k.

Главный аргумент комплексного числа определяется как угол, отсчитываемый от положительной действительной оси, принимающий значения в интервале – π ≤ θ ≤ π .

Углы, измеренные от положительной вещественной оси в направлении против часовой стрелки, положительны.

Углы, измеренные от положительной вещественной оси по часовой стрелке, отрицательны.

Положительный угол аргументаОтрицательный угол аргумента

Как найти аргумент комплексного числа

Чтобы вычислить аргумент комплексного числа z=a+bi:

• Сначала вычислите θ=tan ^-1 (b /а).
• Если комплексное число находится в квадранте 1, аргумент равен θ.
• Если комплексное число находится в квадранте 2, аргумент равен π+θ.
• Если комплексное число находится в квадранте 3, аргумент равен θ-π.
• Если комплексное число находится в квадранте 4, аргумент равен θ.

Например, найдите аргумент .

Шаг 1. Сначала вычислите θ=tan ^-1 ( ^b / _a )

‘a’ — размер действительной части числа, а ‘b ’ — размер мнимой части числа.

В комплексном номере:

Поэтому становится и так, .

Шаг 2. Комплексное число находится в квадранте 1 и аргумент равен θ

Поскольку комплексное число находится в квадранте 1 диаграммы Аргана, аргумент равен θ.

Следовательно, .

---

Пример вычисления аргумента комплексного числа в третьем квадранте:

Комплексное число находится в третьем квадранте, как показано на диаграмме Аргана ниже.

Аргумент показан углом θ, который является отрицательным углом, измеряемым по часовой стрелке от положительной действительной оси.

Шаг 1. Сначала вычислите θ=tan ^-1 ( ^b / _a )

‘a’ размер действительная часть числа и ’b ’ — размер мнимой части числа.

В комплексном номере

Поэтому становится и так, .

Шаг 2. Комплексное число находится в квадранте 3, а аргумент равен θ – π

Аргументом является ближайший угол к направлению комплексного числа, отсчитываемый от положительной действительной оси (от верно).

Поскольку комплексное число находится в третьем квадранте, аргумент рассчитывается как θ – № .

и так далее, .

Поэтому аргумент задается .

Аргумент комплексного числа отрицателен, если ближайший угол к направлению комплексного числа от положительной действительной оси равен по часовой стрелке.

Вот еще несколько примеров вычисления аргумента комплексного числа.

Аргумент вычисляется по следующим правилам:

Для комплексного числа угол .

• Если комплексное число находится в квадранте 1, аргумент равен θ.
• Если комплексное число находится в квадранте 2, аргумент равен π+θ.
• Если комплексное число находится в квадранте 3, аргумент равен θ-π.
• Если комплексное число находится в квадранте 4, аргумент равен θ.

Комплексный номер	Квадрант	Расчет θ	900 07 Расчет аргумента
-1-i	3	arctan(-1/-1) = π /4	π /4 – π = -3 π /4
1-√3i	4	арктан(-√3/1) = – π /3	– π /3
3-√3i	4	арктан(-√3/3) = – π /6 901 52	– № /6
1+√2i	1	арктангенс (2/1) = 0,955	0,955
-1+i	2	арктангенс (1/-1) = – π /4	-π /4 + π = 3 π /4

Вот несколько примеров комплексных чисел без действительная часть

• z= i имеет аргумент π /2
• z=- i имеет аргумент – π /2

Эти аргументы нельзя вычислить с помощью арктангенса, так как их действительная составляющая равна нулю.

Любое комплексное число, не имеющее вещественной части, будет лежать на мнимой оси.

Если это положительное комплексное число, то оно будет располагаться на мнимой оси над действительной осью, поэтому его аргумент будет равен π /2.

Если это отрицательное комплексное число, то оно будет расположено на мнимой оси ниже действительной оси, поэтому его аргумент будет равен -π /2.

Модуль и аргумент комплексного числа, записанного в экспоненциальной форме

Для комплексного числа, записанного в экспоненциальной форме как z = Re ^{i φ} , R — модуль, а φ — аргумент. Например, если z = 3e ^{π i} , модуль равен 3, а аргумент равен π .

Экспоненциальная форма комплексного числа — это простой способ просмотра модуля и аргумента.

Модуль — это коэффициент экспоненты перед числом Эйлера.

Аргумент рядом с i в экспоненциальной степени.

Калькулятор модуля и аргумента комплексного числа

Этот калькулятор вычисляет модуль и аргумент комплексного числа.

Просто введите действительную и мнимую части комплексного числа в калькулятор ниже.

То есть для любого комплексного числа , где a — действительная часть, а b — мнимая часть.

Например, в комплексном числе действительная часть равна, а мнимая часть равна -1, потому что есть -1 партия из я .

Аргумент комплексных чисел. Решаемые примеры

В математике комплексные плоскости играют чрезвычайно важную роль. Мы также называем это z-плоскостью, состоящей из взаимно перпендикулярных линий, известных как оси. Действительные числа представлены горизонтальной линией и поэтому известны как действительная ось, тогда как мнимые числа представлены вертикальной линией и поэтому известны как мнимая ось. В основном мы используем комплексные плоскости для представления геометрической интерпретации комплексных чисел. Это похоже на декартову плоскость, которая имеет как действительную, так и мнимую части комплексного числа вместе с осями X и Y. Комплексные числа разветвляются на две основные концепции, т. е. величину и аргумент. Но пока мы сосредоточимся только на аргументе комплексных чисел и изучим его определение, формулы и свойства. 9{2}\] = −1. Комплексные числа называются продолжением одномерных числовых линий. На комплексной плоскости комплексное число, обозначаемое a + bi, обычно представляется в виде точки (a, b). Мы должны отметить, что комплексное число, в котором нет абсолютно никакой действительной части, например -i, -5i и т. д., называется чисто мнимым. Кроме того, комплексное число, не имеющее абсолютно никакой мнимой части, называется действительным числом.

Что такое аргумент комплексных чисел?

Аргумент комплексного числа представляет собой угол, который наклонен от действительной оси к направлению комплексного числа, представленного на комплексной плоскости. Мы можем обозначить его как «θ» или «φ» и измерить в стандартных единицах «радиан».

 

На приведенной выше диаграмме комплексное число обозначено точкой P. Длина OP представляет собой величину или модуль числа, а угол, под которым OP наклонен к положительной вещественной оси, известен как аргумент числа точка P.

 

Как найти аргументы комплексного числа?

Есть несколько шагов, которые необходимо выполнить, если мы хотим найти аргумент комплексного числа. Эти шаги приведены ниже: 

Шаг 1) Сначала мы должны найти как действительные, так и мнимые части комплексного числа, которое нам дано, и обозначить их x и y соответственно. 9{-1}\] сам по себе.

Шаг 4) Окончательное значение вместе с единицей «радиан» является требуемым значением комплексного аргумента для данного комплексного числа.

С помощью этого метода вы теперь узнаете, как узнать аргумент комплексного числа.

 

Аргумент комплексных чисел Примеры

1. Найдите аргумент -1+i и 4-6i

Ответ: Сначала нам нужно найти два комплексных числа в комплексной плоскости. Это облегчит нам определение квадрантов, в которых лежат ангелы, и даст приблизительное представление о величине каждого угла.

 

Для, z = —+i

 

Мы можем видеть, что Аргумент z представляет собой второй квадрант угла, а тангенс представляет собой отношение мнимой части к действительной части, в таком случае −1 . Таким образом, тангенс исходного угла будет равен 1. Запишите значение второго квадранта угла так, чтобы его исходный угол мог иметь тангенс, равный 1. Если исходный угол содержит тангенс, равный 1, то значение исходного угла будет π/4, поэтому угол второго квадранта равен π − π/4 или 3π/4. 9{-1}\](tan π/3)

arg (z) = π/3

Следовательно, аргумент комплексного числа равен π/3 радиан.

 

Комплексные числа

Комплексные числа — это те числа, которые используются для нахождения квадратного корня из отрицательных чисел. Комплексные числа были впервые введены греческим математиком по имени Герой Александрийский, который пытался найти квадратный корень из отрицательных чисел, но не смог его решить. Эта проблема была решена итальянским математиком по имени Джероламо Кардано, который нашел отрицательные корни кубических и квадратичных полиномиальных выражений, используя комплексные числа. Комплексные числа широко используются в научных исследованиях, гидродинамике, квантовой механике и обработке сигналов.

Комплексное число можно определить как сумму мнимого числа и действительного числа. Он записывается как + ib, который можно обозначить через z. Здесь a и b — действительные числа. Говорят, что значение a является действительной частью, которая обозначается Re(z), а b называется мнимой частью, записываемой как Im(z).