Цилиндр — Умскул Учебник
На этой странице вы узнаете
- Как вода в кружке иллюстрирует сечение цилиндра?
- Как лист бумаги превратить в цилиндр?
Что общего у джентльмена 19 века, Вилли Вонка из «Чарли и шоколадная фабрика», Шерлока Холмса в экранизации «Безобразная невеста» и некоторых сценических костюмов? Цилиндр! О нем, вернее о фигуре цилиндра и поговорим в статье.
Понятие цилиндраСейчас мы говорим про мужской головной убор, который был популярен в 19 веке и стал достаточно узнаваем в массовой культуре. Оказывается, в математике также существует цилиндр. И они похожи по форме.
Цилиндр — тело вращения, полученное при вращении прямоугольника вокруг одной из его сторон.
Возможно, для уточнения некоторых терминов вам захочется заглянуть в статью «Тела вращения».
Если посмотреть на форму шляпы, то она действительно будет похожа на геометрическую фигуру. Встретить цилиндр можно и в наше время. Обычная кружка является цилиндром.
Обычная кружка является цилиндром.
Прямая, вокруг которой мы крутили прямоугольник, чтобы получить цилиндр, — это ось цилиндра.
Также, как у Земли есть ось вращения, она есть и у цилиндра.
Наша кружка стоит на круглом дне. Это дно, как и самый верх кружки, будут называться основаниями цилиндра.
Снова посмотрим на стенки кружки. В цилиндре эта поверхность будет называться цилиндрической поверхностью. Ее также могут называть боковой поверхностью цилиндра.
Представим, что наша кружка раскрашена вертикальными линиями. Эти линии будут лежать на цилиндрической поверхности и перпендикулярны основаниям. У них есть название:
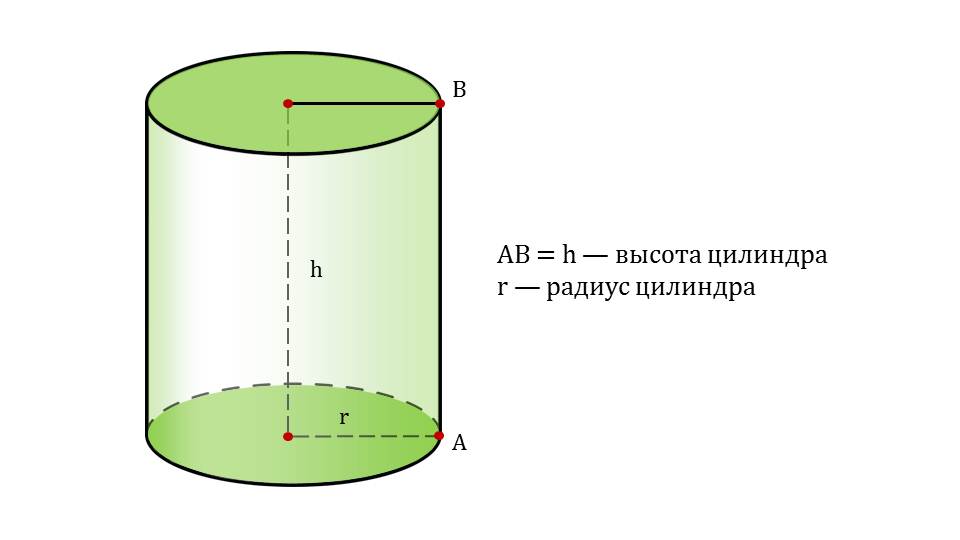
Образующая цилиндра — отрезок, соединяющий точки окружностей основания и перпендикулярный плоскостям оснований.
Все образующие, — а в цилиндре их очень-очень много, —лежат только на цилиндрической поверхности. Эта поверхность и состоит из множества образующих.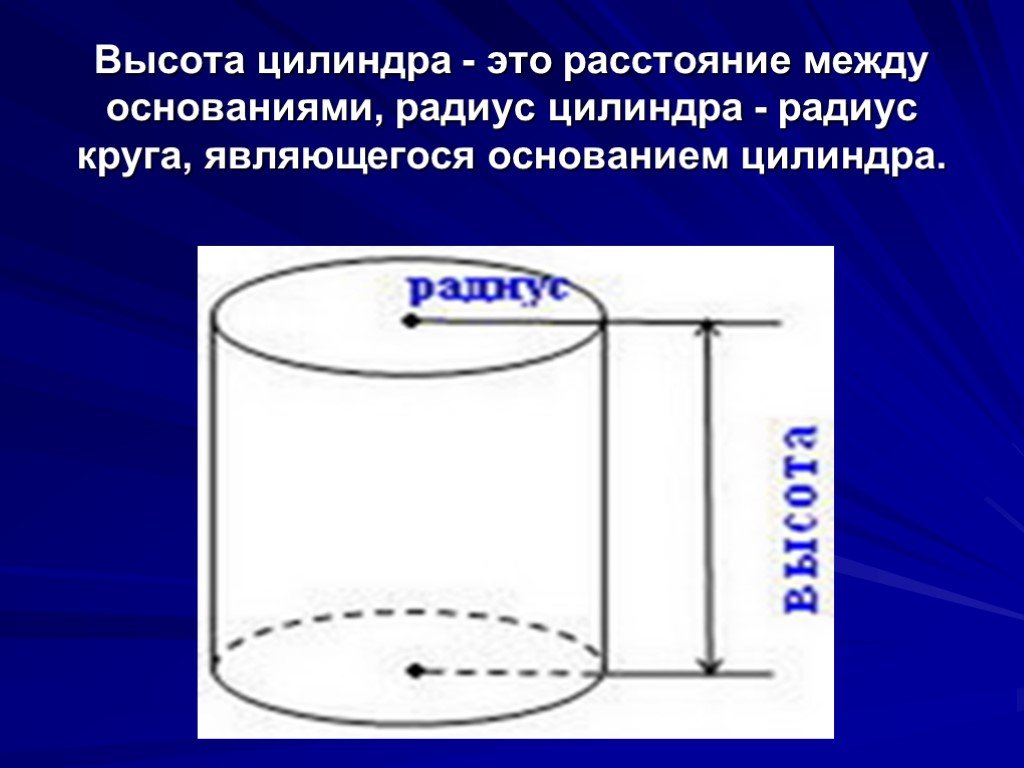
Узнаем ширину кружки. Для этого нужно измерить радиус дна. Этот же радиус будет радиусом основания, а в цилиндре он называется радиусом цилиндра.
Теперь найдем высоту кружки. Для этого нужно измерить расстояние от дна до самого верха кружки.
В математике это будет расстоянием между плоскостями, а ищется оно как длина перпендикуляра, опущенного из одной плоскости на другую. Подробнее про это можно прочесть в статье «Расстояния между фигурами».
Высота цилиндра — перпендикуляр, опущенный из плоскости одного основания на плоскость второго основания.
Свойства цилиндраРассмотрим, какими свойствами обладает цилиндр.
Свойство 1. Основания цилиндра равны и параллельны.
Это всегда два равных круга, лежащих в параллельных плоскостях.
Свойство 2. Образующие цилиндра равны и параллельны.
Поскольку все образующие перпендикулярны основаниям, то они параллельны между собой по свойству прямой и перпендикулярной ей плоскости. Подробнее про это свойство можно прочесть в статье «Углы в пространстве».
Подробнее про это свойство можно прочесть в статье «Углы в пространстве».
А равны они потому, что являются перпендикуляром к основаниям, то есть равны высоте цилиндра.
Свойство 3. Сечение цилиндра, проходящее через ось цилиндра, является прямоугольником. Такое сечение в цилиндре будет называться осевым сечением цилиндра.
Например, если разрезать тортик по диаметру, то место среза как раз будет прямоугольником.
Подробности про сечения фигур можно найти в статье «Сечения».
Свойство 4. Сечение цилиндра, проходящее параллельно оси цилиндра и перпендикулярно его основаниям, будет являться прямоугольником.
Свойство 5. Сечение цилиндра, перпендикулярное оси цилиндра, является кругом с радиусом, равным радиусу цилиндра. Такое сечение в цилиндре называется перпендикулярным сечением цилиндра.
| Как вода в кружке иллюстрирует сечение цилиндра? Если налить в кружку воду, то ее поверхность примет круглую форму. Поскольку поверхность воды параллельна дну кружки, то есть основаниям цилиндра, то она является перпендикулярным сечением цилиндра. Этим опытом можно подтвердить свойство 5. |
Заметим, что все вышеописанные свойства относятся к прямому цилиндру.
Цилиндр также может быть наклонным. В этом случае ось цилиндра и его образующие не будут перпендикулярны основаниям.
Если мы разрежем поверхность цилиндра по одной из его образующих и как бы “развернем” ее, у нас получится прямоугольник.
Это также легко увидеть, если вспомнить художников с тубусами. Тубус имеет форму цилиндра, и свернутый прямоугольный лист принимает такую же форму.
Развертка боковой поверхности цилиндра — прямоугольник, одна сторона которого равна высоте цилиндра, а вторая — длине окружности его основания.
| Как лист бумаги превратить в цилиндр? Поскольку развертка боковой поверхности цилиндра — это прямоугольник, то любой лист бумаги можно превратить в цилиндр. В этой формуле R — радиус цилиндра, Н — высота. Часто формулу объема можно применить для решения жизненных задач. Например, чтобы найти объем детали, погруженной в воду. Пример 1. В цилиндрическом сосуде налито 1650 см3 жидкости. В этот сосуд опустили деталь. При этом уровень жидкости увеличился в 1,2 раза. Найдите объем детали. Ответ выразите в см3. Решение. Шаг 1. Выразим высоту жидкости в первый и второй раз. Пусть вначале уровень жидкости был равен х, значит после того, как в нее опустили деталь, он стал равен 1,2х. Шаг 2. Вспомним физику и заметим, что объем жидкости в сосуде после того, как в него опустили деталь, будет равен сумме объемов жидкости и детали: V = Vж + Vд. Шаг 3. С помощью объема жидкости выразим площадь основания сосуда: Vж = Sосн.H Шаг 4. Подставим площадь основания в формулу объема жидкости после того, как в нее опустили деталь: \(V = S_{осн.}H = \frac{1650}{x} * 1,2x = 1980\) Шаг 5. Тогда объем детали будет равен: Vд = V — Vж Ответ: 330 см3 Фактчек
Задание 1.
Задание 2.
Задание 3.
Задание 4.
Ответы: 1. – 4 2. – 1 3. – 2 4. – 1
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов». Основание пирамиды MABCD — квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD=DM=a. Найдите площадь поверхности пирамиды. Решено основание прямой призмы ромб с острым углом 60градусов.боковое ребро призмы 10см а площадь боковой поверхности 240см в квадрате найдите площадь…В коробке лежат синие,красные и зеленые карандаши.Всего их 22шт. Синих карандашей в 9 раз больше,чем зеленых,а красных меньше ,чем синих.Сколько в Задача: На прошлой неделе Саша прочитал3/7 всей книги, а на этой неделе- половину оставшихся страниц, да еще 20 и дочитал книгу до конца. Сколько Пользуйтесь нашим приложениемКалькулятор высоты цилиндра Этот калькулятор высоты цилиндра быстро находит высоту прямого кругового цилиндра десятью различными способами . Интересно, как найти высоту цилиндра? Просто выберите два известных параметра, введите указанные значения и вычислите высоту. Продолжайте читать, если хотите узнать, какова возможная высота цилиндра. В большинстве случаев вы можете оценить его, зная только две из следующих величин:
Наш калькулятор высоты цилиндра представляет собой удобный инструмент, предназначенный для правильного кругового цилиндра . Этот тип цилиндра состоит из двух конгруэнтных окружностей (называемых основаниями ). Они лежат точно одна над другой, и поэтому мы называем это 9.0003 правый цилиндр. С другой стороны, если одно из оснований сдвинуто, то цилиндр косой . Термин круговой более очевиден — основания имеют форму кругов. Калькулятор отвечает на вопрос как найти высоту цилиндра . Если вы хотите оценить другие параметры, ознакомьтесь с нашим расчетом правильного цилиндра! 92 — \frac{2}{\pi}A_\mathrm{b}}h=d2−π2Ab
Вас интересуют расчеты прямоугольного цилиндра? Вам обязательно нужно проверить калькулятор объема цилиндра и калькулятор площади поверхности цилиндра! Как найти высоту цилиндра Калькулятор высоты цилиндра очень удобен для решения самых разных задач. Иногда вы знаете объем и площадь основания цилиндра, но не знаете его высоту. В другой раз у вас будут указаны только площади поверхности.
Помните, что с помощью калькулятора высоты цилиндра вы можете выбрать единицы измерения любого параметра. Обязательно ознакомьтесь с конвертером длины и инструментами преобразования объема. Они могут быть очень полезны во многих вычислениях. Часто задаваемые вопросыКак найти высоту цилиндра по площади его поверхности?Чтобы найти высоту цилиндра по его общей площади поверхности и радиусу, выполните следующие действия:
Как рассчитать высоту цилиндра по объему и радиусу?Чтобы рассчитать высоту цилиндра по его объему и радиусу, следуйте приведенным инструкциям:
Какова высота цилиндра радиусом 5 см и объемом 900 см³?11,46 см . Формула для расчета высоты цилиндра с учетом его объема и радиуса: высота = объем / (π × радиус²) . Подставляя значения в формулу получаем, высота = 900 см³ / (π × 5 см × 5 см) = 11,46 см Чему равна высота цилиндра, имеющего радиус 8 см и боковую поверхность площадь 1005,5 см²? 20 см . Следовательно, высота цилиндра будет высоты = 1005,5 см² / (2π × 8 см) = 20 см . Калькулятор высоты цилиндра‘ Калькулятор высоты цилиндра ‘ — это бесплатный онлайн-инструмент, который помогает рассчитать высоту цилиндра с заданным радиусом и объемом. Какова высота цилиндра Калькулятор?В калькуляторе высоты цилиндра введите значения радиуса и объема, чтобы найти высоту цилиндра за несколько секунд. Калькулятор высоты цилиндраПРИМЕЧАНИЕ: Введите радиус до трех цифр и объем до пяти цифр. Как пользоваться калькулятором высоты цилиндра?Выполните шаги, указанные ниже, чтобы использовать калькулятор и найти высоту цилиндра:
Как найти высоту цилиндра?Чтобы найти высоту цилиндра, нам нужны входные значения радиуса и объема цилиндра. Объем цилиндра — это вместимость цилиндра или мера занимаемого им пространства. Он рассчитывается по формуле πr 2 h , , где r — радиус круглого основания, h — высота цилиндра, а π(Pi) — математическая константа с приблизительным значением 3.14. Значения радиуса и объема подставляются в формулу для получения объема цилиндра. Таким образом, высота цилиндра рассчитывается по формуле V/ πr 2 . Хотите найти сложные математические решения за считанные секунды? Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами. Записаться на бесплатный пробный урок Решенные примеры расчета высоты цилиндраПример 1: Цилиндр имеет радиус 4 единицы и объем 251,33 куб. . Найдите высоту цилиндра и проверьте ее с помощью калькулятора высоты цилиндра. Решение: Формула для нахождения объема цилиндра = πr 2 ч. Радиус = 4 единицы, объем = 251,33 куб. Итак, подставим значения: Объем цилиндра = πr 2 h высота цилиндра = V/ πr 2 . = 251,33 / 3,14 × 4 2 = 251,33 / 50,24 = 5,002 ед. Следовательно, высота цилиндра = 5,002 единицы. Пример 2: Цилиндр имеет радиус 7 единиц и объем 300 кубических единиц. Найдите высоту цилиндра и проверьте ее с помощью калькулятора высоты цилиндра. Решение: Формула для нахождения объема цилиндра = πr 2 ч. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 При этом совершенно без разницы, сколько воды наливать: поверхность останется кругом.
При этом совершенно без разницы, сколько воды наливать: поверхность останется кругом.  2H\)
2H\)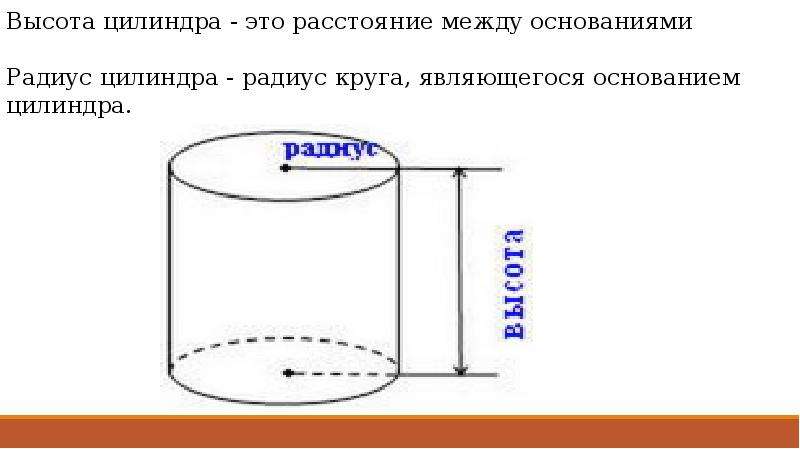 x
x В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра.
В прямом цилиндре образующая равна высоте цилиндра. Образующие равны и параллельны друг другу, а также образуют боковую поверхность цилиндра. 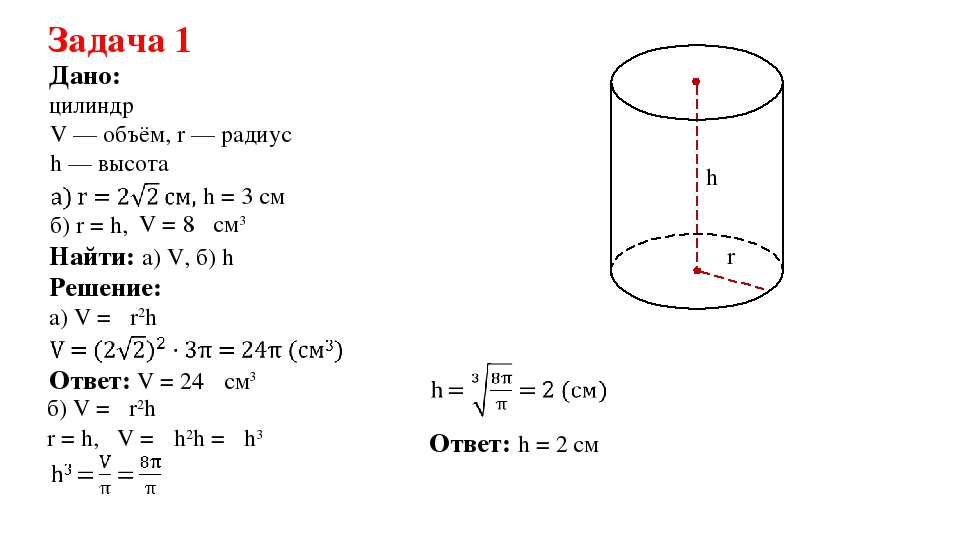
 04.21
04.21 Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше
Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше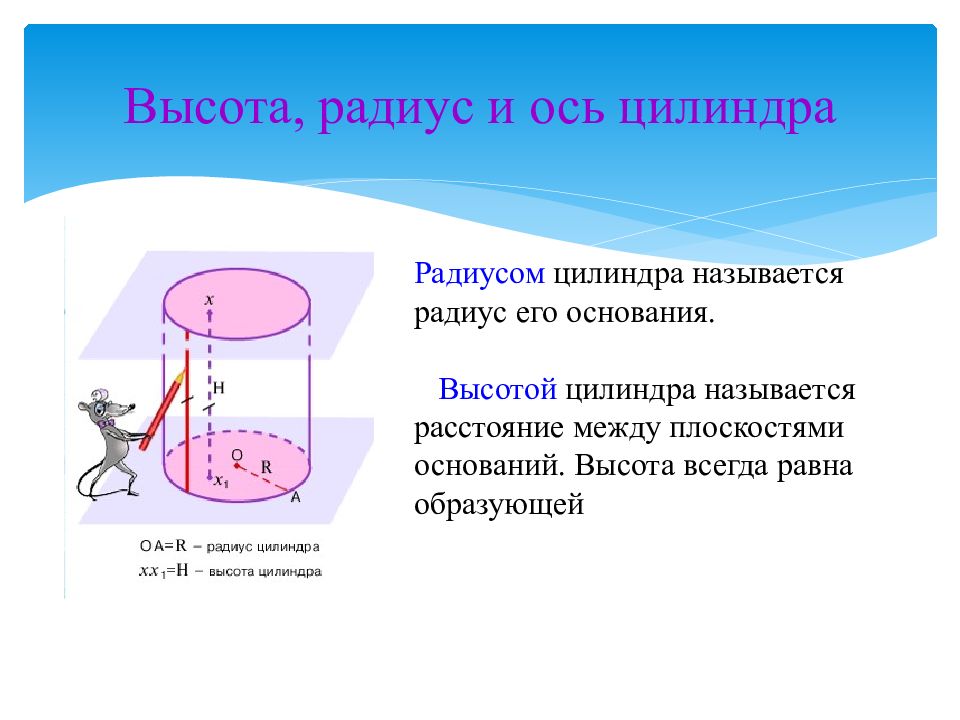
 Вы должны помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр), но обычно мы имеем в виду правильный круговой цилиндр.
Вы должны помнить, что слово цилиндр может соответствовать разным формам (обобщенный цилиндр), но обычно мы имеем в виду правильный круговой цилиндр. Если вы когда-либо сталкивались с такой проблемой, используйте этот калькулятор, чтобы оценить высоту в три простых шага:
Если вы когда-либо сталкивались с такой проблемой, используйте этот калькулятор, чтобы оценить высоту в три простых шага: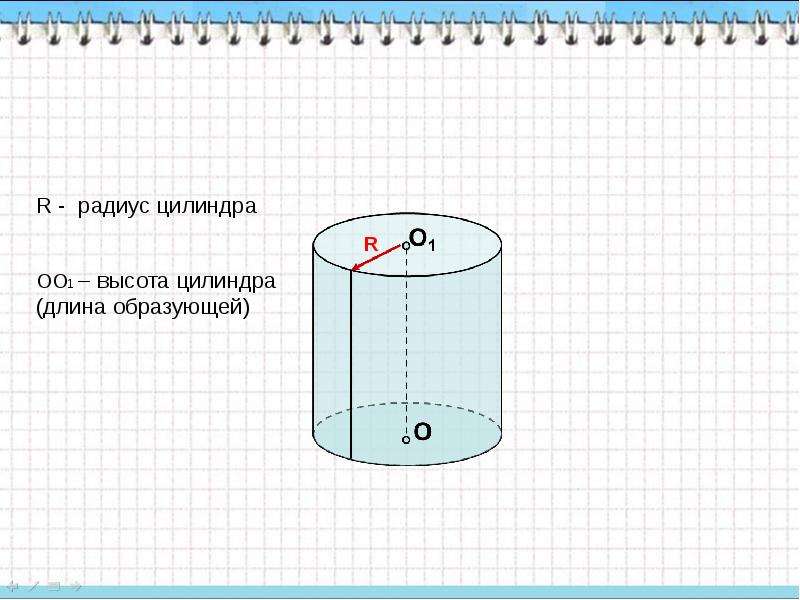
 Для нахождения высоты цилиндра воспользуемся формулой высота = площадь боковой поверхности / (2π × радиус) .
Для нахождения высоты цилиндра воспользуемся формулой высота = площадь боковой поверхности / (2π × радиус) .