Счетные множества — презентация онлайн
1. Лекция 7. Счетные множества
2. Счетные множества
возможно доказать равномощностьпроизвольное множество А
натуральные числа N
Множество А – счетно-бесконечное множество
Способы доказательства
способ, позволяющий
поставить в соответствие
каждому элементу
рассматриваемого множества
А какое-то натуральное число
из множества N
1
методика оценки кардинального
числа множества A сверху и
снизу, что может позволить точно
вычислить реальное значение
мощности исследуемого
множества A
А
N
|A| ≤
2
А
|A| ≥
?..
n
3
א0
א0
=> |A|=
א0
3. Множество целых чисел
– множество, состоящееиз натуральных чисел, числа ноль и чисел,
построенных на основе натуральных только со
знаком «минус» (отрицательных чисел).
Теорема
Множество целых чисел счетно и эффективно
перечислимо.
4.
 ДоказательствоРяд целых чисел: -n, …, -3,-2,-1,0,1,2,3,…, n,…
ДоказательствоРяд целых чисел: -n, …, -3,-2,-1,0,1,2,3,…, n,…Будем обозначать множество целых чисел буквой
Z. Расположим целые числа следующим образом:
0, 1, -1, 2, -2, 3, -3, …., n, -n, …
Тогда каждому числу можно поставить в
соответствие натуральное число
0,
1,
-1, 2,
-2, 3,
…., n, -n, …
1,
2,
3,
4,
5,
6,
…., 2n, 2n+1, …
Таким образом доказано, что множество Z
равномощно множеству N, а значит оно счетно.
5. Доказательство
Для доказательства эффективной перечислимостимножества Z необходимо установить тот факт, что
все элементы множества Z могут быть перебраны по
алгоритму и должны получить в результате такого
перебора порядковые номера, без пропусков и
повторений.
Факт эффективной перечислимости множества Z
напрямую следует из приведенного способа
нумерации элементов натуральными числами. Итак,
множество Z счетно и эффективно перечислимо,
Q.E.D.
6.
 (b=d).
(b=d).Упорядоченную пару элементов обозначают (a,b).
Теорема
Множество упорядоченных пар
натуральных чисел счетно и эффективно
перечислимо.
8. Доказательство
Обычно, употребляя термин «упорядоченная» парасчитают, что допустим пара (1,5) и пара (5,1) имеют
разный смысл и рассматриваются как различные. Чтобы
установить взаимно-однозначное соответствие между
упорядоченными парами натуральных чисел и
натуральными числами, достаточно расположить пары
(p,q) в таблицу так, что (p,q) находится в p-ой строке и в
q-ом столбце.
(1,1) (1,2) (1,3) …
(2,1) (2,2) (2,3) …
…
…
…
Затем указанные пары перечисляются диагональным
методом, начиная с левого верхнего угла.
Последовательность обхода матрицы по сути может быть
любой.
Например, можно расположить пары в последовательность по возрастающей сумме p + q, а
при равной сумме – по возрастанию p. Получим ряд:
n
1
2
3
4
5
6
…
(p,q)
(1,1)
(1,2)
(2,1)
(1,3)
(2,2)
(3,1)
…
Таким образом доказано, что множество упорядоченных пар
натуральных чисел равномощно множеству N, а значит, оно
счетно.

Факт эффективной перечислимости множества упорядоченных
пар натуральных чисел независимо от конкретной трактовки
термина «упорядоченный» представляется вполне очевидным. В
первом случае он напрямую следует из приведенного способа
нумерации элементов натуральными числами. Во втором случае
к предложенному алгоритму перечисления необходимо
добавить процедуру проверки соотношения между элементами p
и q, и если, например, p≤q, то присваивать очередной номер
этой паре, а в противном случае пропускать её. Итак, множество
упорядоченных пар натуральных чисел счетно и эффективно
перечислимо, Q.E.D.
Следствие
Если оперировать трансфинитными числами, то
получим что
א0 • א0 = א0
11. Множество упорядоченных n-ок натуральных чисел
Упорядоченная n-ка натуральных чисел – этонабор из n элементов вида (m1, m2, …, mn), где mi –
натуральное число.
Теорема
Множество упорядоченных n-ок
натуральных чисел счетно и
эффективно перечислимо.

12. Доказательство
Чтобы установить взаимно-однозначноесоответствие между упорядоченными n-ками
натуральных чисел и натуральными числами,
достаточно расположить разложить n-ку вида
(m1, m2, m3,…,mn) следующим образом:
(m1, m2, m3,…,mn) = (m1, (m2, m3,…,mn)) = (m1, (m2,
(m3,…,mn))) = …=(m1, (m2, (m3, (…(mn-1,mn)))))
Расположив по горизонтали таблицы пары
натуральных чисел, а по вертикали – натуральные
числа, диагональным методом получим
нумерацию троек натуральных чисел.
13. Доказательство
Далее по горизонтали таблицы располагаютсятройки натуральных чисел, а по вертикали –
натуральные числа, диагональным методом
получаем нумерацию четверок натуральных чисел
и т.д.
Таким образом доказано, что множество n-ок
натуральных чисел равномощно множеству N, а
значит оно счетно.
Факт эффективной перечислимости множества
напрямую следует из приведенного способа
нумерации элементов натуральными числами.
 (p1+p2+ …+pk -1)
(p1+p2+ …+pk -1)комплексу (2,1,1,1) соответствует следующий код:
p1-1 = 2 -1 = 1
p1+ p2 -1 = 2 + 1 – 1 = 2
p1+ p2 + p3 -1 = 2 + 1 + 1 — 1 = 3
p1+ p2 + p3 + p4 -1 = 2 + 1 + 1 + 1 – 1 = 4
В итоге число n = 0•20 + 1•21 + 1•22 + 1•23 + 1•24 =
=11110 (в двоичном коде) или
2 + 4 + 8 + 16 = 30 ( в десятичном коде).
Таким образом, комплексу (2,1,1,1)
соответствует натуральное число 30.
18. Доказательство
В результате доказано, что множество конечныхкомплексов натуральных чисел равномощно
множеству N, а значит оно счетно.
Факт эффективной перечислимости множества
напрямую следует из приведенного способа
нумерации элементов натуральными числами. Итак,
множество конечных комплексов натуральных чисел
счетно и эффективно перечислимо, Q.E.D.
Если оперировать трансфинитными числами, то
получим:
k
k
א0 + א02 + א03 + … + א0k =
i 1
א0k = א0 = א0 k = א0
i 1
19. Множество рациональных чисел
Рациональное число – число видаn
q
m
, где
n – целое число, m – натуральное число.

Теорема
Множество рациональных чисел счетно и
эффективно перечислимо.
20. Доказательство
Обозначим множество рациональных чисел Q.Рассмотрим сначала положительные рациональные
числа – множество Q+. Определим положительное
рациональное число как q=n/m, где n и m –
натуральные числа.
Запишем их в виде бесконечной матрицы, строки и
столбцы которой пронумерованы натуральными
числами начиная с 1. Элемент, стоящий на
пересечении i-ой строки и j-ого столбца, получит
наименование qij
Используя диагональный метод, перечислим их
(пронумеруем натуральными числами):
21. Доказательство
12
3
4
1
q11
q12
q13
q14
…
2
q21
q22
q23
q24
…
3
q31
q32
q33
q34
…
…………………………….………
n
qn1 qn2……………….……
………………………..……..……
q11 q21 q12 q13 q22 q31 q41 q32 q23 q14 q15 q24 q33
1
2
3
4
5
6 7
8
9
22.
 ДоказательствоВсе (и положительные, и отрицательные) рациональные
ДоказательствоВсе (и положительные, и отрицательные) рациональныечисла в совокупности перечисляются по аналогии с целыми
числами, путем чередования положительной дроби и её
отрицательного аналога. При этом некоторые рациональные
числа мы нумеруем по нескольку раз: например, 1 будет
пронумерована как 1/1, 2/2, и т.д., а например 4/5 как 8/10,
12/15 и т.д.
Т.о. показано, что множество рациональных чисел не
превосходит по мощности множество натуральных чисел,
|Q|≤|N|, т.к. каждое рациональное число получит
соответствующий номер, а если быть точным – то даже
несколько номеров. С другой стороны то, что множество
натуральных чисел не превосходит по мощности множество
рациональных чисел очевидно, |N|≤|Q| (хотя бы потому, что
оно является его подмножеством). Т.о. доказано, что
множество рациональных чисел равномощно множеству
натуральных чисел |Q|=|N| = À0, а значит оно счетно.
23. Доказательство
Факт эффективной перечислимости множества Qнапрямую следует из приведенного способа
нумерации элементов натуральными числами.
 В ходе
В ходеэтой нумерации каждое рациональное число
получает соответствующий номер, и если к алгоритму
добавить процедуру, проверяющую дробь на предмет
сокращаемости (если числитель и знаменатель имеют
общие делители) и исключающую из нумерации
сокращаемые дроби, то мы в чистом виде получим
перечисление рациональных чисел по алгоритму без
пропусков и повторений, что совпадает с
определением эффективной перечислимости.
Итак, множество рациональных чисел счетно
и эффективно перечислимо, Q.E.D.
24. Действительные алгебраические числа
Алгебраическоедействительное
число
–
действительный корень алгебраического уравнения
ненулевой
степени
с
рациональными
коэффициентами.
Общий вид такого уравнения для одной переменной:
a0+a1∙x1+a2∙x2+…+an∙xn=0,
где a0, a1,… – рациональные коэффициенты.
Теорема
Множество алгебраических чисел счетно
и эффективно перечислимо.
25. Доказательство
Предложим процедуру нумерации всехалгебраических чисел числами натурального ряда.

При этом каждое число будем задавать через
образующее его алгебраическое уравнение:
для линейных уравнений будем иметь
упорядоченные пары рациональных чисел
для квадратных уравнений – тройки,
в общем случае получаем
упорядоченную n-ку рациональных чисел:
(ai1,ai2, …, ain) для каждого i-ого алгебраического
уравнения (n-1)-ой степени.
Располагать элементы будем в двусторонне
бесконечной матрице.
26. Доказательство
Выпишем на первой строке будущей матрицы всеупорядоченные пары рациональных чисел.
Это возможно, т.к. пары рациональных чисел
эффективно перечислимы (рациональные числа
эффективно перечисляются, их можно записать в
матрицу и перечислить пары чисел диагональным
способом). Такие пары рациональных чисел
соответствуют линейным уравнениям и имеют по
одному корню.
Т.о. каждая пара однозначно определяет корень
линейного уравнения.
27. Доказательство
На второй строке выпишем все упорядоченные тройкирациональных чисел.

Это возможно, т.к. тройки рациональных чисел
эффективно перечислимы (рациональные числа
эффективно перечисляются, их пары тоже эффективно
перечисляются, значит можно записать в матрицу по
строкам пары, по столбцам числа и перечислить
тройки чисел диагональным способом).
Такие тройки соответствуют квадратным уравнениям и
имеют максимум по два корня: таким образом, в
процессе формирования матрицы каждую тройку
рациональных чисел нужно будет повторить два раза
для обеспечения процесса получения
соответствующего номера для двух чисел, являющихся
решением каждого уравнения.
28. Доказательство
На третьей строке – по три числа на каждое кубическоеуравнение соотв. упорядоченным четверкам и т.д.
Т.о. получим матрицу, которую можно обойти при
помощи диагонального процесса Кантора.
Если часть корней алгебраического уравнения
комплексная, при нумерации их просто пропускаем.
Т.о. каждое алгебраическое число получит
соответствующий номер, и это подтверждает тот факт,
что множество алгебраических действительных чисел
счетно.

29. Доказательство
Факт эффективной перечислимости множества Анапрямую следует из приведенного способа
нумерации элементов натуральными числами, т.к.
попутно указана эффективная процедура нумерации
наборов рациональных чисел, однозначно задающих
алгебраические уравнения соответствующей степени.
При этом важно то, что алгебраическое уравнение
n-ой степени имеет эффективный алгоритм решения,
т.о. процедура полностью эффективна.
Итак, множество алгебраических действительных
чисел счетно и эффективно перечислимо, Q.E.D.
30. Счетные числовые множества: обобщение
Теорема (без доказательства)Множество элементов, которые можно
представить с помощью конечного числа
счетной системы знаков, счетно.
Счетно-бесконечными являются, например:
множество «слов», которое можно составить при
помощи конечного алфавита («слово» здесь комплекс букв, не важно имеющих смысл или
нет),
множество всех книг, которые можно написать
на любом или даже на всех языках,
множество всех симфоний, которые можно
сочинить и т.
 д.
д.МНОЖЕСТВ ТЕОРИЯ | Новая философская энциклопедия | Онлайн словари по философии
МНОЖЕСТВ ТЕОРИЯ – учение о множествах Г.Кантора – наука, зародившаяся в середине 19 в. и изучающая свойства множеств произвольной природы. Создание теории множеств было подготовлено работами математиков 19 в., ставившими целью разработку оснований анализа. Первые работы в этой области были посвящены числовым множествам и множествам функций (Б.Больцано, Р. Дедекинд). Уже в этих работах ставился вопрос о количественном сравнении бесконечных множеств: существуют ли различные ступени математической бесконечности, бесконечные множества разной мощности? В 1871–83 Г.Кантор сделал решительный шаг, изучив множества произвольных элементов, и дал почти современное изложение теории кардинальных и ординальных чисел и теории вполне упорядоченных множеств. Он ввел понятие сравнения двух множеств, опирающееся на понятие взаимнооднозначного их соответствия. Выяснилось, что существует бесконечная шкала неравномощных множеств (напр. , множество натуральных чисел и множество действительных чисел имеют разные мощности). В отмеченном цикле работ 1871–83 Кантор предложил носящую его имя теорию действительных чисел, доказал счетность множества действительных алгебраических чисел и несчетность континуума, ввел общее понятие мощности, доказал равномощность континуумов разного числа измерений и высказал континуум-гипотезу; ввел различные классы точечных множеств, определил операции пересечения и суммирования множеств, провел различение кардинальных и ординальных чисел и их обобщение на трансфиниты. Наконец, в 1895–97 Кантор дал систематизированное изложение своих трудов и положил теорию множеств в фундамент всей математики.
, множество натуральных чисел и множество действительных чисел имеют разные мощности). В отмеченном цикле работ 1871–83 Кантор предложил носящую его имя теорию действительных чисел, доказал счетность множества действительных алгебраических чисел и несчетность континуума, ввел общее понятие мощности, доказал равномощность континуумов разного числа измерений и высказал континуум-гипотезу; ввел различные классы точечных множеств, определил операции пересечения и суммирования множеств, провел различение кардинальных и ординальных чисел и их обобщение на трансфиниты. Наконец, в 1895–97 Кантор дал систематизированное изложение своих трудов и положил теорию множеств в фундамент всей математики.
В теории Кантора понятие множества не определяется, а лишь поясняется на примерах (множество всех четных натуральных чисел, множество всех натуральных решений данного алгебраического уравнения и т.д.). Множество считается заданным, если указано характеристическое свойство его элементов. Основное отношение– принадлежность одного множества другому. Общность понятия «множество» дала возможность применять его в любой математической области, и практически вся математика использует язык теории множеств. Однако самому Кантору шаг обобщения дался трудно, и его идеи были встречены современниками по-разному: Р.Дедекинд и Д.Гильберт признали выдающееся значение теории множеств, в то время как Л.Кронекер был ее убежденным противником. Широкое признание учение Кантора получило на I Международном конгрессе математиков в Цюрихе, в 1897. Однако в это же время в теории множеств обнаружились противоречия, открытие которых (Г.Кантор, С.Бурали-Форти, Б.Рассел) потрясло все основание математики. Кризис этот продолжается и в настоящее время. Но стоит отметить, что противоречия возникают на самых «верхних этажах» иерархии множеств, когда мы образуем «множество всех множеств», или «множество всех порядковых чисел», или «множество всех множеств, не являющихся элементами самих себя» и т.д. Т.о., «наивная» теория множеств, т.е. в том виде, как ее создал Кантор, не может быть использована в полном объеме.
Общность понятия «множество» дала возможность применять его в любой математической области, и практически вся математика использует язык теории множеств. Однако самому Кантору шаг обобщения дался трудно, и его идеи были встречены современниками по-разному: Р.Дедекинд и Д.Гильберт признали выдающееся значение теории множеств, в то время как Л.Кронекер был ее убежденным противником. Широкое признание учение Кантора получило на I Международном конгрессе математиков в Цюрихе, в 1897. Однако в это же время в теории множеств обнаружились противоречия, открытие которых (Г.Кантор, С.Бурали-Форти, Б.Рассел) потрясло все основание математики. Кризис этот продолжается и в настоящее время. Но стоит отметить, что противоречия возникают на самых «верхних этажах» иерархии множеств, когда мы образуем «множество всех множеств», или «множество всех порядковых чисел», или «множество всех множеств, не являющихся элементами самих себя» и т.д. Т.о., «наивная» теория множеств, т.е. в том виде, как ее создал Кантор, не может быть использована в полном объеме. С одной стороны, несмотря на противоречивость, ею продолжали пользоваться в различных областях математики (как языком, удобным для изложения предмета). С другой стороны, необходимо было исправить существующее положение дел. Были предложены различные выходы из создавшейся ситуации, но их пришлось признать в конечном итоге неудовлетворительными. Кратко эти попытки «ремонта» теории множеств резюмируются в характеристике трех основных течений, сложившихся в основаниях математики: логицизма, интуиционизма и формализма. С точки зрения логицизма математика – отрасль логики. Определения и теоремы математики следует давать и доказывать в терминах логических понятий. Приспосабливая логицистическое построение математики к открытиям противоречий, Рассел с помощью разветвленной теории типов исключил непредикативные определения. Однако Рассел не смог обойтись без аксиомы сводимости, утверждающей, что для каждого ненулевого свойства высшего порядка найдется равнообъемное свойство порядка ноль. К числу наиболее современных работ относится работа В.
С одной стороны, несмотря на противоречивость, ею продолжали пользоваться в различных областях математики (как языком, удобным для изложения предмета). С другой стороны, необходимо было исправить существующее положение дел. Были предложены различные выходы из создавшейся ситуации, но их пришлось признать в конечном итоге неудовлетворительными. Кратко эти попытки «ремонта» теории множеств резюмируются в характеристике трех основных течений, сложившихся в основаниях математики: логицизма, интуиционизма и формализма. С точки зрения логицизма математика – отрасль логики. Определения и теоремы математики следует давать и доказывать в терминах логических понятий. Приспосабливая логицистическое построение математики к открытиям противоречий, Рассел с помощью разветвленной теории типов исключил непредикативные определения. Однако Рассел не смог обойтись без аксиомы сводимости, утверждающей, что для каждого ненулевого свойства высшего порядка найдется равнообъемное свойство порядка ноль. К числу наиболее современных работ относится работа В.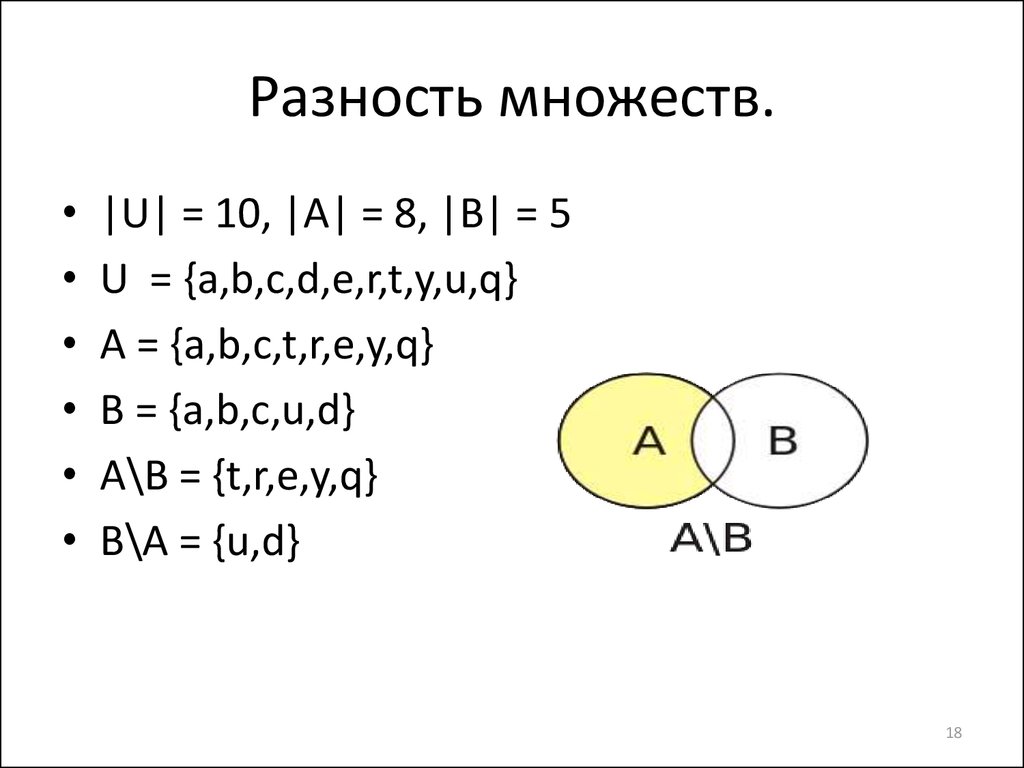 Куайна (W. Quine), предложившего бестиповую аксиоматическую систему теории множеств (конечноаксиоматизируемую) с ограничением на схему аксиом свертывания ∃x ∀ у(у ∊ x ⇔ φ(y)), где φ – стратифицируемая формула, т.е. формула, получающаяся из формулы языка теории типов «стиранием» типов (в системе Куайна существует, напр., множество всех множеств). Логицизм не смог конструктивным путем достичь своей цели.
Куайна (W. Quine), предложившего бестиповую аксиоматическую систему теории множеств (конечноаксиоматизируемую) с ограничением на схему аксиом свертывания ∃x ∀ у(у ∊ x ⇔ φ(y)), где φ – стратифицируемая формула, т.е. формула, получающаяся из формулы языка теории типов «стиранием» типов (в системе Куайна существует, напр., множество всех множеств). Логицизм не смог конструктивным путем достичь своей цели.
В интуиционистской математике Л.Брауэр (L.Brouwer) ограничил использование исключенного третьего закона и ввел новую трактовку логических связок и кванторов. Была построена новая математика, включая теорию континуума. Однако эта другая математика в корне отличалась от той, которая развивалась в течение почти трех тысяч лет. Этот путь также оказался далек от решения вопроса обоснования математики.
Наконец, выход был предложен Д.Гильбертом в виде «финитной установки» (см. Финитизм), однако и этот путь оказался неудовлетворительным. Тем не менее именно на этом пути были сделаны, может быть, самые плодотворные и приемлемые для большинства математиков попытки преодолеть кризис. В 1904–08 Э.Цермело (Е.Zermelo) предложил первую систему аксиом, которой оказалось достаточно, чтобы получить все важные для математики результаты и в которой не получалось ни одно из известных противоречий. В настоящее время существуют несколько общепринятых систем аксиоматической теории множеств, из которых наиболее известной является система Цермело–Френкеля. К последней часто добавляют аксиому выбора, которая носит крайне неконструктивный характер и утверждает существование функции выбора для любого семейства непустых попарно дизъюнктных множеств (формулировка впервые дана Цермело в 1904, и он использовал аксиому выбора для доказательства теоремы о возможности вполне упорядочения любого множества). Попытки доказать или опровергнуть аксиому выбора в рамках системы Цермело–Френкеля оказались тщетными (в 1940 К.Гедель доказал, что аксиома выбора совместна с этой системой (при условии непротиворечивости последней)), а в 1963 П.Коэн (Р.Cohen) доказал совместность отрицания аксиомы выбора с системой (при том же условии непротиворечивости последней).
В 1904–08 Э.Цермело (Е.Zermelo) предложил первую систему аксиом, которой оказалось достаточно, чтобы получить все важные для математики результаты и в которой не получалось ни одно из известных противоречий. В настоящее время существуют несколько общепринятых систем аксиоматической теории множеств, из которых наиболее известной является система Цермело–Френкеля. К последней часто добавляют аксиому выбора, которая носит крайне неконструктивный характер и утверждает существование функции выбора для любого семейства непустых попарно дизъюнктных множеств (формулировка впервые дана Цермело в 1904, и он использовал аксиому выбора для доказательства теоремы о возможности вполне упорядочения любого множества). Попытки доказать или опровергнуть аксиому выбора в рамках системы Цермело–Френкеля оказались тщетными (в 1940 К.Гедель доказал, что аксиома выбора совместна с этой системой (при условии непротиворечивости последней)), а в 1963 П.Коэн (Р.Cohen) доказал совместность отрицания аксиомы выбора с системой (при том же условии непротиворечивости последней). Т.о., одной из попыток выхода из кризиса явилось создание аксиоматической теории множеств, которая занимается изучением фрагментов «наивной» теории множеств, применяя методы математической логики. Для ряда существующих систем аксиоматической теории множеств характерно ограничение схемы аксиом свертывания так, чтобы избежать возникновения противоречий. Это системы Цермело и Цермело–Френкеля. Другой ряд систем характеризуется тем, что в них противоречия устраняются как следствия непредикативных определений. Пример – теория типов Рассела. Наконец, ряд систем преследуют специфические цели (конечность числа аксиом, нестандартные логические средства вывода и т.д.). Это системы Неймана–Геделя–Бернайса, Куайна и появившиеся за последние 25 лет системы, основанные на неклассических логиках (в первую очередь – на интуиционистской логике).
Т.о., одной из попыток выхода из кризиса явилось создание аксиоматической теории множеств, которая занимается изучением фрагментов «наивной» теории множеств, применяя методы математической логики. Для ряда существующих систем аксиоматической теории множеств характерно ограничение схемы аксиом свертывания так, чтобы избежать возникновения противоречий. Это системы Цермело и Цермело–Френкеля. Другой ряд систем характеризуется тем, что в них противоречия устраняются как следствия непредикативных определений. Пример – теория типов Рассела. Наконец, ряд систем преследуют специфические цели (конечность числа аксиом, нестандартные логические средства вывода и т.д.). Это системы Неймана–Геделя–Бернайса, Куайна и появившиеся за последние 25 лет системы, основанные на неклассических логиках (в первую очередь – на интуиционистской логике).
Аксиоматический подход позволил решить ряд вопросов о соотношении различных аксиоматических систем теории множеств, придать точный смысл вопросам неразрешимости ряда математических проблем (континуум-проблемы, в частности), решить некоторые трудные классические проблемы топологии, теории кардинальных и ординальных чисел. Тем не менее вопрос о непротиворечивости всех этих систем остается открытым.
Тем не менее вопрос о непротиворечивости всех этих систем остается открытым.
Тесная связь между теорией множеств и философией математики породила много вопросов о природе противоречий и аксиоматизации этой теории. Во взглядах на то, как можно было бы удовлетворительно обосновать теорию множеств, имеются большие расхождения. Но подавляющее число математиков продолжают с успехом применять понятия, методы и результаты этой теории в большинстве разделов математики и твердо верят в то, что усилия по устранению противоречий приведут к ее реабилитации. «Эта позиция отнюдь не исключает готовности интерпретировать теорию множеств совсем не так, как это обычно делается, что соответствует, очевидно, существующей потребности в пересмотре интерпретации логики и математики вообще» (Френкель Α., Бар-Хиллел И. Основания теории множеств. М., 1966, с. 416).
Литература:
1. Хаудорф Ф. Теория множеств. М. – Л., 1937;
2. Бурбаки Н. Теория множеств. М., 1965;
3. Коэн П.Дж. Теория множеств и континуум-гипотеза. М., 1969;
М., 1969;
4. Куратовский К., Мостовский А. Теория множеств. М., 1970;
5. Йех Т. Теория множеств и метод форсинга. М., 1973;
6. Александров П.С. Введение в теорию множеств и общую топологию. М., 1977;
7. Кантор Г. Труды по теории множеств. М., 1985.
В.X.Хаханян
наборов монет США | 1936-Дата
- АПМЕКС
- Редкие монеты США
- Наборы нумизматических монет США
- Наборы пробных монет США (с 1936 г. по дату)
Пробные наборы США (1968-Дата)
Пробные наборы США (1936–1964)
Наборы Quarter Proof (с 1999 г. )
)
Пробные наборы президентских долларов (дата 2007 г.)
Серебряные пробные наборы (1992-дата)
Смотреть больше категорий
Наборы Silver Quarter Proof (дата 1999 г.)
Наборы Premier Silver Proof (1992–1998)
Престижные пробные наборы Монетного двора США (1983–1997 гг.
См. меньше категорий
APMEX предлагает великолепный выбор наборов Proof, выпущенных с 1936 года по настоящее время. Наборы пруфов — популярный выбор для любого энтузиаста монет. Наша обширная коллекция наборов Proof, которую легко найти и, как правило, доступна по цене, восходит к 1930-м годам и включает большинство лет до настоящего времени. У нас есть несколько труднодоступных наборов серебряных монет и наборов президентских монет, чтобы завершить вашу коллекцию.
Купить наборы пробных монет онлайн
Все наши наборы Proof поставляются в оригинальной упаковке и всегда пользовались популярностью у коллекционеров благодаря своему высокому качеству и красоте. Эти превосходные пробные наборы повысят ценность вашей коллекции.
История крупной валюты США
Зачем мне собирать валюту?
Почему цены на бумажные валюты выше, чем на слитки
Узнайте больше о драгоценных металлах
Покупка драгоценных металлов не должна вас пугать. Независимо от того, делаете ли вы долгосрочные инвестиции или просто восхищаетесь красотой драгоценных металлов, APMEX предоставляет инструменты, которые помогут вам сделать лучший выбор для вашего портфеля.
Посмотреть все статьи
U. S. Proof Sets
| U. S. Proof Sets | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Date/Description | Price | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1951 Proof Set | $630. 00 00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1968 Proof Set | $10.10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1969 Proof Set | 10,10 $ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1970 Proof Set | 15,60 $ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1970 SD Proof Set | $104.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1971 Proof Set | $5.60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1972 Proof Set | $5.60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1974 Proof Set | $13.10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1975 Proof Установка | $ 15.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1976 Доказательство Набор | $ 11,90 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1976 3 ПК ПРЕЗОШЕНИЯ | $ 27.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $ 27.00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $ 27.00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1977 Proof Set | $10.10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1979 Proof Set | $10. 50 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1979 T2 Proof Set | $57.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1980 Proof Set | $6.80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1981 Proof Set | $ 6,80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1982 ПРЕЗИДЕНИЯ | $ 6,80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1983 Доказательство | $ 9.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1984. КОРИТЕЛЬНЫЕ СТАТА | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1984.0059 | $7.50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1985 Proof Set | $6.80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1986 Proof Set | $7.50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1988 Proof Set | $6.40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1989 Proof Set | $6.40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1990 ПРЕЗОШЕНИЯ | $ 6,40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1991 Доказательство | $ 6,40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1992 ПРЕЗОШЕНИЕ | $ 6. 6059 6059 | 1992 ПРЕЗОШЕНИЯ | $ 6.609 | 0059 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1992 Silver Proof Set | $22.95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1992 Premium Silver Proof Set | $26.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1993 Proof Set | $6.80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1993 Silver Proof Set | $31.95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Набор пробных проб 1993 года премиум-класса | 29,40 $ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Набор пробных проб 1994 года | Набор пробных проб 1994 года 6,80 долларов США | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 059 | $30.95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1994 Premium Silver Proof Set | $28.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1995 Proof Set | $12.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1995 Silver Proof Set | $59. 95 95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1995 Premium Silver Proof Set | $ 58,80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1996 ПРЕЗИДЕНИЯ | $ 11.30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1996 СВЕЙСТВЕННЫЙ ПРЕДОСТАВЛЯ0062 1997 Proof Set | $11.30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1997 Silver Proof Set | $36.95 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1997 Premium Silver Proof Set | $36.40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1998 Proof Set | $12.80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1998 Silver Proof Set | 27,95 $ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1998 Premium Silver Proof Set | $ 26,00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1999 Silver Proof Set | $103.60 | ||
| 1999 5 Pc Proof Set | $5. 60 60 | ||
| 2000 Proof Set | $9.00 | ||
| 2000 Silver Proof Set | $48.95 | ||
| 2001 Proof Set | $ 13,50 | ||
| 2001 Серебряный набор Presect | $ 48,95 | ||
| 2001 5PC ПРЕДОСТАВЛЯЕТСЯ | $ 6,009 | 2001 5PC.0059 | |
| 2002 Proof Set | $9.80 | ||
| 2002 Silver Proof Set | $48.95 | ||
| 2002 5pc Proof Set | $7.10 | ||
| 2003 Proof Set | $9.00 | ||
| Серебряный пробный набор 2003 | 48,95 $ | ||
| 2004 Пробный набор | 13,50 $ | ||
| 2004 Серебряный пробный набор | 9004 9095 9095 $5 | ||
| 2004 5pc Proof Set | $6.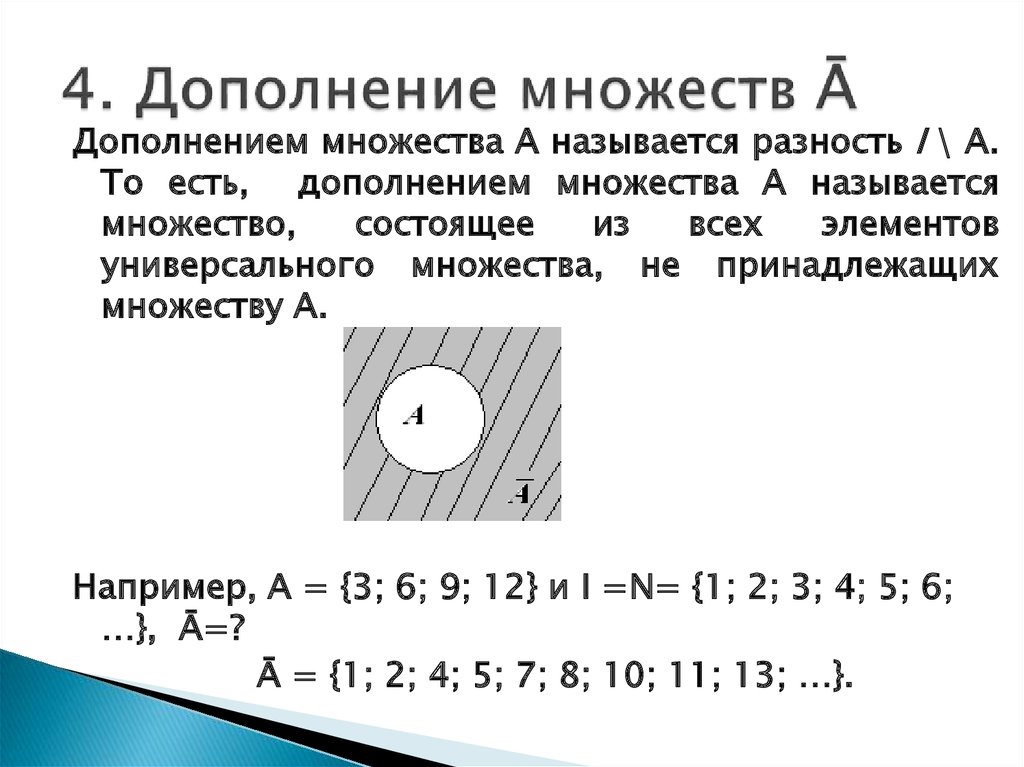 40 40 | ||
| 2004 5pc Silver Proof Set | $34.95 | ||
| 2005 Proof Set | $8.30 | ||
| 2005 Silver Proof Set | $48.95 | ||
| 2005 5pc Silver Presessing Set | $ 34,95 | ||
| 2006 Доказательство Набор | $ 10.50 | ||
| 2006 СЕРИОНСКИЕ ПРЕЗОШЕНИЯ | |||
| 2006 СЕРИНГА. | $48.95 | ||
| 2006 5pc Silver Proof Set | $34.95 | ||
| 2007 Proof Set | $21.00 | ||
| 2007 Silver Proof Set | $54.95 | ||
| 2007 5pc Proof Set | 9,00 $ | ||
| 2007 5 шт. Silver Proof Set | $34,95 | ||
2007 4 шт. 0062 2008 Proof Set 0062 2008 Proof Set | $36.00 | ||
| 2008 Silver Proof Set | $59.95 | ||
| 2008 5pc Proof Set | $18.00 | ||
| 2008 5pc Silver Proof Set | $34.95 | ||
| 2008 Набор из 4 проб $ | |||
| 2009 Proof Set | 34,50 $ | ||
| 94 2009 9075 2996 Silver Proof Set | |||
| 2009 6PC PROUSION SET | $ 7,50 | ||
| 2009 6p Silver Pression | $ 40,95 | ||
| 2009 4PC PREAL $ 50059 | |||
| 2009 4PC PREACT $ 00059 | |||
| 2009 4PC. | $ 18,00 | ||
| 2010 ПРЕЗИДЕНИЯ | $ 44,80 | ||
| 2010 Серебряный доказательство | $ 64. 95 95 | ||
| 2010 5PCET SOTE | |||
| 2010 5PC.0059 | $16.80 | ||
| 2010 5pc Silver Proof Set | $34.95 | ||
| 2010 4pc Pres $ Proof Set | $19.20 | ||
| 2011 Proof Set | $44.80 | ||
| 2011 Silver Proof Set | $69.95 | ||
| 2011 5pc Proof Set | $17.60 | ||
| 2011 5pc Silver Proof Set | $34.95 | ||
| 2011 4pc Pres $ Proof Set | $36.80 | ||
| 2012 Proof Set | $144.00 | ||
| 2012 Silver Proof Set | $225.00 | ||
| 2012 5pc Proof Set | $20.00 | ||
| 2012 5pc Silver Proof Proof Set | $ 49,95 | ||
| 2012 4PC PRES $ PROPEAL SET | $ 80,00 | ||
| 2013 ПРЕЗОШЕНИЕ | 2013 ПРЕЗИДЕНИ0059 | ||
| 2013 Silver Proof Set | $79. 95 95 | ||
| 2013 5pc Proof Set | $17.60 | ||
| 2013 5pc Silver Proof Set | $34.95 | ||
| 2013 4pc Pres $ Proof Set | 17,60 долл. США | ||
| 2014 ПРЕЗОПАССКОЕ УСТАНОВКИ | $ 48,00 | ||
| 2014 Серебряный набор Proof | $ 69,95 | ||
| 2014. | $19.20 | ||
| 2014 5pc Silver Proof Set | $34.95 | ||
| 2014 4pc Pres $ Proof Set | $19.20 | ||
| 2015 Proof Set | $56.00 | ||
| 2015 Silver Proof Set | $ 69,95 | ||
| 2015 5PC PROUSION SET | $ 16.00 | ||
| 2015 5PC Silver Presession | $ 34,95 | ||
| $ 34,95 | |||
| $ 34,95 | |||
| $ 34,95 | |||
| $ 34,95 | |||
| $ 34,95 | |||
| 0062 2016 Proof Set | $75. 00 00 | ||
| 2016 Silver Proof Set | $79.95 | ||
| 2016 5pc Proof Set | $18.00 | ||
| 2016 5pc Silver Proof Set | $39.95 | ||
| 2017 Доказательство набора | $ 59,50 | ||
| 2017 Silver Presessing Set | $ 75,00 | ||
| 2017 5pc Pression Set | $ 18.70 | 9.0060||
| 2017 5pc Silver Proof Set | $39.95 | ||
| 2018 Silver Proof Set | $75.00 | ||
| 2018 5pc Proof Set | $25.00 | ||
| 2018 5pc Silver Proof Set | $42.95 | ||
| 2019 ПРЕЗОПАСНОСТЬ | $ 30.00 | ||
| 2019 Инноизонт $ Proof Set | $ 33. |
