Построение графика функции — презентация онлайн
Похожие презентации:
График функции
Применение производной к исследованию функции и построению графика функции
Функция арифметического квадратного корня, её свойства и график
Обратная пропорциональность. График функции
Функция корень из х. Ее свойства и график
Построение графика квадратичной функции
Функция у=кх², её свойства и график
Исследование функции. Построение графиков
Построение графика функции
Построение графиков кусочных функций
Тема:
Как построить график
функции у=f(х+l),
если известен график
функции у=f(х).
у
Сдвиг на 2
единицы вправо
вдоль оси х
у=х²
Постройте
график
функции:
у=(х-2)²
у=х²
х=2
9
4
-2
у=(х-2)²
1
-3 -2 -1 0
х 0
0 11
У 4
0 11
22
04
1 2 3 4 5
33
19
-1
4
41
х
5-2 -1
-3
94 99
х=-4
у
9
Сдвиг на 4
единицы
влево
вдоль оси х
4
у=(х+4)²
+4
1
Постройте -7 -6 -5 -4 -3 -2 -1 0
график
функции:
х
у=(х+4)²
-1
У 9
-2 -3
4 1
1 2 3
х
-4 -5 -6 -7
0 1
4 9
АЛГОРИТМ 1.

Чтобы построить график функции
y=f(x + l), где l – заданное положительное
число, нужно сдвинуть график функции
y=f(x) вдоль оси х на l единиц масштаба
влево.
Чтобы построить график функции
y=f(x-l), где l – заданное положительное
число, нужно сдвинуть график функции
y=f(x) вдоль оси х на l единиц масштаба
вправо.
Постройте графики функций:
1
у
х 1
4
у
х 3
2
у
х 3
3
у
х 2
у
42
у у
х3
1
х
у
х
5
4
3
2
1
1 3
у y
х 1х
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
3
у
х 2
2
у
4
yх 3
х
Для вывода на экран построений, нужно сделать клики на соответствующих
прямоугольниках (4 раза на каждом)
х
АЛГОРИТМ 2 (экономичный).
Чтобы построить график функции
y=f(x+m) нужно:
1. Перейти к вспомогательной системе
координат, проведя пунктиром
вспомогательные прямые х= -m, y=0, т.
 е.
е.выбрав в качестве начала новой системы
координат точку (-m, 0)
2. К новой системе координат привязать
график функции у=f(х).
Постройте график
функции:
y ( х 2)
2
1.Вспомогательная
система
координат:
х= 2
у= 0
у
х=2
4
3
2
1
-3 -2 -1 0 1 2 3
-1
-2
2. Привязываем к
-3
ней график функции
-4
у=х²
Х 0
У 0
±1 ±2
1 4
y ( х 2)
у=0
2
х
Постройте график
функции:
х=-2
1
х
2
1.Вспомогательная
у
4
3
2
1
система
координат:
х= -2
у= 0
1
y
х 2
2. Привязываем к
у=0 х
-3 -2 -1 0 1 2 3
-1
-2
-3
-4
ней график функции
1
y
х
Х 0,5
У
2
1
2 -0,5 -1 -2
1 0,5 -2 -1 -0,5
Постройте график
функции:
y ( х 4)
2
1.Вспомогательная
система
координат:
у
х=4
4
3
2
1
х= 4
у= 0
-3 -2 -1 0 1 2 3 4 5 6 у=0
-1
-2
-3
2.
 Привязываем к
Привязываем к-4
ней график функции
у=-х²
Х 0
У 0
±1 ±2
-1 -4
y ( х 3)
2
х
Постройте график
функции:
у
х=-5
3
У= х+5
1.Вспомогательная
4
3
2
1
система
координат:
х= -5
у= 0
у=0х
3
У= х+5
2. Привязываем к
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3
-1
-2
-3
-4
ней график функции
3
У=
х
Х
1
У -3
2
3 -1
-0,5 -1 3
-2
-3
0,5 1
Найдите
унаиб. и унаим.
функции
у=2(х-1)²
на отрезке
0 ; 3
Унаиб.= 8
Унаим.= 0
у
11
10
9
8
7
у=2(х-1)² 6
5
4
3
2
1
х=1
у=0
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
х
Найдите
унаиб. и унаим.
функции
у=2(х-1)²
на луче
;1
у
11
10
9
8
7
у=2(х-1)² 6
5
4
3
2
х=1
1
Унаиб.= НЕТ
-6 -5 -4 -3 -2 -1 0 1
Унаим.= 0
у=0
2 3 4 5 6
х
Найдите
унаиб.
 и унаим.
и унаим.у
функции
4
У= х-3
на отрезке
4 ; 7
Унаиб.= 4
Унаим.= 1
у=0
5
4
3
2
1
х=3
-4 -3 -2 -1 0 1 2 3 4 5 6 7
-1
4 -2
х 3 -3
-4
-5
х
Найдите
унаиб. и унаим.
у
функции
4
на
У= х-3
у=0
5
4
3
2
1
х=3
-4 -3 -2 -1 0 1 2 3 4 5 6 7
-1
полуинтервале
4 -2
y
х 3 -3
-4
-5
3; 7
Унаиб.= НЕТ
Унаим.= 1
х
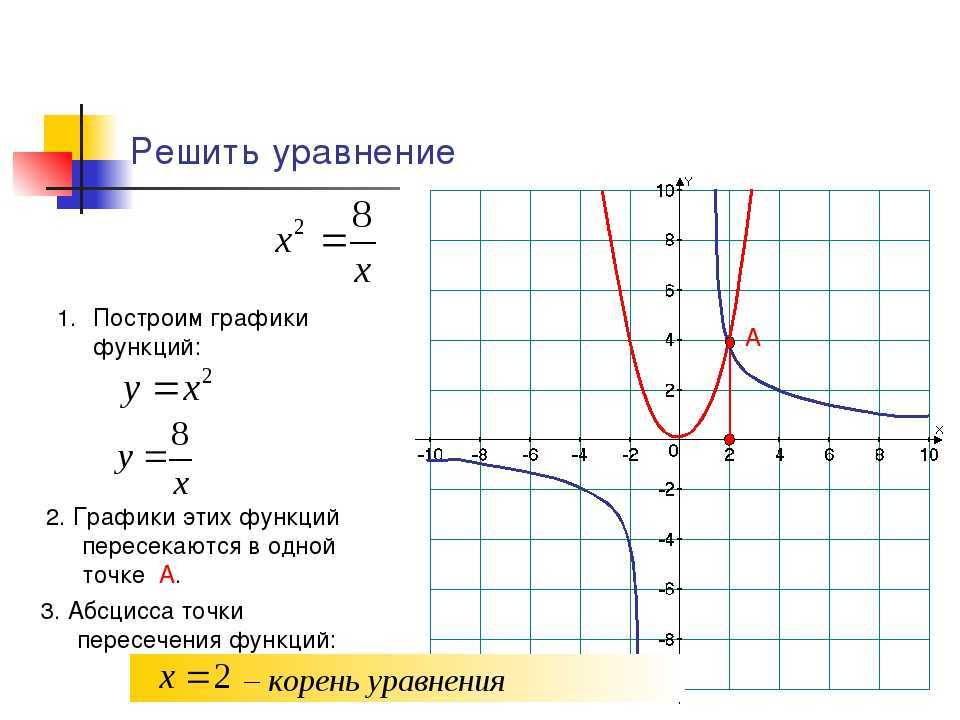
Решить графически уравнение:
(х+1)²=4
1
х=-1
у
9
у=(х+1)²
Построим в одной системе
координат графики функций:
у=4
4
3
у=(х+1)²
В.С.К. х=-1, у=0
у=х²
1
у=0
Х 0 ±1±2±3
-3 -2 -1 0 1 2 3
У 0 1 4 9
Найдём абсциссы точек
0
2
2
Х
пересечения графиков
у=4
У 4 4 3 ОТВЕТ: х=-3, х=1
х
Решить графически систему уравнений:
у=-(х-3)²
у=х-5
1
у
у=0
Построим в одной системе
координат графики функций:
у=-(х-3)²
В.
 С.К. х=3, у=0
С.К. х=3, у=0у=-х²
Х 0 ±1 ±2±3
У 0 -1 -4 -9
Х 0 5
у=х-5
У -5 0
2
Найдём координаты точек
пересечения графиков
х=3
-3 -2 -1 0 1 2 3 4 5 х
-1
(4;-1)
у=х-5
-4
-5
(1;-4)
у=-(х-3)²
-9
3
(1;-4) ,(4;-1)
ОТВЕТ:
Постройте графики функций:
у
у=2(х+2)²
у=(х-1)²
у=-0,5(х-3)²
у=3(х+4)²
у=-4(х+3)²
у=3х²
у=2х²
у=(х-1)²
4
3
2
1
у=2(х+2)²
у=х²
х
-5 -4 -3 -2 -1 0 1 2 3 4 5
у=3(х+4)² -1
-2
-3
-4
-5
у=-0,5х²
у=-4х²
у=-0,5(х-3)²
у=-4(х+3)²
Для вывода на экран построений, нужно сделать клики на соответствующих
прямоугольниках (4 раза на каждом)
Постройте график функции
f(х)=
2 ,если -3≤ х < -1
х+1
-x², если -1≤ х ≤ 2
и опишите её свойства.
f(х)=
2
У= х+1
2 ,если -3≤ х < -1
х+1
-x², если -1≤ х ≤ 2
В.С.К. х= -1, у= 0
2
У=-
х
х 1 2 4 -1 -2 -4
у -2 -1 -0,5 2 1 0,5
у=-х²
Х 0 ±1 ±2
У 0 -1 -4
-1≤ х ≤ 2
х=-1
у
4
3
2
1
у=0 х
-3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
Свойства функции:
1.
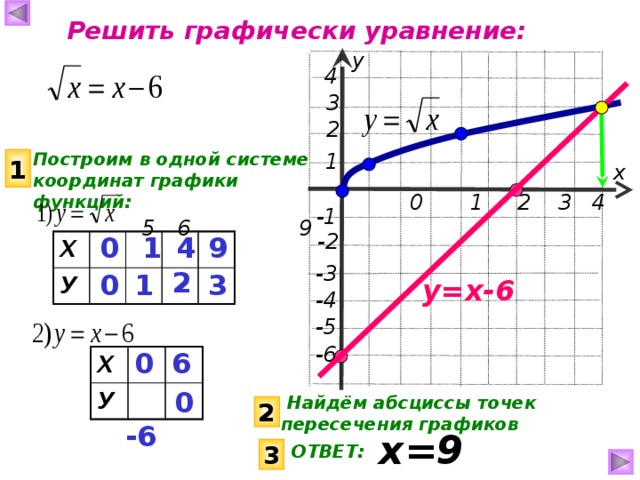 Область
Область1. D ( f ) 3 ; 2
определения
E ( f ) 4 ; 0 1;
у
f(x)=
4
-2/x+1,если -3≤х<1
-х²,если -1≤х≤2
2.
2.Область
значений
3. у=0, если х= 0
у>0, если х 3; 1
у<0, если
х 1; 0 0; 2
1
-3 -2 -1 0 1 2 3 4
-1
4. Функция убывает
при х 0; 2
-4
Функция возрастает
при х 3; 1 1; 0
ограничена снизу и не ограничена
5.Функция
Ограниченность
сверху.
унаиб.= НЕТ
6. унаим.= — 4
7. Непрерывность
Претерпевает разрыв при х = -1.
х
English Русский Правила
Построение графиков с корнями онлайн. Квадратичная и кубическая функции
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.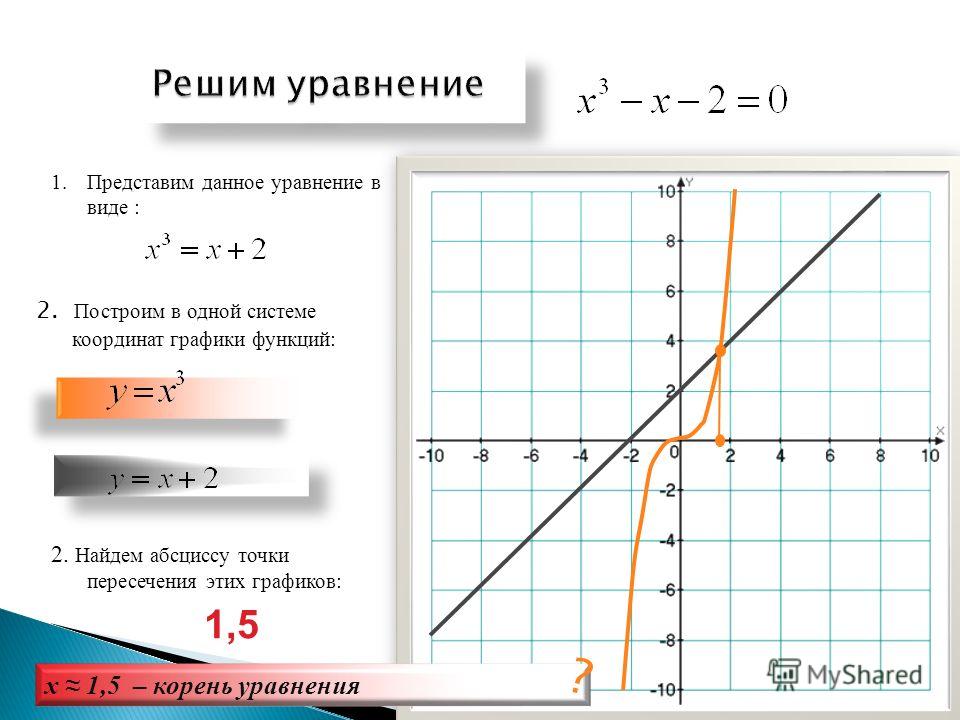 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.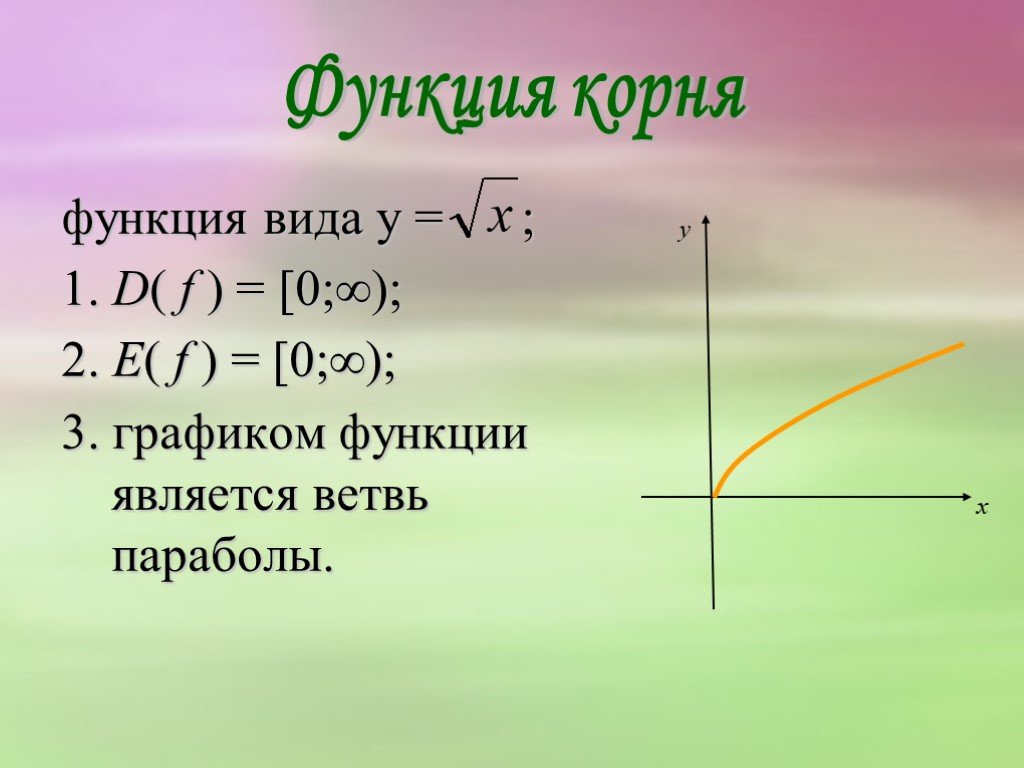
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Онлайн-репетиторство | Репетиторство по математике, английскому языку, естественным наукам
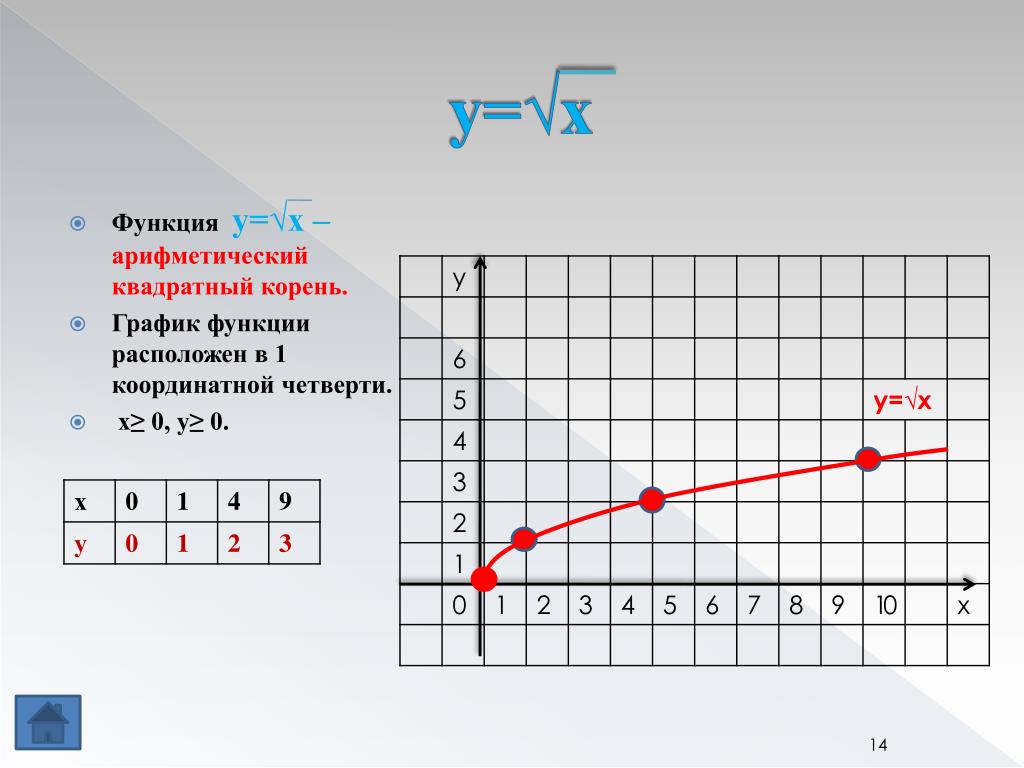
Функция квадратного корня записывается как
y=, где f(x) — линейная функция, а a ≥ 0, где «a» — любое значение в области значений y.
Чтобы построить график функции квадратного корня, нам нужно знать множество упорядоченных пар. Главное помнить, что квадратный корень из отрицательного числа не является действительным числом; поэтому область определения функции квадратного корня принимает только положительное значение, большее или равное нулю.
Самая простая функция извлечения квадратного корня: y=√x. Таблица его функций приведена ниже:
X | у = √x | у(х+1) – у(х) ; х>0 |
0 | 0 | 0 |
1- | 1 | 1 |
2 | 1. | 0,414 |
3 | 1,732 | 0,318 |
4 | 2 | 0,268 |
Мы видим, что при увеличении значения x на 1 разница между последовательными значениями y уменьшается. Это означает, что наклон графика уменьшается по мере увеличения x. График функции квадратного корня приведен ниже:
График других функций извлечения квадратного корня
Зная, как построить график основной функции извлечения квадратного корня, мы можем легко построить график других функций извлечения квадратного корня из графика родительской функции извлечения квадратного корня, т. е. y = √x. Она называется родительской функцией, потому что другие производные от нее графы могут считаться ее дочерними функциями.
е. y = √x. Она называется родительской функцией, потому что другие производные от нее графы могут считаться ее дочерними функциями.
Пример:
График y = +a можно легко вывести из графика родительской функции y =√x.
СОСТОЯНИЕ | РЕЗУЛЬТАТ | КОММЕНТАРИИ |
Когда h>0 | Переместить график влево | При одном и том же значении l x значение y больше по сравнению с родительским графом. |
Когда h<0 | Переместить график вправо | Для одного и того же значения l x значение y меньше по сравнению с родительским графом. |
Когда а>0 | Перевести вверх на единицу |
|
При а<0 | Перевести вниз на единицу |
|
Пример:
Постройте график функции y=
Попробуйте решить эту задачу
1. Найдите приблизительное значение на следующем графике.
- 5.4
- 5,5
- 5,3
- 5,8
Ответ: D
2. Для приведенного ниже графика найдите приблизительное значение √40.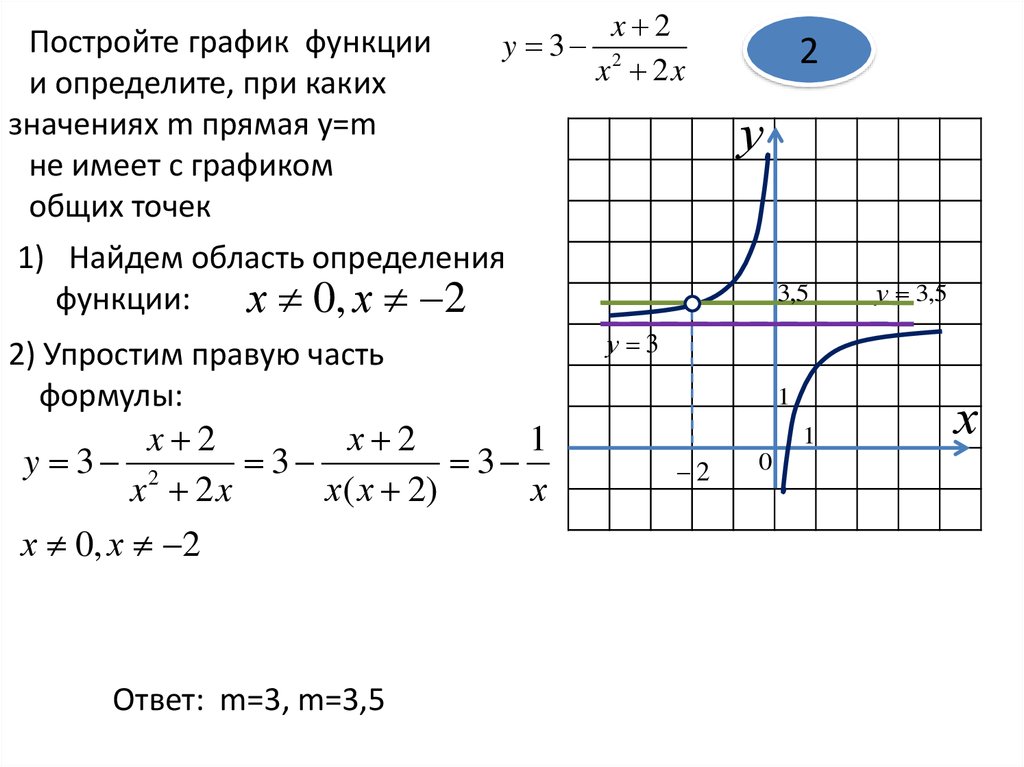
- 6,5
- 6,2
- 6,4
- 6,6
Ответ: C
Объяснение:
Y=√x
Когда x равно 40, y ≈ 6,4.
Следовательно, √40 ≈ 6,4.
BestMaths
Корни из графиков
Графики трех квадратичных функций показаны ниже.
90 109 корней 90 110 соответствующих квадратных уравнений задаются пересечением графика с осью X. т. е. x- перехватывает.
Корни квадратного уравнения называются действительными корнями , если график пересекает ось x или касается ее. Эти корни представляют собой 90 109 действительных 90 110 чисел.
Если график НЕ пересекает ось X, уравнение не имеет действительных корней. Уравнение этого типа можно решить, используя комплексные или мнимые числа, которые обычно изучаются в 12-м классе (13-й год Новой Зеландии).
Уравнение этого типа можно решить, используя комплексные или мнимые числа, которые обычно изучаются в 12-м классе (13-й год Новой Зеландии).
| Графики | |||
| Функция | у = (х + 3) 2 | у = х 2 — 5х + 6 | y = -x 2 + x − 2 |
| Количество и характер корней | Один реальный корень | Два действительных корня | Нет настоящих корней |
Существует более быстрый способ, чем построение графиков или определение количества корней квадратного уравнения. Этот метод использует дискриминант .
Дискриминант квадратного уравнения ax 2 + bx + c = 0 определяется как b 2 — 4ac.
Символ Δ иногда используется для обозначения дискриминанта.
Обратите внимание, что дискриминант — это часть квадратной формулы , которая находится под знаком квадратного корня.
Изучив значение дискриминанта, мы можем определить количество и характер корней.
| Если дискриминант равен нулю | б 2 — 4ас = 0 | есть один (повторяющийся) рациональный корень |
| Если дискриминант положительный | б 2 − 4ас > 0 | есть два действительных корня |
| Если дискриминант отрицательный | б 2 − 4ас < 0 | нет настоящих корней |
Если дискриминант представляет собой полный квадрат, например 49 или 100, то корнями будут рациональных (дробных) чисел.


 414
414