Калькулятор Сумм — Mathcracker.Com
Инструкции: Используйте этот калькулятор сумм для вычисления любого действительного выражения с суммами, которое вы предоставите, показывая все шаги. Пожалуйста, введите дробное вычисление, которое вы хотите выполнить, в поле формы ниже.
Подробнее о калькуляторе сумм
Этот калькулятор позволит вам вычислять и упрощать выражения, включающие суммы наиболее распространенных объектов алгебры, таких как числа, дроби, радикалы и общие функции, показывая все шаги. Вам необходимо ввести правильное выражение, включающее сумму/прибавление. Например, это может быть что-то простое, как «3/4 + 1/3», или что-то более сложное, как «sqrt(1/3+1/4)+(1/8+1/6)».
После того как вы ввели правильное числовое выражение, просто нажмите «Рассчитать», и наш калькулятор покажет вам все шаги.
Выполнение сумм основных терминов алгебры может показаться простым, и это довольно просто, просто это становится трудоемким и чреватым ошибками, когда вам нужно работать над длинным и запутанным термином.
Как добавить выражения?
Складывать простые выражения вместе очень просто, и в вашем распоряжении два мощных инструмента: правила
ассоциативность
и
коммутативность
.
Говоря простым языком, ассоциативность означает, что при сложении терминов можно смело убирать скобки, и результат не изменится. Также коммутативность означает, что вы можете изменить порядок суммы, и результат не изменится.
Каковы шаги для добавления выражения?
- Шаг 1: Определите выражение, которое вы хотите упростить, и выделите часть, которая состоит только из сумм и может быть изолирована
- Шаг 2: Используя правило ассоциативности, вы можете убрать скобки везде, где речь идет только о суммах
- Шаг 3: Выполните сложение член за членом, при этом вы можете менять порядок следования операндов, если это необходимо
- Шаг 4: Приведенные выше правила применимы и к выражениям, состоящим только из умножений, но не обязательно, если вы их смешиваете
Эти правила не работают с вычитаниями или делениями.
Как добавить выражения?
Идея заключается в том, чтобы сгруппировать термины, которые похожи: среди терминов, которые вы складываете, вы можете сгруппировать числа, дроби, а затем оперировать ими.
Идея заключается в том, чтобы оперировать терминами, с которыми легко работать вместе, например, числами и дробями. Затем, если у вас есть более сложные, составные выражения, вы работаете изнутри наружу, но сначала смотрите на простые операции.
Основное внимание нужно уделить скобкам, заметив, что их нельзя просто убрать при смешении операций. Ассоциативное свойство работает только тогда, когда нет смешения различных операций.
Почему полезно добавлять выражения?
Сложение простых выражений — это одна из самых простых операций, которую можно выполнить, и она является краеугольным камнем любой математической операции, точка.
Невозможно переоценить важность правильного сложения дробей и правильного
упрощение выражений
путем группировки и использования правильного порядка операций.
Пример: вычисление суммы выражений
Вычислите следующее: \(\frac{1}{3} + \left(\frac{6}{4} — \frac{5}{6}\right)\)
Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{3}+\left(\frac{6}{4}-\frac{5}{6}\right)\).
Получается следующий расчет:
\( \displaystyle \frac{1}{3}+\left(\frac{6}{4}-\frac{5}{6}\right)\)
Simplifying \(\displaystyle \frac{ 6}{ 4} = \frac{ 2 \cdot 3}{ 2 \cdot 2} = \frac{ \cancel{ 2} \cdot 3}{ \cancel{ 2} \cdot 2} = \frac{ 3}{ 2}\)
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\left(\frac{3}{2}-\frac{5}{6}\right)\)
Amplifying in order to get the common denominator 6
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\frac{3}{2}\cdot\frac{3}{3}-\frac{5}{6}\)
Finding a common denominator: 6
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\frac{3\cdot 3-5}{6}\)
Expanding each term: \(3 \times 3-5 = 9-5\)
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\frac{9-5}{6}\)
Operating the terms in the numerator
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\frac{4}{6}\)
We can factor out 2 for both the numerator and denominator.
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\frac{2\cdot 2}{2\cdot 3}\)
Now we cancel 2 out from the numerator and denominator.
\( = \,\,\)
\(\displaystyle \frac{1}{3}+\frac{2}{3}\)
Finding a common denominator: 3
\( = \,\,\)
\(\displaystyle \frac{1+2}{3}\)
Adding up the terms in the numerator
\( = \,\,\)
\(\displaystyle \frac{3}{3}\)
Now we cancel 3 out from the numerator and denominator
\( = \,\,\)
\(\displaystyle 1\)
Пример: вычисление суммы выражения
Вычислите следующее: \(2 + \frac{5}{4} — \frac{7}{6}\)
Отвечать:
Нам нужно вычислить и упростить следующее выражение: \(\displaystyle 2+\frac{5}{4}-\frac{7}{6}\).
Получается следующий расчет:
\( \displaystyle 2+\frac{5}{4}-\frac{7}{6}\)
Amplifying in order to get the common denominator 12
\( = \,\,\)
\(\displaystyle 2\cdot\frac{12}{12}+\frac{5}{4}\cdot\frac{3}{3}-\frac{7}{6}\cdot\frac{2}{2}\)
We use the common denominator: 12
\( = \,\,\)
\(\displaystyle \frac{2\cdot 12+5\cdot 3-7\cdot 2}{12}\)
Expanding each term: \(2 \times 12+5 \times 3-7 \times 2 = 24+15-14\)
\( = \,\,\)
\(\displaystyle \frac{24+15-14}{12}\)
Adding up the terms in the numerator
\( = \,\,\)
\(\displaystyle \frac{25}{12}\)
чем завершается расчет.
Пример: еще одно вычисление сложения
Рассчитайте \( \left(\frac{4}{3} \times \frac{6}{5} \right)+ \frac{1}{5} \).
Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \left(\frac{4}{3}\cdot\frac{6}{5}\right)+\frac{1}{5}\).
Получается следующий расчет:
\( \displaystyle \frac{4}{3}\cdot\frac{6}{5}+\frac{1}{5}\)
We multiply all the numerators and all the denominators together as in \(\displaystyle\frac{ 4}{ 3} \times \frac{ 6}{ 5}= \frac{ 4 \times 6}{ 3 \times 5} \)
\( = \,\,\)
\(\displaystyle \frac{4\cdot 6}{3\cdot 5}+\frac{1}{5}\)
Factoring the term \(\displaystyle 3\) in the numerator and denominator in \(\displaystyle \frac{ 4 \times 6}{ 3 \times 5}\), which can be further reduced
\( = \,\,\)
\(\displaystyle \frac{4\cdot 2}{5}+\frac{1}{5}\)
After simplifying the common factors from the top and bottom
\( = \,\,\)
\(\displaystyle \frac{8}{5}+\frac{1}{5}\)
We use the common denominator: 5
\( = \,\,\)
\(\displaystyle \frac{8+1}{5}\)
Adding each term
\( = \,\,\)
\(\displaystyle \frac{9}{5}\)
чем завершается расчет.
Другие полезные калькуляторы по алгебре
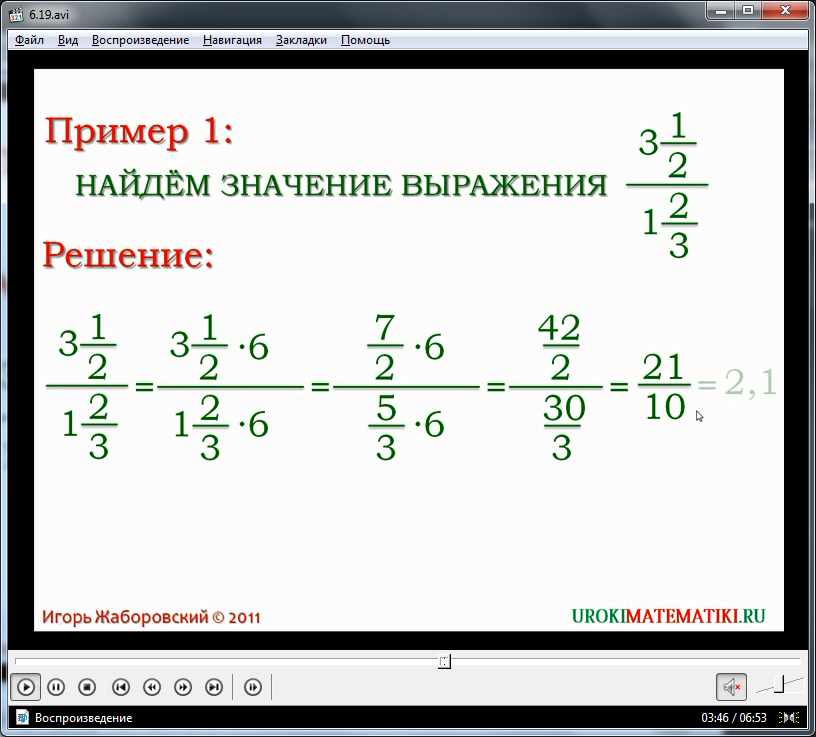
Сложение — это наиболее фундаментальная операция, которую вы можете выполнить. Вы также можете использовать Калькулятор дробей специально для выполнения сложения дробей.
Кроме того, при работе с дробями есть особый случай, связанный с терминами типа «1 1/2», для которых вы можете использовать калькулятор смешанных дробей
§ Наименьшее общее кратное онлайн.
Калькулятор нокСкрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Площадь кругаАлгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Легче отказаться от великих целей, чем от мелких привычек.
Александр Кумор
на главную
Введите тему
Поддержать сайт
←Вернуться в «Калькуляторы онлайн»
| Введите числа через пробел: |
Калькулятор расчёта наименьшего общего кратного онлайн (НОК) поможет вам в нахождении общего знаменателя при сложении и вычитании обыкновенных дробей с разными знаменателями.
Инструкции к калькулятору
- Введите через запятую или пробел натуральные числа в текстовое поле внизу. (Например: 2, 4, 7)
- Нажмите кнопку «Найти НОК» и ожидайте результата под заголовком «Решение».
- Убедитесь, что среди введённых чисел нет нулей.
Важно!
Данный калькулятор поиска онлайн НОК может служить лишь для проверки ваших вычислений.
Научиться находить НОК самостоятельно можно в теме нахождение
наименьшего общего кратного.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Калькулятор рациональных выражений
Онлайн-калькулятор рациональных выражений факторизует заданную функцию и выполняет различные математические операции, чтобы привести ее к максимально упрощенному виду. Вы можете выполнять более одного арифметического действия одновременно для данной задачи, если это применимо.
Этот контент организован с использованием надлежащей органической информации, которая очень важна для оптимизации данного рационального выражения.
Посмотри на это!
Что такое рациональное выражение?
В словаре алгебраических выражений:
«Дробь, содержащая числитель и/или знаменатель в виде алгебраических многочленов, называется рациональным выражением»
Нет ничего сложного в понимании, так как это общая форма дроби состоит из простых или сложных рациональных функций. Лучшее использование бесплатного онлайн-калькулятора рациональных функций поможет вам решить такие задачи одним взглядом.
Например: 92} + 7x + 50}}{1} $$
Это кажется немного странным, но его можно рассматривать как рациональное выражение. Вот почему вы можете рассматривать полином как стандартную рациональную функцию. Вы можете уменьшить сложный многочлен, используя бесплатный онлайн-калькулятор рациональных чисел. Что вам нужно сделать, так это предположить 1 в таких случаях наверняка.
Операции над рациональными выражениями:
Здесь у нас есть ряд алгебраических операций, которые необходимо выполнить над рациональными выражениями.
К ним относятся:
Дополнение:
С помощью бесплатного калькулятора рациональных функций можно сложить два или более рациональных выражения. Но когда дело доходит до ручных вычислений, вам нужно выяснить общие факторы и отменить их, чтобы получить сокращенную форму.
Здесь нужно сделать следующее:
- Запишите все отдельные термины в виде суммы.
- Возьмите общий знаменатель для всех выражений, подвергнув их наименьшему общему кратному (НОК).
- Теперь сложите все члены в числителе, чтобы знаменатель остался прежним.
- Если вы найдете похожие термины с противоположными знаками, сократите их и перепишите все остальные термины в нужной последовательности.
- Вы получаете упрощенную форму.
Вычитание:
Вычитание двух или более рациональных многочленов прямо противоположно сложению, как это определено для чисел. Калькулятор свободного вычитания рациональных выражений может помочь вам выполнить вычитание двух или более рациональных функций.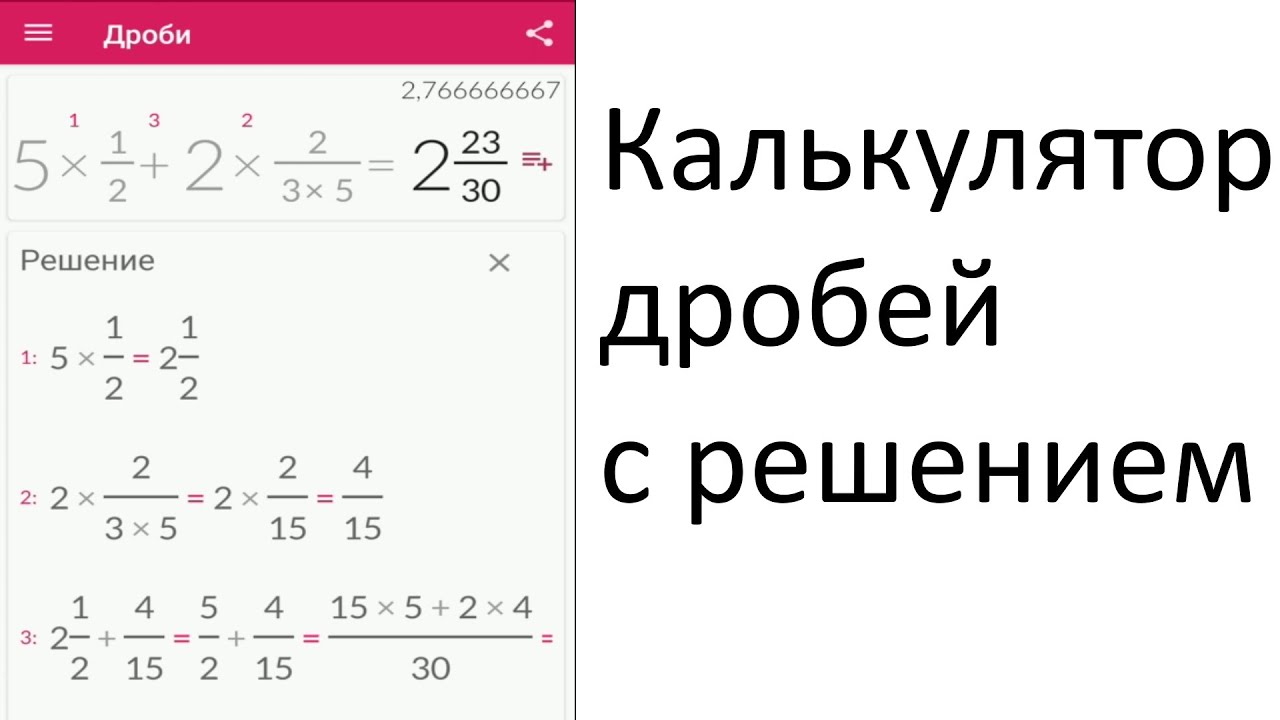
Кроме того, вы должны следовать этим правилам, чтобы вычитать рациональные функции.
- Запишите все отдельные термины в виде вычитания.
- Приведите к общему знаменателю все выражения с помощью НОК.
- Вычесть все члены в числителе.
- Отменить все те, которые имеют противоположные знаки с теми же переменными, и добавить остальные с тем же знаком и переменными степенями.
- Укажите, что знаменатель остается неизменным.
- Так получается упрощенная форма.
Умножение:
Вы можете умножать рациональные многочлены точно так же, как и числа. Но не забывайте следовать приведенным ниже рекомендациям:
- Запишите все выражения, в которых есть знак умножения.
- Произвести произведение всех значений в числителе и знаменателе отдельно.
- Теперь умножьте каждый коэффициент в значениях, следующих за основным распределительным свойством
- Сложите все термины с одинаковыми знаками и переменными и вычтите те, которые имеют противоположные знаки.
- Перепишите выражение в порядке убывания переменной мощности.
- Получено упрощенное рациональное выражение.
Деление:
Подобно отношениям сложения и вычитания, умножение и деление двух или более рациональных выражений также одинаковы. Когда вы сталкиваетесь со сложными терминами, вы можете воспользоваться нашим бесплатным онлайн-калькулятором рациональных выражений с делением, чтобы мгновенно сократить их. Вы обязательно получите пошаговые расчеты, чтобы избежать каких-либо неудобств. Но на практике необходимо обратить внимание на следующие моменты.
- Напишите все термины со знаком деления между ними.
- Заменить числитель и знаменатель всех членов, кроме первого, и заменить знак деления на знак умножения.
- Для остальных вычислений следуйте тем же правилам, что и для умножения рациональных многочленов.
Как упростить рациональные выражения?
Вы можете использовать наш бесплатный онлайн-калькулятор упрощающих рациональных функций, чтобы сократить сложные члены, входящие в выражения, до сокращенного.
Но когда это нужно упростить вручную, мы определили все правила и положения для этого выше. Например, давайте решим несколько примеров, соответствующих каждой из вышеперечисленных операций. 9{2}} $$
Наиболее упрощенная форма данной функции.
Здесь наш бесплатный калькулятор упрощенных рациональных выражений быстро определяет приведенную форму любого рационального многочлена.
Как работает калькулятор Rational Expression?
Вы можете использовать множество методов для упрощения рационального выражения, но лучший из них — бесплатный калькулятор рациональных чисел. Независимо от того, насколько сложна данная функция, наш калькулятор оптимизирует ее до самой общей формы. Позвольте нам помочь вам, как это сделать!
Ввод:
Сначала выберите одну из следующих опций из списка меню:
(1) Сокращенные члены рационального выражения
(2) Сложение, вычитание, умножение и деление рациональных выражений
(3) Упростить любые выражения
Если выбрать вариант 1:
- Введите функцию числителя
- Введите функцию знаменателя
- Нажмите «Рассчитать»
Если вы выберете вариант 2:
- Сначала выберите, нужно ли вам применять операции к двум или трем выражениям
- После этого запишите выражения числителя и знаменателя для каждой рациональной функции в поле ввода
- Нажмите кнопку расчета.
Если вы выбрали вариант 3:
- Запишите функцию ввода в строке меню
- Нажмите кнопку «Рассчитать»
Вывод:
Калькулятор свободных рациональных выражений выполняет следующие операции в соответствии с входными данными, выбранными для рациональных выражений.
Для варианта 1:
- Поэтапно сокращает рациональное выражение для общего ответа
Для варианта 2:
- Складывает, вычитает, умножает и делит две или три функции соответственно.
Для опции 3:
- Упрощает все рациональное выражение и приводит к наиболее оптимальной форме заданного рационального выражения.
Часто задаваемые вопросы:
Как узнать, является ли рациональное выражение правильным или неправильным?
Правильное рациональное выражение:
«Рациональное выражение, в котором числитель имеет наивысшую степень переменной вместо переменной в знаменателе»
Неправильное рациональное выражение:
«Рациональная функция, у которой степень числителя меньше степени переменной в знаменателе, называется неправильной».
Независимо от типа рационального выражения используйте бесплатный онлайн-калькулятор рациональных функций, чтобы упростить его за доли секунд.
Что понимается под степенью многочлена?Наивысшая степень переменной, входящей в полином, называется степенью полинома.
9{2} + 10 $$Как мы видим, для отдельных членов в приведенном выше многочлене степени равны 9, 5, 4 и 2 соответственно. А вот высшая степень это 9 . Поэтому его будем считать степенью всего многочлена. Кроме того, онлайн-калькулятор рациональных выражений поможет вам правильно упростить эту полиномиальную функцию.
Что означает моном?
Алгебраическое предложение, содержащее только один термин, называется мономом.
Например:
5z, 4x, 65y и т. д.
Вывод: Упрощение рациональных выражений позволяет уменьшить сложность ваших задач.
Математики, специалисты по данным, инженеры и физики широко используют рациональные выражения, используя бесплатный онлайн-калькулятор рациональных функций для выполнения быстрых вычислений.
Ссылки:
Из источника википедии: Алгебраическая дробь, Рациональные дроби, Иррациональные дроби, Терминология.
Из истоков академии хана: Сокращение рациональных выражений, Конечное поведение, Разрывы рациональных функций.
Из источника люмен обучения: область рациональной функции, асимптоты, упрощение рационального выражения, частичные дроби.
Рациональные выражения Пошаговое решение математических задач
Добро пожаловать в Quickmath Solvers!
- Решить
- Упростить
- Фактор
- Расширить
- График
- ГКФ
- ЛКМ
Новый Пример
Справка Учебник
Решите уравнение, неравенство или систему.
Пример: 2x-1=y,2y+3=x
Чтобы увидеть учебник, прокрутите вниз
- Математические статьи
- Упрощение выражений
Выражение, представляющее собой частное двух алгебраических выражений (со знаменателем, отличным от 0), называется дробным выражением. Наиболее распространенными дробными выражениями являются те, которые являются частными двух многочленов; они называются рациональными выражениями. Поскольку дробные выражения включают частные, важно отслеживать значения переменной, которые удовлетворяют требованию, чтобы ни один знаменатель не был равен 0. Например, x != -2 в рациональном выражении:
, потому что замена x на -2 делает знаменатель равным 0. Аналогично, в
x!=-2 и x!= -4
Ограничения на переменная находится путем определения значения, при которых знаменатель равен нулю. Во втором приведенном выше примере для нахождения значений x, при которых (x + 2)(x + 4) = 0, необходимо использовать свойство, согласно которому ab = 0 тогда и только тогда, когда a = 0 или b = 0, следующим образом.
(х+2)(х+4)=0
x+2=0 или x+4=0
x=-2 или x=-4
Точно так же, как дробь 6/8 записывается как 3/4, рациональные выражения также могут быть написано в самых низких терминах. Это делается по основному принципу.
Пример 1
Запишите каждое выражение в наименьших терминах.
Разложите числитель и знаменатель на множители, чтобы получить
По фундаментальному принципу
В исходном выражении p не может быть 0 или -4, потому что
Таким образом, этот результат действителен только для значений p, отличных от 0 и -4. Отныне мы всегда будем допускать такие ограничения при редукции рациональных выражений.
Теперь давайте посмотрим, как наш пошаговый решатель дробей решает эту задачу:
Решить похожую задачуВведите свою задачу
Пример 2
Факторы 2 — k и k — 2 имеют противоположные знаки. По этой причине умножьте числитель и знаменатель на -1 следующим образом.