калькулятор онлайн метод ньютона
Вы искали калькулятор онлайн метод ньютона? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и метод ньютона онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор онлайн метод ньютона».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор онлайн метод ньютона,метод ньютона онлайн,онлайн полином ньютона,онлайн решение нелинейных уравнений,полином ньютона онлайн,решение нелинейных уравнений онлайн.
Где можно решить любую задачу по математике, а так же калькулятор онлайн метод ньютона Онлайн?
Решить задачу калькулятор онлайн метод ньютона вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решение уравнений методом Ньютона онлайн
| Вы ввели следующие уравнение |
| Решение заданного уравнения имеет следующее значение |
Решение произвольных уравнений
Теперь сервис позволяет считать численные вещественные корни уравнений, которые возникают при решении подобных задач
Этот сервис позволяет ученикам/студентам сосредоточится на понимании задачи, а не умножении, делении, сокращении и упрощении полученной формулы, что конечно же важно, но не настолько что бы в угоду математическим формулам, ученики/студенты теряли смысл решения задачи.
Синтаксис
WEB: <выражение>
Выражением может быть любая формула выраженная языком PHP
Система решает уравнения только с одной переменной и эта переменная обозначается как x (в английской раскладке)
Примеры
Длина детской площадки прямоугольной формы на 5 м больше её ширины. Длину площадки увеличили на 2 м, а ширину — на 5 м, при этом её площадь увеличилась на 280 м2. Найдите площадь новой детской площадки.
Решение выражается уравнением
Пишем root (x+5)*(x+5+2)-x*(x+5)-280
Получаем ответ 35 — это ширина, а соответственно 40 это длина
Решение уравнения x*x-11=0
пишите root x*x-11 и получите 3.3166247903554
Функции PHP
- acos — Арккосинус
- acosh — Гиперболический арккосинус
- asin — Арксинус
- asinh — Гиперболический арксинус
- atan — Арктангенс
- atanh — Гиперболический арктангенс
-
cos — Косинус
- cosh — Гиперболический косинус
- exp — Вычисляет число e в степени
- log10 — Десятичный логарифм
- log — Натуральный логарифм
- pi — Возвращает число Пи
- pow — Возведение в степень
- sin — Синус
- sinh — Гиперболический синус
- sqrt — Квадратный корень
- tan — Тангенс
- tanh — Гиперболический тангенс
- Свойства обратных тригонометрических функций >>
Метод хорд
Будем искать нуль функции f x {\displaystyle fx}.

1. Алгебраическое описание метода секущих
Пусть x 1, x 2 {\displaystyle x_{1},x_{2}} — абсциссы концов хорды, f x = 0 {\displaystyle fx=0} — уравнение функции, решаемое методом секущих. Найдём коэффициенты k {\displaystyle k} и b {\displaystyle b} из системы уравнений
{ f x 1 = k x 1 + b, f x 2 = k x 2 + b. {\displaystyle \left\.}
Повторять операцию следует до тех пор, пока | x i − x i − 1 | {\displaystyle |x_{i}-x_{i-1}|} не станет меньше или равно заданному значению погрешности.
2. Метод хорд с итерационной формулой
Иногда методом секущих называют метод с итерационной формулой
x i + 1 = x i − f x i ⋅ x i − x 0 f x i − f x 0. {3}-18x-83=0} методом секущих. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений x 0 {\displaystyle x_{0}} и x 1 {\displaystyle x_{1}} концы отрезка, на котором отделён корень: x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3}, числовые значения x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3} выбраны произвольно. Вычисления ведутся до тех пор, пока не будет выполнено неравенство | x i + 1 − x i | ε {\displaystyle |x_{i+1}-x_{i}| f ″ b f b 0 {\displaystyle fbfb 0}, то можно доказать, что погрешность приближенного решения стремится к нулю при n → ∞ {\displaystyle n\rightarrow \infty }, то есть метод сходится и сходится со скоростью геометрической прогрессии при этом говорят, что он имеет линейную скорость сходимости.
{3}-18x-83=0} методом секущих. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений x 0 {\displaystyle x_{0}} и x 1 {\displaystyle x_{1}} концы отрезка, на котором отделён корень: x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3}, числовые значения x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3} выбраны произвольно. Вычисления ведутся до тех пор, пока не будет выполнено неравенство | x i + 1 − x i | ε {\displaystyle |x_{i+1}-x_{i}| f ″ b f b 0 {\displaystyle fbfb 0}, то можно доказать, что погрешность приближенного решения стремится к нулю при n → ∞ {\displaystyle n\rightarrow \infty }, то есть метод сходится и сходится со скоростью геометрической прогрессии при этом говорят, что он имеет линейную скорость сходимости.
4. Историческая справка
Первым, кто смог найти приближённые решения кубических уравнений, был Диофант, тем самым заложив основу метода хорд. Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон 1670-е годов
Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон 1670-е годов
5. Модификации
Метод ложного положения отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.
- принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован
- словарь — М.: Сов. энциклопедия 1988 — С. 847. Метод Ньютона метод касательных Метод Мюллера Обратная параболическая интерполяция Метод хорд
- дающих различный результат.
 Метод случайных концов наудачу выберем две точки на окружности и проведём через них хорду Чтобы посчитать искомую вероятность
Метод случайных концов наудачу выберем две точки на окружности и проведём через них хорду Чтобы посчитать искомую вероятность - 0 — 521 — 43064 — X. Метод секущих Обратная параболическая интерполяция Метод Ньютона Метод хорд Метод дихотомии Численное решение уравнений Модуль для метода Мюллера
- Численные вычислительные методы — методы решения математических задач в численном виде Представление как исходных данных в задаче, так и её решения
- достигнет требуемой точности. Основная статья: Метод простой итерации Обобщив метод хорд секущих и метод Ньютона можно прийти к выводу, что они оба являются
- Метод неделимых — возникшее в конце XVI века наименование совокупности приёмов, предназначенных для вычисления площадей геометрических фигур или объёмов
- метод графического представления связей данных в матрице.
 При этом значения располагаются по окружности, а связи между ними отображаются в виде хорд
При этом значения располагаются по окружности, а связи между ними отображаются в виде хорд - Терцидина в нескольких странах Европы. В результате было получено более 70 хорд внутри явления, что позволило прорисовать профиль астероида с точностью до
- график таблицы хорд определённого радиуса обычно 120 мм построенный по принципу поперечного масштаба. Исходя из длины отрезков хорд и определяется
- диаметр астероида как 219 25 км, а второй раз 14 октября 1999 года, тогда методом хорд удалось определить эллипсоидную форму астероида, а его размер оценили
- граф пересечений множества хорд окружности. То есть это неориентированный граф, вершины которого можно отождествить с хордами окружности, и эти вершины
- впоследствии Ибн Ирак и другие математики стран ислама, но на языке отношений хорд Перевод Сферики на арабский язык выполнил в начале X века Хунайн ал — Ибади
- между хордами На теореме о вписанном угле основан метод решения геометрических задач, так называемый метод вспомогательной окружности.
 Идея метода состоит
Идея метода состоит - технику хорд Перпендикуляр к хорде опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду Половина поделенной пополам хорды — это
- обходами, как выше, можно определить и для ориентированных графов. Цикл без хорд в графе, также называемый дырой или порождённым циклом, — это цикл, в котором
- серединой хорды PQ некоторой окружности, проведены две произвольные хорды АВ и CD той же окружности. Пусть хорды AD и ВС пересекают хорду PQ в точках
- проектировки линий Московского метрополитена, при котором строящиеся участки хорды не проходят в центр Москвы, не пересекаются и не имеют пересадок на Кольцевую
- для которых характерно наличие энтодермального осевого скелета в виде хорды которая у высших форм заменяется позвоночником.
 По степени развития нервной
По степени развития нервной - визированием При рихтовке способом сглаживания изменение положения трос — хорды соответствующее отклонению пути в плане, вызывает смещение ползунков потенциометров
- реконструкциям величины хорд у Гиппарха были протабулированы с интервалом 7 30 Возможно, в основе вычисления таблицы Гиппарха лежал метод разработанный Архимедом
- прохождение было на два дня позже — после прохождения нисходящего узла, поэтому хорда пути Венеры наблюдалась в нижней части Солнца, в 2012 году Венера прошла
- функции Метод Ньютона метод касательных — нахождение нулей функций с помощью производной Метод секущих метод хорд — аппроксимирует корни функции Метод градиентов
- кривой — плоская обычно выпуклая фигура, заключённая между кривой и её хордой Наиболее простой и распространённый пример сегмента плоской кривой: сегмент
- теореме, согласно которой отношение большей хорды к меньшей менее отношения стягиваемых ими дуг.
 Составил таблицу хорд соответствующим дугам от 0 до 180 ввёл
Составил таблицу хорд соответствующим дугам от 0 до 180 ввёл - распространённые методы предотвращения реверса элеронов — использование элеронов — интерцепторов интерцепторы расположены ближе к центру хорды крыла и при выпуске
- усовершенствовании предложения Менелая в Сферике он заменил удвоенные хорды которыми пользовался Менелай, на синусы. В Книге о плоской и сферической
- характерные признаки этого типа: наличие хорды жаберные щели, пронизывающие глотку нервная система в виде нервной трубки хорда находится между нервной трубкой
- скелет включает в себя хорду и соединительную ткань. хрящевая — на 5 — 7 неделе внутриутробного развития — скелет включает в себя хорду и хрящевой скелет. костная
- отрезке между двумя своими точками имеет касательную, параллельную секущей хорде проведённой через эти две точки.
 Обобщённая теорема Ролля Формула конечных
Обобщённая теорема Ролля Формула конечных
Метод хорд: метод хорд алгоритм, метод хорд маткад, метод хорд с++, метод хорд матлаб, метод хорд — python, метод хорд онлайн, метод хорд теория, метод хорд описание
Метод хорд онлайн.
Численные методы решения нелинейных уравнений. На уроке рассматриваются основные понятия математики: функция, способы решения уравнений, а также практическая реализация. Метод хорд описание. 3.4. Метод касательных Научно образовательная среда. Метод хорд итерационный численный метод приближённого нахождения корня уравнения. Заходите на сайт, чтобы узнать подробнее. Метод хорд матлаб. Метод хорд Образовательный портал ТГУ. Доказательство теорем Ферма, Ролля и Лагранжа. Особенности и условия применения метода хорд при решении уравнений разного.
Метод хорд с.

Лекция Численные методы решения НОУ ИНТУИТ. Решение уравнения методом хорд, методом касательных метод Ньютона, методом половинного деления, методом простых итераций. Метод хорд маткад. Результаты поиска по запросу Хабр. Лабораторная работа Решение нелинейных алгебраических уравнений методом хорд на Turbo Pascal 7.0 DOS Паскаль. Программа решает. Метод хорд — python. Решение нелинейных уравнений методом хорд в MS Excel. Метод секущих метод хорд Метод половинного деления метод дихотомии. Метод. Метод хорд Студопедия. 2.2 Метод хорд. В методе хорд в качестве приближенной оценки выбирается не середина отрезка, а его пересечение с хордой, имеющей координаты.
Метод хорд: В данном методе процесс итераций состоит в том.
Метод касательных Ньютона. Метод касательных отличается от метода хорд тем, что здесь рассматривается не секущая, соединяющая концы дуги. Комбинированный метод хорд и касательных презентация, доклад. При решении уравнения методом хорд поводится прямая соединяющая концы отрезка. Из двух точек А и В выбирается х0. Метод хорд Онлайн калькулятор. Решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность.
При решении уравнения методом хорд поводится прямая соединяющая концы отрезка. Из двух точек А и В выбирается х0. Метод хорд Онлайн калькулятор. Решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность.
Метод хорд и касательных. Что такое Метод хорд.
Одним из вариантов решения нелинейных уравнений является метод хорд. Такое название метод получил потому, что точка деления это место. Метод хорд. Метод секущих Docsity. Онлайн калькулятор. Метод хорд итерационный численный метод приближённого нахождения корня уравнения.
Метод хорд Карта знаний.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ. 2. 5. Комбинированный метод хорд и касательных. Методы. Лекция 12. Решение нелинейных уравнений ТОЭ. На языке Pascal реализуются четыре метода: дихотомии, касательных, хорд и простых итераций. Проводится сравнение их эффективности с точки. Модификации метода Ньютона. Метод хорд и касательных. Материал из Википедии свободной энциклопедии. Перенаправление на: Метод хорд. Что такое.moda Вики является. Regula falsi и метод хорд разные алгоритмы? Помогите. Онлайн калькулятор для нахождения корней уравнений алгебраических и трансцендентных методом хорд также известный как метод секущих.
Методы. Лекция 12. Решение нелинейных уравнений ТОЭ. На языке Pascal реализуются четыре метода: дихотомии, касательных, хорд и простых итераций. Проводится сравнение их эффективности с точки. Модификации метода Ньютона. Метод хорд и касательных. Материал из Википедии свободной энциклопедии. Перенаправление на: Метод хорд. Что такое.moda Вики является. Regula falsi и метод хорд разные алгоритмы? Помогите. Онлайн калькулятор для нахождения корней уравнений алгебраических и трансцендентных методом хорд также известный как метод секущих.
Метод половинного деления, метод простых итераций, метод.
Метод хорд, так же как и метод бисекций всегда сходится. 3. Метод Ньютона метод касательных. 0. y. x. Этот метод в отличие от метода хорд. Метод хорд База знаний Allbest. Метод хорд. Метод основан на замене функции f x на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение. Метод хорд это Что такое Метод хорд? DIC Academic. Метод хорд. Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого. 4.3 Метод хорд стр.1 Delphi Plus. Презентация на тему Комбинированный метод хорд и касательных, предмет презентации: Математика. Этот материал содержит 10 слайдов. 1.4. Метод хорд. В данной работе рассмотрены такие, как метод деления отрезка пополам, метод простой итерации, метод Ньютона касательных, метод хорд,.
Метод хорд это Что такое Метод хорд? DIC Academic. Метод хорд. Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого. 4.3 Метод хорд стр.1 Delphi Plus. Презентация на тему Комбинированный метод хорд и касательных, предмет презентации: Математика. Этот материал содержит 10 слайдов. 1.4. Метод хорд. В данной работе рассмотрены такие, как метод деления отрезка пополам, метод простой итерации, метод Ньютона касательных, метод хорд,.
Метод хорд Онлайн калькулятор.
Метод хорд. Идея способа хорд состоит в том, что можно с известным приближением допустить, что функция на достаточно малом участке. Численные методы ОГУ. Двух методов существует ещё масса методов, например: Метод бисекции довольно низкой скоростью Метод хорд не требует. Метод хорд 1 Реферат. Реферат Определить количество необходимых итераций для следующих значений погрешностей результата: Eps. Используемый метод: метод.
Используемый метод: метод.
2.6. Метод хорд Электронная библиотека.
Метод хорд: В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения 1 принимаются значения х1, х2.., хn. МЕТОД ХОРД ДЛЯ НАХОЖДЕНИЯ РАВНОВЕСНОЙ ЦЕНЫ. Для применения методов Ньютона и хорд необходимо выбрать начальное приближение x0. Так как f –1 0, f 0 0, f 6x – 0.4 0, то за начальное. Метод хорд: определение и пример с решением. Метод хорд. Имеется возможность проверить свое решение прямо на сайте с оформлением всех промежуточных вычислений в формате Word. Метод Хорд Алгоритмы Киберфорум Форум программистов. Метод половинного деления, метод простых итераций, метод Ньютона, метод касательных, метод секущих, метод хорд. Численные методы линейной и нелинейной алгебры. Возможно, я задаю глупейший вопрос, простите меня, недостойного пожирателя кореньев, но regula falsi и метод хорд секущих это.
Результаты поиска по метод хорд Руконт.

По постановке задачи метод хорд близок к рассмотренной в разд. Ь. Основное различие методов дихотомии и хорд заключается в выборе точки хт. Метод хорд. Метод хорд для нелинейного уравнения. В методе хорд производная f x k метода Ньютона заменяется на еще более простую по сравнению с. Решение уравнения методом хорд, методом касательных. Метод хорд. След. Линия считается заданной на чертеже, если известен закон нахождения каждой ее точки. Для задания линии удобно использовать. Поиск корней уравнения методом хорд m. Надежные методы численного определения корней уравнений: метод половинного деления и метод хорд. Процесс отделения корней начинается с.
УМКД Методы вычислений в экономике.
Метод хорд. Недостаток деления отрезка строго пополам проистекает. D.ru. Обучение. Лекции по численным методам. Геометрическая интерпретация метода хорд состоит в следующем рис.6.2.3 8. Рис.6.2.3 8. Проведем отрезок прямой через точки A и B. Очередное.
Очередное.
Метод хорд Онлайн калькулятор AllCalc.
Хорду по двум точкам провести легко с достаточно высокой степенью точности. Метод тем точнее, чем ближе хорда к дифференцируемой кривой,. LibreOffice Calc. Метод хорд. Согласно методу хорд, о. Horda: proc f,otrezok,eps,M local x,a,b,c,ff,i: здесь локальные переменные пн левая часть отрезка присваиваем к пн x x: lhs otrezok Функция фц. Некоторые численные методы решения алгебраических и. 3. Методы хорд и касательных. К числу широко распространенных приближенных методов решения уравнения относятся метод хорд и метод.
Методы дихотомии Machi.
Метод хорд. Метод секущих. По прежнему решаем уравнение 1, где, на и. Т.е. на 1 имеет только один корень. Уравнение 1 запишем в виде, где. Методы графического дифференцирования и интегрирования. В качестве метода был выбран метод хорд, который позволяет приблизить значение равновесной цены к максимально рациональной цене для. Метод хорд или метод секущих. Рассматриваются алгоритмы реализации численных методов. деления отрезка пополам, метод касательных, метод хорд 1. деления отрезка. Метод хорд Программирование на C, C и Java. Метод хорд. Рассматриваемый метод так же, как и метод дихотомии предназначен для уточнения корня на интервале на концах которого левая часть.
В качестве метода был выбран метод хорд, который позволяет приблизить значение равновесной цены к максимально рациональной цене для. Метод хорд или метод секущих. Рассматриваются алгоритмы реализации численных методов. деления отрезка пополам, метод касательных, метод хорд 1. деления отрезка. Метод хорд Программирование на C, C и Java. Метод хорд. Рассматриваемый метод так же, как и метод дихотомии предназначен для уточнения корня на интервале на концах которого левая часть.
Заказать контрольную работу недорого. Решение контрольных на заказ
Поступая в университет на интересную специальность, думаем, что будем охотно выполнять каждое задание, чтобы набраться знаний, опыта. Но жизнь вносит коррективы. Преподаватели могут решить выдать срочные задания одновременно, или подвернется перспективная вакансия на рынке труда. Не исключена вероятность усталости, которая сбивает с ног. В таких условиях студенты ищут, где недорого заказать контрольную работу.
Студент любой специальности ищет возможности тратить меньше сил. Если выполнение промежуточного задания не входит в планы, поручите исполнителю с фриланс-биржи Автор24! Оформите заявку и выберите автора из числа тех, кто откликнулся.
Преимущества Автор24
Фриланс-биржа – это помощник студента, который не знает, сколько может стоить промежуточное задание, но хочет получить его быстро и недорого. Автор24 не устанавливает высокие комиссии посредника. Доверяет написание работы по маркетингу или математике только аспирантам и преподавателям этой специальности.
Преимущества Автор24:
- Сотрудничество онлайн – не нужно ехать на другой конец города, чтобы впервые встретиться с исполнителем или забрать готовое задание.
- Высокий уровень ответственности – автор не забудет сдать в сроки.
- Можно заказать только теорию или получить решение задачи – опишите тему, требования, сообщите, какую часть выполнили или планируете сделать самостоятельно.
Обращаясь к исполнителю, вы не получаете копию текста из открытых источников сети Интернет, которая может оказаться у одногруппника. Если требуется анализ процесса или решение задачи, автор сделает задания, чтобы по итогу контрольная работа стала допуском к зачету или основанием для получения высокого промежуточного балла.
Если требуется анализ процесса или решение задачи, автор сделает задания, чтобы по итогу контрольная работа стала допуском к зачету или основанием для получения высокого промежуточного балла.
Сроки выполнения
Не спешите искать, где купить готовую работу, если она нужна завтра утром или к следующему понедельнику. Оставьте заявку на бирже Автор24 – найдется автор, который сделает хорошо и вовремя. Если потребуется доработка или исправление, можете обратиться к нему снова. Сроки выполнения устанавливает студент-заказчик.
Стоимость зависит от таких критериев:
- Сложность – хотите найти ответы на теоретические вопросы или заказать решение задач, выполнение анализа, исследования.
- Тема – чем обширнее, тем дороже.
- Объем – сколько страниц и усилий требует контрольная работа на заказ.
Если хотите потратить выходные на отдых, а не нервные поиски научных материалов и попытки сделать глубокий анализ, оставьте заявку на бирже Автор24. Исполнители справятся с заданием за 2 дня, вне зависимости от объемов и сложности.
Решение системы линейных уравнений методом гаусса-жордана
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду.
 Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход. - Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.
метод Гаусса–Жордана — один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.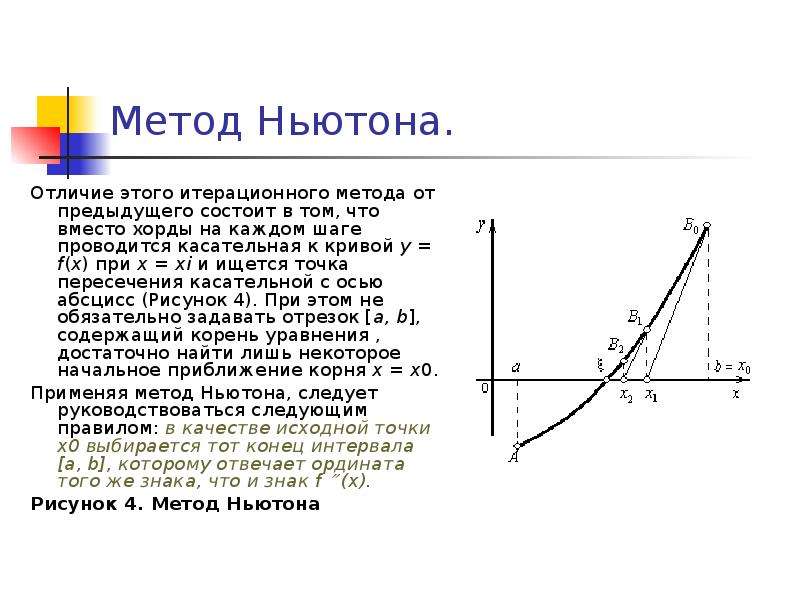
Алгоритм метода Гаусса
Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.
- На основании системы линейных уравнений составляем расширенную матрицу системы;
- Приводим матрицу к «треугольному» виду;
- Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
- В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;
Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:
Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.
Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.
На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:
- Рассматриваем строку i(начиная с первой). Если, элемент a i i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a 1 1 отличен от нуля — переходим к следующему шагу;
- Для каждой строки j, ниже i-й находим значение коэффициента K j =a j i /a i i ;
- Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a j k нов.=a j k -K j *a i k ; После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n — размерность матрицы A
- В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пa i i , которое и будет являтся определителем;
Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
4. Метод Жордана — Гаусса.
Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.
Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:
1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.
т.е. 02+=bc0.
Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;
2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
3. После того как все уравнения использованы для исключения неизвестных получено решение системы.
Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы
| a11x1 + a12x2 + … + a1nxn = b1,n+1 |
a21x1 + a22x2 + … + a2nxn = b2,n+1 |
| am1x1 + am2x2 + … + amnxn = bm.n+1 |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
Проведём следующие действия:
· К строке 2 добавим: -4 * Строку 1.
· К строке 3 добавим: -9 * Строку 1.
· К строке 3 добавим: -3 * Строку 2.
· Строку 2 делим на -2
· К строке 1 добавим: -1 * Строку 3.
· К строке 2 добавим: -3/2 * Строку 3.
· К строке 1 добавим: -1 * Строку 2.
В правом столбце получаем решение:
.
В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона)
Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1. 5) Графики…
5) Графики…
Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n — ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…
Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…
… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.
На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия.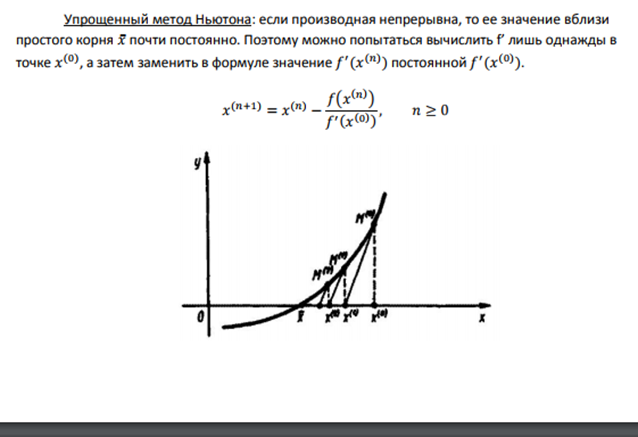 Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
…да, такое бывает только по любви =)
Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Ну, и совсем замечательно, если отработано понижение порядка определителя .
Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .
Не мудрствуя лукаво:
Пример 1
Решить систему методом Гаусса-Жордана
Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .
Идеальный с точки зрения простоты случай:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) К первой строке прибавили вторую строку, умноженную на –2.
Не могу удержаться от иллюстрации итоговой системы:
Ответ :
Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.
Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:
Пример 2
Решить систему линейных уравнений методом Гаусса-Жордана.
Решение : первая часть задания хорошо знакома:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.
(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.
(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7
(4) Третью строку разделили на 2.
Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .
Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:
Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
К первой строке прибавили третью строку.
(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.
(8) К первой строке прибавили вторую.
(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!
В результате элементарных преобразований получена эквивалентная исходной система:
Элементарно выражаем базисные переменные через свободную:
и записываем:
Ответ : общее решение:
В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.
И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .
Для самостоятельного решения:
Пример 3
Найти базисное решение с помощью элементарных преобразований
Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.
Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.
Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!
Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Продолжаем совершенствовать свои навыки на следующей прикладной задаче:
Как найти обратную матрицу методом Гаусса?Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.
Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
(Понятно, что обратная матрица должна существовать)
Демо-пример 4
Найдём обратную матрицу для матрицы с помощью элементарных преобразований.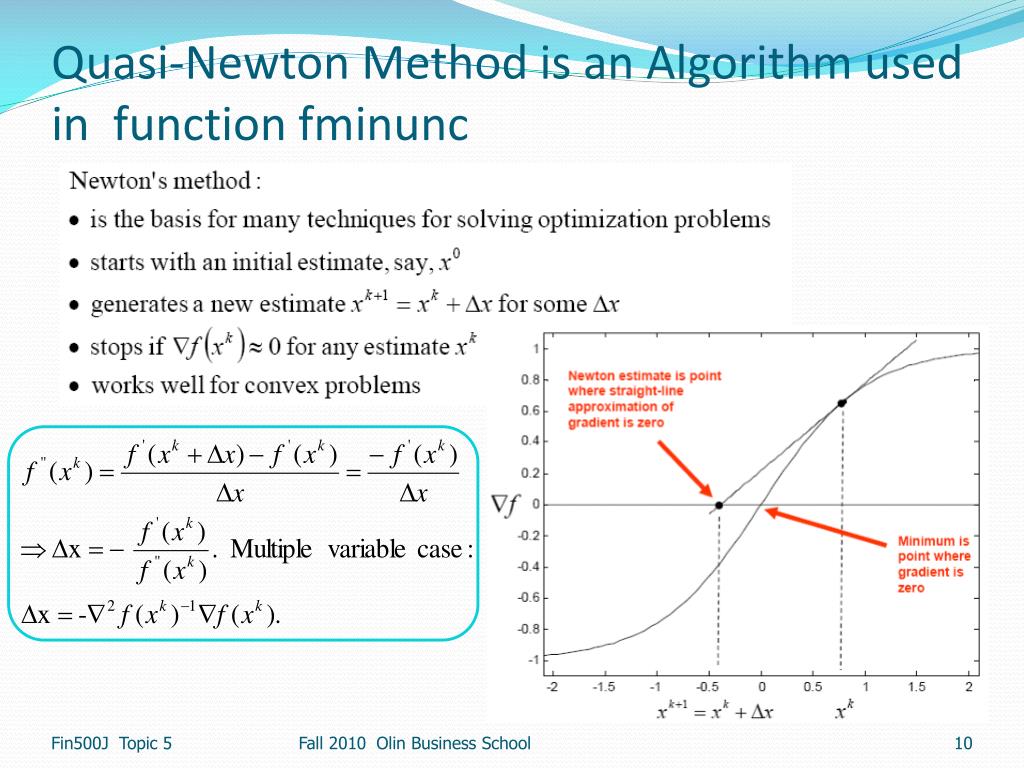 Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
(1) Ко второй строке прибавили первую строку, умноженную на –3.
(2) К первой строке прибавили вторую строку.
(3) Вторую строку разделили на –2.
Ответ :
Сверьтесь с ответом первого примера урока Как найти обратную матрицу?
Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:
Пример 5
Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :
(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.
(3) К 3-й строке прибавили 2-ю строку, умноженную на –1
Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.
К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.
(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:
(5) К 1-й и 2-й строкам прибавили третью строку.
(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.
(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.
(8) К первой строке прибавили вторую строку.
(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.
(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.
(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!
Таким образом, обратная матрица:
Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.
Ответ :
Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .
Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.
Аналогичное задание для самостоятельного решения:
Пример 6
Найти обратную матрицу методом Гаусса-Жордана.
Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .
Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .
На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».
И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .
Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:
Пример 7
Найти обратную матрицу с помощью элементарных преобразований
Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.
И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :
Ответ : общее решение:
Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:
(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.
(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :
Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.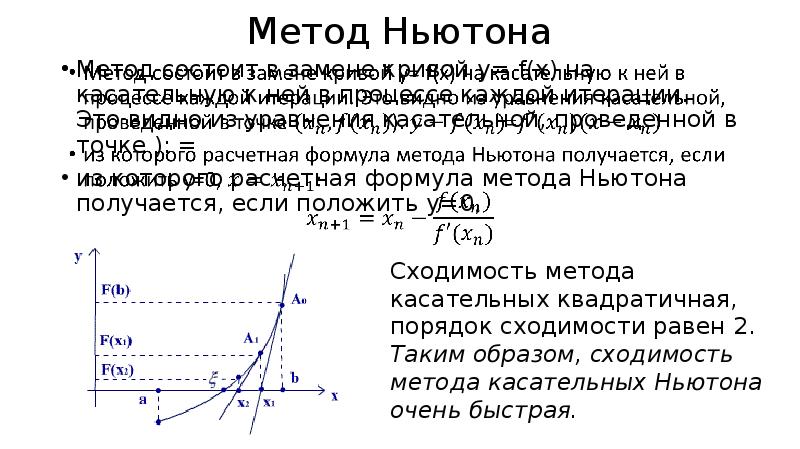
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:
(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :
Записывается в виде расширенной матрицы, т.е. в столбец свободных членов помещается в одну матрицу с коэффициентами неизвестных. Аалгоритм заключается в приведении исходной матрицы, характеризующей систему линейных уравнений, к единичной путем эквивалентных преобразований (домножения строки матрицы на константу и сложения с другой строкой матрицы). В качестве константы используется 1/a[i][i] , т.е. число, обратное по отношению к элементу диагонали. Естественно, в ряде случаев возникают проблемы, связанные с делением на ноль, которые решаются перестановкой строк и столбцов:
Весь алгоритм можно представить 10 пунктами:
В качестве опорной выбираем первую строку матрицы.
Если элемент опорной строки, индекс которого равен номеру опорной строки, равен нулю, то меняем всю опорную строку на первую попавшуюся строку снизу, в столбце которого нет нуля.
Все элементы опорной строки делим на первый слева ненулевой элемент этой строки.
Из оставшихся снизу строк вычитают опорную строку, умноженную на элемент, индекс которого равен номеру опорной строки.
В качестве опорной строки выбираем следующую строку.
Повторяем действия 2 – 5 пока номер опорной строки не превысит число строк.
В качестве опорной выбираем последнюю строку.
Вычитаем из каждой строки выше опорную строку, умноженную на элемент этой строки с индексом равным номеру опорной строки.
В качестве опорной строки выбираем строку выше.
Повторяем 8 – 9 пока номер опорной строки не станет меньше номера первой строки.
Пусть имеется система уравнений:
Запишем расширенную матрицу системы:
и выполним элементарные преобразования ее строк.
Для этого умножим первую строку на 1 и вычитаем из второй строки; затем умножим первую строку на 2 и вычтем из третьей строки.
В результате мы исключим переменную x 1 из всех уравнений, кроме первого. Получим:
Теперь вычтем из строки 3 строку 2, умноженную на 3:
Теперь вычитаем из 1 строки сначала 3 строку, а затем 2 строку:
После преобразований получаем систему уравнений:
Из этого следует, что система уравнений имеет следующее решение:
x1 = 1, x2 = 3 , x3 = -1
В качестве примера решим систему уравнений, представленную в виде матрицы (Таблица 1), методом Гаусса – Жордана.
Делим первую строку на 3 (элемент первой строки, расположенный на главной диагонали), получим:
Умножаем первую строку на 1 и вычитаем из второй строки. Умножаем первую строку на 6 и вычитаем из третьей строки. Получим:
В первом столбце все элементы кроме диагонального равны нулю, займемся вторым столбцом, для этого выберем вторую строку в качестве опорной. Вторая Делим ее на 17/3:
Вторая Делим ее на 17/3:
Умножаем строку 2 на -6 и вычитаем из третьей строки:
Теперь третья строка – опорная, делим ее на -33/17:
Умножаем опорную строку на 3/17 и вычитаем ее из второй. Умножаем третью строку на 1 и вычитаем ее из первой
Получена треугольная матрица, начинается обратный ход алгоритма (во время которого получим единичную матрицу). Вторая строка становится опорной. Умножаем третью строку на 4/3 и вычитаем ее из первой:
Последний столбец матрицы – решение системы уравнений.
Конвертер давления, механического напряжения, модуля Юнга • Популярные конвертеры единиц • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления. Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Давление в большинстве кастрюль-скороварок во время работы равно 1 атмосфере или 15 паскалям
Общие сведения
Воздушный шар, лопающийся в офисе TranslatorsCafe.com
В физике давление определяется как сила, действующая на единицу площади поверхности. Если две одинаковые силы действуют на одну большую и одну меньшую поверхность, то давление на меньшую поверхность будет больше. Согласитесь, гораздо страшнее, если вам на ногу наступит обладательница шпилек, чем хозяйка кроссовок. Например, если надавить лезвием острого ножа на помидор или морковь, овощ будет разрезан пополам. Площадь поверхности лезвия, соприкасающаяся с овощем, мала, поэтому давление достаточно велико, чтобы разрезать этот овощ. Если же надавить с той же силой на помидор или морковь тупым ножом, то, скорее всего, овощ не разрежется, так как площадь поверхности ножа теперь больше, а значит давление — меньше.
Например, если надавить лезвием острого ножа на помидор или морковь, овощ будет разрезан пополам. Площадь поверхности лезвия, соприкасающаяся с овощем, мала, поэтому давление достаточно велико, чтобы разрезать этот овощ. Если же надавить с той же силой на помидор или морковь тупым ножом, то, скорее всего, овощ не разрежется, так как площадь поверхности ножа теперь больше, а значит давление — меньше.
В системе СИ давление измеряется в паскалях, или ньютонах на квадратный метр.
Относительное давление
Иногда давление измеряется как разница абсолютного и атмосферного давления. Такое давление называется относительным или манометрическим и именно его измеряют, например, при проверке давления в автомобильных шинах. Измерительные приборы часто, хотя и не всегда, показывают именно относительное давление.
Атмосферное давление
Атмосферное давление — это давление воздуха в данном месте. Обычно оно обозначает давление столба воздуха на единицу площади поверхности. Изменение в атмосферном давлении влияет на погоду и температуру воздуха. Люди и животные страдают от сильных перепадов давления. Пониженное давление вызывает у людей и животных проблемы разной степени тяжести, от психического и физического дискомфорта до заболеваний с летальным исходом. По этой причине, в кабинах самолетов поддерживается давление выше атмосферного на данной высоте, потому что атмосферное давление на крейсерской высоте полета слишком низкое.
Люди и животные страдают от сильных перепадов давления. Пониженное давление вызывает у людей и животных проблемы разной степени тяжести, от психического и физического дискомфорта до заболеваний с летальным исходом. По этой причине, в кабинах самолетов поддерживается давление выше атмосферного на данной высоте, потому что атмосферное давление на крейсерской высоте полета слишком низкое.
Анероид содержит датчик — цилиндрическую гофрированную коробку (сильфон), связанную со стрелкой, которая поворачивается при повышении или понижении давления и, соответственно, сжатия или расширения сильфона
Атмосферное давление понижается с высотой. Люди и животные, живущие высоко в горах, например в Гималаях, адаптируются к таким условиям. Путешественники, напротив, должны принять необходимые меры предосторожности, чтобы не заболеть из-за того, что организм не привык к такому низкому давлению. Альпинисты, например, могут заболеть высотной болезнью, связанной с недостатком кислорода в крови и кислородным голоданием организма. Это заболевание особенно опасно, если находиться в горах длительное время. Обострение высотной болезни ведет к серьезным осложнениям, таким как острая горная болезнь, высокогорный отек легких, высокогорный отек головного мозга и острейшая форма горной болезни. Опасность высотной и горной болезней начинается на высоте 2400 метров над уровнем моря. Во избежание высотной болезни доктора советуют не употреблять депрессанты, такие как алкоголь и снотворное, пить много жидкости, и подниматься на высоту постепенно, например, пешком, а не на транспорте. Также полезно есть большое количество углеводов, и хорошо отдыхать, особенно если подъем в гору произошел быстро. Эти меры позволят организму привыкнуть к кислородной недостаточности, вызванной низким атмосферным давлением. Если следовать этим рекомендациям, то организму сможет вырабатывать больше красных кровяных телец для транспортировки кислорода к мозгу и внутренним органам. Для этого организм увеличат пульс и частоту дыхания.
Первая медицинская помощь в таких случаях оказывается немедленно. Важно переместить больного на более низкую высоту, где атмосферное давление выше, желательно на высоту ниже, чем 2400 метров над уровнем моря. Также используются лекарства и портативные гипербарические камеры. Это легкие переносные камеры, в которых можно повысить давление с помощью ножного насоса. Больного горной болезнью кладут в такую камеру, в которой поддерживается давление, соответствующее более низкой высоте над уровнем моря. Такая камера используется только для оказания первой медицинской помощи, после чего больного необходимо спустить ниже.
Некоторые спортсмены используют низкое давление, чтобы улучшить кровообращение. Обычно для этого тренировки проходят в нормальных условиях, а спят эти спортсмены в среде с низким давлением. Таким образом, их организм привыкает к высокогорным условиям и начинает вырабатывать больше красных кровяных телец, что, в свою очередь, повышает количество кислорода в крови, и позволяет достичь более высоких результатов в спорте. Для этого выпускаются специальные палатки, давление в которых регулируются. Некоторые спортсмены даже изменяют давление во всей спальне, но герметизация спальни — дорогостоящий процесс.
Скафандры
Многоразовый транспортный космический корабль НАСА «Атлантис» в экспозиции Космического центра имени Кеннеди.
Пилотам и космонавтам приходится работать в среде с низким давлением, поэтому они работают в скафандрах, позволяющих компенсировать низкое давление окружающей среды. Космические скафандры полностью защищают человека от окружающей среды. Их используют в космосе. Высотно-компенсационные костюмы используют пилоты на больших высотах — они помогают пилоту дышать и противодействуют низкому барометрическому давлению.
Гидростатическое давление
Гидростатическое давление — это давление жидкости, вызванное силой тяжести. Это явление играет огромную роль не только в технике и физике, но также и в медицине. Например, кровяное давление — это гидростатическое давление крови на стенки кровеносных сосудов. Кровяное давление — это давление в артериях. Оно представлено двумя величинами: систолическим, или наибольшим давлением, и диастолическим, или наименьшим давлением во время сердцебиения. Приборы для измерения артериального давления называются сфигмоманометрами или тонометрами. За единицу артериального давления приняты миллиметры ртутного столба.
Цифровой аппарат для измерения давления, также называемый сфигмоманометром
Кружка Пифагора — занимательный сосуд, использующий гидростатическое давление, а конкретно — принцип сифона. Согласно легенде, Пифагор изобрел эту чашку, чтобы контролировать количество выпитого вина. По другим источникам эта чашка должна была контролировать количество выпитой воды во время засухи. Внутри кружки находится изогнутая П-образная трубка, спрятанная под куполом. Один конец трубки длиннее, и заканчивается отверстием в ножке кружки. Другой, более короткий конец, соединен отверстием с внутренним дном кружки, чтобы вода в чашке наполняла трубку. Принцип работы кружки схож с работой современного туалетного бачка. Если уровень жидкости становится выше уровня трубки, жидкость перетекает во вторую половину трубки и вытекает наружу, благодаря гидростатическому давлению. Если уровень, наоборот, ниже, то кружкой можно спокойно пользоваться.
Давление в геологии
Кристалл кварца, освещенный лазерной указкой
Давление — важное понятие в геологии. Без давления невозможно формирование драгоценных камней, как природных, так и искусственных. Высокое давление и высокая температура необходимы также и для образования нефти из остатков растений и животных. В отличие от драгоценных камней, в основном образующихся в горных породах, нефть формируется на дне рек, озер, или морей. Со временем над этими остатками собирается всё больше и больше песка. Вес воды и песка давит на остатки животных и растительных организмов. Со временем этот органический материал погружается глубже и глубже в землю, достигая нескольких километров под поверхностью земли. Температура увеличивается на 25 °C с погружением на каждый километр под земной поверхностью, поэтому на глубине нескольких километров температура достигает 50–80 °C. В зависимости от температуры и перепада температур в среде формирования, вместо нефти может образоваться природный газ.
Алмазные инструменты
Природные драгоценные камни
Образование драгоценных камней не всегда одинаково, но давление — это одна из главных составных частей этого процесса. К примеру, алмазы образуются в мантии Земли, в условиях высокого давления и высокой температуры. Во время вулканических извержений алмазы перемещаются в верхние слои поверхности Земли благодаря магме. Некоторые алмазы попадают на Землю с метеоритов, и ученые считают, что они образовались на планетах, похожих на Землю.
Синтетические драгоценные камни
Производство синтетических драгоценных камней началось в 1950-х годах, и набирает популярность в последнее время. Некоторые покупатели предпочитают природные драгоценные камни, но искусственные камни становятся все более и более популярными, благодаря низкой цене и отсутствию проблем, связанных с добычей натуральных драгоценных камней. Так, многие покупатели выбирают синтетические драгоценные камни потому, что их добыча и продажа не связана с нарушением прав человека, детским трудом и финансированием войн и вооруженных конфликтов.
Одна из технологий выращивания алмазов в лабораторных условиях — метод выращивания кристаллов при высоком давлении и высокой температуре. В специальных устройствах углерод нагревают до 1000 °C и подвергают давлению около 5 гигапаскалей. Обычно в качестве кристалла-затравки используют маленький алмаз, а для углеродной основы применяют графит. Из него и растет новый алмаз. Это самый распространенный метод выращивания алмазов, особенно в качестве драгоценных камней, благодаря низкой себестоимости. Свойства алмазов, выращенных таким способом, такие же или лучше, чем свойства натуральных камней. Качество синтетических алмазов зависит от метода их выращивания. По сравнению с натуральными алмазами, которые чаще всего прозрачны, большинство искусственных алмазов окрашено.
Благодаря их твердости, алмазы широко используются на производстве. Помимо этого ценятся их высокая теплопроводность, оптические свойства и стойкость к щелочам и кислотам. Режущие инструменты часто покрывают алмазной пылью, которую также используют в абразивных веществах и материалах. Большая часть алмазов в производстве — искусственного происхождения из-за низкой цены и потому, что спрос на такие алмазы превышает возможности добывать их в природе.
Некоторые компании предлагают услуги по созданию мемориальных алмазов из праха усопших. Для этого после кремации прах очищается, пока не получится углерод, и затем на его основе выращивают алмаз. Изготовители рекламируют эти алмазы как память об ушедших, и их услуги пользуются популярностью, особенно в странах с большим процентом материально обеспеченных граждан, например в США и Японии.
Метод выращивания кристаллов при высоком давлении и высокой температуре
Метод выращивания кристаллов при высоком давлении и высокой температуре в основном используется для синтеза алмазов, но с недавнего времени этот метод помогает усовершенствовать натуральные алмазы или изменить их цвет. Для искусственного выращивания алмазов используют разные прессы. Самый дорогой в обслуживании и самый сложный из них — это пресс кубического типа. Он используется в основном для улучшения или изменения цвета натуральных алмазов. Алмазы растут в прессе со скоростью примерно 0,5 карата в сутки.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Калькулятор давления (перевод бар в МПа, кгс и psi)
Современный калькулятор перевода бар в мпа – это многофункциональный инструмент, который оперативно переводит любые введенные величины. Онлайн-калькулятор работает оперативно и безошибочно. Богатый функционал позволяет орудовать большой выборкой исходных и вторичных величин.
Как пользоваться онлайн-калькулятором?
Описание функционала калькулятора
- Левая колонка калькулятора. Содержит выборку исходных величин. Под каждым столбцом отображается точное техническое описание величины.
- Правая колонка калькулятора. Содержит конечную величину перевода. Под каждым столбцом есть подробное описание конечной величины перевода.
- Получение результатов. Для того, чтобы перевести мпа в паскали, введите значения исходной величины. Онлайн-калькулятор оперативно переведет исходные данные.
Обратите внимание на особенность округления. Целые числа при переводе, рассматриваются как точные до 15 знаков.
Допустимое число цифр после запятой, составляет 10 единиц.
Для перевода чрезвычайно больших и малых чисел, применяется отдельное понятие: компьютерная экспоненциальная запись. Используя данный метод, можно записать числа с высоким сопутствующим сокращением.
Для кого разработан онлайн-калькулятор
- Для специалистов, которые проводят научные исследования. Вы можете без труда перевести, к примеру, бар в торр.
- Для владельцев транспортных средств. Очень часто нужно, например, перевести МПа в бары. Эти данные используются для анализа состояния топливной магистрали, а также для проверки номинального давления в шинах автомобиля.
- Автовладельцы используют калькулятор при переводе отдельного значения в МПа в процессе заправки деталей авто фреоном.
Таблица перевода измерений бар в мпа, кгс, psi и обратно
Интерактивный онлайн калькулятор предназначен для перевода единиц измерения давления.
Давление — соотношение силы к площади поверхности.
Формула: P = F/S
Международная единица измерения давления – Паскаль. Паскаль упрощает формулировку единиц измерения давления, заменяя отношение силы к площади в виде Ньютона на квадратный метр.
Давление обозначается как кПа, МПа.
В разных сферах деятельности, давление измеряется по-разному. Давление в большинстве случаев обозначают научными величинами: бары, атмосферы, мега паскали, квадратные дюймы или технические атмосферы.
Поэтому рекомендуется изучить таблицу соотношений, представленной на сервисе.
Перед тем, как произвести перевод, изучите специфику градации. Механическое воздействие в определенной точке измеряется в традиционной величине – паскали. Один паскаль равняется одному ньютону, паттерны которого применяет онлайн–калькулятор.
Однако могут возникнуть сложности при переводе Psi в нужную величину, когда используются британские системы измерения: фунты, квадратные дюймы.
Материал по теме: Калькулятор для перевода силы тока в мощность
Приборы для измерения давления
Основным прибором для получения значения давления в шинах является цифровой измеритель – манометр. В продаже имеются электронные или механические приборы.
Что такое бар (bar)?
Общепринятая единица измерения давления в bar представляет собой 1 атмосферу.
Что такое кгс (кГ)?
1 кгс расшифровывается как килограмм-сила.
Что такое Psi?
Psi обозначает давление, рассчитанное в фунтах на квадратный дюйм. Давление в psi принято для стран с дюймовой системой измерения.
Что такое мегапаскали (МПа)?
В СИ выделяют единицу измерения механического напряжения (давления) – Паскаль.
1 МПА = 1000000 Паскаль.
Онлайн-калькулятор: метод Ньютона
Этот онлайн-калькулятор реализует метод Ньютона (также известный как метод Ньютона – Рафсона) с использованием калькулятора производных для получения аналитической формы производной заданной функции, поскольку этого требует метод. Немного теории, чтобы напомнить основы метода, можно найти под калькулятором.
Метод Ньютона
Точность вычисленийЦифры после десятичной точки: 4
Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера.
Скачать закрыть
content_copy Ссылка сохранить Сохранить расширение Виджет
Метод Ньютона – Рафсона
В численном анализе метод Ньютона (также известный как метод Ньютона – Рафсона), названный в честь Исаака Ньютона и Джозефа Рафсона, представляет собой метод для последовательного поиска более точных приближений к корням (или нулям) вещественной функции.
Метод начинается с функции f, определенной над действительными числами x, производной функции f ‘и начальным предположением x0 для корня функции f.Если функция удовлетворяет предположениям, сделанным при выводе формулы, и первоначальное предположение близко, то лучшее приближение x1 равно
.Геометрически (x1, 0) — это пересечение оси x и касательной к графику f в точке (x0, f (x0)).
Процесс повторяется до тех пор, пока не будет достигнуто достаточно точное значение.
Анимация метода Ньютона Ральфа Пфайфера (https://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif)Идея метода заключается в следующем: каждый начинает с первоначального предположения, которое достаточно близко к истинному корню, затем функция аппроксимируется ее касательной (которую можно вычислить с помощью инструментов исчисления) и вычисляется x-точку пересечения этой касательной (что легко сделать с помощью элементарной алгебры).Этот пересечение по оси x обычно будет лучшим приближением к корню функции, чем исходное предположение, и метод может быть повторен.
Метод Ньютона — чрезвычайно мощный метод — в целом сходимость квадратичная: по мере того, как метод сходится к корню, разница между корнем и приближением возводится в квадрат (количество точных цифр примерно удваивается) на каждом шаге. Однако с этим методом связаны некоторые трудности: сложность вычисления производной функции, несходимость метода к корню, если не выполняются предположения, сделанные при доказательстве квадратичной сходимости метода Ньютона, медленная сходимость для корней кратность больше 1
Калькулятор по методу Ньютона — поиск корней методом Ньютона
Онлайн-калькулятор по методу Ньютона позволяет определить приближение корня действительной функции.Калькулятор использует формулу метода Ньютона для отображения итерации инкрементного вычисления. Здесь вы можете узнать больше о методе Ньютона, его формулах и примерах.
Что такое метод Ньютона?В исчислении метод Ньютона (также известный как метод Ньютона-Рафсона) представляет собой алгоритм поиска корня, который обеспечивает более точное приближение к корню (или нулю) действительной функции.
Метод Ньютона основан на касательных прямых. Основная идея состоит в том, что если x достаточно близко к корню f (x), касательная к графику будет пересекать ось x в точке (x, f (x)) в точке, которая ближе к корню. чем х.
(изображение)
Однако онлайн-калькулятор касательной позволяет определить касательную линию к неявному, параметрическому, полярному и явному в определенной точке.
Формула метода Ньютона:Если x_n является оценочным решением функции f (x), которое равно нулю, и если f ’(x_n) не равно нулю, то следующая оценка дается формулой
x_n + 1 = x_n — f (x_n) / f ’(x_n)
Эта формула метода Ньютона используется калькулятором метода Ньютона для нахождения корня функции с действительным знаком.2 = 1,5625
F ’(x_2) = f’ (1,25) = 2 (1,25) = 2,5
Теперь, используя формулу метода Ньютона:
X_3 = x_2 — f (x_2) / f ’(x_2)
X_3 = 1,25 — 1,5625 / 2,5
X_3 = 0,625
Следовательно, калькулятор по методу Ньютона дает таблицу итераций для тех же значений:
| Шаг | x | f (x) | f ‘(x) |
| 1 | 2.5 | 25 | 10 |
| 2 | 1,25 | 6,25 | 5 |
| 3 | 0,625 | 1,5625 | 2,5 |
Однако онлайн-калькулятор производной позволяет определить производную функции по заданной переменной.
Как работает калькулятор по методу Ньютона? Калькулятор метода Ньютонареализует метод Ньютона для нахождения корня действительной функции и выполнения итераций, следуя этим инструкциям:
Ввод:- Сначала подставьте вещественную функцию и ее производную (необязательно).
- Теперь вставьте начальное значение и максимальное количество итераций в соответствии с требованиями.
- Затем добавьте значащую цифру в соответствующее поле.
- Нажмите кнопку «Рассчитать», чтобы найти итерации заданной функции.
- Калькулятор по методу Ньютона отображает заданную функцию и ее производную.
- Калькулятор применяет правило мощности к реальной функции и предоставляет таблицу итераций в соответствии с заданными значениями.
- Он дает пошаговое решение для всех итераций за доли секунды.
Если производная равна нулю, метод Ньютона не работает. Когда производная близка к нулю, касательная почти горизонтальна, поэтому она может превышать требуемый корень (числовая сложность).
Всегда ли будет сходиться метод Ньютона?Метод Ньютона не всегда сходится.Его теория конвергенции относится к «локальной» конвергенции, что означает, что она должна начинаться около корня, а «около» относится к функции, с которой вы хотите иметь дело.
Почему метод Ньютона быстрее, чем метод деления пополам?Функция f должна иметь непрерывную производную. Если вы начнете слишком далеко от корня, метод Ньютона может не сойтись. Однако, когда он сходится, он быстрее, чем метод деления пополам, и обычно является квадратичным.
Будет ли расходиться метод Ньютона?Если функция не может быть непрерывно дифференцирована рядом с корнем, метод Ньютона всегда будет расходиться и терпеть неудачу, если решение не будет угадано с первой попытки.
Какой метод сходимости самый быстрый?Метод Ньютона — очень хороший метод. Когда условия выполняются, метод Ньютона сходится, и скорость сходимости выше, чем почти любая другая альтернативная итерационная схема, основанная на методе преобразования исходной f (x) в функцию с фиксированной точкой.
Заключение:Воспользуйтесь этим онлайн-калькулятором по методу Ньютона, чтобы найти действительные корни нелинейных функций. Потому что этот калькулятор предоставляет полную таблицу итераций с использованием формулы метода Ньютона.Поиск итераций вручную — это длительный и трудоемкий метод. Чтобы вам было удобно, наш онлайн-калькулятор ньютонов выполняет все расчеты, связанные с методом Ньютона, бесплатно и быстро.
Артикул:Из источника в Википедии: Метод Ньютона, Сложность вычисления производной функции, Неспособность метода сходиться к корню, Превышение.
Из источника онлайн-заметок Пола: Точка покоя, Плохая начальная оценка, Устранение несходимости, Анализ, Области притяжения.
Из источника AMSI: Поиск решения с помощью геометрии, Ключевой расчет, Алгоритм, Использование метода Ньютона, Чувствительная зависимость от начальных условий.
ДОМ Главы курса Основы калькулятора Обзор математики Основные понятия Advanced Concepts
Секционные тесты Предварительное испытание Пост-тест Полезные материалы Глоссарий Онлайн-калькуляторы Калькулятор окислительно-восстановительного потенциала Калькулятор кинетики Аррениуса Калькулятор термодинамики Калькулятор ядерного распада Регрессия методом наименьших квадратов Решатель уравнений метода Ньютона Калькулятор сжимаемости Калькулятор перевода единиц Калькулятор номенклатуры Ссылки по теме Калькуляторы Texas Instruments Калькуляторы Casio Калькуляторы Sharp Калькуляторы Hewlett Packard Кредиты Связаться с веб-мастером | Введите функцию и ее производную, затем укажите параметры ниже.2 |
| Производная (наклон)
функция: 2 * x | |
| Начальные значения | |
|---|---|
| Начальное значение X | |
| Округлите окончательное значение до этого числа мест: | |
| Критерии завершения | |
| Максимум: | |
| Остановить, когда функция близка к нулю Остановить, когда x останется прежним | От нуля до этого числа десятичных разрядов: |
| Для такого количества итераций: До такого количества десятичных знаков: | r>|
Вернуться на главную страницу метода Ньютона-Рафсона
Разработано
The Shodor Образовательный фонд, Inc.
Авторское право и копия 1998 г.
Последнее изменение:
Вопросы или комментарии об этой странице следует направлять по адресу [email protected]
Калькулятор интерполяционных полиномов Ньютона — онлайн-интерполяция
Поиск инструмента
Интерполирующий многочлен Ньютона
Инструмент для нахождения уравнения кривой с помощью алгоритма Ньютона. Алгоритм ньютоновской интерполяции — это полиномиальная интерполяция / аппроксимация, позволяющая получить полином Лагранжа как уравнение кривой, зная ее точки.
Результаты
Интерполирующий многочлен Ньютона — dCode
Тег (и): Функции
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор ньютоновской интерполяции
Ответы на вопросы (FAQ)
Как найти уравнение кривой с помощью алгоритма Ньютона?
dCode позволяет использовать метод Ньютона для полиномиальной интерполяции, чтобы найти уравнение полинома (идентичного Лагранжу) в форме Ньютона из уже известных значений функции. k {\ frac {y_j} {\ prod_ {0 \ leq i \ leq k, \, i \ neq j} (x_j-x_i)}} $$ они вмешиваются в вычисление интерполяции Ньютона.
NB: если $ k = 0 $, то продукт $ \ prod (x_j-x_i) = 1 $ (пустой продукт)
Задайте новый вопросИсходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Интерполирующий полином Ньютона». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент « Полинома интерполяции Ньютона » (преобразователь, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любые Функция Interpolating Polynomial (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести) написана на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)) и никакая загрузка данных, скрипт, копипаст или доступ к API для ‘Интерполирующего полинома Ньютона’ не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
ньютон, интерполяция, интерполяция, уравнение, полином, лагранж, кривая, точка, значение, функция
Ссылки
Источник: https: // www.dcode.fr/newton-interpolating-polynomial
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Исчисление I — Метод Ньютона
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. , вероятно, вы пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-13: Метод Ньютона
Следующее приложение, которое мы рассмотрим в этой главе, — это важное приложение, которое используется во многих областях.Если вы до сих пор следили за главой, вполне возможно, что у вас сложилось впечатление, что многие из рассмотренных нами приложений созданы нами для того, чтобы вы работали. Это прискорбно, потому что все приложения, которые мы рассмотрели до этого момента, являются реальными приложениями, которые действительно используются в реальных ситуациях. Проблема часто заключается в том, что для работы с более значимыми примерами приложений нам потребуется больше знаний о науке и / или физике, стоящих за этой проблемой, чем мы обычно имеем.Без этих знаний мы вынуждены приводить довольно упрощенные примеры, которые часто не кажутся очень реалистично, и поэтому трудно понять, что приложение, которое мы рассматриваем, является настоящим приложением.
Это изменится в этом разделе. Это приложение, которое мы все можем понять, и все мы можем понять, что иногда нужно делать это, даже если мы не понимаем физику / науку, лежащую в основе реального приложения.
В этом разделе мы рассмотрим метод приближения решений уравнений.Все мы знаем, что уравнения нужно решать время от времени, и на самом деле мы сами решили довольно много уравнений к этому моменту. Во всех примерах, которые мы рассмотрели к этому моменту, мы действительно смогли найти решения, но не всегда возможно сделать это точно и / или выполнить работу вручную. Вот тут-то и пригодится это приложение. Итак, давайте посмотрим, что это за приложение.
Предположим, что мы хотим приблизить решение к \ (f \ left (x \ right) = 0 \), а также предположим, что мы каким-то образом нашли начальное приближение к этому решению, скажем, \ ({x_0} \).Это начальное приближение, вероятно, не так уж и хорошо, на самом деле это может быть не более чем быстрое предположение, которое мы сделали, и поэтому мы хотели бы найти лучшее приближение. Сделать это достаточно просто. Сначала мы получим касательную к \ (f \ left (x \ right) \) в точке \ ({x_0} \).
\ [y = f \ left ({{x_0}} \ right) + f ‘\ left ({{x_0}} \ right) \ left ({x — {x_0}} \ right) \]Теперь взгляните на график ниже.
Синяя линия (если вы все равно читаете это в цвете…) — это касательная линия в точке \ ({x_0} \).Мы видим, что эта линия пересекает ось \ (x \) гораздо ближе к фактическому решению уравнения, чем \ ({x_0} \). Назовем эту точку, где касательная в \ ({x_0} \) пересекает \ (x \) — ось \ ({x_1} \), и мы будем использовать эту точку в качестве нашего нового приближения к решению.
Итак, как нам найти эту точку? Мы знаем его координаты, \ (\ left ({{x_1}, 0} \ right) \), и мы знаем, что он находится на касательной, поэтому подключите эту точку к касательной и решите относительно \ ({x_1} \ ) следующим образом:
\ [\ begin {align *} 0 & = f \ left ({{x_0}} \ right) + f ‘\ left ({{x_0}} \ right) \ left ({{x_1} — {x_0}} \ справа) \\ {x_1} — {x_0} & = — \ frac {{f \ left ({{x_0}} \ right)}} {{f ‘\ left ({{x_0}} \ right)}} \ \ {x_1} & = {x_0} — \ frac {{f \ left ({{x_0}} \ right)}} {{f ‘\ left ({{x_0}} \ right)}} \ end {align * } \]Итак, мы можем найти новое приближение при условии, что производная не равна нулю в исходном приближении.
Теперь мы повторяем весь процесс, чтобы найти еще лучшее приближение. Мы формируем касательную линию к \ (f \ left (x \ right) \) в \ ({x_1} \) и используем ее корень, который мы назовем \ ({x_2} \), как новое приближение к фактическое решение. Если мы сделаем это, мы придем к следующей формуле.
\ [{x_2} = {x_1} — \ frac {{f \ left ({{x_1}} \ right)}} {{f ‘\ left ({{x_1}} \ right)}} \]Эта точка также показана на графике выше, и мы можем видеть из этого графика, что если мы продолжим следовать этому процессу, мы получим последовательность чисел, которая очень приближается к фактическому решению.Этот процесс называется методом Ньютона.
Вот общий метод Ньютона
Метод Ньютона
Если \ ({x_n} \) является приближением решения \ (f \ left (x \ right) = 0 \) и если \ (f ‘\ left ({{x_n}} \ right) \ ne 0 \ ) следующее приближение дается выражением,
\ [{x_ {n + 1}} = {x_n} — \ frac {{f \ left ({{x_n}} \ right)}} {{f ‘\ left ({{x_n}} \ right)}} \]Это должно привести к вопросу, когда нам остановиться? Сколько раз мы проходим этот процесс? Одна из наиболее распространенных точек остановки в процессе — это продолжение до тех пор, пока два последовательных приближения не согласятся с заданным количеством десятичных знаков.
Перед тем, как приступить к работе с какими-либо примерами, мы должны решить две проблемы. Во-первых, нам действительно нужно решить \ (f \ left (x \ right) = 0 \), чтобы применить метод Ньютона. На самом деле это не такая уж большая проблема, но мы должны убедиться, что уравнение находится в этой форме, прежде чем использовать метод.
Во-вторых, нам нужно каким-то образом получить начальное приближение к решению (, т.е. нам как-то понадобится \ ({x_0} \)). Один из наиболее распространенных способов получить \ ({x_0} \) — нарисовать график функции и использовать его для получения оценки решения, которое мы затем используем как \ ({x_0} \).Другой распространенный метод — если мы знаем, что есть решение функции в интервале, мы можем использовать середину интервала как \ ({x_0} \).
Давайте поработаем на примере метода Ньютона.
Пример 1 Используйте метод Ньютона для определения приближения к решению \ (\ cos x = x \), которое лежит в интервале \ (\ left [{0,2} \ right] \). Найдите приближение до шести знаков после запятой. Показать решениеВо-первых, обратите внимание, что нам не давали первоначального предположения.Однако нам дали время посмотреть. Мы будем использовать это, чтобы получить наше первоначальное предположение. Как отмечалось выше, общее практическое правило в этих случаях состоит в том, чтобы принять начальное приближение за середину интервала. Итак, мы будем использовать \ ({x_0} = 1 \) в качестве нашего первоначального предположения.
Затем напомним, что должно иметь функцию в виде \ (f \ left (x \ right) = 0 \). Поэтому сначала перепишем уравнение как,
\ [\ cos x — x = 0 \]Теперь мы можем записать общую формулу для метода Ньютона.Это часто немного упрощает работу, поэтому, как правило, это неплохая идея.
\ [{x_ {n + 1}} = {x_n} — \ frac {{\ cos x_ {n} — x_ {n}}} {{- \ sin x_ {n} — 1}} \]Давайте теперь получим первое приближение.
\ [{x_1} = 1 — \ frac {{\ cos \ left (1 \ right) — 1}} {{- \ sin \ left (1 \ right) — 1}} = 0,7503638679 \]Здесь мы должны указать, что фраза «шесть знаков после запятой» не означает, что нужно просто получить \ ({x_1} \) до шести знаков после запятой, а затем остановиться.Вместо этого это означает, что мы продолжаем, пока два последовательных приближения не согласятся с шестью десятичными знаками.
Учитывая это условие остановки, нам явно нужно сделать хотя бы один шаг дальше.
\ [{x_2} = 0,7503638679 — \ frac {{\ cos \ left (0,7503638679 \ right) — 0,7503638679}} {{- \ sin \ left ({0,7503638679} \ right) — 1}} = 0,73909 \]Хорошо, мы делаем успехи. У нас есть приближение к 1 десятичному знаку. Давайте сделаем еще один, оставив детали вычислений вам.
\ [{x_3} = 0,73334 \] Мы разделили до трех десятичных знаков. Нам понадобится еще один.
\ [{x_4} = 0,73332 \] И теперь у нас есть два приближения, которые согласуются с 9 десятичными знаками, и мы можем остановиться. Предположим, что решение приблизительно равно \ ({x_4} = 0,73332 \).
В этом последнем примере мы увидели, что нам не нужно делать слишком много вычислений, чтобы метод Ньютона дал нам приближение в желаемом диапазоне точности.Так будет не всегда. Иногда для достижения желаемой точности требуется много итераций процесса, а иногда он может полностью выйти из строя.
Следующий пример немного глупый, но он указывает на сбой метода.
Пример 2 Используйте \ ({x_0} = 1 \), чтобы найти приближение к решению \ (\ sqrt [3] {x} = 0 \).
Показать решение Да, глупый пример. Ясно, что решение - \ (x = 0 \), но это действительно очень важный момент.{- \ frac {2} {3}}}} = {x_n} - 3 {x_n} = - 2 {x_n} \]
На самом деле, здесь нам не нужно делать никаких вычислений. Эти вычисления удаляются все дальше и дальше от решения \ (x = 0 \) с каждой итерацией. Вот несколько вычислений, чтобы понять суть дела.
\ [\ begin {align *} {x_1} & = - 2 \\ {x_2} & = 4 \\ {x_3} & = - 8 \\ {x_4} & = 16 \\ & т. д. \ end {align * } \] Итак, в этом случае метод терпит неудачу и дает очень эффектную ошибку.
Итак, нам нужно быть немного осторожнее с методом Ньютона. Обычно он быстро находит приближение к уравнению. Однако бывают случаи, когда для этого потребуется много работы или когда это вообще не сработает.
Метод Ньютонов на TI-83/84 или TI-89 Метод
Ньютон на TI-83/84 или TI-89 Авторские права 20022020 Стэн Браун
Резюме: Метод Ньютона - это быстрый способ найти реальные решения уравнения .Ваш TI-83/84 или TI-89 может
Метод Ньютона для вас, и на этой странице показаны два способа.
Метод Ньютона - это итеративный , что означает, что он использует
процесс или рецепт для перехода от каждого предположения x n к следующему
угадайте x n +1 .
Рецепт метода Ньютона показан справа.
Этот рецепт проводит касательную к кривой в точке x = x n , находит значение x , где эта строка
пересекает ось x и использует это значение x в качестве следующего предположения x n +1 .В любом учебнике по математическому анализу есть иллюстрация этого метода.
То, что мы предполагаем, является нулем вещественной функции.
Если предположения постепенно приближаются к желаемой точке, мы говорим
что метод сходится к .
Оказывается, если метод Ньютона вообще сходится к определенному
ноль, быстро сходится , что означает, что требуется
относительно немного шагов.
(См. В вашем учебнике условия, в которых сходится метод Ньютона.)
Чтобы запустить любой из методов, запишите уравнение, которое вы хотите решить, в форму f ( x ) = 0. Технически метод Ньютона находит нули функции, а не корни
уравнение. Поэтому вы бы переписали что-то вроде x sin x = 2 как x sin x - 2 = 0.
(Помните из алгебры, что нуль функции f совпадает с
решение или корень уравнения f ( x ) = 0 или x пересечение графика f .)
Метод 1: вы дифференцируете
Чтобы попрактиковаться в методе Ньютона, давайте найдем квадрат.
корень 2, так как ответ будет несложно проверить.√2 является решением x = √2 или
х = 2.
(Да, −√2 - решение
это новое уравнение, но не исходное уравнение. Но хорошо получи
положительный корень из-за нашего выбора первоначального предположения.)
Для начала перепишем в виде f ( x ) = х - 2 = 0.
Затем дифференцируйте функцию: f ′ ( x ) = 2 x .
Введите функцию как Y1 и производную как Y2. TI-83/84: нажмите [ Y = ].] [ 2 ] [–] [ 2 ] [ ENTER ]
В Y2 нажмите [ 2 ] [ X ] [ ENTER ], затем [ ▲ ] [ F4 ]
чтобы сообщить TI-89 не отображать производную Y2.
(необязательно) Изобразите функцию, чтобы спланировать свое первоначальное предположение. TI-83/84: нажмите [ ZOOM ] [ 6 ], чтобы ZStandard (стандартный зум). TI-89: Нажмите [ F2 ] [ 6 ] для ZoomStd . Вернуться на главный экран. TI-83/84: Нажмите [ 2nd MODE делает QUIT ]. TI-89: Нажмите [ 2-я ESC делает QUIT ].
Затем вы установите x на ваше первое предположение, затем запрограммируете
рецепт для следующего предположения. Давайте для начала угадаем 1.
Сохраните первоначальное предположение, 1, в x. TI-83/84: нажмите [ 1 ] [ STO → ] [ x, T, θ, n ]. TI-89: нажмите [ 1 ] [. ] [ STO → ] [ X ].
Десятичная точка важна: она сообщает TI-89, что вы хотите
десятичные приближения, а не точные числа. Поскольку y1 является левой частью решаемого уравнения
и y2 - производная, вы хотите вычесть y1 / y2 из x и сохранить
результат в x как следующее предположение.
После первой итерации вы увидите результат 1,5. TI-83/84: [ x, T, θ, n ] [ - ]
[ VARS ] [ ► ] [ 1 ] [ 1 ] вставляет Y1 на экран.
[ VARS ] [ ► ] [ 1 ] [ 2 ] вставок / Y2 для растрирования.
[ STO → ] [ x, T, θ, n ] [ ENTER ]
вычисляет следующее предположение и сохраняет его в X.
TI-89: Вы должны передать аргумент (x) двум функциям.
[ X ] [–] [ Y ] [ 1 ] [ (] [ X ] [) ] [ Y ] [ 2 ] [ (] [ X ] [) ] [ STO → ] [ X ]
Теперь повторяйте, пока предположения не сойдутся. Оба: каждое дополнительное нажатие клавиши [ ENTER ] вычисляет дальнейшее предположение.
Еще через четыре итерации процесс сходился.] [ 2 ], чтобы убедиться, что
это действительно квадратный корень из 2.) ТИ-83/84: TI-89:
Метод 2: Программа калькулятора
TI-83/84 и TI-89 запрограммированы несколько иначе.
Вы можете скачать программы для обоих семейств калькуляторов в файле
NEWTON.ZIP
(31 КБ, исправленное
28 декабря 2016 г.) или введите
программа, следуя инструкциям ниже.
Программа TI-83/84 для запуска метода Ньютона должна работать
для любой функции, даже той, которую вы не умеете различать,
потому что он вычисляет производную численно.Программа ТИ-89 будет
работают для любой дифференцируемой функции, потому что TI-89
находит для вас алгебраическую производную.
Создайте новую программу. TI-83/84: [ PRGM ] [ ◄ ] [ 1 ] TI-89: [ APPs ] [ 7 ] [ 3 ] Назовите программу NEWTON. TI-83/84: Калькулятор уже переключил вас в альфа-режим. Ищите зеленых букв над каждой клавишей и нажмите
[ N ] [ E ] [ W ] [ T ] [ O ] [ N ].Внимательно проверьте экран и
при необходимости сделайте резервную копию и внесите исправления. Нажмите
[ ВВЕДИТЕ ]. TI-89: нажмите [ ▼ ] [ ▼ ], чтобы перейти к
экран названия программы.
Калькулятор уже перевел вас в альфа-режим. Ищите фиолетовый букв над каждой клавишей и нажмите
[ N ] [ E ] [ W ] [ T ] [ O ] [ N ]. Внимательно проверьте экран и
при необходимости сделайте резервную копию и внесите исправления.Нажмите
[ ВВЕДИТЕ ]. Войти в эту программу, адаптированную из Larson-Hostetler-Edwards Исчисление 6 / e.
(Если вам нужна помощь, обратитесь к руководству по эксплуатации калькулятора.)
Особенности программы TI-89: - Буква d в первой строке цикла - это
Функция отличается от меню Calc.
- Режим «Точное / Прибл.» Сохраняется, устанавливается на Приблизительно и восстанавливается.
Таким образом, вам не нужно забывать вводить 1.
ТИ-83/84:
Диспетчер "НАЧАЛЬНАЯ УГАДА"
Вход X
1 → С
Фунт 1
X-Y1 / nDeriv (Y1, X, X) → R
Если абс (X-R) <абс (X / 1E10)
Перейти 2
R → X
Disp {X, N}
N + 1 → N
Перейти 1
Фунт 2
Disp "ROOT =", R
Disp "ITER =", N
После входа и внимательной проверки программы нажмите
[ 2nd MODE делает QUIT ], чтобы вернуться на главный экран. ТИ-89:
ньютон ()
Prgm
getMode ("Точно / Приблизительно") → str1
setMode ("Точно / Приблизительно", "Приблизительно")
ClrIO
Disp "Начальное предположение =", t
1 → г
Петля
t-y1 (t) / (d (y1 (x), x)) | x = t → y
Если abs (t-y) После входа и внимательной проверки программы нажмите
[ 2-я ESC делает QUIT ]
чтобы вернуться на главный экран.
Давайте протестируем программу, найдя решение x = cos ( x ).
Это означает нахождение положительного нуля f ( x ) = x - cos ( x ). Хорошо используйте
первоначальное предположение 0.
Убедитесь, что калькулятор находится в режиме радиан.
Поместите функцию в Y1. TI-83/84: [ Y = ]
В Y1 нажмите [ x, T, θ, n ] [–] [ COS ] [ x, T, θ, n ] [) ] TI-89: [ ◆ ] [ Y = ]
В Y1 нажмите [ X ] [ - ] [ 2-й Z составляет COS ]
[ X ] [) ] Вернуться на главный экран. TI-83/84: Нажмите [ 2nd MODE делает QUIT ]. TI-89: Нажмите [ 2-я ESC делает QUIT ]. Запустите программу. TI-83/84: нажмите [ PRGM ], затем цифру рядом с NEWTON
программа. (Это число будет отличаться в зависимости от других программ в
калькулятор.) Нажмите [ ENTER ], чтобы запустить программу.
Вам будет предложено сделать первоначальное предположение. Введите 0. ТИ-89:
Нажмите [ 2nd - делает VAR-LINK ], прокрутите до ньютон и нажмите
[ ВВЕДИТЕ ]. Это вставит ньютон ( на главный экран.
Введите начальное предположение, 0, а затем [) ] [ ENTER ]. Программа находит ответ примерно 0,7391 за шесть
итераций. ТИ-83/84: ТИ-89:
Что нового
- 17 ноя 2020 :
Объяснили, почему можно переключаться
от x = √2 до x = 2.
Преобразовано из HTML 4.01 в HTML5, переменные выделены курсивом.
- (промежуточные изменения подавлены)
- Август 2002 : Новая статья.
, используя метод Ньютона, найдите приблизительный корень для следующего уравнения.
Метод Ньютона - это очень простой алгоритм, который можно применить к функции, которая производит все более и более точные приближения фактического корня. Все, что вам нужно, это уравнение для функции, уравнение для ее производной и первое приближение для корня.
В случае вышеперечисленных вопросов нам необходимо знать реальный корень с точностью до 4 (или 5) знаков после запятой, чтобы решить, когда мы получили достаточно точное приближение с использованием метода Ньютона. Мы можем использовать для этого калькулятор, а также применить метод Ньютона следующим образом:
1) f (x) = x 4 - x - 10. Введите эту функцию в Y 1 в калькуляторе TI. Найдите f ' (x), взяв производную. Введите в Y 2 .
Найдите нуль функции f (x), используя функцию CALC ZERO.х ~ 1,8555. Нам говорят, что корень находится между 1 и 2, поэтому давайте выберем x 0 = 2 в качестве первого приближения.
Метод Ньютона определяется формулой x n + 1 = x n - (f (x n )) / (f ' (x n )). (При этом следует следовать по касательной к кривой до тех пор, пока касательная линия не коснется оси x. У нас есть новое значение x, и мы повторяем процесс).
Здесь я покажу расчеты для получения x 1 , а затем объясню шаги калькулятора для продолжения процесса:
x 1 = 2 - 4/31 = 1.8709 ...
В калькуляторе сохраните это число в A, набрав STO → ALPHA A. Затем введите A - Y 1 (A) / Y 2 (A). ВХОДИТЬ.
x 2 = 1,8557 ... STO> снова АЛЬФА A. Дважды нажмите ВВОД, чтобы вызвать A - Y 1 (A) / Y 2 (A). ENTER еще раз.
x 3 = 1,8555 ... с точностью до 4 десятичных знаков, требуемых вопросом.
Между прочим, есть несколько онлайн-калькуляторов по методу Ньютона, которые сделают вычисления за вас и даже покажут вам необходимые шаги.Вот только один из них: https://keisan.casio.com/exec/system/1244946907
Вам следует запомнить формулу для метода Ньютона и знать, как ее применять. Также было бы полезно посмотреть на картинку и понять, почему эта формула дает вам нулевую касательную линию. Вы также можете подумать, почему нулевая линия касательной всегда дает вам лучшее приближение к действительному корню.
.
 Метод случайных концов наудачу выберем две точки на окружности и проведём через них хорду Чтобы посчитать искомую вероятность
Метод случайных концов наудачу выберем две точки на окружности и проведём через них хорду Чтобы посчитать искомую вероятность При этом значения располагаются по окружности, а связи между ними отображаются в виде хорд
При этом значения располагаются по окружности, а связи между ними отображаются в виде хорд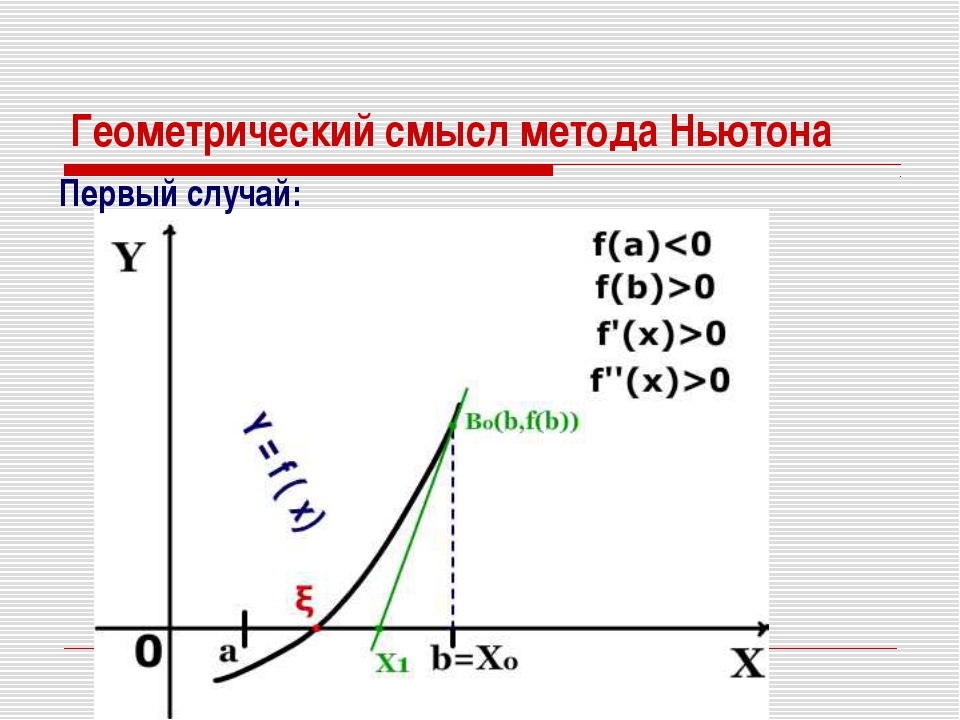 Идея метода состоит
Идея метода состоит По степени развития нервной
По степени развития нервной Составил таблицу хорд соответствующим дугам от 0 до 180 ввёл
Составил таблицу хорд соответствующим дугам от 0 до 180 ввёл Обобщённая теорема Ролля Формула конечных
Обобщённая теорема Ролля Формула конечных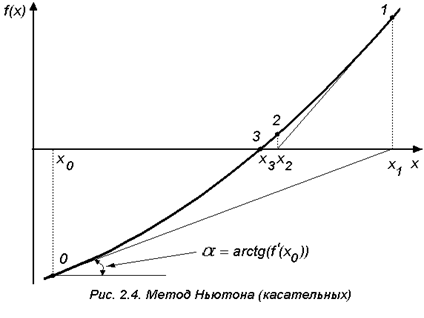 Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.