Метод гаусса решения слау. Решение систем линейных уравнений методом гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) с троки матрицыможно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .
4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.
5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду:
элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»).
Например, к такому виду:
Например, к такому виду:Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования.
Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг . Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка.
То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23)
, и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1
Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.
х 2 = 3 и х 1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов .
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.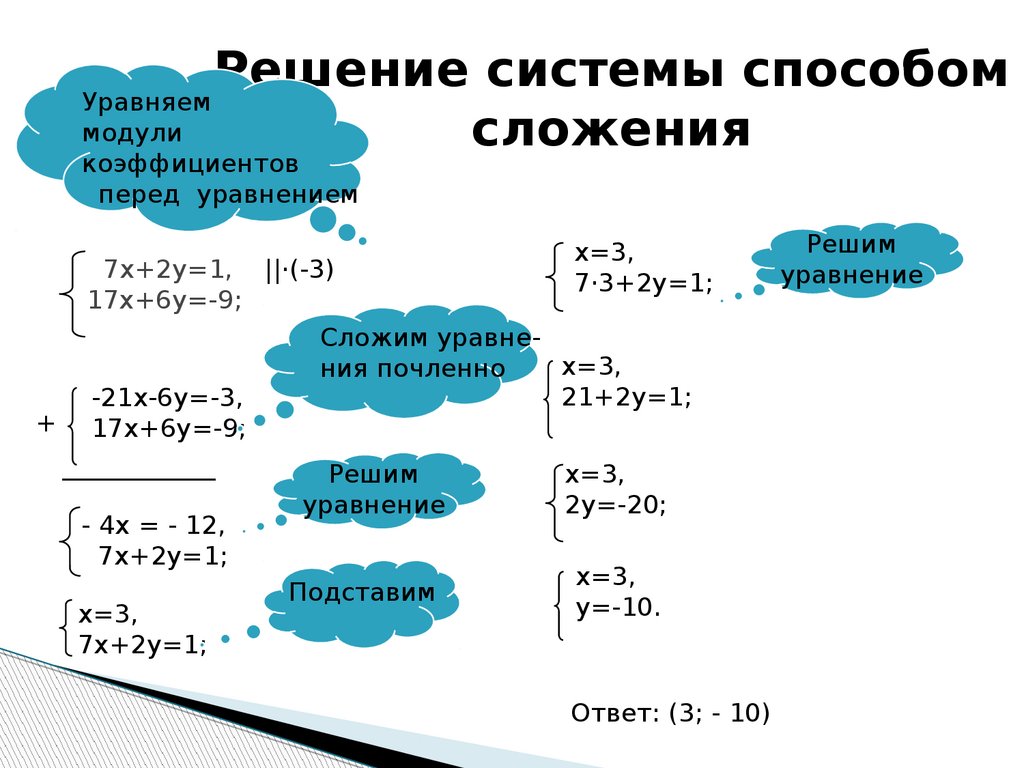
Одним из универсальных и эффективных методов решения линейных алгебраических систем является метод Гаусса , состоящий в последовательном исключении неизвестных.
Напомним, две системы называются эквивалентными (равносильными), если множества их решений совпадают. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой и наоборот. Эквивалентные системы получаются приэлементарных преобразованиях уравнений системы:
умножение обеих частей уравнения на число отличное от нуля;
прибавление к некоторому уравнению соответствующих частей другого уравнения, умноженных на число отличное от нуля;
перестановка двух уравнений.
Пусть дана система уравнений
Процесс решения этой системы по методу
Гаусса состоит из двух этапов. На первом
этапе (прямой ход) система с помощью
элементарных преобразований приводится
к ступенчатому , илитреугольному виду, а на
втором этапе (обратный ход) идет
последовательное, начиная с последнего
по номеру переменного, определение
неизвестных из полученной ступенчатой
системы.
Предположим, что коэффициент данной
системы
,
в противном случае в системе первую
строку можно поменять местами с любой
другой строкой так, чтобы коэффициент
прибыл отличен от нуля.
Преобразуем систему, исключив неизвестное во всех уравнениях, кроме первого. Для этого умножим обе части первого уравнения наи сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения наи сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
Здесь
– новые значения коэффициентов и
свободных членов, которые получаются
после первого шага.
Аналогичным образом, считая главным
элементом
,
исключим неизвестноеиз всех уравнений системы, кроме первого
и второго. Продолжим этот процесс, пока
это возможно, в результате получим
ступенчатую систему
,
где
,
,…,–
главные элементы системы
.
Если в процессе приведения системы к
ступенчатому виду появятся уравнения
,
т. е. равенства вида
,
их отбрасывают, так как им удовлетворяют
любые наборы чисел
.
Если же при
появится уравнение вида,
которое не имеет решений, то это
свидетельствует о несовместности
системы.
При обратном ходе из последнего уравнения
преобразованной ступенчатой системы
выражается первое неизвестное
через все остальные неизвестные
. Аналогичным образом последовательно определяются переменные
. Переменные
, выраженные через свободные переменные, называютсябазисными (зависимыми). В результате получается общее решение системы линейных уравнений.
Чтобы найти частное решение системы, свободным неизвестным
в общем решении придаются произвольные
значения и вычисляются значения
переменных
.
Технически удобнее подвергать элементарным преобразованиям не сами уравнения системы, а расширенную матрицу системы
.
Метод Гаусса — универсальный метод,
который позволяет решать не только
квадратные, но и прямоугольные системы,
в которых число неизвестных
не равно числу уравнений
.
Достоинство этого метода состоит
также в том, что в процессе решения мы
одновременно исследуем систему на
совместность, так как, приведя расширенную
матрицу
к ступенчатому виду, легко определить
ранги матрицыи расширенной матрицы
и применитьтеорему Кронекера —
Капелли .
Пример 2.1 Методом Гаусса решить систему
Решение . Число уравнений
и число неизвестных
.
Составим расширенную матрицу системы, приписав справа от матрицы коэффициентов столбец свободных членов.
Приведём матрицу к треугольному виду; для этого будем получать «0» ниже элементов, стоящих на главной диагонали с помощью элементарных преобразований.
Чтобы получить «0» во второй позиции первого столбца, умножим первую строку на (-1) и прибавим ко второй строке.
Это преобразование запишем числом (-1) против первой строки и обозначим стрелкой, идущей от первой строки ко второй строке.
Для получения «0» в третьей позиции
первого столбца, умножим первую строку
на (-3) и прибавим к третьей строке; покажем
это действие с помощью стрелки, идущей
от первой строки к третьей.
.
В полученной матрице, записанной второй в цепочке матриц, получим «0» во втором столбце в третьей позиции. Для этого умножили вторую строку на (-4) и прибавили к третьей. В полученной матрице вторую строку умножим на (-1), а третью — разделим на (-8). Все элементы этой матрицы, лежащие ниже диагональных элементов — нули.
Так как , система является совместной и определенной.
Соответствующая последней матрице система уравнений имеет треугольный вид:
Из последнего (третьего) уравнения
.
Подставим во второе уравнение и получим
.
Подставим
и
в первое уравнение, найдём
.
Решение систем линейных уравнений методом Гаусса. Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n .
Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а .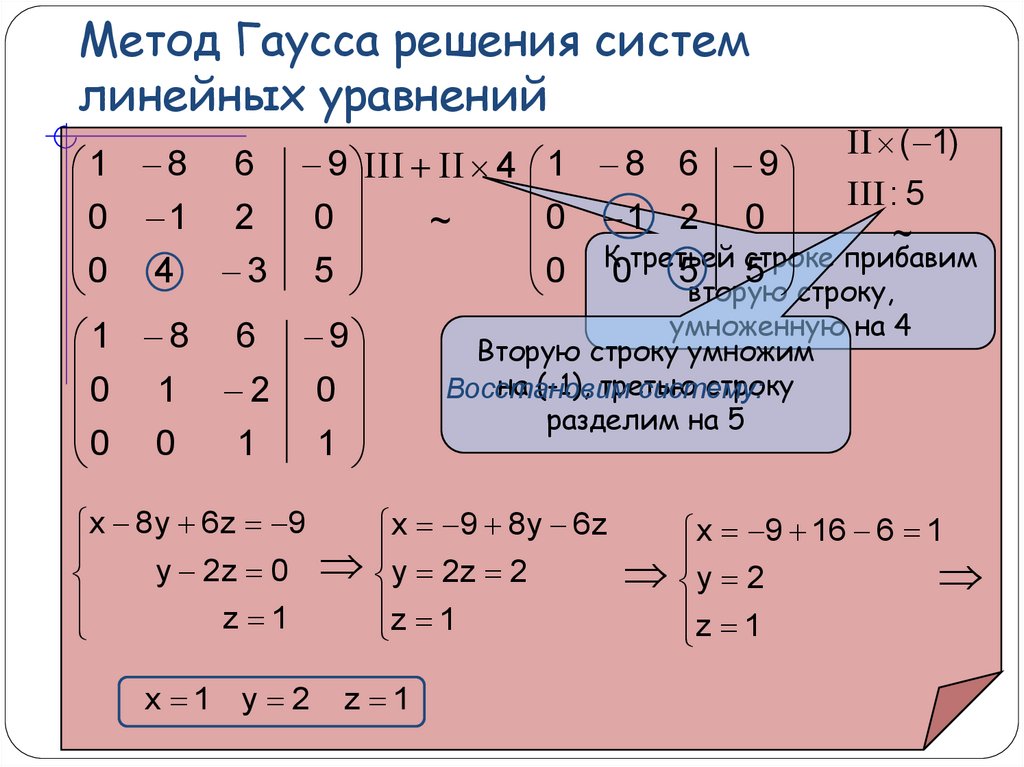
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а . Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3 , при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.
Пример.
Решите систему линейных уравнений методом Гаусса.
Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения. Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант — все можно посчитать, не используя сложных операций.
Что представляет собой СЛАУ
В математике существует понятие СЛАУ — система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить методом Гаусса данную систему — означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.
Наиболее популярные методы решения СЛАУ
В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное. Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами — и получится достоверный результат.
Где используются СЛАУ на практике
Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата.
Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.
Критерий совместимости СЛАУ
Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) — это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.
Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы.
В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».
Почему СЛАУ можно представить в матричном виде
Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде. Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.
Преобразования матриц
Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:
- Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
- Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями.
- Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.
Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями.Метод Жордана-Гаусса
Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные. Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие.
Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Простой пример решения системы 2х2
Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.
Перепишем ее в расширенную матрицу.
Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 — получившиеся ответы в процессе решения.
- Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
- Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.
Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.
Пример решения СЛАУ 3х3
Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.
Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.
Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.
- Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном.
- Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
- Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
- Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
- Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
- Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.
Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном.
Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.Как видно, решение уравнений методом Гаусса довольно простое.
Пример решения системы уравнений 4х4
Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.
Ниже описана пошаговая инструкция решения такого примера.
В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных.
Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений — это целые числа. Иногда решение может быть из дробных чисел.
Проверка правильности решения
Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком «равно». Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика — это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.
Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ
Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид. Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.
Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй — второму, и так далее.
Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением.
Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.
Калькулятор охлаждения ветром
Этот калькулятор оценивает температуру, ощущаемую телом в зависимости от скорости ветра и фактической температуры воздуха.
Калькулятор работает при температуре воздуха от -50°F до 50°F.
Калькулятор связанного теплового индекса | Калькулятор точки росы
Что такое охлаждение ветром?
Зимой температура, ощущаемая телом, обычно ниже фактической температуры воздуха. Это похоже на то, как тело ощущает более высокую температуру в условиях высокой влажности летом. Обратитесь к Калькулятору теплового индекса для получения дополнительной информации.
Поверхность, такая как кожа на теле человека, теряет тепло посредством теплопроводности, конвекции и излучения. Хотя проводимость и излучение имеют отношение к теплопередаче, температура охлаждения ветром в основном является результатом конвекции. Конвекция определяется как передача тепла из-за объемного движения молекул внутри жидкостей, таких как газы и жидкости, такие как ветер. По сути, когда воздух вокруг тела движется, он разрушает теплый воздух, окружающий тело, позволяя более прохладному воздуху заменить теплый воздух. Чем выше скорость ветра и, следовательно, движение окружающего воздуха, тем быстрее остывает поверхность.
Результатом охлаждения ветром является увеличение скорости потери тепла. Физиологической реакцией организма на повышенную скорость теплоотдачи является выделение большего количества тепла для поддержания температуры поверхности, что приводит к восприятию более низких температур из-за большей теплоотдачи.
Как рассчитать охлаждение ветром
Восприятие более низких температур, вызванных ветром, привело к разработке множества различных формул, которые пытаются качественно предсказать влияние ветра на эту воспринимаемую температуру. Поскольку температура охлаждения ветром не является точной наукой, метеорологические службы в разных странах используют стандарты, относящиеся к их конкретному региону, и поэтому ее оценки могут отличаться от оценок, предоставляемых местными метеорологическими службами в других регионах. В этом калькуляторе используется формула, разработанная Национальной метеорологической службой США, которая указана ниже.
Температура охлаждения ветра = 35,74 + 0,6215 × T — 35,75 × V 0,16 + 0,4275 × T × V 0,16
- , где T — температура воздуха в Farenheit, V — скорость ветра в MPH.
Обморожение
Обморожение может произойти, когда кожа или другие ткани подвергаются воздействию низких температур. Обычно первые признаки обморожения включают онемение, изменение цвета кожи и ощущение холода, как правило, в конечностях тела. Более серьезные осложнения включают гипотермию (о которой будет сказано ниже) и компартмент-синдром, состояние, которое приводит к недостаточному кровоснабжению тканей в определенном пространстве.
Скорость обморожения зависит от температуры и уровня воздействия. Обморожение чаще всего поражает людей, подвергающихся воздействию низких температур в течение длительного периода времени, например, тех, кто занимается зимними видами спорта, на работе, связанной с длительным нахождением на улице при низких температурах, а также бездомных.
Признаки и симптомы:
Обморожение исторически описывалось с точки зрения степени обморожения, аналогичной степени ожога:
Обморожение первой степени:
- Поверхностное повреждение, которое обычно не является постоянным
- Онемение/потеря чувствительности кожи с возможным отеком
- Кожа может отслоиться в ближайшие недели
Обморожение второй степени:
- Образуются волдыри и твердеет поверхность кожи
- Кожа с волдырями сохнет, чернеет и шелушится в ближайшие недели
- Возможна постоянная холодовая чувствительность и онемение
Обморожение третьей степени:
- Замерзание тканей под кожей
- Возникают волдыри и синюшность кожи
- Почерневшая корка развивается, а боль сохраняется в ближайшие недели
- Может возникнуть долгосрочное повреждение пластинок роста и изъязвление
Обморожение четвертой степени:
- Поражаются сухожилия, кости и мышцы
- Твердая текстура кожи и бесцветный внешний вид, повторное согревание происходит без боли
- Позже кожа становится черной и мумифицируется, а степень необратимого повреждения может быть неизвестна в течение месяца
Профилактика:
Обморожение можно предотвратить, принимая определенные меры предосторожности, когда обстоятельства ставят человека в ситуацию, связанную с низкими температурами.
К ним относятся:
- Покрытие кожи и волосистой части головы, отказ от тесной обуви и одежды и сохранение активности
- Избегайте температур ниже -15°C
- Отказ от алкоголя и наркотиков
- Многослойная одежда
- Использование согревающих устройств
- Осведомленность о ранних признаках обморожения (аналогично обморожению, но без образования кристаллов льда на коже)
Гипотермия
Гипотермия возникает, когда тело рассеивает больше тепла, чем поглощает, что приводит к снижению температуры тела. У людей гипотермия определяется как температура тела ниже 95,0°F (35,0°C). Симптомы могут варьироваться от легкого озноба до остановки сердца.
Гипотермия чаще всего возникает в результате воздействия сильного холода. Это также может произойти из-за других состояний, таких как алкогольная интоксикация, низкий уровень сахара в крови, анорексия и пожилой возраст.
Легкая гипотермия:
- Физиологические реакции на сохранение тепла тела
- Дрожь
- Повышенная частота сердечных сокращений и частота дыхания
- Повышенное кровяное давление
- Повышенное образование мочи
- Спутанность сознания
Умеренная гипотермия:
- Дальнейшая спутанность сознания
- Амнезия
- Невнятная речь
- Потеря мелкой моторики и снижение рефлексов
Тяжелая гипотермия:
- Начинается отказ физиологических систем, что приводит к снижению частоты сердечных сокращений, частоты дыхания и артериального давления.
- Парадоксальное раздевание — раздевание, происходящее в результате дезориентации и спутанности сознания человека, страдающего гипотермией от умеренной до тяжелой степени. На это приходится 25-50% смертей, вызванных гипотермией.
- Терминальное закапывание — поведение, возникающее на последних стадиях гипотермии, когда человек, страдающий от гипотермии, входит в небольшие закрытые помещения.
Оденьтесь тепло на зиму
Обморожение и переохлаждение могут возникнуть как в результате низких температур, так и привести к серьезным необратимым, а иногда и опасным для жизни осложнениям. Таким образом, важно правильно одеваться и понимать риски, связанные с воздействием низких температур в течение длительного периода времени. Ниже приведены некоторые общие советы о том, как оставаться в тепле и в безопасности при разной степени низких температур. При температуре ниже определенных температур следует полностью избегать пребывания на улице из-за серьезного риска для здоровья человека.
от 32 до 15°F (от 0 до -10°C): Одевайтесь тепло с учетом температуры наружного воздуха.
от 15 до -15°F (от -10 до -25°C): Существует риск гипотермии, если вы долгое время находитесь на улице без надлежащей защиты. Оденьтесь в несколько слоев теплой одежды. Хорошим началом будет тонкий впитывающий слой для удаления пота с кожи, за которым следует более толстый слой флиса, полиэстера или шерсти, который будет изолировать тело. Внешний слой должен быть ветроустойчивым, а в идеале водонепроницаемым в зависимости от погоды. Наденьте шапку, варежки и шарф.
от -15 до -50°F (от -25 до -45°C): Существует риск обморожения открытых участков кожи и риск переохлаждения, если вы долгое время находитесь на улице без надлежащей защиты. Подобно тому, как вы одеваетесь при температуре от 15 до -15 ° F, следует носить тонкий влагоотводящий базовый слой, флис, ветрозащитный и водостойкий внешний слой. Накройте все открытые участки кожи, особенно лицо и руки.
При необходимости можно добавить слои, например, синтетическую или пуховую куртку для дополнительной изоляции.
От -50 до -75°F (от -45 до -60°C): Открытая кожа может замерзнуть (обморожение) за считанные минуты, что может привести к длительному, потенциально необратимому повреждению. Существует серьезный риск переохлаждения, если вы остаетесь на улице слишком долго. Оденьтесь в несколько слоев очень теплой одежды, как описано в предыдущих диапазонах температур, с более изолирующими слоями и ветрозащитным и водоотталкивающим внешним слоем. Накройте все открытые участки кожи, особенно лицо и руки. Ограничьте мероприятия на свежем воздухе короткими периодами времени или, в идеале, полностью отмените мероприятия на свежем воздухе.
-75°F (-60°C) и ниже: Наружные условия опасны. Открытая кожа может замерзнуть менее чем за две минуты. Оставаться дома.
Калькулятор сохранения прибрежной среды обитания в Пьюджет-Саунд
Приоритетом в Пьюджет-Саунд является сохранение прибрежной среды обитания, включая водно-болотные угодья, эстуарии и приливные зоны, которые являются одними из наиболее ценных мест обитания лосося и стальноголового лосося в этом регионе.
Находящиеся под угрозой исчезновения южные косатки зависят от этого лосося в качестве добычи, что делает эту среду обитания важной и для китов. Прибрежная среда обитания также является краеугольным камнем региональной экономики, поддерживая рыболовство, разведение моллюсков, туризм и многое другое.
К сожалению, большая часть прибрежной среды обитания в Пьюджет-Саунд исчезла, и более 90 процентов приливных водно-болотных угодий были потеряны для освоения. Это оставляет лосося без необходимой среды обитания, в которой он нуждается, чтобы кормить и расти, чтобы повысить свою дальнейшую выживаемость в открытом океане. Это особенно касается лосося чавычи Пьюджет-Саунд, который внесен в список находящихся под угрозой исчезновения в соответствии с Законом об исчезающих видах.
Дальнейшая утрата прибрежной среды обитания увеличивает риск исчезновения, подрывая шансы видов на восстановление. В регионе были устранены другие серьезные угрозы для лосося путем улучшения прохода рыбы мимо плотин, снижения промыслового давления и адаптации методов разведения рыбы, чтобы помочь сохранить находящиеся под угрозой популяции.
Продолжающаяся потеря прибрежной среды обитания, столь тесно связанная с выживанием лосося, остается самым большим риском для зарегистрированного в Пьюджет-Саунд чавычи.
Предотвращение дальнейших потерь
Те, кто работает над развитием и обслуживанием прибрежных проектов, таких как причалы и доки, которые воздействуют на эту среду обитания в Пьюджет-Саунд, могут продолжать свои проекты без дальнейшего ухудшения важнейшей среды обитания на береговой линии в целом. Они могут добиваться компенсаций за сохранение через банк сохранения среды обитания.
Узнайте больше о природоохранных банках и аналогичных подходах к сохранению среды обитания, используемых на Западном побережье
Планы восстановления, разработанные в соответствии с Законом об исчезающих видах лосося и стальноголового лосося в Пьюджет-Саунд, предусматривают защиту и восстановление прибрежной среды обитания. Тем не менее, первый шаг — избежать дальнейших потерь, поскольку проекты по развитию и обслуживанию береговой линии продолжают поддерживать рост и экономику региона.
Чтобы компенсировать воздействие на среду обитания, связанное с проектом, и избежать чистой потери прибрежной среды обитания, разработчики проекта могут, например, решить улучшить свою проектную зону (например, удалить креозотовые сваи). Еще один способ компенсировать воздействие — улучшить прибрежную среду обитания в других местах, например, восстановить исторические приливные водно-болотные угодья.
Прочтите здесь о других примерах, которые уменьшают и компенсируют воздействие, связанное с калькулятором
Многие инициаторы проекта задаются вопросом, насколько достаточно смещения? NOAA Fisheries использовала новейшие научные данные о среде обитания, чтобы предоставить инструменты, которые объективно дают ответ.
Прибрежный калькулятор для определения воздействия на среду обитания
Чтобы определить объем восстановления, необходимый для компенсации воздействия развития на эту среду обитания и виды, которые от нее зависят, в настоящее время доступен «прибрежный калькулятор», основанный на последних научных данных.
использовать.
Калькулятор определяет изменения стоимости среды обитания в общей валюте, которая представляет воздействие на среду обитания как дебет, а улучшение среды обитания – как кредит. Затем застройщики могут компенсировать дебет эквивалентным количеством кредитов, избегая дальнейших чистых потерь прибрежной среды обитания. Кредиты могут быть получены за улучшения, предпринятые в рамках того же проекта, или за улучшения в других областях в регионе Пьюджет-Саунд.
- Прибрежный калькулятор
- Руководство пользователя калькулятора (PDF, 62 страницы)
- Картографические ресурсы для прибрежного калькулятора: устья рек и карманные пляжи Натала
- Часто задаваемые вопросы
- Публикации по анализу эквивалентности среды обитания
- Программа восстановления эстуариев и лосося
Совместная работа над решениями
NOAA Fisheries готова помочь разработчикам проектов в Пьюджет-Саунд в снижении воздействия на прибрежную среду обитания и оценке вариантов компенсации этого воздействия.
Мы также готовы проявлять гибкость в отношении того, как инициаторы проекта получают кредиты на среду обитания, чтобы компенсировать воздействия или дебеты, связанные с развитием. Мы понимаем, что это новый подход, при котором существует лишь несколько природоохранных банков. Мы работаем над тем, чтобы улучшить это. А пока мы можем помочь разными способами:
- Мы можем помочь вам найти и/или приобрести кредиты. Хотя у нас может не быть полного списка всех поставщиков или возможностей, мы можем знать о возможностях.
- Мы не будем требовать использования определенного поставщика кредитов, но, тем не менее, одобрим использование кредитов.
- Мы не определяем стоимость кредитов — ее определяет продавец и рынок.
Семинары, презентации и обучающие материалы
Каждый год мы проводим виртуальный публичный семинар по работе с Калькулятором охраны природы, который включает сеанс вопросов и ответов в реальном времени. Вот некоторые из проведенных нами семинаров и презентаций:
- Инструменты кредитования/дебетования для эстуарной среды обитания в штате Вашингтон (2020)
- Семинар по расчету параметров сохранения звука Пьюджет | NOAA Рыболовство (2021)
- Новый рынок охраны природы в Пьюджет-Саунд (2021 г. )
)Дополнительные ресурсы можно найти на странице «Семинары, презентации и ресурсы для обучения».
Прибрежный калькулятор Часы работы эксперта
Теперь мы предлагаем помощь виртуального прибрежного калькулятора! Запишитесь на 20-минутный сеанс, и член прибрежной группы рыболовства NOAA присоединится к вам для видеовстречи (или вы можете связаться по телефону). Мы рекомендуем также пригласить представителя агентства действий на встречу, если ваши вопросы касаются конкретного проекта. Вы можете включить примечание, чтобы пригласить дополнительных людей на собрание, через поле «Комментарии» на странице регистрации. Мы позаботимся о том, чтобы все стороны получили приглашение и ссылку. Вы также сможете поделиться ссылкой на встречу с другими людьми, которые хотели бы принять участие. Перед встречей, пожалуйста, отправьте по электронной почте проект Калькулятора консервации по адресу [email protected], если это уместно, вместе с любой дополнительной информацией, которая может помочь нам подготовиться к вашей встрече.
Запись на рабочее время
Биологическое заключение программы побережья Салишского моря (SSNP)
5 января 2022 года Национальное управление океанических и атмосферных исследований и Министерство армии подписали меморандум, касающийся проектов инфраструктуры и технического обслуживания. В результате NMFS и Инженерный корпус армии США совместно работали над программным биологическим заключением для побережья Салишского моря (Salish Sea Nearshore Programmatic, SSNP). Эта программа касается невыполненных проектов и будущих прибрежных проектов в этой важной экологической области. Биологическое заключение было окончательно оформлено 29 июня., 2022.
Для многих действий, подпадающих под алгоритмическую программу SSNP, требуется компенсация сохранения. Более подробную информацию о проектах, требующих компенсаций, см. в размещенной ниже публичной презентации информационно-пропагандистского мероприятия. Самый быстрый способ привести проект в соответствие с программным обеспечением, если необходимы смещения, — это использовать калькулятор сохранения среды обитания в прибрежной зоне Пьюджет-Саунд.
Представление калькулятора для каждого проекта настоятельно рекомендуется.
SSNP Biological Opinion
SSNP Public Outreach Presentation, март 2022 г.
Salish Sea Biological Opinion обеспечивает путь для прибрежных проектов при сохранении видов
Поставщики кредитов на сохранение и ресурсы восстановления лосося
Зона обслуживания Координационного совета канала Худ
Координационный совет канала Худ
Для проектов в бассейне канала Худ, кредиты могут быть можно получить через Координационный совет канала Худ. Пожалуйста, обращайтесь:
Майк Лисица
Менеджер программы смягчения последствий
Координационный совет канала Худ
Электронная почта: [email protected]
Телефон (360) 517-5714
Зона обслуживания Blue Heron
Банк сохранения Blue Heron
Банк сохранения Blue Heron Slough имеет природоохранные кредиты в более ограниченной зоне обслуживания, которая включает устье реки Снохомиш, впадающее в морские воды вокруг острова Вашон и на юг примерно до города Де-Мойн (заявители должны будут связаться с этим берегом, чтобы узнать точное местоположение).