Онлайн калькулятор собственные числа и собственные векторы матрицы: Собственные числа матрицы онлайн

Содержание

Собственные числа и собственные векторы матрицы

Определение 13.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом матрицы А.

Подставив в формулы (13.3) x`_j = λx_j, получим систему уравнений для определения координат собственного вектора:

Отсюда

. (13.5)

Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

| A -λE | = 0, (13.6)

поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A — λE| называется характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

Характеристический многочлен линейного преобразования не зависит от выбора базиса.

▀ (см. (9.4)), но следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.▄

Если матрица А линейного преобразования является симметрической (т.
е. а_ij=a_ji), то все корни характеристического уравнения (13.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

Если выбрать базис из собственных векторов х₁, х₂, х₃, соответствующих собственным значениям λ₁, λ₂, λ₃ матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

(13.7)

Доказательство этого свойства следует из определения собственных векторов.

Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.
Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

Пример.Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: (1- λ)(5 — λ)(1 — λ) + 6 — 9(5 — λ) — (1 — λ) — (1 — λ) = 0,

λ³ — 7λ² + 36 = 0, λ₁= -2, λ₂= 3, λ₃= 6.

Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (13.5) следует, что если х₍₁₎={x₁,x₂,x₃} – собственный вектор, соответствующий

λ₁=-2, то

— совместная, но неопределенная система. Ее решение можно записать в виде х₍₁₎={a,0,-a}, где а – любое число. В частности, если потребовать, чтобы |x₍₁₎|=1, х₍₁₎=

Подставив в систему (13. 5) λ₂=3, получим систему для определения координат второго собственного вектора — x₍₂₎={y₁,y₂,y₃}:

, откуда х₍₂₎={b,-b,b} или, при условии |x₍₂₎|=1, x₍₂₎=

Для λ₃

= 6 найдем собственный вектор x₍₃₎={z₁, z₂, z₃}:

, x₍₃₎={c,2c,c} или в нормированном варианте

х₍₃₎ = Можно заметить, что х₍₁₎х₍₂₎= ab – ab = 0, x₍₁₎x₍₃₎= ac – ac = 0, x₍₂₎x₍₃₎= bc — 2bc + bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.

Лекция 14.

Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.

Определение 14.1. Квадратичной формой действительных переменных х₁, х₂,…,х_n называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Примеры квадратичных форм:

(n = 2),

(n = 3). (14.1)

Напомним данное в прошлой лекции определение симметрической матрицы:

Определение 14.2. Квадратная матрица называется симметрической, если , то есть если равны элементы матрицы, симметричные относительно главной диагонали.

Свойства собственных чисел и собственных векторов симметрической матрицы:

Все собственные числа симметрической матрицы действительные.

Доказательство (для n = 2).

Пусть матрица А имеет вид: . Составим характеристическое уравнение:

(14.2)

Найдем дискриминант:

следовательно, уравнение имеет только действительные корни.

Собственные векторы симметрической матрицы ортогональны.

Доказательство (для n = 2).

Координаты собственных векторов и должны удовлетворять уравнениям:

Следовательно, их можно задать так:

. Скалярное произведение этих векторов имеет вид:

По теореме Виета из уравнения (14.2) получим, что Подставим эти соотношения в предыдущее равенство: Значит, .

Определение 14.3. Матрицей квадратичной формы называется симметрическая матрица

. (14.3)

Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (14.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.

Приведение квадратичной формы к каноническому виду

Определение 14.4. Каноническим видом квадратичной формы (14.1) называется следующий вид: . (14.4)

Покажем, что в базисе из собственных векторов квадратичная форма (14.1) примет канонический вид. Пусть

— нормированные собственные векторы, соответствующие собственным числам λ₁,λ₂,λ₃ матрицы (14.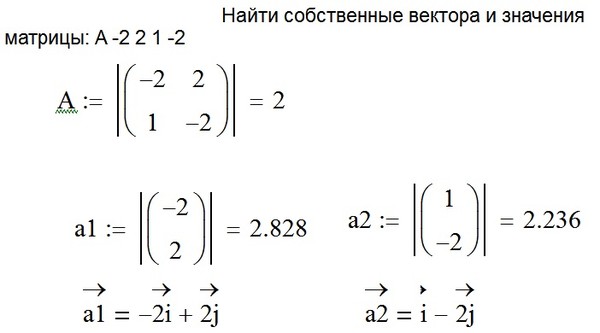 3) в ортонормированном базисе . Тогда матрицей перехода от старого базиса к новому будет матрица

. В новом базисе матрица А примет диагональный вид (по свойству собственных векторов). Таким образом, преобразовав координаты по формулам:

получим в новом базисе канонический вид квадратичной формы с коэффициентами, равными собственным числам λ₁, λ₂, λ₃:

. (14.5)

Замечание 1. С геометрической точки зрения рассмотренное преобразование координат представляет собой поворот координатной системы, совмещающий старые оси координат с новыми.

Замечание 2. Если какие-либо собственные числа матрицы (14.3) совпадают, к соответствующим им ортонормированным собственным векторам можно добавить единичный вектор, ортогональный каждому из них, и построить таким образом базис, в котором квадратичная форма примет канонический вид.

Пример. Приведем к каноническому виду квадратичную форму

x² + 5y² + z² + 2xy + 6xz + 2yz.

Ее матрица имеет вид В предыдущем примере найдены собственные числа и ортонормированные собственные векторы этой матрицы:

Составим матрицу перехода к базису из этих векторов:

(порядок векторов изменен, чтобы они образовали правую тройку). Преобразуем координаты по формулам:

^.Получим:

Итак, квадратичная форма приведена к каноническому виду с коэффициентами, равными собственным числам матрицы квадратичной формы.

Лекция 15.

Кривые второго порядка. Эллипс, гипербола и парабола, их свойства и канонические уравнения. Приведение уравнения второго порядка к каноническому виду.

Определение 15.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.

Эллипс.

Определение 15.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F₁ и F₂ эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему

у М(х,у)

координат так, чтобы ось Ох совпала с прямой F₁F₂, начало координат – с серединой отрезка F₁F₂. Пусть длина этого отрезка равна 2с, тогда в выбранной системе координат F₁(-c, 0), F₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F₁ и F₂ равна 2а.

Тогда r₁+ r₂= 2a, но ,

поэтому Введя обозначение b² = a²-c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:

(15.1)

Определение 15.3. Эксцентриситетом эллипса называется величина е=с/а (15.2)

Определение 15.4. Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (15.1), а уравнением второй степени другого вида.

Калькулятор собственных значений и собственных векторов для матриц 3×3

Калькулятор собственных значений и собственных векторов для матриц 3×3 | Минимум слепого расчета

Нравится:

Нравится Загрузка. ..

Запись опубликована 19 декабря 2017 г. автором dlandmj в рубрике Другое.

Поиск:

Блогролл

Последние сообщения

Площадь прямоугольника 13 июня 2020 г.
Формулы площади треугольника: два кейса в «форме ответа» 25 мая 2020 г.
ШАГ 2/2012/7 7 мая 2020 г.
ШАГ 2/2011/5 5 мая 2020 г.
ШАГ 1/2016/6 1 мая 2020 г.

Мета

Регистрация
Вход в систему
Лента записей
Лента комментариев
WordPress.com

Блог на WordPress.com.

%d блоггерам нравится это:

— Примеры, Калькулятор собственных значений онлайн

e Калькулятор помогает вычислить собственные значения матрицы 2 × 2. Собственные значения связаны с собственными векторами и используются для анализа линейных преобразований.

Что такое калькулятор собственных значений?

Калькулятор собственных значений — это онлайн-инструмент, который помогает вычислять собственные значения для заданной матрицы 2 × 2. Собственные значения также можно определить как специальный набор скаляров, связанных с системой линейных уравнений. Использование калькулятора собственных значений введите значения в указанные поля ввода.

Калькулятор собственных значений

Как пользоваться калькулятором собственных значений?

Выполните следующие действия, чтобы вычислить собственные значения матрицы 2 × 2 с помощью калькулятора собственных значений.

Шаг 1: Перейдите к онлайн-калькулятору собственных значений Cuemath.
Шаг 2: Введите значения в указанные поля ввода калькулятора собственных значений.
Шаг 3: Нажмите на Кнопка «Вычислить» , чтобы найти собственные значения для заданной матрицы 2 x 2.
Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.

Как работает калькулятор собственных значений?

Предположим, у нас есть квадратная матрица, заданная как \(A_{n\times n}\). Пусть λ — скалярная величина. Тогда [A — λI] называется собственной или характеристической матрицей. Здесь I используется для представления единичной матрицы. Определитель этой характеристической матрицы может быть задан как | А — λI | и собственное уравнение будет | А — λI | = 0. Чтобы найти собственные значения этого уравнения, используются следующие шаги.

Пусть A — квадратная матрица 2 × 2.
Единичная матрица I = \(\begin{bmatrix} 1 & 0\\ 0& 1 \\\end{bmatrix}\)
Теперь умножим единичную матрицу I на некоторое числовое значение λ. Это дает нам λI
Далее из матрицы A вычитаем λI; А — λI
Затем находим определитель полученной матрицы. То есть | А — λI |.
В результате получается квадратное выражение.
Приравниваем это выражение к нулю. Таким образом, | А — λI | = 0,
Наконец, мы решаем квадратное уравнение, чтобы получить два значения λ. Эти два значения будут собственными значениями.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Решенные примеры на калькуляторе собственных значений

Пример 1:

Найдите собственное значение \(\begin{bmatrix} 0 & 1\\ 2& 3 \\\end{bmatrix}\) и проверьте это с помощью калькулятора собственных значений.

Решение:

Данная матрица: A = \(\begin{bmatrix} 0 & 1\\ 2& 3 \\\end{bmatrix}\)

| А — λI | = 0, где I — единичная матрица, т. е.

A — λI = \(\begin{bmatrix} 0 & 1\\ 2& 3 \\\end{bmatrix}\) — λ\(\begin{bmatrix} 1 & 0\\ 0& 1 \\\end{bmatrix}\)

A — λI = \(\begin{bmatrix} — λ & 1\\ 2 & 3 — λ \\\end{bmatrix}\)

| А — λI | = λ ² — 3λ — 2

Подставляя эти значения в | А — λI | = 0 получаем

λ ² — 3λ — 2 = 0

При решении

λ = -0,56 , 3,56

Пример 2: trix

.
No related posts.