дробно рациональные уравнения калькулятор онлайн
дробно рациональные уравнения калькулятор онлайнВы искали дробно рациональные уравнения калькулятор онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и дробно рациональные уравнения онлайн калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дробно рациональные уравнения калькулятор онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Где можно решить любую задачу по математике, а так же дробно рациональные уравнения калькулятор онлайн Онлайн?
Решить задачу дробно рациональные уравнения калькулятор онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Дробно-рациональные уравнения их решения — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тема урока: «Дробно-рациональные уравнения и их решения»
2. Сформулируем понятие дробно рационального уравнения
Дробным рациональным уравнениемназывается уравнение, обе части
которого являются рациональными
выражениями, причем хотя бы одно
из них- дробным выражением.
2
Целое рациональное
уравнение
Дробные рациональные
уравнения
Левая и правая части каждого равенства являются
рациональными выражениями. Такие уравнения
называются рациональными уравнениями.
Рациональные уравнения
Целые рациональные уравнения
2х 3
5 х;
5
2
х 6 х 8 0;
х 5 х 9
.
4
6
Дробно-рациональные уравнения
2х 3
4 х;
5 х
х2 6х 8
0;
х 2
х 5 х 9
.
4х
6
5. Алгоритм решения дробно-рациональных уравнений
Алгоритм решения дробнорациональных уравнений• Найти
общий знаменатель дробей, входящих в
уравнение;
• Умножить обе части уравнения на этот общий
знаменатель, чтобы получить целое уравнение;
• Решить полученное целое уравнение;
• Исключить корни, обращающие каждый знаменатель в
нуль
или найти ОДЗ (Область допустимых значений
переменных в знаменателях данных дробей)
6. Уравнения
х 72
х 5
— дробно-рациональное уравнение
х 7
15
5
— целое рациональное уравнение
х 9 х 17 х 8
х 5
х
2
х 7 х 2
5
7
— дробно-рациональное уравнение
2
— целое рациональное уравнение
Решим целое уравнение
∙6
Ответ: 1,5
Наименьший общий знаменатель
Решим дробное рациональное уравнение
Алгоритм решения дробнорационального уравнения:
1) найти общий знаменатель дробей,
входящих в уравнение;
2) умножить обе части уравнения на
общий знаменатель;
3) решить получившееся целое
уравнение;
Если x= 5, то
Если x= — 2, то
Ответ: х= — 2
4) исключить из его корней те, которые
обращают в нуль общий знаменатель.
Решим целое уравнение
Решим дробное рациональное уравнение
∙6
Если x= 5, то
Ответ: х=1,5
Если x= — 2, то
Ответ: х= — 2
Пример.
Алгоритм решения дробнорационального уравнения:
1) найти общий знаменатель дробей,
входящих в уравнение;
2) умножить обе части уравнения на
общий знаменатель;
3) решить получившееся целое
уравнение;
4) исключить из его корней те, которые
обращают в нуль общий знаменатель.
Ответ: х=3
English Русский Правила
1.3: Рациональные уравнения — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 38264
Рациональное выражение есть частное двух многочленов.
Рациональное уравнение — это \( \underline{\textrm{уравнение}} \), содержащее одно или несколько рациональных выражений.
Рациональные выражения обычно содержат переменную в знаменателе. По этой причине необходимо позаботиться о том, чтобы знаменатель не был равен \(0\), отметив ограничения и проверив, что никакое решение не делает знаменатель равным нулю в исходном уравнении. Решение рациональных уравнений включает в себя очистку дробей путем умножения обеих частей уравнения на наименьший общий знаменатель (LCD).
Как: решить рациональное уравнение.
- Умножьте все знаменатели, чтобы определить ЖК-дисплей.
Обратите внимание на ограничения для \(x\). Это значения \(x\), при которых знаменатель равен нулю. Это значения, которыми \(x\) не может быть, потому что дробь с нулевым знаменателем не определена. - Умножьте обе стороны знака равенства на ЖК-дисплее. Каждый член уравнения умножается на LCD. Это приводит к тому, что дроби «вычищаются» из уравнения.
9{ 2 } }\quad\quad\quad\:\:\color{Cerulean}{Distribute.} \\ 2 x + 4 & = x + 9\quad\quad\quad\quad\quad\quad\color{Cerulean }{Упростить\:и\:затем\:решить.} \\ x & = 5 \end{выравнивание}\) - Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- да
- Теги
- Решение рациональных уравнений
- Решение рациональных уравнений путем очистки знаменателей
- Найдите посторонние решения в рациональном уравнении
- Найти переменную в рациональной формуле
- Приложения рациональных уравнений
- Определение компонентов уравнения работы
- Решите уравнение работы
- Определите и напишите пропорцию
- Решение пропорциональных задач на чертежах в масштабе
- Определение прямой вариации и решение задач, связанных с прямой вариацией
- Определение обратной вариации и решение задач с обратной вариацией
- Определить совместную вариацию и решить задачи, связанные с совместной вариацией
- Прямое изменение: [латекс]у=кх[/латекс]
- Обратная вариация: [латекс] y=\frac{k}{x}[/latex]
- Вариант соединения: [латекс]y=kxz[/латекс]
- «Текущее население мира». Часы мирового населения: 7,4 миллиарда человек (2016 г.). По состоянию на 21 июня 2016 г. http://www.worldometers.info/world-population/. «Текущее население мира». Часы мирового населения: 7,4 миллиарда человек (2016 г.). По состоянию на 21 июня 2016 г. http://www.worldometers.info/world-population/. «Текущее население мира». Часы мирового населения: 7,4 миллиарда человек (2016 г.). По состоянию на 21 июня 2016 г. http://www.worldometers.info/world-population/. ↵
- Обиалор, Амвросий, Черчилль Ихентуге и Фрэнк Акапуака. «Определение роста с использованием длины бедренной кости у взрослого населения района местного самоуправления Огута штата Имо, Нигерия». Федерация американских обществ экспериментальной биологии, апрель 2015 г. По состоянию на 22 июня 2016 г.
Ответ всегда должен проверяться на то, что это не ограниченное значение. Другими словами, ответы должны быть проверены, чтобы при подстановке обратно в исходное уравнение не происходило деления на ноль.
Набор решений: \( \{5 \}\).
После умножения обеих частей предыдущего примера на LCD нам осталось решить линейное уравнение. Это не всегда так; иногда мы останемся с квадратным уравнением.
Пример \(\PageIndex{2}\):
Решить: \(\dfrac { 3 ( x + 2 ) } { x — 4 } — \ dfrac { x + 4 } { x — 2 } = \ dfrac { х — 2 } { х — 4 }\).
Решение
В этом примере есть два ограничения: \(x≠4\) и \(x≠2\). Начните с умножения обеих сторон на LCD, \((x−2)(x−4)\).
\(\begin{aligned} \color{Cerulean}{(x-2)(x-4)}\color{black}{\cdot} \left( \frac{3(x+2)}{x -4}-\frac{x+4}{x-2} \right) &= \color{Cerulean}{(x-2)(x-4)}\color{black}{\cdot} \left( \frac{x-2}{x-4} \right)\\ \color{Cerulean}{(x-2)\cancel{(x-4)}}\color{black}{\cdot} \frac{ 3(x+2)}{\cancel{x-4}} — \color{Cerulean}{\cancel{(x-2)}(x-4)}\color{black}{\cdot} \frac{ x+4}{\cancel{x-2}} &= \color{Cerulean}{(x-2)\cancel{(x-4)}}\color{black}{\cdot} \frac{x- 2}{\cancel{x-4}} \\ 3 ( x + 2 ) ( x — 2 ) — ( x + 4 ) ( x — 4 ) & = ( x — 2 ) ( x — 2 ) \\ 3 \left( x ^ { 2 } — 4 \right) — \left( x ^ { 2 } — 16 \ right) & = x ^ { 2 } — 2 x — 2 x + 4 \\ 3 x ^ { 2 } — 12 — x ^ { 2 } + 16 & = x ^ { 2 } — 4 x + 4\\ 2x^{2} + 4 & = x^{2}-4x+4 \end{aligned}\) 9{ 2 } + 4 x = 0 } \\ { x ( x + 4 ) = 0 } \end{массив}\)
\(\begin{aligned} x = 0 \text {или } x + 4 & = 0 \\ x & = — 4 \end{aligned}\)
Эти значения проверяются, подтверждая, что они находятся в домене исходного уравнения.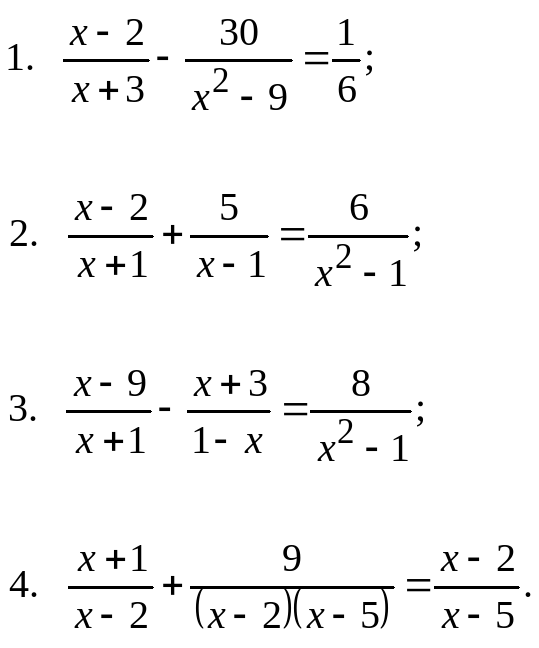
Набор решений равен \( \{ 0, −4 \} \).
До этого момента все возможные решения решали исходное уравнение. Однако это может быть не всегда так. Умножение обеих частей уравнения на переменные коэффициенты может привести к 9{ 2 } — 14 x — 5 } } \\ { \dfrac { 2 x } { ( 3 x + 1 ) } = \ dfrac { 1 } { ( x — 5 ) } — \ dfrac { 4 ( x — 1 ) } { ( 3 x + 1 ) ( x — 5 ) } } \end{массив}\)
ЖК-дисплей имеет вид \((3x+1)(x−5)\).
Определите ограничения. В этом случае \(x≠−\frac{1}{3}\) и \(x≠5\).
Шаг 2: Умножьте обе части уравнения на ЖК-дисплей. Тщательно распределите, а затем упростите.
\(\begin{align} \color{Cerulean}{( 3 x + 1 ) ( x — 5 )}\color{black}{ \cdot} \ frac { 2 x } { ( 3 x + 1 ) } &=\color{Cerulean}{ ( 3 x + 1 ) ( x — 5 )}\color{black}{ \cdot} \left( \frac { 1 } { ( x — 5 ) } — \ frac { 4 ( x — 1 ) } { ( 3 x + 1 ) ( x — 5 ) }\right)\\ \color{Cerulean}{\cancel{(3x+1)}(x-5)}\color{black}{ \cdot}\frac{2x}{\cancel{(3x+1)}} &= \color{Cerulean}{(3x+1)\cancel{(x-5)}}\color{black}{\cdot } \frac{1}{\cancel{(x-5)}} -\color{Cerulean}{\cancel{ (3x+1)}\cancel{(x-5)}}\color{black}{ \ cdot} \frac{4(x-1)}{\cancel{(3x+1)}\cancel{(x-5)}} \\ 2x(x-5) &=(3x+1)-4( х-1) \конец{выровнено}\) 9{ 2 } — 9 x — 5 & = 0 \\ ( 2 x + 1 ) ( x — 5 ) & = 0 \end{aligned}\)
\(\begin{align} 2 x + 1 & = 0 \quad\quad \text { or } &x — 5 &= 0 \\ 2 x & = — 1 & x &= 5 \\ x &= — \frac { 1 } { 2 } \end{aligned}\)
Шаг 4: Проверьте наличие посторонних решений.
{ 2 } + 9{ 2 } — 9 &= 0 \\ ( 2 x + 3 ) ( 2 x — 3 ) &= 0 \end{aligned}\)
\(\begin{align} 2 x + 3 & = 0 \quad \quad \text { или }& 2 x — 3& = 0 \\ 2 x & = — 3 &2 x& = 3 \\ x &= — \frac { 3 } { 2 } & x& = \frac { 3 } { 2 } \end{aligned}\)
Оба эти значения являются ограничениями исходного уравнения; следовательно, оба являются посторонними, а набор решений равен \(Ø\)
Рациональные выражения и рациональные уравнения
Важно отметить, что этот метод очистки алгебраических дробей работает только для уравнений. Не пытайтесь очищать алгебраические дроби при упрощении выражений. Напоминаем, что ниже приведен пример каждого из них.
| Выражение | Уравнение | ||
|---|---|---|---|
\(\dfrac { 1 } { x } + \ dfrac { x } { 2 x + 1 } \) | \(\dfrac { 1 } { x } + \ dfrac { x } { 2 x + 1 } = 0 \) |
Необходимо упростить выражения и решить уравнения.
Если мы умножим выражение на LCD, \(x (2x + 1)\), мы получим другое выражение, которое не эквивалентно. 9{ 2 } + x — 1 & = 0 \\ ( 3 x — 1 ) ( 2 x + 1 ) & = 0 \end{aligned}\)
\(\begin{align} 3 x — 1 &= 0 \quad\quad \text { or } & 2 x + 1 &= 0 \\ 3 x &= 1 & 2 x & = — 1 \\ x &= \frac { 1 } { 3 } &x &= — \frac { 1 } { 2 } \end{aligned}\)
Ни одно из решений не является ограниченным значением и не приводит к делению на ноль в исходном уравнении, поэтому набор решений равен \( \Large\{−\frac{1} {2}, \frac{1}{3} \Large\} \)
Пропорции
Пропорция является выражением равенства двух отношений, \(\frac{a}{b}=\frac{c}{d}\). Эта пропорция часто читается как «\(a\) к \(b\), как \(c\) к \(d\)». Для любых ненулевых действительных чисел \(a, b, c\) и \(d\), которые удовлетворяют пропорции, умножьте обе части на произведение знаменателей, чтобы получить следующее:
\(\begin{aligned} \ frac {a} {b} & = \frac {c} {d} \\ \color{Cerulean}{b d}\color{black}{\cdot} \frac{a} {b} & = \color{Cerulean }{b d}\color{black}{\cdot} \frac { c } { d } \\ a d & = b c \end{aligned}\)
Это показывает, что перекрестные произведения равны, и обычно называется перекрестным умножением .
Если \(\dfrac{a}{b}=\dfrac{c}{d}\), то \(ad = bc\)
Перемножить, чтобы решить пропорции, члены которых неизвестны.
Пример \(\PageIndex{7}\):
Решите: \(\dfrac { 5 n — 1 } { 5 } = \dfrac { 3 n } { 2 }\).
Решение
При перекрестном умножении обязательно группируйте \(5n−1\).
\(( 5 n — 1 ) \cdot 2 = 5 \cdot 3 n\)
Примените свойство распределения на следующем шаге.
\(\begin{aligned} ( 5 n — 1 ) \cdot 2 & = 5 \cdot 3 n \\ 10 n — 2 & = 15 n \quad \color{Cerulean} { Распределить. } \\ — 2 & = 5 n \quad\:\:\color{Cerulean}{Solve.} \\ \frac { — 2 } { 5 } & = n \end{aligned}\)
Ни одна дробь не может иметь знаменатель равен нулю, поэтому посторонних решений нет, а набор решений равен \( \{−\frac{2}{5} \} \)
Перекрестное умножение можно использовать как альтернативный метод решения рациональных уравнений, но для того, чтобы использовать этот метод, каждая часть уравнения должна быть упрощена до одной алгебраической дроби, а затем может быть выполнено перекрестное умножение .
Пример \(\PageIndex{8}\):
Решите: \(\dfrac { 1 } { 2 } — \dfrac { 4 } { x } = — \ dfrac { x } { 8 } \).
Решение
Получить одну алгебраическую дробь в левой части путем вычитания эквивалентных дробей с общим знаменателем.
\(\begin{align} \frac { 1 } { 2 } \cdot \color{Cerulean}{\frac { x } { x }}\color{black}{ -} \frac { 4 } { x } \cdot \color{Cerulean}{\frac { 2 } { 2 }} & \color{black}{=} — \ frac { x } { 8 } \\ \ frac { x } { 2 x } — \ frac { 8 } { 2 x } & = — \ frac { x } { 8 } \\ \ frac { x — 8 } { 2 x } & = — \ frac { x } { 8 } \ end {aligned} \) 9{ 2 } + 4 x — 32 \right) & = 0 \\ 2 ( x — 4 ) ( x + 8 ) & = 0 \end{aligned}\)
Затем установите каждую переменную factor равной нулю.
\(\begin{align} x — 4 & = 0 \quad\quad\text { or } &x + 8 &= 0 \\ x & = 4 \quad &x &= — 8 \end{align}\)
Ограничения на \( x \) равны \( x \ne 0 \), поэтому оба решения допустимы. Набор решений: \( \{−8, 4 \} \)
Попробуйте \(\PageIndex{3}\)
Решите: \(\dfrac { 2 ( 2 x — 5 ) } { x — 1 } = — \ dfrac { x — 4 } { 2 x — 5 }\).
92 — 2x\), которое легко решается. Набор решений равен \( \{ 1 \pm \sqrt{6} \} \).
Во избежание подобных осложнений перед выполнением перекрестного умножения следует проверить знаменатели, а также сначала исключить все общие множители в знаменателях. В приведенном выше примере два знаменателя равны \((x-1)(x+1)\) и \(2(x-1)\). Если общий множитель в обоих знаменателях \( (x-1) \) удалить (путем умножения обеих сторон знака равенства на \( (x-1) \), то при перекрестном умножении результат будет быть квадратным числом \( 2(2x+3) = (x+1)(x+1) \), которое легче решить, чем кубическое.
1.3: Rational Equations распространяется по незадекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.
Решение рациональных уравнений | Начальная алгебра
Результаты обучения
Уравнения, содержащие рациональные выражения, называются рациональными уравнениями .
Например, [латекс] \frac{2x+1}{4}=\frac{x}{3}[/latex] является рациональным уравнением. Рациональные уравнения могут быть полезны для представления ситуаций из реальной жизни и для поиска ответов на реальные проблемы. В частности, они неплохо подходят для описания различных пропорциональных отношений.
Один из самых простых способов решить рациональное уравнение — исключить знаменатели с общим знаменателем, а затем использовать свойства равенства, чтобы изолировать переменную. Этот метод часто используется для решения линейных уравнений с дробями, как в следующем примере:
Решите [латекс]\frac{1}{2}x-3=2-\frac{3}{4}x[/latex], сначала удалив дроби в уравнении.
Умножьте обе части уравнения на 4, общий знаменатель дробных коэффициентов.
[латекс]\begin{array}{c}\frac{1}{2}x-3=2-\frac{3}{4}x\\ 4\left(\frac{1}{2} x-3\right)=4\left(2-\frac{3}{4}x\right)\\\text{}\\\,\,\,\,4\left(\frac{1} {2}x\справа)-4\слева(3\справа)=4\слева(2\справа)+4\слева(-\frac{3}{4}x\справа)\\2x-12=8 -3x\\\подчеркивание{+3x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\подчеркивание{+3x}\\5x-12=8\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\ ,\underline{+12}\,\,\,\,\underline{+12} \\5x=20\\x=4\end{массив}[/latex]
Мы могли бы найти общий знаменатель и работать с дробями, но это часто приводит к большему количеству ошибок.
Мы можем применить ту же идею к решению рациональных уравнений. Отличие линейного уравнения от рационального уравнения в том, что рациональные уравнения могут иметь многочлены в числителе и знаменателе дробей. Это означает, что очистка знаменателя иногда может означать умножение всего рационального уравнения на многочлен. В следующем примере мы очистим знаменатели рационального уравнения с членами, имеющими многочлен в числителе.
В следующем примере мы покажем, как решить рациональное уравнение с биномом в знаменателе одного члена. Мы будем использовать общий знаменатель, чтобы исключить знаменатели из обеих дробей. Обратите внимание, что LCD является произведением обоих знаменателей, потому что они не имеют общих множителей.
Вы также можете решить эту задачу, умножив каждый член уравнения на 3, чтобы полностью исключить дроби. Вот как это будет выглядеть.
В следующем видео мы представляем два способа решения рациональных уравнений как с целыми, так и с переменными знаменателями.
Исключенные значения и посторонние решения
Некоторые рациональные выражения имеют переменную в знаменателе. Когда это так, есть дополнительный шаг в их решении. Поскольку деление на 0 не определено, вы должны исключить значения переменной, знаменатель которых будет равен 0. Эти значения называются исключенными значениями . Давайте посмотрим на пример.
В следующем видео мы представляем пример решения рационального уравнения с переменными в знаменателе.
Вы видели, что существует несколько способов решения рациональных уравнений. Поскольку оба этих метода манипулируют и переписывают члены, иногда они могут давать решения, которые не работают в исходной форме уравнения. Такие ответы называются посторонними решениями .
Вот почему всегда важно проверять все решения в исходных уравнениях — вы можете обнаружить, что они дают неверные утверждения или производят неопределенные выражения.
Рациональные формулы
Рациональные формулы могут быть полезными инструментами для представления реальных ситуаций и поиска ответов на реальные проблемы. Уравнения, представляющие прямую, обратную и совместную вариацию, являются примерами рациональных формул, которые могут моделировать многие ситуации из реальной жизни. Как вы увидите, если вы можете найти формулу, вы обычно можете разобраться в ситуации.
При решении задач с использованием рациональных формул часто полезно сначала решить формулу для указанной переменной. Например, в рабочих задачах вас просят рассчитать, сколько времени потребуется разным людям, работающим с разной скоростью, чтобы выполнить задание. Алгебраические модели таких ситуаций часто включают рациональные уравнения, полученные из формулы работы [latex]W=rt[/latex].
Объем выполненной работы ( W ) есть произведение нормы труда ( r ) и времени, затраченного на работу ( t ). Используя алгебру, вы можете написать формулу работы тремя способами:
[латекс]W=rt[/латекс]
Найдите время (t): [латекс] t=\frac{W}{r}[/ латекс] (разделить обе части на r)
Найти скорость (r): [латекс] r=\frac{W}{t}[/latex] (разделить обе части на t)
Теперь рассмотрим пример с использованием формулы объема цилиндра.
В следующем видео мы приводим еще один пример решения для переменной в формуле или, как их еще называют, буквальном уравнении.
Применение рациональных уравнений
Рациональные уравнения могут использоваться для решения различных задач, связанных со скоростью, временем и работой. Использование рациональных выражений и уравнений может помочь вам ответить на вопросы о том, как объединить рабочих или машины, чтобы выполнить работу в срок.
Хороший рабочий день
Работа
«Рабочая задача» — это пример реальной жизненной ситуации, которую можно смоделировать и решить с помощью рационального уравнения. Рабочие задачи часто требуют подсчитать, сколько времени потребуется разным людям, работающим с разной скоростью, чтобы выполнить задание. Алгебраические модели таких ситуаций часто включают рациональные уравнения, полученные из формулы работы [latex]W=rt[/latex]. (Обратите внимание, что формула работы очень похожа на соотношение между расстоянием, скоростью и временем, или [латекс]d=rt[/латекс].) Объем выполненной работы ( W ) есть произведение нормы труда ( r ) и времени, затраченного на работу ( t ). Формула работы имеет 3 варианта.
[латекс]\begin{array}{l}W=rt\\\\\,\,\,\,\,t=\frac{W}{r}\\\\\,\,\, \,\,r=\frac{W}{t}\end{array}[/latex]
Некоторые рабочие проблемы связаны с тем, что несколько машин или людей работают над проектом вместе в течение одинакового времени, но с разной скоростью.
В этом случае вы можете сложить их индивидуальные показатели работы вместе, чтобы получить общую скорость работы. Давайте посмотрим на пример.
Другие рабочие проблемы решаются иначе. Вы можете рассчитать, сколько времени потребуется одному человеку, чтобы выполнить работу в одиночку, если вы знаете, сколько времени требуется людям, работающим вместе, чтобы завершить работу.
В следующем видеоролике мы показываем еще один пример определения скорости работы одного человека по комбинированной скорости работы.
Как показано выше, многие рабочие задачи могут быть представлены уравнением [латекс] \frac{t}{a}+\frac{t}{b}=1[/latex], где t время, чтобы сделать работу вместе, a — это время, которое требуется человеку А, чтобы выполнить работу, а b — это время, которое требуется человеку Б, чтобы выполнить работу.
1 относится к общей проделанной работе — в данном случае работа заключалась в покраске 1 дома.
Ключевая идея здесь состоит в том, чтобы выяснить индивидуальную норму труда каждого работника. Затем, как только эти скорости определены, сложите их вместе, умножьте на время t , установите его равным количеству выполненной работы и решите рациональное уравнение.
В следующем видео мы представляем еще один пример двух людей, рисующих с разной скоростью.
Пропорции
Матрешка, или матрешка.
Пропорция — это утверждение о том, что два отношения равны друг другу. Есть много вещей, которые можно представить с помощью соотношений, включая фактическое расстояние на земле, которое представлено на карте. На самом деле, вы, вероятно, регулярно используете пропорциональные рассуждения и не осознаете этого. Например, скажем, вы вызвались принести напитки для общественного мероприятия.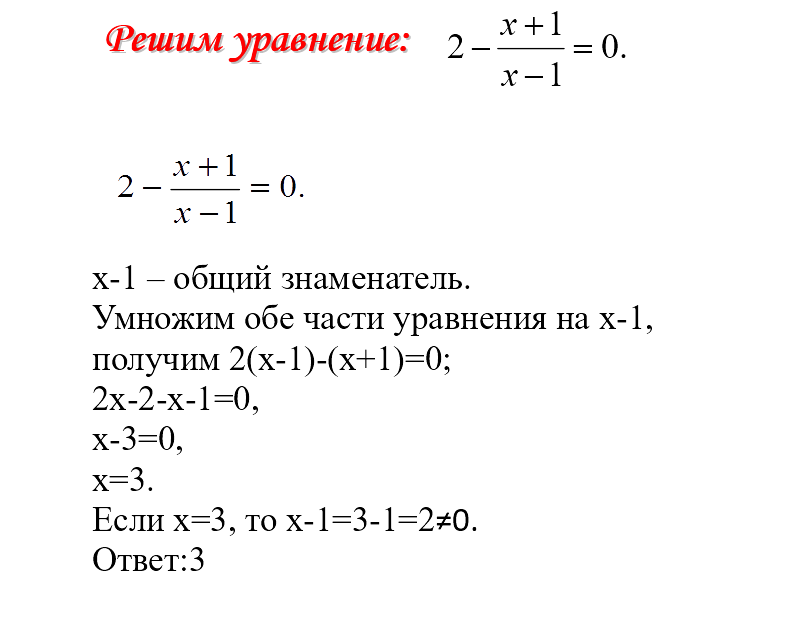
Вас просят принести достаточно напитков для 35-40 человек. В магазине вы видите, что напитки продаются в упаковках по 12 штук. Вы умножаете 12 на 3 и получаете 36 — этого может быть недостаточно, если придет 40 человек, поэтому вы решаете купить 4 упаковки напитков, чтобы быть уверенным.
Этот процесс также может быть выражен в виде пропорционального уравнения и решен с использованием математических принципов. Во-первых, мы можем выразить количество напитков в упаковке в виде отношения:
[latex]\frac{12\text{ drinks }}{1\text{ package }}[/latex]
Затем мы выражаем число людей, для которых мы покупаем напитки, в соотношении с неизвестным количеством необходимых нам упаковок. Мы будем использовать максимум, чтобы нам хватило.
[латекс]\frac{40\text{люди}}{x\text{пакеты}}[/latex]
Мы можем узнать, сколько пакетов нужно приобрести, установив выражения равными друг другу:
[латекс]\frac{12\text{ напитки }}{1\text{ пакет }}=\frac{40\text { people }}{x\text{packages }}[/latex]
Чтобы найти x, мы можем использовать технику решения линейных уравнений, или мы можем сократить путь умножения.
[латекс]\begin{array}{l}\,\,\,\,\,\,\,\frac{12\text{напитки}}{1\text{пакет}}=\frac{40 \text{ люди }}{x\text{ пакеты }}\\\text{}\\x\cdot\frac{12\text{ напитки }}{1\text{ пакет }}=\frac{40\text { люди }}{x\text{ пакеты }}\cdot{x}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,12x=40\\\text{}\\\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x= \frac{40}{12}=\frac{10}{3}=3,33\end{массив}[/latex]
Можно округлить до 4, так как на 0,33 упаковки напитков нет смысла. Конечно, вы не записываете таким образом свои мысли, когда находитесь в продуктовом магазине, но это помогает вам применять концепции к менее очевидным проблемам. В следующем примере мы покажем, как использовать пропорцию, чтобы найти количество людей на планете, у которых нет доступа к туалету.
Пример
По состоянию на март 2016 года население мира оценивалось в 7,4 миллиарда человек. [1] . По данным water.org, каждый третий человек на планете живет без туалета.
Найдите количество людей на планете, у которых нет туалета.
Показать раствор
В следующем примере мы будем использовать длину бедренной кости человека для оценки его роста. Этот процесс используется в криминалистике и антропологии, и во многих научных исследованиях было обнаружено, что это очень хорошая оценка.
Пример
Было показано, что рост человека пропорционален длине бедра [2] . Учитывая, что у человека ростом 71 дюйм длина бедра составляет 17,75 дюйма, какой рост у человека с длиной бедра 16 дюймов?
Показать раствор
Другой способ описать отношение длины бедренной кости к высоте, которое мы нашли в последнем примере, состоит в том, что существует отношение 1:4 между длиной бедренной кости и высотой, или 1 к 4.
Соотношения также используются в чертежах в масштабе. Чертежи в масштабе — это увеличенные или уменьшенные изображения объектов, зданий, дорог и карт.
Карты меньше, чем они представляют, а рисунок дендритных клеток в вашем мозгу, скорее всего, больше, чем он представляет. Масштаб чертежа представляет собой соотношение, которое представляет собой сравнение длины фактического объекта и его представления на чертеже. На изображении ниже показана карта США с масштабом 1 дюйм, что соответствует 557 милям. Мы могли бы записать масштабный коэффициент в виде дроби [латекс]\фракция{1}{557}[/латекс] или, как мы сделали с отношением высоты бедренной кости, 1:557.
Карта с масштабным коэффициентом
В следующем примере мы будем использовать масштабный коэффициент, указанный на изображении выше, чтобы найти расстояние между Сиэтлом, штат Вашингтон, и Сан-Хосе, штат Калифорния.
Пример
Учитывая коэффициент масштаба 1:557 на карте США, если расстояние от Сиэтла, штат Вашингтон, до Сан-Хосе, Калифорния составляет 1,5 дюйма на карте, определить пропорцию, чтобы найти фактическое расстояние между ними.
Показать раствор
В следующем примере мы найдем масштабный коэффициент, учитывая расстояние между двумя городами на карте и их фактическое расстояние друг от друга.
Пример
Два города на карте находятся на расстоянии 2,5 дюйма друг от друга. Их фактическое расстояние друг от друга составляет 325 миль. Напишите пропорцию для представления и найдите коэффициент масштабирования для одного дюйма карты.
Показать раствор
В следующем видео показан еще один пример определения фактического расстояния с использованием масштабного коэффициента карты.
В следующем видео мы представляем пример использования пропорций для получения правильного количества лекарства для пациента, а также для поиска желаемой смеси кофе.
Вариация
Так много машин, так много шин.
Прямая вариация
Вариационные уравнения являются примерами рациональных формул и используются для описания отношений между переменными.
Например, представьте себе парковку, заполненную автомобилями. Общее количество шин на стоянке зависит от общего количества автомобилей. Алгебраически эту связь можно представить уравнением.
[латекс]\текст{количество шин}=4\cdot\текст{количество автомобилей}[/латекс]
Цифра 4 говорит о том, насколько связаны автомобили и шины. Вы называете скорость константой вариации . Это константа, потому что это число не меняется. Поскольку количество автомобилей и количество шин связаны константой, изменение количества автомобилей приводит к пропорциональному и постоянному изменению количества шин. Это пример прямой вариации , где количество шин напрямую зависит от количества автомобилей.
Вы можете использовать уравнение автомобиля и шины в качестве основы для написания общего алгебраического уравнения, которое будет работать для всех примеров прямой вариации. В примере количество шин является выходом, 4 — константой, а количество автомобилей — входом.
Давайте введем эти общие термины в уравнение. Вы получаете [латекс]у=кх[/латекс]. Это формула для всех уравнений прямой вариации.
[латекс]\текст{количество шин}=4\cdot\текст{количество автомобилей}\\\текст{выход}=\текст{константа}\cdot\текст{ввод}[/латекс]
В В следующем видео мы представляем пример решения уравнения прямой вариации.
Обратная вариация
Другой вид вариации называется обратная вариация . В этих уравнениях выход равен константе, деленной на изменяющуюся входную переменную. В символической форме это уравнение [латекс] y=\frac{k}{x}[/latex].
Одним из примеров обратного изменения является скорость, необходимая для перемещения между двумя городами за заданный промежуток времени.
Допустим, вам нужно ехать из Бостона в Чикаго, а это около 1000 миль. Чем больше у вас есть времени, тем медленнее вы можете двигаться.
Если вы хотите добраться туда за 20 часов, вам нужно ехать со скоростью 50 миль в час (при условии, что вы не перестанете ехать!), потому что [латекс] \frac{1,000}{20}=50[/latex]. Но если вы можете добраться туда за 40 часов, то вам нужно в среднем 25 миль в час, так как [латекс] \frac{1,000}{40}=25[/latex].
Уравнение для определения того, как быстро можно путешествовать по количеству времени, которое у вас есть, выглядит следующим образом: [latex] speed=\frac{miles}{time}[/latex]. Это уравнение должно напомнить вам формулу расстояния [латекс] d=rt[/латекс]. Если вы решите [латекс] d=rt[/латекс] для r , вы получите [латекс] r=\frac{d}{t}[/латекс], или [латекс] скорость=\фрак{миль}. время}[/латекс].
В случае поездки из Бостона в Чикаго вы можете написать [latex] s=\frac{1,000}{t}[/latex]. Обратите внимание, что это та же форма, что и формула обратной функции вариации, [латекс] y=\frac{k}{x}[/latex].
В следующем примере мы найдем температуру воды в океане на глубине 500 метров.
Температура воды обратно пропорциональна глубине океана.
Температура воды в океане обратно пропорциональна глубине.
Пример
Температура воды в океане обратно пропорциональна глубине воды. Чем глубже ныряет человек, тем холоднее становится вода. На глубине 1000 метров температура воды составляет 5º по Цельсию. Какая температура воды на глубине 500 метров?
Показать решение
В следующем видео мы представляем пример обратной вариации.
Совместная вариация
Третий тип вариации называется Совместная вариация . Совместная вариация аналогична прямой вариации, за исключением двух или более величин. Например, площадь прямоугольника можно найти по формуле [латекс]А=lw[/латекс], где х — длина прямоугольника, а х — ширина прямоугольника. Если вы измените ширину прямоугольника, то изменится площадь, и точно так же, если вы измените длину прямоугольника, то изменится и площадь.
Вы можете сказать, что площадь прямоугольника «зависит от длины и ширины прямоугольника». 9{2}}h[/latex] — еще один пример совместной вариации. Объем цилиндра зависит от квадрата радиуса и высоты цилиндра. Константа вариации [латекс] \пи [/латекс].
Обнаружение k как [латекс] \frac{1}{2}[/latex] не должно удивлять. Вы знаете, что площадь треугольника равна половине основания, умноженной на высоту, [латекс] A=\frac{1}{2}bh[/латекс]. [latex] \frac{1}{2}[/latex] в этой формуле точно такой же [latex] \frac{1}{2}[/latex], который вы рассчитали в этом примере!
В следующем видео мы показываем пример нахождения постоянной вариации для совместно меняющегося отношения.
Прямая, совместная и обратная вариация
k — постоянная вариации. Во всех случаях [латекс]k\neq0[/латекс].
Резюме
Рациональные формулы могут использоваться для решения множества задач, связанных с нормами, временем и работой.
Прямые, обратные уравнения и уравнения совместной вариации являются примерами рациональных формул. При прямом изменении переменные находятся в прямой зависимости — при увеличении одной величины будет увеличиваться и другая величина. При уменьшении одной величины уменьшается другая величина. При обратной вариации переменные находятся в обратной зависимости: при увеличении одной переменной другая уменьшается, и наоборот. Совместная вариация такая же, как и прямая вариация, за исключением двух или более переменных.
Резюме
Вы можете решать рациональные уравнения, находя общий знаменатель. Переписав уравнение так, чтобы все члены имели общий знаменатель, вы можете найти переменную, используя только числители. Или вы можете умножить обе части уравнения на наименьшее общее кратное знаменателей, чтобы все члены стали полиномами, а не рациональными выражениями.
Важным шагом в решении рациональных уравнений является исключение любых посторонних решений из окончательного ответа.
Посторонние решения — это решения, которые не удовлетворяют исходной форме уравнения, поскольку они дают неверные утверждения или являются исключенными значениями, делающими знаменатель равным 0,9.0026
