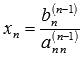Онлайн система уравнений методом гаусса онлайн: Метод Гаусса онлайн

Решение системы линейных алгебраических уравнений методом Гаусса

Система линейных уравнений вида:

может быть решена методом Гаусса при помощи нашего калькулятора.

Система уравнений задается в виде расширенной матрицы, т. е. матрицы коэффициентов и свободных членов размерности [n : n+1] вида:

Описание метода Гаусса следует сразу за калькулятором.

Решение системы линейных уравнений методом Гаусса

8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51

СЛАУ в матричном виде

Точность вычисления

Знаков после запятой: 2

Количество решений

 

Вектор решения системы уравнений

 

save Сохранить extension Виджет

Метод Гаусса

Метод был назван в честь гениального немецкого математика XIX века Карла Фридриха Гаусса. Сам Гаусс не был первооткрывателем метода (метод был известен и ранее (еще в I-II веке до н. э. метод упоминался в китайском труде «Математика в девяти книгах»).

Приведение матрицы к ступенчатому виду

На первом шаге решения системы уравнений методом Гаусса матрица коэффициентов и свободных членов приводится к ступенчатому виду:

Матрица превращается в ступенчатую форму путем элементарных преобразований — перемена строк местами, умножение строки на коэффициент, сложение строк.
В нашем калькуляторе для перехода к ступенчатому виду осуществляется последовательное вычитание из нижних строк матрицы, помноженных на , верхних строк , помноженных на коэффициент , где i — индекс текущей строки (индекс строки, которую вычитают из нижних строк).
При осуществлении этой операции требуется, чтобы коэффициент главной переменной был не нулевым. В случае нулевого коэффициента, строка меняется местами с любой другой нижней строкой, в которой в текущем столбце значение отлично от нуля.

Выражение базисных переменных

Получив ступенчатую матрицу, мы переходим к выражению базисных переменных, для этого сначала выполняется деление текущей строки на коэффициент , затем производится обратное вычитание из верхних строк , этой строки , помноженных на коэффициент , где j — индекс текущей строки (индекс строки, которую вычитают из верхних строк). Операция повторяется с каждой строкой, начиная от n-й до 1-й.

В результате матрица приобретает диагональный вид:
,
далее, поделив строки матрицы на коэффициент , в столбце свободных членов получаем вектор решений системы уравнений.

Решение системы линейных уравнений методом Гаусса онлайн

Для решения любой системы линейных уравнений метод Гаусса или метод последовательного исключения неизвестных является наиболее универсальным и достаточно простым при небольшом количестве переменных. Этот метод универсален, его применяют, когда система уравнений имеет:

• единственное решение;
• бесконечное множество решений;
• вовсе не имеет решений.

Суть метода состоит в переходе от заданной системы линейных уравнений к более простой с помощью таких эквивалентных преобразований в системе, как:

• перемена двух уравнений местами;
• умножение обеих частей уравнения на любое действительное число, не равное 0;
• прибавление к одному уравнению соответствующих частей другого, умноженных на произвольное число.

С помощью преобразований последовательно исключаем одну переменную за другой пока в одной из строк не будет определена переменная x_i.

Метод Гаусса позволяет решать СЛАУ при небольшом числе вычислительных операций.

Алгоритм решения:

• записываем систему в виде расширенной матрицы;
• прямой ход — приводим матрицу к ступенчатому виду;
• обратный ход — приводим матрицу к специальному ступенчатому виду.

Пусть дана система из n уравнений с n неизвестными переменными: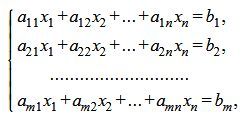

Определитель основной матрицы не равен 0.

Исключим из всех уравнений системы переменную х

1, начиная со 2-го, для чего:

• ко 2-му уравнению прибавим 1-е, умноженное на — а₂₁/а₁₁;
• к 3-му уравнению прибавим 1-е, умноженное на — а₃₁/а₁₁, и т.д.;
• к n-му уравнению прибавим 1-е, умноженное на — а_n1/а₁₁.

В результате преобразований система приняла вид: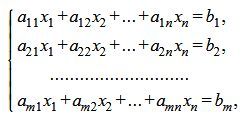

Далее таким же путем исключаем неизвестную переменную х₂ из всех уравнений, начиная с 3-го.

Для этого к 3-му уравнению прибавляем 2-е, умноженное на — а₃₂/а₂₂ и т.д. К n-му уравнению прибавим 2-е, умноженное на — а_n2/а₂₂.

Таким же способом исключаем неизвестную х₃ из всех уравнений системы, начиная с 4-го.

Прямой ход продолжается, пока в последнем уравнении не останется единственная неизвестная. Система будет иметь вид:

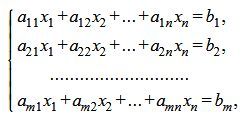
а_nn^(n-1) х_n = b_n^(n-1)

После окончания прямого хода метода Гаусса — последовательного исключения неизвестных, вычисляем неизвестную в последнем уравнении:

• из последнего уравнения системы находим х_n по формуле:
• из предпоследнего уравнения находим х^n-1 и т.д.
• из первого уравнения находим х₁.

Последовательное нахождение неизвестных, начиная с последнего уравнения к первому, называется обратным ходом.

Заметим, если в матрице есть хоть одна нулевая строка, у которой правая часть (свободный член) не равна 0, система несовместима, решения отсутствуют.

Для быстрого и правильного решения СЛАУ методом Гаусса можно воспользоваться калькулятором онлайн.


Решение системы линейных уравнений методом Гаусса

123456  — количество неизвестных

Количество знаков после разделителя дроби в числах: 0123456789101112

Как решить линейное уравнение методом Гаусса онлайн

Карл Фридрих Гаусс — немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса является самым действующим способом решения систем линейных уравнений, поскольку ни метод Крамера, ни матричный метод не работают в условиях, когда система имеет бесконечное количество решений или несовместна. Однако последовательное исключение неизвестных, что и заложено в основу метода Гаусса, приведет к решению любых линейных систем.

Так же читайте нашу статью «Решить логарифмическое уравнение онлайн решателем»

Решим следующую систему линейных уравнений методом Гаусса:

\[\left\{\begin{matrix} x_1+2x_2+3x_3-2_x4=1\\ 2x_1-x2-2x_3-3x_4=2\\ 3×1+2x_2-x_3+2x_4=-5\\ 2x_1-3x_2+2x_3+x_4=11 \end{matrix}\right.\]

Сделаем расширенную матрицу:

\[\begin{pmatrix} 1&2&3&-2\\ 2&-1&-2&-3\\ 3&2&-1&2\\ -2&-3&2&1 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&-5&-8&1\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\]

Используя 2 уравнение, избавимся от переменной \[x_2\] в последующих уравнениях:

\[\begin{pmatrix} 1&2&3&-2\\ 0&-5&-8&1\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\0&-7&-4&5 \end{pmatrix}\]

Выполним исключение переменной \[x_2\] из 3 и 4 уравнений. К 3 строке добавим 2, умноженную на \[\frac{1}{4}, \] а к \[4 — 2,\] умноженную на \[\frac{7}{1}. \]

\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&-4&-10&8\\ 0&-7&-4&5 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&-18&54 \end{pmatrix}\]

Теперь с помощью третьего уравнения исключим переменную \[x_3\] из четвёртого уравнения. Для этого к четвёртой строке прибавим третью, умноженную на \[-\frac{18}{18}=-1.\] Получаем расширенную матрицу трапециевидной формы.

\[\begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&-18&54 \end{pmatrix}\sim \\ \sim \begin{pmatrix} 1&2&3&-2\\ 0&1&-2&7\\ 0&0&-18&36\\ 0&0&0&18 \end{pmatrix}\]

Заданная система эквивалентна, таким образом, следующей:

\[\left\{\begin{matrix} x_1+2x_2+3x_3-2x_4=1\\ x_2-2x_3+7x_4=-8\\ -18x_3+36x_4=-40\\ 18x_4-7 \end{matrix}\right.\]

Основываясь на полученных данных, делаем вывод, что полученная и данная системы — совместны и определённы. Искомое решение находим «с конца». Из четвёртого уравнения имеем

\[x_4=-\frac{7}{18}.\]

Это значение подставляем в третье уравнение системы и получаем

\[-18x_3+36(-\frac{7}{18})=-40,\]

откуда

\[x_3=\frac{13}{9}.\]

Далее, подставляем значения \[x_3\] и \[x_4\] во второе уравнение системы:

\[x_2=2\frac{13}{9}+7(-\frac{7}{18})-8,\]

т.е.

\[x_2=-\frac{43}{18}.\]

Наконец, подстановка значений \[x_2, x_3, x_4\] в первое уравнение даёт:

\[x_1+2(-\frac{43}{18})+3(\frac{13}{9})-2(-\frac{7}{18})=1,\]

Получаем:

\[x_1=\frac {2}{3}.\]

Ответ:

\[(x_1=\frac {2}{3}, x_2=-\frac{43}{18}, x_3=\frac{13}{9}, x_4=-\frac{7}{18}).\]

Где можно решить линейные уравнения методом Гаусса онлайн?

Решить систему уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Решение системы линейных уравнений методом Гаусса-Жордана

метод Гаусса–Жордана — один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.

Алгоритм метода Гаусса

1. На основании системы линейных уравнений составляем расширенную матрицу системы;
2. Приводим матрицу к «треугольному» виду;
3. Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
4. В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через
   переменные которые могут принимать произвольные значения;

Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

1. Рассматриваем строку i(начиная с первой). Если, элемент aⁱ_i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a¹₁ отличен от нуля — переходим к следующему шагу;
2. Для каждой строки j, ниже i-й находим значение коэффициента K_j=a^j_i/aⁱ_i;
3. Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a^j_kнов.=a^j_k-K_j*aⁱ_k;
   После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n — размерность матрицы A
4. В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пaⁱ_i, которое и будет являтся определителем;

Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.

Комментарий к шагу 3 Метода Гаусса. Рангом матрицы A размера m × n называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы A обозначается через r(A) = rangA = rankA.
Минором M (от латинского “minor” меньший) k-го порядка матрицы A называется определитель некоторой матрицы, составленной из элементов матрицы A, стоящих на пересечении произвольно выбранных k
строк и k столбцов с сохранением их порядка. Если номера столбцов, в которых расположен минор M, совпадают с номерами строк, то этот минор называется главным. Каждая матрица A порядка n имеет
(C^k_n)2 миноров k-го порядка. Минорами 1-го порядка являются сами элементы матрицы A.

Основываясь на сравнении полученных значений рангов для основной и расширенной матрицы можно сделать следующие выводы о разрешимости системы:

• если ранг основной системы равен рангу расширенной и равен числу уравнений системы (rangA=rangA’=n), то система совместна и имеет единственное решение;
• если ранг основной системы равен рангу расширенной, но меньше числа уравнений в системе (rangA=rangA’
• если ранг основной системы меньше ранга расширенной (rangA

Выполненные готовые работы

Так же вы можете купить уже выполненные похожие работы. Для удобства покупки работы размещены на независимой бирже. Подробнее об условиях покупки тут.

Калькулятор исключения Гаусса

Как найти неизвестные переменные в уравнениях методом исключения Гаусса?

Исключение Гаусса или редукция строки — это алгоритм решения системы линейных уравнений. Этот метод также называется исключением Гаусса-Жордана. Он представлен последовательностью операций, выполняемых над матрицей. Метод назван в честь Карла Фридриха Гаусса (1777-1855), хотя был известен китайским математикам.Метод решения системы линейных уравнений методом исключения Гаусса аналогичен методу решения матриц. Например, существует связь между системой трех линейных уравнений и ее матрицей коэффициентов. $$ \ begin {align} & a_1x + b_1y + c_1z = {d_1} \\ & a_2x + b_2y + c_2z = {d_2} \\ & a_3x + b_3y + c_3z = {d_3} \\ \ end {align} \ quad \ longmapsto \ left ( \ BEGIN {массив} {} ссс {a_1} & b_1 & c_1 \\ {a_2} & b_2 & c_2 \\ {a_3} & b_3 & c_3 \\ \ {Конец массива} \ Справа) $$ Есть три типа операций с элементарными строками:

• Замена двух рядов;
• Умножение строки на ненулевое число;
• Добавление числа, кратного одной строке, к другой строке.

Метод исключения Гаусса состоит из двух частей. Первая часть сводит данную систему к \ underline {форме эшелона строк}. Из формы эшелона строк мы можем сделать вывод, что у системы нет решений, единственное решение или бесконечно много решений. Во второй части используются строковые операции, пока не будет найдено решение. Форма рядного эшелона удовлетворяет следующим свойствам:

• Старший коэффициент каждой строки должен составлять 1 доллар;
• Все элементы в столбце ниже $ 1 $ должны быть $ 0 $;
• Все строки, содержащие нули, находятся внизу матрицы.

Например, следующие матрицы представлены в виде эшелона строк $$ \ влево ( \ BEGIN {массив} {} куб.см 1 и 5 \\ 0 и 1 \\ \ {Конец массива} \ справа), \ quad \ left ( \ BEGIN {массив} {} сссс 1 и 1 и 0 и 5 \\ 0 и 1, 3 и 4 \\ 0 & 0 & 1 & 2 \\ \ {Конец массива} \ справа), \ quad \ left ( \ BEGIN {массив} {} сссс 1 и 2 и 3 и 4 \\ 0 и 1, 3 и 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \\ \ {Конец массива} \ Справа) $$ Матрица находится в форме сокращенного эшелона строк , если, кроме того, в каждом столбце, содержащем ведущий коэффициент, все другие записи в этом столбце равны нулю.Например, матрицы, показанные ниже, являются примерами матриц в сокращенной форме эшелона строк. $$ \ влево ( \ BEGIN {массив} {} куб.см 1 & 0 \\ 0 и 1 \\ \ {Конец массива} \ справа), \ quad \ left ( \ BEGIN {массив} {} сссс 1 & 0 & 0 & 7 \\ 0 & 1 & 0 & -2 \\ 0 & 0 & 1 & 2 \\ \ {Конец массива} \ справа), \ quad \ left ( \ BEGIN {массив} {} сссс 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & -2 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \\ \ {Конец массива} \ Справа) $$ Расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц.В случае решения системы нам необходимо увеличить матрицу коэффициентов и постоянную матрицу. Вертикальная линия указывает разделение между матрицей коэффициентов и постоянной матрицей. Итак, для системы трех уравнений $$ \ begin {align} & a_1x + b_1y + c_1z = {d_1} \\ & a_2x + b_2y + c_2z = {d_2} \\ & a_3x + b_3y + c_3z = {d_3} \\ \ Конец {Выравнивание} $$ расширенная матрица $$ \ влево ( \ BEGIN {массив} {ссс | с} a_1 & b_1 & c_1 & d_1 \\ a_2 & b_2 & c_2 & d_2 \\ a_3 & b_3 & c_3 & d_3 \\ \ {Конец массива} \ Справа) $$ Количество решений системы зависит только от ранга матрицы, представляющей систему, и ранга соответствующей расширенной матрицы.На основании теоремы Кронекера-Капелли любая система из трех линейных уравнений не имеет решений, если ранг расширенной матрицы больше, чем ранг матрицы коэффициентов. Если ранги этих двух матриц равны, система должна иметь хотя бы одно решение. Решение уникально тогда и только тогда, когда ранг равен количеству переменных, в данном случае, если ранг равен 3 $. Например, решим решение системы методом исключения Гаусса $$ \ begin {align} & 4x + 5y + 3z = {10} \\ & 3x + 6y + 7z = {8} \\ & 2x + 3y + 0z = {8} \\ \ Конец {Выравнивание} $$ Коэффициенты и постоянные члены системы дают матрицы $$ \ влево ( \ BEGIN {массив} {} ссс 4 и 5 и 3 \\ 3 и 6 и 7 \\ 2 и 3 и 0 \\ \ {Конец массива} \ справа), \ quad \ left ( \ BEGIN {массив} {с} 10 \\ 8 \\ 8 \\ \ {Конец массива} \ Справа) $$ Расширенная матрица $$ \ влево ( \ BEGIN {массив} {ссс | с} 4 и 5 и 3 и 10 \\ 3 и 6 и 7 и 8 \\ 2 и 3 и 0 и 8 \\ \ {Конец массива} \ Справа) $$ Чтобы решить эту систему, приведите расширенную матрицу к сокращенной форме эшелона строк следующим образом.

• Разделите строку $ 1 $ на $ 4 $ ($ R_1 = \ frac {R_1} 4) $, чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 3 и 6 и 7 и 8 \\ 2 и 3 и 0 и 8 \\ \ {Конец массива} \ Справа) $$
• Вычтите строку $ 1 $, умноженную на $ 3 $, из строки $ 2 $ ($ R_2 = R_2-3R_1 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & \ frac 94 & \ frac {19} 4 & \ frac 12 \\ 2 и 3 и 0 и 8 \\ \ {Конец массива} \ справа) $$
• Вычтите строку $ 1 $, умноженную на $ 2 $, из строки $ 3 $ ($ R_3 = R_3-2R_1 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & \ frac 94 & \ frac {19} 4 & \ frac 12 \\ 0 & \ frac12 & — \ frac 32 & 3 \\ \ {Конец массива} \ справа) $$
• Умножьте строку $ 2 $ на $ \ frac 49 $ ($ R_2 = \ frac49 R_2 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\\ 0 & \ frac12 & — \ frac 32 & 3 \\ \ {Конец массива} \ справа) $$
• Вычтите строку $ 2 $, умноженную на $ \ frac 54 $, из строки $ 1 $ ($ R_1 = R_1- \ frac54 R_2 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & 0 & — \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & \ frac12 & — \ frac 32 & 3 \\ \ {Конец массива} \ справа) $$
• Вычтите строку $ 2 $, умноженную на $ \ frac 12 $, из строки $ 3 $ ($ R_3 = R_3- \ frac12R_2 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & 0 & — \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & — \ frac {23} 9 & \ frac {26} 9 \\ \ {Конец массива} \ Справа) $$
• Умножьте строку $ 3 $ на $ — \ frac9 {23} $ ($ R_3 = — \ frac9 {23} R_3 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & 0 & — \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & 1 & — \ frac {26} {23} \\ \ {Конец массива} \ справа) $$
• Добавьте строку $ 3 $, умноженную на $ \ frac {17} 9 $, в строку $ 1 $ ($ R_1 = R_1 + \ frac {17} 9R_3 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & 0 & 0 & \ frac2 {23} \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & 1 & — \ frac {26} {23} \\ \ {Конец массива} \ справа) $$
• Вычтите строку $ 3 $, умноженную на $ \ frac {19} 9 $, из строки $ 2 $ ($ R_2 = R_2- \ frac {19} 9R_3 $), чтобы получить $$ \ влево ( \ BEGIN {массив} {ссс | с} 1 & 0 & 0 & \ frac2 {23} \\ 0 & 1 & 0 & \ frac {60} {23} \\ 0 & 0 & 1 & — \ frac {26} {23} \\ \ {Конец массива} \ Справа) $$ Итак, решение системы: $ (x, y, z) = (\ frac {2} {23}, \ frac {60} {23}, — \ frac {26} {23}) $.

Работа с устранением Гаусса с шагами показывает полное пошаговое вычисление для поиска решения линейной системы трех уравнений с использованием метода исключения Гаусса. Для любой другой системы просто введите двенадцать действительных чисел в качестве коэффициентов линейных уравнений и нажмите кнопку «Создать работу». Ученики начальной школы используют этот калькулятор исключения Гаусса для создания работы, проверки результатов решения систем линейных уравнений, выведенных вручную, или для эффективного выполнения домашних заданий.Во многих приложениях необходимо вычислить исключение матрицы, когда этот онлайн-калькулятор исключения матрицы Гаусса может помочь легко упростить вычисления для соответствующих входных данных. ,

Онлайн калькулятор: Метод исключения Гаусса

Система линейных уравнений:

может быть решена методом исключения Гаусса с помощью нашего калькулятора.

В методе исключения Гаусса система линейных уравнений представлена ​​как расширенная матрица, то есть матрица, содержащая коэффициенты уравнения и постоянные члены с размерами [n: n + 1]:

Исключение по Гауссу

8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51

Матрица системы линейных уравнений

Точность вычисления

Цифры после десятичной точки: 2

сохранить Сохранить расширение Виджет

Исключение по Гауссу

Метод назван в честь Карла Фридриха Гаусса, гениального немецкого математика 19 века.Сам Гаусс не изобрел этот метод. Метод редукции строк был известен древним китайским математикам, он был описан в книге «Девять глав математического искусства», китайской книге по математике, изданной во II веке.

Ликвидация вперед

Первым этапом исключения Гаусса является получение матрицы строковой формы. Левая нижняя часть этой матрицы содержит только нули, и все нулевые строки находятся ниже ненулевых строк:

Матрица приведена к этой форме с помощью элементарных операций со строками: поменять местами две строки, умножить строку на константу, добавить к одной строке скалярное кратное другой.
Наш калькулятор получает эшелонную форму путем последовательного вычитания верхних строк, умножения на нижние строки, умножения на, где i — ведущая строка коэффициентов (ведущая строка).
Важно получить отличный от нуля ведущий коэффициент. Если он становится равным нулю, строка заменяется на более низкую с ненулевым коэффициентом в той же позиции.

Обратная замена

На этом этапе операции с элементарными строками продолжаются до тех пор, пока не будет найдено решение. Наконец, матрица преобразуется в сокращенный вид эшелона строк:
,
.

.

Уравновешивание химических уравнений методом исключения Гаусса

с использованием метода исключения Гаусса

Этот калькулятор использует метод исключения Гаусса для определения стехиометрических коэффициентов химического уравнения. Исключение Гаусса (также известное как сокращение строк) — это численный метод решения системы линейных уравнений. Метод назван в честь немецкого математика Карла Фридриха Гаусса (1777-1855).

Все химические уравнения должны быть сбалансированы.Что значит быть сбалансированным? Это означает, что соблюдается закон сохранения массы. Закон сохранения массы гласит, что при обычной химической реакции материя не создается и не разрушается, то есть химическое уравнение должно иметь одинаковое количество атомов каждого элемента на обеих сторонах уравнения.

Запишите несбалансированное химическое уравнение в поле ввода, используя следующие правила, и нажмите «Баланс» (например: ca3 (po4) 2 (s) + h3so4 (aq) = h4po4 (aq) + caso4 (s)).

Правила набора уравнений

• В действительном уравнении должны быть одинаковые элементы с обеих сторон уравнения
• Пробелы не имеют значения, например ag no3 равно agno3
• Все скобки правильные, например Na2Zn3 [Fe (CN) 6] 2 * 9h3O
• Чтобы ввести виды заряда, просто введите их как есть (Al3 +, Nh5 +, SO42-) или явно объявите (Hg2 ^ 2 +)
• Чтобы ввести знак уравнения, вы можете использовать символы «=», «->» или «→».
• Уравнение можно записать строчными буквами. Если элементы в химической формуле правильно написаны с заглавной буквы, преобразователь смарт-кейсов оставит их так, как вы ввели.
• Для обозначения физических состояний, которые вы можете использовать для твердого тела, (l) для жидкостей, (g) для газов и (aq) для веществ, растворенных в воде.

Примеры химических уравнений

Балансировка окислительно-восстановительных реакций

Две проблемы могут возникнуть при балансировании окислительно-восстановительных реакций математическими методами:

1.Уравновешивание уравнений окислительно-восстановительных реакций путем проверки или математического метода (например, метода исключения Гаусса) может дать результаты, которые будут математически точными, но не химическими. Это связано с тем, что уравнения окислительно-восстановительных реакций также должны удовлетворять электронному балансу, то есть количество электронов, высвобождаемых в реакции окисления, должно быть равно количеству электронов, полученных в реакции восстановления.

Метод изменения окислительного числа

2.Уравнения окислительно-восстановительного потенциала часто записываются таким образом, что вода и ее ионы не учитываются. H ₂ O, H ⁺ или OH ^— (в зависимости от среды) могут быть добавлены по мере необходимости, поскольку предполагается, что реакция протекает в воде. Напротив, математический метод требует, чтобы все виды, участвующие в реакции, были явно указаны.

Метод изменения окислительного числа

,{-1} $.

Обращение матриц 2 $ \ times $ 2

Пример 1. Найти обратное

.

$ A = \ left [{\ begin {array} {* {20} {c}} 1 & 3 \\ 2 & 7 \ end {array}} \ right]

долл. США

Решение:

Шаг 1: Присоедините единичную матрицу к правой части $ A $:

$ A = \ left [{\ begin {array} {* {20} {c}} 1 & 3 \\ 2 & 7 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} \ Цвет {синие} {1} & \ {цвет синего} {0} \\ \ Цвет {синие} {0} & \ {цвет синего} {1} \ end {array}} \ right.} \право] $

Шаг 2: Применяйте к этой матрице операции со строками, пока левая часть не уменьшится до $ I $. Вычисления:

$$ \ Начать {выравниваются} & \ left [{\ begin {array} {* {20} {c}} \ Цвет {красный} {1} & \ цвет {красный} {3} \\ {2 — \ color {blue} {2} \ cdot \ color {red} {1}} & {7 — \ color {blue} {2} \ cdot \ color {red} {3}} \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} \ Цвет {красный} {1} & \ цвет {красный} {0} \\ {0 — \ color {blue} {2} \ cdot \ color {red} {1}} & {1 — \ color {blue} {2} \ cdot \ color {red} {0}} \ end {array}} \ right.} \ right] \ \ Row2 = Row2 — \ color {blue} {2} \ cdot \ color {red} {Row1} \\ & \ left [{\ begin {array} {* {20} {c}} 1 & 3 \\ 0 & 1 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 \\ {- 2} & 1 \ end {array}} \ right.} \ right] \\ & \ left [{\ begin {array} {* {20} {c}} {1 — \ color {blue} {3} \ cdot \ color {red} {0}} & {3 — \ color {blue} {3} \ cdot \ color {red} {1}} \\ \ Цвет {красный} {0} & \ цвет {красный} {1} \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} {1 — \ color {blue} {3} \ cdot \ color {red} {(- 2)}} & {0 — \ color {blue} {3} \ cdot \ color {red} {1}} \\ \ color {красный} {- 2} & \ color {красный} {1} \ end {array}} \ right.{-1} = \ left [{\ begin {array} {* {20} {c}} 7 & {- 3} \\ {-2} & 1 \ end {array}} \ right] $

Необратимая матрица

Если $ A $ необратимо , то слева появится нулевая строка.

Пример 2: Найдите обратное

$ A = \ left [{\ begin {array} {* {20} {c}} 1 & {- 3} \\ {- 2} и 6 \ end {array}} \ right] $

Решение:

Шаг 1: Присоедините единичную матрицу к правой части A:

$ \ left [{\ begin {array} {* {20} {c}} 1 & {- 3} \\ {- 2} и 6 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} \ Цвет {синие} {1} & \ {цвет синего} {0} \\ \ Цвет {синие} {0} & \ {цвет синего} {1} \ end {array}} \ right.} \право] $

Шаг 2: Применить операции со строками

$ \ left [{\ begin {array} {* {20} {c}} \ color {красный} {1} & \ color {красный} {- 3} \\ {- 2 + \ color {blue} {2} \ cdot \ color {red} {1}} & {6 + \ color {blue} {2} \ cdot \ color {red} {(- 3)}} \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} \ Цвет {красный} {1} & \ цвет {красный} {0} \\ {0 + \ color {blue} {2} \ cdot \ color {red} {1}} & {1 + \ color {blue} {2} \ cdot \ color {red} {0}} \ end {array}} \ right.} \ right] Row2 = Row2 + \ color {red} {2} \ cdot \ color {blue} {Row1} $

$ \ left [{\ begin {array} {* {20} {c}} 1 & {- 3} \\ \ Цвет {красный} {0} & \ цвет {красный} {0} \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 \\ 0 & 1 \ end {array}} \ right.} \ right] _ {\ color {red} {\ leftarrow ZERO \ \ ROW}} $

Шаг 3: Вывод: Эта матрица необратима.

Обратная матрица 3 $ \ умноженная на 3 $

Пример 1. Найти обратное

.

$ A = \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 2 & 5 & 3 \\ 1 & 0 & 8 \ end {array}} \ right] $

Решение:

Шаг 1: Присоедините единичную матрицу к правой части A:

$ \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 2 & 5 & 3 \\ 1 & 0 & 8 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array}} \ right.} \право] $

Шаг 2: Применяйте операции со строками к этой матрице, пока левая часть не уменьшится до I. Вычисления:

$ \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 2 & 5 & 3 \\ 1 & 0 & 8 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array}} \ right.} \ right] \ mathop {- — — — — — — \ to} \ limits_ {R3 = R3 \ color {red} {-} R1} ^ {R2 = R2 — \ color {синий} {2} \ cdot R1} \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ {2 — \ color {blue} {2} \ cdot 1} & {5 — \ color {blue} {2} \ cdot 2} & {3 — \ color {blue} {2} \ cdot 3} \\ {1 \ color {red} {-} 1} & {0 \ color {red} {-} 2} & {8 \ color {red} {-} 3} \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ {0 — \ color {blue} {2} \ cdot 1} & {1 — \ color {blue} {2} \ cdot 0} & {0 — \ color {blue} {2} \ cdot 0} \\ {0 \ color {red} {-} 1} & {0 \ color {red} {-} 0} & {1 \ color {red} {-} 0} \ end {array}} \ right.{} \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 0 & 1 & {- 3} \\ {0 \ color {blue} {+ 2} \ cdot 0} & {- 2 \ color {blue} {+ 2} \ cdot 1} & {5 \ color {blue} {+ 2} \ cdot (- 3) } \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ {- 1 \ color {blue} {+ 2} \ cdot (- 2)} & {0 \ color {blue} {+ 2} \ cdot 1} & {1 \ color {blue} {+ 2} \ cdot 0 } \ end {array}} \ right.} \ right] $

$ \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 0 & 1 & {- 3} \\ 0 & 0 & {- 1} \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ {- 5} & 2 & 1 \ end {array}} \ right.{} \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 0 & 1 & {- 3} \\ 0 & 0 & 1 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ 5 & ​​{- 2} & {- 1} \ end {array}} \ right.} \ right] $

$ \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 3 \\ 0 & 1 & {- 3} \\ 0 & 0 & 1 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} 1 & 0 & 0 \\ {- 2} & 1 & 0 \\ {- 5} & {- 2} & 1 \ end {array}} \ right.{R1 = R1 — 3 \ cdot R3} \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} {- 14} & 6 и 3 \\ {13} & {- 5} & {- 3} \\ 5 & ​​{- 2} & {- 1} \ end {array}} \ right.} \ right] $

$ \ left [{\ begin {array} {* {20} {c}} 1 & 2 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ Конец {массив} \ влево | {\ BEGIN {массив} {* {20} {с}} {- 14} & 6 и 3 \\ {13} & {- 5} & {- 3} \\ 5 & ​​{- 2} & {- 1} \ end {array}} \ right.{- 1} = \ left [{\ begin {array} {* {20} {c}} {- 40} & {16} & 9 \\ {13} & {- 5} & {- 3} \\ 5 & ​​{- 2} & {- 1} \ end {array}} \ right] $

,