Решение нестандартных математических задач
Большинство задач, решаемых в школьном курсе математики, являются стандартными. Для их решения необходимо умение работать «по образцу». Существует определенный алгоритм, с помощью которого можно решить все задачи данного типа. При решении стандартных задач так же могут возникнуть затруднения, но методика их преодоления хорошо известна – это тренировка, ведь в большинстве случаев все проблемы носят чисто технический характер.
Но не всякая задача в результате различных преобразований или с помощью удачно подобранной замены переменной может быть сведена к решению стандартного уравнения или неравенства, для которых существуют определенные алгоритмы решения. В таких случаях необходимо использовать нестандартные методы решения, о которых и пойдет речь в статье.
При решении сложных задач, например, олимпиадных или заданий из части С единого государственного экзамена, не всегда следует идти по стандартному пути, пытаясь решить предложенные задания «в лоб».
Рассмотрим несколько задач.
Пример 1.
Доказать, что если все коэффициенты квадратного уравнения ax2 + bx + c = 0 – нечетные числа, то его корни не могут быть рациональными числами.
Доказательство.
Предположим, что корнями уравнения ax2 + bx + c = 0 являются рациональные числа.
В таком случае его дискриминант D = b2 – 4ac должен быть полным квадратом, т.е. b2 – 4ac = у2.
Так как b – нечетное число, а 4ас – четное, то отсюда следует, что у так же является нечетным числом.
Далее, из равенства b2 – 4ac = у2 получаем (b – y)(b + y) = 4ac.
Поскольку b и y нечетные, то (b – y) и (b + y) являются четными. Если при этом учесть, что ac – нечетное число, то из равенства (b – y)(b + y) = 4ac вытекает, что b – y = 2t и b + y = 2u, где t и u – нечетные числа.
Из системы равенств
{b – y = 2t,
{b + y = 2u
получаем b = t + u.
Однако числа t, u являются нечетными, поэтому b – четное число. А это противоречит тому, что по условию задачи коэффициенты a, b и c уравнения ax2 + bx + c = 0 являются нечетными числами. Значит, данное уравнение может иметь только иррациональные корни.
Пример 2.
Числа a, b, c и d таковы, то а2 + b2 = 1, c2 + d2 = 1 и ac + bd = 0. Вычислить ab + cd.
Решение.
Так как а2 + b2 = 1, c2 + d2 = 1, то положим
a = sin α, b = cos α, c = sin β, c = cos β, где 0 ≤ α ≤ 2п, 0 ≤ β ≤ 2п.
В таком случае ac + bd = sin α · sin β + cos α · cos β = cos (α – β).
Однако, по условию ac + bd = 0, поэтому cos (α – β) = 0.
Поскольку
ab + cd = sin α · cos α + sin β · cos β = ½ (sin 2α + sin 2β) = sin(α + β) · cos (α – β) и cos (α – β) = 0,
то ab + cd = 0.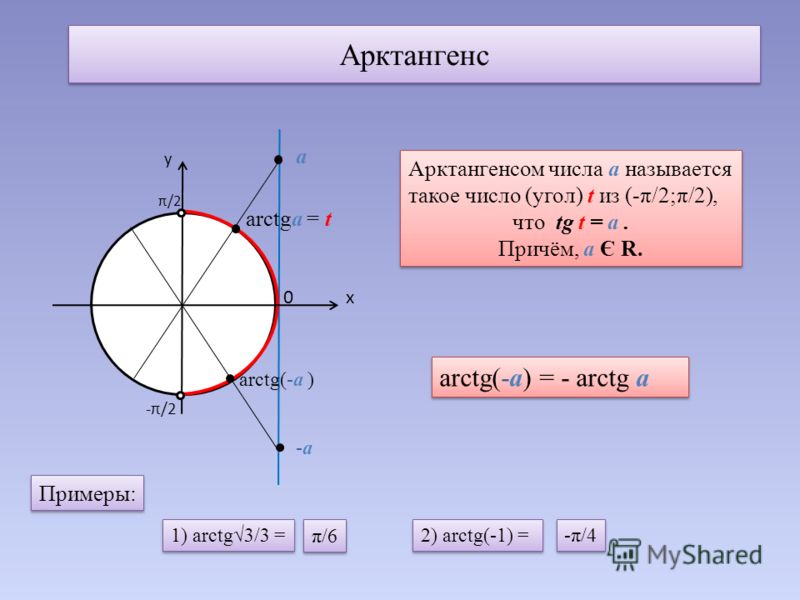
Ответ: ab + cd = 0.
Пример 3.
Вычислить х + у + z, если
{arctg x + arctg y + arctg z = п,
{хyz = 4.
Решение.
Из первого уравнения системы следует, что arctg x + arctg y = п – arctg z.
Отсюда tg(arctg x + arctg y) = tg(п – arctg z),
tg(arctg x + arctg y) = -tg(arctg z),
(x + y)/(1 – xy) = -z и
x + y + z = xyz.
Из системы уравнений имеем хyz = 4.
Так как x + y + z = xyz,
то х + y + z = 4.
Ответ: х + y + z = 4.
Пример 4.
Разложить на множители А = (а + 1)(а + 3)(а + 5)(а + 7) + 15.
Решение.
Преобразуем выражение А следующим образом:
А = ((а + 1)(а + 7)) · ((а + 3)(а + 5)) + 15 = (а2 + 8a + 7) · (а2 + 8a + 15) + 15.
Обозначим а2 + 8a + 7 = b, тогда
А = b(b + 8) + 15 = b2 + 8b + 15 = (b + 3)(b + 5).
Отсюда получаем А = (а2 + 8a + 10) · (а2 + 8a + 12).
Поскольку корнями квадратных уравнений а2 + 8a + 10 = 0 и а2 + 8a + 12 = 0 являются соответственно
х1 = -4 – √6,
х2 = -4 + √6,
х3 = -2,
х4 = -6,
то из равенства А = (а2 + 8a + 10) · (а2 + 8a + 12) получаем
А = (а + 4 + √6) · (а + 4 – √6) · (а + 2) · (а + 6).
Ответ: А = (а + 4 + √6) · (а + 4 – √6) · (а + 2) · (а + 6).
Пример 5.
Вычислить значение А = arctg 8 + arctg (19/22) + arcctg (-3/2).
Решение.
Пусть α = arctg 8, β = arctg (19/22), γ = arcctg (-3/2).
Тогда tg α = 8, tg β = 19/22, ctg γ = -3/2 и 0 < α < п/2, 0 < β < п/2, п/2 < γ < п.
Так как A = α + β + γ, то п/2 < А < 2п.
Так как tg (α + β) = (tg α + tg β) / (1 – tg α · tg β) = (8 + 19/22) / (1 – 8 · (19/22)) = -3/2 и tg γ = -2/3, то
tg А = tg ((α + β) + γ) = ((tg α + tg β) + tg γ) / (1 – tg (α + β) · tg γ) = (-3/2 – 2/3) / (1 – (-3/2)(-2/3)) = (-13/6) / (1 – 1).
Так как в знаменателе дроби получено нулевое значение, то можно сделать вывод о том, что tg A не определен. А это возможно только в том случае, когда А = п/2 + пn, где n – целое число.
Так как ранее было установлено, что
п/2 < А < 2п, то А = 3п/2.
Ответ: А = 3п/2.
Систематическое решение нестандартных задач способствует умственному развитию и формированию математических представлений.
Остались вопросы? Не знаете, как решать задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
tangent-graph-calculator — Googlesuche
AlleBilderShoppingVideosMapsNewsBücher
suchoptionen
tangent line Calculator — Symbolab
www.
symbolab.com › … › 9004 Калькулятор производных линий 9004 касательная с заданной точкой или точкой пересечения шаг за шагом.
Калькулятор касательной — Wolfram|Alpha
www.wolframalpha.com › input
Вычисляйте ответы, используя революционную технологию и базу знаний Wolfram, на которые полагаются миллионы студентов и профессионалов. Для математики, естественных наук, питания, …
Калькулятор свободной касательной — Mathepower
www.mathepower.com › tangent
Калькулятор касательной находит касательную через точку заданной функции.
Калькулятор касательной — eMathHelp
www.emathhelp.net › калькуляторы › calculus-1 › tang…
Калькулятор найдет касательную к явной, полярной, параметрической и неявной кривой в заданной точке , с показанными шагами.
Калькулятор касательной линии — Mathway
www.mathway.com › Калькулятор › Калькулятор касательной
Бесплатный калькулятор касательной – пошаговые решения, помогающие найти уравнение касательной к заданной кривой в заданной точке.
Ähnliche Fragen
Как найти тангенс графика?
Что такое калькулятор касательной?
графическое представление функции tan(x) — Solumaths
www.solumaths.com ›графический калькулятор › график › t…
Операторы, которые будут использоваться в графическом калькуляторе для записи … Онлайн-плоттер позволяет нарисовать касательную функции в точке, чтобы сделать это, …
Найти наклон и уравнение касательной линии — калькулятор Онлайн
калькулятор-online.net › калькулятор касательной
Лучший калькулятор касательной поможет вам рассчитать касательную к уравнению, а также наклон линии к заданной кривой в заданной точке.
Калькулятор функции TAN и график — Программное обеспечение MedCalc
www.medcalc.org › … › Тригонометрические функции
Касательная функция. TAN(x) возвращает тангенс угла x. Аргумент x должен быть выражен в радианах. Чтобы преобразовать градусы в радианы, используйте RADIANS .
..
Калькулятор касательной — Бесплатный онлайн калькулятор — Byju’s
byjus.com › Калькуляторы › Математические калькуляторы
19.10.2020 · Точка пересечения прямой и кривой называется точкой касания. Что такое уравнение касательной прямой? Уравнение касательной …
Касательная функция — онлайн калькулятор, формулы, график — Calculat.org
www.calculat.org › ru › тригонометрические функции
Bewertung 5,0
(1)
-угольный треугольник как отношение противоположных… График. α tan α [°] [рад] 0 90° 180° 270° 360° 0,5 π π 1,5 π 2 π …
Ähnlichesuchanfragen
Калькулятор производных
Уравнение касательной
Касательная калькулятор самолета
Online calculator
Multivariable function calculator
Mathe calculator
Lab Calculator
Definite integral Calculator
graphing angles in standard position calculator
AlleBilderShoppingVideosMapsNewsBücher
Suchoptionen
Reference Angle Calculator | Квадранты графика
www.
omnicalculator.com › математика › опорный угол
02.02.2023 · Калькулятор опорного угла находит соответствующий угол в первом квадранте.
Калькулятор опорного угла с графиком
calculate-online.net › калькулятор опорного угла
Бесплатный стандартный калькулятор положения вычисляет: угол в градусах; Угол в радианах; Угол в π радианах …
Формула опорного угла · Как найти опорный угол?
Draw Angles — Программа для черчения — Rechneronline
rechneronline.de › winkel › angles
Программа для черчения углов. Положение первого рычага сохраняется, второй рычаг вращается против часовой стрелки на увеличивающийся угол. … См. также Калькулятор треугольников …
Калькулятор опорного угла — Pi Day
www.piday.org › Калькуляторы
Используйте этот простой калькулятор, чтобы найти опорный угол любого угла. Узнайте, как найти опорный угол без калькулятора.
Поиск опорного угла и квадранта — тригонометрический калькулятор
www.
analyzemath.com › Калькуляторы › find_referen…
Калькулятор опорного угла и квадранта. Этот онлайн-калькулятор находит опорный угол и квадрант тригонометрического угла в стандартном положении.
Ähnliche Fragen
Как найти исходный угол в градусах в стандартном положении?
Какой исходный угол для 240 в стандартном положении?
Калькулятор углов рисования в стандартном положении {CVN9VR}
epvuuws.deliziedachef.it
4-й круговой рабочий лист математический график градусы рисования градусы печатаемые углы рабочие листы печатаются ниже расчет. Q: Нарисуйте угол 190° в стандартном положении.
угол эскиза в стандартном калькуляторе положения
zkbhmxoq.elisastella.it
Бесплатная пробная версия доступна на KutaSoftware. Интерактивный геометрический калькулятор. Онлайн-викторина BYJU: зарисовка углов в стандартном положении Примечание: …
6.1 Триггерные коэффициенты для любого любого угла в стандартном положении — Desmos
www.