4.1.3. Операции над множествами
Глава 4. Комбинаторика
4.1.
4.1.3.
Рассмотрим некоторое множество E, которое будем называть основным, и не будем интересоваться его природой. Будем считать, что все множества, которые рассматриваются в данном пункте, являются подмножествами основного множества.
|
Объединением двух множеств A и B называется множество A B, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B. |
||
|
Пересечением множеств A и B называется множество A B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B. |
||
Аналогично определяется пересечение и объединение любого числа множеств.
Для удобства множества изображают в виде кругов, а основное множество в виде прямоугольника, их содержащего. Такие рисунки называются диаграммами Эйлера–Венна.
|
Модель 4. |
Пример 1
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти и
Показать решение
Пример 2
Пусть A = [−2; 1] и B = (0; 3). Найти и
Показать решение
Операции объединения и пересечения множеств обладают следующими свойствами. |
Если то |
Например,
Следует заметить, что мощность объединения и пересечения двух конечных множеств связаны следующим соотношением:

Для бесконечных множеств это равенство неверно. Если хотя бы одно из множеств A и B бесконечно, то мощность объединения
Пусть теперь A и B − некоторые множества в основном множестве E.
|
Разностью множеств A и B называется множество A \ B, которое состоит из тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B. Разность между основным множеством E и множеством A называется дополнением множества A в E и обозначается |
||
Кратко это можно записать так:
Очевидно, что для любого
Пример 3
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}.
Показать решение
Для любых двух множеств A и B основного множества E справедливы законы де Моргана. |
Законы де Моргана можно проиллюстрировать при помощи диаграмм Эйлера–Венна.
Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн |
|||||||||
|
|||||||||
|
|
|||||||||
Операции над множествами с примерами решения
Содержание:
- Примеры с решением
- Разность двух множеств
Множества можно определять и при помощи операций над другими множествами.
Равенство множеств. Множества А и В считаются разными (совпадающими), если они состоят из одних и тех же элементов. Равенство множеств обозначают так: Если множества не равны, то пишут:
Доказательство равенства множеств состоит из двух частей:
1) для любого элемента множества А (формальная запись — ) доказывается, что он принадлежит и множеству В. Формально это записывается так:
Формально это записывается так:
2) для любого элемента В доказывается, что он принадлежит и множеству К. формально это можно записать так:
Отсюда следует, что запись равенства двух множеств «А = В» эквивалентна записи
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Примеры с решением
Пример 1.
Доказать, что множество равно множеству В корней уравнения то есть Для доказательства этого утверждения решим уравнение. Получим: Следовательно,
Затем непосредственной подстановкой убеждаемся, что любое из чисел 0, 2, 3 удовлетворяет уравнению, следовательно:
Только теперь можно записать, что
Объединение (сумма) множеств. Объединением множеств А и В называется такое множество С, каждый элемент которого содержится хотя бь/в одном из множеств А или В.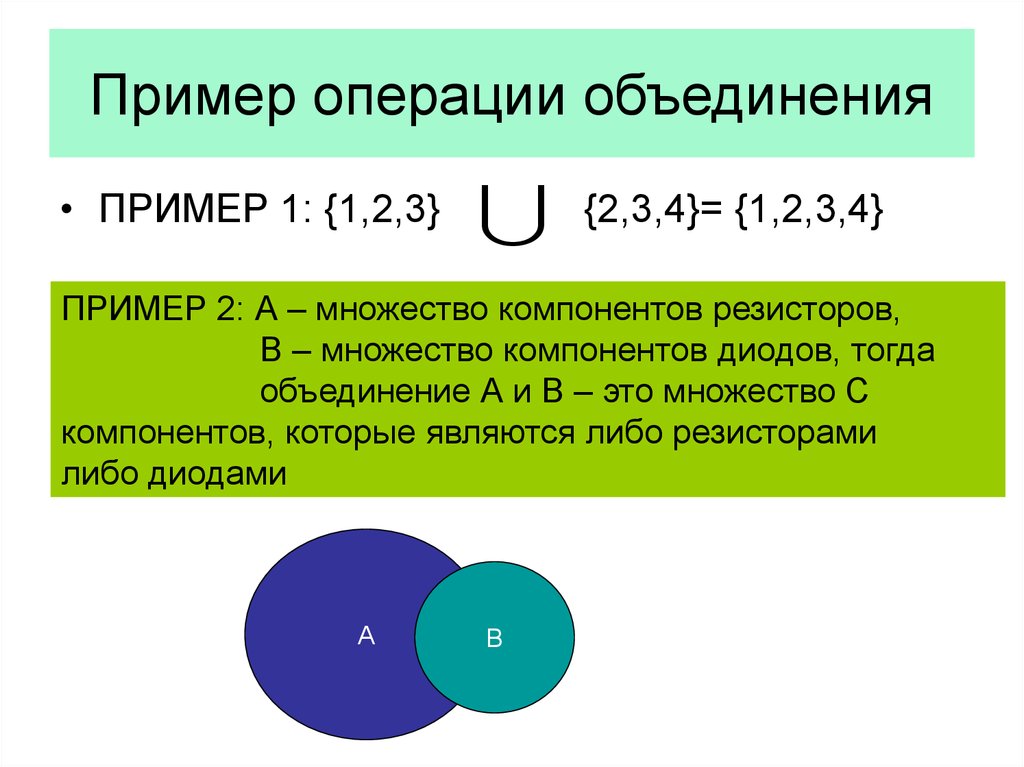 Обозначается:
Обозначается:
Возможно вам будут полезны данные страницы:
Уравнение плоскости по трем точкам |
Метод Симпсона |
Что такое производная |
Определение производной |
Пример 2.
Если , то
Можно рассматривать объединение п множеств:
при этом в А входят все элементы, которые входят хотя бы в одно из множеств
Например, множество всех действительных чисел R состоит из множества положительных чисел R\ множества отрицательных чисел R’ и множества , содержащего один элемент — ноль, то есть
Для наглядного представления соотношений между несколькими подмножествами какого-либо универсума часто используются круги Эйлера или диаграммы Венна.
Универсум представляется множеством всех точек некоторого прямоугольника, а его подмножества — соответствующими кругами. Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1—1.5.
Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1—1.5.
Пересечение (умножение) множеств. Пересечением множеств А и В называется множество D, составленное из общих для множеств А и В элементов. Обозначение: Для множеств из примера 5 имеем:
Можно рассматривать пересечение множеств:
при этом в А входят только, те элементы, которые входят во все множества
Пересечение двух множеств иллюстрируется на рис 1.2.
Пусть есть некоторое множество А. Говорят, что задано разбиение множества А на классы если
Классы — это такие подмножества разбиваемого множества, которые не имеют общих элементов, а их объединение образует исходное множество А. Следовательно, каждый элемент множества А входит в один и только в один класс. Например, разбиение всех студентов одного факультета университета на учебные группы, разбиение книги на страницы, а страницы на абзацы, разбиение уголовного кодекса на статьи и т. п.
Разность двух множеств
Разностью двух множеств называется множество G, содержащее лишь те элементы из А, которые не входят в В. Обозначение: . Отметим, что в А могут находиться не все элементы из вычитаемого множества В (см. рис.1.3). Например,
Обозначение: . Отметим, что в А могут находиться не все элементы из вычитаемого множества В (см. рис.1.3). Например,
Если В — подмножество то разность . называется дополнением к В до А. Например, если и то множество — дополнение к В до А. Операция дополнения иллюстрируется на рис. 1.4.
Дополнение к А до универсума U имеет особое обозначение: (см. рис. 1.5).
Пример 3.
Пусть Такое множество называется множеством неотрицательных чисел. Тогда это множество отрицательных чисел.
Перечисляемые ниже свойства операций над множествами справедливы для любых множеств, поэтому их часто называют законами, часть которых имеет специальные наименования.
1. Коммутативный, или переместительный, закон имеет место, как для операции объединения, так и для операции пересечения:
2. Ассоциативный, или сочетательный, закон также имеет место и для операции объединения и для операции пересечения:
Так как порядок выполнения операций несущественен, то скобки в записи опускают.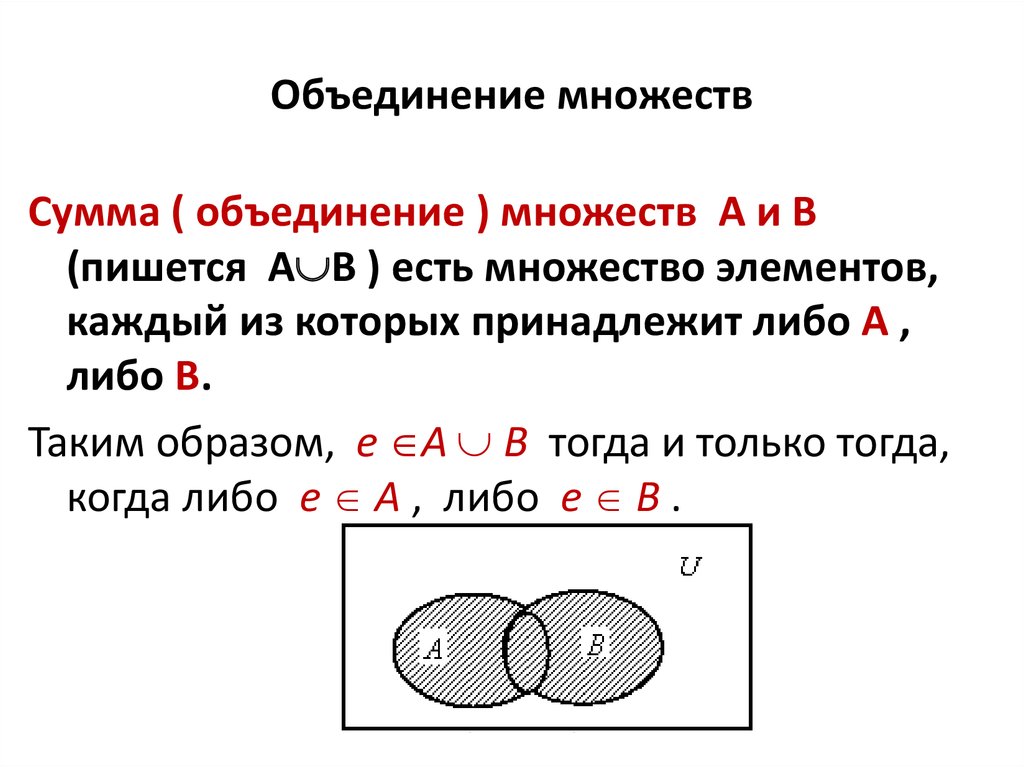 3. Дистрибутивный, или распределительный, закон:
3. Дистрибутивный, или распределительный, закон:
4. Закон идемпотентности:
5. Закон поглощения:
6. Закон двойственности де Моргана: 7. 8. 9.
10. Если и одновременно 11. 12.
Анализируя свойства 1—13, можно сформулировать принцип двойственности: всякое равенство, тождественно выполняемое в теории множеств, переходит также в тождественно выполняющееся равенство при замене знака объединения на знак пересечения множество универсум на пустое множество и наоборот.
04. Множества и операции над ними. Числовые множества. Некоторые обозначения
Множества изображают Диаграммами (кругами) Эйлера-Венна (рис. 1.2).
Рис.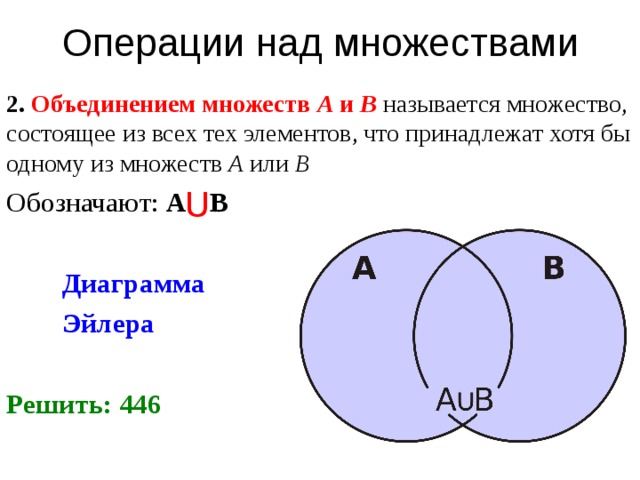 1.2
1.2
Если элемент А принадлежит множеству А, то пишут A Î A; если элемент А не принадлежит множеству А, то пишут A Ï A.
Множество может задаваться с указанием его характеристического свойства. Например, если A состоит из элементов X, для которых выполняется свойство P(X), то пишут
Если каждый элемент множества A есть элемент множества B, то множество A называется Подмножеством множества B (или говорят, что A Включено в B), пишут A Ì B (или B É A) (рис. 1.3). Два множества A, B называются Равными (A = B), если они состоят из одних и тех же элементов: A = B тогда и только тогда, когда A Ì B и B Ì A. Множество, которое не имеет элементов, называется Пустым И обозначается символом Æ.
К основным операциям над множествами относят пересечение, объединение, разность, дополнение.
Пересечением множеств A, B называется множество A Ç B, состоящее из всех тех элементов, которые принадлежат и множеству A, и множеству B (рис. 1.4).
Объединением множеств A, B называется множество A È B, состоящее из всех тех элементов, которые принадлежат или множеству A, или множеству B (хотя бы одному из множеств A, B) (рис. 1.5).
Разностью множеств A\B называется множество, состоящее из всех тех элементов, которые принадлежат множеству A и не принадлежат множеству B (рис. 1.6).
Дополнением множества A до конкретного (универсального) множества U называется множество , которое определяется равенством (рис. 1.7).
A Ì B A Ç B A È B
Рис. 1.3 Рис. 1.4 Рис. 1.5
А\В
Рис.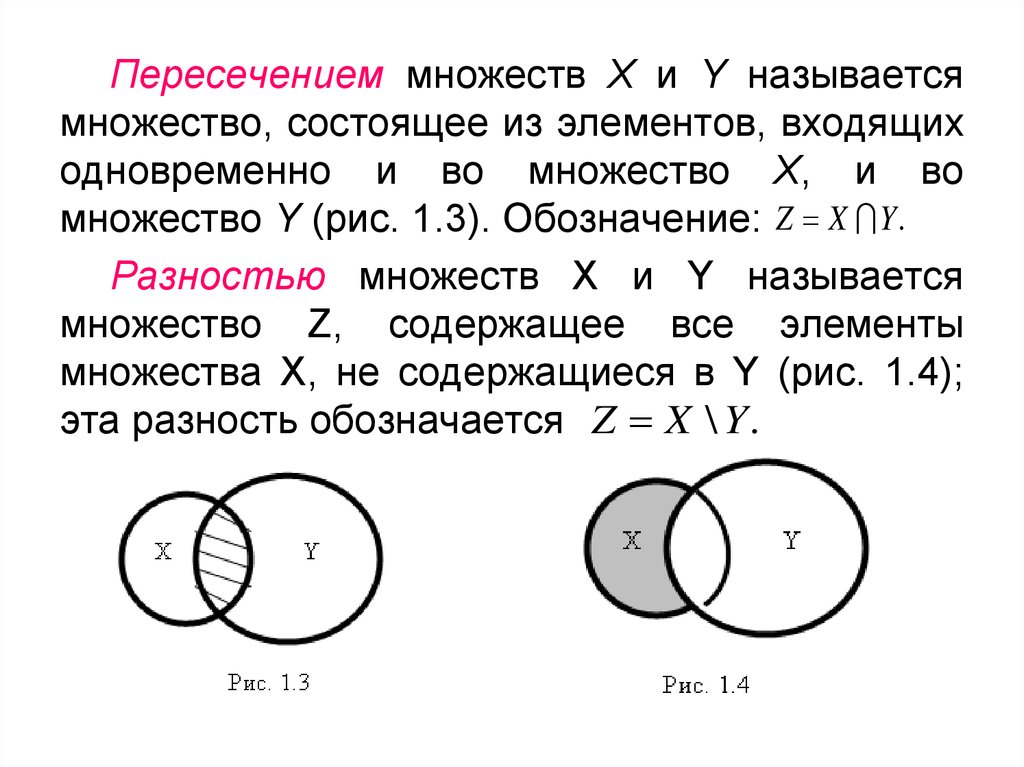 1.6 Рис. 1.7
1.6 Рис. 1.7
Для произвольных множеств A, B, C справедливы свойства:
1) Коммутативность объединения;
2) коммутативность пересечения;
3) Ассоциативность объединения;
4) Ассоциативность пересечения;
5) , дистрибутивность;
6) ;
7) ;
8) ;
9) .
Пусть – количество элементов множеств А и В соответственно, тогда справедлива формула
(1.8)
Рассматривают следующие числовые множества:
1) Множество натуральных чисел;
2) Множество целых чисел;
3) Q – Множество рациональных чисел: это множество всех обыкновенных дробей, т. е. чисел вида где
Множество Q определяется также, как множество всех бесконечных десятичных периодических дробей;
4) I – Множество иррациональных чисел: это множество всех бесконечных десятичных непериодических дробей;
5) R – Множество действительных чисел: .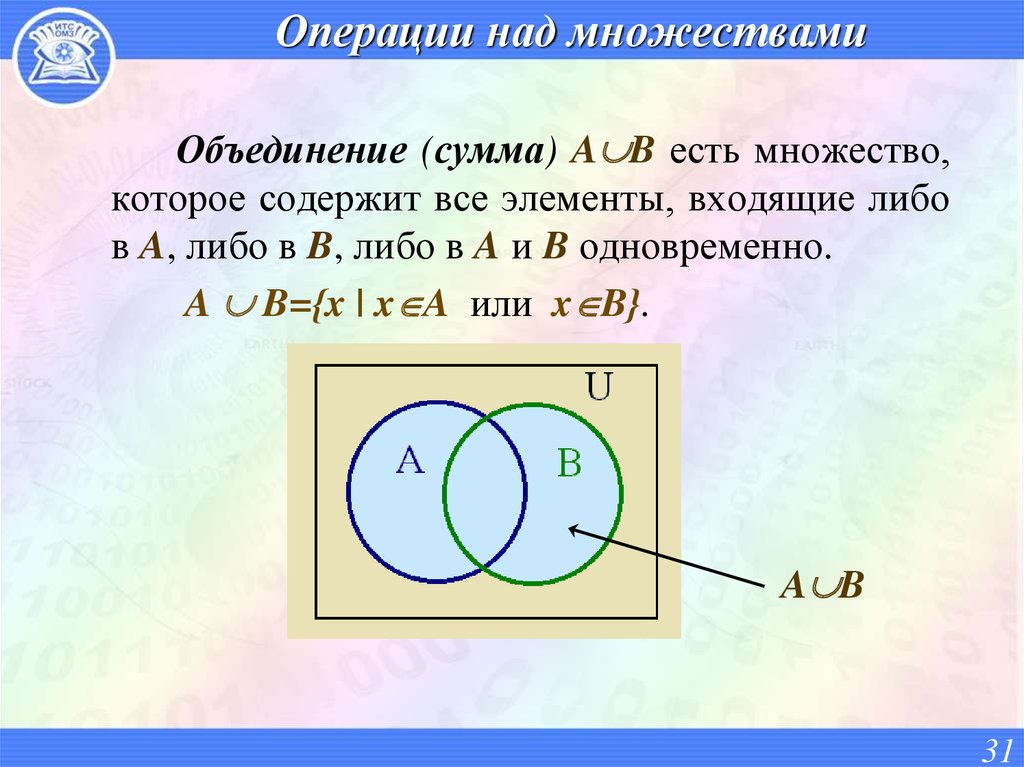
Верны соотношения:
, , .
Произведение первых N натуральных чисел называется Факториалом, для него введен специальный символ:
.
По определению принимают 0! = 1.
Для всякого определены следующие понятия:
Целая часть (антье) числа X, определяется как целое число такое, что
;
Дробная часть (мантисса), определяется равенством
;
– Знак числа (сигнум), определяется следующим образом:
Если некоторые действительные числа, то Сумму Этих величин обозначают с использованием Знака суммы:
,
Где K – Индекс суммирования.
Свойства суммы:
1) – сумма не зависит от того, какой буквой обозначен индекс суммирования;
2)
3)
4) – свойство сдвига индекса суммирования.
Пример 1. Доказать равенство
(1.9)
Доказательство. Пусть Согласно определению разности, получаем и Поскольку выполняются оба эти условия, то это возможно только в случае Получаем, что и т. е. Этим мы доказали, что
Пусть Согласно определению разности, получаем и Поскольку выполняются оба эти условия, то это возможно только в случае Получаем, что и т. е. Этим мы доказали, что
(1.10)
Допустим, что Тогда и но это означает, что
Два условия и которые имеют место, означают, что т. е.
(1.11)
Равенство (1.9) доказано, поскольку установлена справедливость включений (1.10) и (1.11).
Пример 2. На первом курсе учатся 200 студентов. Из них своевременно сдали зачет по математике 175 человек, а по физике – 185 человек. Не сдали зачет ни по математике, ни по физике 10 человек. Сколько студентов сдали оба зачета?
Решение. Пусть A – множество всех студентов курса; B – множество студентов, которые сдали зачет по математике, C – по физике (рис. 1.8).
Согласно условию задачи, , , , и надо найти .
Рис. 1.8
Находим, сколько человек сдали хотя бы один зачет:
Используем далее формулу (1.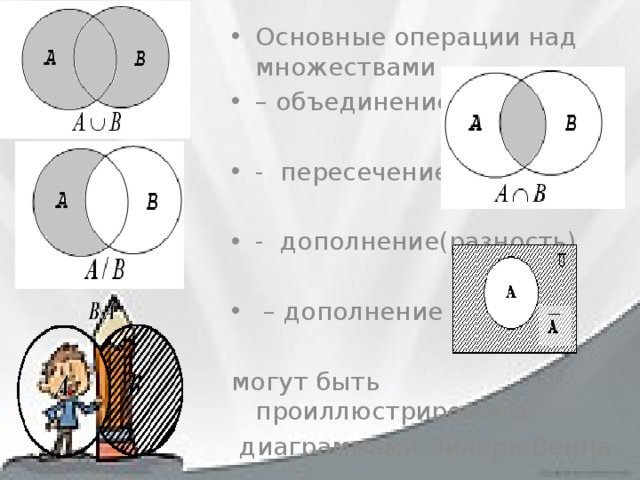 8), из которой выражаем
8), из которой выражаем
Получаем
Пример 3. Сократить дробь
Решение. Выделим общий множитель в числителе и знаменателе. Очевидно, что
Поэтому
Пример 4. Вычислить сумму
Решение. Получим последовательно слагаемые, придавая значения 1, 2, …, 7:
Вычисляя, приходим к ответу
| < Предыдущая | Следующая > |
|---|
6.2. Операции над множествами
Объединение множеств. Объединением множеств и называется множество , элементы которого принадлежат либо множеству , либо множеству . Принятое обозначение: . Аналогично определяется объединение любого (конечного или счётного) числа множеств : множество содержит элементы, принадлежащие хотя бы одному из множеств .
Пересечение множеств. Пересечением множеств и называется множество , элементы которого принадлежат как множеству , так и множеству . Обозначение: . Пересечением любого (конечного или счётного) числа множеств называется множество элементов, содержащееся в каждом из множеств .
Обозначение: . Пересечением любого (конечного или счётного) числа множеств называется множество элементов, содержащееся в каждом из множеств .
Операции объединения и пересечения множеств коммутативны, ассоциативны и взаимно дистрибутивны.
Разность множеств. Разностью множеств и называется множество , состоящее из тех элементов множества , которые не принадлежат множеству . Обозначение: . Дизъюнктивная сумма (симметрическая разность) двух множеств и определяется как объединение разностей и . Для её обозначения используют символ , т. е. по определению .
Дополнение множества. Дополнением множества до универсального множества называется множество , определяемое из соотношения: .
Очевидно, , т. е. если то , а значит, В общем случае имеет место формула:
Разбиение множества. Рассмотрим некоторое множество и систему множеств . Систему множеств называют разбиением множества , если выполняются следующие условия: 1) , 2) , 3) .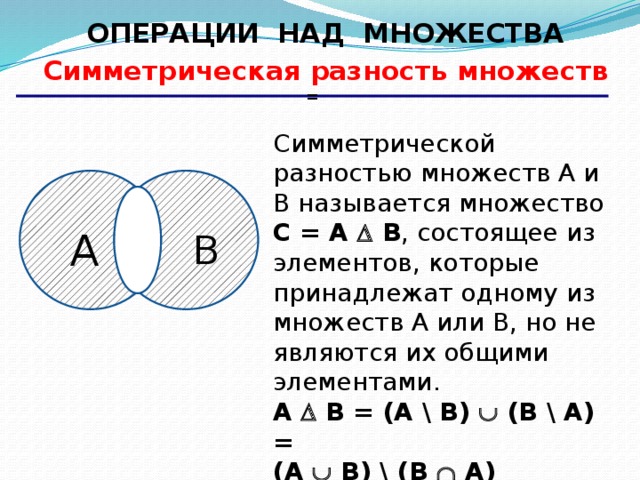
Пример 25. Пусть – универсальное множество, – его подмножество, т. е. , например,
Выпишем для каждого элемента из степень его принадлежности множеству : Это позволяет представить множество через все элементы множества с указанием для каждого из них значения функции принадлежности:
.
Очевидно,
Выясним, как задаётся функция принадлежности пересечению и объединению множеств и . По определению:
Т. е. где «» – операция булева произведения, которую можно задать такой таблицей: .
Аналогично, т. е. , где «» – булева сумма, значения которой определяются таблицей: .
Пример 26. Пусть задано универсальное множество и его подмножества и . Найти , , , и .
Решение. Представим множества и в виде:
Тогда:
И для дополнений к этим множествам имеем:
Так как:
То для дизъюнктивной суммы множеств и получим:
.
Пример 27. На первом курсе факультета компьютерных информационных технологий обучается 80 студентов.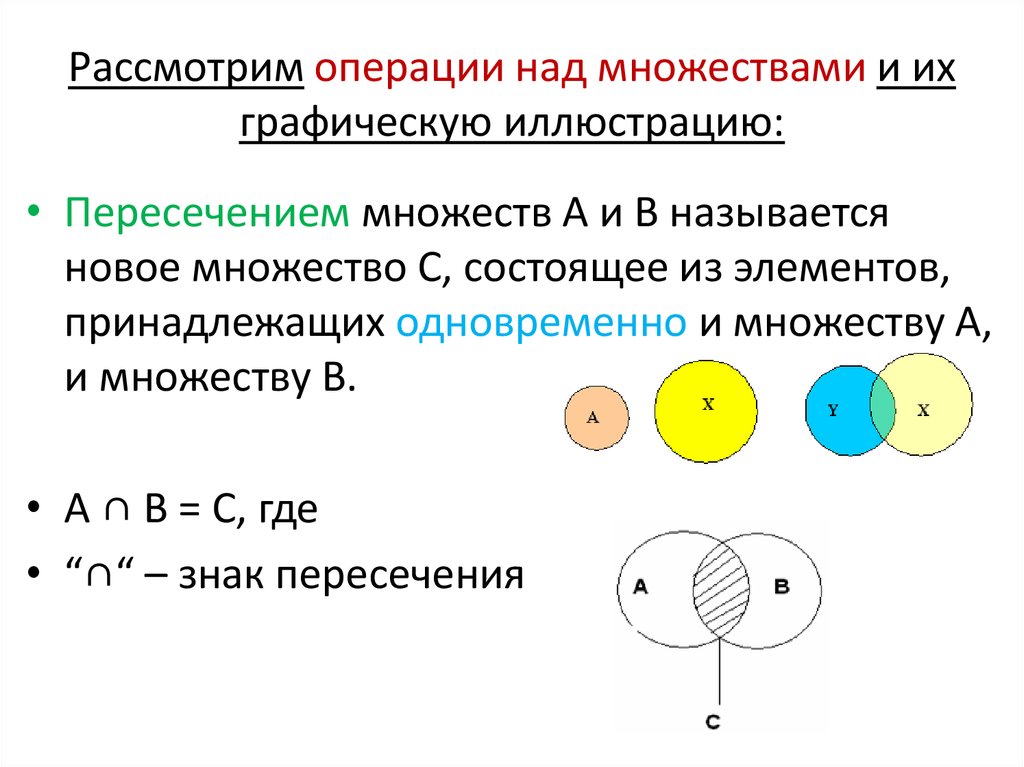 Известно, что из них легкой атлетикой занимаются 35 студентов, посещают бассейн 23, играют в настольный теннис 30, занимаются легкой атлетикой и посещают бассейн 10, занимаются легкой атлетикой и играют в настольный теннис 11, посещают бассейн и играют в настольный теннис 7, занимаются во всех трех спортивных секциях 4 студента. Остальные студенты не посещают ни одной спортивной секции. Дайте ответы на следующие вопросы:
Известно, что из них легкой атлетикой занимаются 35 студентов, посещают бассейн 23, играют в настольный теннис 30, занимаются легкой атлетикой и посещают бассейн 10, занимаются легкой атлетикой и играют в настольный теннис 11, посещают бассейн и играют в настольный теннис 7, занимаются во всех трех спортивных секциях 4 студента. Остальные студенты не посещают ни одной спортивной секции. Дайте ответы на следующие вопросы:
Сколько студентов посещают только бассейн? Сколько студентов занимаются легкой атлетикой, но при этом не играют в настольный теннис? Сколько студентов не посещают ни одной спортивной секции? Сколько студентов не занимаются легкой атлетикой и не посещают бассейн?
Решение. Построим диаграмму Венна в виде пересекающихся кругов, изображающих множества студентов, занимающихся легкой атлетикой, плаванием и настольным теннисом соответственно (рисунок 3).
Введем обозначения:
– множество всех студентов курса (= 80),
– множество студентов, занимающихся легкой атлетикой (= 35),
– множество студентов, посещающих бассейн (= 23),
– множество студентов, играющих в настольный теннис (= 30),
– множество студентов, занимающихся легкой атлетикой и посещающих бассейн (, = 10),
– множество студентов, занимающихся легкой атлетикой и играющих в настольный теннис (, = 11),
– множество студентов, посещающих бассейн и играющих в настольный теннис (, = 7),
– множество студентов, посещающих эти три спортивные секции (, = 4).
Определим множество студентов, занимающихся легкой атлетикой и посещающих бассейн, но не играющих в настольный теннис . Ясно, что .
Множество студентов, занимающихся легкой атлетикой и играющих в настольный теннис, но не посещающих бассейн , и .
Аналогично, множество студентов, посещающих бассейн и играющих в настольный теннис, но не занимающихся легкой атлетикой: , а .
Теперь с помощью диаграммы Венна можно определить число студентов, занимающихся только в одной из трех спортивных секций.
Только легкой атлетикой занимаются студентов; только в бассейн ходят студентов; только в настольный теннис играют студентов.
Множество студентов, занимающихся хотя бы в одной из этих спортивной секций . Таких студентов . Следовательно, студентов, не занимающихся ни в одной из трех спортивных секций .
Окончательно, диаграмма Венна примет вид, представленный на рис. 3.
Ответим на поставленные в задаче вопросы:
Количество студентов, посещающих только бассейн . Количество студентов, занимающихся легкой атлетикой, но при этом не играющих в настольный теннис . Количество студентов, которые не посещают ни одной спортивной секции . Количество студентов, которые не занимаются легкой атлетикой и не посещают бассейн , поскольку в это число входят студенты, которые не занимаются ни в одной спортивной секции либо занимаются только настольным теннисом.
Количество студентов, занимающихся легкой атлетикой, но при этом не играющих в настольный теннис . Количество студентов, которые не посещают ни одной спортивной секции . Количество студентов, которые не занимаются легкой атлетикой и не посещают бассейн , поскольку в это число входят студенты, которые не занимаются ни в одной спортивной секции либо занимаются только настольным теннисом.
Рисунок 3
| < Предыдущая | Следующая > |
|---|
Операции над множествами
Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = { | Том, Фред, Макс, Джорж } |
| Друзья Майкла = { | Лео, Том, Фред, Эван } |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.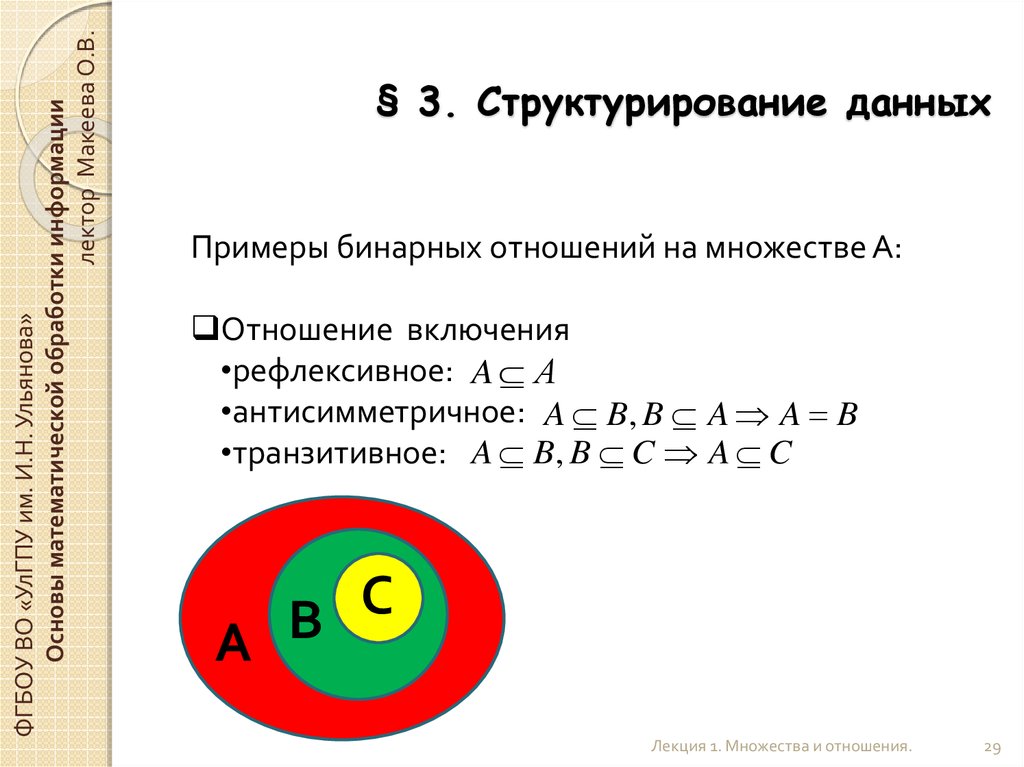
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда:
| Общие друзья Джона и Майкла | = { Том, Фред } |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Обозначим множество друзей Джона через букву A, множество друзей Майкла — через букву B, а множество общих друзей Джона и Майкла обозначим через букву C:
A = { Том, Фред, Макс, Джордж }
B = { Лео, Том, Фред, Эван }
C = { Том, Фред }
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
A ∩ B = C
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
Или еще проще:
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
Теперь представим, что у Джона и Майкла нет общих друзей. Для удобства, как и прежде обозначим множество друзей Джона через букву A, а множество друзей Майкла через букву B
A = { Макс, Джордж }
B = { Лео, Эван }
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
A ∩ B = ∅
Пример 2.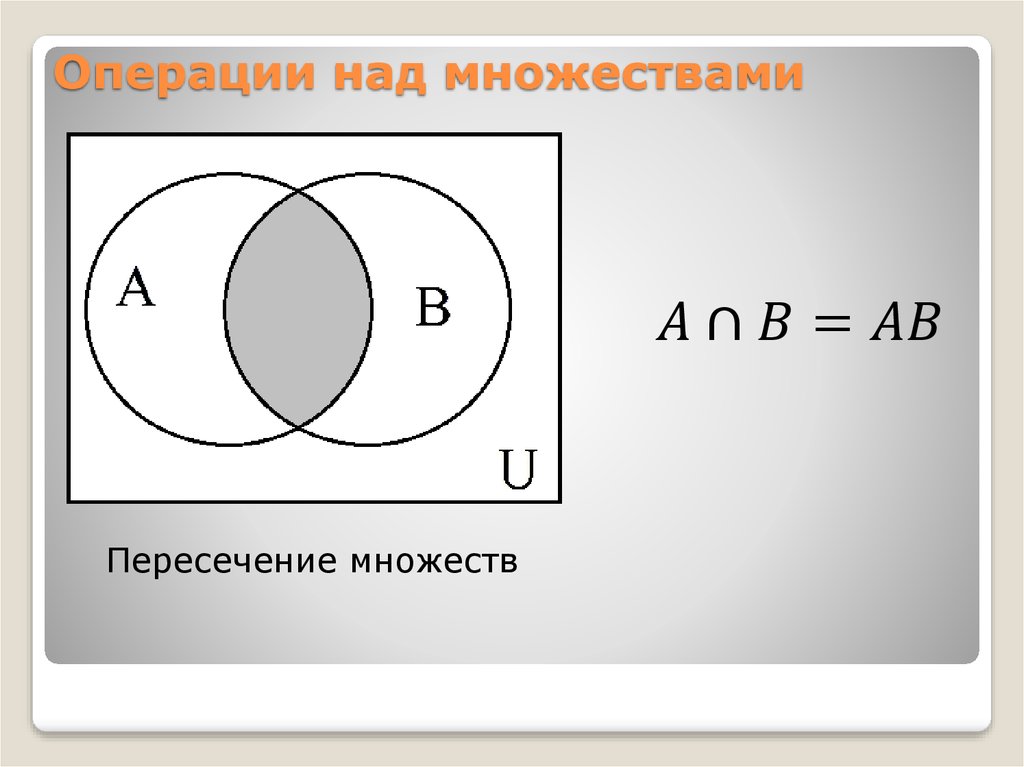 Рассмотрим два множества: множество A, состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Рассмотрим два множества: множество A, состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
A = { 1, 2, 3, 5, 7 }
B = { 1, 2, 3, 4, 6, 12, 18 }
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
C = { 1, 2, 3 }
Множество С является пересечением множеств A и B, поскольку элементы множества C одновременно принадлежат множеству A и множеству B
Пример 3. Рассмотрим два множества: множество A, состоящее из чисел 1, 5, 7, 9 и множество B, состоящее из чисел 1, 4, 5, 7
A = { 1, 5, 7, 9 }
B = { 1, 4, 5, 7 }
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
C = { 1, 5, 7 }
Множество С является пересечением множеств A и B, поскольку элементы множества C одновременно принадлежат множеству A и множеству B.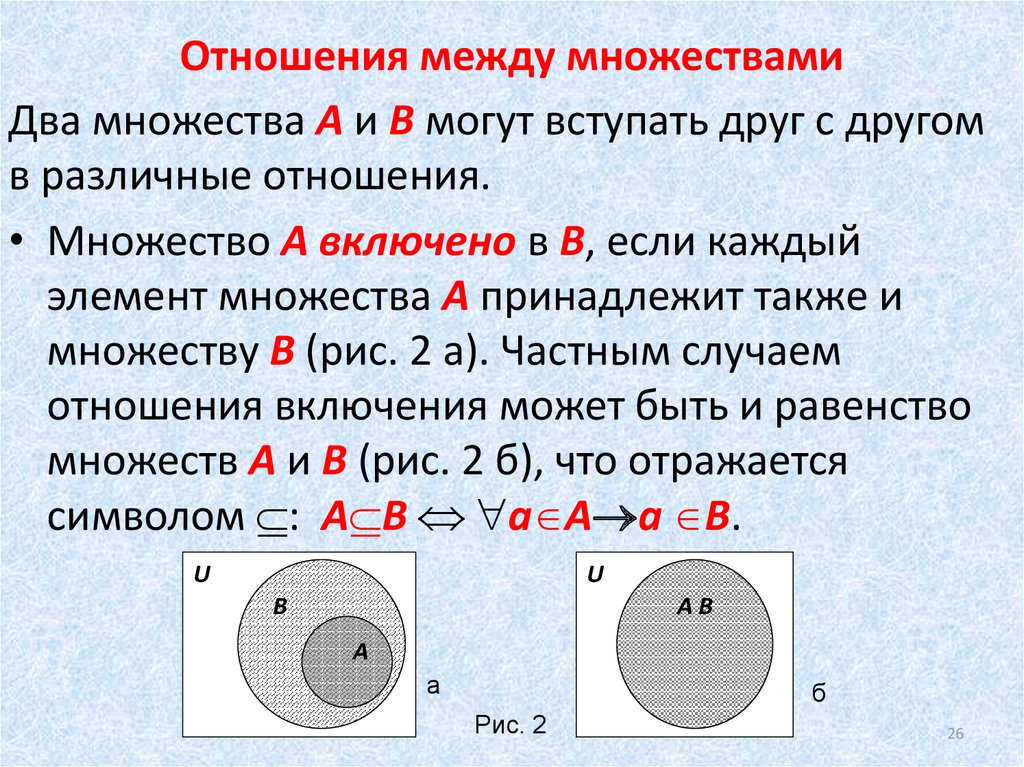
Пример 4. Найти пересечение следующих множеств:
A = { 1, 2, 3, 7, 9 }
B = { 1, 3, 5, 7, 9}
С = { 3, 4, 5, 8, 9}
Пересечением множеств A, B и C будет множество, состоящее из элементов, принадлежащих каждому из множеств A, B и C. Этими элементами являются числа 3 и 9.
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
D = { 3, 9}
A ∩ B ∩ C = D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
К примеру, пусть первое множество состоит из элементов 1, 3, 5, а второе из элементов 2, 3, 5. Пересечением в данном случае является множество, состоящее из элементов 3 и 5. Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Чтобы записать пересечение, можно воспользоваться прямым перечислением:
{ 1, 3, 5 } ∩ { 2, 3, 5 } = { 3, 5 }
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
2, 3, 4, 5, 6 ∈ [2; 6]
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6):
3, 4, 5 ∈ (2; 6)
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Рассмотрим несколько примеров.
Пример 5. Даны два числовых промежутка: [2; 6] и [4; 8]. Найти их пересечение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8]:
2, 3, 4, 5, 6 ∈ [2; 6]
4, 5, 6, 7, 8 ∈ [4; 8]
Видно, что числа 4, 5, 6 принадлежат как первому промежутку [2; 6], так и второму [4; 8].
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
[2; 6] ∩ [4; 8] = [4; 6]
Изобразим промежутки [2; 6] и [4; 8] на координатной прямой. На верхней области отметим числовой промежуток [2; 6], на нижней — промежуток [4; 8]
Видно, что числа, принадлежащие промежутку [4; 6], принадлежат как промежутку [2; 6], так и промежутку [4; 8]. Можно также заметить, что штрихи, входящие в промежутки [2; 6] и [4; 8] пересекаются в промежутке [4; 6]. В такой ситуации, когда перед глазами есть координатная прямая, понятие пересечения множеств можно понимать в прямом смысле что очень удобно.
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7]:
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
4, 5, 6, 7 ∈ [4; 7]
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
[−2; 3] ∩ [4; 7] = Ø
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента { 2 }. Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента { 2 }, на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества { 2 } и числового промежутка (−3; 4) будет множество, состоящее из одного элемента { 2 }, поскольку элемент 2 принадлежит как множеству { 2 }, так и числовому промежутку (−3; 4)
{ 2 } ∩ (−3; 4) = { 2 }
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств.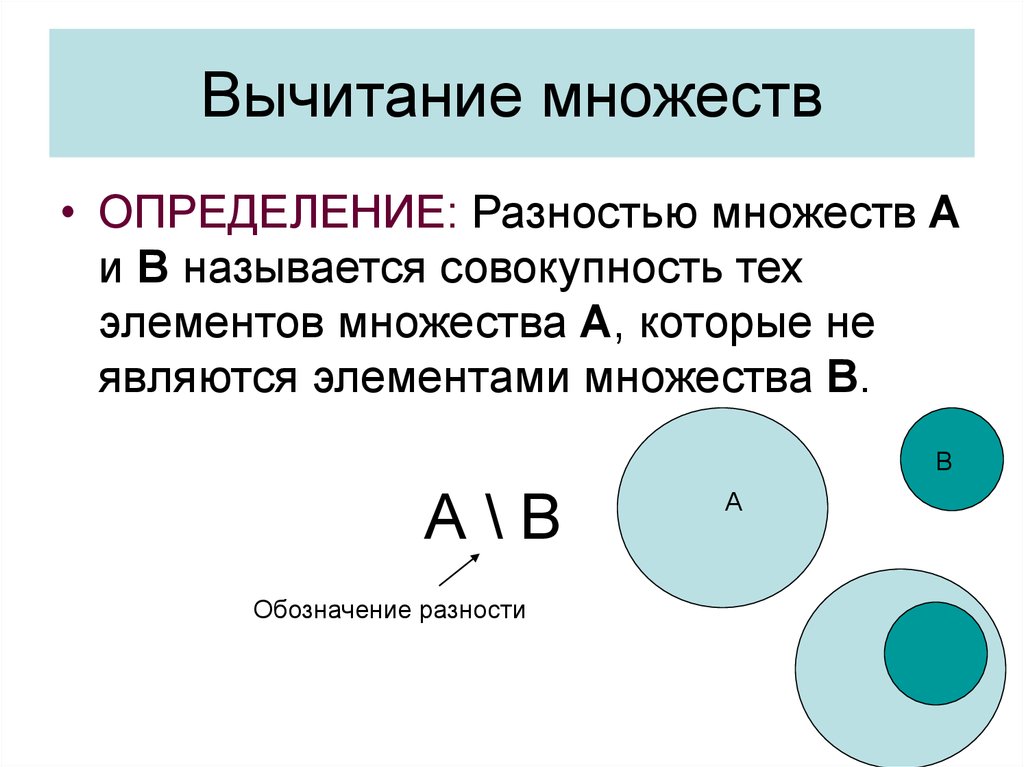 Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств , мы должны сначала найти множества решений каждого неравенства, затем найти пересечение этих множеств.
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Если мы изобразим множество решений системы на координатной прямой, то увидим, что эти решения принадлежат промежутку [3; 6], который в свою очередь является пересечением промежутков [3; +∞) и (−∞; 6]
[3; +∞) ∩ (−∞; 6] = [3; 6]
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
x ∈ [3; 6]
Пример 2.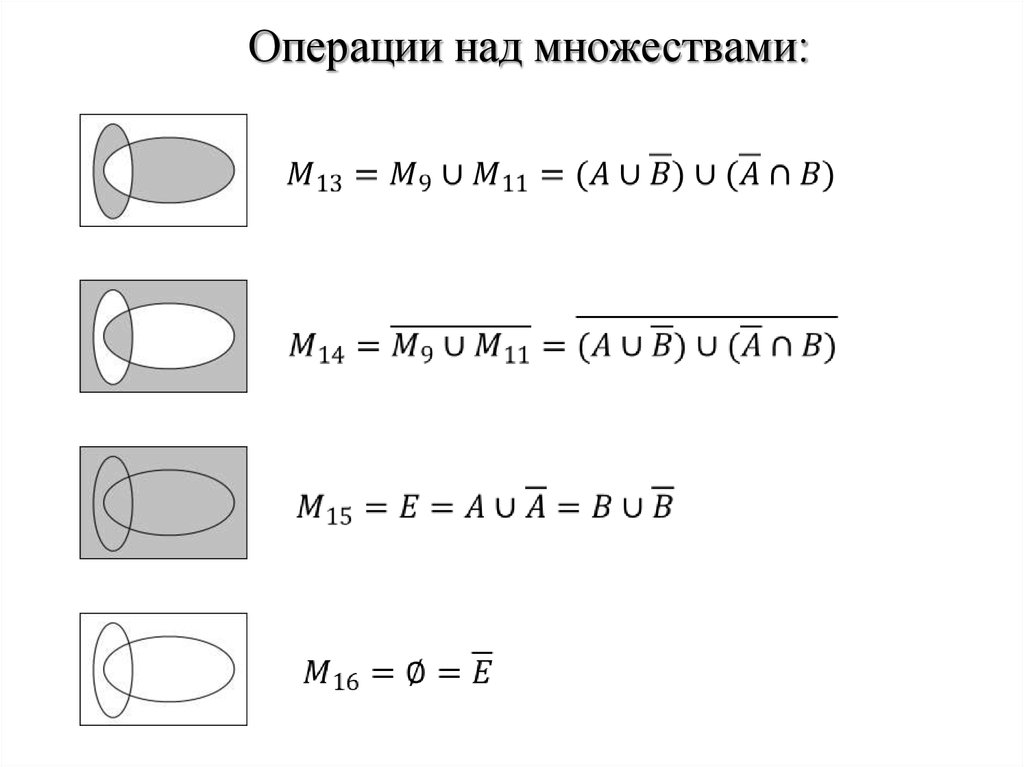 Решить неравенство
Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
Решением первого неравенства является числовой промежуток (−∞; −1).
Решением второго неравенства является числовой промежуток (−∞; −5).
Решением третьего неравенства является числовой промежуток (−∞; 4).
Решением системы будет пересечение числовых промежутков (−∞; −1), (−∞; −5) и (−∞; 4). В данном случае этим пересечением является промежуток (−∞; −5).
(−∞; −1) ∩ (−∞; −5) ∩ (−∞; 4) = (−∞; −5)
На рисунке представлены числовые промежутки и неравенства, которыми эти числовые промежутки заданы. Видно, что числа, принадлежащие промежутку (−∞; −5), одновременно принадлежат всем исходным промежуткам.
Запишем ответ к системе с помощью числового промежутка:
x ∈ (−∞; −5)
Пример 3. Решить неравенство
Решением первого неравенства y > 7 является числовой промежуток (7; +∞).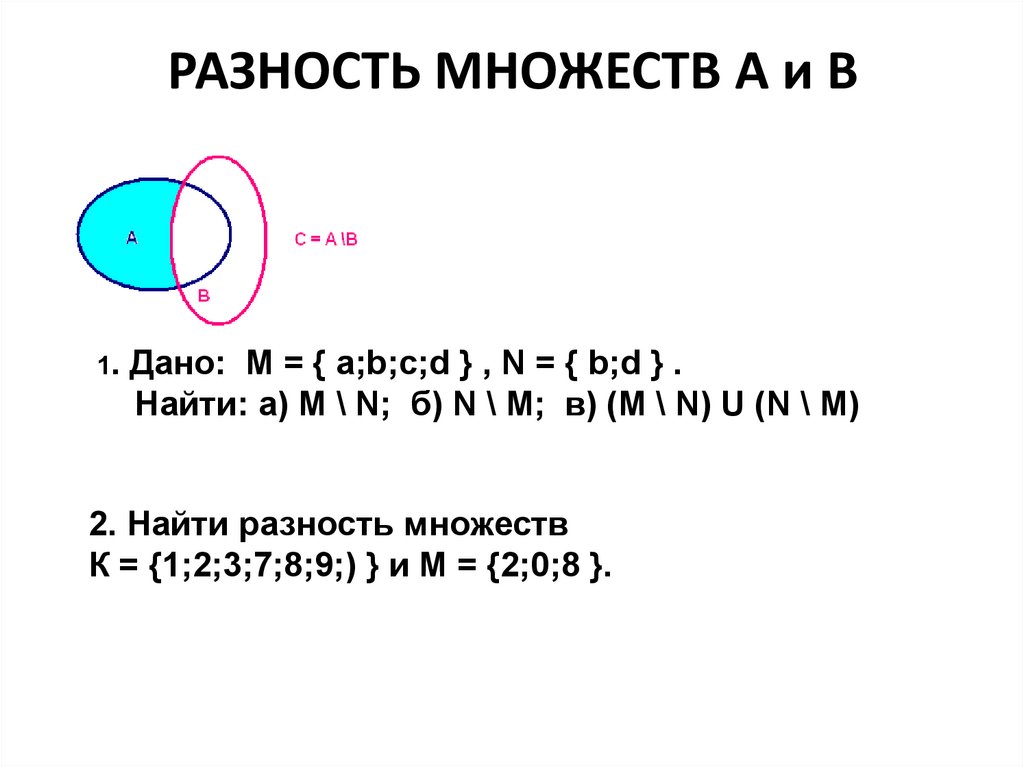
Решением второго неравенства y < 4 является числовой промежуток (−∞; 4).
Решением системы будет пересечение числовых промежутков (7; +∞) и (−∞; 4).
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
(7; +∞) ∩ (−∞; 4) = ∅
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.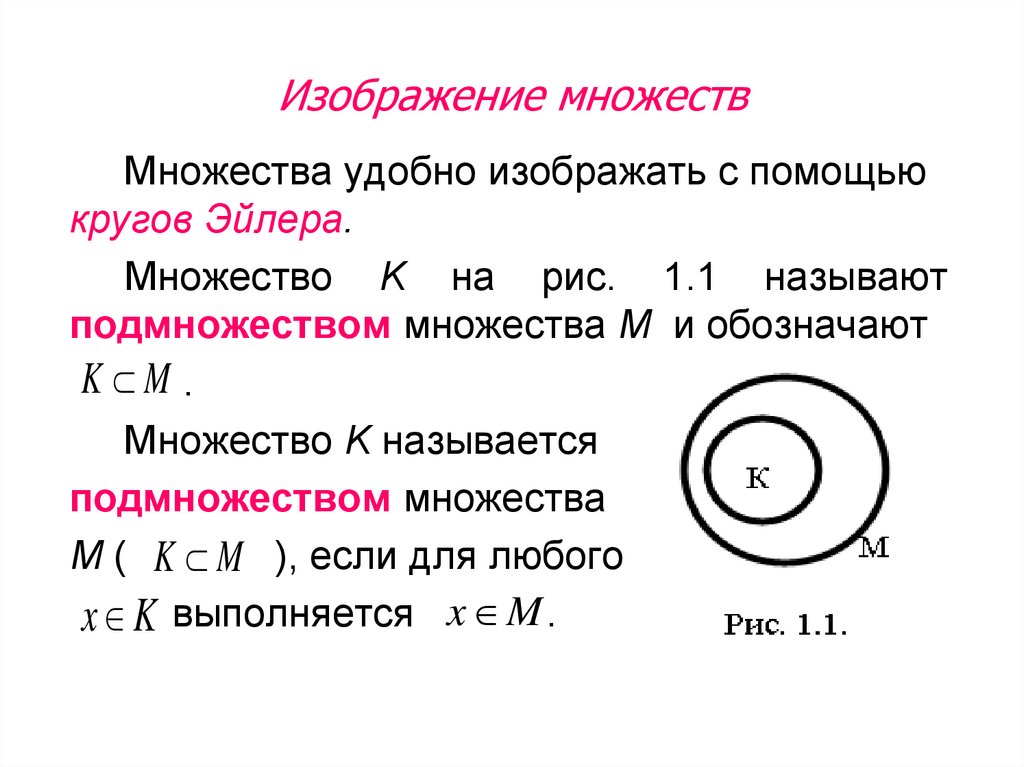
A = { 1, 2, 3 }
B = { 4, 5, 6 }
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
C = { 1, 2, 3, 4, 5, 6 }
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
A ∪ B = C
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Вернёмся к созданному нами множеству C, куда входят все элементы множеств A и B. Возьмём для примера из этого множества элемент 5. Что можно про него сказать?
Что можно про него сказать?
Если 5 является элементом множества C, а множество С является объединением множеств A и B, то можно с уверенностью заявить, что элемент 5 принадлежит хотя бы одному из множеств A и B. Так оно и есть:
A = { 1, 2, 3 }
B = { 4, 5, 6 }
C = { 1, 2, 3, 4, 5, 6 }
Возьмем ещё один элемент из множества С, например, элемент 2. Что можно про него сказать?
Если 2 является элементом множества C, а множество С является объединением множеств A и B, то можно с уверенностью заявить, что элемент 2 принадлежит хотя бы одному из множеств A и B. Так оно и есть:
A = {1, 2, 3}
B = {4, 5, 6}
C = { 1, 2, 3, 4, 5, 6 }
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
A = {1, 2, 3, 4}
B = {2, 4, 5, 6}
Видим, что элементы 2 и 4 одновременно принадлежат и множеству A, и множеству B. Если мы захотим объединить множества A и B, то новое множество C будет содержать элементы 2 и 4 только один раз. Выглядеть это будет так:
C = { 1, 2, 3, 4, 5, 6 }
Чтобы при объединении не допустить ошибок, обычно поступают так: сначала в новое множество добавляют все элементы первого множества, затем добавляют элементы второго множества, которые не принадлежат первому множеству. Попробуем сделать такое объединение с множествами A и B.
Итак, у нас имеются следующие исходные множества:
A = { 1, 2, 3, 4 }
B = { 2, 4, 5, 6 }
Зададим новое множество С и добавим в него все элементы множества A
C = { 1, 2, 3, 4,
Теперь добавим элементы из множества B, которые не принадлежат множеству A. Множеству A не принадлежат элементы 5 и 6. Их и добавим во множество C
Множеству A не принадлежат элементы 5 и 6. Их и добавим во множество C
C = { 1, 2, 3, 4, 5, 6 }
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = { | Том, Фред, Макс, Джорж } |
| Друзья Майкла = { | Лео, Том, Фред, Эван } |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.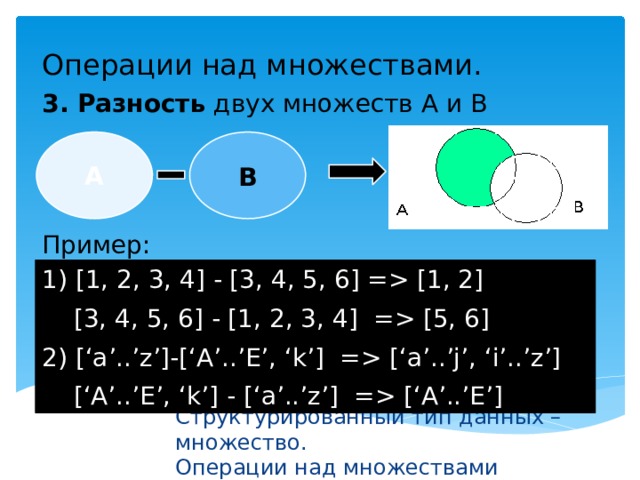
| Все друзья Джона и Майкла | = { Том, Фред, Макс, Джордж, Лео, Эван } |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
Пример 3. Даны два числовых промежутка: [−7; 0] и [−3; 5]. Найти их объединение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1, 0 ∈ [−7; 0]
−3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
Объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5], который содержит все числа промежутка [−7; 0] и [−3; 5] без повторов некоторых из чисел
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
[−7; 0] ∪ [−3; 5] = [−7; 5]
Изобразим на координатной прямой промежутки [−7; 0] и [−3; 5]. На верхней области отметим числовой промежуток [−7; 0], на нижней — промежуток [−3; 5]
Ранее мы выяснили, что промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5]. Здесь полезно вспомнить про определение объединения множеств, которое было приведено в самом начале. Объединение трактуется, как множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств.
Действительно, если взять любое число из промежутка [−7; 5], то окажется, что оно принадлежит хотя бы одному из промежутков: либо промежутку [−7; 0] либо промежутку [−3; 5].
Возьмём из промежутка [−7; 5] любое число, например число 2. Поскольку промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5], то число 2 будет принадлежать хотя бы одному из этих промежутков.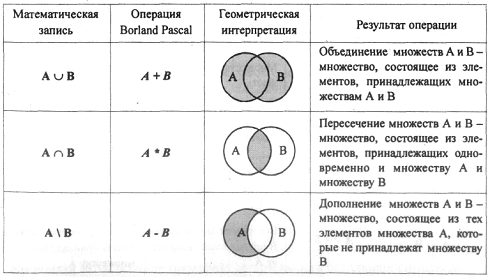 В данном случае число 2 принадлежит промежутку [−3; 5]
В данном случае число 2 принадлежит промежутку [−3; 5]
Возьмём ещё какое-нибудь число. Например, число −4. Это число будет принадлежать хотя бы одному из промежутков: [−7; 0] или [−3; 5]. В данном случае оно принадлежит промежутку [−7; 0]
Возьмём ещё какое-нибудь число. Например, число −2. Оно принадлежит как промежутку [−7; 0], так и промежутку [−3; 5]. Но на координатной прямой оно указывается только один раз, поскольку в одной точке сразу два числа −2 не бывает.
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2; −1] и [4; 7].
Идея остаётся та же самая — объединением числовых промежутков [−2;−1] и [4; 7] будет множество, состоящее из элементов, принадлежащих хотя бы одному из промежутков: [−2; −1] или [4; 7]. Но это множество не будет являться числовым промежутком. Для наглядности перечислим все целые числа, принадлежащие этому объединению:
[−2; −1] ∪ [4; 7] = { −2, −1, 4, 5, 6, 7 }
Получили множество { −2, −1, 4, 5, 6, 7 }.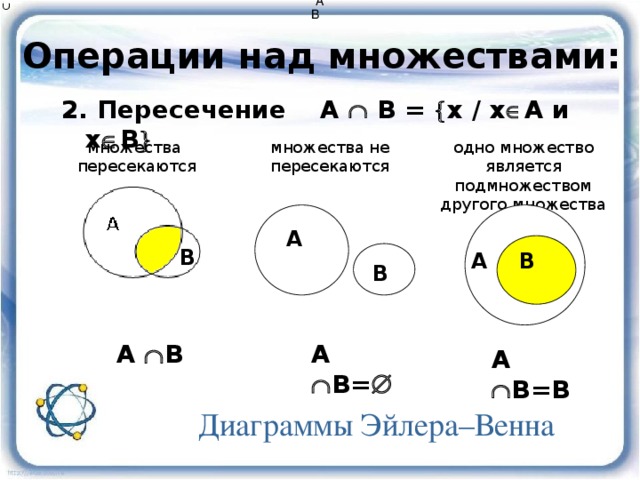 Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4, не вошли в полученное множество
Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4, не вошли в полученное множество
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Эта линейка не является линейкой в 15 см, и её нежелательно использовать для измерения. Также, её нельзя назвать числовым промежутком [0; 15], поскольку она не содержит все числа, которые должна была содержать.
Решение неравенств, содержащих знак ≠
Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8. Чтобы решить такое неравенство, нужно найти множество значений переменной x, при которых левая часть не равна правой части.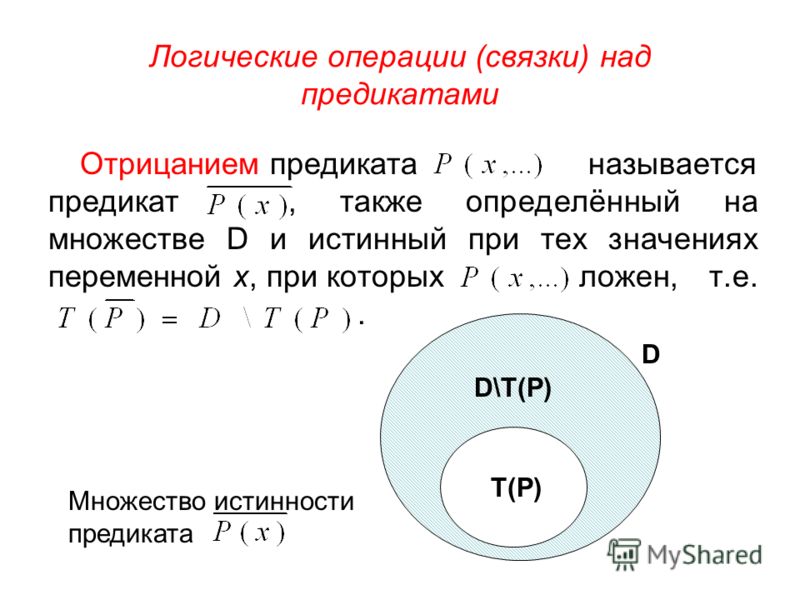
Решим неравенство 2x ≠ 8. Разделим обе части данного неравенства на 2, тогда получим:
Получили равносильное неравенство x ≠ 4. Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
Подставим 7
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8, то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8. Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8.
2 × 5 ≠ 8
2 × 7 ≠ 8
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪
Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪
x ∈ (−∞; 4) ∪ (4; +∞)
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат промежутку (−∞; 4) или промежутку (4; +∞).
Неравенства, содержащие знак ≠, также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак =. Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.
Решим предыдущее неравенство 2x ≠ 8, как обычное уравнение. Заменим знак ≠ на знак равенства =, получим уравнение 2x = 8. Разделим обе части данного уравнения на 2, получим x = 4.
Видим, что при x, равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2.
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
x ∈ (−∞; 1,2) ∪ (1,2; +∞)
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Решением первого неравенства x ≥ 3 является числовой промежуток [3; +∞). Решением второго неравенства x ≤ 6 является числовой промежуток (−∞; 6].
Множество значений x, при которых верно хотя бы одно из неравенств, будет принадлежать промежутку [3; +∞) или промежутку (−∞; 6]. Так и записываем:
Так и записываем:
x ∈ [3; +∞) ∪ (−∞; 6]
В этом выражении говорится, что переменная x, входящая в
совокупность принимает все значения, принадлежащие промежутку [3; +∞) или промежутку (−∞; 6]. А это то, что нам нужно. Ведь решить совокупность означает найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность. А любое число из промежутка [3; +∞) или промежутка (−∞; 6] будет удовлетворять хотя бы одному неравенству.
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Посмотрите внимательно на выражение x ∈ [3; +∞) ∪ (−∞; 6], а именно на его правую часть. Ведь выражение [3; +∞) ∪ (−∞; 6] представляет собой объединение числовых промежутков [3; +∞) и (−∞; 6]. Точнее, объединение множеств решений первого и второго неравенства.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.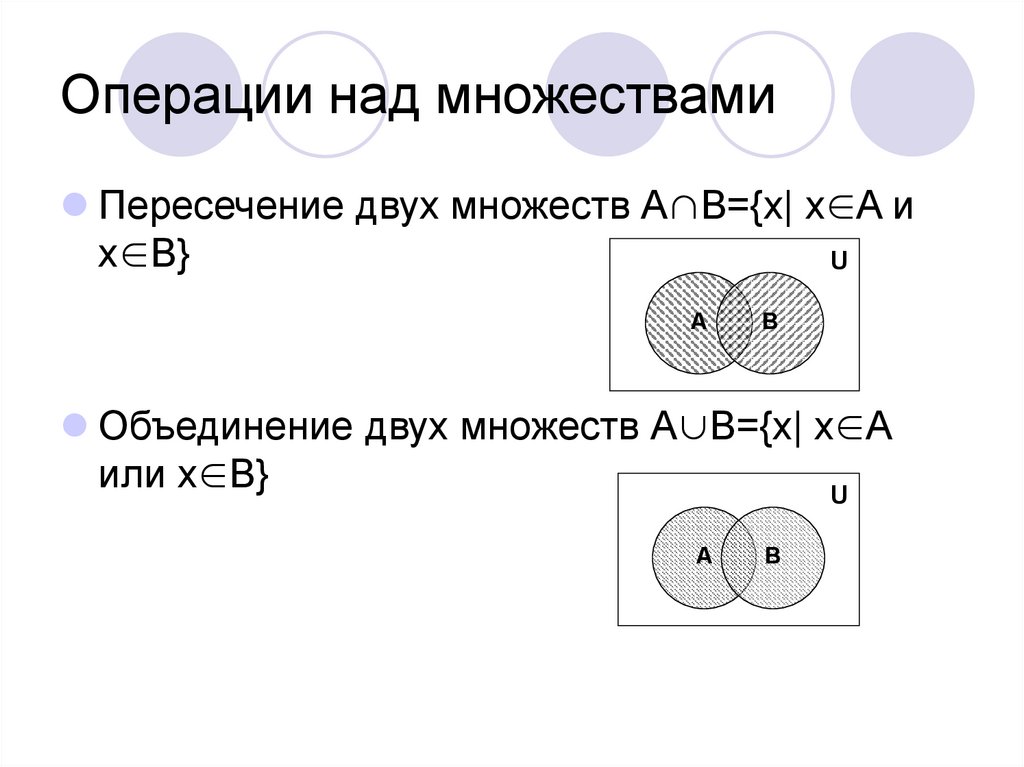
Иначе говоря, решением совокупности будет объединение числовых промежутков [3; +∞) и (−∞; 6]
Объединением числовых промежутков [3; +∞) и (−∞; 6] является промежуток (−∞; +∞). Точнее, объединением числовых промежутков [3; +∞) и (−∞; 6] является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
[3; +∞) ∪ (−∞; 6] = (−∞; +∞)
Ответ можно оставить таким, каким мы его записали ранее:
x ∈ [3; +∞) ∪ (−∞; 6]
либо заменить на более короткий:
x ∈ (−∞; +∞)
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
8 ≥ 3
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
1 ≤ 6
Возьмем еще какое-нибудь число, например, число 5. Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6
Пример 2. Решить совокупность неравенств
Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Для начала найдём множество решений первого неравенства x < −0,25. Этим множеством является числовой промежуток (−∞; −0,25).
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.
x ∈ (−∞; −0,25) ∪ [−7; +∞)
Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −0,25) и [−7; +∞)
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
(−∞; −0,25) ∪ [−7; +∞) = (−∞; +∞)
Ответ можно оставить таким, каким мы его записали ранее:
x ∈ (−∞; −0,25) ∪ [−7; +∞)
либо заменить на более короткий:
x ∈ (−∞; +∞)
Пример 3.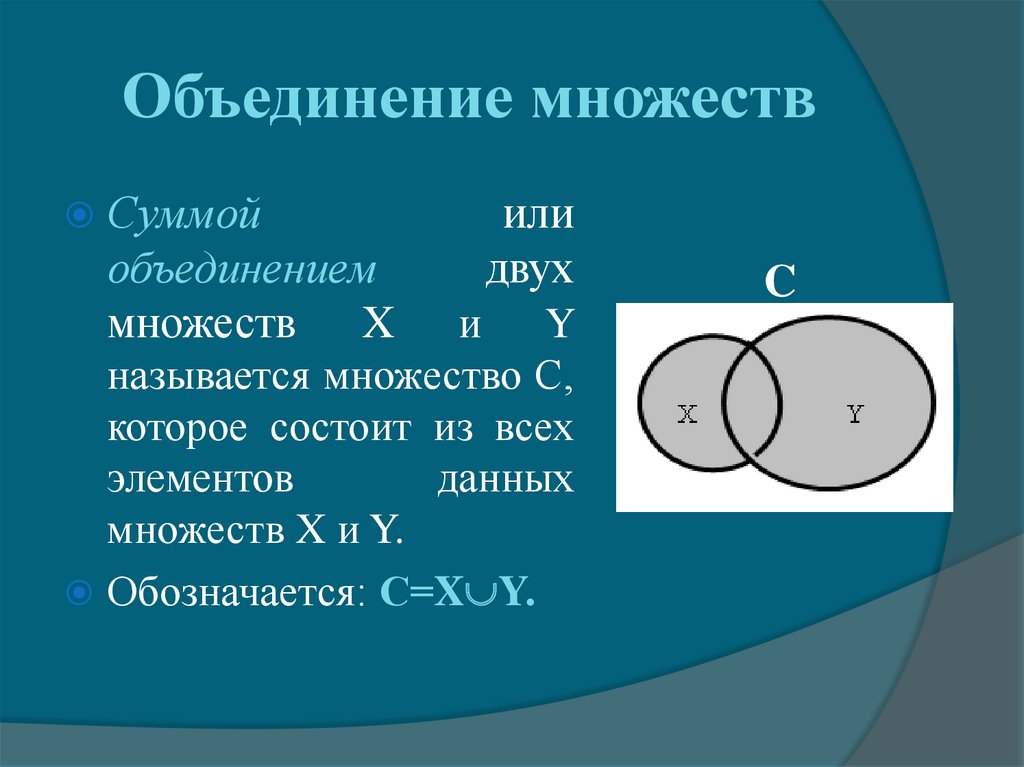 Решить совокупность неравенств
Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Множеством решений первого неравенства x < −3 является числовой промежуток (−∞; −3).
Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0].
Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.
x ∈ (−∞; −3) ∪ (−∞; 0]
Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −3) и (−∞; 0]
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
(−∞; −3) ∪ (−∞; 0] = (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее:
x ∈ (−∞; −3) ∪ (−∞; 0]
либо заменить на более короткий:
x ∈ (−∞; 0]
Задания для самостоятельного решения
Задание 1. Найдите пересечение и объединение следующих множеств:
А = { 1, 2, 5 }
B = { 3, 4, 5 }
Решение:
A ∩ B = { 5 }
A ∪ B = { 1, 2, 3, 4, 5 }
Показать решение
Задание 2.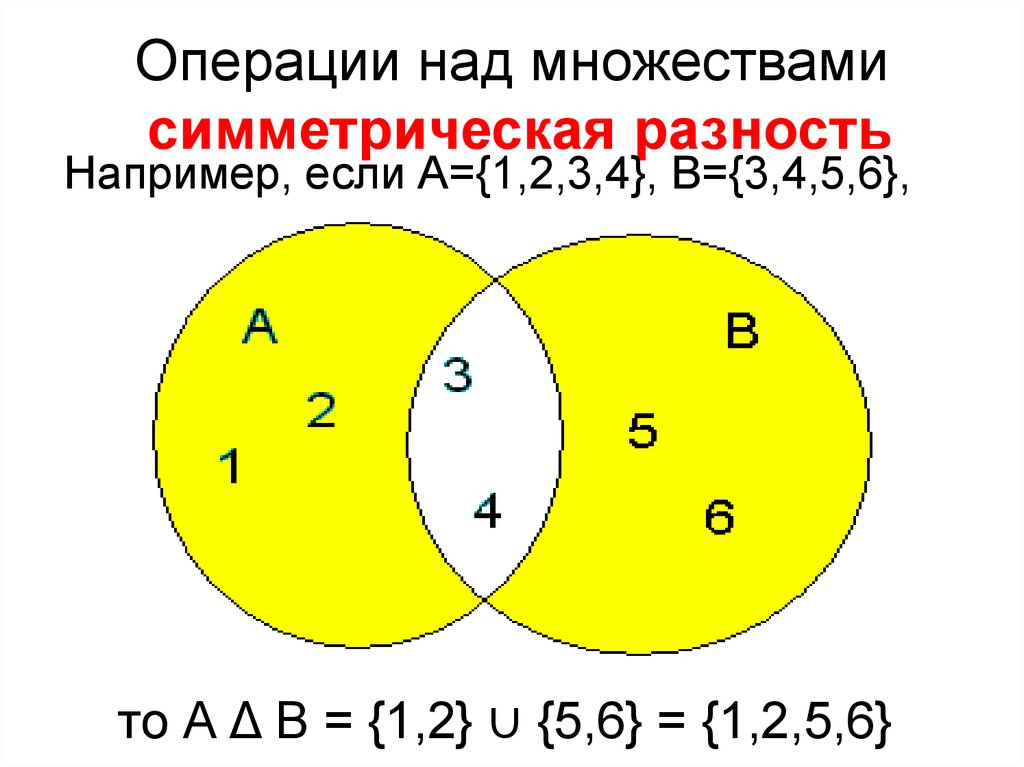 Найдите пересечение и объединение следующих множеств:
Найдите пересечение и объединение следующих множеств:
А = { −3, −2, −1, 0, 1, 2 }
B = { 1, 2, 3, 4, 5 }
Решение:
A ∩ B = { 1, 2 }
A ∪ B = { −3, −2, −1, 0, 1, 2, 3, 4, 5 }
Показать решение
Задание 3. Найдите пересечение и объединение следующих множеств:
А = { 1, 2, 3 }
B = { 3, 4 }
Решение:
A ∩ B = { 3 }
A ∪ B = { 1, 2, 3, 4 }
Показать решение
Задание 4. Найдите пересечение и объединение следующих числовых промежутков:
[−2; 7) и (0; 10]
Решение:
[−2; 7) ∩ (0; 10] = (0; 7)
[−2; 7) ∪ (0; 10] = [−2; 10]
Показать решение
Задание 5. Найдите пересечение и объединение следующих числовых промежутков:
(−∞; 3] и [−2; 1)
Решение:
(−∞; 3] ∩ [−2; 1) = [−2; 1)
(−∞; 3] ∪ [−2; 1) = (−∞; 3]
Показать решение
Задание 6. Найдите пересечение и объединение следующих числовых промежутков:
(3; +∞) и [2; +∞)
Решение:
(3; +∞) ∩ [2; +∞) = (3; +∞)
(3; +∞) ∪ [2; +∞) = [2; +∞)
Показать решение
Задание 7. Найдите пересечение и объединение следующих числовых промежутков:
Найдите пересечение и объединение следующих числовых промежутков:
[−3; −1] и (−2; 4]
Решение:
[−3; −1] ∩ (−2; 4] = (−2; −1]
[−3; −1] ∪ (−2; 4] = [−3; 4]
Показать решение
Задание 8. Решите неравенство:
Решение:
Показать решение
Задание 9. Решите неравенство:
Решение:
Показать решение
Задание 10. Решите совокупность неравенств:
Решение:
Показать решение
Задание 11. Решите совокупность неравенств:
Решение:
Показать решение
Задание 12. Решите совокупность неравенств:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Решение некоторых задач по теории множеств
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
, где
“” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.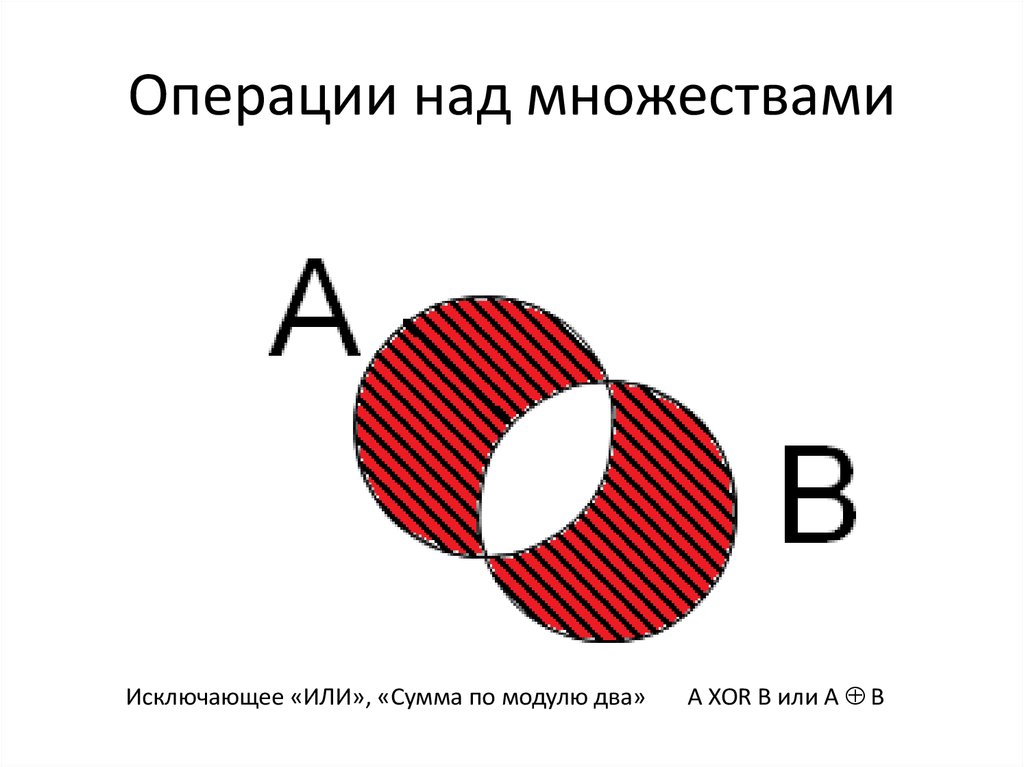 е. если , то , где “С” знак подмножества или включения.
е. если , то , где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):
(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
(рис.3)
Обозначим буквой Е основное или универсальное множество, где A С Е (“”- любо число), т.е. А Е = Е; АЕ =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕ или Ā (рис.4)
Е
(рис.4)
Примерами для понимания этих понятий являются свойства:
_
А Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
АВ = А∩В
________ _ _
АВ = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (AB) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (АВ)
m (ABC) = m (A) + m (В) + m (С)– m (А∩В) — m (А∩С) – m (В∩С) – m (А∩В∩С).
А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек.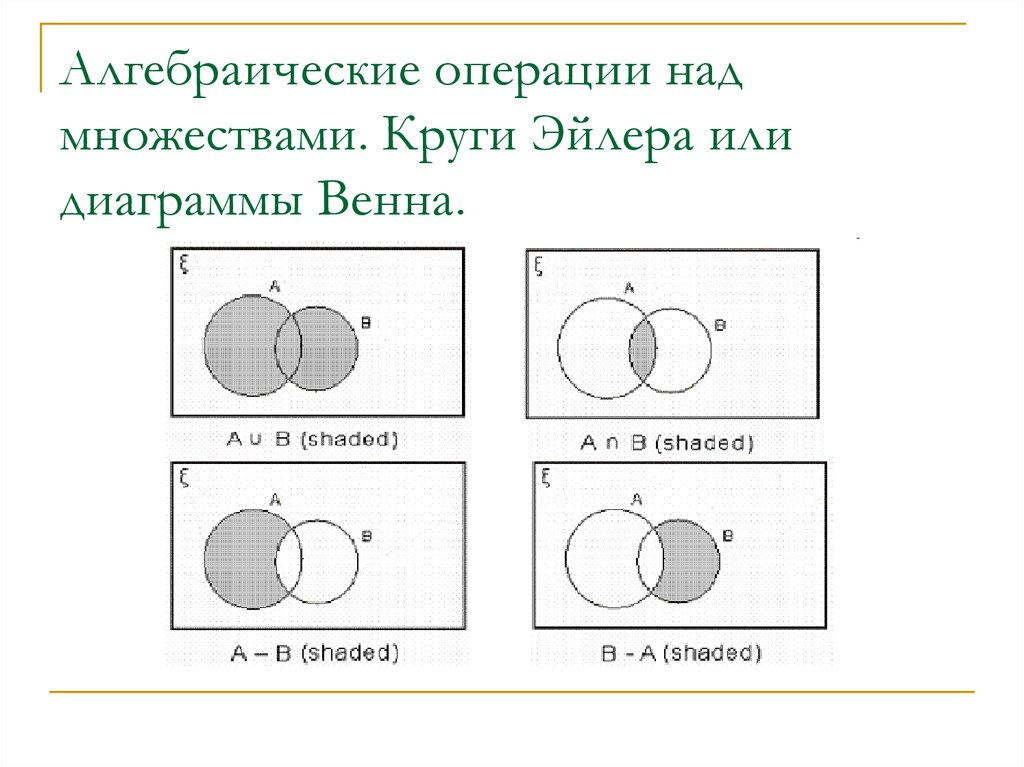 Ни одной задачи не решили 3 человека.
Ни одной задачи не решили 3 человека.
- Сколько учащихся решили все задачи?
- Сколько учащихся решили только две задачи?
- Сколько учащихся решили только одну задачу?
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
- m (Е) = 40
- m (А) = 20
- m (В) = 18
- m (С) = 18
- m (А∩В) = 7
- m (А∩С) = 8
- m (В∩С) = 9
___________
m (АВС) = 3 => m (АВС) = 40 – 3 = 37
Обозначим разбиение универсального множества Е множествами А, В, С (рис.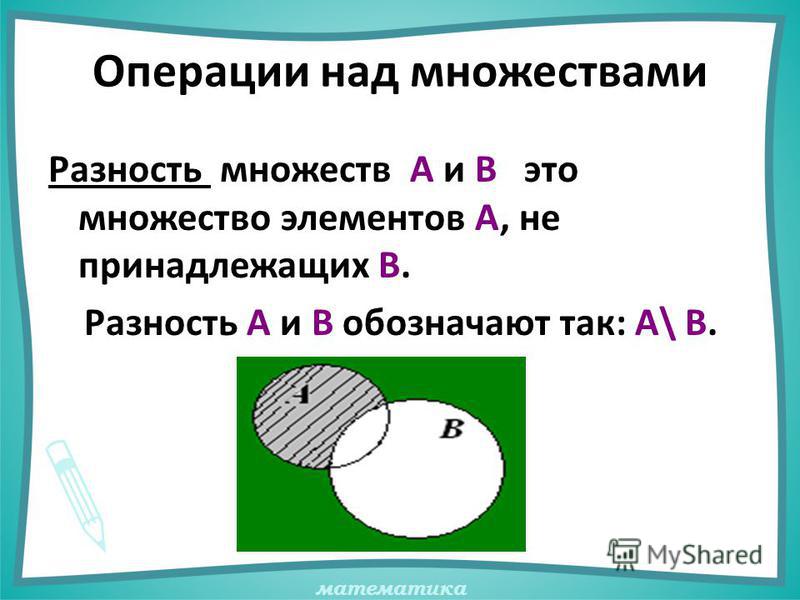 5).
5).
(рис.5)
К1 – множество учеников, решивших только одну задачу по алгебре;
К2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К3 – множество учеников, решивших только задачу по геометрии;
К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К5 – множество всех учеников, решивших все три задачи;
К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К7 – множество всех учеников, решивших только задачу по тригонометрии;
К8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
- m (К5) = m (А∩В∩С)= m (АВС) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
- m (К5) = 37-20-18-18+7+8+9=5
- m (К2) = m (А∩В) — m (К5) = 7-5=2
- m (К4) = m (А∩С) — m (К5) = 8-5=3
- m (К6) = m (В∩С) — m (К5) = 9-5=4
- m (К1) = m (А) — m (К2) — m (К4) — m (К5) = 20-2-3-5=10
- m (К3) = m (В) — m (К2) — m (К6) — m (К5) = 18-2-4-5=7
- m (К7) = m (С) — m (К4) — m (К6) — m (К5) = 18-3-4-5 =6
- m (К2) + m (К4) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
- m (К1) + m (К3) + m (К7) = 10+7+6=23 – число учеников решивших только одну задачу.

Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
- m (АВ) = 33
- m (АС) = 31
- m (ВС) = 32
- m (К2) + m (К4) + m (К6) + m (К5) = 20
Найти m (К1) + m (К3) + m (К7)
- m (АUВ) = m (К1) + m (К2) + m (К3) + m (К4) + m (К5) + m (К6) = m (К1) + m (К3) + 20 = 33 =>
- m (К1) + m (К3) = 33 – 20 = 13
- m (АUС) = m (К1) + m (К4) + m (К2) + m (К5) + m (К6) + m (К7) = m (К1) + m (К7) + 20 = 31 =>
- m (К1) + m (К7) = 31 – 20 = 11
- m (ВUС) = m (К3) + m (К2) + m (К5) + m (К6) + m (К7) + m (К4) = m (К3) + m (К7) + 20 = 32 =>
- m (К3) + m (К7) = 32 – 20 = 12
- 2m (К1) + m (К3) + m (К7) = 13+11=24
- 2m (К1) + 12 = 24
- m (К3)= 13-6=7
- m (К7)=12-7=5
- m (К1) + m (К3) + m (К7) = 6+7+5=18
Ответ:
Только одну контрольную работу решили 18 учеников.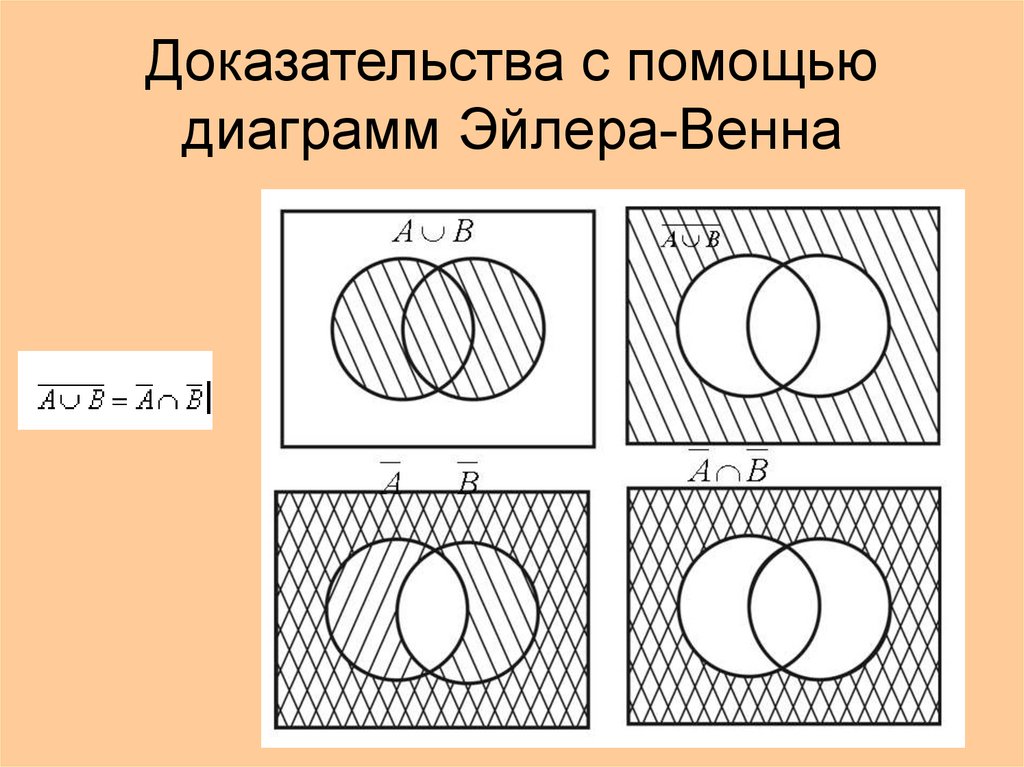
Решение задачи № 3
- m (Е) = 35
- m (А∩В∩С)= m (К5) = 6
- m (А∩В)= 15
- m (А∩С)= 13
- m (В∩С)= 9
Найти m (К1) + m (К3) + m (К7)
- m (К2) = m (А∩В) — m (К5) = 15-6=9
- m (К4) = m (А∩С) — m (К5) = 13-6=7
- m (К6) = m (В∩С) — m (К5) = 9-6=3
- m (К1) + m (К3) + m (К7) = m (Е) — m (К4) — m (К2) — m (К6) — m (К5) = 35-7-9-3-6=10
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
Набор операций | Союз | Пересечение | Дополнение | Разница | Взаимоисключающие | Перегородки | Закон де Моргана | Распределительный закон
← предыдущий
следующий →
Объединение двух множеств представляет собой множество, содержащее все элементы, находящиеся в $A$ или в
$B$ (возможно, оба). Например, $\{1,2\}\cup\{2,3\}=\{1,2,3\}$. Таким образом, мы можем написать $x\in(A\cup B)$
тогда и только тогда, когда $(x\in A)$ или $(x\in B)$. Обратите внимание, что $A \cup B=B \cup A$. На рисунке 1.4,
объединение множеств $A$ и $B$ показано заштрихованной областью на диаграмме Венна. 9{n} A_i.$$
Например, если $A_1=\{a,b,c\}, A_2=\{c,h\}, A_3=\{a,d\}$, то $\bigcup_{i} A_i=A_1 \cup А_2
\cup A_3=\{a,b,c,h,d\}$. Аналогичным образом мы можем определить объединение бесконечного числа множеств
$A_1 \чашка A_2 \чашка A_3 \чашка\cdots$.
Например, $\{1,2\}\cup\{2,3\}=\{1,2,3\}$. Таким образом, мы можем написать $x\in(A\cup B)$
тогда и только тогда, когда $(x\in A)$ или $(x\in B)$. Обратите внимание, что $A \cup B=B \cup A$. На рисунке 1.4,
объединение множеств $A$ и $B$ показано заштрихованной областью на диаграмме Венна. 9{n} A_i.$$
Например, если $A_1=\{a,b,c\}, A_2=\{c,h\}, A_3=\{a,d\}$, то $\bigcup_{i} A_i=A_1 \cup А_2
\cup A_3=\{a,b,c,h,d\}$. Аналогичным образом мы можем определить объединение бесконечного числа множеств
$A_1 \чашка A_2 \чашка A_3 \чашка\cdots$.
Пересечение двух множеств $A$ и $B$, обозначаемое $A \cap B$, состоит из всех элементов которые оба находятся в $A$ $\underline{\textrm{and}}$ $B$. Например, $\{1,2\}\cap\{2,3\}=\{2\}$. На рис. 1.5 пересечение множеств $A$ и $B$ показано заштрихованной областью с помощью диаграммы Венна. 9с$.
Рис.1.8 — Заштрихованная область показывает множество $A-B$. Два множества $A$ и $B$ являются взаимоисключающими или непересекающимися , если они не имеют общих
элементы; т. е. их пересечение есть пустое множество $A \cap B=\emptyset$. В общем, несколько наборов
называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов.
На рис. 1.9 показаны три непересекающихся множества.
е. их пересечение есть пустое множество $A \cap B=\emptyset$. В общем, несколько наборов
называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов.
На рис. 1.9 показаны три непересекающихся множества.
Если земная поверхность является нашим эталонным пространством, мы можем захотеть разделить его на разные континенты. Точно так же страна может быть разделена на разные провинции. В общем, набор непустых наборы $A_1, A_2,\cdots$ — это разбивает множества $A$, если они не пересекаются и их объединение равно $A$. На рис. 1.10 множества $A_1, A_2, A_3$ и $A_4$ образуют разбиение универсального множества $S$.
Рис.1.10 — Набор множеств $A_1, A_2, A_3$ и $A_4$ является разбиением $S$.Вот несколько правил, которые часто бывают полезны при работе с множествами. Вскоре мы увидим примеры их использования.
Теорема : Закон Де Моргана
Для любых множеств $A_1$, $A_2$, $\cdots$, $A_n$ имеем
9с$.
Теорема : Закон распределения
Для любых множеств $A$, $B$ и $C$ имеем
- $A \cap (B \cup C)=(A \cap B) \cup (A\cap C)$;
- $A \чашка (B \крышка C)=(A \чашка B) \крышка (A\чашка C)$.
Пример
Если универсальный набор задан как $S=\{1,2,3,4,5,6\}$ и $A=\{1,2\}$, $B=\{2, 4,5\}, C=\{1,5,6\} $ — три множества, найдите следующие множества:
- $A\чашка B$
- $A\cap B$ 9c=\{3,4,5,6\} \cap \{1,3,6\}=\{3,6\}.$$
- Имеем $$A \cap (B \cup C)=\{1,2\} \cap \{1,2,4,5,6\}=\{1,2\},$$, что равно такой же как $$(A \cap B) \cup (A\cap C)=\{2\} \cup \{1\}=\{1,2\}.$$
A Декартово произведение двух множеств $A$ и $B$, записанное как $A\times B$, представляет собой множество, содержащее упорядоченных пары из $A$ и $B$. То есть, если $C=A \times B$, то каждый элемент $C$ имеет вид $(x,y)$, где
$x \in A$ и $y \in B$:
$$A \times B = \{(x,y) | x \in A \textrm{ и } y \in B \}. $$
Например, если $A=\{1,2,3\}$ и $B=\{H,T\}$, то
$$A \times B=\{(1,H),(1,T),(2,H),(2,T),(3,H),(3,T)\}.$$
Обратите внимание, что здесь пары упорядочены, например, $(1,H)\neq (H,1)$. Таким образом, $A \times B$ равно не то же, что $B \times A$.
$$
Например, если $A=\{1,2,3\}$ и $B=\{H,T\}$, то
$$A \times B=\{(1,H),(1,T),(2,H),(2,T),(3,H),(3,T)\}.$$
Обратите внимание, что здесь пары упорядочены, например, $(1,H)\neq (H,1)$. Таким образом, $A \times B$ равно не то же, что $B \times A$.
Если у вас есть два конечных множества $A$ и $B$, где $A$ состоит из $M$ элементов, а $B$ состоит из $N$ элементов, то $A \times B$
имеет $M \times N$ элементов. Это правило называется принципом умножения на и очень полезно при подсчете
количества элементов в наборах. Количество элементов в множестве обозначается $|A|$, поэтому здесь мы пишем $|A|=M,
|B|=N$ и $|A \times B|=MN$. В приведенном выше примере $|A|=3, |B|=2$, поэтому $|A \times B|=3 \times 2 = 6$.
Аналогично можно определить декартово произведение $n$ множеств $A_1, A_2, \cdots, A_n$ как
$$A_1 \times A_2 \times A_3 \times \cdots \times A_n = \{(x_1, x_2, \cdots, x_n) | x_1 \in A_1 \textrm{ и }
x_2 \in A_2 \textrm{ и }\cdots x_n \in A_n \}.$$
Принцип умножения утверждает, что для конечных множеств $A_1, A_2, \cdots, A_n$, если $$|A_1|=M_1, |A_2|=M_2,
\cdots, |A_n|=M_n,$$ затем $$\mid A_1 \times A_2 \times A_3 \times \cdots \times A_n \mid=M_1 \times M_2
\times M_3 \times \cdots \times M_n.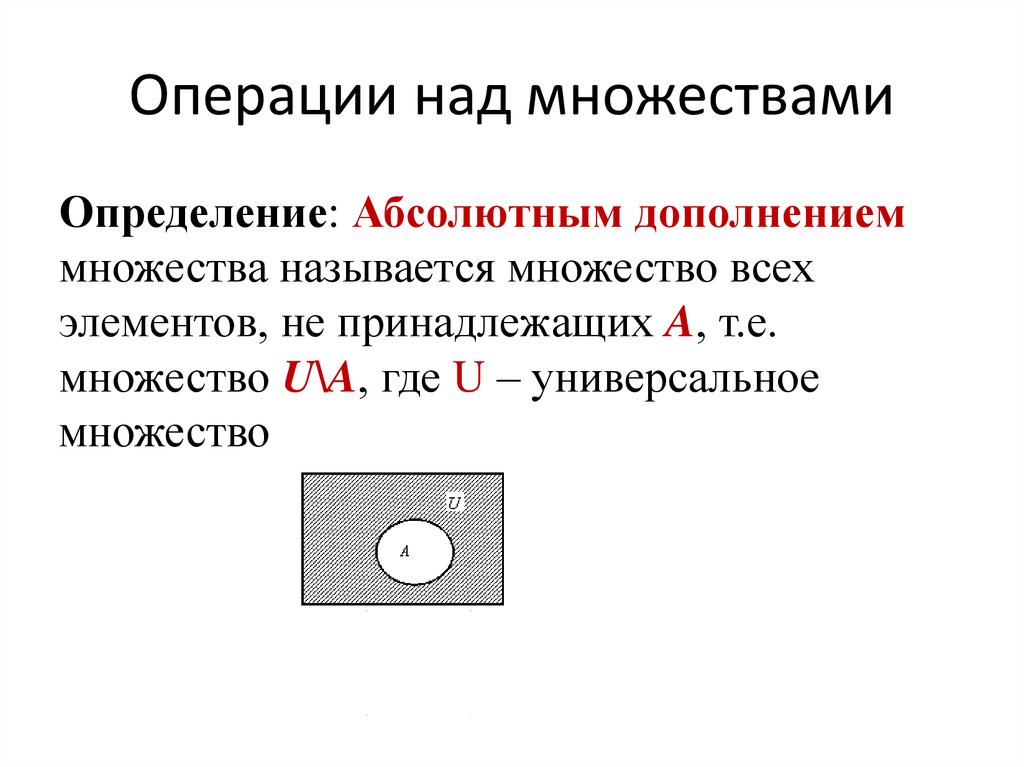 $$ 93=\mathbb{R}\times \mathbb{R} \times \mathbb{R}$ и так далее.
$$ 93=\mathbb{R}\times \mathbb{R} \times \mathbb{R}$ и так далее.
← предыдущая
следующая →
Печатная версия книги доступна на Amazon здесь.
Операции над множествами – формула, свойства, примеры
Операции над множествами – это концепция, аналогичная основным операциям над числами. Множества в математике имеют дело с конечным набором объектов, будь то числа, алфавиты или любые объекты реального мира. Иногда возникает необходимость установить связь между двумя или более множествами. Возникает понятие операций над множествами.
Существует четыре основных операции над множествами, включая объединение множеств, пересечение множеств, дополнение множеств и разность множеств. В этой статье мы изучим различные операции с множествами, обозначения представления множеств, способы работы с множествами и их использование в реальной жизни.
| 1. | Что такое операции над множествами? |
2. | Базовый набор операций |
| 3. | Свойства операций над множествами |
| 4. | Часто задаваемые вопросы по операциям набора |
Что такое операции над множествами?
Набор определяется как набор объектов. Каждый объект внутри набора называется «Элемент». Множество может быть представлено в трех формах. Это форма заявления, форма списка и нотация построителя наборов. Операции над множествами — это операции, которые применяются к двум или более множествам для установления связи между ними. Существует четыре основных типа операций над множествами, которые заключаются в следующем.
- Набор комплектов
- Пересечение наборов
- Дополнение к набору
- Разница между комплектами/относительное дополнение
Прежде чем мы перейдем к обсуждению различных операций над множествами, давайте вспомним концепцию диаграмм Венна, поскольку она важна для понимания операций над множествами. Диаграмма Венна — это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Диаграмму Венна можно представить следующим образом.
Диаграмма Венна — это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Диаграмму Венна можно представить следующим образом.
Базовый набор операций
Теперь, когда мы знаем концепцию множества и диаграммы Венна, давайте подробно обсудим каждую операцию над множеством. Различные операции над множествами:
Объединение множеств
Для двух заданных множеств A и B, A∪B (читается как объединение B) представляет собой множество различных элементов, которые принадлежат множеству A и множеству B или обоим. Количество элементов в A ∪ B определяется выражением n(A∪B) = n(A) + n(B) − n(A∩B), где n(X) — количество элементов в множестве X. Чтобы Чтобы лучше понять эту операцию объединения множеств, давайте рассмотрим пример: если A = {1, 2, 3, 4} и B = {4, 5, 6, 7}, то объединение A и B равно определяется как A ∪ B = {1, 2, 3, 4, 5, 6, 7}.
Пересечение множеств
Для двух заданных множеств A и B, A ∩ B (читается как пересечение A B) — это множество общих элементов, принадлежащих множествам A и B.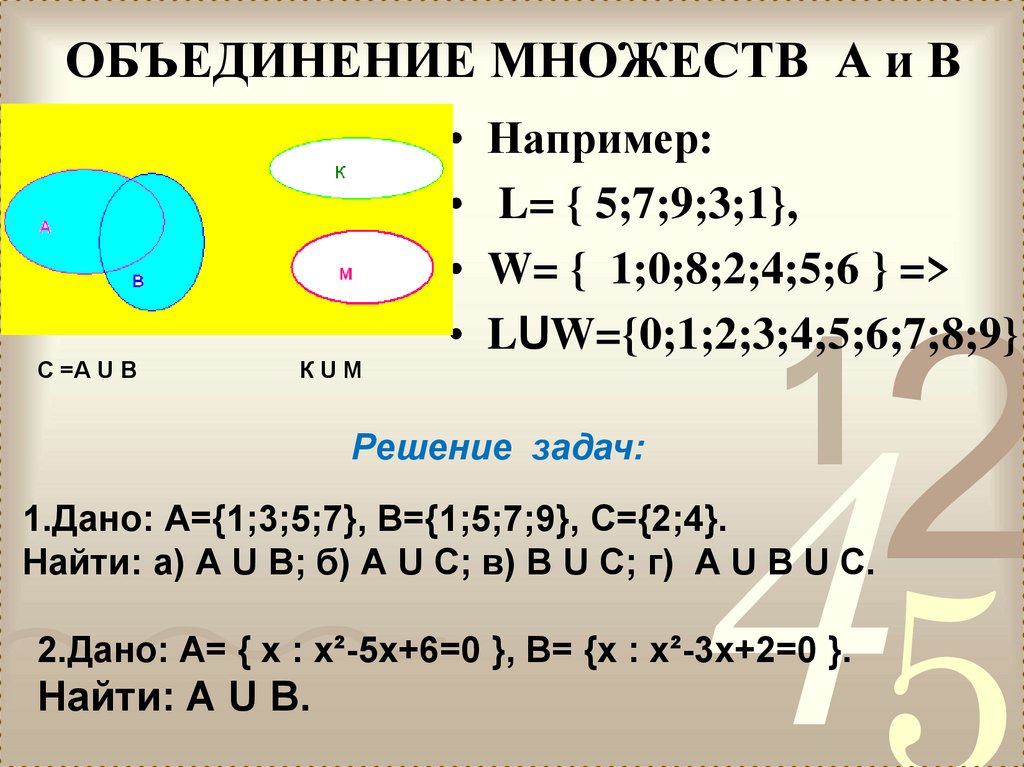 Количество элементов в A ∩ B определяется выражением n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы лучше понять эту операцию пересечения множеств, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4} .
Количество элементов в A ∩ B определяется выражением n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы лучше понять эту операцию пересечения множеств, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4} .
Установить разницу
Разность между множествами подразумевает вычитание элементов из множества, что аналогично понятию разности между числами. Разница между наборами A и набором B, обозначенная как A − B, перечисляет все элементы, которые находятся в наборе A, но не в наборе B. Чтобы лучше понять эту операцию над набором разности наборов, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то разница между множествами A и B определяется соотношением A — B = {1, 2}.
Дополнение к наборам
Дополнение множества A, обозначаемое как A′ или A c (читается как дополнение A), определяется как множество всех элементов данного универсального множества (U), которые не присутствуют в множестве A.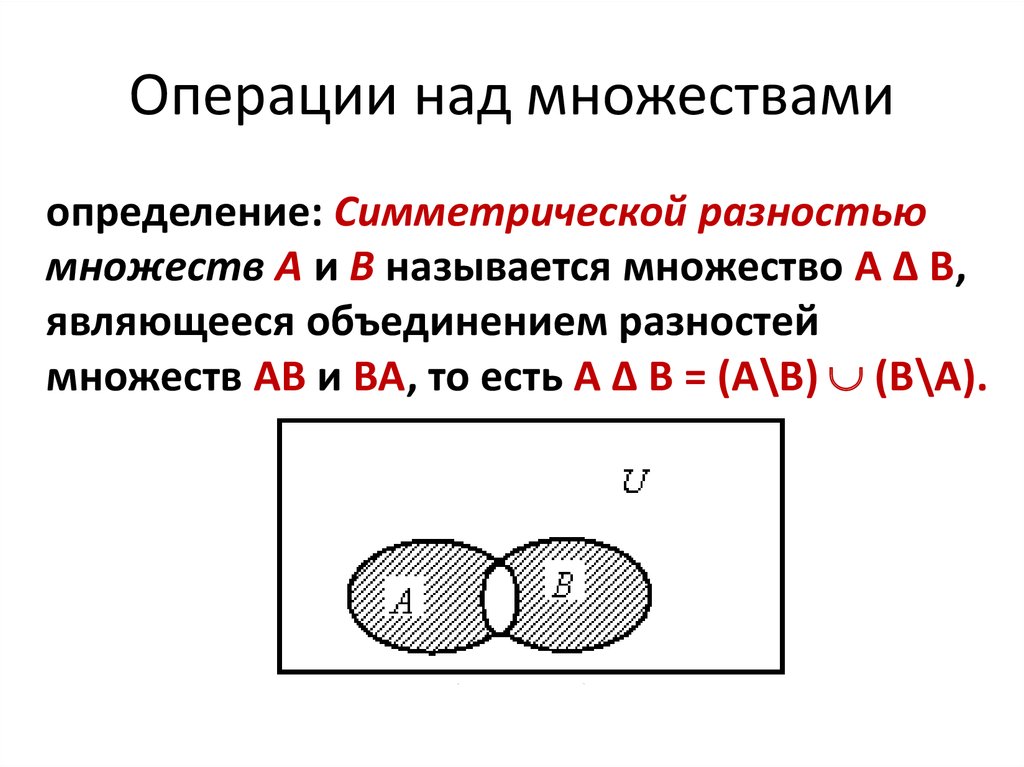 Чтобы понять эту операцию дополнения множеств лучше, рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4}, тогда дополнение множества A задается как A’ = {5, 6, 7, 8, 9}.
Чтобы понять эту операцию дополнения множеств лучше, рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4}, тогда дополнение множества A задается как A’ = {5, 6, 7, 8, 9}.
На изображении выше показаны различные операции над наборами с помощью диаграмм Венна. Когда элементы одного множества B полностью лежат в другом множестве A, то B называется собственным подмножеством A. Когда два множества не имеют общих элементов, они называются непересекающимися множествами. Теперь давайте рассмотрим свойства операций над множествами.
Свойства операций над множествами
Свойства операций над множествами аналогичны свойствам основных операций над числами. Важные свойства операций над множествами указаны ниже:
- Закон перестановочности . Для любых двух заданных множеств A и B свойство перестановочности определяется как
A ∪ B = B ∪ A
Это означает, что множественная операция объединения двух множеств коммутативна.
А ∩ В = В ∩ А
Это означает, что множественная операция пересечения двух множеств коммутативна. - Ассоциативный закон — Для любых трех заданных наборов A, B и C свойство ассоциативности определяется как
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Это означает, что операция объединения множеств ассоциативна.
(А ∩ В) ∩ С = А ∩ (В ∩ С)
Это означает, что операция пересечения множеств ассоциативна. - Закон Де-Моргана — Закон Де Моргана гласит, что для любых двух множеств A и B мы имеем (A ∪ B)’ = A’ ∩ B’ и (A ∩ B)’ = A’ ∪ B’
- А ∪ А = А
- А ∩ А = А
- А ∩ ∅ = ∅
- А ∪ ∅ = А
- А ∩ В ⊆ А
- А ⊆ А ∪ В
Важные примечания по операциям над множествами
- Формула операции над множествами для объединения множеств: n(A∪B) = n(A) + n(B) − n(A∩B) множества есть n(A∩B) = n(A)+n(B)−n(A∪B).

- Объединение любого множества с универсальным множеством дает универсальное множество, а пересечение любого множества A с универсальным множеством дает множество A.
- Объединение, пересечение, разность и дополнение — это различные операции над множествами.
- Дополнением универсального множества является пустое множество U′ = ϕ. Дополнением пустого множества является универсальное множество ϕ′ = U.
Темы, связанные с операциями над множествами
- Надмножество
- Силовой набор
- Конечные и бесконечные наборы
Часто задаваемые вопросы по операциям набора
Что такое
Операции над множествами в теории множеств?Операции над множествами — это операции, применяемые к двум или более множествам для установления связи между ними. Существует четыре основных вида операций над множествами.
Каковы различные операции над наборами?
Существует четыре основных вида операций с наборами:
- Набор комплектов
- Пересечение наборов
- Дополнение к набору
- Разница между комплектами/относительное дополнение
Как мы используем операции над множествами в реальной жизни?
Набор — это набор элементов. Некоторыми реальными примерами множеств являются список всех штатов в стране, список всех фигур в геометрии, список всех целых чисел от 1 до 100. Мы можем определить общие области, используя операцию пересечения множества.
Некоторыми реальными примерами множеств являются список всех штатов в стране, список всех фигур в геометрии, список всех целых чисел от 1 до 100. Мы можем определить общие области, используя операцию пересечения множества.
Как вы решаете проблемы с работой набора?
Для решения задач с операциями над множествами мы используем диаграмму Венна для представления отношений между множествами и применяем формулу операций над множествами для объединения, пересечения, разности или дополнения множества.
Какие из операций над множествами являются коммутативными и некоммутативными?
Объединение и пересечение множеств являются коммутативными операциями над множествами, в то время как разность множеств не является коммутативной.
Что такое набор символов операций?
Существуют различные символы, используемые для различных операций с множествами, которые называются обозначениями множеств. Для объединения множеств мы используем ‘ ∪ ‘, для пересечения множеств используем ‘∩’, для разности множеств используем ‘-‘, а для дополнения множества A мы пишем как A’ или A c .
Как найти разницу между двумя наборами?
Для любых двух наборов A и B разность A-B перечисляет все элементы набора A, которых нет в наборе B.
Как найти дополнение к набору?
Для заданного универсального множества U и множества A дополнение множества A определяется как множество всех элементов универсального множества, отсутствующих в множестве A.
Что такое операции объединения и пересечения множеств ?
Для любых двух наборов A и B объединение определяется как комбинация элементов как в наборе A, так и в наборе B. Пересечение наборов дает общие элементы в наборе A и наборе B.
Операции над множествами — теория, отношения, приложения & Примеры
Теория множеств и ее Операции , вероятно, являются наиболее фундаментальной областью математики, необходимой для любого тщательного изучения математики.
Математики, такие как Джордж Кантор , Ричард Дедекинд , Цермело и Франкель , расширили наши современные знания о теории множеств.
Теория множеств включает в себя математические объекты, называемые множествами, и их операции называются операциями над множествами. Это исследование расширяет наши знания, чтобы узнать о различных типах операций над множествами и их важности.
Георг Кантор (Источник) ИсторияСтатья, посвященная теории множеств: «О свойстве совокупности всех действительных алгебраических чисел» (1874) Джорджа Кантора.
Около 1900 года Джордж Кантор обнаружил несколько парадоксов в теории множеств.
Самым известным парадоксом был « парадокс Рассела ». Эти парадоксы вызвали потребность в более совершенной теории множеств. Ernst Zermelo и Abraham Fraenkel разработали Теория множеств Цермело-Френкеля сегодня как современная теория, свободная от парадоксов.
Операция с множествами — это математический процесс, который принимает набор(ы) в качестве входных данных и дает результат (число или набор).
Примеры операций над множествами: объединение, пересечение, разность, дополнение, мощность, декартово произведение, множество мощности и т. д.
Объединение множестваПусть A и B — два множества. Объединение A и B, обозначаемое \(A \cup B\), представляет собой множество, содержащее те элементы, которые находятся либо в A, либо в B, либо в обоих. Ни один элемент не повторяется.
Диаграмма Венна \(A \cup B\) (Источник)\(A \cup B = \{ x : x \in A \mbox{ or } x \in B \}\)
Пример: Если \(A = \{ 1,2,3,4 \}\) и \(B = \{ 2, 5, 4, 6, 7 \}\), то \(A \cup B = \{ 1, 2, 3, 4, 5, 6, 7 \}\) .
Вот некоторые существенные соотношения:
- Если A непустое множество, а B нулевое множество, то \(A \cup B = A\).

- Если S — универсальное множество, а A — непустое множество, то \(A \cup S = S\).
- \(A \чашка B = B \чашка A\) ( Коммутативный )
- \((A \cup B ) \cup C = A \cup ( B \cup C)\) ( Ассоциативный )
Пусть A и B два набора. Пересечение A и B, обозначаемое \(A \cap B\), представляет собой множество, содержащее те элементы, которые есть как в A, так и в B. Ни один элемент не повторяется.
Диаграмма Венна \(A \cap B\) (Источник)\(A \cap B = \{ x : x \in A \mbox{ и } x \in B \}\)
Пример: Если \(A =\{1, 2, 3, 4 \}\) и \(B = \{ 2, 5, 4, 6, 7 \}\), то \(A \cap B =\{ 2, 4 \}\).
Вот некоторые важные соотношения:
- Если A — непустое множество, а B — нулевое множество, то \(A \cap B = \phi\).
- Если S — универсальное множество, а A — непустое множество, то \(A \cap S = A\).
- \(A \cap B = B \cap A\) ( Коммутативный )
- \((A \cap B) \cap C = A \cap (B \cap C)\) ( Ассоциативный )
Пусть A и B — два множества.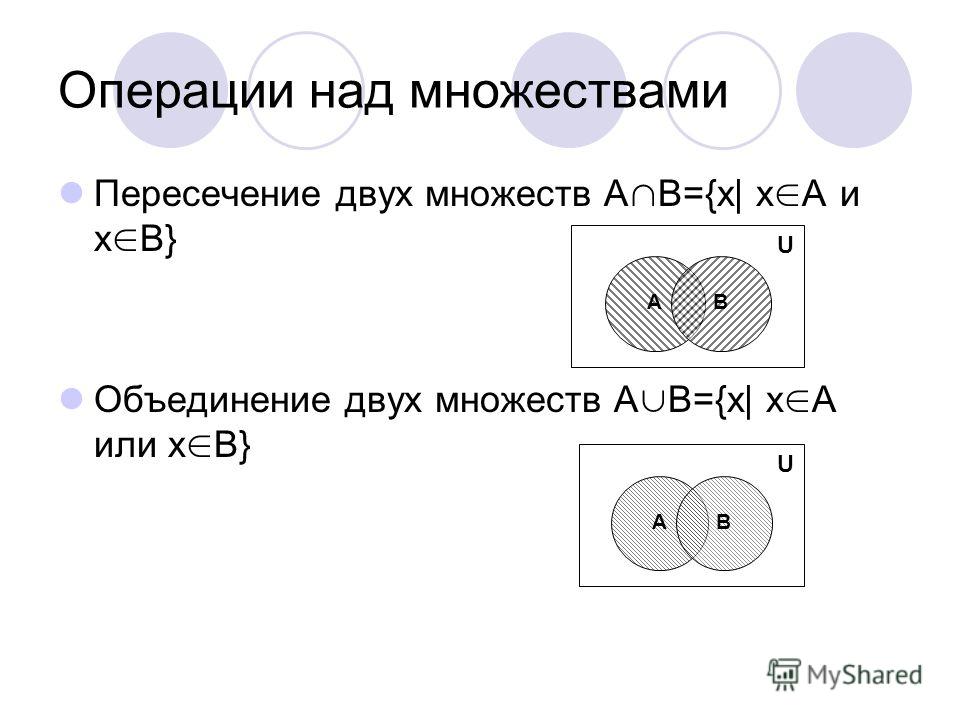 Разность A и B, обозначаемая \(A – B\), представляет собой множество всех элементов A, которые не входят в B .
Разность A и B, обозначаемая \(A – B\), представляет собой множество всех элементов A, которые не входят в B .
\(A – B = \{ x : x \in A \mbox{ и } x \not \in B \}\)
Пример: Если \( A = \{1, 2, 3, 4 \}\) и \(B = \{ 2, 5, 4, 6, 7 \}\), тогда \(A – B = \{ 1\}\) . Точно так же \(B – A = \{ 5, 6, 7 \}\).
Читать о типах отношений
Дополнение множестваПусть A — любое множество, а S — универсальное множество. Тогда A является подмножеством S (\(A \subset S\)).
Дополнение A, обозначаемое A’ или \(\bar{A}\), равно \(A’ = S – A = \bar{A}\).
Дополнительная диаграмма Венна (Источник)Пример: Если \(S = \{ 1, 2, \ldots, 10 \}\) и \(A = \{ 1, 2 , 3 \}\), то \ (A’ = \{ 4, 5, \ldots , 10 \}\)
Вот некоторые существенные соотношения:
- Если A — нулевое множество, то \(A’ = S\) .
- Если S универсальное множество, то \(S’ = \phi\).

- \((А’)’ = А\).
Мощность набора есть не что иное, как количество элементов набора ( неповторяющийся ).
Пример: Если \(A = \{ 0, 1, 2, \ldots , 10 \}\) , то мощность A , обозначаемая через \(n(A)\), равна \(n(A) = 11\).
Декартово произведение множествПусть A и B — любые два множества. Декартово произведение или перекрестное произведение A и B — это множество \(A \times B\), содержащее все упорядоченные пары элементов A и B.
\(A \times B = \{ (x, y) : \forall x \in A , y \in B \}\)
Пример: Если \(A = \{ 1, 2, 3 \}\) и \(B = \{ 3, 4 \}\) тогда, 92 = 4\).
Некоторые важные отношения с операциями над множествами чашка B \чашка C ) = n(A) +n (B) + n(C) — n(A \крышка B) — n (A \крышка C) + n( A \крышка B \крышка C)\) Теория множеств и алгебра множеств находят применение в широком спектре областей — Статистика, физика, теория чисел, теория групп, теория вероятностей, инженерия, экономика и т.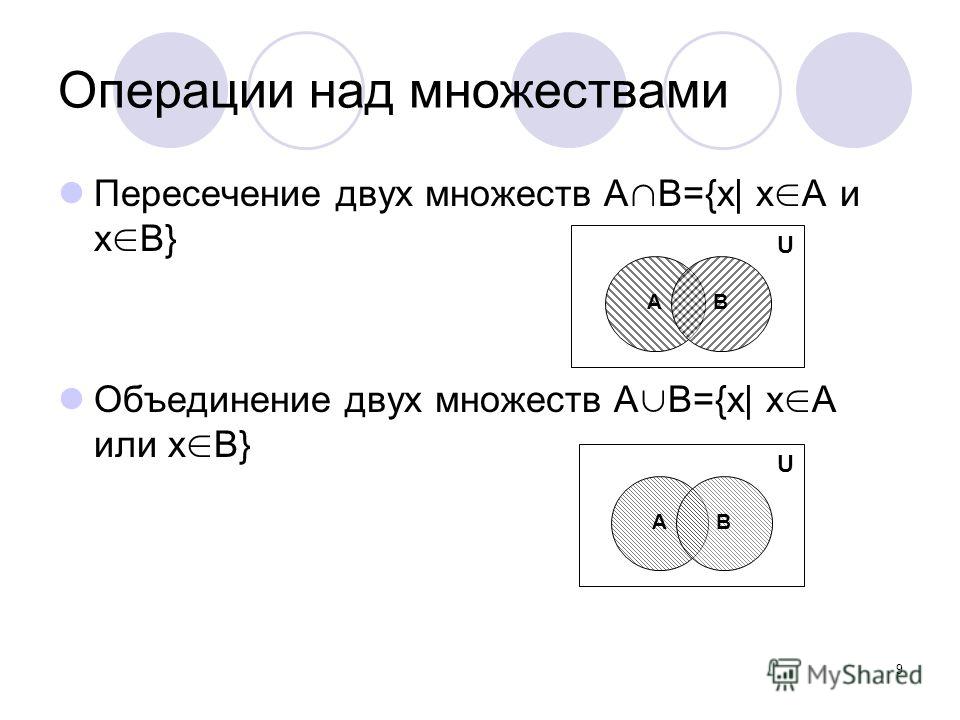 д. Теория множеств в основном используется в Исследование аксиоматической вероятности .
д. Теория множеств в основном используется в Исследование аксиоматической вероятности .
Наиболее распространенные наборы:
\(\mathbb(R)\) — Набор действительных чисел.
\(\mathbb(Z)\) – множество целых чисел.
\(\mathbb(C)\) — Набор комплексных чисел.
\(\mathbb(N)\) — Набор натуральных чисел.
\(\mathbb(Q)\) — Набор рациональных чисел.
\(\mathbb(W)\) – Набор целых чисел.
Вопрос 1. Нарисуйте диаграммы Венна для законов Де Моргана.
Ответ. Диаграмма закона Венна Де Морганса (Источник)
Вопрос 2. При опросе 400 учащихся в школе 100 были указаны как употребляющие яблочный сок, 150 – как употребляющие апельсиновый сок, а 75 – употребляющие оба яблока как а также апельсиновый сок. Найдите, сколько студентов не употребляли ни яблочный, ни апельсиновый сок.
Ответ. Пусть \(U\) обозначает множество опрошенных студентов, \(A\) обозначает множество студентов, пьющих яблочный сок, а \(B\) обозначает множество студентов, пьющих апельсиновый сок. Затем
Пусть \(U\) обозначает множество опрошенных студентов, \(A\) обозначает множество студентов, пьющих яблочный сок, а \(B\) обозначает множество студентов, пьющих апельсиновый сок. Затем
\(n (U) = 400, n (A) = 100, n (B) = 150\) и \(n (A \cap B) = 75\).
Теперь \(n (A′ \cap B′) = n (A \cup B)′\)
\(= n(U) – n(A \cup B)\)
\(= n (U) – n (A) – n (B) + n (A \cap B) \)
=>\(= 400 – 100 – 150 + 75 = 225\).
Таким образом, 225 учащихся не употребляли ни яблочный, ни апельсиновый сок.
Вопрос 3. Перечислите все подмножества множества {–1, 0, 1}.
Ответ. Подмножества: \(\phi , \{ -1\} , \{ 0 \} , \{ 1 \} , \{ -1, 0 \} , \{ -1, 1\} , \{ 0, 1 \} , \{ -1, 0 , -1 \} \).
Часто задаваемые вопросыДля чего используются декартовы произведения?
Декартовы произведения составляют основу для определения домена и ко-домена функций и отношений.
Например, вещественная функция — это отображение из \(\mathbb(R) \times \mathbb(R)\) в \(\mathbb(R) \times \mathbb(R)\).
Какова мощность набора нулей?
Набор мощностей нулевого набора является нулевым набором. Он имеет нулевую мощность.
Какое кардинальное уравнение для объединения 4 множеств?
\(n(A \чашка B \чашка C \чашка D ) = n(A) + n(B) + n(C) + n(D) – n(A \cap B)\)
\(– n(B \cap C ) – n(C \cap D) + n(A \cap B \cap C) + n(A \cap B \cap D)\)
\(– n ( A \ крышка B \ крышка C \ крышка D )\).
Наборы Python — операции и примеры
Если вы новичок в Python, скорее всего, вы сталкивались со списками. Но слышали ли вы о множествах в Python?
В этом уроке мы рассмотрим, что такое наборы, как их создавать и какие операции с ними можно использовать.
В Python наборы точно такие же, как списки, за исключением того факта, что их элементы являются неизменяемыми (это означает, что вы не можете изменить/мутировать элемент набора после его объявления). Однако вы можете добавлять/удалять элементы из набора.
Если это сбивает с толку, позвольте мне попытаться резюмировать:
Набор — это изменяемая неупорядоченная группа элементов, где сами элементы неизменны.
Еще одной характеристикой набора является то, что он может включать в себя элементы разных типов. Это означает, что вы можете иметь группу чисел, строк и даже кортежей в одном наборе!
РЕКЛАМА
Наиболее распространенный способ создания набора в Python — использование встроенной функции set() .
>>> first_set = set(("Коннор", 32, (1, 2, 3)))
>>> первый_набор
{32, "Коннор", (1, 2, 3)}
>>>
>>> second_set = set("Коннор")
>>> второй_набор
{'н', 'С', 'р', 'о'} Вы также можете создавать наборы с помощью фигурной скобки {} синтаксис:
>>> Third_set = {"Яблоки", ("Бананы", "Апельсины")}
>>> тип (третий_набор)
Функция set() принимает итерируемый и возвращает список объектов, которые будут вставлены в набор.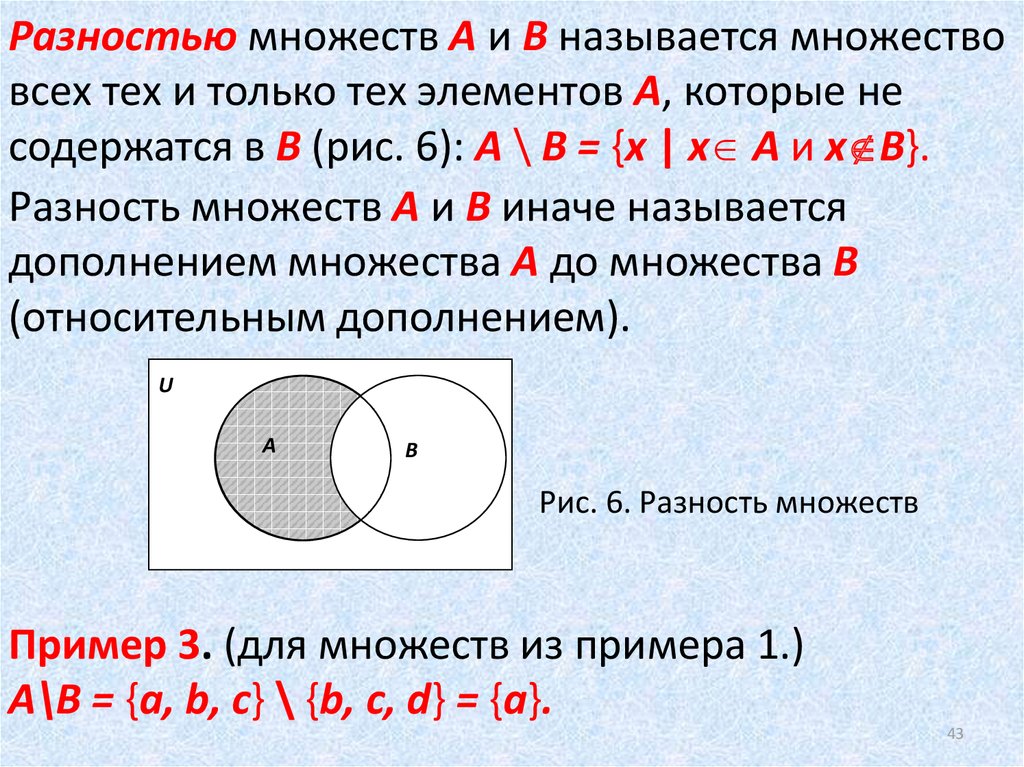 Синтаксис
Синтаксис {} помещает сами объекты в набор.
Как вы, наверное, поняли, используете ли вы set() или {} для создания набора, каждый элемент должен быть неизменяемым объектом. Поэтому, если вы добавите список (который является изменяемым объектом) в набор, вы столкнетесь с ошибкой:
>>> correct_set = {"Яблоки", ["Бананы", "Апельсины"]}
Traceback (последний последний вызов):
Файл "", строка 1, в
TypeError: unhashable type: 'list'
Мы уже знаем, что наборы изменяемы. Это означает, что вы можете добавлять/удалять элементы в наборе.
Вот пример добавления элементов в набор с помощью update() функция.
>>> add_set = набор ((1, 2, 3, 4))
>>> add_set
{1, 2, 3, 4}
>>>
>>> add_set.update((1,))
>>> add_set
{1, 2, 3, 4}
>>> add_set.update(("виолончель", "скрипка"))
>>> add_set
{1, 2, 3, 4, 'скрипка', 'виолончель'} Но обратите внимание, что ничего не меняется, когда мы снова пытаемся добавить в набор «виолончель»:
>>> add_set.update(("виолончель" ,)) >>> add_Set {1, 2, 3, 4, "скрипка", "виолончель"}
Это связано с тем, что наборы в Python не могут содержать дубликаты. Итак, когда мы попытались снова добавить «виолончель» в набор, Python распознал, что мы пытаемся добавить повторяющийся элемент, и не обновил набор. Это одно предостережение, которое отличает наборы от списков.
Вот как можно удалить элементы из набора:
>>> sub_set = add_set
>>> sub_set.remove("скрипка")
>>> подмножество
{1, 2, 3, 4, "виолончель"} remove(x) 9Функция 0699 удаляет элемент x из набора. Он возвращает KeyError , если x не является частью набора:
>>> sub_set.remove("гитара")
Traceback (последний последний вызов):
Файл "", строка 1, в
KeyError: 'гитара' Есть несколько других способов удалить элемент(ы) из набора:
- метод
discard(x)удаляетxиз набора, но не вызвать любую ошибку, еслихв комплекте нету.
- метод
pop()удаляет и возвращает случайный элемент из набора. - метод
clear()удаляет все элементы из набора
Вот несколько примеров для иллюстрации:
>>> m_set = set((1, 2, 3, 4))
>>>
>>> m_set.discard(5) # ошибка не возникает, хотя '5' отсутствует в наборе
>>>
>>> m_set.pop()
4
>>> m_set
{1, 2, 3}
>>>
>>> m_set.clear()
>>> m_set
установить() Если вы помните базовую математику в средней школе, вы, вероятно, вспомните математические операции над множествами, такие как объединение , пересечение , разность и симметричная разность . Что ж, вы можете добиться того же с наборами Python.
РЕКЛАМА
1. Объединение множеств
Объединением двух множеств является множество всех элементов обоих множеств без дубликатов. Вы можете использовать метод union() или метод | Синтаксис для поиска объединения набора Python.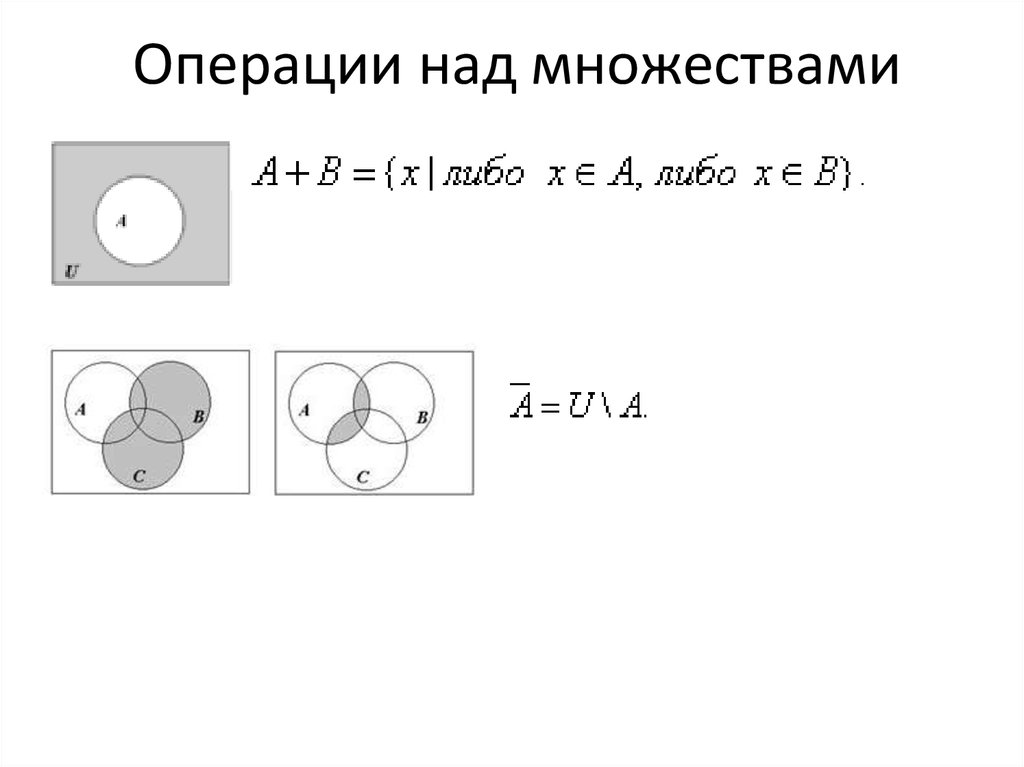
>>> first_set = {1, 2, 3}
>>> второй набор = {3, 4, 5}
>>> first_set.union(second_set)
{1, 2, 3, 4, 5}
>>>
>>> первый_набор | second_set # с использованием оператора `|`
{1, 2, 3, 4, 5}
2. Пересечение множеств
Пересечением двух множеств является множество всех общих элементов обоих множеств. Вы можете использовать метод пересечения() и , чтобы найти пересечение набора Python.
>>> first_set = {1, 2, 3, 4, 5, 6}
>>> second_set = {4, 5, 6, 7, 8, 9}
>>> first_set.intersection(second_set)
{4, 5, 6}
>>>
>>> first_set и second_set # с помощью оператора `&`
{4, 5, 6} 3. Разница между наборами
Разница между двумя наборами представляет собой набор всех элементов первого набора, которые отсутствуют во втором наборе. Вы бы использовали метод разницы() или оператор - для достижения этого в Python.
>>> first_set = {1, 2, 3, 4, 5, 6}
>>> second_set = {4, 5, 6, 7, 8, 9}
>>> first_set. difference(second_set)
{1, 2, 3}
>>>
>>> first_set - second_set # с использованием оператора `-`
{1, 2, 3}
>>>
>>> второй_набор - первый_набор
{8, 9, 7}
difference(second_set)
{1, 2, 3}
>>>
>>> first_set - second_set # с использованием оператора `-`
{1, 2, 3}
>>>
>>> второй_набор - первый_набор
{8, 9, 7} РЕКЛАМА
4. Set Symmetric Difference
Симметричная разность между двумя наборами — это набор всех элементов, равных 9` оператор {1, 2, 3, 7, 8, 9}
Каждая из операций set() , которые мы обсуждали выше, может использоваться для модификации существующего набора Python. Подобно тому, как вы использовали бы расширенный синтаксис присваивания, такой как += или *= , для обновления переменной, вы можете сделать то же самое для наборов:
>>> a = {1, 2, 3, 4, 5, 6}
>>> б = {4, 5, 6, 7, 8, 9}
>>>
>>> a.update(b) # операция "объединения"
>>> а
{1, 2, 3, 4, 5, 6, 7, 8, 9= b # операция "симметричная разность"
>>> а
{7, 8, 9} Они встречаются не так часто, но помогают увидеть, как наборы соотносятся с другими.
- метод
a.issubset(b)или<=возвращает true, еслиaявляется подмножеством = Оператор возвращает true, еслиaявляется надмножеством изb - метод
a.возвращает true, если нет общих элементов между наборами isdisjoint(b)
isdisjoint(b) aиb
означает, что вы не можете использовать их в качестве ключей словаря.
Python позволяет обойти это, используя вместо этого замороженный набор . Он имеет все свойства набора, за исключением того, что он неизменяемый (это означает, что вы не можете добавлять/удалять элементы из замороженного набора). Его также можно хешировать, поэтому его можно использовать в качестве ключей к словарю.
Тип данных frostset имеет все методы множества (такие как Different() , symmetric_difference и union ), но поскольку он неизменяем, у него нет методов для добавления/удаления элементов.
>>> а = замороженный набор ((1, 2, 3, 4)) >>> b = заморозка((3, 4, 5, 6)) >>> >>> a.issubset(b) ЛОЖЬ >>> a.update(b) # вызывает ошибку Traceback (последний последний вызов): Файл "", строка 1, в AttributeError: объект «замороженный» не имеет атрибута «обновление»
И использовать замороженный набор s в качестве ключей словаря так же просто, как 1, 2, 3:
>>> a = замороженный набор ((1, 2, 3, 4))
>>> b = замороженный набор(("w", "x", "y", "z"))
>>>
>>> d = {а: "привет", б: "мир"}
>>> д
{frozenset({1, 2, 3, 4}): 'привет', frostset({'w', 'x', 'y', 'z'}): 'world'} Вот и все! Вы узнали о том, что такое наборы, как их создавать и работать с ними, а также о различных операциях, которые вы можете с ними использовать.
После того, как наборы были готовы, вы должны освоиться с большинством встроенных функций Python. Все, что вам нужно сделать сейчас, это практика. Удачи!
Не забудьте подписаться на меня в Твиттере, чтобы быть в курсе новых новостей. Удачи!
Научитесь программировать бесплатно. Учебная программа freeCodeCamp с открытым исходным кодом помогла более чем 40 000 человек получить работу в качестве разработчиков. Начать
РЕКЛАМА
операторов набора SQL | Работа и типы операторов множества в SQL
Операторы набора SQL используются для объединения результатов, полученных из двух или более запросов, в один результат. Запросы, содержащие два или более подзапросов, называются составными запросами.
Существует четыре основных типа операторов SQL, а именно:
- Union
- Все соединения
- Пересечение
- Минус
Вот абстрактная таблица всего, что мы будем изучать в этой статье.
Оператор набора SQL | Функция |
| Союз | Объединяет разные результаты двух или более операторов SELECT. |
| Соединение Все | Объединяет все результаты двух или более операторов SELECT, включая дубликаты. |
| Пересечение | Возвращает только общие записи, полученные из двух или более операторов SELECT. |
| Минус | Возвращает только те записи, которые являются эксклюзивными для первой таблицы. |
Syntax and Parameters of SQL Set Operators
The generic syntax for working with SQL set operators is as follows:
Syntax:
SELECT column_name
FROM table_name_1
SET OPERATOR
SELECT column_name
FROM table_name_2
SET OPERATOR
SELECT имя_столбца
FROM имя_таблицы_3
.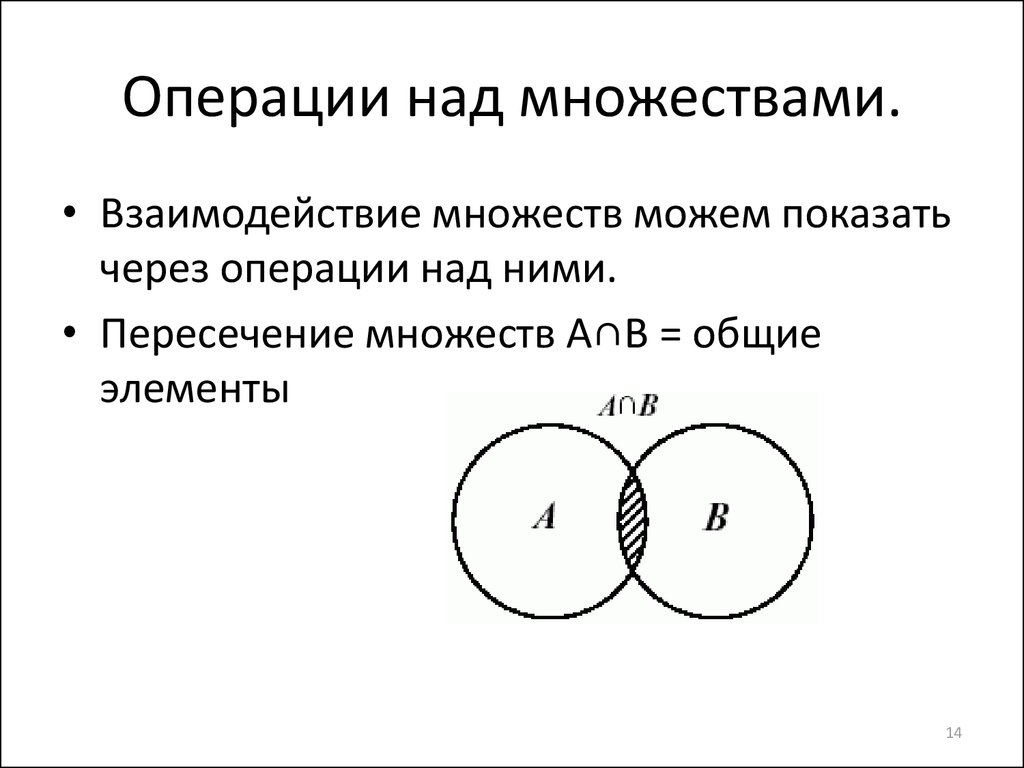
.
.
Параметры:
Различные параметры, используемые в синтаксисе:
- ОПЕРАТОР НАСТРОЙКИ: Укажите тип операции с множествами, которую вы хотите выполнить из {Объединение, Объединение всех, Пересечение, Минус}
- имя_столбца: Укажите имя столбца, над которым вы хотите выполнить операцию над набором и хотите получить в наборе результатов
- FROM table_name_1: Укажите имя первой таблицы, из которой должен быть извлечен столбец
- FROM table_name_2: Укажите имя второй таблицы, из которой должен быть извлечен столбец
Из вышеперечисленных параметров все параметры являются обязательными. Вы можете использовать предложения WHERE GROUP BY и HAVING в зависимости от ваших требований.
Работа
Вот несколько моментов, о которых следует помнить при работе с операторами набора SQL:
- Количество столбцов в операторе SELECT, к которым мы применили операторы набора SQL, должно быть одинаковым.

- Выбранные столбцы должны иметь одинаковый тип данных.
- Порядок столбцов должен быть таким же, как указано в операторе SELECT.
Далее мы подробно обсудим вышеупомянутые функции.
- Чтобы эффективно продемонстрировать и объяснить операторы множества в SQL, мы будем использовать следующие таблицы. Эти примеры таблиц — «customers_jan» и «customers_dec». Эти таблицы содержат 10 записей, каждая из которых содержит идентификатор, имя, город и страну клиента.
- Давайте посмотрим на записи в таблицах customers_jan и customers_dec. Чтобы позже мы могли понять, чем полезны операции над множествами.
Схема для обсуждаемых таблиц заключается в следующем. :
1. Оператор множества Union
Оператор множества UNION используется для объединения результатов, полученных из двух или более операторов SELECT. Вот пример, иллюстрирующий использование оператора UNION.
Пример:
Найдите имена всех клиентов
ВЫБЕРИТЕ имя ИЗ customers_dec
ОБЪЕДИНЕНИЕ
ВЫБЕРИТЕ имя ИЗ customers_jan;
Примечание : Уникальный выбор только различных значений.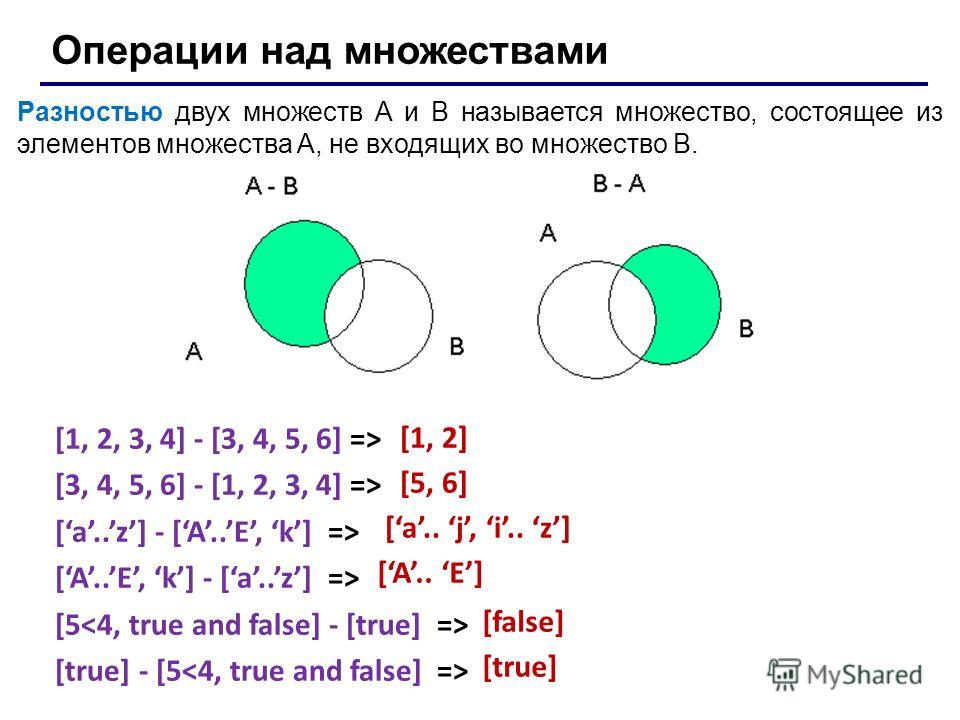 Это может создать проблемы, когда у нас есть клиенты с одним и тем же именем, но в разных странах или городах.
Это может создать проблемы, когда у нас есть клиенты с одним и тем же именем, но в разных странах или городах.
Вы заметите, что есть два клиента по имени Акшай Гупта, один из Дели, а другой из Бангалора. Но оператор Union вернул только одно имя клиента. То же самое для Аканши Сингха. Чтобы решить вышеупомянутую проблему, мы можем использовать оператор UNION ALL.
2. Оператор объединения всех множеств
Оператор множества UNION используется для объединения всех результатов, полученных из двух или более операторов SELECT. В отличие от оператора Union, он учитывает повторяющиеся значения и включает их в окончательный результат.
Вот пример, иллюстрирующий использование оператора UNION ALL.
Пример:
Найдите имена всех клиентов, которые зарегистрировались в декабре или январе.
ВЫБЕРИТЕ имя ИЗ customers_dec
ОБЪЕДИНЕНИЕ ВСЕХ
ВЫБЕРИТЕ имя ИЗ customers_jan;
Вы заметите, что есть два разных клиента по имени Акшай Гупта, один из Дели, а другой из Бангалора.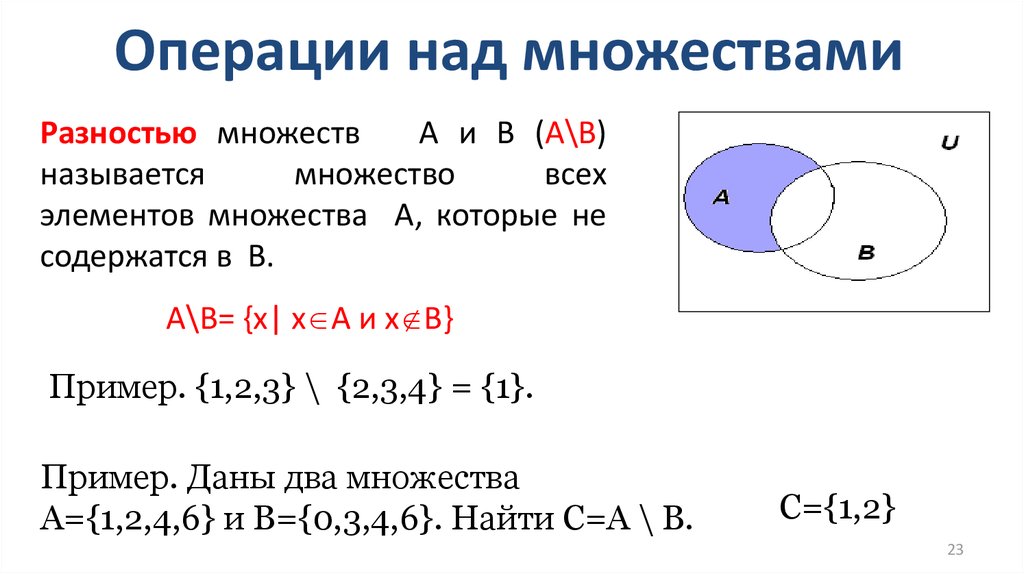 Оператор Union ALL тоже принял во внимание и дважды вернул Акшая Гупту. То же самое и с Аканшей Сингхом.
Оператор Union ALL тоже принял во внимание и дважды вернул Акшая Гупту. То же самое и с Аканшей Сингхом.
3. Оператор множества пересечений
Оператор множества пересечений, используемый для объединения всех результатов двух операторов SELECT. Но возвращает только те записи, которые являются общими для обоих операторов SELECT.
Примечание . Оператор INTERSECT не поддерживается в базах данных MYSQL. Мы можем использовать предложение IN или EXIST IN для выполнения подобных операций.
Вот пример, иллюстрирующий использование оператора INTERSECT.
Пример:
Найдите информацию о покупателях, совершивших покупки в декабре и январе.
ВЫБЕРИТЕ имя, город ОТ customers_dec
INTERSECT
ВЫБЕРИТЕ имя, город ОТ customers_jan;
4. Оператор минус-сет
Оператор набора МИНУС используется для объединения всех результатов двух или более операторов SELECT. Но возвращает только те записи, которые присутствуют исключительно в первой таблице.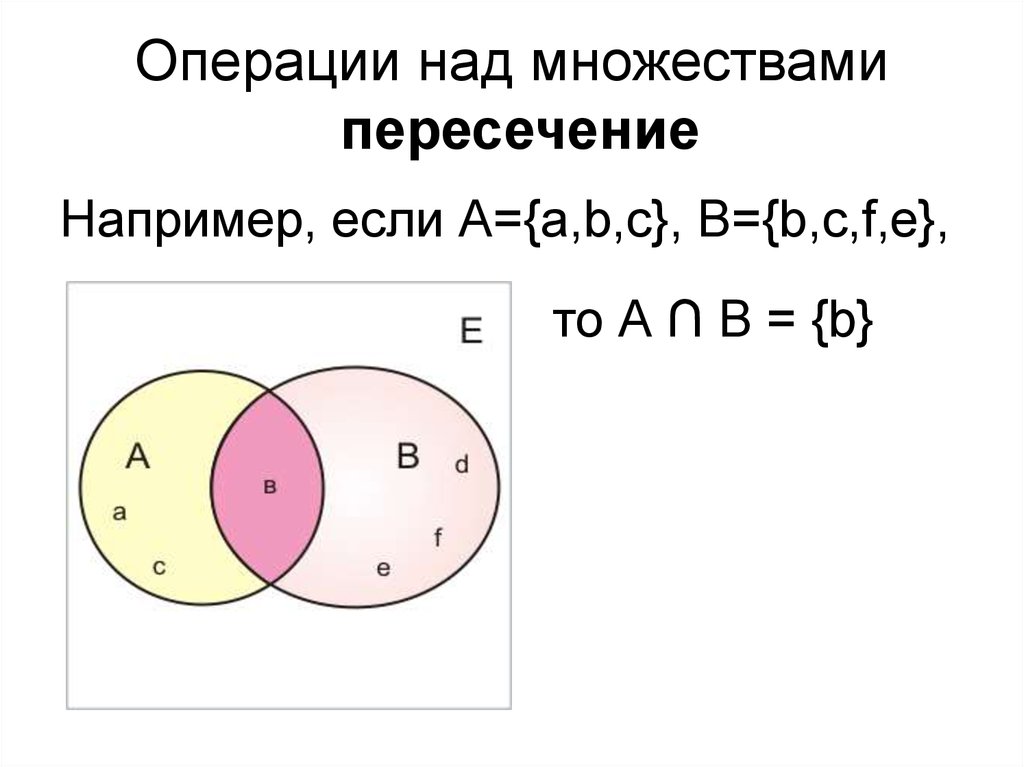
Примечание . Оператор МИНУС поддерживается только в базах данных Oracle. Для других баз данных, таких как SQL Server, PostgreSQL и SQLite, мы можем использовать оператор EXCEPT для выполнения аналогичных операций.
Вот пример, иллюстрирующий использование оператора EXCEPT.
Пример:
Найдите сведения о покупателях, которые совершали покупки только в декабре, но не в январе.
ВЫБЕРИТЕ имя, город ИЗ customers_dec
ЗА ИСКЛЮЧЕНИЕМ
ВЫБЕРИТЕ имя, город ИЗ customers_jan;
Рекомендуемые статьи
Это руководство по операторам набора SQL. Здесь мы обсуждаем работу, типы и функции операторов множества SQL, а также синтаксис и параметры. Вы также можете просмотреть следующие статьи, чтобы узнать больше –
- Список предложений SQL | Синтаксис и пример
- Как использовать запрос LIKE в SQL?
- Как НЕ работает условие в MySQL?
- Оператор SQL IN
Узнайте значение, операции, примеры и свойства!
Алгебра операций над множествами выполняется над двумя или более множествами для получения смеси элементов в соответствии с операцией, выполняемой над заданными множествами.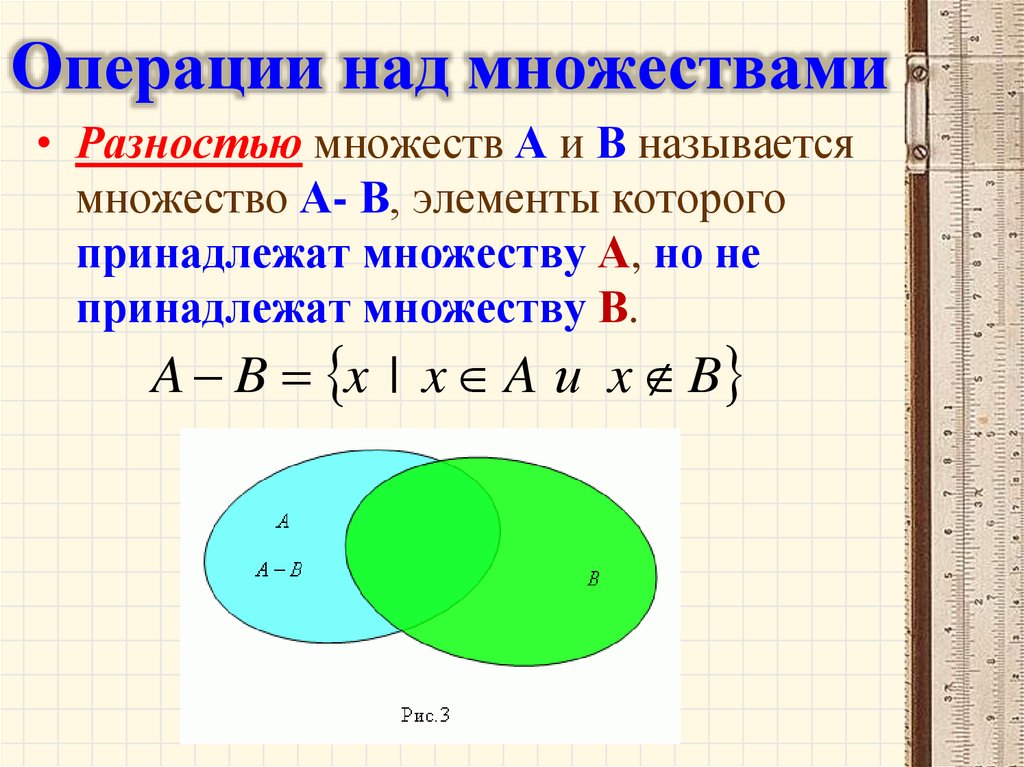 Набор определяется как четко определенный набор объектов, и эти объекты известны как элементы набора. Набор обозначается заглавными буквами.
Набор определяется как четко определенный набор объектов, и эти объекты известны как элементы набора. Набор обозначается заглавными буквами.
Например:
P = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Компоненты множества в математике, как видно из приведенного выше примера, вложены в фигурные скобки, разделенные запятыми.
Основные операции, которые можно выполнять над отношениями множества: пересечение множеств, объединение множеств, дополнение множества и разность множеств. В этой статье мы постараемся изучить основные операции теории множеств, свойства с примерами и многое другое.
Что такое набор операций? В математике совокупность элементов или групп вещей означает заданное значение. Существуют различные типы наборов, такие как пустой набор, конечный набор, бесконечный набор, равный набор, набор мощности, эквивалентный набор, подмножество, надмножество и универсальный набор. Фундаментальная операция над множествами — это понятие, аналогичное операциям над числами. Там, где требуется установить связь между двумя или более множествами, возникает понятие операций над множествами.
Там, где требуется установить связь между двумя или более множествами, возникает понятие операций над множествами.
Существует четыре основных операции набора, а именно:
- Объединение множеств
- Пересечение множеств
- Дополнение множества
- Различие между множествами
К множеству можно обращаться в трех формах. а именно; форма оператора, форма реестра, форма построителя набора и операции с наборами являются фундаментальными операциями, которые используются на двух или более чем двух наборах для установления отношений между данными наборами. Теперь давайте узнаем и поймем диаграмму Венна, прежде чем переходить к различным операциям на съемочной площадке.
Диаграмма Венна — это логическое представление данных, показывающее возможную взаимосвязь между различными конечными множествами. Пример показан ниже. Мы узнаем больше об использовании диаграммы Венна через различные операции над множествами.
Если мы рассмотрим два множества, скажем P и Q, то объединение P и Q содержит все элементы, существующие в множестве P и множестве Q. Объединение множеств обозначается как P∪Q и представлено как:
P ∪ Q = {a: a ∈ P или a ∈ Q}
Здесь «а» обозначает элементы, которые присутствуют как в P, так и в Q.
Количество элементов в P ∪ Q определяется по формуле:
n(P∪Q) = n(P) + n(Q) − n(P∩Q) .
Объединение множеств Диаграмма Венна выглядит следующим образом:
Заштрихованная область указывает P∪Q.
Пример:
Чтобы лучше понять эту операцию объединения множеств, рассмотрим пример: если P = {1, 2, p, q} и Q = {3, 4, s, t} , то объединение P и Q берется в виде P ∪ Q = {1, 2, 3, 4, p, q, s, t}. 9nP_i\)
Пересечение множеств Для любых двух заданных множеств, скажем P и Q, пересечение P и Q содержит все общие элементы, принадлежащие множествам P и Q. Символически представляется как:
Символически представляется как:
P∩Q
Операция пересечения представлена в виде:
P∩Q = {x : x ∈ P и x ∈ Q}
Здесь x — общая компонента обоих множеств P и Q.
Пересечение множеств P и Q также можно рассчитать по формуле, как показано:
P∩Q = n(P) + n(Q) – n(P∪Q)
Здесь
- n(P) обозначает кардинальное число множества P.
- n(B) обозначает кардинальное число множества Q.
- n(P ∪ Q) обозначает кардинальное число объединения множеств P и Q.
Диаграмма Венна пересечения множеств выглядит следующим образом:
Заштрихованное место показывает P ∩Q.
Заштрихованная область на приведенной выше диаграмме Венна показывает P∩Q∩R.
Пример:
Если P = {3, 5, r, s} и Q = {4, 5, p, s}, то пересечение P и Q определяется как P ∩ B = {5, s}, как ' 5' и 's' являются общими для обоих данных наборов.
Если \(P_1, P_2, P_3,⋯, P_n\) — n множеств, то их множество пересечений включает все элементы, присутствующие во всех заданных множествах.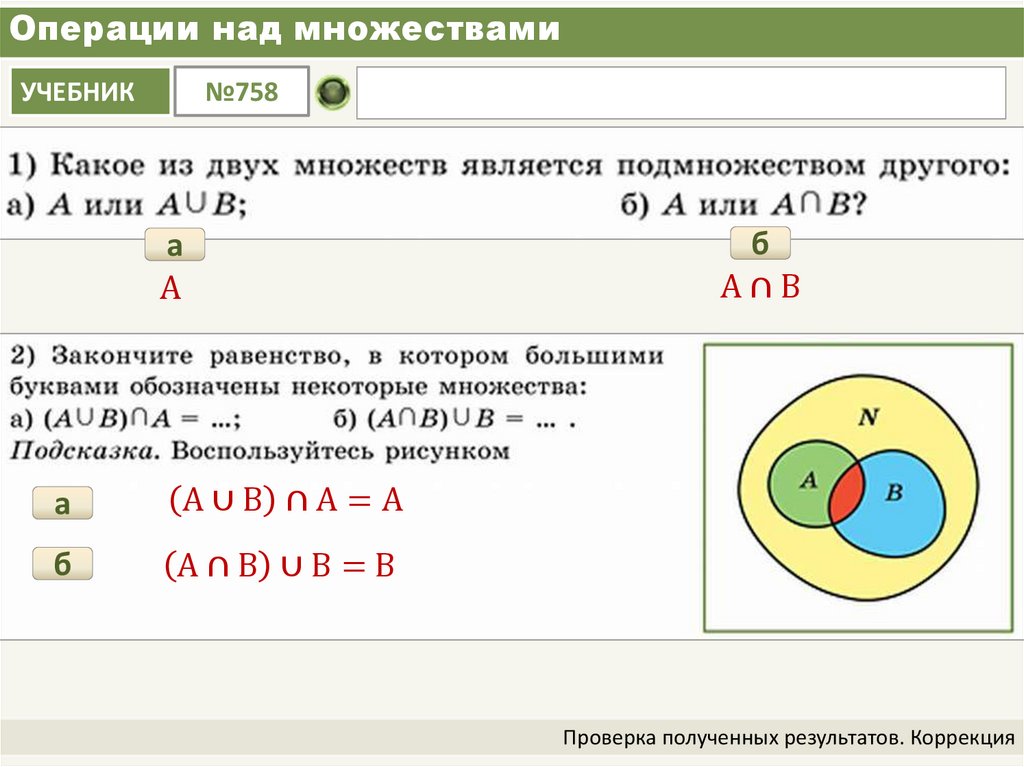 Мы можем составить это пересечение по формуле:
Мы можем составить это пересечение по формуле:
\(\cap_iP_i\)
Ознакомьтесь с этой статьей о декартовом произведении множеств.
Установить разницуРазность наборов указывает на вычитание компонентов из набора, что эквивалентно вычислению разницы между числами/цифрами.
Если нам даны два множества P и Q, то разница между двумя множествами эквивалентна множеству, которое охватывает элементы, присутствующие в P, но не в Q. Разность множеств представляется как P-Q.
Диаграмма Венна разности множеств.
Заштрихованное пространство указывает P-Q.
Установить разницу Пример 9{с}\).
Пример:
Если U = {a, b, c, d, e, f, g, i} и P = {a, b, c, d}, то дополнение множества P определяется выражением Р' = {е, е, г, я}.
Непересекающееся множество Два заданных множества считаются непересекающимися, если их пересечение приводит к пустому множеству. т. е. множества не содержат общих элементов.
т. е. множества не содержат общих элементов.
Выше приведена диаграмма Венна непересекающегося Q.
Пример
Пусть P = {a, e, i, o, u} и Q = {b, c, d, f, g }0003
Здесь P и Q непересекающиеся множества, поскольку оба они не содержат общих элементов.
Ознакомьтесь с другими темами по математике здесь.
Свойства операций над множествамиМножество представлено как совокупность объектов, элементы которых фиксированы и не могут быть изменены. В свойствах множества используется понятие, аналогичное свойствам основных операций в системе счисления. Различные свойства перечислены ниже:
Коммутативное свойствоДля любых двух заданных множеств P и Q свойство коммутативности представлено в виде: как и пересечение двух множеств, носит коммутативный характер.
Ассоциативное свойствоДля заданных 3 множеств P, Q и R ассоциативное свойство изображается как:
(P ∪ Q) ∪ R = P ∪ (Q ∪ R)
Также: ∩ Q) ∩ R = P ∩ (Q ∩ R)
Это означает, что объединение множеств, а также пересечение множеств носят ассоциативный характер.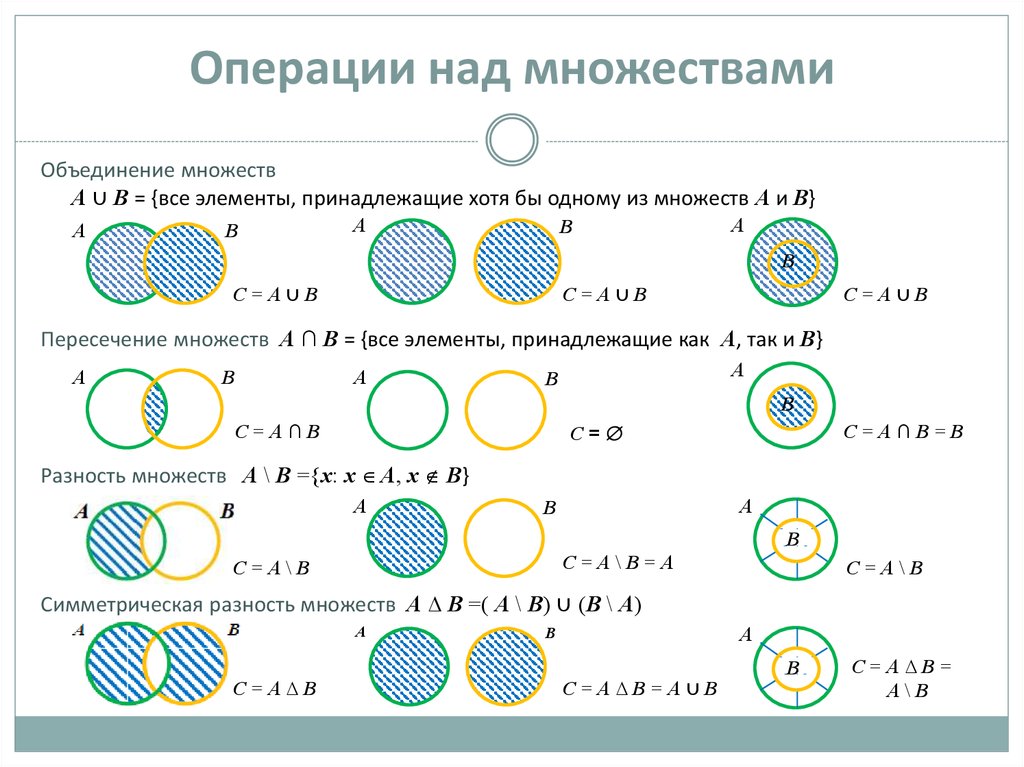
Для заданных 3 множеств P, Q и R распределительное свойство изображается как:
P ∩ (Q ∪ R) = (P ∩ Q) ∪ (P ∩ R) (Q ∩ R) = (P ∪ Q) ∩ (P ∪ R)
Узнайте больше об отношениях и функциях здесь.
Закон Де-МорганаЗакон гласит, что для любых двух множеств P и Q мы имеем (P ∪ Q)’ = P’ ∩ Q’ и (P ∩ Q)’ = P’ ∪ Q’ 92-4y-5=0\right\}\) можно представить в обжарщике следующим образом: B = {-1, 5}.
Пусть C = (A ∩ B) = {-1}.
⇒ A ∪ C = {-1, 3}
Следовательно, A ∪ (A ∩ B)={-1, 3}
Также читайте о последовательностях и сериях здесь.
Вопрос 2: Какое из следующих утверждений верно для любых двух множеств A и B?
I (A∪B)′=A′∩B′
- (A∩B)′=A′∪B′
III. (A−B)=A∩B′
Решение:
По закону Деморгана:
Для любых двух множеств A и B имеем (A∪B)′=A′∩B′ и (A∩B)′=A′∪B′
Кроме того, A – B = {c | c ∈ A и c ∉ B} = A ∩ B’.
Следовательно, все три варианта верны.
Пример 3: В классе каждый ученик изучает либо английский, либо математику, либо и то, и другое. Было обнаружено, что 300 студентов изучают английский язык, 250 студентов изучают математику и 150 студентов изучают и то, и другое. Найдите, сколько учеников было в классе, используя формулу операции над множествами.
Решение: Пусть количество студентов, изучающих английский язык, равно n(E), а количество студентов, изучающих математику, равно n(M). Имеем n(E) = 300, n(M) = 250 и n(E ∩ M) = 150. Мы знаем, что
n(E∪M) = n(E) + n(M) − n (E∪M)
Следовательно, n(E∪M)=(300+250)−150
n(E∪M) = 400
Общее количество студентов в вызовах равно 400.
Мы надеемся что приведенная выше статья об операциях над множествами полезна для вашего понимания и подготовки к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам.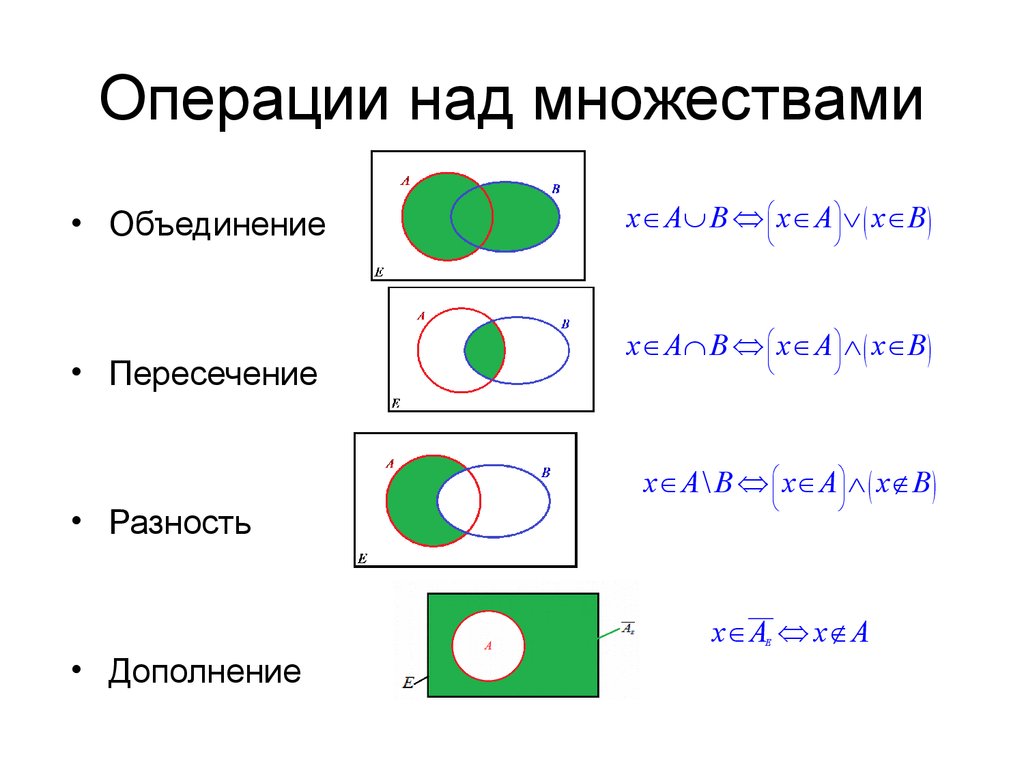 Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
В.1. Какие существуют типы наборов?
Ответ 1 Различные типы множеств: пустое множество, конечное множество, одноэлементное множество, эквивалентное множество, подмножество, множество мощности, универсальное множество, надмножество и бесконечное множество.
Q.2 Что означает набор?
Ответ 2 В математике совокупность элементов или групп вещей означает набор значений.
Q.3 В чем разница между набором и набором?
Ответ 3 Коллекция может содержать различные типы элементов. Однако набор — это четко определенная группа отдельных компонентов, заключенная в квадратные скобки.
Q.4 Каковы некоторые приложения теории множеств в реальной жизни?
Ans. 4 Приложения теории множеств чаще всего используются в науке, физике и математике, а также в компьютерной и электрической технике. При подготовке логических основ по геометрии, по созданию алгебры топологии и многого другого.
4 Приложения теории множеств чаще всего используются в науке, физике и математике, а также в компьютерной и электрической технике. При подготовке логических основ по геометрии, по созданию алгебры топологии и многого другого.
В.5 В чем разница между наборами?
Ответ 5 Разность множеств указывает на вычитание компонентов из множества, что эквивалентно вычислению разницы между числами.
Q.6 Каковы 4 операции множеств?
Ответ 6 Четыре важные операции над множествами: Объединение множеств. Пересечение множеств. Комплектация наборов. Разница между наборами
Q.7 Каковы основные свойства наборов?
Ответ 7 Основные свойства множеств: Коммутативность. Ассоциативное свойство. Распределительное свойство.
Q.8 Что вы подразумеваете под операцией на съемочной площадке?
Ответ 8 Когда два или более набора объединяются для создания одного набора при данных обстоятельствах, выполняются операции над наборами.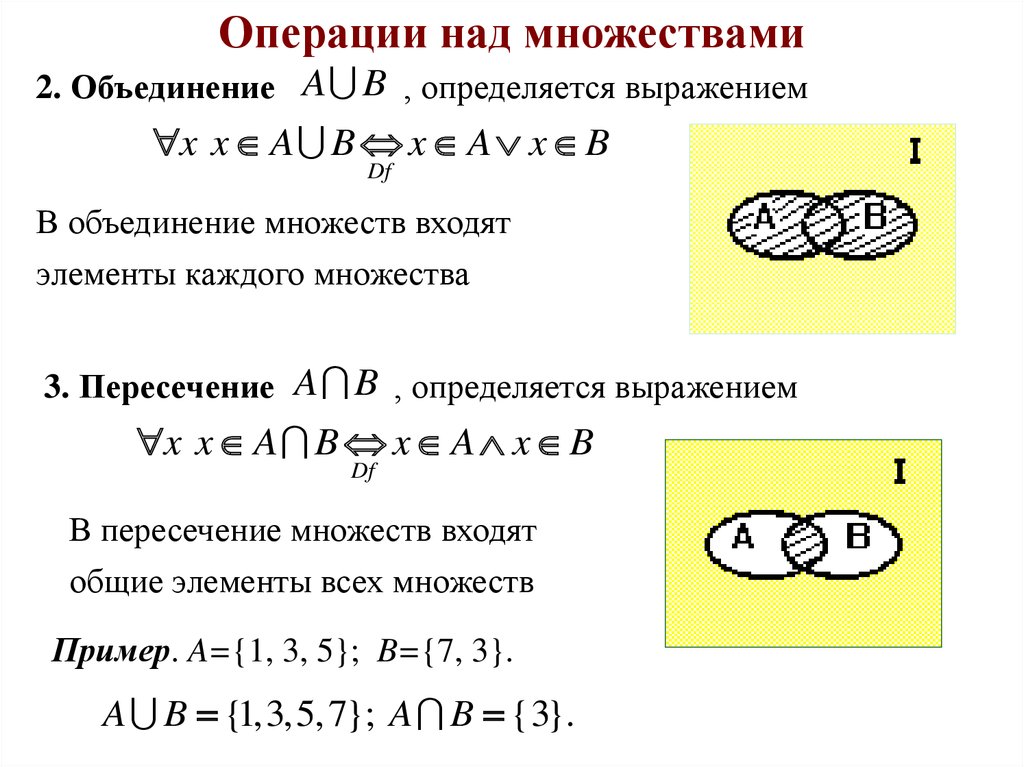


 1.
Множества на плоскости
1.
Множества на плоскости
 ru
ru
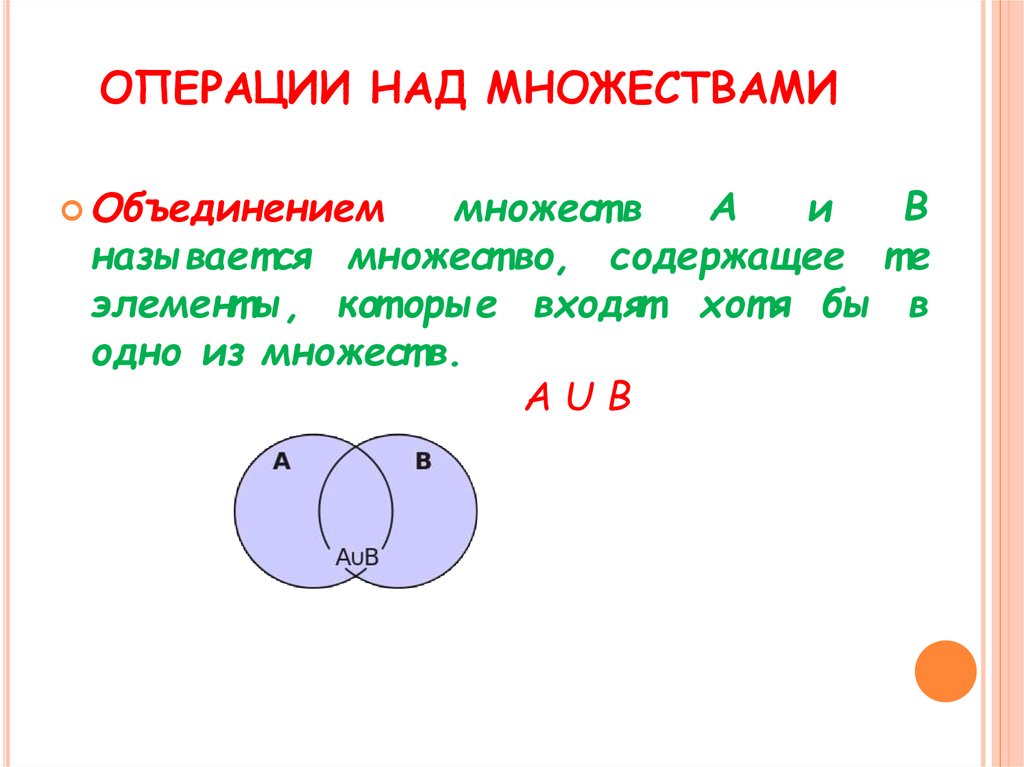



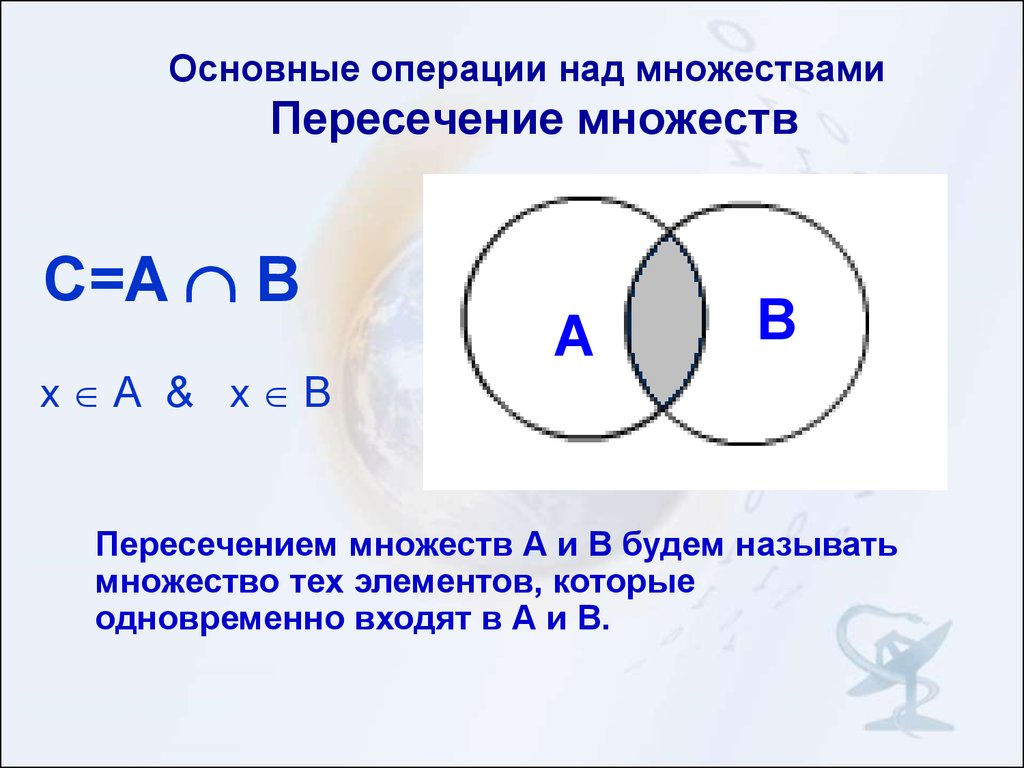 update(("виолончель" ,))
>>> add_Set
{1, 2, 3, 4, "скрипка", "виолончель"}
update(("виолончель" ,))
>>> add_Set
{1, 2, 3, 4, "скрипка", "виолончель"} 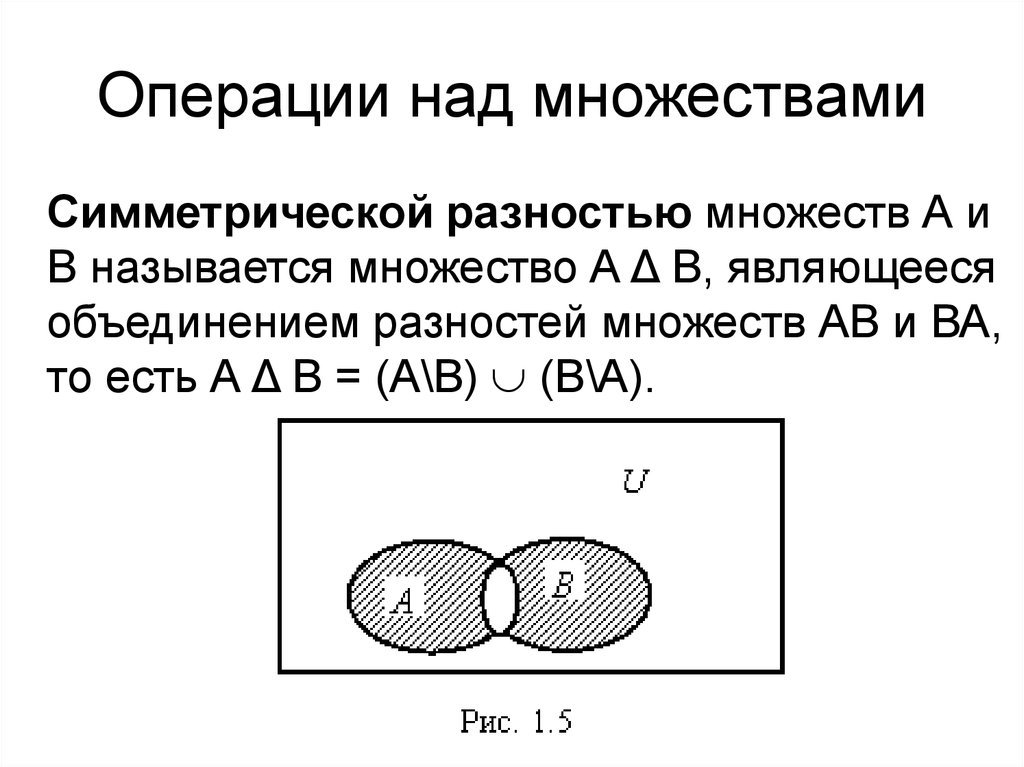
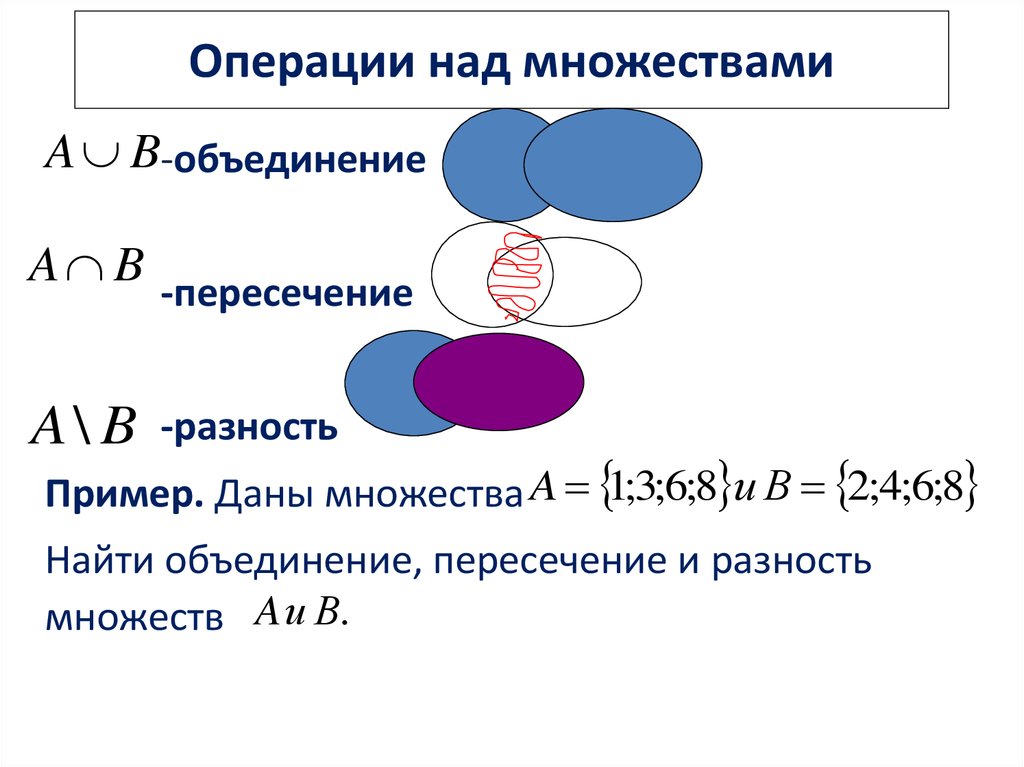 difference(second_set)
{1, 2, 3}
>>>
>>> first_set - second_set # с использованием оператора `-`
{1, 2, 3}
>>>
>>> второй_набор - первый_набор
{8, 9, 7}
difference(second_set)
{1, 2, 3}
>>>
>>> first_set - second_set # с использованием оператора `-`
{1, 2, 3}
>>>
>>> второй_набор - первый_набор
{8, 9, 7} 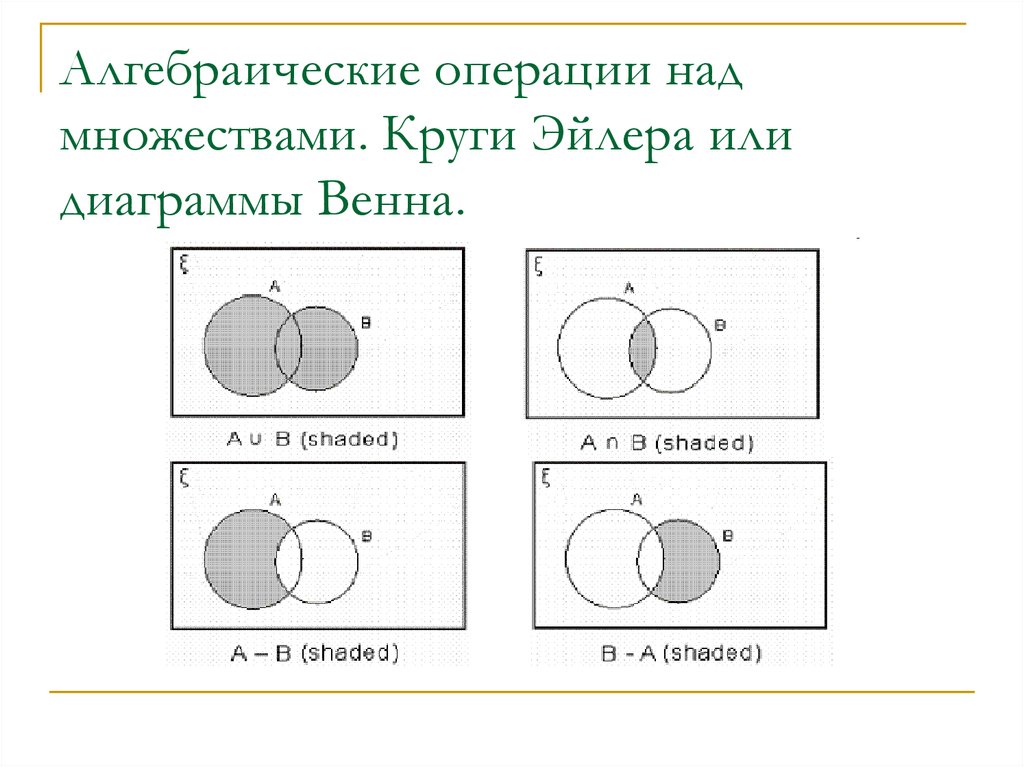 isdisjoint(b)
isdisjoint(b) 