Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.
4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
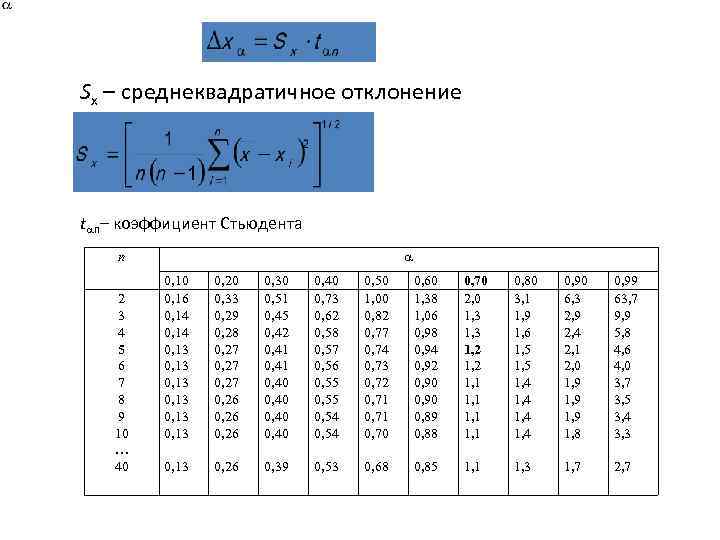
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.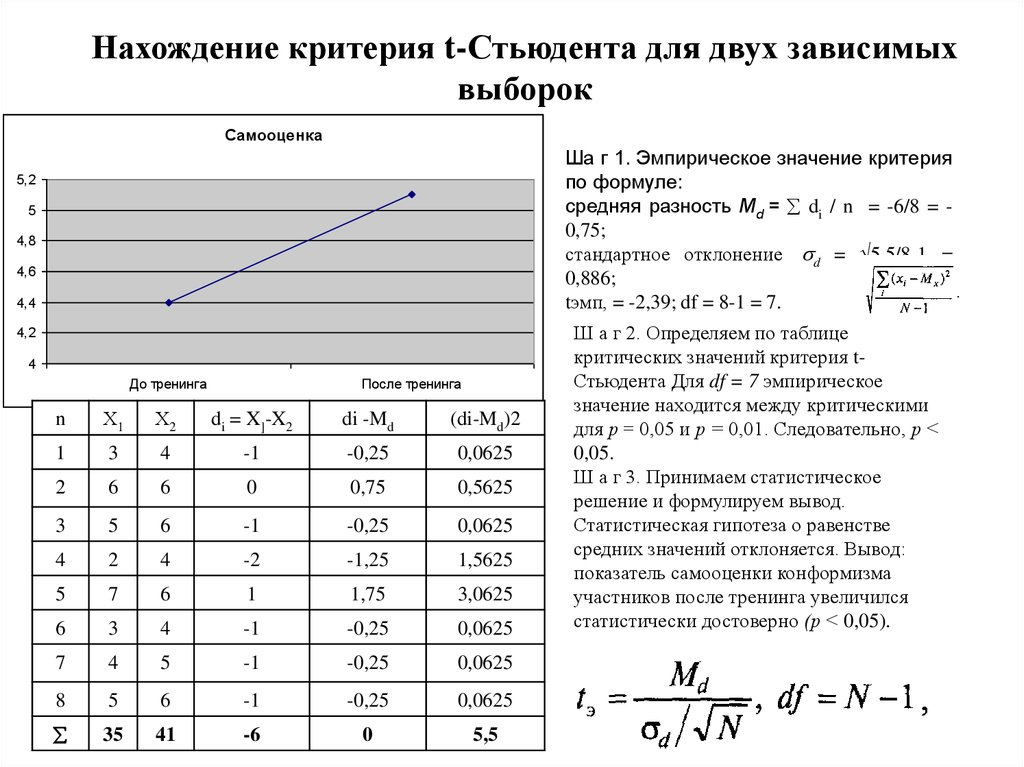
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.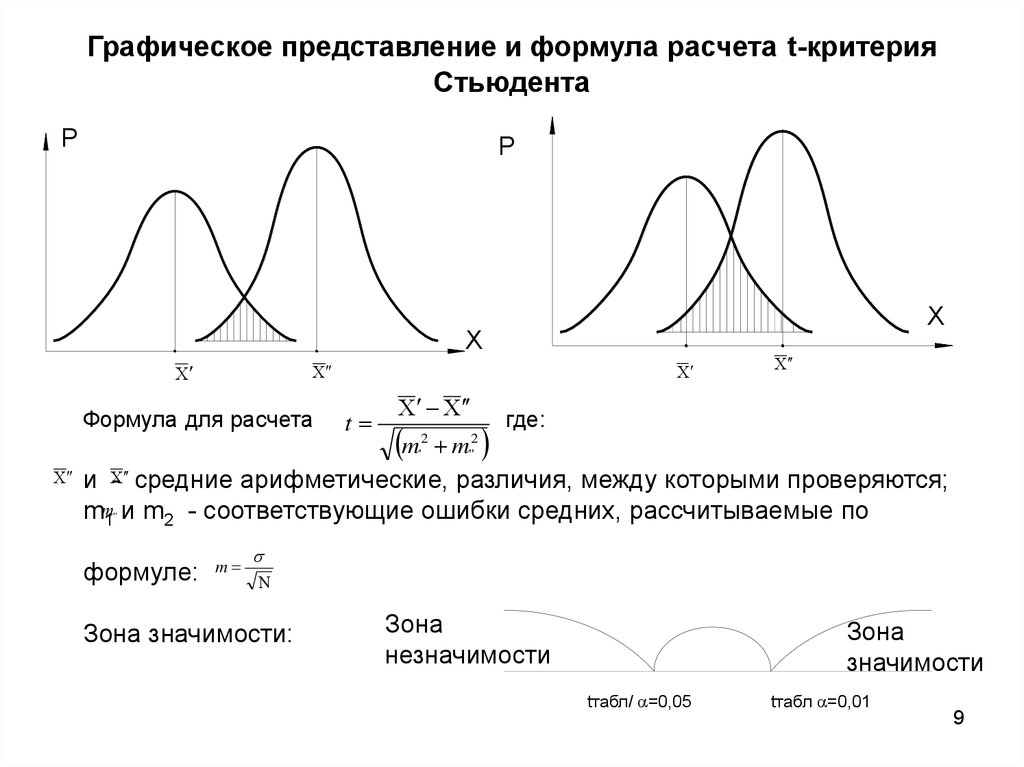
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.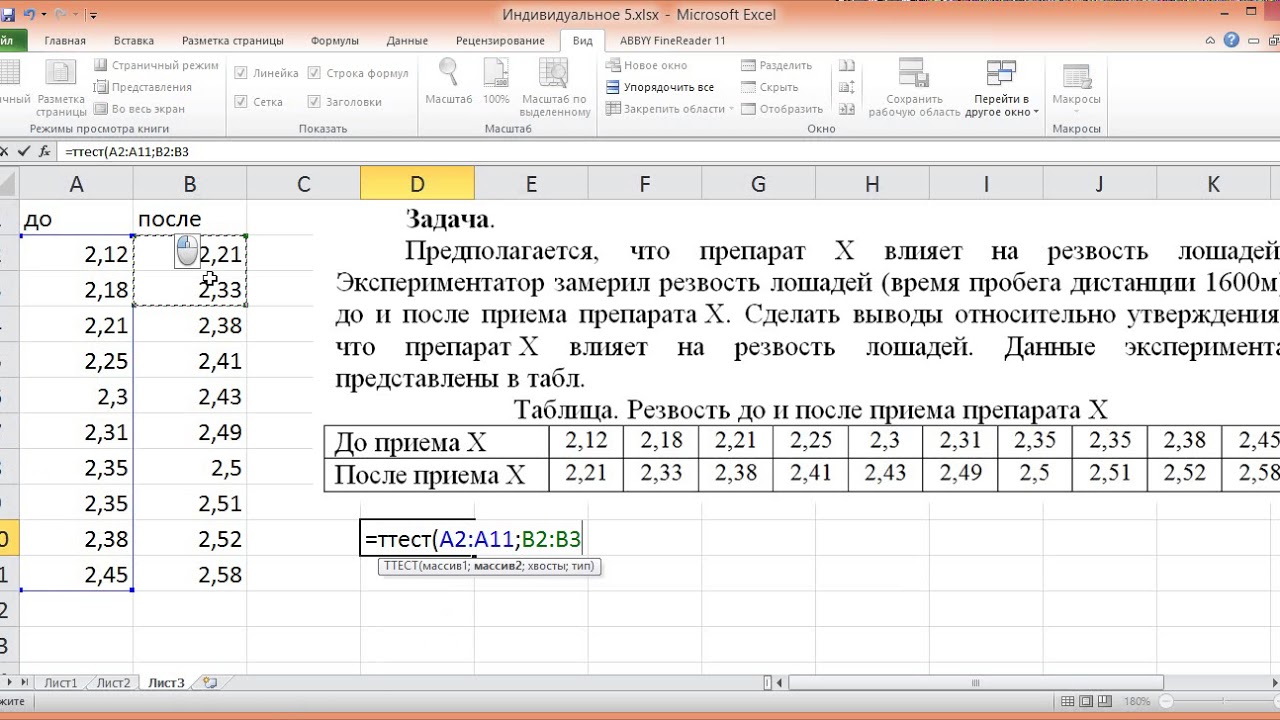
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Comparison of mean dependent sample populations with unknown variances of general populationsРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Как найти t критическое в excel. Распределение t-критерия Стьюдента для проверки гипотезы о средней и расчета доверительного интервала в MS Excel
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок.
То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ . В версиях Excel 2007 года и ранее она называлась ТТЕСТ . Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ . Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ
можно вызвать также путем перехода во вкладку «Формулы»
с помощью специальной кнопки на ленте.
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
1. История разработки t-критерия
Данный критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых ), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата ).
3. В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение
. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства (гомоскедастичности) дисперсий
.
При несоблюдении этих условий при сравнении выборочных средних должны использоваться аналогичные методы непараметрической статистики , среди которых наиболее известными являются U-критерий Манна — Уитни (в качестве двухвыборочного критерия для независимых выборок), а также критерий знаков и критерий Вилкоксона (используются в случаях зависимых выборок).
4. Как рассчитать t-критерий Стьюдента?
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
где М 1 — средняя арифметическая первой сравниваемой совокупности (группы), М 2 — средняя арифметическая второй сравниваемой совокупности (группы), m 1 — средняя ошибка первой средней арифметической, m 2 — средняя ошибка второй средней арифметической.
5. Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n 1 и n 2).
Находим число степеней свободы f
по следующей формуле:
f = (n 1 + n 2) — 2
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже ).
Сравниваем критическое и рассчитанное значения критерия:
- Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
6. Пример расчета t-критерия Стьюдента
Для изучения эффективности нового препарата железа были выбраны две группы пациентов с анемией. В первой группе пациенты в течение двух недель получали новый препарат, а во второй группе — получали плацебо.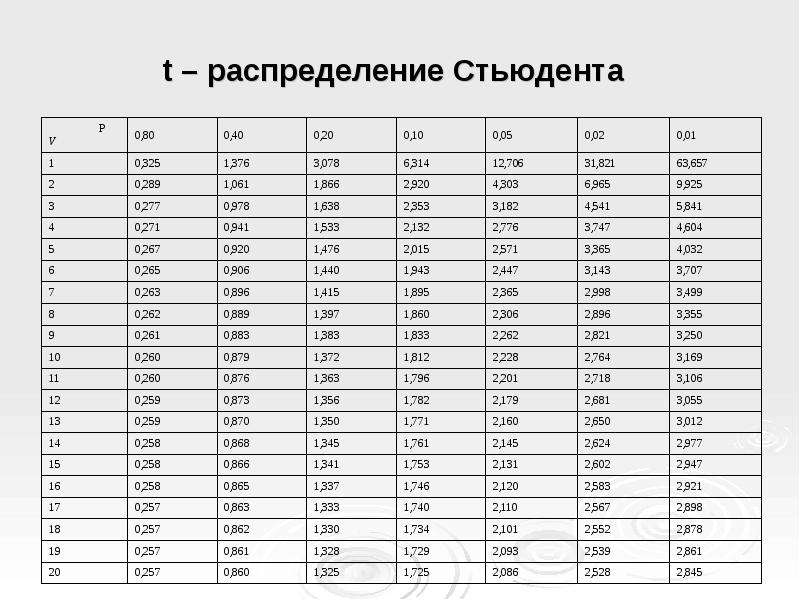
После этого было проведено измерение уровня гемоглобина в периферической крови. В первой группе средний уровень гемоглобина составил 115,4±1,2 г/л, а во второй — 103,7±2,3 г/л (данные представлены в формате M±m
), сравниваемые совокупности имеют нормальное распределение. При этом численность первой группы составила 34, а второй — 40 пациентов. Необходимо сделать вывод о статистической значимости полученных различий и эффективности нового препарата железа.
Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:
После выполнения расчетов, значение t-критерия оказалось равным 4,51. Находим число степеней свободы как (34 + 40) — 2 = 72. Сравниваем полученное значение t-критерия Стьюдента 4,51 с критическим при р=0,05 значением, указанным в таблице: 1,993. Так как рассчитанное значение критерия больше критического, делаем вывод о том, что наблюдаемые различия статистически значимы (уровень значимости р
Таблица распределения Стьюдента
Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности.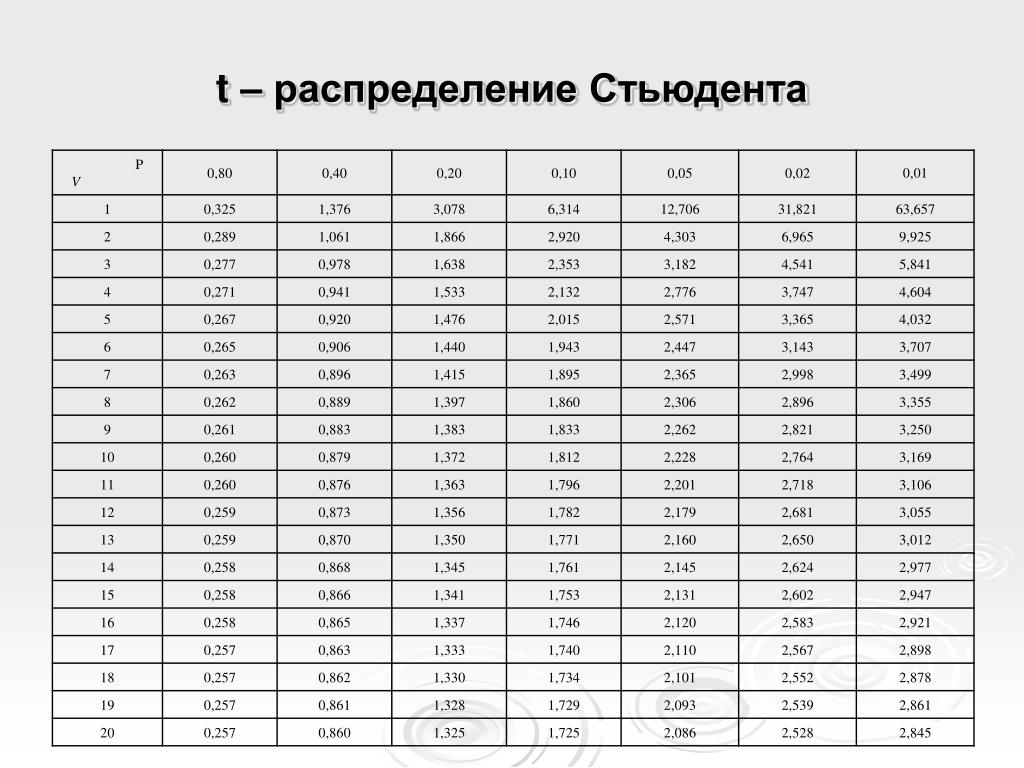
Но уже при (n
)
табличными данными и вероятностью предела; при (n )
ральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормаль-
ным. В выборках небольшого объема (n )
вокупности, имеющей нормальное распределение. Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В
1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить (t ) и доверительную вероятность F(t ). При (n ) > 100, таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30
100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц).
Использование малых выборок в ряде случаев обусловлено характером обследуемой совокупности.
Так, в селекционной работе «чистого» опыта легче добиться на небольшом числе
делянок. Производственный и экономический эксперимент, связанный с экономическими затратами, также проводится на небольшом числе испытаний. Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней.
Плотность вероятностей распределения Стьюдента описывается функцией.
1 + t2 |
|||
f (t ,n) := Bn | |||
n − 1 | |||
t — текущая переменная;n — объем выборки;
B — величина, зависящая лишь от (n ).
Распределение Стьюдента имеет только один параметр: (d.
f.
) -число степеней свободы (иногда обозначается (к
)). Это распределение — как и нормальное, симметрично относительно точки (t
) = 0, но оно более пологое. При увеличении объема выборки, а, следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно рас-
полагать для определения искомой характеристики. Так, для расчета дисперсии должна быть известна средняя величина. Поэтому при расчете дисперсии применяют (d.f. )= n — 1 .
Таблицы распределения Стьюдента публикуются в двух вариантах:
1. аналогично таблицам интеграла вероятностей приводятся значения ( t ) и соответствую-
щие вероятности F(t ) при разном числе степеней свободы;
2. значения (t ) приводятся для наиболее употребляемых доверительных вероятностей
0,70; 0,75; 0,80; 0,85; 0,90; 0,95 и 0,99 или для 1 — 0,70 = 0,3; 1 — 0,80 = 0,2; …… 1 — 0,99 = 0,01.
3.
при разном числе степеней свободы.
Такого рода таблица приведена в приложении
(Таблица 1 — 20 ), а также значение (t )- критерий Стьюдента при уровне значимости от0,7
В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение . В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства (гомоскедастичности) дисперсий .
При несоблюдении этих условий при сравнении выборочных средних должны использоваться аналогичные методы непараметрической статистики , среди которых наиболее известными являются U-критерий Манна — Уитни (в качестве двухвыборочного критерия для независимых выборок), а также критерий знаков и критерий Вилкоксона (используются в случаях зависимых выборок).
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
где М 1
— средняя арифметическая первой сравниваемой совокупности (группы), М 2
— средняя арифметическая второй сравниваемой совокупности (группы), m 1
— средняя ошибка первой средней арифметической, m 2
— средняя ошибка второй средней арифметической.
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n 1 и n 2). Находим число степеней свободы f по следующей формуле:
f = (n 1 + n 2) — 2
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже ).
Сравниваем критическое и рассчитанное значения критерия:
· Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
· Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
Пример расчета t-критерия Стьюдента
Для изучения эффективности нового препарата железа были выбраны две группы пациентов с анемией.
В первой группе пациенты в течение двух недель получали новый препарат, а во второй группе — получали плацебо. После этого было проведено измерение уровня гемоглобина в периферической крови. В первой группе средний уровень гемоглобина составил 115,4±1,2 г/л, а во второй — 103,7±2,3 г/л (данные представлены в формате M±m
), сравниваемые совокупности имеют нормальное распределение. При этом численность первой группы составила 34, а второй — 40 пациентов. Необходимо сделать вывод о статистической значимости полученных различий и эффективности нового препарата железа.
Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:
После выполнения расчетов, значение t-критерия оказалось равным 4,51. Находим число степеней свободы как (34 + 40) — 2 = 72. Сравниваем полученное значение t-критерия Стьюдента 4,51 с критическим при р=0,05 значением, указанным в таблице: 1,993.
Так как рассчитанное значение критерия больше критического, делаем вывод о том, что наблюдаемые различия статистически значимы (уровень значимости р
Распределение Фишера – это распределение случайной величины
где случайные величины Х 1 и Х 2 независимы и имеют распределения хи – квадрат с числом степеней свободы k 1 и k 2 соответственно. При этом пара (k 1 , k 2) – пара «чисел степеней свободы» распределения Фишера, а именно, k 1 – число степеней свободы числителя, а k 2 – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики.
Таблица критических значений Стьюдента.
Начало формы
| Число степеней свободы, f | Значение t-критерия Стьюдента при p=0. 05
|
| 12.706 | |
| 4.303 | |
| 3.182 | |
| 2.776 | |
| 2.571 | |
| 2.447 | |
| 2.365 | |
| 2.306 | |
| 2.262 | |
| 2.228 | |
| 2.201 | |
| 2.179 | |
| 2.160 | |
| 2.145 | |
| 2.131 | |
| 2.120 | |
| 2.110 | |
| 2.101 | |
| 2.093 | |
| 2.086 | |
| 2.080 | |
| 2.074 | |
| 2.069 | |
| 2.064 | |
| 2.060 | |
| 2.056 | |
| 2.052 | |
2. 048
|
|
| 2.045 | |
| 2.042 | |
| 2.040 | |
| 2.037 | |
| 2.035 | |
| 2.032 | |
| 2.030 | |
| 2.028 | |
| 2.026 | |
| 2.024 | |
| 40-41 | 2.021 |
| 42-43 | 2.018 |
| 44-45 | 2.015 |
| 46-47 | 2.013 |
| 48-49 | 2.011 |
| 50-51 | 2.009 |
| 52-53 | 2.007 |
| 54-55 | 2.005 |
| 56-57 | 2.003 |
| 58-59 | 2.002 |
| 60-61 | 2.000 |
| 62-63 | 1.999 |
| 64-65 | 1.998 |
| 66-67 | 1.997 |
| 68-69 | 1. 995
|
| 70-71 | 1.994 |
| 72-73 | 1.993 |
| 74-75 | 1.993 |
| 76-77 | 1.992 |
| 78-79 | 1.991 |
| 80-89 | 1.990 |
| 90-99 | 1.987 |
| 100-119 | 1.984 |
| 120-139 | 1.980 |
| 140-159 | 1.977 |
| 160-179 | 1.975 |
| 180-199 | 1.973 |
| 1.972 | |
| ∞ | 1.960 |
Функция Т.ТЕСТ — служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Дополнительно…Меньше
Возвращает вероятность, связанную с критерием Стьюдента.
Используйте T.TEST, чтобы определить, вероятно ли, что две выборки получены из одних и тех же двух базовых совокупностей, имеющих одинаковое среднее значение.
Синтаксис
Т.ТЕСТ(массив1,массив2,хвосты,тип)
Синтаксис функции Т.ТЕСТ имеет следующие аргументы:
-
Массив1 Обязательно. Первый набор данных.
-
Массив2 Обязательно. Второй набор данных.
-
Хвосты Обязательно. Определяет количество хвостов распределения. Если хвосты = 1, T.TEST использует одностороннее распределение.
Если хвосты = 2, T.TEST использует двустороннее распределение. -
Введите Обязательно. Тип t-теста для выполнения.
Параметры
|
Если тип равен |
Этот тест выполняется |
|
1 |
В паре |
|
2 |
Равная дисперсия по двум выборкам (гомоскедастическая) |
|
3 |
Двухвыборочная неравная дисперсия (гетероскедастическая) |
Примечания
-
Аргументы хвоста и типа усекаются до целых чисел.
-
Если хвост или тип не являются числовыми, T.TEST возвращает #VALUE! значение ошибки.
-
Если решка имеет значение, отличное от 1 или 2, функция Т.ТЕСТ возвращает ошибку #ЧИСЛО! значение ошибки.
-
T.TEST использует данные массивов1 и массив2 для вычисления неотрицательной t-статистики.
Если хвосты=1, T.TEST возвращает вероятность более высокого значения t-статистики в предположении, что array1 и array2 являются выборками из совокупностей с одинаковым средним значением. Значение, возвращаемое T.TEST, когда хвосты = 2, в два раза больше, чем возвращаемое, когда хвосты = 1, и соответствует вероятности более высокого абсолютного значения t-статистики при допущении «одинаковые средние значения населения».
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
|
Данные 1 |
Данные 2 |
|
|
3 |
6 |
|
|
4 |
19 |
|
|
5 |
3 |
|
|
8 |
2 |
|
|
9 |
14 |
|
|
1 |
4 |
|
|
2 |
5 |
|
|
4 |
17 |
|
|
5 |
1 |
|
|
Формула |
Описание |
Результат |
|
=Т. |
Вероятность, связанная с парным критерием Стьюдента, с двусторонним распределением. |
0,196016 |
Парный образец t-тест | Реальная статистика с использованием Excel
Основные понятия
В парной выборке проверяется гипотеза, из генеральной совокупности выбирается выборка и выполняются два измерения для каждого элемента в выборке. Каждый набор измерений считается образцом. В отличие от проверки гипотез с двумя выборками (см. Стьюдентный критерий с двумя выборками), две выборки не являются независимыми друг от друга. Парные образцы также называются согласованные образцы или повторные измерения .
Например, если вы хотите определить, влияет ли употребление бокала вина или бокала пива на память одинаково или по-разному, один из подходов состоит в том, чтобы взять выборку, скажем, из 40 человек, и дать половине из них выпить стакан вина, а другая половина выпивает стакан пива, а затем дайте каждому из 40 человек тест на память и сравните результаты. Это подход с независимыми выборками.
Другой подход состоит в том, чтобы взять выборку из 20 человек и предложить каждому выпить по бокалу вина и пройти тест на память, а затем предложить тем же людям выпить стакан пива и снова пройти тест на память, после чего мы сравним результаты двух тестов. Этот подход используется с парными выборками.
Преимущества
Преимущество второго подхода заключается в том, что выборка может быть меньше. Кроме того, поскольку выборка для пива и вина одинакова, вероятность того, что какой-либо внешний фактор ( смешанная переменная ) повлияет на результат, меньше. Проблема с этим подходом заключается в том, что результаты второго теста памяти могут оказаться ниже просто потому, что человек выпил больше алкоголя. Это можно исправить, разделив тесты во времени, например. путем проведения пробы с пивом через сутки после пробы с вином.
Также возможно, что порядок, в котором люди проходят тесты, влияет на результат (например, испытуемые узнают что-то в первом тесте, что поможет им во втором тесте, или, возможно, прохождение теста во второй раз вызывает некоторую скуку, которая снижает оценку). Один из способов справиться с этими эффектами порядка состоит в том, чтобы половина людей пила вино в первый день и пиво во второй день, в то время как для другой половины порядок был обратным (так называемый уравновешивающий ).
В следующей таблице приведены преимущества тестирования парных образцов по сравнению с тестированием независимых образцов:
| Парные образцы | Независимые образцы |
| Нужно меньше участников | Меньше проблем с усталостью или тренировочными эффектами |
| Больше контроля над мешающими переменными | Участники с меньшей вероятностью поймут цель исследования |
Рисунок 1 – Сравнение независимых и парных выборок
Очевидно, что не во всех экспериментах можно использовать план парных выборок. Например. если вы тестируете различия между мужчинами и женщинами, то потребуются независимые выборки.
Как вы увидите из следующего примера, анализ парных образцов выполняется путем просмотра разницы между двумя измерениями. В результате в этом случае используются те же методы, что и для случая с одной выборкой, хотя обычно проще использовать либо инструмент анализа данных парного t-теста, либо функцию рабочего листа T.TEST с type = 1.
Проверка гипотез
Пример 1: Клиника предлагает программу, помогающую своим клиентам похудеть, и просит агентство по работе с потребителями изучить эффективность этой программы. Агентство берет выборку из 15 человек, взвешивая каждого человека в выборке до начала программы и через 3 месяца, чтобы составить таблицу на рис. 2. Определите, эффективна ли программа.
Рисунок 2 – Данные для парной выборки пример
Пусть x = снижение веса через 3 месяца после запуска программы. Нулевая гипотеза:
H 0 : μ = 0; т. е. любые различия в весе обусловлены случайностью (двусторонний критерий)
Используя столбец разностей D, мы можем сделать следующие вычисления:
s.e. = стандартное отклонение / = 6,33 / = 1,6343534
t обс = ( x̄ – μ) /s.e. = (10,93 – 0)/1,63 = 6,6896995
T CRIT = T.Inv.2T ( α, DF) = T.Inv.2T (.05, 14) = 2,1447867
с T OBS > T . нулевой гипотезы и сделать вывод с 95% уверенностью, что разница в весе до и после программы не является исключительно случайной.
В качестве альтернативы мы можем использовать T.TEST типа 1 для выполнения анализа следующим образом: α
и, таким образом, еще раз отвергаем нулевую гипотезу.
Как обычно, чтобы результаты были достоверными, мы должны убедиться, что выполняются предположения для t-критерия, а именно, что меры разности нормально распределены или, по крайней мере, достаточно симметричны. Из рисунка 3 мы видим, что дело обстоит именно так:
Рисунок 3 – Блок-диаграмма для разностных показателей (столбец D на рисунке 2)0276: Мы можем использовать t-тест Excel : инструмент анализа данных «Парные две выборки для средств ». Результат работы этого инструмента анализа данных показан на рис. 4.
Инструмент анализа данных Real Statistics : Мы также можем использовать T-тест и инструмент анализа данных непараметрических эквивалентов в пакете ресурсов Real Statistics, чтобы получить тот же результат.
Чтобы использовать этот инструмент, нажмите Ctrl-m и выберите Т-тесты и непараметрические эквиваленты в меню (или на вкладке Разное при использовании многостраничного интерфейса). Появится диалоговое окно (как на рисунке 3 двухвыборочного t-теста: неравные отклонения). Введите B3:C18 в поле Input Range 1 (или B3:B18 в Input Range 1 и C3:C18 в Input Range 2 ) и выберите Заголовки столбцов, включенные в данные , Парные выборки и варианты T Test . При нажатии кнопки OK отображается вывод, показанный на рис. 5.
Рисунок 5 – Анализ данных реальной статистики для парных выборок
Отсутствующие данные
данные. Такие ячейки будут игнорироваться при анализе.
Пример 2 : Повторить пример 1, используя данные в диапазоне B24:C396.
В этом примере отсутствуют данные для субъектов 5, 7 и 10. Анализ повторяется с удалением данных для этих людей. Обратите внимание, что некоторые формулы были изменены для учета недостающих данных. Например. когда нет пропущенных данных, ячейка h37 может содержать простую формулу =СРЗНАЧ(B25:B39), но поскольку отсутствуют данные, вместо нее используется следующая формула:
=СУММПРОИЗВ(ЧИСЛО(B25:B39)*ЧИСЛО(C25 :C39),B25:B39)/G27
Рисунок 6 – Парный t-критерий с отсутствующими данными
Внимание : Если у вас есть отсутствующие данные, вы можете изменить значения данных и даже заполнить отсутствующие данные числовыми значениями, и результирующий анализ будет правильным. Если, однако, входные данные не содержат отсутствующих данных, вы можете изменить любое из значений данных и по-прежнему получать достоверный анализ, но если вы измените числовое значение на нечисловое, тогда анализ будет неправильным, и вы необходимо повторно запустить инструмент анализа данных, чтобы получить правильные результаты.
Сравнение парных выборок с тестами независимых выборок
Предположим, мы проводим тот же анализ данных в Примере 1 из двухвыборочного t-критерия с равными дисперсиями, используя t-критерий с независимыми выборками, и сравниваем результаты с результатами, полученными для парные образцы:
Рисунок 6 – Анализ данных Excel для независимых образцов
Мы суммируем результаты двух анализов, как показано на рисунке 7.
Рисунок 7 – Сравнение парных и независимых выборочных t-тестов
Обратите внимание, что средние различия одинаковы, но стандартное отклонение для случая парной выборки ниже, что приводит к более высокому t-stat и более низкому p -ценить. В целом это правда.
Одновыборочный тест
Хотя Real Statistics предоставляет инструмент анализа данных для одновыборочных тестов, Excel не предоставляет стандартный инструмент анализа данных для этого случая. Функция T.TEST с введите = 1, а инструмент анализа данных парных выборок можно, однако, использовать для случая одной выборки, просто создав нулевую парную выборку со всеми нулевыми данными.
Пример 3 : Повторите пример 1 t-критерия одной выборки, используя указанное выше наблюдение.
На рис. 8 показано, как это сделать с помощью инструмента анализа данных парного t-критерия Excel.
Рисунок 8 – Использование анализа данных парной выборки для одного выборочного теста
Величина эффекта
Поскольку случай парных данных с двумя выборками эквивалентен случаю с одной выборкой, мы можем использовать те же подходы для расчета размера и мощности эффекта, что и в t-тесте одной выборки.