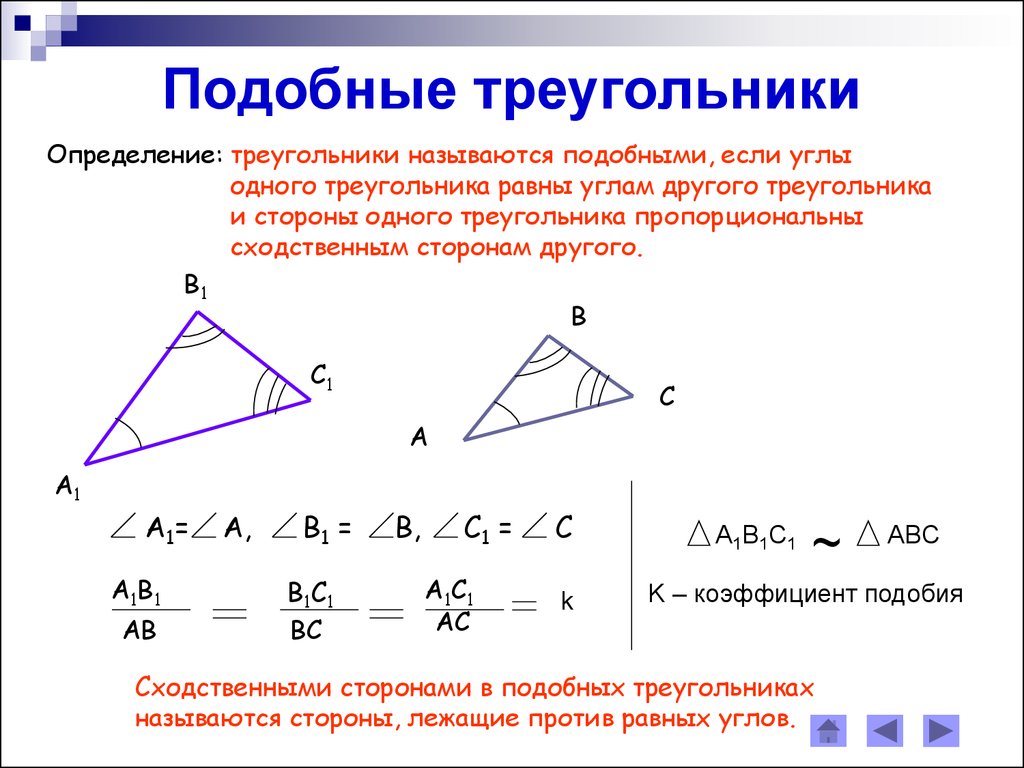
Что такое треугольник: определение, классификация, свойства
В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.
- Определение треугольника
- Классификация треугольников
- Свойства треугольника
- Примеры задач
Определение треугольника
Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.
- Точки A, B и C – вершины треугольника.
- Отрезки AB, BC и AC – стороны треугольника, которые часто обозначаются в виде одной латинской буквы. Например, AB = a, BC = b, AC = c.
- Внутренность треугольника – часть плоскости, ограниченная сторонами треугольника.
Стороны треугольника в вершинах образуют три угла, традиционно обозначающиеся греческими буквами – α, β, γ и т.д. Из-за этого треугольник еще называют многоугольником с тремя углами.
Углы можно, также, обозначать с помощью специального знака “∠“:
- α – ∠BAC или ∠CAB
- β – ∠ABC или ∠CBA
- γ – ∠ACB или ∠BCA
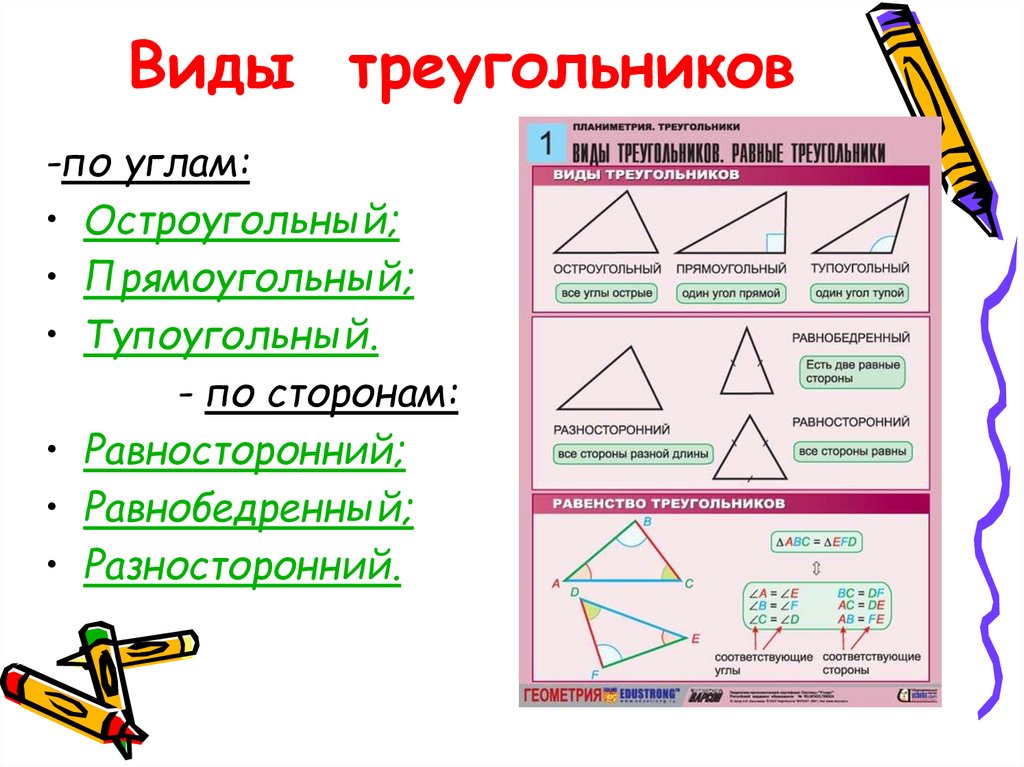
Классификация треугольников
В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:
1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.
2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°.
В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).
4. Разносторонний – треугольник, у которого все стороны имеют разную длину.
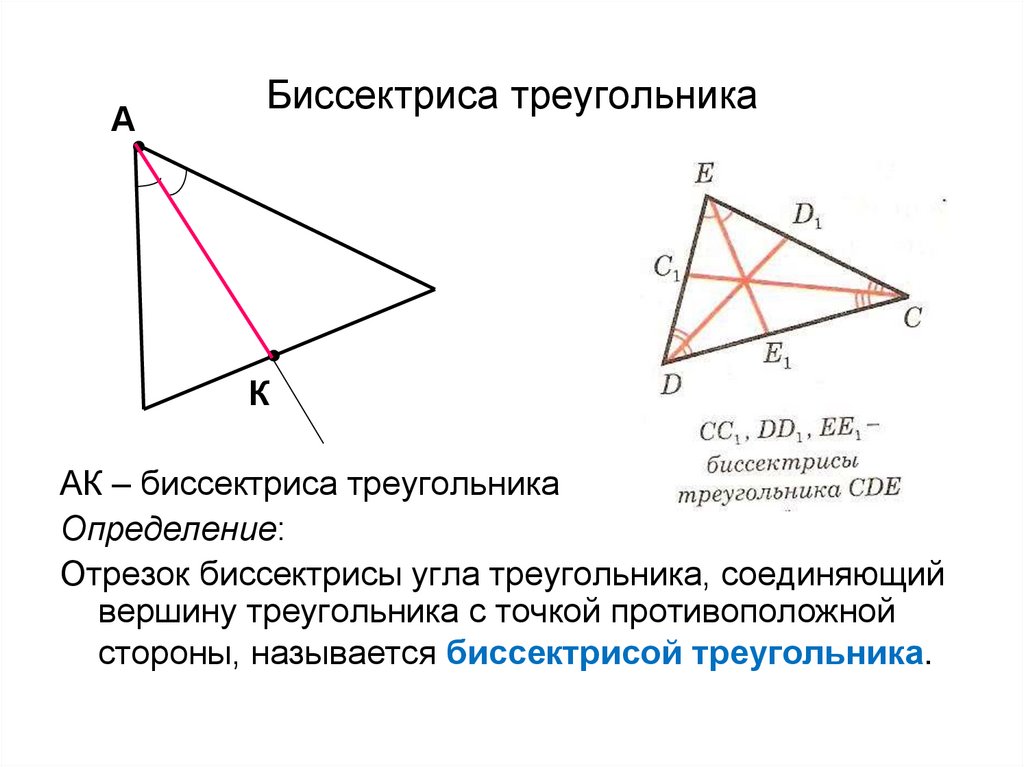
5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).
6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
Свойства треугольника
1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:
b – c < a < b + c, при b > с
Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.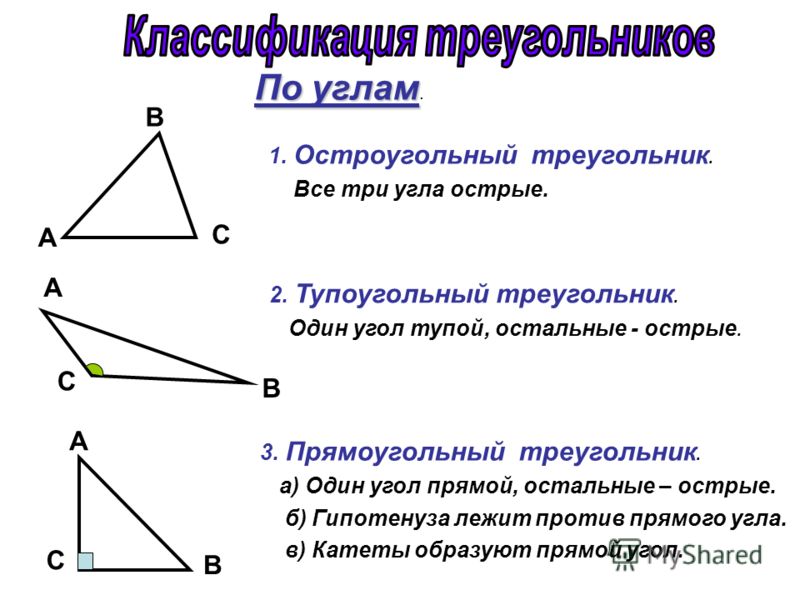
2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.
3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.
Примеры задач
Задание 1
В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.
Решение
Примем известные углы за α (32°) и β (56°), а неизвестный – за γ.
Согласно свойству о сумме всех углов, α + β + γ = 180°.
Следовательно, γ = 180° – α – β = 180° – 32° – 56° = 92°.
Задание 2
Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.
Решение
Составим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:
11 – 4 < 8 < 11 + 4
8 – 4 < 11 < 8 + 4
11 – 8 < 4 < 11 + 8
Все они верны, следовательно, данные отрезки могут быть сторонами треугольника.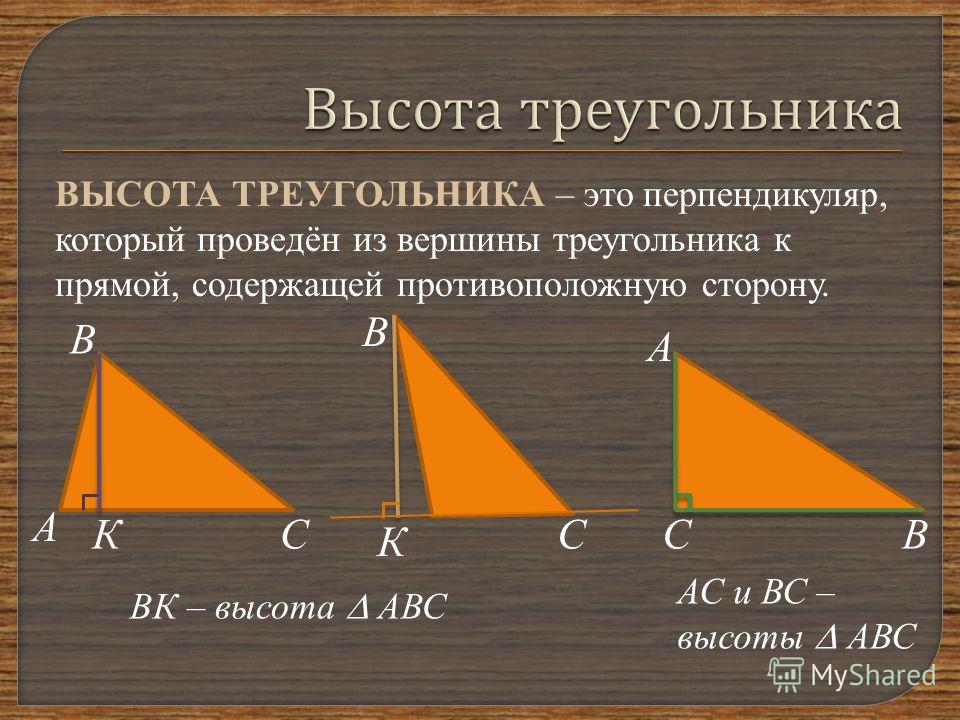
Что такое треугольник? Ответ на webmath.ru
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение треугольника
- Свойства сторон и углов треугольника
- Примеры решения задач
Определение треугольника
Определение
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, трех отрезков, которые последовательно соединяют эти точки и ограниченной ними части плоскости.
Точки $A$, $B$ и $C$ называются \lt strong>вершинами \lt /strong>, а отрезки $AB$, $BC$, $AC$ — сторонами треугольника.
Углы $\angle A B C, \angle B A C, \angle A C B$ — углы треугольника
$\triangle A B C$. Их можно обозначать также одной буквой: $\angle A, \angle B, \angle C$ или
$\alpha, \beta, \gamma$ — соответственно.
Стороны, которые лежат против углов $\angle A, \angle B, \angle C$ также обозначают $a, b, c$.
{\circ}$.
Подробнее в теореме о сумме углов треугольника.
Примеры решения задач
Пример
Задание. Проверить могут ли данные отрезки образовывать треугольник:
1) $a=3 ; b=4 ; c=2$
2) $a=3 ; b=4 ; c=7$
Решение. 1) Наибольшим из этих отрезков является отрезок $b=4$, сумма двух других $a+c=3+2=5$, получаем $b \lt a +c$. Значит, отрезки $a=3 ; b=4 ; c=2$ образуют треугольник.
2) Среди отрезков $a=3 ; b=4 ; c=7$, наибольшим является отрезок $c=7$. Сумма оставшихся $a+b=3+4=7$. Получаем $c=a+b$, поэтому отрезки $a=3 ; b=4 ; c=7$ не могут образовывать треугольник.
Ответ. Oтрезки $a=3 ; b=4 ; c=2$ образуют треугольник.
Отрезки $a=3 ; b=4 ; c=7$ не могут образовывать треугольник.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.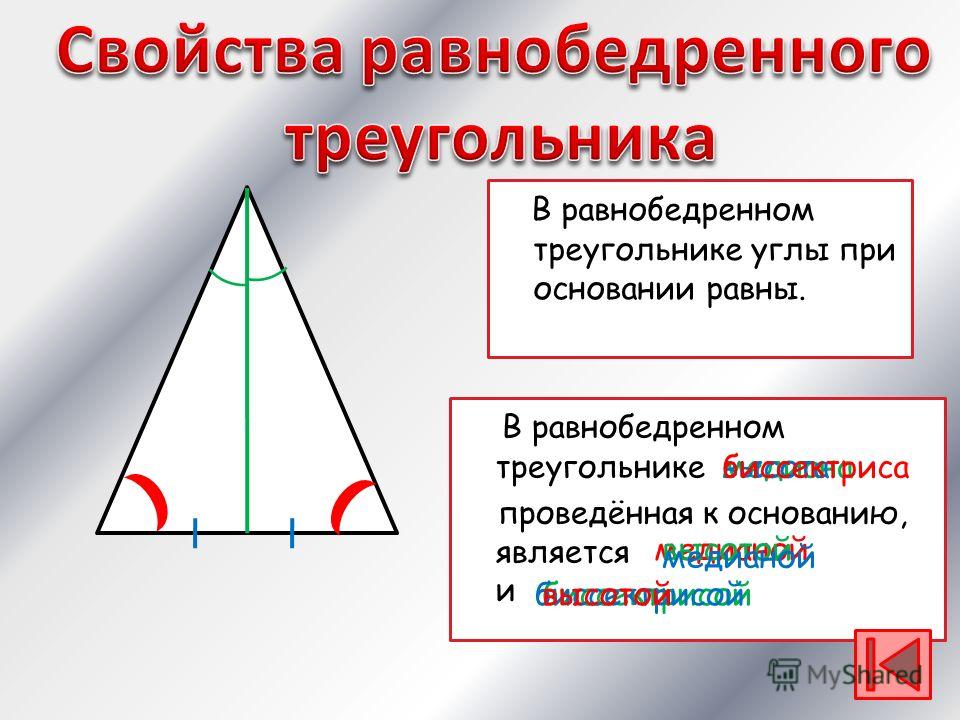
{\circ}$
Читать дальше: что такое внешний угол треугольника.
Определение и значение треугольника — Merriam-Webster
треугольник ˈtrī-ˌaŋ-gəl
1
: многоугольник с тремя сторонами
сравнить сферический треугольник
2
а
: ударный инструмент, состоящий из стального стержня, изогнутого в форме треугольника, открытого под одним углом и издаваемого ударами металлического стержня
б
: чертежный инструмент, состоящий из тонкого плоского прямоугольного треугольника из дерева или пластмассы с острыми углами 45° или 30° и 60°
3
: ситуация, в которой один из членов пары вовлечен в любовную связь с третьим лицом
Иллюстрация треугольника
- 1 равносторонний
- 2 острый
- 3 тупой
- 4 разносторонний
- 5 равнобедренный
- 6 прямоугольный треугольник
Примеры предложений
Она разрезала бутерброды на треугольника .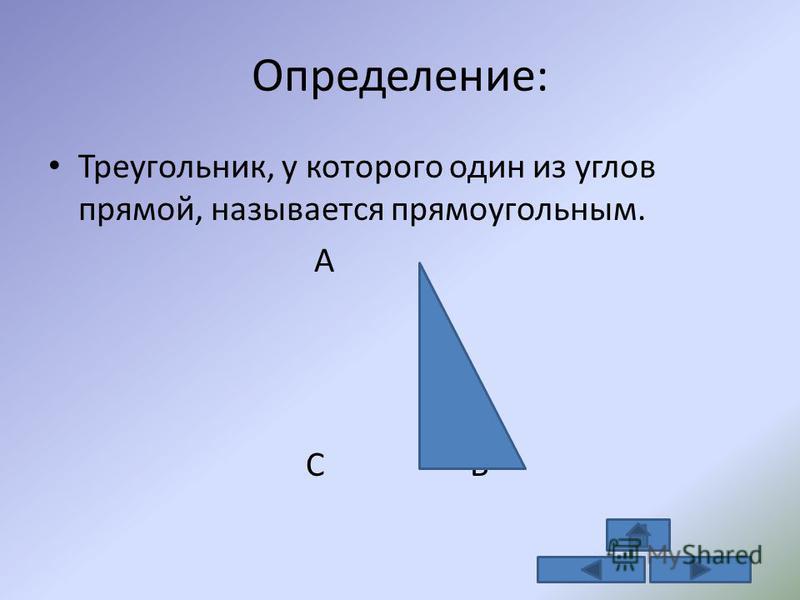
Недавние примеры в Интернете Некоторые современные дизайны в стиле ар-деко включают в себя отдельные элементы этого стиля, в том числе эта спальня, спроектированная Джошуа Грином, в которой есть 9Обои с принтом 0063 треугольник
в более нейтральной цветовой гамме. — Келли Аллен, Красивый дом , 7 декабря 2022 г. Картер объясняет, что ромбовидная полоса и линия треугольника на исиколо и воротнике (вверху) представляют южноафриканский народ ндебеле. — Фавния Су Ху, The Hollywood Reporter , 7 декабря 2022 г. Взяв свое название из вымышленной биографии Тейлора Дженкинса Рида, сериал рассказывает о группе в стиле Fleetwood Mac через ее взлет, падение и потрясающую столетие любовь 9.
0063 треугольник , который почти уничтожает всех на своем пути.
— Кт Джонс, Rolling Stone 
В 50-х Берджесс путешествует по своей любви треугольник , но затем, 40 лет спустя, напряженные отношения Тома и Марион становятся еще более сложными, поскольку Патрик возвращается к их жизни после перенесенного инсульта.
— Карсон Бертон, Variety , 15 июня 2022 г.
И ставки действительно высоки; одно из противоречивых изменений в сюжете включает в себя превращение младшей сестры Кейт в серьезную соперницу в их любовном треугольнике .
— Инейе Комонибо, 9 лет.0063 refinery29.com , 5 апреля 2022 г.
Узнать больше Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «треугольник».
История слов
Этимология
Среднеанглийский, от англо-французского, от латинского triangulum , от среднего рода triangulus треугольный, от tri- + angulus angle
Первое известное использование
14 век, в значении 14 век
Путешественник во времени
Первое известное использование треугольника было в 14 веке
Посмотреть другие слова того же века
Словарные статьи Рядом с
треугольниктреугольный
треугольник
треугольный краб
Посмотреть другие записи поблизости
Процитировать эту запись «Треугольник.
» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/triangle. По состоянию на 15 декабря 2022 г.Копировать цитирование
Детское определение
треугольник
существительное
треугольник ˈtrī-ˌaŋ-gəl
1
: фигура, имеющая три стороны и три угла : многоугольник, имеющий три стороны
2
: ударный инструмент, изготовленный из стального стержня, согнутого в треугольник, открытый одним углом
3
: чертежный инструмент, состоящий из тонкого плоского прямоугольного треугольника
Medical Definition
треугольник
существительное
треугольник ˈtrī-ˌaŋ-gəl
: трехсторонняя область или пространство и особенно анатомическое
см.
передний треугольник, каротидный треугольник, бедренный треугольник, задний треугольник, подзатылочный треугольник
More from Merriam-Webster on
triangleNglish: Translation of triangle for Spanish Speakers
Britannica English: Translation of triangle for Arabic Speakers
Britannica.com: Encyclopedia article about triangle
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
Определение треугольника
Определение треугольникаОпределение треугольника
Примеры треугольников Свойства треугольников Классификация треугольников Содержание Примеры треугольников Треугольник — это особая форма. Как вы думаете, что делает фигуру треугольником?
Обязательно подумайте над этим вопросом, прежде чем продолжить урок 9.0003
Свойства треугольников Прежде чем мы решим, что именно делает фигуру треугольником, нам нужно понять, что такое замкнутая фигура.
Фигура закрыта , если все ее стороны соединены.
Эти цифры закрыты. Эти фигуры не закрыты. Треугольник представляет собой замкнутую фигуру с тремя сторонами.
Используйте это определение, чтобы выяснить, какие из следующих фигур являются треугольниками, а какие нет.
Щелкните здесь, чтобы проверить свои ответы.
Можете ли вы вспомнить какие-нибудь треугольники, которые вы видите в своей повседневной жизни?
(Подсказка: посмотрите на мосты или радиомачты.)
Классификация треугольников Треугольники бывают разных видов.
В следующей таблице представлены некоторые основные типы треугольников.
Остроугольные треугольники — это треугольники, в которых все три угла меньше 90 градусов. Тупоугольные треугольники — это треугольники, в которых градусная мера одного угла больше 90 градусов. Прямоугольные треугольники — это треугольники, в которых градусная мера одного угла равна 90 градусам.
