Ортогональная проекция вектора: Как найти проекцию вектора на прямую?

Содержание

1.8. Ортогональная проекция вектора на ось

Определение 10. Проектирование называется ортогональным, Если плоскость П ортогональна оси.

При ортогональном проектировании достаточно из данной точки опустить на ось перпендикуляр.

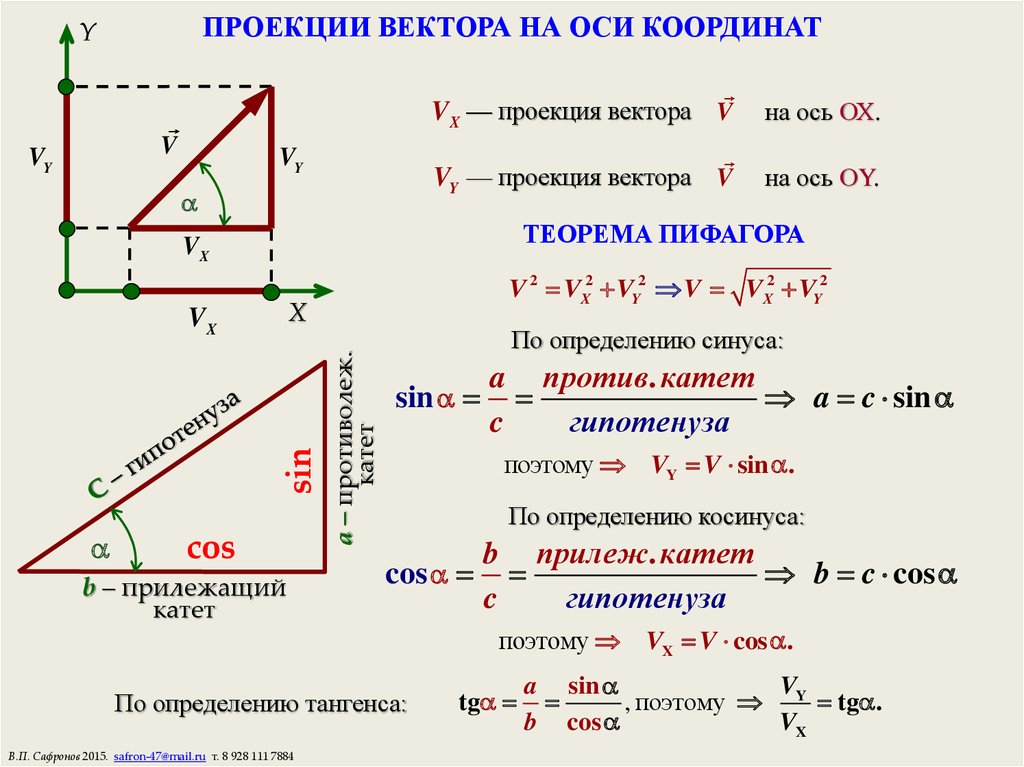
Теорема 7. Числовая ортогональная проекция вектора на ось равна произведению длины этого вектора на косинус его угла с осью.

Доказательство. Пусть l – ось,  её орт,  произвольный вектор. Если , топр_l = 0, поэтому можно считать, что утверждение теоремы верно. Пусть и = (l).

Возможны следующие случаи.

1)  = 0. В этом случае (рис. 17а) ипр=.

Рис. 17 а)

Рис. 17 б)

2) 0    90⁰. В этом случае (рис. 17б) ,пр.

Рис. 17 в)

Рис. 17 г)

Рис. 17 д)

3)  = 90⁰ (рис. 17в). В этом случае пр= 0 и, следовательно, пр= .

4) 90⁰    180⁰ (рис. 17г). В этом случае ,пр.

5)  = 180⁰ (рис. 17д). В этом случае пр=.

Итак, во всех случаях пр.

В разделе «Линейные пространства» в линейных пространствах над полем действительных чисел вводилась ещё одна операция: скалярное произведение векторов, с помощью которой линейное пространство превращалось в евклидово пространство.

Если в данном линейном пространстве по разному вводить скалярное произведение, то получатся различные евклидовы пространства. В векторном пространстве геометрических векторов существует «стандартное» (исторически сложившееся благодаря потребностям физики) определение скалярного произведения векторов.

Определение 11. Скалярным произведением упорядоченной пары ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из перемножаемых векторов нулевой, то скалярное произведение считается равным нулю.

Обозначение: (), или. Из определения

= (1)

Свойства скалярного произведения.

1⁰. Скалярное произведение любой упорядоченной пары векторов определено и однозначно.

2⁰. =для любых векторови(коммутативный закон).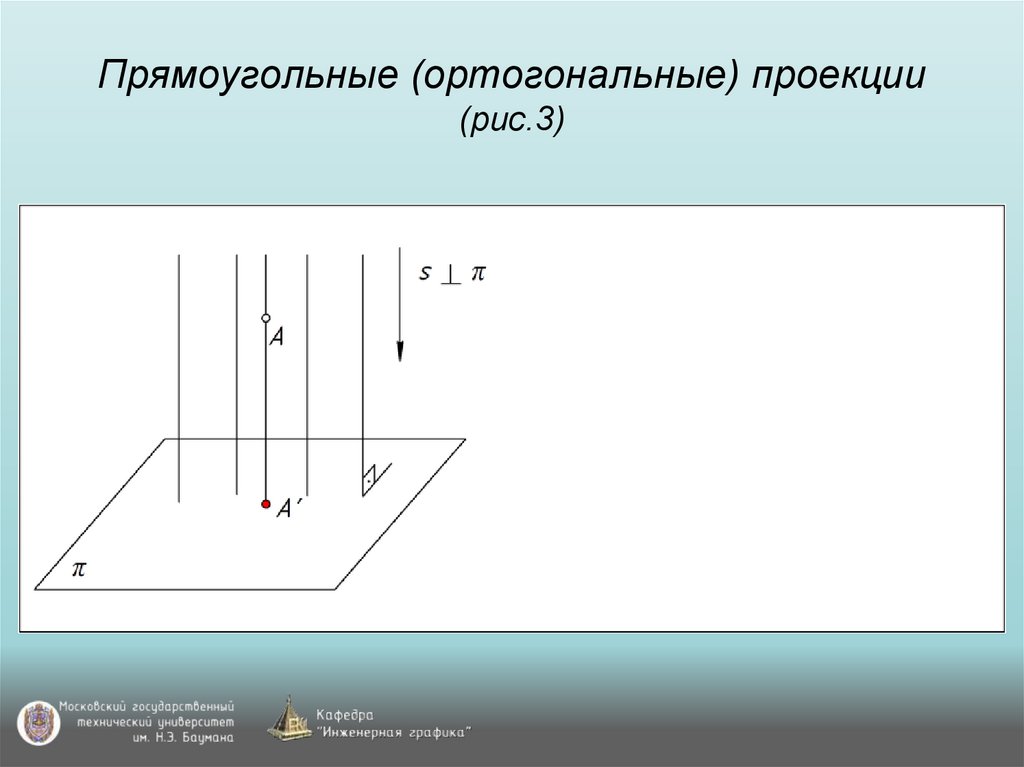

Доказательство. Если =или=, то= 0 и= 0, т.е. равенство верно.

Пусть  и . Тогда==.

3⁰. Если  и , то=пр. Если  , а=, то тоже=пр.Следовательно, при  имеет место формула= пр(2)

4⁰. = 0 либо =, либо=, либо .

5⁰. (+)=, для любых векторов,и.

Доказательство. Если вектор , то доказываемое равенство имеет вид 0 = 0 + 0, т.е. оно верно. Пусть. Тогда (по формуле 2)

(+)==.

6⁰. для любых векторов,и любого действительного числа.

Доказательство. Если либо  = 0, либо хотя бы один из векторов ,нулевой, то равенство очевидно. Пусть  0 и векторы ,нулевые. Тогда

Произведение называется скалярным квадратом вектораи обозначается

= .

7⁰. =для любого вектора. Отсюда следует

. (3)

Из формулы (7) следует, что  0 для любого вектора и= 0 .

Теорема 8. Множество всех геометрических векторов, любое множество всех компланарных векторов и любое множество всех коллинеарных векторов являются евклидовыми пространствами.

Доказательство следует из свойств 1⁰, 2⁰, 4⁰, 7⁰.

8⁰. Если  , то. (4)

Формула (4) следует из (2).

9⁰. Если  и , то

. (5)

Замечание. Формулы 4⁰, 7⁰– 10⁰ определяют применение скалярного произведения для решения задач.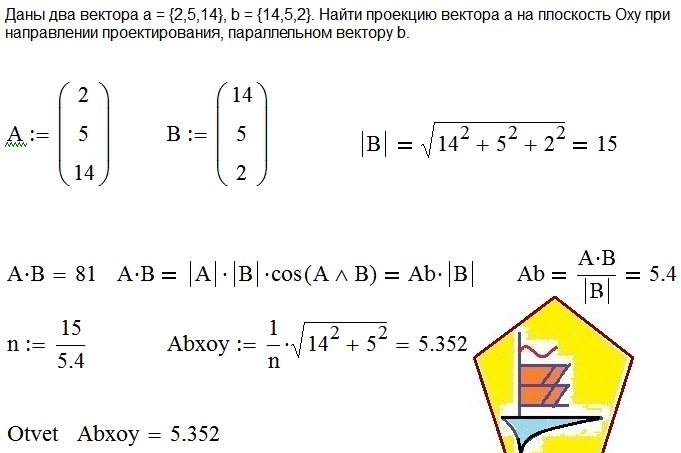

10⁰. (Скалярное произведение в координатах)

Пусть В =  базис, ,. Тогда

)=. (6)

Если базис В = ортонормированный, то

= . (7)

Из формулы (3) получаем, что в ортонормированном базисе

. (8)

Замечание. Формулы (6), (7) и (8) выведены в векторном пространстве всех геометрических векторов. Во множестве компланарных векторов, в базисе В = получим, а в ортонормированном базисе=и. Во множестве коллинеарных векторов, в базисеВ = получим=. Если= 1, то=и.

Задача 7. В параллелограмме АВСD угол DАВ = 60⁰, ,,

, AB = 6, AD = 4.

Найдите QNP (рис. 18).

Решение. Решим задачу векторным методом. Для этого выберем базис , где(),. УголQNP равен углу между векторами и. Используя формулу (5), получим

Cos(QNP) = . Найдём эти

Рис. 18

векторы: ,. Поэтому. Так как= 2² = 4, = 2² = 4, (= 22Cos60⁰ = 2, то =. Аналогично,,. Следовательно,

Cos(QNP) = .

Задача 8. Докажите, что в правильном тетраэдре а) противоположные рёбра взаимно перпендикулярны, б) отрезок, соединяющий середины противоположных рёбер, перпендикулярен к ним и найдите длину этого отрезка, если длина ребра равна а.

Решение. Решим задачу векторным методом. В качестве базиса выберем векторы ,,. Так как тетраэдр правильный, то достаточно рассмотреть одну пару противоположных рёбер и один из отрезков, соединяющих середины противоположных рёбер. Покажем, что,и. Для этого достаточно найти скалярные произведения,и. Выражая

Рис. 19

векторы через базис, получим ,,

. Следовательно,===ааCos60⁰  ааCos60⁰ = 0, т.е. .

= Отсюда. Аналогично доказывается, что.

По формуле (8) получаем, что

аналитическая-геометрия / Как найти ортогональную проекцию вектора? / Математика

Найти ортогональную проекцию вектора $%\overline{V} (2, 4, 4)$% на плоскость с базисом $%\overline{a} \ (1, 0, 1)$%, $%\overline{b} \ (1, 2, -1)$%.

аналитическая-геометрия

задан 9 Окт ’14 16:45

Bob1995
70●3●15
81% принятых

изменен 9 Окт ’14 18:18

Виталина
99●1●7

старыеновыеценные

Проекция $%w$% вектора $%v$% обладает следующими свойствами: 1) она принадлежит плоскости, то есть представляется в виде $%xa+yb$% с некоторыми коэффициентами; 2) разность векторов $%v-w$% ортогональна плоскости, то есть скалярное произведение этого вектора на оба базисных равно нулю. Отсюда получаем два уравнения: $%(w,a)=(v,a)$% и $%(w,b)=(v,b)$%, то есть $%x(a,a)+y(a,b)=(v,a)=6$% и $%x(a,b)+y(b,b)=(v,b)=6$%. Ясно, что $%(a,b)=0$%, что облегчает вычисления; $%(a,a)=2$%, $%(b,b)=6$%, откуда $%x=3$%, $%y=1$%. В итоге $%w=3a+b=(4;2;2)$%.

ссылка

отвечен 9 Окт ’14 18:15

falcao
284k●9●37●51

Ваш ответ

Если вы не нашли ответ, задайте вопрос.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

регистрация »

отмечен:

аналитическая-геометрия ×961

задан
9 Окт ’14 16:45

показан
6967 раз

обновлен
9 Окт ’14 22:04

Связанные исследования

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

Ортогональные проекции — Mathonline

Ортогональные проекции

Сгиб

Содержание

Ортогональные проекции

Рассмотрим вектор $\vec{u}$. Этот вектор можно представить в виде суммы двух векторов, перпендикулярных друг другу, то есть $\vec{u} = \vec{w_1} + \vec{w_2}$, где $\vec{w_1} \perp \ vec{w_2}$.

Сначала постройте вектор $\vec{b}$, начальная точка которого совпадает с $\vec{u}$:

Теперь мы построим $\vec{w_1}$, начальная точка которого также совпадает с $\vec{v}$ и $\vec{u}$. Этот вектор будет проходить вдоль $\vec{b}$.

Теперь мы опустим перпендикулярный вектор $\vec{w_2}$, начальная точка которого находится в конечной точке $\vec{w_1}$, а конечная точка — в конечной точке $\vec{u} $. Таким образом, мы получаем, что $\vec{u} = \vec{w_1} + \vec{w_2}$ и $\vec{w_1} \perp \vec{w_2}$, как мы и хотели.

Вектор $\vec{w_1}$ имеет специальное имя, которое мы формально определим следующим образом. 92} \vec{b}$.

Доказательство: Заметим, что $\vec{b}$ и $\vec{w_1}$ параллельны друг другу и, таким образом, для некоторого скаляра $k$ $\vec{w_1} = k\vec {б}$.

2} \end{align} 92} \vec{b} \\ \blacksquare \end{align}

Конечно, нам также нужна формула для вычисления нормы $\mathrm{proj}_{\vec{b}} \vec{u} $. Следующая теорема дает нам относительно удобную формулу.

Теорема 2: Если $\vec{u} = \vec{w_1} + \vec{w_2}$, $\vec{w_1} \| \vec{b}$ и $\vec{w_1} \perp \vec{w_2}$, затем $\| \mathrm{proj}_{\vec{b}} \vec{u} \| = \| \vec{и} \| \| \vec{b} \| \cos\тета$.

Доказательство: Доказательство формулы теоремы 2 довольно простое. Отметив, что $\vec{u} \cdot \vec{b} = \| \vec{и} \| \| \vec{b} \| \cos \theta$ у нас есть это: 92} \| \vec{b} \| \\\| \mathrm{proj}_{\vec{b}} \vec{u} \| = \frac{\mid \vec{u} \cdot \vec{b}\mid}{\| \vec{b} \|} \\ \| \mathrm{proj}_{\vec{b}} \vec{u} \| = \ гидроразрыв {\ середина \ | \vec{и} \| \| \vec{b} \| \cos\тета\mid}{\| \vec{b} \|} \\ \| \mathrm{proj}_{\vec{b}} \vec{u} \| = \ гидроразрыва {\ | \vec{и} \| \| \vec{b} \| \mid \cos \theta \mid}{\| \vec{b} \|} \\ \| \mathrm{proj}_{\vec{b}} \vec{u} \| = \ середина \ соз \ тета \ середина \ | \vec{и} \| \quad \blacksquare \end{align}
Если не указано иное, содержимое этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 3. 0 License
линейная алгебра — ортогональная проекция одного вектора на другой
спросил 4 года 3 месяца назад
Изменено 4 года, 3 месяца назад
Просмотрено 13 тысяч раз
$\begingroup$
Я пытаюсь понять проекцию вектора $\operatorname{proj}_{b} (a)$ $a$ на вектор $b$. 9{2}} \cdot b$
Насколько я понимаю, скалярное произведение $a$ и $b$ равно величине проекции $a$ на $b$, умноженной на величину $b$ (и наоборот), поэтому
$a \cdot b = \operatorname{proj}_{b} (a) \cdot ||b||_{2}$
почему нельзя просто разделить на $ ||b||_{2}$, чтобы получить проекцию?
$\operatorname{proj}_{b} (a) = \frac{a \cdot b}{||b||_{2}}$
- линейная алгебра
- проекция
$\endgroup$
1
$\begingroup$
Неформально мне нравится думать о скалярном произведении как о проекции. Итак, $a\cdot b$ сообщает нам кое-что о том, как $a$ проецируется на $b$. Однако мы хотим, чтобы скалярное произведение было симметричным, поэтому мы не можем просто определить $a\cdot b$ как длину проекции $a$ на $b$. Мы фиксируем это, также умножая на длину проецируемого вектора.
Используя простой триггер, обратите внимание, что проекция $a$ на $b$ равна $|a|\cos\theta$, где $\theta$ — угол между ними. Чтобы сделать скалярное произведение, мы определяем $a\cdot b$ как проекцию $a$ на $b$, умноженную на длину $b$. То есть $$a\cdot b=|a||b|\cos \theta$$ и это явно симметрично. Теперь, поскольку $|a|\cos\theta$ — это длина проекции $a$ на $b$, если мы хотим найти фактический вектор, мы умножаем эту длину на a 92}. \end{align}
Я действительно думаю об этом так:
$$\text{Проекция $a$ на $b$}=\color{blue}{\underbrace{{\frac{a\cdot b}{|b|}}}_{\text{скалярная проекция}}}\qquad\text{times}\color{red}{\qquad \underbrace{\frac{b}{|b|}}_{ \text{единичный вектор}}}$$
$\endgroup$
$\begingroup$
Проблема с вашими рассуждениями заключается в том, что предложенная вами формула дает скаляр, а не вектор.
No related posts.