Четные цифры списком
4.6
Средняя оценка: 4.6
Всего получено оценок: 537.
4.6
Средняя оценка: 4.6
Всего получено оценок: 537.
Четные числа – достаточно интересная и простая тема в курсе математики. Многие ученики не задумываясь, пользуются основными свойствами четных чисел, что иногда вызывает ошибки. Чтобы разобраться в вопросе раз и навсегда – разберем тему четных чисел во всех подробностях.
Что такое четное число?
Четным числом называют любое целое число, которое делиться на два нацело. Для того, чтобы лучше понять, какие числа относятся к четным, вспомним классификацию чисел по множествам.
Ноль в натуральные числа не входит, а потому первое множество чисел, где встречается ноль – целые числа.
Формула четного числа
Существует формула четного числа, она выглядит так:
k=2m – где k – четное число, m – любое целое число. Если любое целое число подставить в формулу, то результатом будет всегда четное значение.
Можно обратить внимание на число 2 в формуле, именно это значение делает любой конечный результат формулы четным. Так же есть формула нечетного числа: k=2m+1.
Сколько всего четных чисел?
Полного списка четных чисел нет и никогда не будет. Как мы помним, чисел – бесконечное множество. Это значит, что четных чисел так же бесконечно много. Но часто у учеников возникает вопрос: сколько существует четных цифр. Список четных цифр привести можно: 0,2,4,6,8 – всего пять значений.
Четные числа на числовой прямой
Еще один интересный вопрос в изучении темы, это четные числа на числовой прямой. Интересно посмотреть, являются ли отрицательные числа и ноль – четными. Ответ прост – да, являются. Исходя из определения, мы знаем, что четным числом может быть только целое значение. Попробуем подставить в формулу четных чисел 0:
k=2*0=0
Значение нуля сохранилось, а значит ноль – число четное.
Теперь подставим в формулу целое отрицательное число:
k=2*(-5)=-10 – получилось отрицательное число, то есть отрицательные числа так же могут быть четными.
Что мы узнали?
Мы поговорили о четных числах. Разобрались, сколько четных чисел существует в математике. Привели формулу четного числа.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Алина Шабунина
5/5
Майрам Мажидова
4/5
Новиков Елисей
5/5
Лира Нургалиева
5/5
Алексей Кабанов
5/5
Захар Никулин
5/5
Лизочка Толстых
4/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 537.
А какая ваша оценка?
Какое число считается четным?
Какое число считается четным?
— характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится на два, оно называется чётным (примеры: 2, 28, —8, 40), если нет — нечётным (примеры: 1,3, 75, —19). Ноль считается чётным числом. Чётное число — целое число, которое делится на 2 без остатка: …
Если целое число делится на два, оно называется чётным (примеры: 2, 28, —8, 40), если нет — нечётным (примеры: 1,3, 75, —19). Ноль считается чётным числом. Чётное число — целое число, которое делится на 2 без остатка: …
Какие нечетные числа?
Чётные и нечётные числа в числовом ряду чередуются. К чётным числам относятся 2, 4, 6, 8, 10, так как они делятся на 2. К нечётным числам относятся 1, 3, 5, 7, 9, так как они не делятся на 2.
Как объяснить ребенку что такое четные и нечетные числа?
Поделитесь секретом: определять, четное число или нечетное, нужно по последней цифре. Следовательно числа, оканчивающиеся на 0, 2, 4, 6, 8 — четные, а на 1, 3, 5, 7, 9 — нечетные.
Как получить нечетное число?
Проверка чисел на четность выполняется путем определения остатка от деления числа на 2. Если остаток равен нулю, значит, число четное. Если нет, то нечетное.
Почему 0 четное число?
Число называют чётным, если это число кратно 2. Например, причиной того, что число 10 является чётным, является то, что оно равно 5 × 2. В то же время, ноль также является целым кратным 2, то есть 0 × 2, следовательно, ноль является чётным.
Можно ли разменять 25 лир десятью монетами в 1 3 и 5 лир?
Можно ли разменять 25 лир десятью монетами в 1, 3 и 5 лир? Решение. Нет, так как сумма чётного количества (в данном случае 10) нечётных слагаемых будет чётным число. … Если бы такие числа существовали, то для того, чтобы их произведение было нечётным, нужно, чтобы они оба были нечётными.
Как понять натуральные числа?
Натуральные числа принято обозначать символом N.
Как это целые числа?
Целые числа — это множество чисел, которые состоят из натуральных чисел, целых отрицательных чисел и нуля. Отрицательные целые числа — это целые числа со знаком «минус».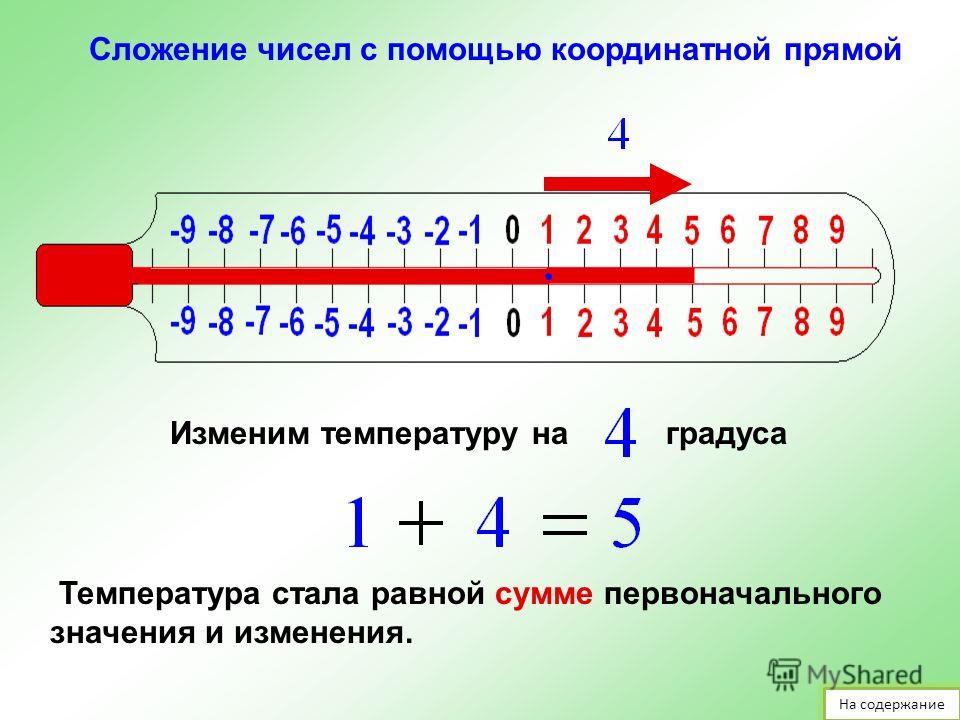 … Примеры целых отрицательных чисел: -944, -1287, -1, -19. Положительные целые числа — это целые числа со знаком «плюс».
… Примеры целых отрицательных чисел: -944, -1287, -1, -19. Положительные целые числа — это целые числа со знаком «плюс».
Что такое положительные рациональные числа?
Положительным рациональным числом называется класс дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа. Например, о дроби Положительные рациональные числа мы должны говорить, что она является записью некоторого рационального числа.
Как определить рациональное и иррациональное число?
Любое рациональное число представимо в виде периодической бесконечной десятичной дроби. Множество рациональных чисел обозначается Q. Если действительное число не является рациональным, то оно иррациональное число. Десятичные дроби, выражающие иррациональные числа бесконечны и не периодичны.
Для чего нужны рациональные числа?
А для того, чтобы записывать часть целого (например, возвращение долга частями), стали использовать дроби. Именно поэтому математикам необходимо было как-то объединить такие характерные числа, дать им общее название. Так появились рациональные числа (от латинского ratio – «отношение»).
Именно поэтому математикам необходимо было как-то объединить такие характерные числа, дать им общее название. Так появились рациональные числа (от латинского ratio – «отношение»).
Как узнать какое число является рациональным?
Чтобы вычислить сумму рациональных чисел , нужно отдельно сложить все положительные числа (заключив в скобки и поставив перед скобкой знак «+») и отдельно сложить все отрицательные числа (заключив в скобки и поставив перед скобкой знак «-»).
Какие числа являются иррациональными примеры?
Самыми известными примерами иррациональных чисел в такой записи являются арифметический квадратный корень из двух , число «пи» π=3,141592…, число e=2,718281… и золотое число . Иррациональные числа также можно определить через действительные числа, которые объединяют рациональные и иррациональные числа.
Какие числа называются целыми числами?
Целыми числами называются все натуральные числа, все числа противоположные им по знаку и нуль. … На множестве целых чисел можно ввести четыре арифметические операции: сложение, вычитание, умножение и деление.
… На множестве целых чисел можно ввести четыре арифметические операции: сложение, вычитание, умножение и деление.
Какие числа называют дробными?
Понятие дроби. … Дробью или обыкновенной дробью называется число, состоящее из одной или нескольких равных частей (долей) единицы.
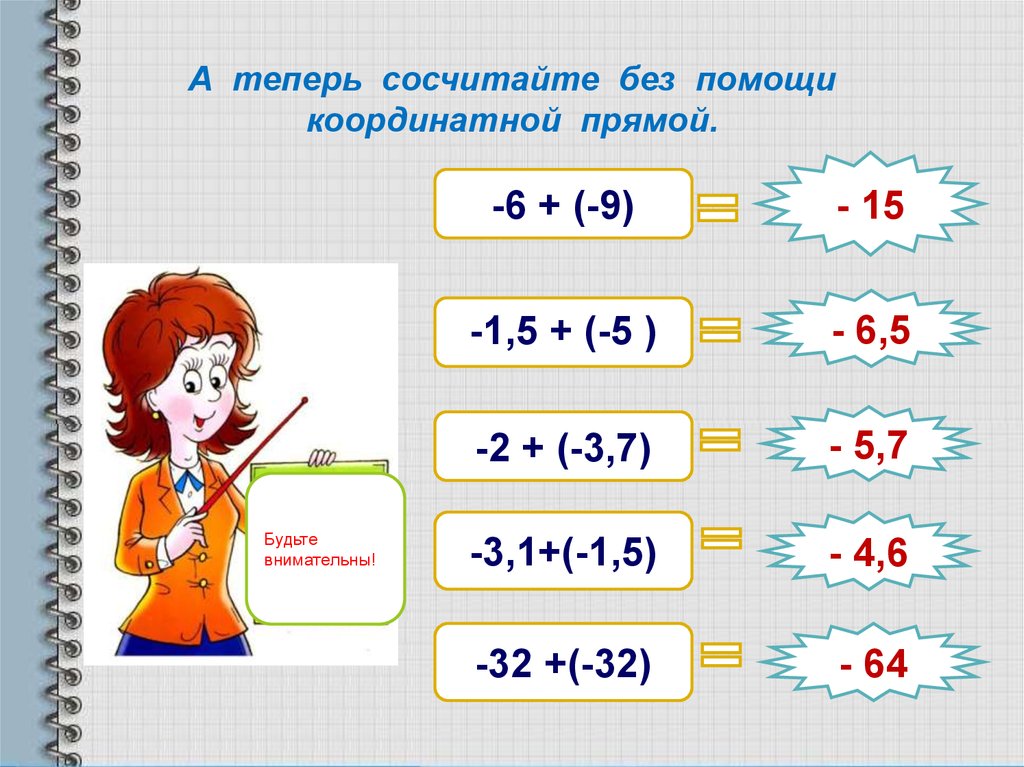
Как складывать числа с разными знаками?
Вспомним, как складывают два числа с разными знаками. Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.
Что значит целое решение?
Целое решение неравенства — это целое число, входящее в область решений неравенства. В этот интервал входят, например, целые числа -6; 0; 1; 5; 7 и т. д. Эти числа и будут называться целыми решениями неравенства.
Программа для проверки числа на положительное, отрицательное, нечетное, четное, ноль
Просмотреть обсуждение
Улучшить статью
Сохранить статью
- Уровень сложности: Базовый
- Последнее обновление: 09 сент, 2022
Посмотреть обсуждение
Улучшить статью
Сохранить статью
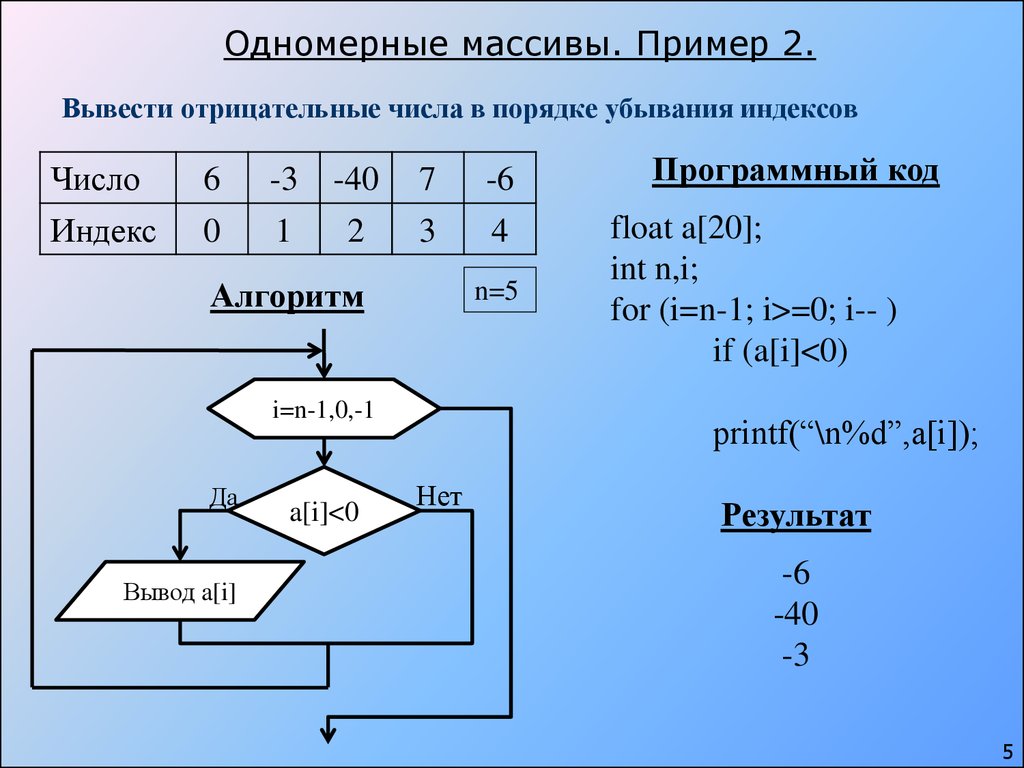
Предварительное условие: Циклы в Python Чтобы проверить, является ли число положительным, отрицательным, нечетным, четным или нулем. Эта проблема решается с помощью if…elif…else и вложенного оператора if…else.
Эта проблема решается с помощью if…elif…else и вложенного оператора if…else.
Подход:
- Число считается положительным, если оно больше нуля. Проверяем это в выражении if.
- Если False, число будет либо нулем, либо отрицательным.
- Это также проверяется в последующем выражении.
- В случае нечетного и четного числа Число является четным, если оно полностью делится на 2.
-
- Когда число делится на 2, мы используем оператор остатка % для вычисления остатка.
- Если остаток не равен нулю, число нечетное.
Примеры:
Ввод: 10 Выход : Положительное число 10 — четное
Ввод: 0 Вывод: 0 равно четному
Рекомендуется: сначала попробуйте свой подход на {IDE} , прежде чем переходить к решению.
Python
:
|
print ( "Positive number" )
|
8 Вывод: Положительное число
20 is Even Python3
num = - 10
x = str (num)
if x.startswith( "-" ):
print ( "Negative number" )
elif x = = "0" :
print ( "Zero" ) else :
print ( "Positive number" )
if (num % 2 ) = = 0 :
print ( "{0} is Even" .
format (num))
else :
print ( "{0} is Odd" . format (num))
Выход
Отрицательное число
-10 равно четному
Временная сложность: O(1), так как выполняются постоянные операции
Вспомогательное пространство: O(1), поскольку используется постоянное пространство для переменных
Давайте изучим четные и нечетные числа
В математике четные числа — это целые числа, которые делятся на 2, то есть при делении целого числа на два не остается остатка. С другой стороны, нечетные числа являются целыми числами, при делении на 2 в остатке будет 1. Нечетные числа всегда находятся между четными числами и наоборот. Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным.
Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным.
Важность изучения четных и нечетных чисел
Определение четных и нечетных чисел является важным математическим навыком, которым должны овладеть учащиеся. Расширенная программа обучения математике будет предоставляться учителями в классах, где учащиеся изучают эту концепцию, а не просто относиться к этому уроку как к «нестандартному». Студенты упускают важные знания, которые имеют решающее значение для овладения математическими понятиями на более высоком уровне. Учителя должны изучить более глубокие подходы к четным и нечетным числам, т. е. четность отрицательных целых чисел.
Учащиеся больше оценят урок, если они усвоят его через конкретное исследование. В зависимости от того, в каком классе он изучается, этот урок можно проводить с творческими идеями. Например, вместо того, чтобы учить первоклассников четным и нечетным числам путем деления, более уместно и более творчески говорить, что число четное, если все его можно соединить без остатка, в противном случае оно будет нечетным. Учителя также могут использовать наглядные материалы для представления этого определения.
Учителя также могут использовать наглядные материалы для представления этого определения.
Четные и нечетные числа также можно изучать в старших классах, и они могут иметь такой же уровень важности. В этом блоге Learn ZOE будут рассмотрены такие понятия, как четность и краткое определение четных и нечетных чисел.
Что такое четность? Свойство того, является ли целое число четным или нечетным, называется четностью. Любые два последовательных целых числа имеют противоположную четность. Например, 15 нечетно, а 16 четно. Четные числа можно формально определить как целые числа вида n=2k, где k — целое число. Отсюда следует, что нечетные числа — это целые числа вида n=2k+1 или n=2k-1. Обратите внимание, что эти определения четности применимы только к целым числам. Рациональные числа, такие как 25 и -5,369, и иррациональные числа, такие как π и 5, не имеют четности. Эти краткие определения представляют собой формулы для создания четных и нечетных чисел, а также для доказательства четности целых чисел.
Пример 1. Укажите, является ли число 18 596 четным или нечетным.
Четность 18 596 можно определить, разделив на 2.
Поскольку остатка нет, четность 18 596 четна. Мы также можем использовать правило делимости на 2, чтобы определить четность числа. 18 596 оканчивается на 6, поэтому оно делится на 2 и, следовательно, является четным числом.
Пример 2: Определить четность 458 963.
Разделить 458 963 на 2.
458 963 нечетно, так как мы получили остаток от 1. Число также заканчивается на 3, нечетное число, поэтому наше решение должно быть правильным.
Четность целых чисел также включает следующие свойства.
- четный четный = четный
- четный нечетный = нечетный
- нечетный нечетный = четный
- четный × четный = четный
- четный × нечетный = четный
- нечетный × нечетный = нечетный 17+863 даст четную или нечетную сумму.

Поскольку 17 нечетно, 863 четно, а сумма четного и нечетного числа четна, мы можем заключить, что их сумма нечетна. Проверьте, найдя сумму двух чисел.
880 заканчивается нулем, четным числом, поэтому сумма действительно четная.
Пример 4: Определить четность произведения 27 и 15.
27 и 15 нечетные. Следовательно, их произведение также должно быть нечетным. Проверьте, найдя произведение двух чисел.
405 заканчивается четным числом. Поэтому продукт действительно странный.
Четность отрицательных целых чисел Многие, вероятно, скажут, что отрицательные целые числа нельзя классифицировать как четные или нечетные. Но оказывается, мы действительно можем! Четность отрицательных целых чисел кажется озадачивающей, но это довольно простая концепция, которую должны знать учащиеся. Чтобы понять концепцию четных и нечетных отрицательных целых чисел, мы должны начать с обобщения отношения чисел в делении.
Любой делитель n равен сумме произведения делителя d на частное q и остатка r.
n=dq+r,
, где 0r
Это обобщение можно перевести на определение четных и нечетных чисел. Поскольку мы определяем четность целых чисел делением на 2, d=2. Значение r может быть либо 0, либо только 1.
n=2q+1 или n=2q.
Мы можем использовать эти два определения для проверки четности любого отрицательного целого числа.
Пример 5. Докажите, что четность -37 нечетна.
Пусть n= -37. Мы будем использовать n=2q+1, чтобы доказать его нечетную четность. Мы покажем, что q существует
-37=2q+1
q=-19
Поскольку мы можем показать, что существует целое число q такое, что -37=2q+1, мы видим, что -37 нечетно. .
Образцы текстовых задач
Вот несколько примеров текстовых задач, которые можно использовать для улучшения навыков определения четных и нечетных чисел.
- x и y — целые числа, такие что x четно, а y нечетно. Какова четность xy?
Мы знаем, что четное нечетное = четное. Следовательно, xy должно быть четным.
- Какова четность произведения простых чисел на отрезке (2,1001]?
Поскольку на отрезке есть четные числа, мы можем сказать, что произведение простых чисел на отрезке интервал также должен быть четным
- Если a нечетно, а b четно, что из следующего должно быть верно относительно (a2+b)3+ab? Выберите все подходящие варианты.
- Четность (a2+b)3+ab четна.
- абис четный.
- Четность (a2+b)3+abadd.
- (a2+b)3четно.
Упрощая выражение, используя свойства четных и нечетных чисел, получаем:
[(нечетное)2+четное]3+(нечетное)(четное)
=[нечетное+четное]+четное 0 900
=нечетный+четный
= нечетный
Следовательно, варианты B и C верны.
- Если x — целое число, какое из следующих чисел всегда нечетное?
- 2x+8
- 3x-5
- 10×2-6
- 34x+17
Вариант A можно переписать как 2(x+4). Умножение на любое четное число всегда дает четное произведение.
Вариант B четный, если x нечетный.
Выбор можно переписать как 2(5×2-3). Умножение на любое четное число всегда дает четное произведение.
Вариант D можно переписать как 17(2x+1). (2x+1) — это определение нечетного числа, а 17 — нечетное. Произведение двух нечетных чисел всегда нечетно. Следовательно, правильный ответ — вариант D.
- Докажите: если x — нечетное целое число, то 15x+5 — четное.
Любое нечетное целое число x может быть записано как 2n+1, где n — целое число. Следовательно,
15x+2=15(2n+1)+2
=30n+15+5
=30n+20
Обратите внимание, что 30n+20 можно переписать в 2(15n+10), где 15n+10 — элемент множества целых чисел.




 Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным.
Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным. 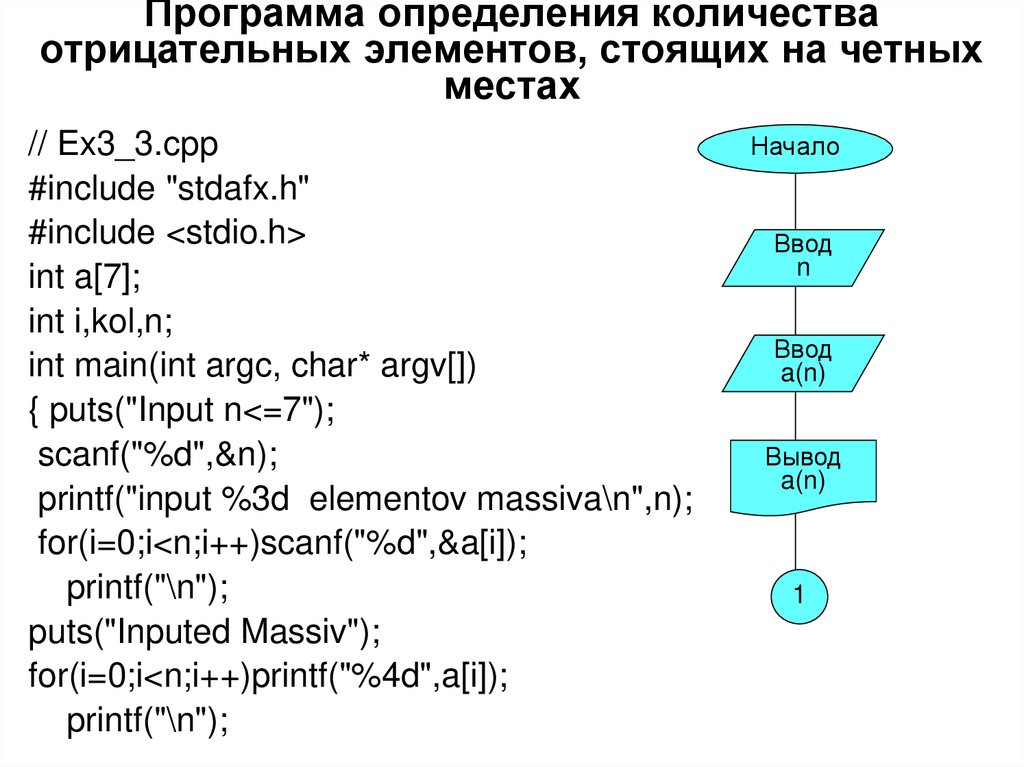 Учителя также могут использовать наглядные материалы для представления этого определения.
Учителя также могут использовать наглядные материалы для представления этого определения.