Перестановки без повторений: Перестановка без повторений | matematicus.ru

определение понятия, примеры из комбинаторики

1. Выборки
2. Перестановка без повторений
3. Перестановка с повторениями
4. Примеры

п.1. Выборки

Рассмотрим некоторое непустое конечное множество A мощностью |A| = n (т.е. состоящее из n элементов). Из этого множества всегда можно выбрать k элементов.

Выборка (кортеж) – набор из k элементов из некоторого множества n элементов. Назовём её 〈n,k〉  – выборка.

Важной характеристикой выборки является её упорядоченность.

Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки с одинаковым набором элементов, но разными порядками следования, являются различными.
Если порядок следования не задан (не важен), выборка называется неупорядоченной.

Второй важной характеристикой выборки является повторение элементов.

Если элементы в выборке не повторяются, она называется выборкой без повторений.
В отличие от множества, элементы в выборке могут повторяться; в этом случае она называется выборкой с повторениями. При этом может оказаться, что k > n – количество элекментов выборки больше мощности исходного множества.

Например:
Пусть задано множество A={a,b,c,d,e,f,g}. Его мощность |A|=7.
(a,c,d) – это 〈7,3〉– выборка без повторений
Если мы работаем с неупорядоченными выборками, то
(a,c,d) = (c,d,a) = (d,a,c) = …
Если мы определяем наши выборки как упорядоченные, то
(a,c,d) ≠ (c,d,a) ≠ (d,a,c) ≠ …
(a,a,a,g,c,d,e,e,g) – это 〈7,9〉– выборка с повторениями. Она также может быть упорядоченной или неупорядоченной, в зависимости от задачи.

п.2. Перестановка без повторений

Перестановка без повторений – это упорядоченная 〈n,n〉– выборка без повторений.
Общее количество перестановок без повторений:

$P_n=n!$

Лексикографический порядок – способ упорядочения перестановок, основанный на сравнении. Меньшей считается та перестановка, у которой на первом месте стоит меньший элемент. Если оба первых элементов равны, сравниваются вторые элементы; и т.д. Отношение лексикографического «меньше» обозначается ≺
Читается «меньше» или «предшествует».

Например:
1) Пусть задано множество A={a,b}, n=2
Его перестановки без повторений: (a,b) и (b,a) – итого два варианта (2!=2)
2) Для A={a,b,c}, n=3
Все перестановки без повторений:
(a,b,c),(b,c,a),(c,a,b),(b,a,c),(a,c,b),(c,b,a) – итого шесть вариантов (3!=6)
В лексикографическом порядке:

(a,b,c)≺(a,c,b)≺(b,a,c)≺(b,c,a)≺(c,a,b)≺(c,b,a)

п.3. Перестановка с повторениями

Перестановка с повторениями – это упорядоченная〈n,k〉 – выборка с повторениями, в которой элемент a₁ повторяется k₁ раз, элемент a₂ повторяется k₂ раз, и так далее, до последнего элемента a_s, который повторяется k_s раз (s ≤ n). При этом
k = k₁ + k₂ + … + k_s.
Общее количество перестановок с повторениями: $$ \mathrm{ P_k(k_1,k_2,…,k_s)=\frac{k!}{k_1!k_2!…k_s!} } $$

Например:
Сколько различных 6-тибуквенных слов можно написать из 3 букв {a,b,c}, если буква a должна повторяться 3 раза, буква b – 2 раза, буква c – 1 раз.
Пример такого слова: (a,b,a,a,b,c) – это 〈3,6〉 – выборка с повторениями.
По условию k₁=3, k₂=2, k₃=1, k=3+2+1=6 $$ \mathrm{ P_6(3,2,1)=\frac{6!}{3!\ 2!\ 1!}=\frac{720}{6\cdot 2\cdot 1}=60 } $$ Всего – 60 слов.

п.4. Примеры

Пример 1. Сколько 4-значных чисел можно составить из 4-х карточек с цифрами 0,1,3,5?
У нас только 4 карточки – значит, исследуем перестановки без повторений для 〈4,4〉-выборки. Таких перестановок P₄ = 4! = 24.
Кроме того, нужно учесть, что число не может начинаться с 0. Отложим карточку «0» в сторону, и посчитаем, сколько перестановок без повторений у выборки (1,3,5), т. е. у 〈3,3〉- выборки: P₃ = 3! = 6.
Получаем искомое число вариантов: N = P₄ – P₃ = 24 – 6 = 18
Ответ: 18.

Пример 2. У Маши четыре вазы. Сколькими способами Маша может расставить их по углам комнаты, если вазы разноцветные: белая, голубая, розовая и красная? Сколько способов останется, если все вазы — совершенно одинаковые?

1) Для разноцветных ваз рассматриваем 〈4,4〉-выборку вида (a,b,c,d). Количество перестановок без повторений P₄ = 4! = 24.
2) Для одинаковых ваз рассматриваем 〈4,4〉-выборку вида (a,a,a,a). В выборке один элемент, который повторяется 4 раза. Количество перестановок с повторениями: \(\mathrm{P_4(4)=\frac{4!}{4!}}\). Для одинаковых ваз есть только 1 вариант.
Ответ: 24; 1.

Пример 3. Сколькими способами можно разместить на полке 7 книг? Если среди книг – один трёхтомник, тома которого нужно ставить рядом (в любом порядке), сколько способов размещения останется?
1) Для 7 книг рассматриваем 〈7,7〉-выборку. Количество перестановок без повторений P₇ = 7! = 5040.
2) Для трёхтомника рассматриваем 〈3,3〉-выборку. Расставить 3 тома можно P₃ = 3! = 6 способами. Теперь рассматриваем трёхтомник как одно целое: получатся, что нужно расставить 5 книг, т.е. посчитать перестановки без повторений для 〈5,5〉-выборки: P

5 = 5! = 120 вариантов. Общее количество расстановок ищем по правилу произведения: N = P₃ · P₅ = 720.
Ответ: 5040; 720.

Пример 4. Сколько различных слов можно составить, переставляя буквы слова «МАТЕМАТИКА»? Сколько слов останется, если потребовать, чтобы три буквы «А» не стояли рядом?
1) По условию рассматриваем перестановки с повторениями.

a₁=M, k₁=2,    a₂=A, k₂=3,    a₃=T, k₃=2,   
a₄=E, k₄=1,    a₅=И, k₅=1,    a₆=K, k₆=1,   
k = k₁ + k₂ + . .. + k₆ = 2+3+2+1+1+1 = 10

$$ \mathrm{ P_{10}(2;3;2;1;1;1)=\frac{10!}{2!\ \cdot\ 3!\ \cdot\ 2!}=\frac{3628800}{2\ \cdot\ 6\ \cdot\ 2}=151200 } $$ 2) Найдем количество слов с тремя «А» подряд. Условие для перестановок с повторениями изменится так:

a₁=M, k₁=2,    a₂=»AAA», k₂=1,    a₃=T, k₃=2,   
a₄=E, k₄=1,    a₅=И, k₅=1,    a₆=K, k₆=1,   
k = k₁ + k₂ + … + k₆ = 2+1+2+1+1+1 = 8

$$ \mathrm{ P_{8}(2;1;2;1;1;1)=\frac{8!}{2!\ \cdot\ 2!}=\frac{40320}{2\ \cdot\ 2}=10080 } $$ Исключим слова с тремя «А» подряд из общего набора.
Останется N = 151200 – 10080 = 141120 слов.
Ответ: 151200 слов; 141120 слов.

Перестановки без повторений

Пусть дано множество А, содержащее m элементов. Упорядочим его элементы, пронумеровав их.

При этом всякий раз будем получать кортежи длины m.

Пример: Пусть . Упорядочим его элементы:

1) (a,b.c), 2) (a,c,b), 3) (b,a,c), 4) (b,c,a), 5) (c,a,b), 6) (c,b,a).

Получили 6 кортежей длины 3. Все они содержат одни и те же элементы, однако отличаются друг от друга порядком следования элементов.

Определение: Всякое упорядоченное n – элементное множество называется перестановкой без повторений из n элементов.

Теорема: Число перестановок без повторений из n элементов равно произведению n последовательных натуральных чисел от 1 до n.

Доказательство:

При упорядочивании элементов множества

А, содержащего n элементов, первый элемент можно выбрать n способами; второй – (n—1) способами; третий – (n-2) способами и т. д.; n-ый элемент можно выбрать 1 способом. Тогда n-ку ( по правилу произведения можно выбрать способами.

Пример: Сколькими способами можно четырех человек посадить на четырех различных стульях?

В задаче речь идет о перестановках без повторений: (способа).

Пример: Сколько различных пятизначных чисел можно составить из цифр: 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?

Цифр всего 5 и число должно быть пятизначным, т.е. в образовании числа должны быть задействованы все цифры. Известно, что значение числа зависит от того, какое место в числе занимает та или иная цифра. Налицо все характерные признаки перестановок без повторений. Следовательно, таких чисел будет:

.

Замечание: По определению считают: 0! = 1.

Задача 3: Сколько различных трехзначных чисел можно составить из цифр: 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?

В этой задаче в отличие от предыдущей для образования трехзначного числа необходимо задействовать лишь три цифры, а выбрав три цифры из пяти, их нужно упорядочить, чтобы получить различные трехзначные числа. Например, выберем цифры: 2, 3, 5. С их помощью можно получить числа: 235; 253; 523; 532; 325; 352. Выбрав другую тройку цифр, получим другие трехзначные числа и т.д.

Таким образом, мы из множества, содержащего n элементов, образуем

упорядоченные k – элементные подмножества.

Определение: Всякое упорядоченное k – элементное подмножество множества, содержащего n элементов, называется размещением без повторений из n элементов по k.

Два различных размещения без повторений могут отличаться друг от друга элементами, а также порядком следования элементов.

Теорема: Число размещений без повторений из n элементов по k равно

Тогда решение нашей задачи будет выглядеть так:

При составлении k — элементных подмножеств из элементов множества А, содержащего n элементов, нас не всегда будет интересовать порядок, в котором располагаются элементы.

Например, если из 10 сортов ткани нужно выбрать 4, то порядок выбора сортов ткани значения не имеет. В таких задачах речь идет о подмножествах, не являющихся упорядоченными.

Определение: Всякое неупорядоченное k – элементное подмножество множества, содержащего n элементов, называется сочетанием без повторений из n элементов по k.

Как следует из определения, два различных сочетания без повторений отличаются друг от друга элементами, порядок следования элементов роли не играет.

Теорема: Число сочетаний без повторений из n элементов по k определяется по формуле:

Доказательство:

Очевидно, что, если составить все сочетания без повторений из n элементов по k, (то есть все неупорядоченные k – элементные подмножества множества, содержащего

n элементов), а затем каждое из них упорядочить, то получим все размещения из n элементов по k. Число перестановок в каждом сочетании будет равно k!, а сочетаний всего , тогда . Отсюда

Задача: Из 12 человек нужно выбрать 3 человека для участия в соревнованиях. Сколькими способами это можно сделать ?

При выборе трех человек из 12 для участия в соревнованиях порядок выбора не важен. следовательно, в задаче речь идет о сочетаниях без повторений из 12 по 3: (способов).

Задача: Сколькими способами из 12 человек можно составить команду для участия в эстафете?

Здесь при выборе тройки человек важен порядок, в котором побегут спортсмены, поэтому решение задачи будет таким:

=1320

Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок

Узнайте, сколькими способами можно выбрать k предметов из n предметов набора. С/без повторения, с/без порядка.

Расчет:

Ck​(n)=(kn​)=k!(n−k)!n!​  n=10 k=4 C4​(10)=(410​)=4!(10 −4)!10!​=4⋅3⋅2⋅110⋅9⋅8⋅7​=210

Количество комбинаций: 210

Вариантов

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, образованная из множества n элементов. Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).

Количество вариаций можно легко подсчитать, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5 и мы должны сделать вариации третьего класса, их V ₃ (5) = 5 * 4 * 3 = 60. Vk​(n)=n(n−1)(n−2)…(n−k+1)=(n−k)!n!​ н! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначение с факториалом только более понятное, эквивалентное. Для вычислений вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.

Перестановки

Перестановка является синонимом вариации n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе. P(n)=n(n−1)(n−2)…1=n! Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?

Вариации с повторением

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, состоящая из множества n элементов, причем элементы могут повторяться и зависят от их порядка. Типичным примером является образование чисел из цифр 2,3,4,5 и нахождение их числа. Рассчитываем их количество по комбинаторному правилу произведения: Vk′(n)=n⋅n⋅n⋅n…n=nk

Перестановки с повторением

Повторяющаяся перестановка представляет собой упорядоченную группу k-элементов из n-элементов, при этом некоторые элементы повторяются в группе. Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок. Pk1​k2​k3​…km​′​​(n)=k1​!k2​!k3​!…km​!n!​ Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.

Комбинации

Комбинация k-го класса из n элементов представляет собой неупорядоченную группу k-элементов, образованную из множества n элементов. Элементы не повторяются, и порядок элементов группы не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами. Их количество является комбинационным числом и рассчитывается следующим образом: Ck​(n)=(kn​)=k!(n−k)!n!​ Типичный пример комбинаций: у нас 15 учеников, и мы должны выбрать троих. Сколько их будет?

Комбинации с повтором

Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться.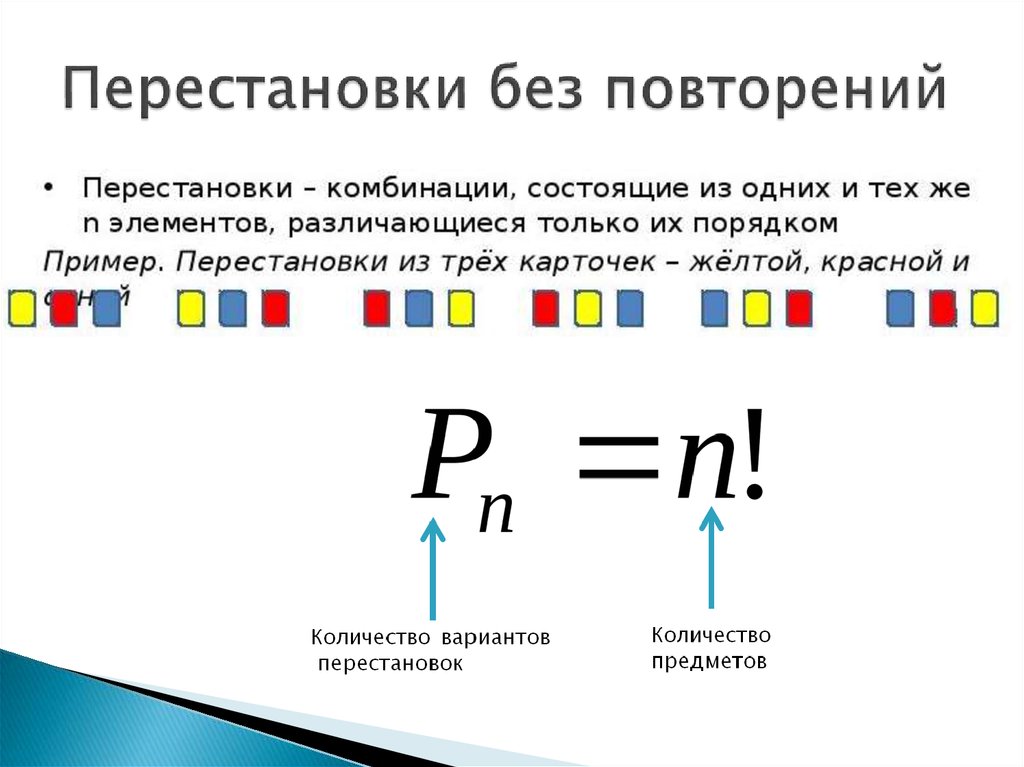 k логически больше n (иначе мы получили бы обычные комбинации). Их счет: Ck′(n)=(kn+k−1​)=k!(n−1)!(n+k−1)!​ Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n − 1 разделителей на n-1 + k местах. Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть? к = 6, п = 3.

Основы комбинаторики в текстовых задачах

• ПИН-коды
  Сколько пятизначных ПИН-кодов мы можем составить, используя четные числа?
• Усвоение
  Учащийся усваивает предмет для экзамена по чешскому языку на 98%, по математике на 86% и по экономике на 71%. Какова вероятность того, что он потерпит неудачу по математике, а другие преуспеют?
• Пересечение) 1566
  В скольких точках пересекаются девять прямых на плоскости, из которых четыре параллельны, а из пяти других нет двух параллельных (а если предположить, что через каждое пересечение проходят только две прямые)?
• Блюда
  Из 5 разных блюд HOD должен протестировать не менее трех разных блюд, прежде чем выставлять оценки учащимся. Сколькими способами он может выбрать блюда?
• MATES
  В MATES (Малый телевизионный прогноз) из 35 случайных чисел выпадает пять выигрышных номеров. Сколько возможных комбинаций существует?
• Произвольно 69194
  На плоскости есть десять произвольных точек. Сколько кругов мы можем сделать из них?
• Тест из шести вопросов
  В тесте шесть вопросов. На каждый есть три ответа, правильный только один. Для сдачи экзамена студенты должны правильно ответить не менее чем на четыре вопроса. Алан не выучил, поэтому обвел ответы, только угадывая. Какова вероятность
• 7 героев
  9 героев скачут на 9 лошадях позади. Сколькими способами мы можем отсортировать их сзади?
• Шахматная доска 80533
  Сколькими способами можно выбрать одну белую и одну черную клетку на шахматной доске 8×8, если выбранные клетки не могут лежать в одной строке или столбце?
• Определить 79634
  В корзине 12 яблок и 10 груш. Питер должен выбрать из них либо яблоко, либо грушу, чтобы у Виры, выбравшей после него 1 яблоко и 1 грушу, был как можно больший выбор. Определите, что выберет Питер.
• Три кости
  Игрок, бросающий три кости, спросил Г. Галилея: «На сумму 11 или на сумму 12?» Что ответил ему Галилей? Подсказка: запишите все три тройки чисел, которые можно выбросить, всего 11, всего 12 и сравните proba
• Вероятность 3219
  В последние годы в марте 12 дней шел дождь. Какова вероятность того, что 18 марта шел дождь?
• Семисегментный дисплей
  Электронные устройства иногда используют тип цифр ниже, где каждая цифра использует несколько коротких полос. Например, семерка использует три маленькие полоски. Какое самое большое трехзначное число можно составить, если использовать двадцать полосок?
• Равносторонний 75284
  Даны 6 отрезков длиной 3 см, 4 см, 5 см, 7 см, 8 см и 9 см. Сколько равносторонних треугольников можно составить из них? Перечислите все варианты.
• Следующий
  Следующие данные представляют собой количество ящиков кофе или фильтров, проданных четырьмя торговыми представителями в ходе недавнего конкурса продаж. продавец; Гурман; Единая чашка; фильтры; Тотал Коннор; 142; 325; 30; 497 Пейдж ; 42; 125; 40; 207 Брайс ; 9; 100; 10; 119 Молл
• Четырехзначный код
  Даны цифры 0-7. Если повторение запрещено, сколько возможны четырехзначные коды, которые больше 2000 и делятся на 4?

more math problems »

• decimals
• fractions
• triangle ΔABC
• percentage %
• permille ‰
• prime factors
• complex numbers
• LCM
• GCD
• LCD
• combinatorics
• equations
• статистика
• … все математические калькуляторы

комбинаций — Количество перестановок без повторения без выбора всех элементов

спросил 8 лет, 4 месяца назад

Изменено 8 лет, 4 месяца назад

Просмотрено 894 раза

$\begingroup$

Я ищу формулу для расчета числа или возможных перестановок, когда: а) повторение не допускается и б) вам не нужно выбирать все элементы из пула.

Итак, у меня есть n элементов, и я хочу знать, сколько комбинаций я могу получить, когда позиция имеет значение, я не могу выбрать элемент дважды и мне не нужно использовать все элементы.

Заранее спасибо!

• перестановки
• комбинации

$\endgroup$

$\begingroup$

Если мы собираемся использовать $k$ элементов, их можно выбрать $\binom{n}{k}$ способами и выстроить в ряд $k!$ способами. Это дает число, которое упрощается до $\frac{n!}{(n-k)!}$. Сложите от $k=0$ до $k=n$, если вы позволите «пустую» строку, или от $k=1$ до $n$, если вы этого не сделаете. (Мне нравится пустая строка, она непритязательна.)

Для привлекательности поменяйте порядок суммирования. Мы получаем $$n!\left(1+\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{n!}\right)$$ если мы допустим пустую строку. В противном случае мы остановимся на члене $\frac{1}{(n-1)!}$. Я не знаю точной «закрытой формы» этого выражения.