Перестановки сочетания: Перестановки, размещения и сочетания: понятия и формулы

О нумерации перестановок и сочетаний для организации параллельных вычислений в задачах проектирования управляющих систем

%PDF-1.4 % 1 0 obj > endobj 6 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > /Encoding > >> /DA (/Helv 0 Tf 0 g ) >> endobj 5 0 obj > stream

О нумерации перестановок и сочетаний для организации параллельных вычислений в задачах проектирования управляющих систем

Тимошевская Н. Е. endstream endobj 7 0 obj > endobj 8 0 obj > endobj 9 0 obj > endobj 10 0 obj > endobj 11 0 obj > endobj 12 0 obj > endobj 13 0 obj > endobj 14 0 obj > endobj 15 0 obj > endobj 16 0 obj > endobj 17 0 obj > endobj 18 0 obj > endobj 19 0 obj > /ExtGState > /Font > /Properties > /ProcSet [/PDF /Text] >> >> endobj 20 0 obj > endobj 21 0 obj > endobj 22 0 obj > endobj 23 0 obj > stream HWMoMf5YyK+d7;$$l$9c!|H

Методы принятия решений

Методы принятия решений

Эддоус М. , Стэнсфилд Р. Методы принятия решений/ Пер. с англ. под ред. член-корр. РАН И.И. Елисеевой. — М.: Аудит, ЮНИТИ, 1997. — 590 с. Предлагаемая книга представляет собой учебное пособие, которое подготовлено и используется Ассоциацией присяжных дипломированных бухгалтеров Великобритании (The Chartered Association of Certified Accountants — ACCA) в подготовке дипломированных бухгалтеров. Излагаются теоретические основы принятия управленческих решений в условиях неопределенности и оценки риска: элементы теории вероятностей, минимаксные правила принятия решений, статистический анализ для принятия решений, включающий процедуры статистического вывода, контроля качества, анализа временных рядов и прогнозирования, методы оптимизации решений. Оглавление ОТ НАУЧНОГО РЕДАКТОРА Часть 1. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕДОСТАТКА ИНФОРМАЦИИ 1.2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ 1.2.2. Свойства вероятности 1. 2.3. Как найти значение вероятности 1.3. ВЕРОЯТНОСТЬ СЛОЖНЫХ СОБЫТИЙ 1.4. ДЕЙСТВИЯ С ВЕРОЯТНОСТЯМИ 1.4.2. Условная вероятность 1.4.3. Правило умножения вероятностей 1.4.4. Правило вычисления вероятностей для более чем двух событий 1.5. ФОРМУЛА БАЙЕСА 1.6. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ 1.7. ПЕРЕСТАНОВКИ И СОЧЕТАНИЯ 1.7.1. Использование перестановок и сочетаний для вычисления вероятности РЕЗЮМЕ УПРАЖНЕНИЯ Глава 2. ВЕРОЯТНОСТНЫЕ РАСПРЕДЕЛЕНИЯ 2.2. ВЕРОЯТНОСТНЫЕ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 2.2.2. Распределение дискретной случайной величины 2.2.3. Графическое представление распределения дискретной случайной величины 2.2.4. Математическое ожидание и стандартное отклонение вероятностного распределения 2.3. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 2.3.2. Биномиальное распределение 2.3.3. Математическое ожидание и стандартное отклонение для биномиального распределения 2.4. РАСПРЕДЕЛЕНИЕ ПУАССОНА 2.4.2. Математическое ожидание и дисперсия распределения Пуассона 2. 5. РАСПРЕДЕЛЕНИЕ ПУАССОНА КАК АППРОКСИМАЦИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ 2.6. РАСПРЕДЕЛЕНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 2.6.2. Равномерное распределение 2.7. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 2.7.2. Стандартное нормальное распределение 2.8. ИСПОЛЬЗОВАНИЕ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ В КАЧЕСТВЕ АППРОКСИМАЦИИ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ 2.9. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК ЗАМЕНА РАСПРЕДЕЛЕНИЯ ПУАССОНА 2.10. КОМБИНАЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН 2.10.2. Особый случай зависимых случайных величин 2.10.3. Природа распределения объединенных случайных величин РЕЗЮМЕ УПРАЖНЕНИЯ Глава 3. ПРАВИЛА И СХЕМЫ ПРИНЯТИЯ РЕШЕНИЙ 3.2. ПРАВИЛА ПРИНЯТИЯ РЕШЕНИЙ 3.2.2. Критерий Гурвича — компромиссный способ принятия решений 3.2.3. Правила принятия решений с использованием численных значений вероятностей исходов 3.2.4. Зависимость решения от изменений значений вероятностей 3.2.5. Стоимость достоверной информации 3.3. ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И СТАНДАРТНОГО ОТКЛОНЕНИЯ ДЛЯ ОЦЕНКИ РИСКА 3. 4. ИСПОЛЬЗОВАНИЕ ПОНЯТИЯ ПОЛЕЗНОСТИ ПРИ ОПРЕДЕЛЕНИИ РАЗМЕРОВ РИСКА 3.4.1. Преимущества шкалы полезности 3.5. «ДЕРЕВО» РЕШЕНИЙ 3.5.1. Расчет двухуровневого “дерева” решений 3.5.2. «Дерево» и анализ чувствительности решений РЕЗЮМЕ УПРАЖНЕНИЯ Часть 2. АНАЛИЗ ДАННЫХ КАК СОСТАВНАЯ ЧАСТЬ ПРИНЯТИЯ РЕШЕНИЙ Глава 4. ВЫБОРКА И ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ 4.2. ПРИЧИНЫ ПРИМЕНЕНИЯ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ 4.3. СЛУЧАЙНЫЙ ОТБОР 4.4. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ 4.4.1. Выборочное распределение выборочных средних 4.4.2. Выборочное распределение выборочной дисперсии 4.4.3. Оценка стандартной ошибки выборочного распределения выборочных средних 4.4.4. Стандартные выборочные распределения РЕЗЮМЕ УПРАЖНЕНИЯ 5.2. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ГЕНЕРАЛЬНОЙ СРЕДНЕЙ «мю» 5.2.2. Генеральная дисперсия неизвестна 5.3. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ГЕНЕРАЛЬНОЙ ДОЛИ (ОТНОСИТЕЛЬНОЙ ВЕЛИЧИНЫ) р 5.4. ОПРЕДЕЛЕНИЕ СООТВЕТСТВУЮЩЕГО ОБЪЕМА ВЫБОРКИ 5.4.2. Объем выборки, необходимый для оценки генеральной доли РЕЗЮМЕ УПРАЖНЕНИЯ Глава 6. СТАТИСТИЧЕСКИЙ ВЫВОД 2: ИСПЫТАНИЕ ГИПОТЕЗ 6.2. ПРОЦЕДУРА ИСПЫТАНИЯ ГИПОТЕЗ 6.2.1. Правила испытания гипотез 6.2.2. Одно- и двусторонние тесты 6.3. ИСПЫТАНИЕ ГИПОТЕЗЫ НА ОСНОВЕ ВЫБОРОЧНОЙ СРЕДНЕЙ: ГЕНЕРАЛЬНАЯ ДИСПЕРСИЯ ИЗВЕСТНА 6.4. ИСПЫТАНИЕ ГИПОТЕЗЫ НА ОСНОВЕ ВЫБОРОЧНОЙ СРЕДНЕЙ — ГЕНЕРАЛЬНАЯ ДИСПЕРСИЯ НЕИЗВЕСТНА 6.5. ИСПЫТАНИЕ ГИПОТЕЗЫ НА ОСНОВЕ ВЫБОРОЧНОЙ ДОЛИ 6.6. ИСПЫТАНИЕ ГИПОТЕЗ О ДВУХ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЯХ 6.7. СРАВНЕНИЕ СРЕДНИХ ВЕЛИЧИН ДВУХ ВЫБОРОК ПРИ ИЗВЕСТНЫХ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЯХ 6.8. ИСПЫТАНИЕ ГИПОТЕЗЫ ПО ВЫБОРОЧНЫМ СРЕДНИМ — ГЕНЕРАЛЬНЫЕ ДИСПЕРСИИ НЕИЗВЕСТНЫ 6.9. ИСПЫТАНИЕ ГИПОТЕЗЫ ПО ДВУМ ВЫБОРОЧНЫМ ДОЛЯМ 6.10. ИСПЫТАНИЕ ГИПОТЕЗЫ ПО СПАРЕННЫМ ДАННЫМ — ЗАВИСИМЫЕ ВЫБОРКИ 6.11. НЕПАРАМЕТРИЧЕСКИЕ ИСПЫТАНИЯ ГИПОТЕЗ-КРИТЕРИЙ ХИ-КВАДРАТ РЕЗЮМЕ УПРАЖНЕНИЯ Глава 7. СТАТИСТИЧЕСКИЙ КОНТРОЛЬ КАЧЕСТВА 7.2. ИЗМЕНЧИВОСТЬ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА 7. 3. ПРОИЗВОДСТВЕННЫЕ ВОЗМОЖНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА 7.4. КОНТРОЛЬНЫЕ КАРТЫ 7.4.2. Контрольные карты количественных признаков при неизвестных «мю» и «сигма» 7.4.3. Контрольные карты качественных признаков 7.5. СТАТИСТИЧЕСКИЙ ПРИЕМОЧНЫЙ КОНТРОЛЬ КАЧЕСТВА НЕКОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ РЕЗЮМЕ УПРАЖНЕНИЯ Глава 8. ЛИНЕЙНАЯ РЕГРЕССИЯ 8.2. ПРОСТАЯ МОДЕЛЬ ЛИНЕЙНОЙ РЕГРЕССИИ 8.3. ТЕСНОТА ЛИНЕЙНОЙ СВЯЗИ — КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ r 8.4. ПРЕДСКАЗАНИЯ И ПРОГНОЗЫ НА ОСНОВЕ ЛИНЕЙНОЙ МОДЕЛИ РЕГРЕССИИ 8.5. СТАТИСТИЧЕСКИЙ ВЫВОД В АНАЛИЗЕ ЛИНЕЙНОЙ РЕГРЕССИИ 8.5.2. Испытание гипотезы для оценки линейности связи 8.5.3. Доверительный интервал в линейном регрессионном анализе 8.6. МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ 8.8. РАНГОВЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ СПИРМЕНА РЕЗЮМЕ УПРАЖНЕНИЯ Глава 9. ВРЕМЕННЫЕ РЯДЫ И ПРОГНОЗИРОВАНИЕ 9.2. ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА 9.3. АНАЛИЗ МОДЕЛИ С АДДИТИВНОЙ КОМПОНЕНТОЙ 9.3.2. Десезонализация данных при расчете тренда 9. 3.3. Расчет ошибок 9.3.4. Прогнозирование по аддитивной модели 9.4. АНАЛИЗ МОДЕЛИ С МУЛЬТИПЛИКАТИВНОЙ КОМПОНЕНТОЙ 9.4.2. Десезонализация данных и расчет уравнения тренда 9.4.3. Расчет ошибок 9.4.4. Прогнозирование по модели с мультипликативной компонентой РЕЗЮМЕ УПРАЖНЕНИЯ Часть 3. ПЛАНИРОВАНИЕ В БИЗНЕСЕ 10.2. СЕТЕВЫЕ ГРАФЫ 10.2.2. Вершинные графы 10.3. АНАЛИЗ КРИТИЧЕСКОГО ПУТИ 10.3.2. Анализ критического пути с применением стрелочных графов 10.4. СТОИМОСТЬ ПРОЕКТА 10.5. НЕОПРЕДЕЛЕННОСТЬ ВРЕМЕНИ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ 10.6. РАСПРЕДЕЛЕНИЕ РЕСУРСОВ РЕЗЮМЕ УПРАЖНЕНИЯ Глава 11. ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ ЗАПАСАМИ 11.2. ОСНОВНАЯ МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ 11.2.2. Издержки хранения запасов 11.2.3. Уравнение общей стоимости 11.2.4. Оптимальный размер заказа 11.2.5. Уровень и интервал повторного заказа 11.2.6. Модель экономичного размера партии 11.3. СКИДКА НА КОЛИЧЕСТВО 11.4. ДРУГИЕ МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ 11. 4.2. Модель планирования дефицита 11.5. НЕОПРЕДЕЛЕННОСТЬ И ОСНОВНАЯ МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ 11.5.1. Уровневая система повторного заказа 11.5.2. Циклическая система повторного заказа 11.6. ДРУГИЕ АСПЕКТЫ ТЕОРИИ УПРАВЛЕНИЯ ЗАПАСАМИ РЕЗЮМЕ УПРАЖНЕНИЯ Часть 4. МОДЕЛИРОВАНИЕ В БИЗНЕСЕ 12.2. ФОРМУЛИРОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 12.3. РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 12.4. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ 12.4.2. Воздействие на оптимальное решение изменений в обеспечении нелимитирующими ресурсами 12.4.3. Воздействие на оптимальное решение изменений в коэффициентах целевой функции 12.5. СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С МНОЖЕСТВОМ ПЕРЕМЕННЫХ 12.6. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ И СИМПЛЕКС-МЕТОД 12.7. ДВОЙСТВЕННАЯ МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ РЕЗЮМЕ УПРАЖНЕНИЯ Глава 13. ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ 13.2. ТРАНСПОРТНАЯ ЗАДАЧА И АЛГОРИТМ ЕЕ РЕШЕНИЯ 13.2.2. Алгоритм решения транспортной задачи 13. 2.3. Поиск начального распределения ресурсов 13.2.4. Проверка на оптимальность 13.2.5. Поиск оптимального решения 13.2.6. Анализ чувствительности 13.2.7. Модификации транспортной задачи 13.3. ЗАДАЧА О НАЗНАЧЕНИЯХ 13.3.2. Особые случаи задачи о назначениях РЕЗЮМЕ УПРАЖНЕНИЯ Глава 14. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ 14.2. ПРИНЦИПЫ ПОСТРОЕНИЯ ДИСКРЕТНЫХ ИМИТАЦИОННЫХ МОДЕЛЕЙ 14.3. ПРИМЕНЕНИЕ ИМИТАЦИОННЫХ МОДЕЛЕЙ В СИСТЕМАХ МАССОВОГО ОБСЛУЖИВАНИЯ 14.4. ПРИМЕНЕНИЕ ИМИТАЦИОННЫХ МОДЕЛЕЙ В УПРАВЛЕНИИ ЗАПАСАМИ РЕЗЮМЕ УПРАЖНЕНИЯ ОТВЕТЫ К УПРАЖНЕНИЯМ АССОЦИАЦИЯ ДИПЛОМИРОВАННЫХ АУДИТОРОВ (The Chartered Association of Certified Accountants) НОВЫЕ ФОРМУЛЫ И ВЫДЕРЖКИ ИЗ ТАБЛИЦ ОТВЕТЫ АВТОРОВ МОДЕЛЕЙ НА ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО ТЕМЕ “КОЛИЧЕСТВЕННЫЙ АНАЛИЗ” МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ

Комбинации и перестановки

Расследовать!

У вас есть набор фишек пяти разных цветов: красного, синего, зеленого, фиолетового и желтого.

1. Сколько различных стопок по две фишки можно составить, если нижняя фишка должна быть красной или синей? Объясните свой ответ, используя как аддитивный, так и мультипликативный принцип.

2. Сколько различных стопок по три фишки можно составить, если нижняя фишка должна быть красной или синей, а верхняя фишка должна быть зеленой, фиолетовой или желтой? Как эта проблема связана с предыдущей?

3. Сколько существует различных стопок по три фишки, в которых ни один цвет не повторяется? Как насчет стеков из четырех фишек?

4. Предположим, вы хотите взять три фишки разного цвета и положить их в карман. Сколько различных вариантов у вас есть? Что, если вы хотите четыре фишки разного цвета? Как эти проблемы связаны с предыдущими?

Перестановка — это (возможная) перестановка объектов. Например, есть 6 перестановок букв 9.0027 а, б, в :

\begin{уравнение*} abc, ~~ acb, ~~ bac, ~~bca, ~~ cab, ~~ cba\text{. } \end{уравнение*}

Мы знаем, что у нас есть все перечисленные выше — есть 3 варианта, какую букву поставить первой, затем 2 варианта, какая буква будет следующей, что оставляет только 1 вариант для последней буквы. Мультипликативный принцип говорит, что мы умножаем \(3\cdot 2 \cdot 1\text{.}\)

Пример 1.3.1.

Сколько существует перестановок букв a, b, c, d, e, f ?

Раствор.

Мы НЕ хотим пытаться перечислить все это. Однако, если бы мы это сделали, нам нужно было бы выбрать букву для записи в первую очередь. Есть 6 вариантов этой буквы. Для каждого выбора первой буквы есть 5 вариантов для второй буквы (мы не можем повторить первую букву, мы переставляем буквы и имеем только по одной каждой), и для каждого из них есть 4 варианта для третьей, 3 варианты для четвертого, 2 варианта для пятого и, наконец, только 1 вариант для последней буквы. Итак, есть \(6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\) перестановки 6 букв.

Здесь будет полезна небольшая запись: \(n!\text{,}\) читать как «\(n\) факториал», это произведение всех положительных целых чисел, меньших или равных \(n\) (для из соображений удобства мы также определяем 0! как 1). Таким образом, количество перестановок из 6 букв, как видно из предыдущего примера, равно \(6! = 6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\text{.}\) Это обобщает:

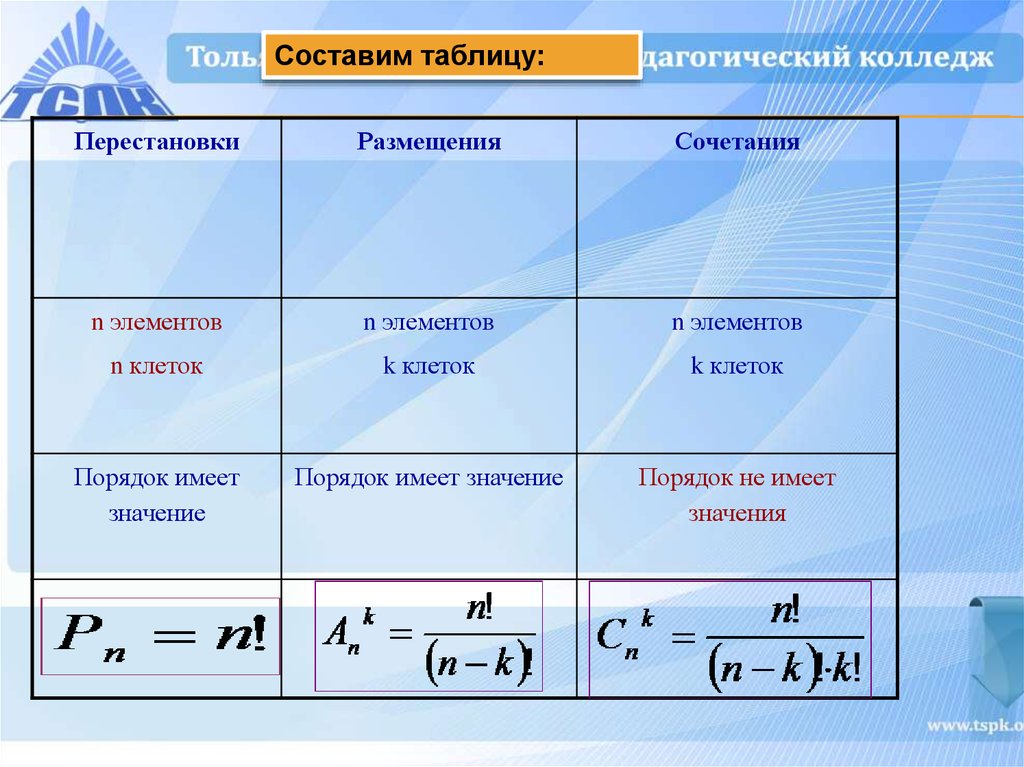
Перестановки \(n\) элементов.

Существуют \(n! = n\cdot (n-1)\cdot (n-2)\cdot \cdots \cdot 2\cdot 1\) перестановки \(n\) (различных) элементов.

Пример 1.3.2. Счетные биективные функции.

Сколько функций \(f:\{1,2,\ldots,8\} \to \{1,2,\ldots, 8\}\) являются биективными ?

Раствор.

Вспомните, что означает биективность функции: каждый элемент домена кода должен быть образом ровно одного элемента домена. Используя двухстрочную запись, мы могли бы записать одну из этих биекций как

\begin{equation*} f = \twoline{1 \amp 2 \amp 3 \amp 4 \amp 5 \amp 6 \amp 7 \amp 8} {3 \amp 1 \amp 5 \amp 8 \amp 7 \amp 6 \amp 2 \amp 4}\текст{. } \end{уравнение*}

На самом деле мы просто переставляем элементы кодового домена, поэтому мы создаем перестановку из 8 элементов. На самом деле «перестановка» — это еще один термин, используемый для описания биективных функций из конечного множества в себя.

Если вы в это верите, то вы видите, что ответ должен быть \(8! = 8 \cdot 7 \cdot\cdots\cdot 1 = 40320\text{.}\) Это можно увидеть и непосредственно: для каждого элемента домена, мы должны выбрать отдельный элемент кодового домена для сопоставления. Есть 8 вариантов, куда отправить 1, затем 7 вариантов, куда отправить 2, и так далее. Умножаем по принципу мультипликативности.

Иногда мы не хотим переставлять все буквы/цифры/элементы, которые нам даны.

Пример 1.3.3.

Сколько 4-буквенных «слов» можно составить из букв от a до f без повторяющихся букв?

Раствор.

Это похоже на задачу перестановки 4 букв, только теперь у нас больше вариантов для каждой буквы. Для первой буквы есть 6 вариантов. Для каждого из них есть 5 вариантов второй буквы. Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно \(6\cdot 5\cdot 4 \cdot 3 = 360\text{.}\). Это не \(6!\), потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6!\), а затем сократите 2 и 1 и, таким образом, напишите \(\frac{6!}{2!}\text{.}\)

В общем, мы можем спросить, сколько существует перестановок \(k\) объектов, выбирающих эти объекты из большего набора \(n\) объектов. (В приведенном выше примере \(k = 4\text{,}\) и \(n = 6\text{.}\)) Мы пишем это число \(P(n,k)\) и иногда называем его \(k\)-перестановка \(n\) элементов . Из приведенного выше примера мы видим, что для вычисления \(P(n,k)\) мы должны применить принцип умножения к \(k\) числам, начиная с \(n\) и считая в обратном порядке. Например

\begin{уравнение*} P(10, 4) = 10\cdot 9 \cdot 8 \cdot 7\text{.} \end{уравнение*}

Еще раз обратите внимание, что \(P(10,4)\) начинается с вида \(10!\text{,}\), но мы останавливаемся после 7. Мы можем формально объяснить эту «остановку», отделив часть факториал нам не нужен:

\begin{уравнение*} P(10,4) = \frac{10\cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = \frac{10!}{6!}\text{.} \end{уравнение*}

Осторожно: факториал в знаменателе равен не \(4!\), а \((10-4)!\text{.}\)

\(k\)-перестановок \(n\) элементов.

\(P(n,k)\) — количество \(k\)-перестановок \(n\) элементов , количество способов расположить \(k\) объектов, выбранных из \( п\) различных объектов.

\begin{уравнение*} P(n,k) = \frac{n!}{(n-k)!} = n(n-1)(n-2)\cdots (n-(k-1))\text{.} \end{equation*}

Обратите внимание, что когда \(n = k\text{,}\) мы имеем \(P(n,n) = \frac{n!}{(n-n)!} = n!\ ) (поскольку мы определили \(0!\) равным 1). Это имеет смысл — мы уже знаем, что \(n!\) дает количество перестановок всех \(n\) объектов.

Пример 1.3.4. Счетные инъективные функции.

Сколько функций \(f:\{1,2,3\} \to \{1,2,3,4,5,6,7,8\}\) являются инъективными ?

Раствор.

Обратите внимание, что здесь не имеет смысла запрашивать число биекций , поскольку их нет (поскольку кодовый домен больше домена, сюръекций нет). Но чтобы функция была инъективной, мы просто не можем использовать элемент кодового домена более одного раза.

Нам нужно выбрать элемент из кодового домена, который будет изображением 1. Есть 8 вариантов. Затем нам нужно выбрать один из оставшихся 7 элементов, чтобы он был образом 2. Наконец, один из оставшихся 6 элементов должен быть образом 3. Таким образом, общее количество функций равно \(8\cdot 7 \cdot 6 = Р(8,3)\текст{.}\)

В целом это демонстрирует, что число инъекций \(f:A \to B\text{,}\), где \(\card{A} = k\) и \(\card{B} = n \text{,}\) равно \(P(n,k)\text{.}\)

Вот еще один способ найти число \(k\)-перестановок \(n\) элементов: сначала выберите, какие \(k\) элементов будут в перестановке, затем посчитайте, сколько существует способов их расположить. После того, как вы выбрали \(k\) объектов, мы знаем, что есть \(k!\) способов упорядочить (переставить) их. Но как выбрать \(k\) объектов из \(n\text{?}\) У вас есть \(n\) объектов, и вам нужно выберите \(k\) из них. Вы можете сделать это \({n \выбрать k}\) способами. Тогда для каждого выбора из этих \(k\) элементов мы можем переставить из \(k!\) способов. Используя принцип умножения, мы получаем другую формулу для \(P(n,k)\text{:}\)

\begin{уравнение*} P(n,k) = {n \выберите k}\cdot k!\text{.} \end{уравнение*}

Теперь, поскольку у нас уже есть замкнутая формула для \(P(n,k)\), мы можем подставить ее в:

\begin{уравнение*} \frac{n!}{(n-k)!} = {n \выберите k} \cdot k!\text{.} \end{уравнение*}

Если мы разделим обе части на \(k!\), мы получим закрытую формулу для \({n \choose k}\text{.}\)

Замкнутая формула для \({n \выбрать k}\).

\begin{уравнение*} {n \выберите k} = \frac{n!}{(n-k)!k!} = \frac{n(n-1)(n-2)\cdots(n-(k-1))}{k (к-1)(к-2)\cdots 1}\текст{. } \end{equation*}

Мы говорим, что \(P(n,k)\) подсчитывает перестановок , а \({n \choose k}\) подсчитывает комбинаций . Формулы для каждого из них очень похожи, просто в знаменателе \({n \choose k}\text{.}\) есть лишний \(k!\) что \({n \choose k}\) не различает различные порядки, в которых могут появляться \(k\) объекты. Мы просто выбираем (или выбираем) \(k\) объекты, а не упорядочиваем их. Возможно, «комбинация» — обманчивый ярлык. Мы не имеем в виду кодовый замок (где порядок определенно имеет значение). Возможно, лучшая метафора — это сочетание вкусов — вам просто нужно решить, какие вкусы сочетать, а не в каком порядке их комбинировать.

Чтобы еще больше проиллюстрировать связь между комбинациями и перестановками, мы закончим пример.

Пример 1.3.5.

Вы решили устроить званый ужин. Несмотря на то, что вы невероятно популярны и у вас 14 разных друзей, у вас достаточно стульев, чтобы пригласить только 6 из них.

1. Сколько у вас есть вариантов, кого из 6 друзей пригласить?

2. Что делать, если вам нужно решить не только, кого из друзей пригласить, но и где их рассадить за длинным столом? Сколько вариантов у вас есть тогда?

Раствор.

1. Вы должны просто выбрать 6 друзей из 14. Это можно сделать \({14 \выбрать 6}\) способами. Мы можем найти это число либо с помощью треугольника Паскаля, либо по закрытой формуле: \(\frac{14!}{8!\cdot 6!} = 3003\text{.}\)

2. Здесь вы должны подсчитать все способы, которыми вы можете переставить 6 друзей, выбранных из группы из 14. Таким образом, ответ равен \(P(14, 6)\text{,}\), который можно рассчитать как \(\frac{14 !}{8!} = 2162160\текст{.}\)

   Заметьте, что мы можем думать об этой задаче на счет как о вопросе о счетных функциях: сколько инъективных функций имеется в вашем наборе из 6 стульев и в вашем наборе из 14 друзей (эти функции инъективны, потому что ни один стул не может двигаться). двум твоим друзьям).

Как связаны эти числа? Обратите внимание, что \(P(14,6)\) намного на больше, чем \({14 \choose 6}\text{.}\) Это имеет смысл. \({14 \выбрать 6}\) выбирает 6 друзей, но \(P(14,6)\) упорядочивает 6 друзей, а также выбирает их. На самом деле, мы можем точно сказать, насколько больше \(P(14,6)\). В обеих задачах на подсчет мы выбираем 6 из 14 друзей. Для первого мы останавливаемся там, на 3003 способах. Но во второй задаче на подсчет каждый из этих 3003 вариантов выбора из 6 друзей можно упорядочить ровно \(6!\) способами. Итак, теперь у нас есть \(3003\cdot 6!\) вариантов, и это ровно \(2162160\text{.}\)

В качестве альтернативы, посмотрите на первую проблему с другой стороны. Мы хотим выбрать 6 из 14 друзей, но нас не волнует порядок, в котором они выбираются. Чтобы выбрать 6 из 14 друзей, мы можем попробовать следующее:

\begin{equation*} 14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9\text{.} \end{equation*}

Это разумное предположение, поскольку у нас есть 14 вариантов для первого гостя, затем 13 для второго и так далее. Но догадка неверна (на самом деле это произведение равно \(2162160 = P(14,6)\)). Он различает разные порядки, в которых мы могли бы пригласить гостей. Чтобы исправить это, мы могли бы разделить на количество различных расстановок 6 гостей (чтобы все они считались одним исходом). Существует ровно \(6!\) способов разместить 6 гостей, поэтому правильный ответ на первый вопрос —

\begin{уравнение*} \frac{14 \cdot 13 \cdot 12 \cdot 11\cdot 10 \cdot 9}{6!}\text{.} \end{equation*}

Обратите внимание, что это можно записать по-другому:

\begin{equation*} \frac{14!}{8!\cdot 6!}\text{.} \end{equation*}

, что у нас было изначально.

Упражнения Упражнения

1.

Пиццерия предлагает 10 начинок.

1. Сколько пицц с тремя начинками они могли включить в свое меню? Предположим, что двойная начинка не допускается.

2. Сколько всего пицц возможно с от нуля до десяти начинок (но не с двойной начинкой)?

3. Пиццерия перечислит 10 начинок в двух колонках одинакового размера в своем меню. Сколькими способами они могут расположить начинки в левой колонке?

Раствор.

1. \({10 \выберите 3} = 120\) пиццы. Мы должны выбрать (в произвольном порядке) 3 из 10 начинок. {10} = 1024\) пиццы. Скажите «да» или «нет» каждой начинке.

2. \(P(10,5) = 30240\) способов. Назначьте каждому из 5 мест в левой колонке уникальную начинку для пиццы.

2.

Кодовый замок состоит из циферблата с 40 цифрами. Чтобы открыть замок, вы поворачиваете циферблат вправо, пока не дойдете до первой цифры, затем влево, пока не дойдете до второй цифры, затем снова вправо до третьей цифры. Числа должны быть разными. Сколько различных комбинаций возможно?

Раствор. 93\)).

3.

Используя цифры со 2 по 8, найдите количество различных пятизначных чисел, таких что:

1. Цифры могут использоваться более одного раза.

2. Цифры не могут повторяться, но могут идти в любом порядке.

3. Цифры не могут повторяться и должны быть записаны в возрастающем порядке.

4. Какой из приведенных выше вопросов на подсчет является комбинацией, а какой перестановкой? Объясните, почему это имеет смысл. 95 = 16807\) таких чисел.

5. Теперь у нас есть 7 вариантов для первого числа, 6 для второго и т. д. Итак, есть \(7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 = P(7,5) = 2520\) таких чисел .

6. Чтобы построить такое число, нам просто нужно выбрать 5 разных цифр. После этого будет только один способ упорядочить их в 5-значное число. Таким образом, таких чисел \({7 \выберите 5} = 21\).

7. Перестановка в части (b), а комбинация в части (c). Сначала это кажется обратным, поскольку обычно мы используем комбинации, когда порядок не имеет значения. Здесь похоже, что в части (c) порядок имеет значение. Лучший способ провести различие между комбинациями и перестановками — спросить, считаем ли мы разные схемы разными результатами. В части (c) есть только одно расположение любого набора из 5 цифр, тогда как в части (b) каждый набор из 5 цифр дает \(5!\) разные результаты.

4.

Пытаясь навести порядок в своей комнате, вы купили новую плавающую полку, чтобы поставить некоторые из ваших 17 книг, которые вы сложили в углу. Все эти книги написаны разными авторами. Новая книжная полка достаточно большая, чтобы вместить 10 книг.

1. Сколькими способами вы можете выбрать и расставить 10 из 17 книг на полке? Обратите внимание, что здесь мы позволим книгам располагаться в любом порядке. Объяснять.

2. Сколькими способами можно расположить 10 из 17 книг на полке, если вы настаиваете на том, чтобы они были расположены в алфавитном порядке по авторам? Объяснять.

Подсказка.

Ответ на какой вопрос должен быть больше? Один из них является комбинацией, другой — перестановкой.

5.

Предположим, вы хотите нарисовать четырехугольник, используя точки внизу в качестве вершин (углов). Точки разнесены на одну единицу по горизонтали и на две единицы по вертикали.

Сколько четырехугольников возможно?

Сколько квадратов?

Сколько прямоугольников?

Сколько параллелограммов?

Сколько трапеций? (Здесь, как и в математическом анализе, трапеция определяется как четырехугольник с по крайней мере одной парой параллельных сторон. В частности, параллелограммы являются трапециями.)

Сколько трапеций не являются параллелограммами?

Раствор.

Вы можете составить \({7\выбрать 2}{7\выбрать 2} = 441\) четырехугольников.

Есть 5 квадратов.

Есть \({7 \выберите 2}\) прямоугольников.

Есть \({7 \выберите 2} + ({7 \выберите 2}-1) + ({7 \выберите 2} — 3) + ({7 \выберите 2} — 6) + ({7 \выберите 2} — 6) + ({7 \выберите 2} — 1) выберите 2} — 10) + ({7 \выберите 2} — 15) = 91\) параллелограммы.

Все четырехугольники являются трапециями. Чтобы подсчитать непараллелограммные трапеции, вычислите \({7\выберите 2}{7\выберите 2} — \left[ {7 \выберите 2} + ({7 \выберите 2}-1) + ({7 \выберите 2}-1) + ({7\выберите 2} 2} — 3) + ({7 \выбрать 2} — 6) + ({7 \выбрать 2} — 10) + ({7 \выбрать 2} — 15) \right]\text{.}\)

6.

Сколько существует треугольников с вершинами из точек, показанных ниже? Обратите внимание, что мы не допускаем вырожденных треугольников, у которых все три вершины лежат на одной линии, но допускаем непрямоугольные треугольники. Объясните, почему ваш ответ правильный.

Подсказка.

Если выбрать любые три точки, можно получить треугольник, если только эти три точки не лежат на оси \(x\) или на оси \(y\). Есть и другие способы начать это, и любой правильный метод должен давать тот же ответ.

Раствор.

7.

Анаграмма слова — это просто перестановка его букв. Сколько существует различных анаграмм слова «не защищено авторским правом»? (Это самое длинное общеупотребительное английское слово без повторяющихся букв.)

Решение.

Поскольку существует 15 различных букв, у нас есть 15 вариантов для первой буквы, 14 для следующей и так далее. Таким образом, имеется \(15!\) анаграмм.

8.

Сколько существует анаграмм слова «оценки», начинающихся на букву «а»?

Подсказка.

Нам просто нужна строка из 7 букв: 4 одного типа, 3 другого.

Раствор.

Есть \({7 \выберите 2} = 21\) анаграммы, начинающиеся с «а».

9.

Сколько существует анаграмм слова «анаграмма»?

Раствор.

Сначала решите, где поставить «а». Есть 7 позиций, и мы должны выбрать 3 из них, чтобы заполнить «а». Это можно сделать \({7 \выбрать 3}\) способами. Оставшиеся 4 места получают разные буквы, так что есть \(4!\) способов закончить анаграмму. Всего получается \({7 \выберите 3}\cdot 4!\) анаграмм. Как ни странно, это 840, что также равно \(P(7,4)\text{.}\) Чтобы получить такой ответ, начните с выбора одного из 7 позиций заполнить буквой «n», одну из оставшихся 6 позиций заполнить буквой «g», одну из оставшихся 5 позиций заполнить буквой «r», одну из оставшихся 4 позиций заполнить заполнить буквой «м», а затем поставить «а» в оставшиеся 3 позиции.

10.

На деловом выезде ваша компания из 20 руководителей играет в гольф.

1. Вам нужно разбиться на четверки (группы по 4 человека): первая четверка, вторая четверка и так далее. Сколько способов вы можете сделать это?

2. После всей вашей тяжелой работы вы понимаете, что на самом деле вы хотите, чтобы каждая четверка включала одного из пяти членов Совета. Сколько способов вы можете сделать это?

Раствор.

1. \({20 \выбрать 4}{16 \выбрать 4}{12 \выбрать 4}{8 \выбрать 4}{4 \выбрать 4}\) способов.

2. \(5!{15 \выбрать 3}{12 \выбрать 3}{9 \выбрать 3}{6 \выбрать 3}{3 \выбрать 3}\) способов.

11.

Сколько различных рассадок возможно для короля Артура и его 9рыцари вокруг своего круглого стола?

Подсказка.

Вокруг стола сидят 10 человек, но не имеет значения, где сидит король Артур, только кто сидит слева от него, два места слева от него и так далее. Так что ответ не \(10!\text{. }\)

Решение.

\(9!\text{.}\)

12.

Рассмотрим множества \(A\) и \(B\) с \(|A| = 10\) и \(|B| = 17\text{.}\)

1. Сколько функций \(f: А\к Б\) есть?

2. 9{10}\) функций. Существует 17 вариантов изображения каждого элемента в домене.

3. \(P(17, 10)\) инъективные функции. Существует 17 вариантов изображения первого элемента домена, затем только 16 вариантов для второго и так далее.

13.

Рассмотрим функции \(f: \{1,2,3,4\} \to \{1,2,3,4,5,6\}\text{.}\)

1. Сколько функций там всего?

2. Сколько функций инъективны?

   94 = 1296\) функций.

3. \(P(6, 4) = 6 \cdot 5 \cdot 4 \cdot 3 = 360\) функций.

4. \({6 \выберите 4} = 15\) функций.

14.

Мы видели, что формула для \(P(n,k)\) равна \(\dfrac{n!}{(n-k)!}\text{.}\) Ваша задача здесь состоит в том, чтобы объяснить почему это это правильная формула.

1. Предположим, у вас есть 12 фишек разного цвета. Сколько разных стопок по 5 фишек можно составить? Объясните свой ответ и почему он аналогичен формуле для \(P(12,5)\text{.}\)

2. Снова используя сценарий с 12 фишками, сколько будет считаться \(12!\)? Что значит \(7!\)? Объяснять.

3. Объясните, почему имеет смысл делить \(12!\) на \(7!\) при вычислении \(P(12,5)\) (в терминах чипов).

4. Ваше объяснение подходит для чисел, отличных от 12 и 5? Объясните формулу \(P(n,k) = \frac{n!}{(n-k)!}\), используя переменные \(n\) и \(k\text{.}\)

Перестановки и комбинации | Гуру качества

Перестановки и комбинации — это два взаимосвязанных понятия в математике, которые связаны с расположением элементов или чисел. Перестановки — это расположения, в которых порядок элементов имеет значение, а комбинации — это расположения, в которых порядок не имеет значения.

Эти понятия используются в различных областях, таких как вероятность и статистика, информатика, финансы и т.д. Понимание основ перестановок и комбинаций может помочь вам разобраться в более сложных математических задачах.

Основы перестановок

Перестановки — это перестановки, в которых порядок элементов имеет значение . Формула перестановок вычисляет количество способов, которыми данный набор элементов можно расположить в определенном порядке.

Без повторения:

Например, если у вас есть три элемента (A, B и C) и вы хотите расположить их по порядку, возможные перестановки: ABC, ACB, BAC, BCA, CAB и CBA.

Формула часто записывается как «nPr», где n — количество элементов в наборе, а r — количество элементов, расположенных в определенном порядке.

Формула перестановок (без повторения) определяется следующим образом:
$$nPr = \frac{n!}{(n-r)!}$$

Где n — количество элементов в наборе, r — количество элементов, расположенных в определенном порядке, и ! обозначает факториальную операцию.

Например, если у вас есть набор из трех букв, скажем, A, B и C, и вы хотите узнать, сколько способов вы можете расположить их в определенном порядке, вы должны использовать формулу перестановки для вычисления этого . Количество перестановок будет 3P3 = 3! / (3-3)! = 3! / 0! = 3! / 1 = 6, потому что есть 6 различных способов расположить три буквы в определенном порядке. 93 или 27 аранжировок с повторением.

Основы комбинаций

Комбинации используются для определения того, сколько различных групп может быть сформировано из набора объектов. Комбинации — это схемы, в которых порядок не имеет значения.

Без повторения:

Например, если у вас есть набор из четырех букв, скажем A, B, C и D, и вы хотите узнать, сколько способов выбрать две из них. Возможные комбинации: AB, AC, AD, BC, BD и CD.

Формула часто записывается как «nCr», где n — общее количество элементов в наборе, r — количество выбираемых элементов, а ! обозначает факториальную операцию.

Формула для комбинаций (без повторения) определяется следующим образом:

$$nCr = \frac{n!}{r!(n-r)!}$$

Где n — общее количество элементов в наборе , r — количество выбираемых элементов, а ! обозначает факториальную операцию.

В приведенном выше примере у нас было четыре буквы (A, B, C и D), и мы хотели выбрать из них две буквы. Количество комбинаций будет

$$4C2 = \frac{4!}{2!(4-2)!} = \frac{4!}{(2!)(2!)} = 6$$

Существует 6 различных способов что вы можете выбрать две буквы из набора независимо от их порядка.

С повторением:

Формула для комбинаций с повторением:
$$(n+r-1)Cr = \frac{(n+r-1)!}{r!(n-1)!}$ $

Понимание различий между перестановками и комбинациями

Перестановки — это расположения объектов, порядок которых важен, а сочетания — это расположения объектов, порядок которых не важен.

Применение перестановок и комбинаций в реальном мире

Перестановки и комбинации — это фундаментальные математические понятия, которые имеют многочисленные применения в реальном мире.

Перестановки — это расположение элементов в определенном порядке. Одним из распространенных примеров перестановок является создание пароля, где важен порядок символов. Например, «пароль» и «дроуссап» — это разные сочетания одного и того же набора символов.

Комбинации, однако, представляют собой расположение предметов, порядок которых не имеет значения. Примером комбинации является выбор команды игроков из большого пула игроков, где конкретный порядок выбора игроков не важен.

Другие реальные применения перестановок и комбинаций включают:

• Статистика: Перестановки и комбинации используются в статистическом анализе для расчета вероятности возникновения определенных событий и определения вероятности конкретных результатов.
• Криптография: Перестановки и комбинации используются в криптографии для создания безопасных паролей и ключей шифрования.

  No related posts.