| 1. Организационный момент | – Ребята, наш урок мы сегодня начнем с
пословицы. Перед вами представлены формулы,
среди них выберите те, которые указывают на
нахождение периметра прямоугольника (Презентация,
слайд 2)
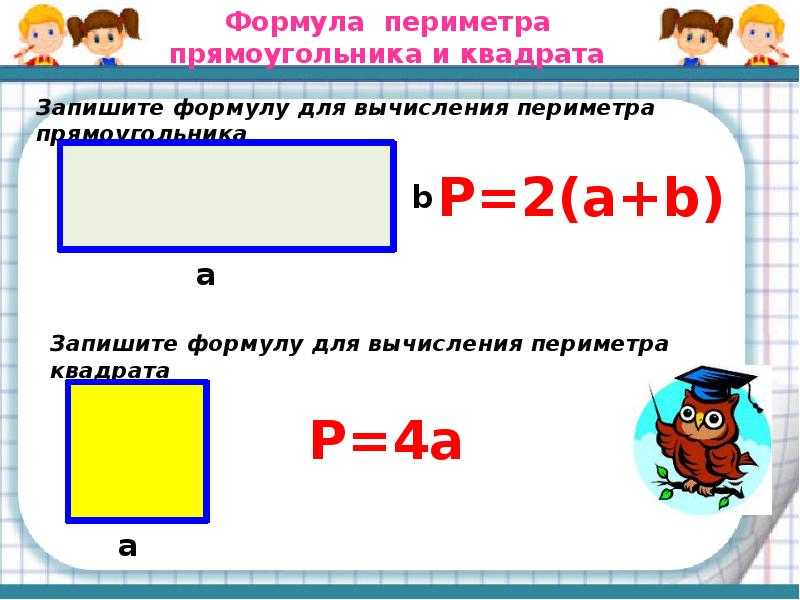
– Какой формулой мы воспользуемся для
нахождения площади? |
||||||||||||||
2. Самоопределение к деятельности Самоопределение к деятельностиАктуализация знаний |
– Ребята, вы выбрали верные формулы для
нахождения периметра и площади. Появляются
напротив каждой формулы слова. «Уменье –… найдет применение» – Вы заметили, что в пословице не хватает еще одного слова. Подумайте, за какой же формулой скрывается недостающее слово. Узнав его, мы сможем сказать девиз нашего урока. (Слайд 2) – Эти формулы будут нам сегодня помогать решать задачи на нахождение периметра и площади прямоугольника. На слайде представлены геометрические фигуры. (Слайд 3) Назовите номера фигур, которые являются прямоугольниками. Д: фигуры под номерами 1, 2, 3. Лишние фигуры исчезают по щелчку. – Ребята, среди высказываний, выберите истинные высказывания о прямоугольнике (Слайд 4) Д: Высказывания под номерами 1, 4 являются ложными, а высказывания под номерами 2, 3, 5 – истинными.  самостоятельно. (Слайд 5) – Молодцы, ребята. Следующее задание решить задачу. Найдите площадь прямоугольника со сторонами 8см и 5см |
||||||||||||||
| Устные упражнения | 8 * 5 + 2 * 5 = 50 (см2) 8 * 5 = 40 (см2) 8 * 5 + 2 * 5 = 50 (см) 8 * 5 = 40 (см) 8 * 2 + 5 = 21 (см) (8 + 5) * 2 = 26 см – Найдите правильно
записанное решение задачи и запишите ответ в
тетрадь. Проверка решения. |
||||||||||||||
| Ученики записывают величины в нужном порядке у себя в рабочих тетрадях | – Ребята, расположите величины в
порядке убывания . При верном составлении у вас
должно поучится слово. (Слайд 6) При верном составлении у вас
должно поучится слово. (Слайд 6)
|
||||||||||||||
3. Постановка учебной задачи Постановка учебной задачи |
Самопроверка записи – на слайде (клик
мышкой) Дети: 50м2 – Какое слово у вас получилось? (Квадрат) |
||||||||||||||
| Исследование общих признаков геометрических фигур | – Определите содержание двух понятий
прямоугольника и квадрата:
Вывод: Чем больше содержание понятия,
тем меньше его объем. |
||||||||||||||
| Работа над построением графической модели | – Сравните объемы понятий
«прямоугольник» и «квадрат» (Слайд 7) Д: Объем понятия прямоугольник шире, чем объем понятия квадрат – Употребляя слова «все», «некоторый», «каждый», «ни один», установите отношения между понятиями квадрат и прямоугольник (Слайд 8) Д: Некоторые прямоугольники являются квадратами. Каждый квадрат является прямоугольником. – Как изобразить отношения между понятиями прямоугольник и квадрат? (Слайд 9) Д: С помощью кругов Эйлера-Венна. |
||||||||||||||
| Физпауза | Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Головою три кивка, На четыре руки шире.  Пять, шесть – тихо сесть. |
||||||||||||||
| Использование проблемной ситуации. Своими вопросами учитель подводит учащихся к новым знаниям. | Можно ли вычислить периметр и площадь
квадрата, используя формулы? (Слайд 10)
Появляется формула: S = а * а. – Что это за формула? |
||||||||||||||
| 4. Закрепление (фронтальная работа) | – Сейчас, используя, формулы мы с вами
будем решать задачи. Учебник с.173 №590. – Прочитайте условие задачи. Длина школьного бассейна в 3раза больше его ширины. Чему равен P бассейна, если его ширина равна 9м. – О какой фигуре идет речь в задаче? (Прямоугольник) – Что известно в задаче? (Ширина прямоугольника, известно что длина в 3 раза больше его ширины) – Что мы можем узнать, используя эти данные? (Можем найти длину) – Как мы узнаем длину? а = 9 * 3 = 27 м – Можем ли мы зная длину и ширину прямоугольника, найти Р? (Можем, используя формулу Р = (а + в)* 2 Р б.  = (9 + 27) * 2 = 72 м = (9 + 27) * 2 = 72 мВывод: Где в жизни можно применить полученные умения и навыки при решении задач на нахождение периметра и площади? Д: В строительстве, на дачном участке, в ремонтных работах. |
||||||||||||||
| Групповая работа (задания предложенные учащимся, имеют компетентностно-ориентированное содержание) Создание ситуации успеха. У группы ориентир на мыслительную деятельность « Мы группа, значит мы способны действовать. В ходе рассуждений при решении технического задания, предоставляется свобода для самовыражения. |
Класс делится на группы (бригады) по 4
человека. Каждой бригаде предлагается выполнить
техническое задание. (Слайд 11) Каждый участник представляет отдельный этап работы. Роли в группе показаны на магнитной доске: – организатор – спикер – секрет – контролер Группа, которая безошибочно справится с работой, выигрывает право принять участие в проведении ремонтных работ на территории школы во время осенних каникул. 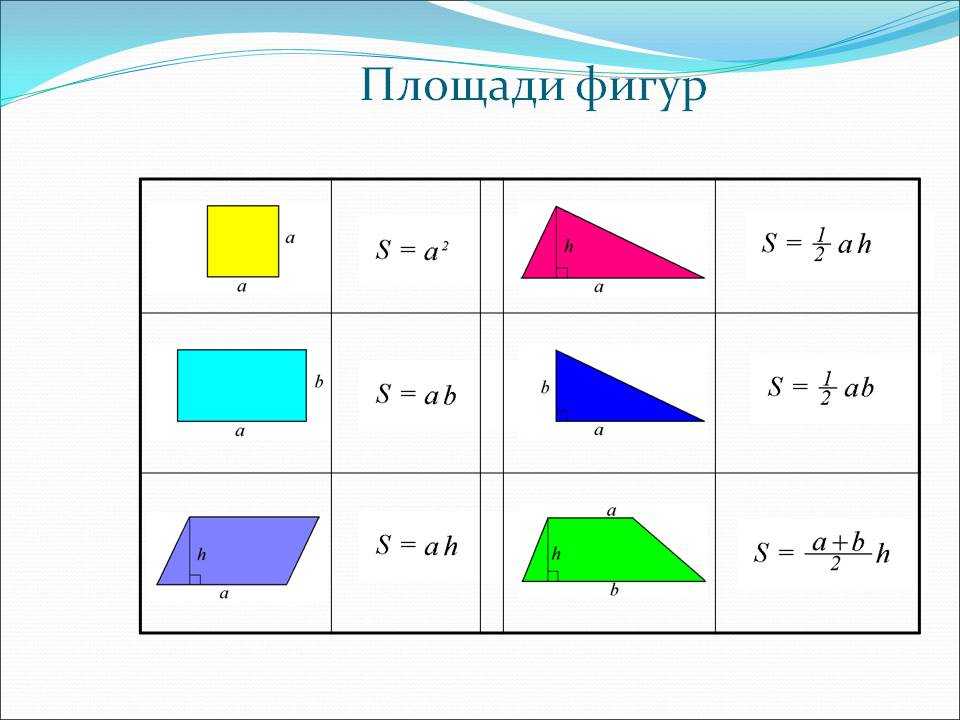 Лучшая бригада награждается
путевкой в зимний пришкольный лагерь. (Слайд 12) Лучшая бригада награждается
путевкой в зимний пришкольный лагерь. (Слайд 12) | ||||||||||||||
| Использование метода моделирования.
Наиболее удобные способы записи. Ребята при выполнении работы используют материальную и математическую модели |
1 задание. На пришкольном
участке необходимо установить бордюр вокруг 2-х
детских площадок. Сколько потребуется материала,
если длина 1 бордюра 1 м? Д: Мы
воспользовались формулой для нахождения
периметра?
2 задание. Вычислите площади фигур,
если дана мерка. (Слайд 13) Д: Мы вычислили S фигур, используя мерку величиной 10м2. Путем переложения квадрата мерки на фигуры. Мы нашли а и b. Вторую фигуру, мы превратили в прямоугольник, пререложив квадраты, для быстроты вычисления. (Слайды 14, 15) 3 задание (Слайд 16). Часть покрытия на теннисном корте испортилась. Необходимо в ходе ремонтных работ заменить покрытие и установить ограждение вокруг корта. Сколько материала потребуется? Д: Чтобы найти площадь и периметр, надо
знать его длину. От данного прямоугольника
осталась часть, нам известна ширина 30 м2.
Слева мы добавляем до 20 м2 Длина 80 м2 и
вверху добавляем 60м2 . Используя, свойства
прямоугольника, у него противоположные стороны
равны.
– Молодцы, ребята вы отлично справились с техническим заданием! |
||||||||||||||
| 5. Домашнее задание | Составить задачу по вариантам. Составить 2 задачи на нахождение периметра и площади, используя числовые данные в пределах второго десятка. В будущем мы все должны научиться решать задачи на нахождение периметра и площади только на 5. |
||||||||||||||
| 6. Рефлексия | – Что удалось нам сегодня открыть на
уроке? Расскажите. (Решали практические задачи,
учились строить модели, взаимодействовать друг с
другом в группах, учились обосновывать свой
выбор, сравнивать, упорядочивать информацию) –
Какое задание показалось наиболее трудным? А
какое наиболее интересным. Д: Уроки математики учат нас знаниям, навыкам, что нам может пригодиться и найти применение в нашей жизни. – Девизом нашего урока были слова «Умение –
везде найдет применение». И мы это доказали,
применяя нужные формулы для решения задач.
Данное умение вам пригодится при выполнении
домашнего задания. |
| Расчет периметра квадрата, прямоугольника, треугольника, круга (периметры фигур). | |
| Периметры фигур |
S это площадь или периметр
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде – книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ.
 Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b).
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
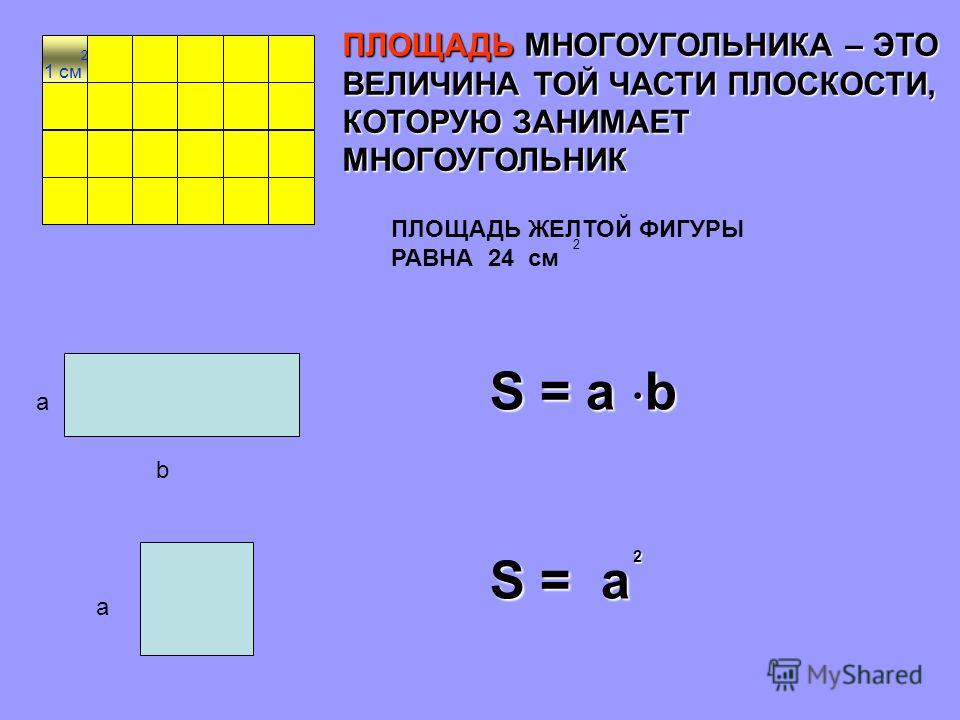
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.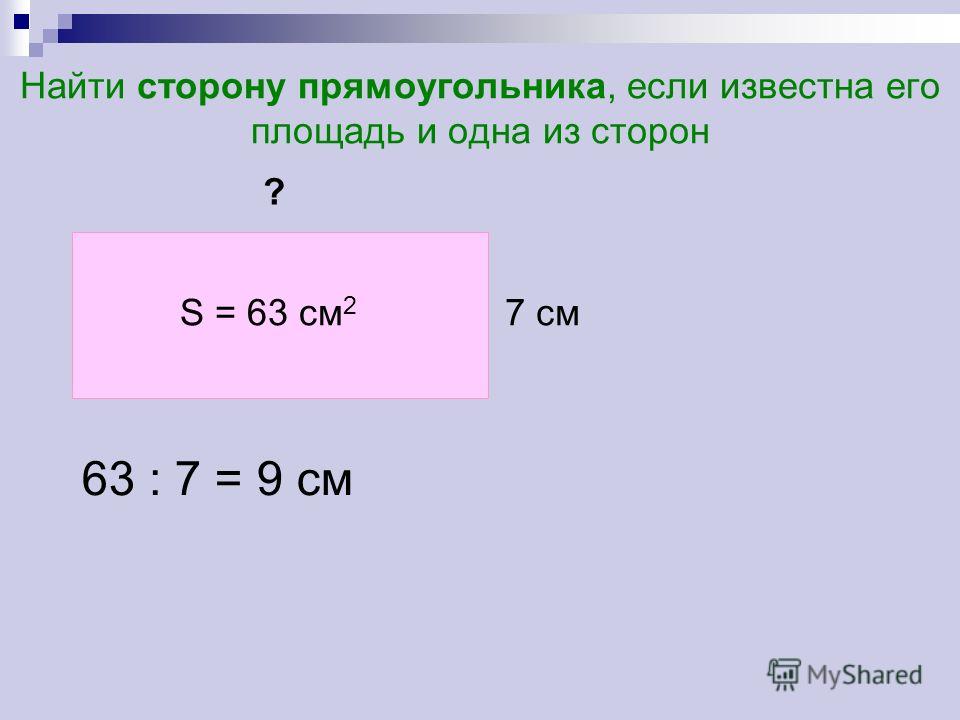
- Теорема Пифагора: a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Пери́метр (др. -греч. περίμετρον — окружность, др. -греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры [1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Периметр фигуры обладает только одним параметром — протяжённостью, или длиной, выраженной в единицах длины: метр, ярд, аршин, локоть. Или производных от них: километр, сантиметр, дециметр.
Площадь фигуры обладает двумя параметрами — например, длиной и шириной, или радиусом и коэффициентом Пи, в зависимости от формы. Величина площади выражается в единицах в квадрате: квадратных метрах, гектарах, квадратных милях
Периметр и его определение
Периметром принято называть протяжённость границы плоской фигуры, состоящей из прямых отрезков, где начало каждого последующего примыкает к окончанию предыдущего.
Строго говоря, окружность тоже обладает периметром, но для криволинейных границ принято говорить о длине окружности, или длине дуги
Для определения длины периметра, необходимо измерить, или вычислить, длину каждой стороны фигуры, а затем суммировать полученные числа.
Площадь фигуры и её определение
Площадь простейших геометрических фигур определяется по формулам.
Площадь прямоугольника равна произведению длин сторон.
Площадь круга равна произведению квадрата радиуса на число Пи=3,1415
Свои формулы есть для треугольника, сектора, трапеции, параллелограмма.
Площадь сложных криволинейных фигур вычисляется интегралом. Взятие интеграла формулы, описывающей границу фигуры, даст в результате площадь. В этом и есть геометрический смысл интеграла — он вычисляет площадь, ограниченную графиком функции на заданном участке.
Сложная фигура, lkz которой нет общей формулы, для определения площади мысленно разбивается на простейшие фигуры. Площади простых фигур вычисляются и затем суммируются.
Периметр и площадь геометрической фигуры связаны и один параметр всегда может быть вычислен из другого с минимальными дополнительными данными.
Площадь и периметр – две численные характеристики, часто используемые в геометрии. Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).
Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).
Определение
Площадь – величина, характеризующая размер поверхности, которую занимает геометрическая фигура.
Периметр – размер границ (контура) геометрической фигуры.
Понятия применимы для каждой геометрической фигуры и выражаются в различных единицах. Расчет периметра и площади определяется единицами измерения параметров, используемых для их вычисления: длин сторон, диаметра, высоты. В геометрии указанные параметры чаще всего измеряются в мм, см, м.
Сравнение
Периметр обозначается заглавной буквой P, используется при измерении многоугольников и определяется как сумма длин его сторон. Площадь обозначается буквой S и может быть использована как численная характеристика поверхности, имеющей различный контур, в том числе искривленный. Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.
Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.
Простейший случай – квадрат. Длины его сторон равны, поэтому для вычисления периметра достаточно умножить одну сторону на 4. Формула выглядит так:
Р = a + a + a + a = a х 4, где а – сторона квадрата.
Для вычисления площади квадрата используется другая формула:
Периметр и площадь прямоугольника. Что такое периметр? Как найти периметр прямоугольника разными способами
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.

- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .

- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Класс: 2
Цель: ознакомить с приёмом нахождения
периметра прямоугольника.
Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.
Оборудование: ИКТ (мультимедийный проектор, презентация к уроку), картинки с геометрическими фигурами для физминутки, модель магического квадрата, у учеников – модели геометрических фигур, маркерные доски, линейки, учебники, тетради.
ХОД УРОКА
1. Организационный момент
Проверка готовности к уроку. Приветствие.
Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.
2. Устный счёт
а) Использование магических фигур. (Приложение 1 )
– Заполним клетки магического квадрата,
назовите его особенности (сумма чисел по
горизонталям, вертикалям и диагоналям равны) и
определите волшебное число. (39)
(39)
По цепочке дети заполняют квадрат на доске и в тетрадях .
б) Знакомство со свойствами магических треугольников. (Приложение 2 )
– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.
3. Подготовка к изучению нового материала
– Перед Вами геометрические фигуры. Назовите
их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение
3 )
– Что такое прямоугольники. (Прямоугольники –
четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон
четырёхугольников? Периметр – сумма длин сторон
фигур.
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все
стороны?
– Какие свойства у противолежащих сторон
прямоугольников? (У прямоугольника
противоположные стороны равны).
– Если противоположные стороны равны, надо ли
измерять все стороны? (Нет. )
)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом? (Учащиеся
работают устно с комментированием.)
4. Изучение новой темы
– Прочитайте тему нашего урока: «Периметр
прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её
длина равна – а , а ширина – в .
Желающие находят Р у доски. Учащиеся в тетрадях записывают решение.
– Как записать это по-другому?
Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.
– Мы получили формулу нахождения периметра прямоугольника. (Приложение 5 )
5. Закрепление
Стр. 44 № 2.
Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.
6. Физминутка. Сигнальные карточки
Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.
7. Практическая работа
– У Вас на партах лежат в конвертах
геометрические фигуры. Как мы их назовём?
– Что такое прямоугольники?
– Что вы знаете о противолежащих сторонах
прямоугольников?
– Измерьте стороны фигур по вариантам,
найдите периметр разными способами.
– Проверяем у соседа.
Взаимопроверка тетрадей .
– Прочитайте: Как нашли периметр? Что можно
сказать о периметрах данных фигур? (Они равны) .
– Начертите прямоугольник с таким же Р, но
другими сторонами.
Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16
Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16
8. Графический диктант
Слева 6 клеток. Поставили точку. Начинаем
движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4
– вправо вверх. Какая фигура? Преврати её в
прямоугольник. Дострой. Найди Р разными
способами.
Поставили точку. Начинаем
движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4
– вправо вверх. Какая фигура? Преврати её в
прямоугольник. Дострой. Найди Р разными
способами.
Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.
9. Пальчиковая гимнастика
Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.
(Слова сопровождаются движениями)
10. Составление и решение задачи по условию (Приложение 8 )
Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) –
ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм
11. Самостоятельная работа
Самостоятельная работа
12. Итог урока
– Чему учились. Как находили Р прямоугольника?
13.Оценивание
Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.
14.Домашнее задание
С. 44 № 5 (с пояснениями).
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.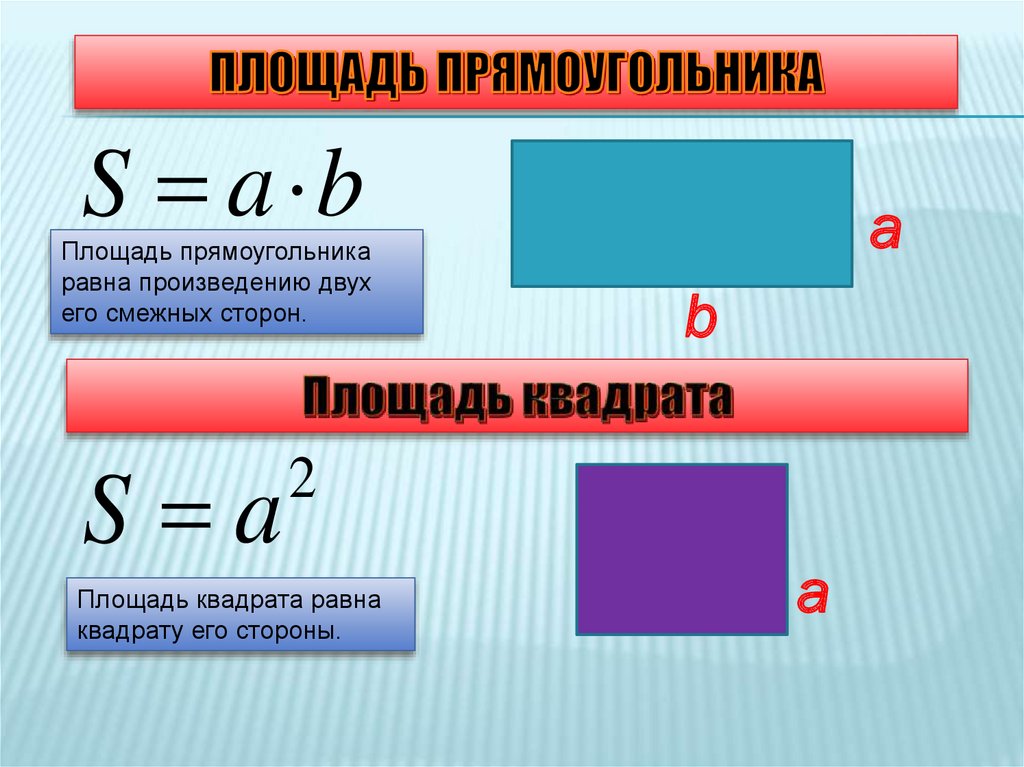
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс.
 — М.: Дрофа, 2004.
— М.: Дрофа, 2004. - Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис. 1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2.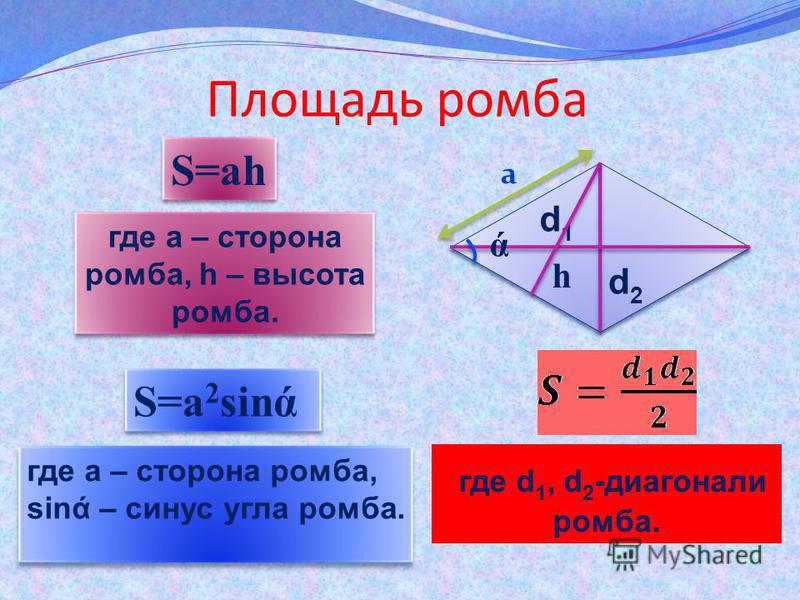 Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины.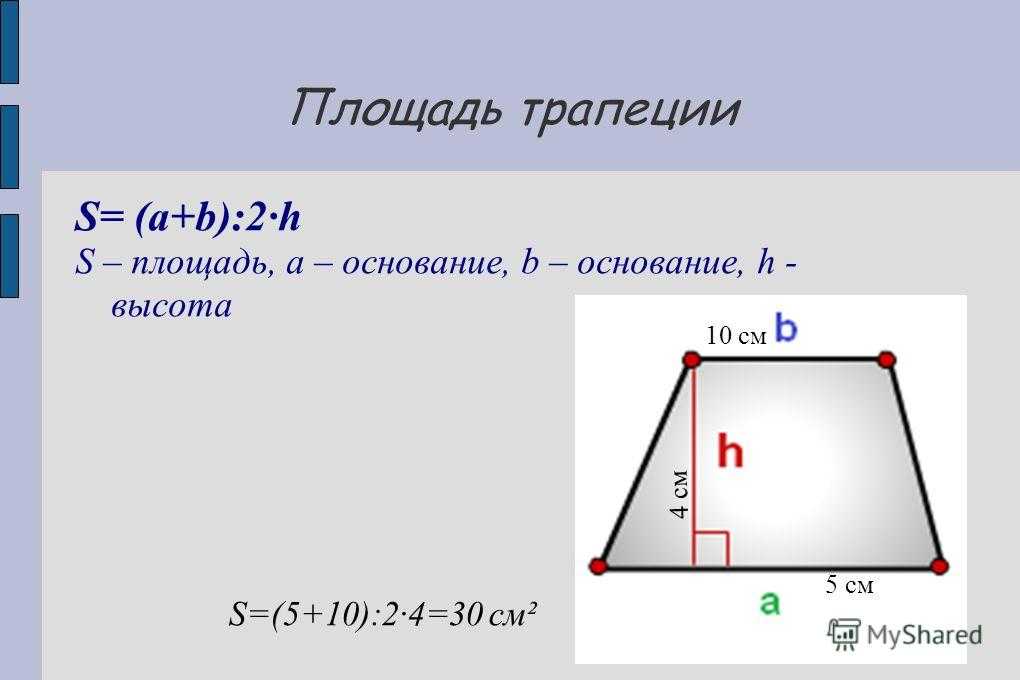 Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.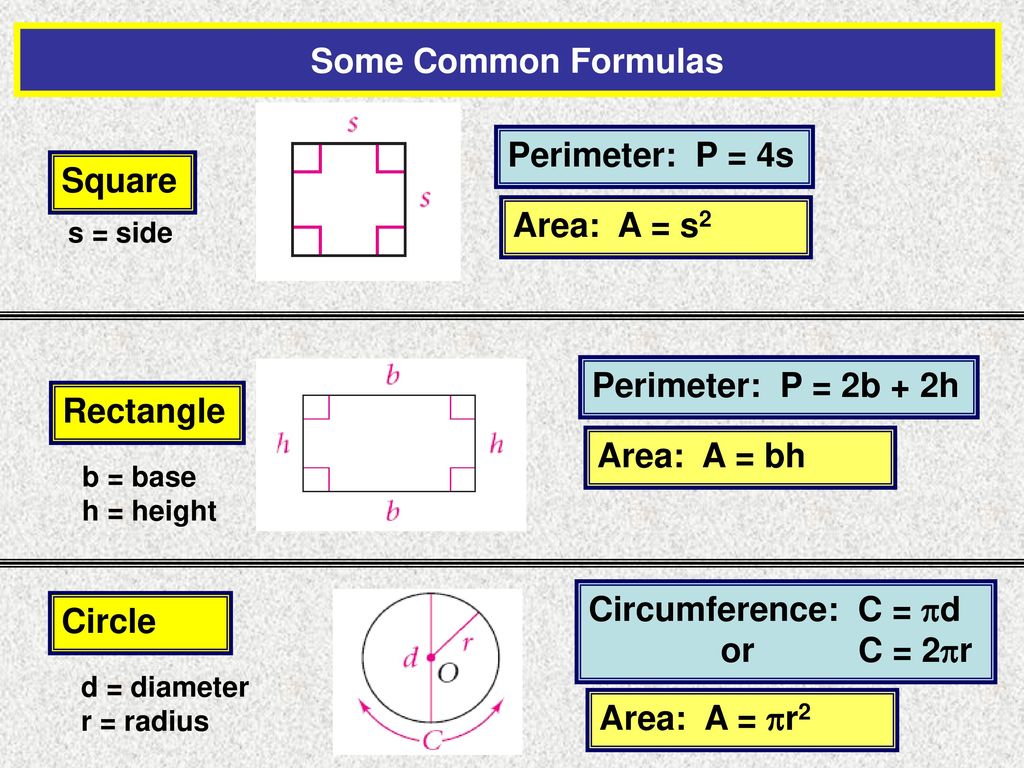
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
- Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
- Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD.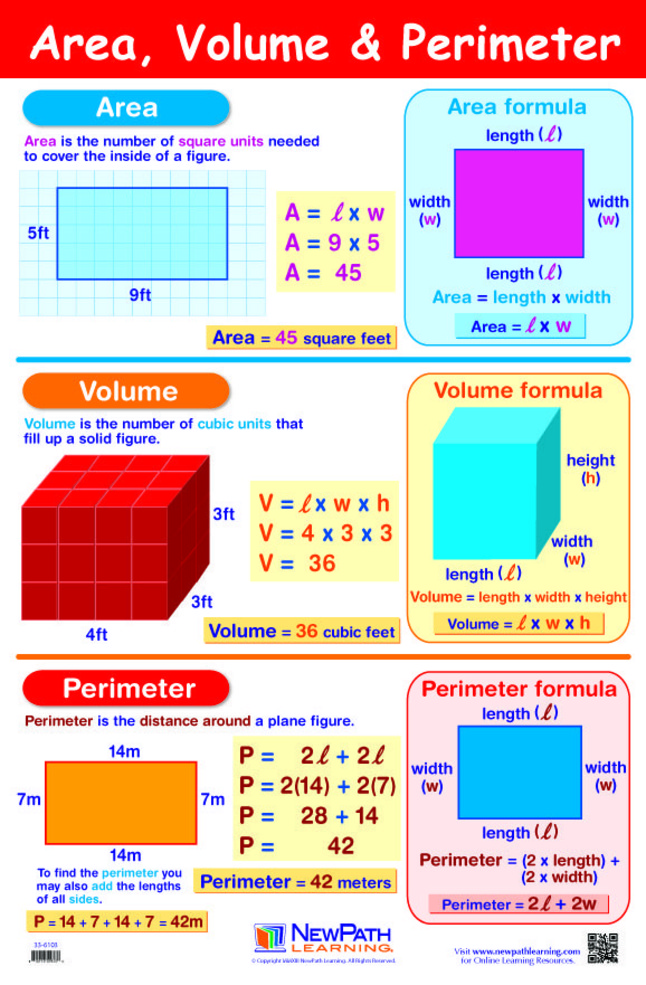 Найдите периметр прямоугольника ABCD».
Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.
Ответ: 50 (м).
Вычисление площади
Более сложной величиной является площадь фигуры.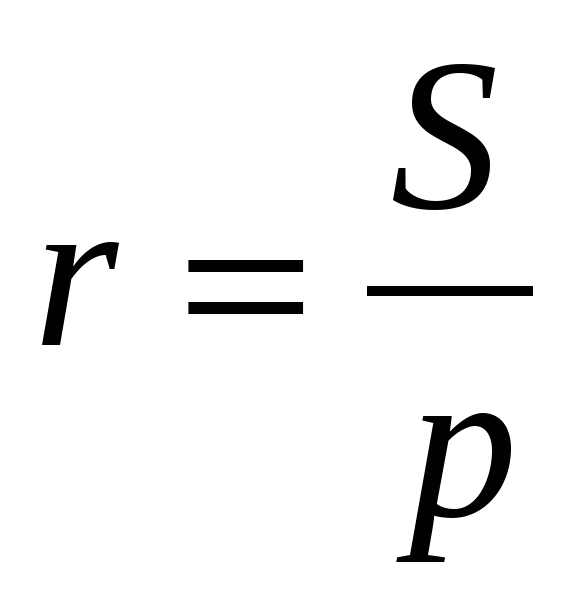 Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.
- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду.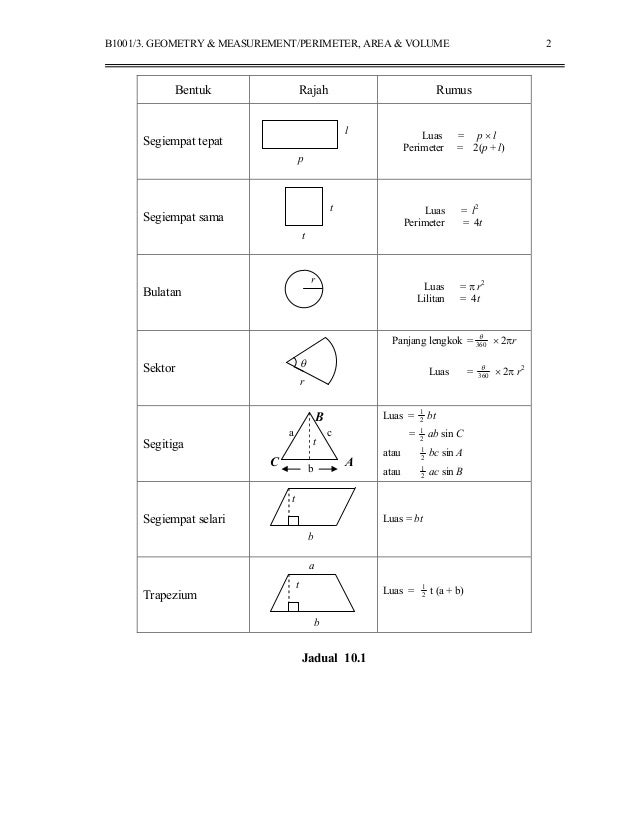 После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Ответ: 30 (м).
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».
Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).
Ответ: 18 (м²).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями.Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости./918870b1bc4a305.s.siteapi.org/img/fa91516c043aa701896b5ea126baf73168f97729.jpg) Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь.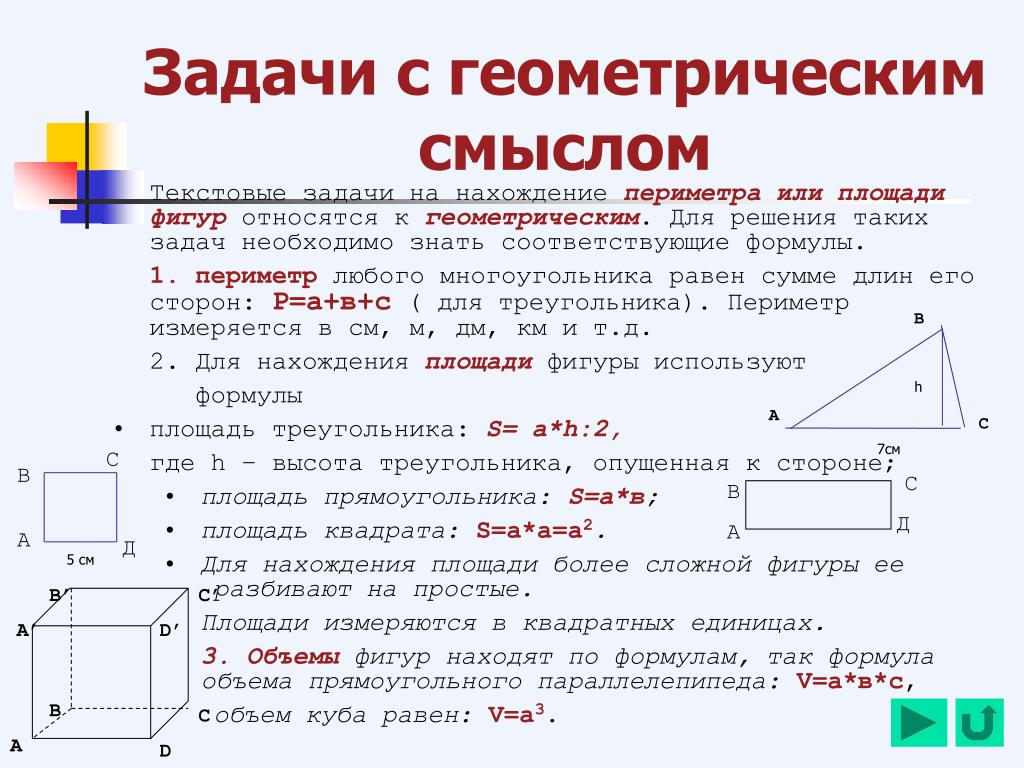 В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).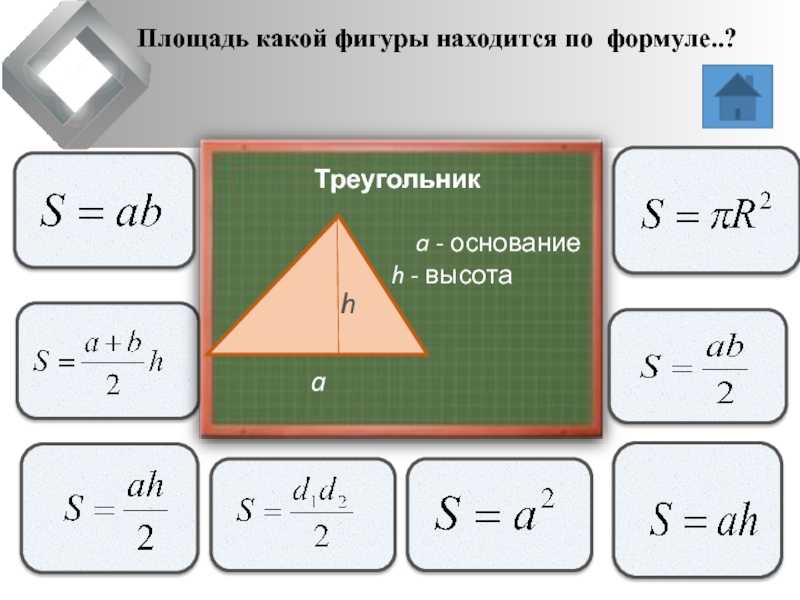
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины.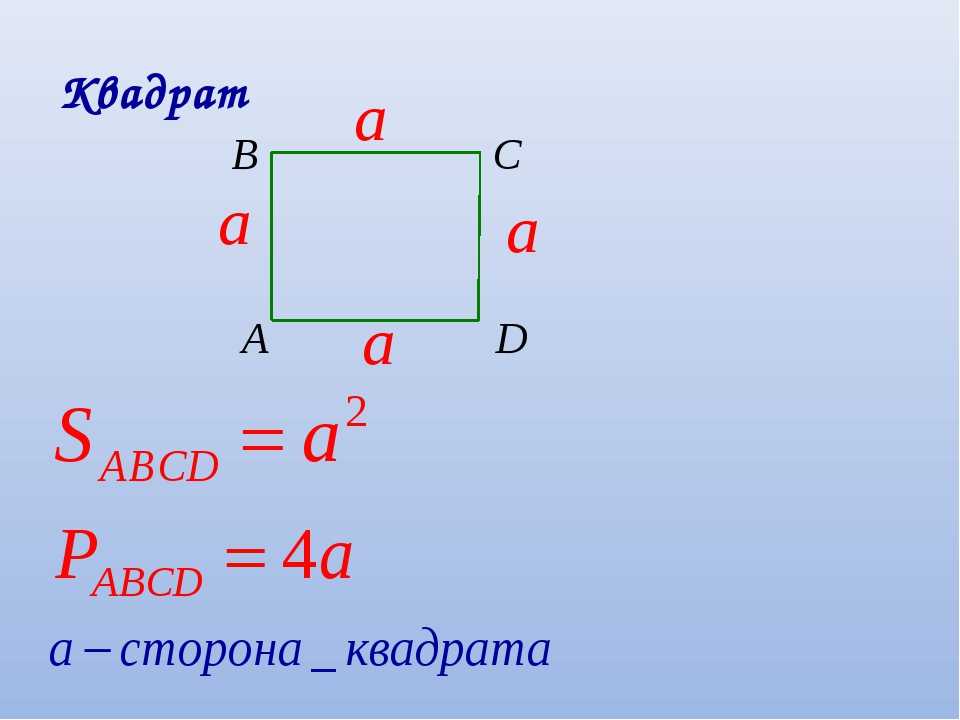 Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).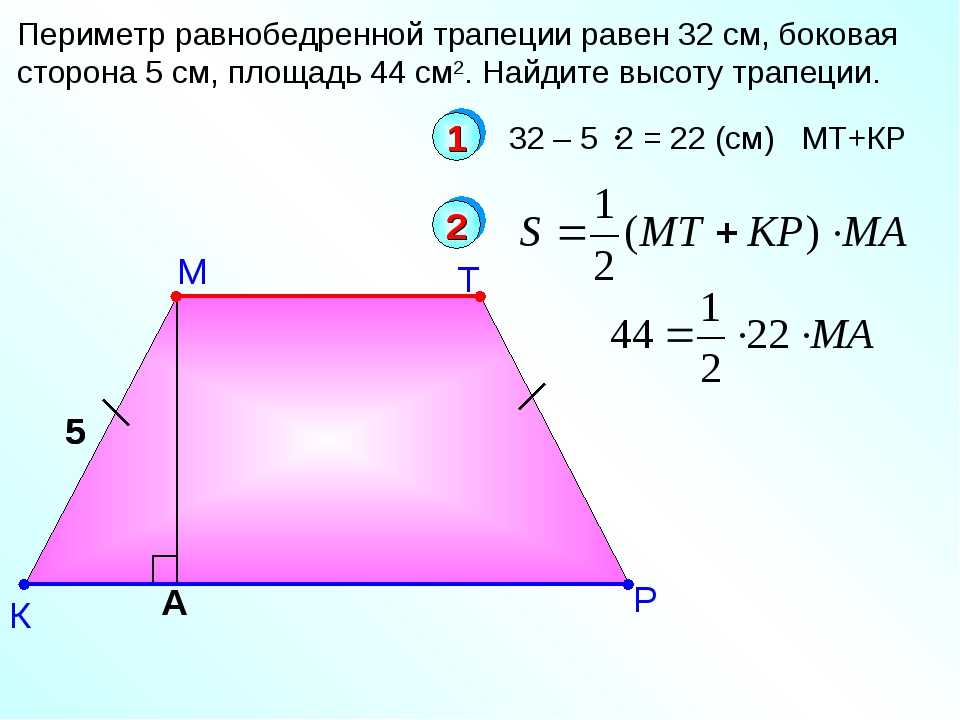
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.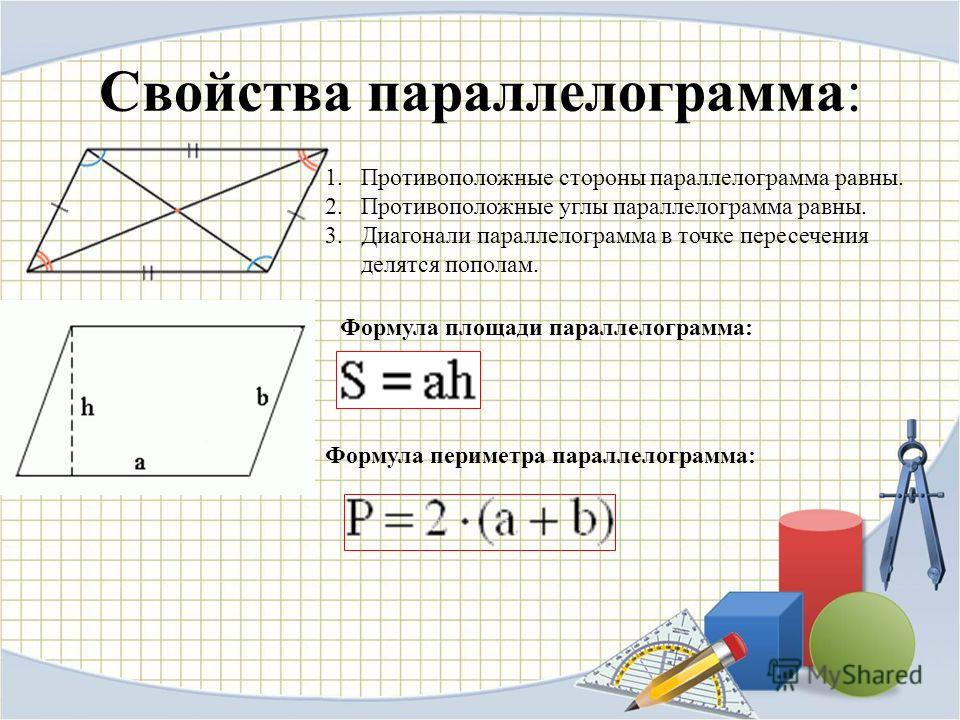
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3.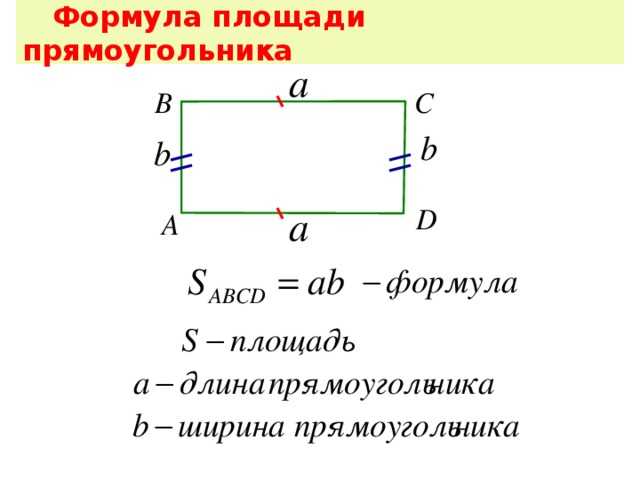 Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.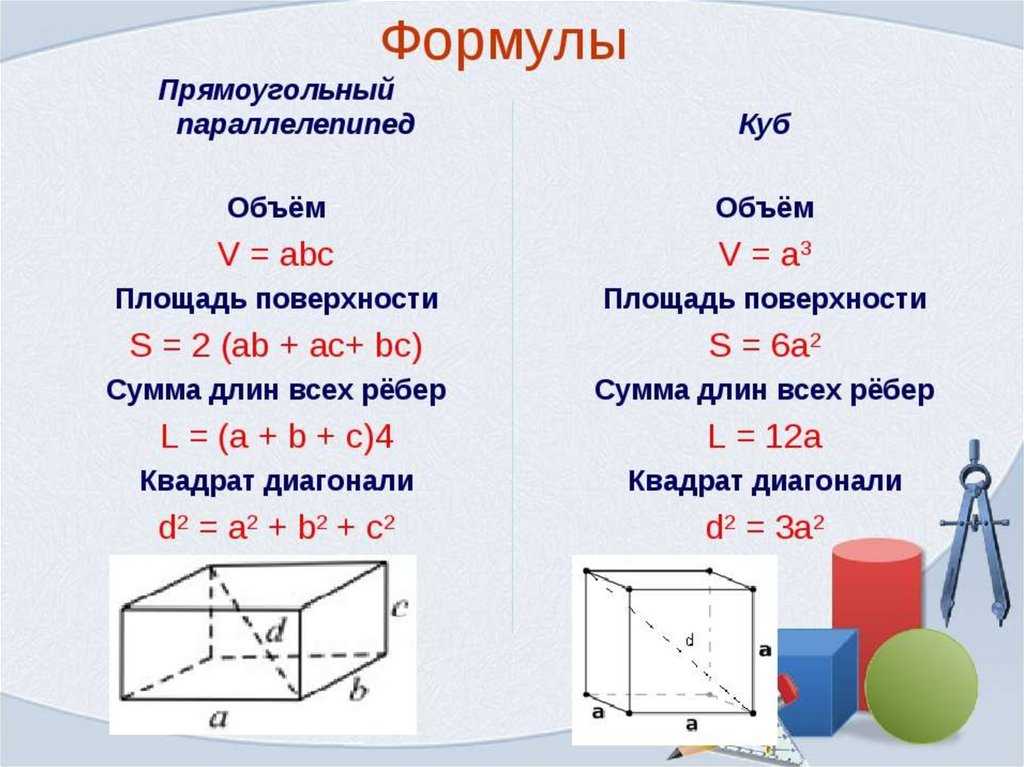
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.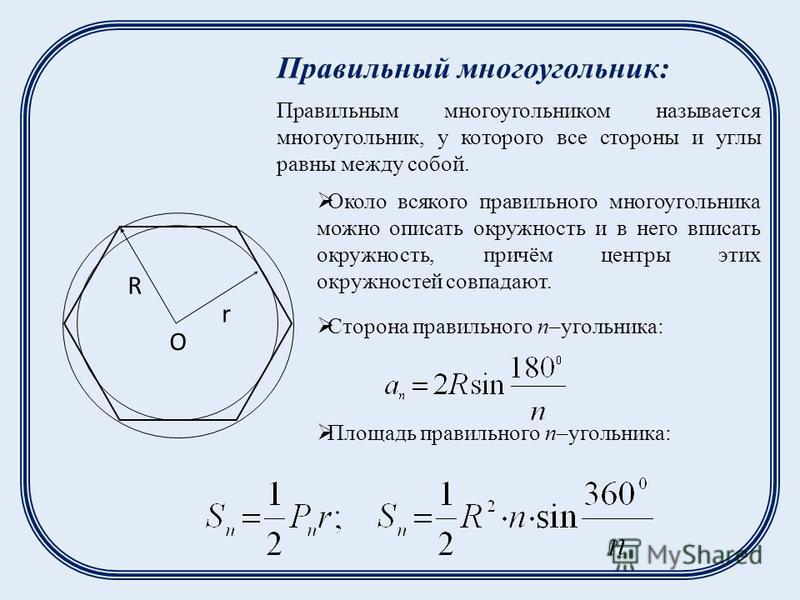
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Показать решение
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Показать решение
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Показать решение
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Показать решение
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Показать решение
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.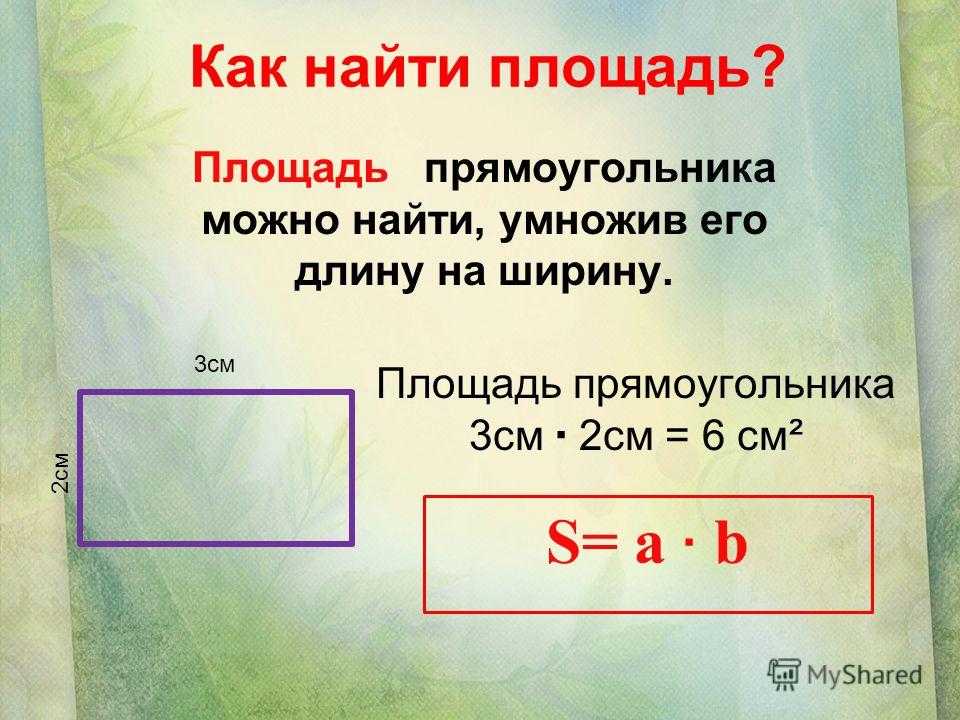
Показать решение
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Показать решение
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Показать решение
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Периметр и площадь геометрических фигур
- Периметр
- Площадь
- Таблица перевода квадратных единиц
Существует много плоских геометрических фигур: точка, линия (прямая или кривая), отрезок, угол, ломаная и т. д.:
д.:
Если внимательно посмотреть на все эти фигуры, то можно выделить две из них, которые образованы замкнутыми линиями (окружность и треугольник). Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:
Периметр
Периметр – это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.
Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P
:
Площадь
Площадь – это часть плоскости, занимаемая замкнутой плоской геометрической фигурой.
Любая плоская замкнутая геометрическая фигура имеет определённую площадь. На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Обычно за единицу измерения площади принимается квадрат, у которого сторона равна единице измерения длины: миллиметру, сантиметру, метру и т. д.
На рисунке изображён квадратный сантиметр. Квадратный сантиметр — квадрат, у которого каждая сторона имеет длину 1 см:
Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д.
Таблица перевода квадратных единиц
| мм2 | см2 | дм2 | м2 | ар (сотка) | гектар (га) | км2 | |
|---|---|---|---|---|---|---|---|
| мм2 | 1 мм2 | 0,01 см2 | 10-4 дм2 | 10-6 м2 | 10-8 ар | 10-10 га | 10-12 км2 |
| см2 | 100 мм2 | 1 см2 | 0,01 дм2 | 10-4 м2 | 10-6 ар | 10-8 га | 10-10 км2 |
| дм2 | 104 мм2 | 100 см2 | 1 дм2 | 0,01 м2 | 10-4 ар | 10-6 га | 10-8 км2 |
| м2 | 106 мм2 | 104 см2 | 100 дм2 | 1 м2 | 0,01 ар | 10-4 га | 10-6 км2 |
| ар | 108 мм2 | 106 см2 | 104 дм2 | 100 м2 | 1 ар | 0,01 га | 10-4 км2 |
| га | 1010 мм2 | 108 см2 | 106 дм2 | 104 м2 | 100 ар | 1 га | 0,01 км2 |
| км2 | 1012 мм2 | 1010 см2 | 108 дм2 | 106 м2 | 104 ар | 100 га | 1 км2 |
| 104 = 10 000 | 10-4 = 0,000 1 |
| 106 = 1 000 000 | 10-6 = 0,000 001 |
| 108 = 100 000 000 | 10-8 = 0,000 000 01 |
| 1010 = 10 000 000 000 | 10-10 = 0,000 000 000 1 |
| 1012 = 1 000 000 000 000 | 10-12 = 0,000 000 000 001 |
Периметр прямоугольника с заданной площадью
Создано Вишнувардханом Шактибалой
Отзыв Александры Зайонц, доктор медицины
Последнее обновление: 14 марта 2022 г.
- Что такое периметр прямоугольника?
- Как использовать периметр прямоугольника с калькулятором заданной площади?
- Захватим прямоугольники!
- Часто задаваемые вопросы
Вы ищете способ найти периметр прямоугольника, зная площадь и сторону? Тогда вы в правильном месте. Наш калькулятор периметра прямоугольника с заданной площадью поможет вам быстро найти периметр прямоугольника. Сразу после того, как вы вставите площадь A и сторону Side 1 (это сторона, которая вам известна), наш калькулятор выдаст вам периметр P .
Читайте дальше, чтобы узнать больше о:
- Периметр прямоугольника;
- Уравнения, используемые для нахождения периметра прямоугольника; и
- Другие калькуляторы, которые помогут вам ответить на любые вопросы, связанные с прямоугольником.
Чему равен периметр прямоугольника?
Периметр — это величина , которая измеряет общую длину внешней границы 2-D или 3-D геометрии : измерение начинается с одной точки (скажем, точки z) и заканчивается в той же точке (точка z).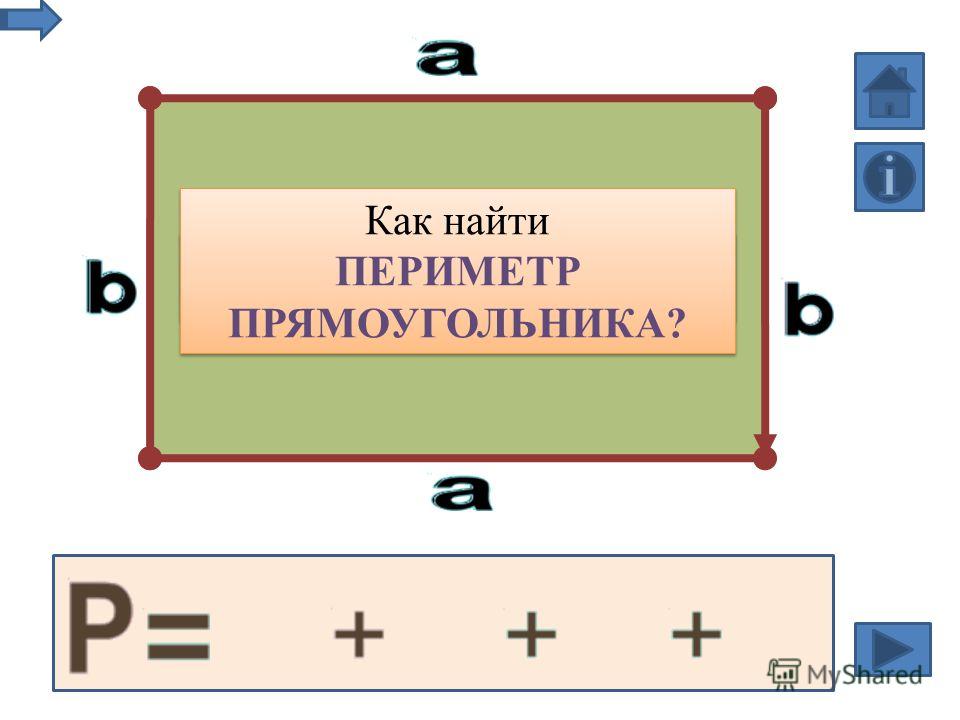 Прямоугольник замкнут четырьмя перпендикулярными сторонами, две из которых единственные. Периметр уравнения прямоугольника равен
Прямоугольник замкнут четырьмя перпендикулярными сторонами, две из которых единственные. Периметр уравнения прямоугольника равен P=(a+b+a+b) , что в основном измеряет все стороны. В упрощенном виде: P=2×(a+b) .
Как использовать периметр прямоугольника с калькулятором заданной площади?
Чтобы использовать наш калькулятор, выполните следующие пункты:
- Во-первых, вы должны знать площадь
Aи хотя бы одну сторону прямоугольника; - Вставьте значение площади и известное значение стороны в поля Area (A) и Side 1 (a) ;
- После вставки наш калькулятор покажет недостающую сторону 9.0019 Сторона 2 (b) и периметр прямоугольника P .
- Ура! Мы считаем, что теперь вы можете использовать наш калькулятор периметра прямоугольника с заданной площадью, чтобы быстро найти периметр прямоугольника. Если вы ищете способы найти все возможные параметры, связанные с прямоугольником, вам следует проверить следующий раздел.

Захватим прямоугольники!
Здесь мы представляем вам все калькуляторы, которые помогут вам найти ответы на любые вопросы, связанные с прямоугольниками:
- Калькулятор площади прямоугольника
- Размеры прямоугольного калькулятора
- Калькулятор диагонали прямоугольника
- Калькулятор угла диагонали прямоугольника
- Периметр прямоугольника
- Калькулятор площади поверхности прямоугольника
- Калькулятор длины прямоугольника
- Калькулятор ширины прямоугольника
- Калькулятор длины и ширины прямоугольника с учетом площади
- Калькулятор длины и ширины прямоугольника с учетом периметра
- Калькулятор масштабного коэффициента прямоугольника
- Квадратные футы прямоугольника калькулятор
- Калькулятор золотого прямоугольника
Часто задаваемые вопросы
Как найти периметр прямоугольника по заданной площади?
Вы можете использовать следующие точки, чтобы найти периметр прямоугольника с заданной площадью:
- Вам нужно , чтобы знать хотя бы одну сторону прямоугольника: назовите ее
Сторона 1; - Теперь используйте уравнение площади, т.
 2, а длина 4 м? 9 по длине
2, а длина 4 м? 9 по длине l =4 см, т. е.w=20/4=5; и - После того, как ширина
wнайдена, периметр вычисляется какP=2×(w+l)=2×(5+4)=20 м.
В чем разница между площадью и периметром прямоугольника?
Разница между площадью и периметром следующая:
- Площадь — это величина, которая показывает сколько места занимает геометрия , тогда как периметр дает нам измерение общей длины внешней границы геометрии ;
- Площадь уравнения прямоугольника задается как
A=длина×ширина, а периметр уравнения прямоугольника задается какP=2×(длина+ширина) Единица площади - СИ равна м 2 , а для периметра — м .
Чему равен периметр прямоугольника 11м х 5м?
Периметр этого прямоугольника равен 32 м . 11 м и 5 м — длина и ширина прямоугольника соответственно.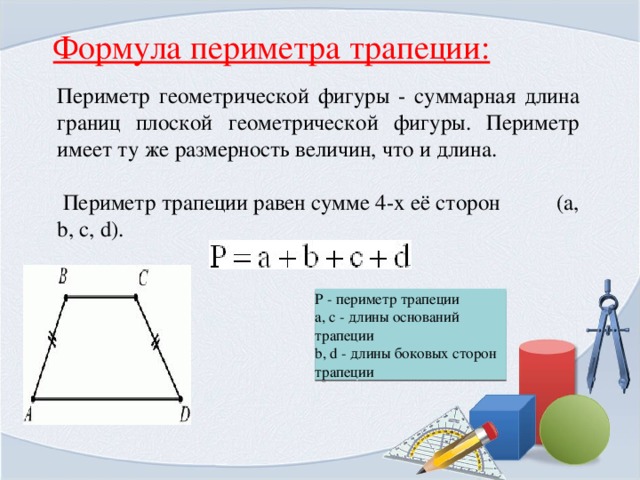 Зная длину и ширину, можно вычислить периметр как 9.0021 Р=2×(11+5)=32 .
Зная длину и ширину, можно вычислить периметр как 9.0021 Р=2×(11+5)=32 .
Vishnuvardhan Shakthibala
Область (A)
Сторона 1 (A)
Сторона 2 (B)
Периметр (P)
Проверьте 21 Аналогичные геометрические расчеты. … еще 18
Как найти периметр прямоугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 5 6 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти периметр прямоугольника
Учитывая прямоугольник на диаграмме, каков периметр прямоугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Периметр прямоугольника находится путем сложения длин всех четырех сторон. Поскольку две длинные стороны равны 12 см, а две более короткие стороны равны 7 см, периметр можно найти по формуле:
Поскольку две длинные стороны равны 12 см, а две более короткие стороны равны 7 см, периметр можно найти по формуле:
Периметр 38 см.
Сообщить об ошибке
Одна сторона прямоугольника равна 7 дюймам, а другая — 9 дюймам. Чему равен периметр прямоугольника в дюймах?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти периметр прямоугольника, сложите длины его четырех сторон. Если у вас есть только ширина и высота, то вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине). Умножьте высоту и ширину на два и сложите результаты.
Сообщить об ошибке
Площадь прямоугольника равна . Ширина в четыре раза меньше длины. Что такое периметр?
Возможные ответы:
Правильный ответ:
Объяснение:
Для прямоугольника площадь равна , а периметр – , где длина и ширина.
Пусть = длина и = ширина.
Уравнение площади для решения становится , или .
Чтобы разложить на множители, найдите сумму двух чисел до -4 и умножьте на -96. -12 и 8 будут работать:
x 2 + 8x — 12x — 96 = 0
x(x + 8) — 12(x + 8) = 0
(x — 12)(x + 8) = 0
Приравняйте каждый множитель к нулю и решите:
или .
Следовательно, длина равна , а ширина равна , что дает периметр .
Сообщить об ошибке
Владелец ранчо хочет окружить свое прямоугольное поле забором из колючей проволоки, который стоит 1,75 доллара за фут. Размер поля 200 ярдов на 400 ярдов. Сколько будет стоить забор?
Возможные ответы:
Правильный ответ:
Объяснение:
Преобразуйте размеры из ярдов в футы, умножив их на 3: Это дает размеры 600 футов и 1200 футов. Таким образом, периметр этой фермы равен
Таким образом, периметр этой фермы равен
.
Умножьте это на стоимость забора за фут:
Сообщить об ошибке
Длина прямоугольника дюймы, а ширина дюймы, найдите периметр прямоугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти периметр любого прямоугольника, сложите все стороны:
20 + 20 + 12 + 12 = 64 дюйма
Вы также можете использовать эту формулу:
, где P = периметр , l = длина, w = ширина
Эта формула исходит из того, что в каждом прямоугольнике есть 2 длины и 2 ширины.
Сообщить об ошибке
Найдите периметр этого прямоугольника.
Возможные ответы:
Правильный ответ:
Пояснение:
Помните, что периметр прямоугольника равен сумме всех четырех сторон:
Из рисунка видно, что A=6 и B=24.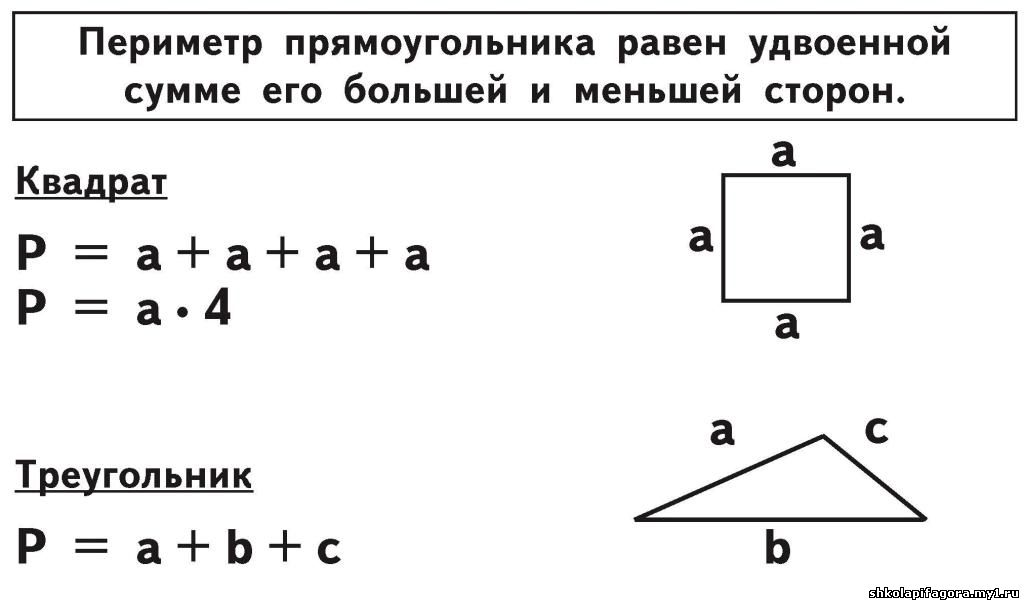
Сообщить об ошибке
Прямоугольник имеет площадь 56 квадратных футов и ширину 4 фута. Чему равен периметр прямоугольника в футах?
Возможные ответы:
36
14
30
120
28
90 90 Пояснение:
Разделите площадь прямоугольника на ширину, чтобы найти длину 14 футов. Периметр — это сумма длин сторон, которая в данном случае равна 14 футам + 4 футам + 14 футам + 4 футам или 36 футам.
Сообщить об ошибке
Площадь прямоугольника , а ширина этого прямоугольника в два раза больше его высоты. Чему равен периметр прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь прямоугольника равна произведению ширины на высоту, и нам говорят, что в этом прямоугольнике ширина в два раза больше высоты.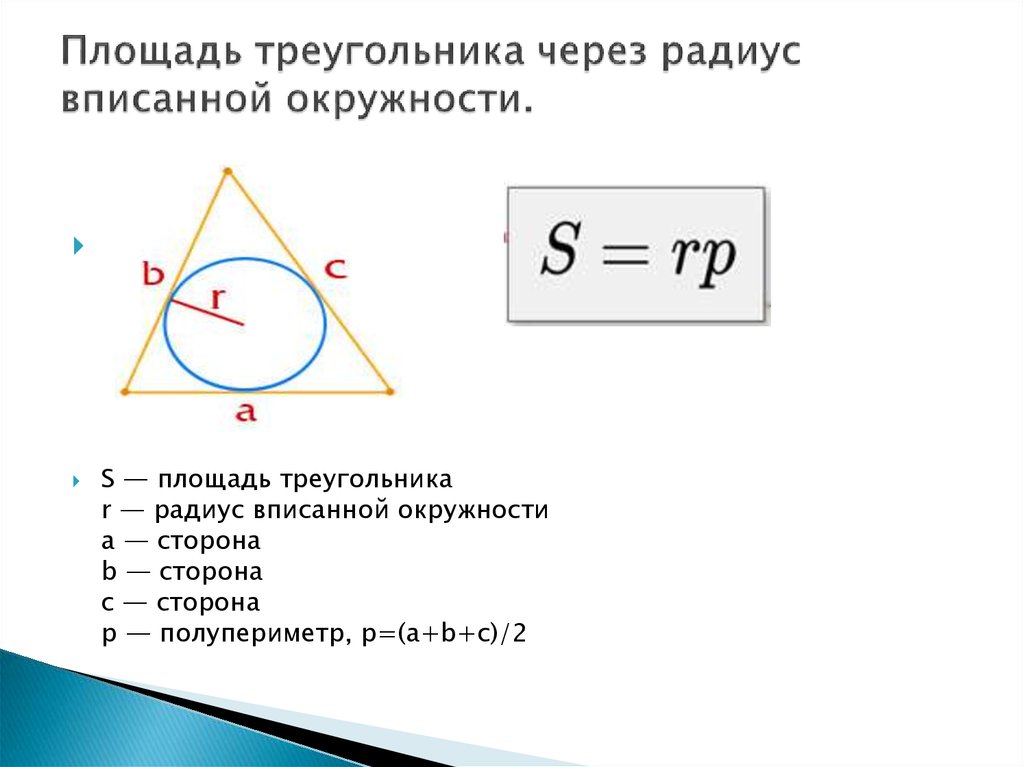
Следовательно, .
Подставьте значение площади:
Решите для , чтобы найти ширину 4 дюйма. Используя нашу формулу выше, высота должна быть 8 дюймов. Затем складываем все стороны прямоугольника вместе, чтобы найти периметр:
Сообщить об ошибке
Роберт проектирует прямоугольный сад. Он хочет, чтобы площадь сада составляла 9 квадратных метров. Если длина участка будет на три метра меньше, чем удвоенная ширина, то каков будет периметр участка в метрах?
Возможные ответы:
1,5
10
12
6
3
Правильный ответ:
12
Объяснение:
Пусть l — длина сада, а w — ширина.
По условиям задачи l = 2w-3.
Подставьте это для длины в формулу площади:
A = l x w = (2w — 3) x w = 9
Найдите ширину:
2w²- 3w — 9 =0
(2w + 3) (w — 3) = 0
w равно 3 или -3/2, но у нас не может быть отрицательной ширины, поэтому w = 3.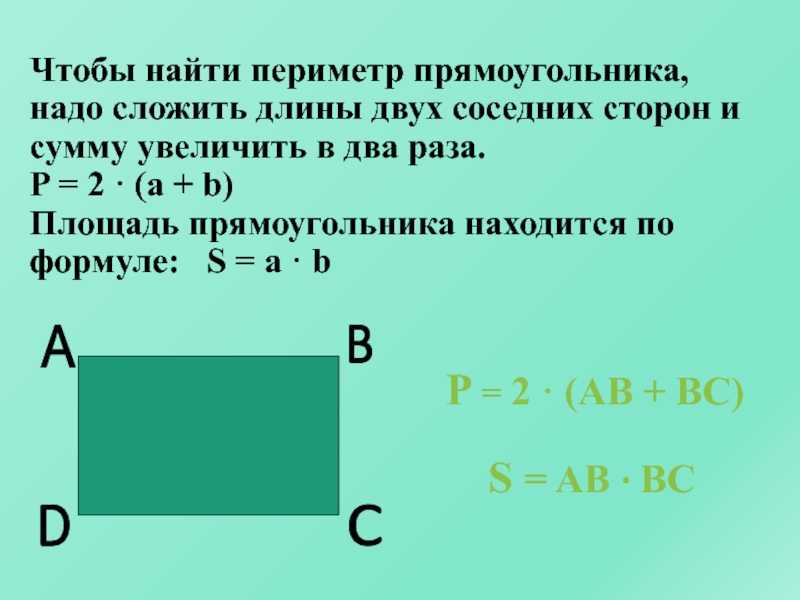
Если w = 3, то длина = 2(3) — 3 = 3.
Теперь подставьте ширину и длину в формулу периметра:
P = 2 l + 2w = 2(3) + 2(3) = 12
Сообщить об ошибке
Найдите периметр прямоугольника, длина которого равна , а ширина .
Возможные ответы:
Правильный ответ:
Пояснение:
Напомним, как найти периметр прямоугольника:
Для данного прямоугольника
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
Вычисление периметра прямоугольников (примеры вопросов)
Решение задач с прямоугольным периметром — это навык, который имеет множество интересных практических применений. Например, мы можем использовать расчеты периметра для таких ситуаций, как требования к ограждению вокруг игрового поля, размеры рамы картины, расстояния вокруг пешеходной дорожки или размеры большого окна. Вычисление периметра прямоугольников — полезный навык, потому что он часто используется в нашей повседневной жизни.
Например, мы можем использовать расчеты периметра для таких ситуаций, как требования к ограждению вокруг игрового поля, размеры рамы картины, расстояния вокруг пешеходной дорожки или размеры большого окна. Вычисление периметра прямоугольников — полезный навык, потому что он часто используется в нашей повседневной жизни.
Примеры вопросов по периметру прямоугольников
Давайте вспомним, что периметр относится к расстоянию по внешней стороне двумерной формы. Может быть полезно визуализировать периметр в виде ограждения, окружающего парк или задний двор. Когда мы вычисляем периметр, мы, по сути, вычисляем общее расстояние вокруг этой двумерной формы.
Расчет задач периметра можно выполнять разными способами, но наиболее эффективная стратегия — просто использовать формулу периметра.
Чему равен периметр прямоугольника?
Формула периметра прямоугольника гласит, что P = (L + W) × 2, где P представляет периметр, L представляет длину, а W представляет ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр. Например, если прямоугольник ниже представляет собой сад, который нуждается в кирпичной рамке, мы можем использовать формулу периметра, чтобы определить, сколько футов кирпичной бордюры нам нужно всего.
Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр. Например, если прямоугольник ниже представляет собой сад, который нуждается в кирпичной рамке, мы можем использовать формулу периметра, чтобы определить, сколько футов кирпичной бордюры нам нужно всего.
Формула периметра прямоугольника
Формула утверждает, что P = (L + W) × 2, поэтому давайте подставим 14 футов вместо L и 6 футов вместо W. Теперь у нас есть P = (14 + 6) × 2 , что упрощается до 40 или 40 футов.
Использование формулы периметра экономит нам немного времени, избегая альтернативной стратегии, которая заключалась бы в суммировании длин каждой стороны отдельно. 14 + 6 + 14 + 6 даст правильный ответ, но эта стратегия обычно занимает больше времени, поэтому рекомендуется использовать формулу.
Однако не во всех задачах о периметре можно получить длину и ширину таким простым способом. На самом деле, некоторые задачи о периметре дадут вам одно измерение, а также площадь прямоугольника.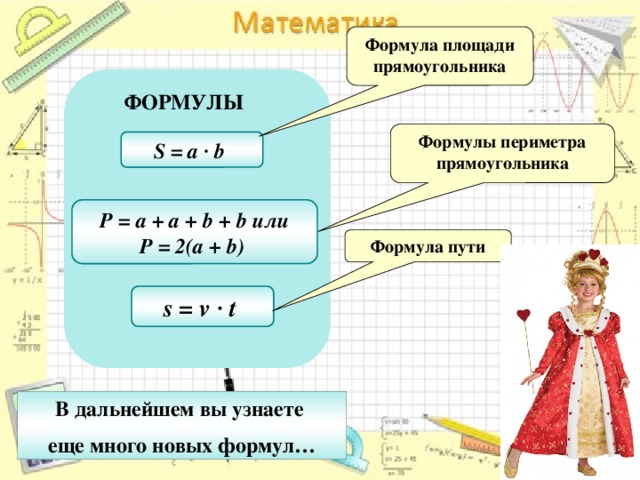 Чтобы решить такую проблему периметра, нам нужно пересмотреть наше понимание площади. Помните, чтобы вычислить площадь прямоугольника, мы просто умножаем длину на ширину. Прямоугольник размером 3,5 см на 4 см будет иметь площадь 14 см 2 , потому что 3,5 × 4 = 14. Давайте воспользуемся этим знанием площади и применим его к задаче периметра.
Чтобы решить такую проблему периметра, нам нужно пересмотреть наше понимание площади. Помните, чтобы вычислить площадь прямоугольника, мы просто умножаем длину на ширину. Прямоугольник размером 3,5 см на 4 см будет иметь площадь 14 см 2 , потому что 3,5 × 4 = 14. Давайте воспользуемся этим знанием площади и применим его к задаче периметра.
Например, предположим, что вам нужно обрамить большое прямоугольное окно площадью 35 квадратных футов и длиной 7 футов. Давайте используем то, что мы знаем о вычислении площади, чтобы найти периметр.
Мы знаем, что площадь поверхности находится путем умножения длины на ширину. Это означает, что семь умножить на что-то равно 35, 7 × ? = 35. Мы можем найти недостающую длину стороны, разделив 35 на 7, что равно 5. Теперь мы можем применить формулу периметра, потому что мы знаем, что длина равна 7 футам, а ширина 5 футам.
P = (L + W) × 2 становится P = (7 + 5) × 2, что упрощается до 24 или 24 футов.
Теперь, когда мы рассмотрели формулу периметра и ее различные приложения, рассмотрим следующий вопрос. Есть ли у прямоугольника площадью 20 квадратных футов более одного возможного варианта периметра? Если вы сказали да, то вы правы. Прямоугольники с ограниченной площадью, например 20 квадратных футов, могут иметь различные периметры. Например, прямоугольник площадью 20 квадратных футов может иметь размеры 1 фут × 20 футов, 2 фута × 10 футов или 4 фута × 5 футов. Все эти варианты будут давать разные периметры, хотя все они имеют одинаковую площадь. . Давайте докажем эту концепцию, рассчитав периметр трех только что упомянутых возможных прямоугольников: 1 фут × 20 футов, 2 фута × 10 футов и 4 фута × 5 футов.
Есть ли у прямоугольника площадью 20 квадратных футов более одного возможного варианта периметра? Если вы сказали да, то вы правы. Прямоугольники с ограниченной площадью, например 20 квадратных футов, могут иметь различные периметры. Например, прямоугольник площадью 20 квадратных футов может иметь размеры 1 фут × 20 футов, 2 фута × 10 футов или 4 фута × 5 футов. Все эти варианты будут давать разные периметры, хотя все они имеют одинаковую площадь. . Давайте докажем эту концепцию, рассчитав периметр трех только что упомянутых возможных прямоугольников: 1 фут × 20 футов, 2 фута × 10 футов и 4 фута × 5 футов.
1 фут × 20 футов: P = (Д + Ш) × 2 = (1 + 20) × 2 = 42 фута
2 фута × 10 футов = Д + Ш × 2 = (2 + 10) × 2 = 24 футов
4 фута × 5 футов = Д + Ш × 2 = 4 + 5 × 2 = 18 футов
*Также важно отметить, что формула P = (Д + Ш) × 2 применима только к прямоугольникам. Эта формула будет работать только для четырехугольников, у которых два набора конгруэнтных сторон.
Вот несколько примеров вопросов, касающихся площади прямоугольника.
Вопрос №1:
Какая формула используется для вычисления периметра прямоугольника?
\(Периметр=4+(длина+ширина)\)
\(Периметр=\frac{(\text{длина}×\текст{ширина})}{2}\)
\(Периметр=( длина+ширина)×4 \)
\(Периметр=(длина+ширина)×2 \)
Показать Ответ
Ответ:
Прямоугольник имеет две равные длины и две равные ширины. Чтобы найти периметр или расстояние вокруг прямоугольника, нам нужно сложить длины всех четырех сторон. Это можно сделать эффективно, просто добавив длину и ширину, а затем умножив эту сумму на два, поскольку каждой длины по две. \(Периметр=(длина+ширина)×2\) — это формула для периметра.
Скрыть ответ
Вопрос №2:
Вычислите периметр данного прямоугольника.
22 фута
44 фута
86,5 футов
108,75 футов
Показать ответ
Ответ:
Мы можем рассчитать периметр прямоугольника, используя формулу \ (Периметр = Длина+Wideth). ×2\). Мы видим, что длина равна 14,5 футам, а ширина — 7,5 футам, поэтому наша формула принимает вид \(Периметр=(14,5+7,5)×2\), что упрощается до 44. Периметр прямоугольника равен 44 футам.
Скрыть Ответ
Вопрос №3:
Определите периметр прямоугольника, если его площадь 64 м 2 , а длина 16 м.
40 метров
45 метров
30 метров
38 метров
Показать Ответ
Ответ:
Для того, чтобы определить ширину прямоугольника, нужно сначала определить метр. Площадь прямоугольника вычисляется путем умножения \(длина×ширина\), поэтому мы можем использовать следующее уравнение, чтобы найти недостающее значение (w).
Площадь прямоугольника вычисляется путем умножения \(длина×ширина\), поэтому мы можем использовать следующее уравнение, чтобы найти недостающее значение (w).
Площадь = l × w
64 м 2 =16 × w
Разделите обе стороны на 16, чтобы найти w.
w = 4 или 4 м
Теперь, когда мы знаем длину и ширину, мы можем использовать формулу \(Периметр=(длина+ширина)×2\), чтобы найти периметр. Подставив 16 м в длину и 4 м в ширину, мы получим следующее: \(Периметр=(16 м+4 м)×2\), что упрощается до 40 м. Периметр прямоугольника 40 метров.
Скрыть ответ
Вопрос № 4:
Стороны прямоугольной песочницы в Санниленд-парке имеют длину 15 и 8,5 футов. Определить периметр песочницы. Ответ: 2\). Мы знаем, что длина равна 15 футам, а ширина — 8,5 футам, поэтому мы можем подставить эти значения в формулу, чтобы найти периметр. Теперь наша формула принимает вид \(Периметр=(15+8,5)×2\), что упрощается до 47 или 47 футов.
Скрыть ответ
Вопрос № 5:
Глория проектирует сад для своего заднего двора. Она знает, что хочет иметь 24 квадратных фута в саду, но она гибка в отношении размеров. Она хочет поставить забор вокруг сада, но забор (за метр) может быть довольно дорогим, поэтому она хочет сравнить варианты. Вариант А состоит в том, чтобы построить сад размером 8 футов на 3 фута. Вариант Б – построить сад размером 6 футов на 4 фута. Какой вариант потребует меньшего количества ограждений и, следовательно, меньшей стоимости?
Вариант А дешевле
Вариант Б дешевле
Показать ответ
Ответ:
Вариант А имеет длину 8 футов и ширину 3 фута. Периметр этого сада составляет 22 фута.
Вариант B имеет длину 6 футов и ширину 4 фута. Периметр этого сада составляет 20 футов.
Вариант B требует меньшего количества ограждений; следовательно, это менее дорогой вариант.
Скрыть ответ
Вернуться к примерам вопросов по математике
Формулы периметра – определение, вывод и примеры
Периметр – это путь или граница вокруг фигуры, или его также называют контуром фигуры. В геометрии мы сталкиваемся с различными формами, от 2D до 3D. Формулы периметра охватывают формулы различных двумерных фигур в геометрии. Давайте изучим различные формулы различных форм, а также решим несколько примеров.
Значение формул периметра
Формулы периметра используются для нахождения расстояния вокруг двумерной фигуры путем сложения длин ее сторон. Периметром считается сумма длин сторон различных фигур. Формулу периметра можно определить, если известны размеры формы. Каждый полигон имеет свою формулу периметра в зависимости от формы объекта. На изображении ниже показаны все формулы для различных фигур в геометрии.
Формула периметра различных фигур
Формула периметра может быть определена как сумма длин всех сторон любой геометрической формы.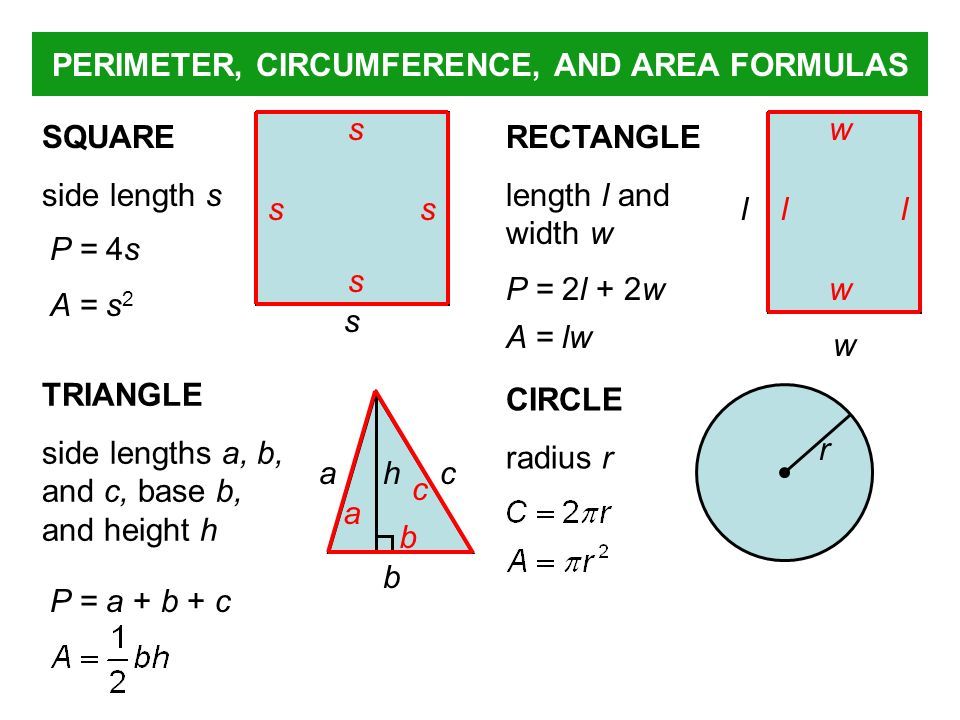 Различные фигуры в геометрии имеют формулу периметра в зависимости от формы и размера. Давайте посмотрим на формулы периметра этих фигур.
Различные фигуры в геометрии имеют формулу периметра в зависимости от формы и размера. Давайте посмотрим на формулы периметра этих фигур.
Формула периметра квадрата
Как мы уже знаем, периметр – это длина сторон, границы или пути фигуры. Формула периметра квадрата может быть рассчитана путем сложения длин всех его сторон. Формула для вычисления периметра квадрата может быть дана как,
Периметр квадрата, (P) = 4 × стороны
Формула периметра прямоугольника
Формула периметра прямоугольника зависит от расстояния, пройденного всего прямоугольника, т. е. границы или охвата всех 4 сторон прямоугольник. l + b + l + b = 2l + 2b = 2(l+b). Периметр прямоугольника равен удвоенной сумме его длины и ширины. Следовательно, формула для периметра прямоугольника:
Периметр прямоугольника, (P) = 2(l + b) единиц
Где
- l длина прямоугольника
- b — ширина прямоугольника
Формула периметра треугольника
Формула периметра треугольника может быть рассчитана путем сложения всех сторон, в данном случае, всех трех сторон треугольника. Для разных типов треугольников используются разные формулы периметра. Но общая формула, используемая для нахождения периметра треугольника, такова:
Для разных типов треугольников используются разные формулы периметра. Но общая формула, используемая для нахождения периметра треугольника, такова:
.Периметр треугольника = сумма всех трех сторон
Формулы периметра для различных типов треугольников:
- Периметр разностороннего треугольника = a + b + c, где a, b и c – три разные стороны.
- Периметр равнобедренного треугольника = 2a + b, где a – длина каждой из двух сторон равной длины, а b – третья сторона.
- Периметр равностороннего треугольника = 3 × a, где a – длина каждой стороны треугольника
- Периметр прямоугольного треугольника = p + b + h или p + b + √(p2 + b2), где h — гипотенуза прямоугольного треугольника, p — перпендикуляр прямоугольного треугольника, а b — основание прямоугольный треугольник
- Периметр прямоугольного равнобедренного треугольника = h + 2l, где h — высота, а l — длина
Формула периметра параллелограмма
Формула периметра параллелограмма определяется суммой всех сторон, равных друг другу. Однако формулу периметра параллелограмма можно найти и в том случае, если не указаны стороны объекта, а указаны диагонали или угол. Следовательно, формула для вычисления периметра параллелограмма:
Однако формулу периметра параллелограмма можно найти и в том случае, если не указаны стороны объекта, а указаны диагонали или угол. Следовательно, формула для вычисления периметра параллелограмма:
- Периметр параллелограмма (со сторонами), P = 2 (a + b), где a и b — две смежные стороны
- Периметр параллелограмма (с одной стороной и диагоналями), P = 2a + √(2x 2 + 2y 2 — 4a 2 ), где a — одна сторона, а x и y — диагонали
- Периметр параллелограмма (со стороной, высотой и углом), P = 2a + 2h / sin θ, где a — сторона, h — высота, а θ — угол
Формула периметра круга
Формула периметра окружности состоит из двух основных компонентов — 2 констант и одного радиуса окружности. Формула для периметра круга представляет собой длину окружности круга, а формула для расчета периметра или окружности круга:
Периметр круга = 2 π r = π d
Где
- r — радиус окружности
- d — диаметр окружности
- π(pi) приблизительно измерено как 3,412
Формула периметра ромба
Формула периметра ромба рассчитывается путем сложения длин всех сторон фигуры. Есть два параметра, по которым можно вычислить формулу периметра ромба — когда даны стороны и когда даны углы. Отсюда формула для периметра ромба:
Есть два параметра, по которым можно вычислить формулу периметра ромба — когда даны стороны и когда даны углы. Отсюда формула для периметра ромба:
- Периметр ромба (со сторонами), P = 4a, где a длина стороны
- Периметр ромба (с углами), P = 2√(d1) 2 +(d2) 2 , где d1 и d2 — длины диагоналей
Формула периметра трапеции
Формула для вычисления периметра трапеции состоит в сложении длин всех четырех сторон объекта. Формула периметра трапеции гарантирует, что она покрывает всю границу трапеции. Следовательно, формула для вычисления периметра трапеции:
Периметр трапеции, P = сумма всех сторон = a + b + c + d , где a, b, c и d — длины сторон
Формула периметра воздушного змея
Формула периметра воздушного змея рассчитывается путем сложения всех сторон воздушного змея, а расстояние рассчитывается путем сложения стороны каждой пары. Следовательно, формула для расчета периметра воздушного змея:
Периметр воздушного змея, P = 2(a+b) , где a и b – длины двух пар воздушных змеев
Формула периметра многоугольников
Поскольку многоугольники представляют собой замкнутые плоские формы, периметр многоугольников также лежит в двумерной плоскости. Формула периметра многоугольника может быть рассчитана путем измерения общей длины многоугольника. Периметр многоугольников рассчитывается двумя способами: относительно правильных многоугольников и неправильных многоугольников. Формула для вычисления периметра правильного многоугольника:
Формула периметра многоугольника может быть рассчитана путем измерения общей длины многоугольника. Периметр многоугольников рассчитывается двумя способами: относительно правильных многоугольников и неправильных многоугольников. Формула для вычисления периметра правильного многоугольника:
Правильные многоугольники:
- Периметр шестиугольника = 6 × (длина одной стороны)
- Периметр пятиугольника = 5 × (длина одной стороны)
Неправильные многоугольники:
Периметр неправильных многоугольников = сумма всех сторон
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Забронируйте бесплатный пробный урок
Примеры использования формулы периметра
Пример 1: Джози хочет добавить кружево в качестве украшения по краям своей столешницы. Лист столешницы имеет форму прямоугольника. Длина листа столешницы составляет 140 дюймов, а ширина — 95 дюймов. Какой длины понадобится шнурок?
Лист столешницы имеет форму прямоугольника. Длина листа столешницы составляет 140 дюймов, а ширина — 95 дюймов. Какой длины понадобится шнурок?
Решение: Дана длина l = 140 дюймов, ширина b = 95 дюймов
Длина шнурка = периметр листа
Мы знаем формулу периметра прямоугольника = 2(l+b).
Применяя значения длины и ширины в этой формуле, мы получаем Периметр = 2(l+b) = 2 (140 + 95) = 2 × 235 = 470 дюймов.
Следовательно, Джози понадобится 470 дюймов кружева.
Пример 2: Определить длину стороны равностороннего треугольника, если его периметр равен 30 единицам.
Решение: Дан периметр равностороннего треугольника = 30
Пусть длина стороны равностороннего треугольника равна а.
а вычисляется по формуле периметра равностороннего треугольника.
Р = 3 х а
30 = 3 × a
a = 30/3
a = 10 единиц
Следовательно, длина стороны равностороннего треугольника равна 10 единицам.
Пример 3. Если периметр квадрата равен 74 единицам, найдите его сторону.
Решение: Дано: периметр квадрата P = 74 единицы
Используя формулу периметра квадрата,
P = 4 × боковые панели
74 = 4 × сторона
Сторона = 74/4
Сторона = 18,5 единиц
Следовательно, сторона квадрата равна 18,5 единицам
Часто задаваемые вопросы о формулах периметра
Что такое формулы периметра?
Формулы периметра используются для определения периметра различных геометрических фигур, таких как квадрат, треугольник, прямоугольник и т. д. Каждая фигура имеет свою формулу для вычисления периметра. Формула периметра представляет собой общую длину сторон всех этих фигур, и она варьируется в зависимости от размера и формы объекта.
Какие формы охватывают формулы периметра?
Существуют разные формулы периметра для различных фигур в зависимости от их формы и размера.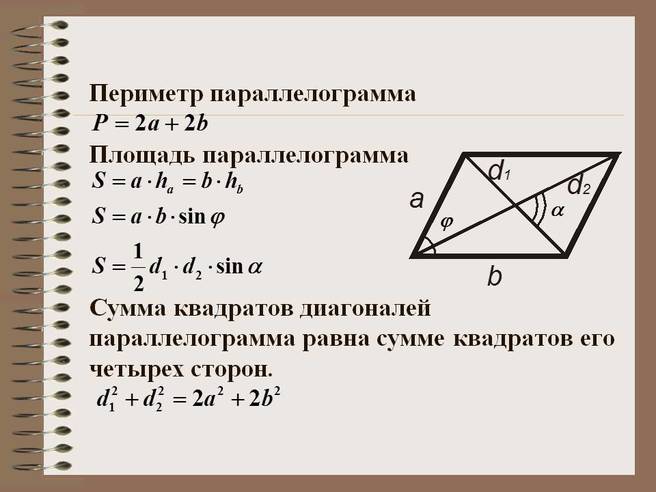 Различные объекты:
Различные объекты:
- Квадрат
- Прямоугольник
- Треугольник
- Круг
- Воздушный змей
- Ромб
- Параллелограмм
- Трапеция
Что такое формула периметра многоугольников?
Формула периметра для многоугольников разделена на две части: правильные многоугольники и неправильные многоугольники. Формула для расчета периметра многоугольника:
- Периметр правильного многоугольника = (количество сторон) × (длина одной стороны)
- Периметр неправильного многоугольника = Сумма всех сторон
Какова формула периметра различных типов треугольников?
Формулы периметра для различных типов треугольников:
- Периметр разностороннего треугольника = a + b + c, где a, b и c – три разные стороны
- Периметр равнобедренного треугольника = 2a + b, где a – две стороны равной длины, а b – третьи стороны
- Периметр равностороннего треугольника = 3 × a, где a – длина каждой стороны треугольника
- Периметр прямоугольного треугольника = p + b + h или p + b + √(p2 + b2), где h — гипотенуза прямоугольного треугольника, p — перпендикуляр прямоугольного треугольника, а b — основание прямоугольный треугольник
- Периметр прямоугольного равнобедренного треугольника = h + 2l, где h — высота, а l — длина
Периметр квадрата – формула, определение, примеры
Периметр квадрата определяется как общая длина, которую покрывает его граница. Периметр любой замкнутой геометрической формы рассчитывается путем нахождения расстояния вокруг этой формы. Для квадрата периметр можно вычислить, найдя сумму всех сторон. Поскольку все четыре стороны равны, длина каждой стороны квадрата в четыре раза больше. Давайте узнаем о периметре квадрата подробно в этой статье.
Периметр любой замкнутой геометрической формы рассчитывается путем нахождения расстояния вокруг этой формы. Для квадрата периметр можно вычислить, найдя сумму всех сторон. Поскольку все четыре стороны равны, длина каждой стороны квадрата в четыре раза больше. Давайте узнаем о периметре квадрата подробно в этой статье.
| 1. | Что такое периметр квадрата? |
| 2. | Вычисление периметра квадрата по формуле |
| 3. | Как найти периметр квадрата? |
| 4. | Часто задаваемые вопросы по периметру площади |
Каков периметр квадрата?
Периметр любой формы — это либо путь, который охватывает/окружает/очерчивает форму (в двух измерениях), либо ее длина (в одном измерении). Периметр квадрата можно вычислить, сложив длины всех его сторон.
Периметр квадрата Формула
Формула для вычисления периметра квадрата может быть математически выражена как;
Периметр квадрата, (P) = 4 × сторона
Пример: Вычислите периметр квадрата, каждая сторона которого равна 7 единицам.
Решение: Дано: Длина стороны квадрата = 7 единиц.
Мы знаем, используя формулу периметра квадрата,
Периметр квадрата = 4 × Сторона
⇒ 4 × 7 = 28 единиц
Вычисление периметра квадрата по формуле
Периметр квадрата определяется как общая длина границы квадрата. Чтобы вычислить периметр квадрата, найдем сумму всех его сторон. Поскольку все стороны квадрата равны для квадрата, каждая сторона измеряется в единицах «s», поэтому периметр будет задан как
Периметр квадрата = s + s + s + s
⇒ Периметр квадрата = 4s, где «s» — длина стороны квадрата.
Как найти периметр квадрата?
Периметр квадрата можно рассчитать различными способами в зависимости от известных параметров. В этом разделе рассматривается метод с использованием
- Длина стороны
- Диагональ
- Район
Периметр квадрата, используя длину стороны
В этом случае мы обычно находим периметр, умножая длину стороны на 4.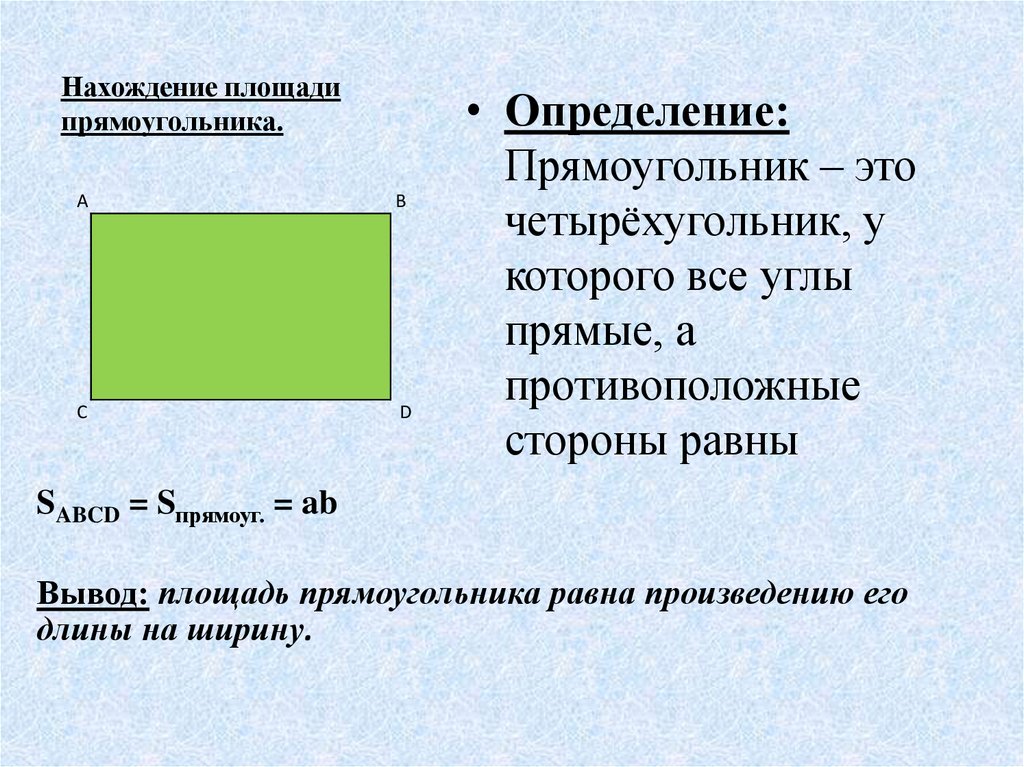 Чтобы найти периметр квадрата, используя длину стороны, мы можем выполнить шаги, указанные ниже,
Чтобы найти периметр квадрата, используя длину стороны, мы можем выполнить шаги, указанные ниже,
- Шаг 1: Запишите размер стороны.
- Шаг 2: Умножьте указанную длину на 4.
- Шаг 3: Выразите полученный результат в соответствующей единице.
Периметр квадрата с использованием диагонали
Периметр квадрата также можно вычислить, если нам известна длина его диагонали. Чтобы найти периметр квадрата по диагонали, мы можем выполнить шаги, указанные ниже:
- Шаг 1: Запишите размер диагонали квадрата.
- Шаг 2: Рассчитайте длину стороны по диагонали.
Сторона = диагональ/√2 = √2 × диагональ/ 2 - Шаг 3: Умножьте полученное значение длины стороны (√2 × диагональ/2) на 4 и выразите ответ в единицах.
Периметр = (√2 × диагональ/2) × 4 = (2√2 × диагональ) единиц.
Периметр квадрата с использованием площади квадрата
Мы можем найти периметр квадрата, зная его площадь. Чтобы найти периметр квадрата, используя площадь, мы можем выполнить шаги, указанные ниже:
Чтобы найти периметр квадрата, используя площадь, мы можем выполнить шаги, указанные ниже:
- Шаг 1: Запишите площадь квадрата.
- Шаг 2: Рассчитайте длину стороны, используя площадь.
Сторона = √площадь - Шаг 3: Умножьте полученное значение длины стороны (√площадь) на 4 и выразите ответ в единицах.
Периметр = (√площадь) × 4 = 4√единицы площади.
Давайте посмотрим на несколько решенных примеров, чтобы лучше понять периметр квадрата.
Периметр квадрата Примеры
Пример 1: Если периметр квадрата равен 64 единицам, найдите его сторону.
Решение:
Дано: периметр квадрата = 64 единицы.
Используя формулу периметра квадрата,
Периметр = (4 × сторона) единиц
Подставляя значение периметра, получаем,
64 = 4 × сторона
⇒ Сторона = 64/4 = 16 единицОтвет: Длина стороны данного квадрата равна 16 единицам.

Пример 2: Площадь квадрата равна 225 квадратных единиц. Используя формулу периметра квадрата, вычислите его периметр.
Решение:
Дано: Площадь квадрата = 225 квадратных единиц.
Мы знаем, что площадь квадрата = (сторона) 2 квадратных единиц
⇒ 225 = (сбоку) 2
⇒ сторона = √ 225 = 15 единицТеперь, используя формулу периметра квадрата,
Периметр, P = 4 × боковые блоки
⇒ P = 4 × 15 = 60 единицОтвет: Периметр данного квадрата = 60 единиц.
Пример 3: Если диагональ квадрата равна 3√2 дюйма, каков будет периметр квадрата?
Решение:
Дано: Диагональ квадрата = 3√2 дюйма.
Поскольку мы знаем, что по диагонали периметр квадрата равен P = (2√2 × диагональ) единиц.
⇒ P = (2√2 × 3√2) дюймов
P = 6 × 2 дюйма
p = 12 дюймовОтвет: Периметр данного квадрата = 12 дюймов.

перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по периметру площади
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по периметру квадрата
Что такое периметр квадрата в математике?
Периметр квадрата в математике — это общая длина вокруг его границы. Формула периметра квадрата выражается как сумма всех сторон. Он представлен как P = 4 × боковые единицы.
☛Также проверьте:
- Формулы периметра
- Формулы площади
Что такое Формула Периметра Квадрата?
Периметр квадрата определяется как длина, которую покрывает его граница. Формула для вычисления периметра квадрата выглядит так: P = 4 × сторона.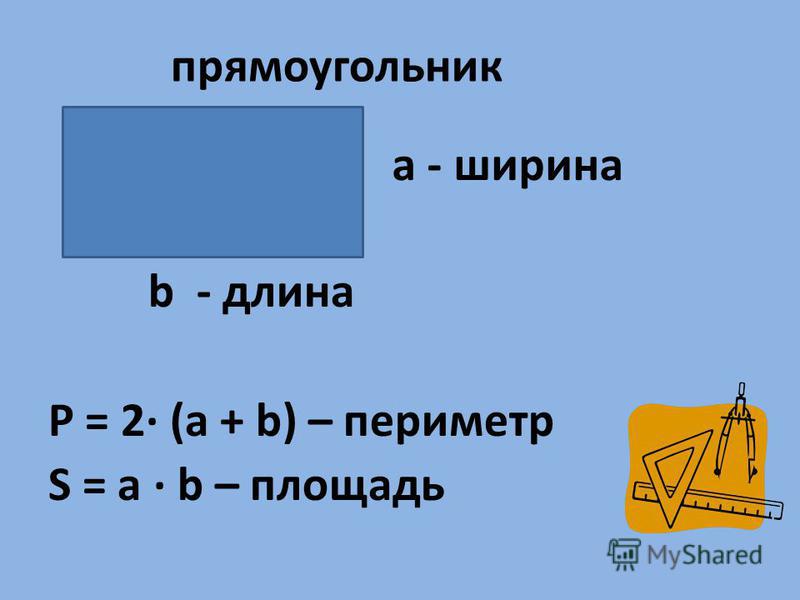
Как рассчитать периметр квадрата?
Периметр квадрата можно вычислить, найдя общую сумму всех его сторон. Поскольку мера всех сторон квадрата одинакова, чтобы вычислить периметр квадрата, мы можем просто умножить 4 на длину его стороны.
Что такое площадь и периметр квадрата?
Площадь квадрата – это пространство, занимаемое в пределах границы квадрата. Он рассчитывается по формуле: Площадь = (сторона × сторона) квадратных единиц. С другой стороны, периметр квадрата — это общая длина его границы. Его можно найти, сложив все четыре стороны квадрата или умножив любую из сторон на 4. Формула для нахождения периметра квадрата: (4 × сторона) единиц.
Как найти длину стороны квадрата, зная периметр?
Периметр квадрата определяется как P = 4 × сторона. Преобразовав приведенную выше формулу для вычисления длины стороны квадрата, когда задан периметр, мы получим сторону = P/4. Следовательно, длину стороны квадрата можно вычислить, разделив заданный периметр на 4.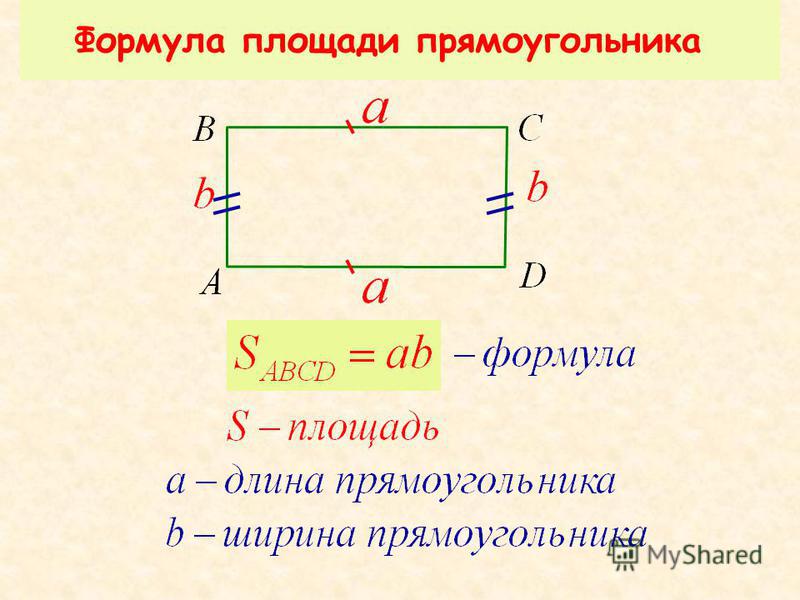
Как найти периметр квадрата, зная площадь?
Площадь квадрата можно рассчитать по формуле площадь = сторона × сторона. Преобразовав эту формулу для вычисления длины стороны квадрата с использованием площади, мы получим, что сторона = √ район. Поскольку периметр квадрата задается как: 4 × сторона, мы можем вычислить периметр квадрата, когда площадь дана по формуле: 4 √ площади.
Какова единица периметра квадрата?
Периметр квадрата — это общее расстояние вокруг его границы или длины его сторон, сложенные вместе. Периметр (P) измеряется в таких единицах, как дюймы (дюймы), ярды (ярды), миллиметры (мм), сантиметры (см), метры (м) и т. д.
Как пользоваться калькулятором периметра квадрата?
Калькулятор периметра квадрата используется для быстрых расчетов и быстрого получения желаемого результата периметра квадрата. Чтобы вычислить периметр квадрата с помощью калькулятора, нам нужно ввести определенные параметры, такие как длина стороны квадрата. Попробуйте калькулятор периметра квадрата Cuemath прямо сейчас и получите ответы одним щелчком мыши.
Попробуйте калькулятор периметра квадрата Cuemath прямо сейчас и получите ответы одним щелчком мыши.
☛ Проверьте листы периметра квадратов для большей практики .
Как найти периметр квадрата по диагонали?
Диагональ квадрата определяется как √2 × сторона. Преобразовав эту формулу для вычисления стороны квадрата, мы получим: сторона = диагональ/√2 = (√2 × диагональ)/2. Таким образом, периметр квадрата можно рассчитать по формуле P = 2√2 × диагональ.
Скачать БЕСПЛАТНЫЕ учебные материалы
Периметр квадрата Рабочий лист
Исчисление — Можно ли найти площадь фигуры по ее периметру?
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 15 тысяч раз
$\begingroup$
Можно ли найти площадь фигуры произвольной формы, зная периметр? Примером может служить форма листа клевера. Если периметр равен 96, как я узнаю, какой будет площадь?
Если периметр равен 96, как я узнаю, какой будет площадь?
область исчисления геометрии
$\endgroup$
2
$\begingroup$
Вопреки всем другим ответам, я говорю да, вы можете найти площадь $a$ известной формы (клеверного листа) по длине ее периметра $p$.
Взяв аналогичную модель листа клевера, измерьте его площадь $A$ и периметр $P$ с помощью курвиметра и планиметра. Вы также можете сделать это с цифрового изображения (фотоскан), но я не знаю готовых инструментов для этого. 92.$$
Для любой формы существует соответствующий коэффициент преобразования, который можно вычислить раз и навсегда.
Например, по картинке ниже вы можете оценить площадь в $19852$ пикселей и периметр в $750$ пикселей (это неточное измерение).
Тогда $F_{clover3hearts}\приблизительно 0,0353$, и ваш лист имеет площадь $325$ квадратных единиц.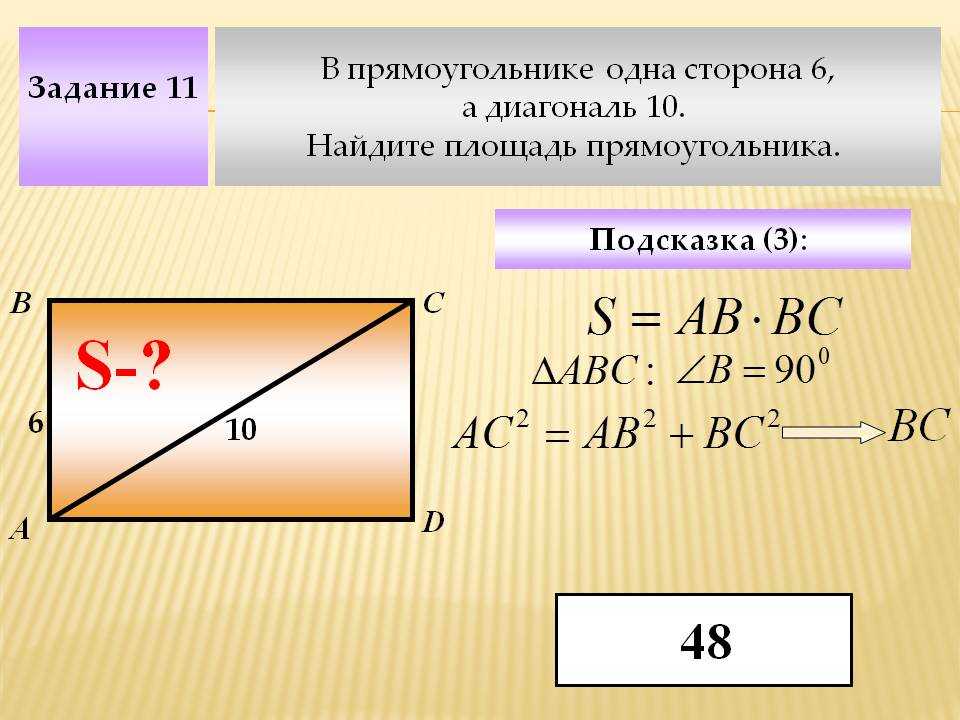
$\endgroup$
$\begingroup$
Это невозможно. Мы можем доказать это, построив две фигуры с одинаковым периметром, но разными площадями.
Рассмотрим, например, единичный равносторонний треугольник с периметром $3$ и площадью $\sqrt{3}/4$ и квадрат со сторонами $3/4$ и площадью $9/16$. Поскольку эти две фигуры имеют одинаковый периметр, но разные площади, невозможно однозначно определить площадь по периметру.
$\endgroup$
0
$\begingroup$
Периметр в основном представляет собой длину дуги. Вы могли бы так же легко иметь отрезок длины 92}{16}$, что (поскольку $\pi < 4$) меньше.
Если вы знаете форму границы, вы можете вычислить площадь области, вычислив интеграл непосредственно по границе, например, с помощью теоремы Грина. Это принцип, используемый планиметром, машиной, которая делает именно это.
Это принцип, используемый планиметром, машиной, которая делает именно это.
$\endgroup$
$\begingroup$
Нет, это невозможно, потому что вы можете легко увеличить периметр любого многоугольника (при сохранении его площади), изменив его края следующим образом:
(Источник: http://en.wikipedia.org/wiki/File:Quadratic_Koch_curve_type2_iterations.png)
Вы даже можете использовать эту технику для создания фракталов с бесконечным периметром, таких как «Колбаса Минковского».
PS: Как отметили Ив Дауст и Трэвис, этот ответ применим только в том случае, если форма неизвестна.
$\endgroup$
$\begingroup$
Если «периметр» равен длине …, это невозможно, как уже ответили. Но если форма известна тем, что можно вычислить площадь, используя теоремы Грина.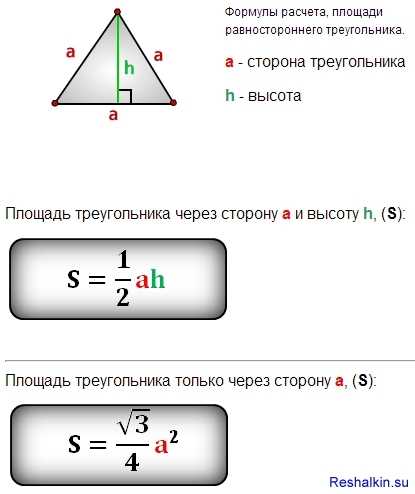



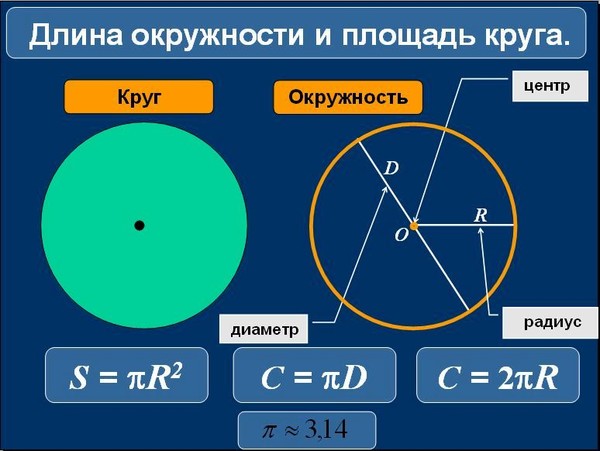 Вычислите, сколько
материала уйдет на каждый участок?
Вычислите, сколько
материала уйдет на каждый участок?

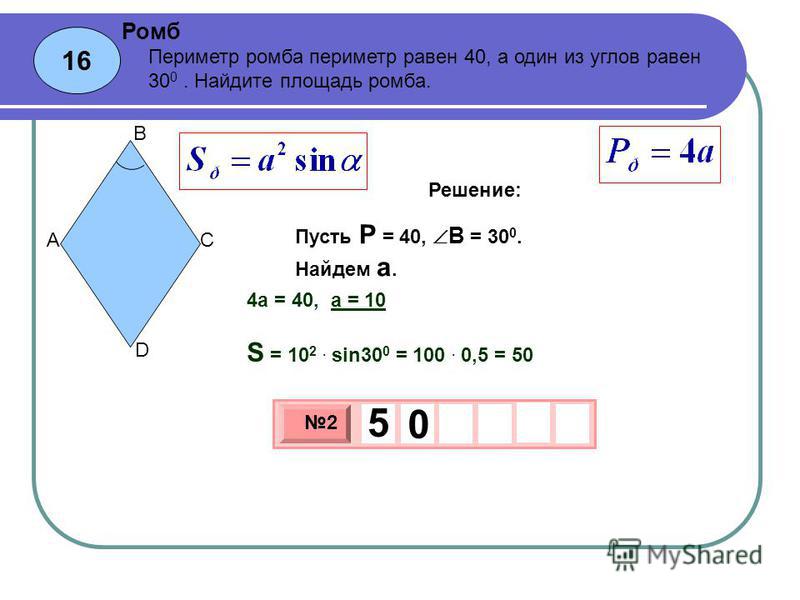 В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.
В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.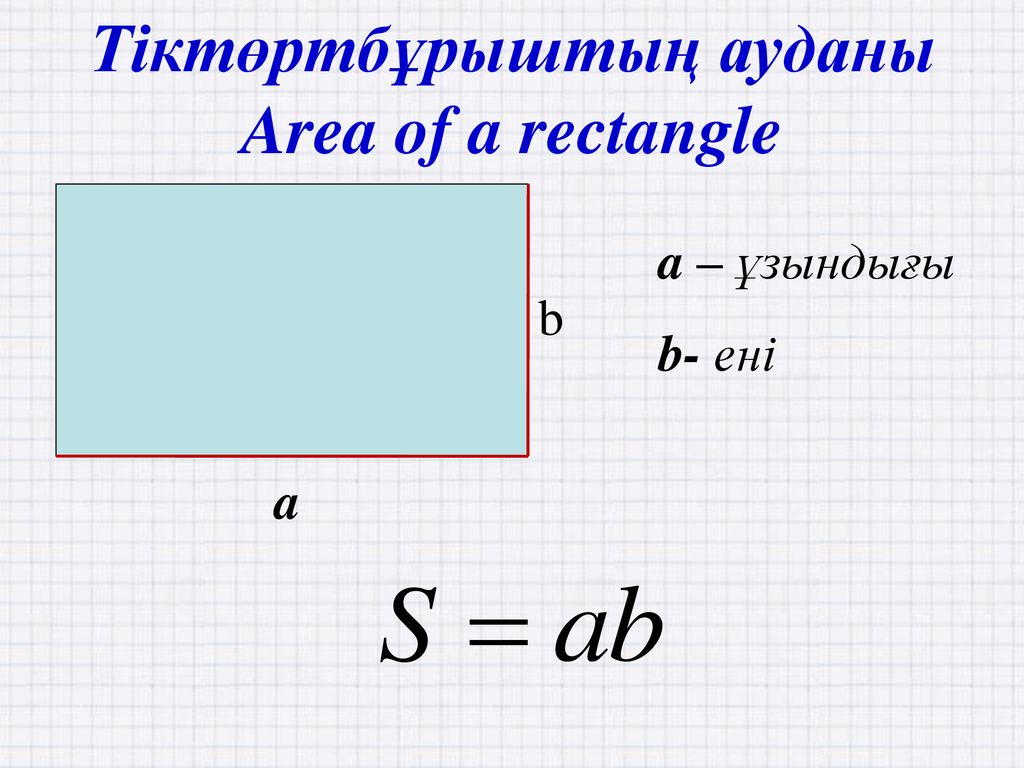
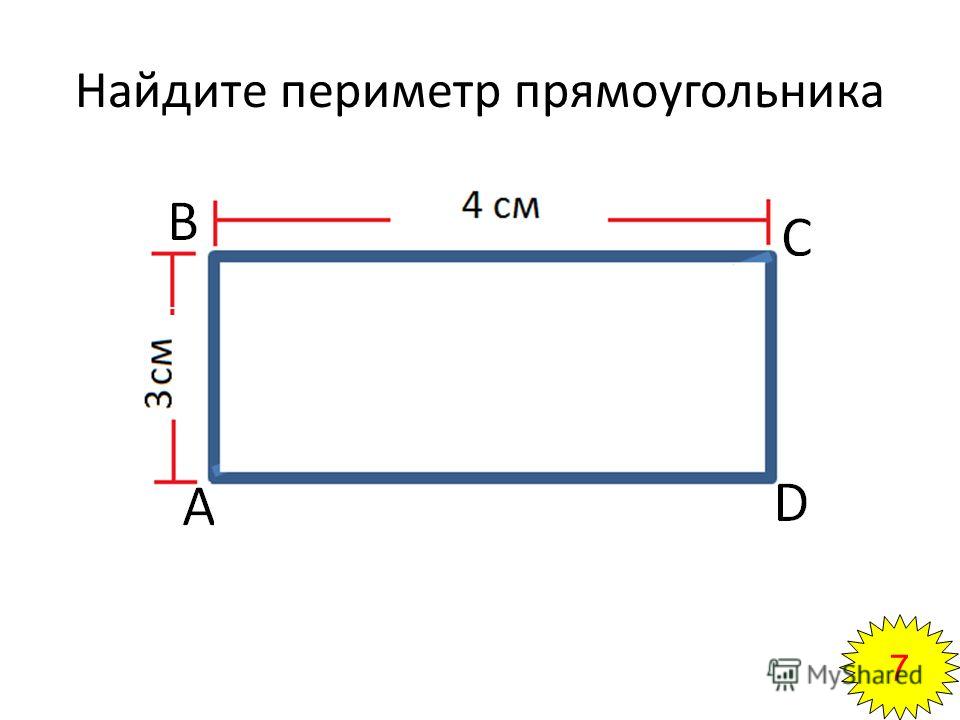 Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.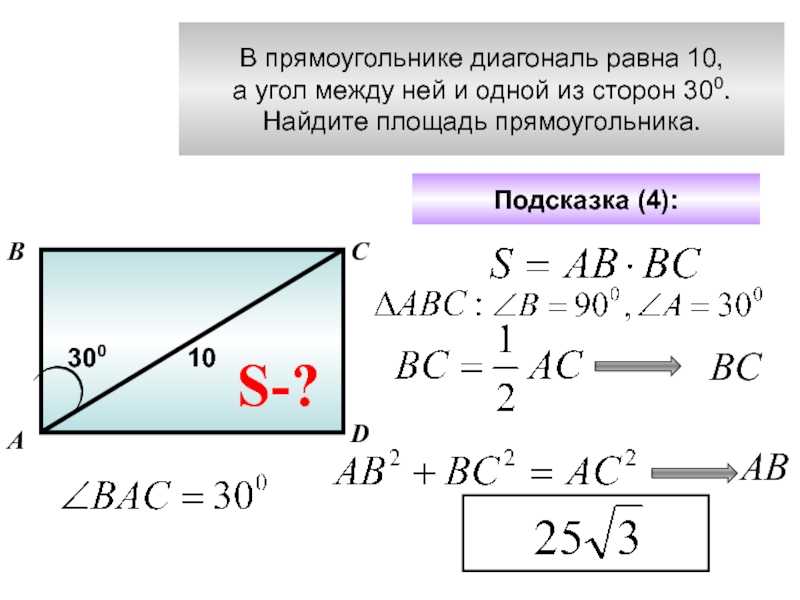 Найдем его периметр.
Найдем его периметр. А уже после периметр вычисляется по стандартной формуле.
А уже после периметр вычисляется по стандартной формуле.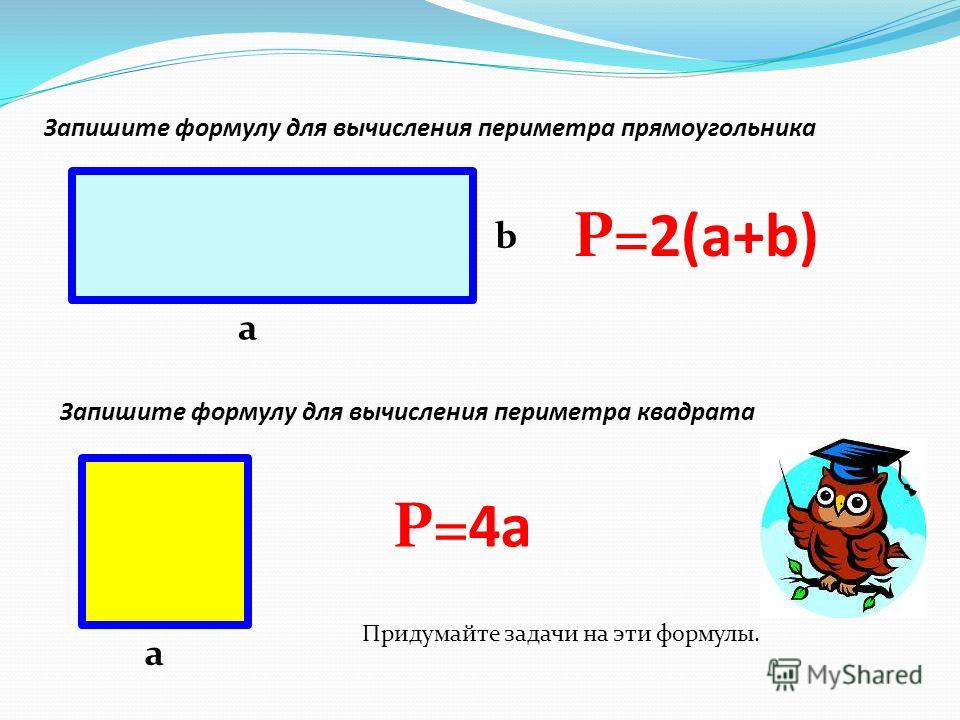 2})}, где d — диагональ прямоугольника, a — сторона прямоугольника.
2})}, где d — диагональ прямоугольника, a — сторона прямоугольника. Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон (MN=a-b).
Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон (MN=a-b). 2) или
2) или
 ru/voprosy-i-otvety/ploshchad-pryamougolnika-najti-formule-diagonal-perimetr.html
ru/voprosy-i-otvety/ploshchad-pryamougolnika-najti-formule-diagonal-perimetr.html Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

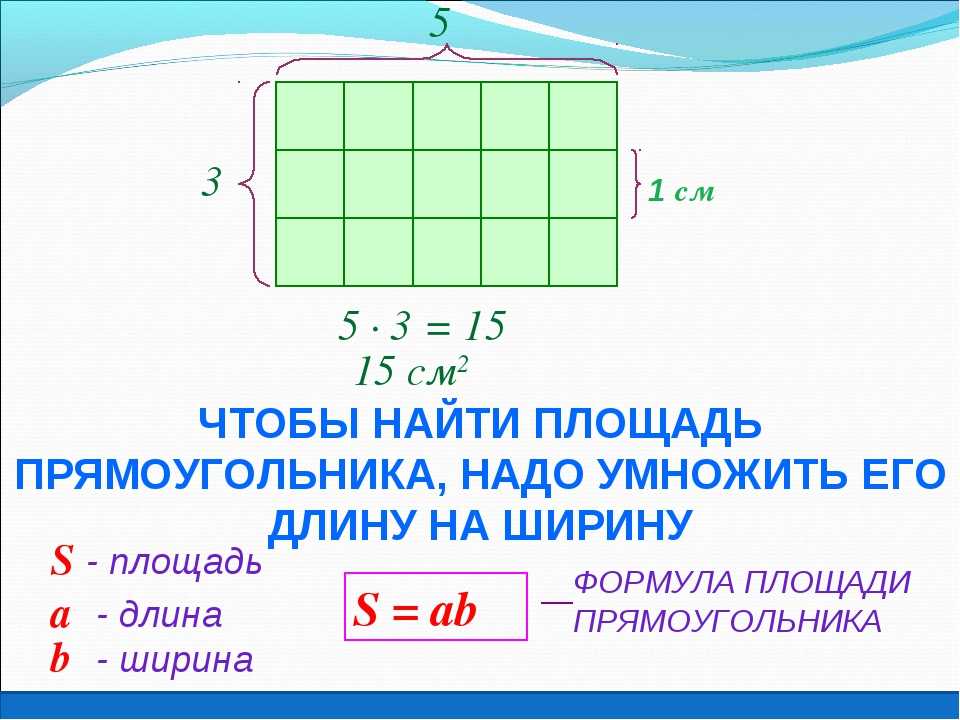
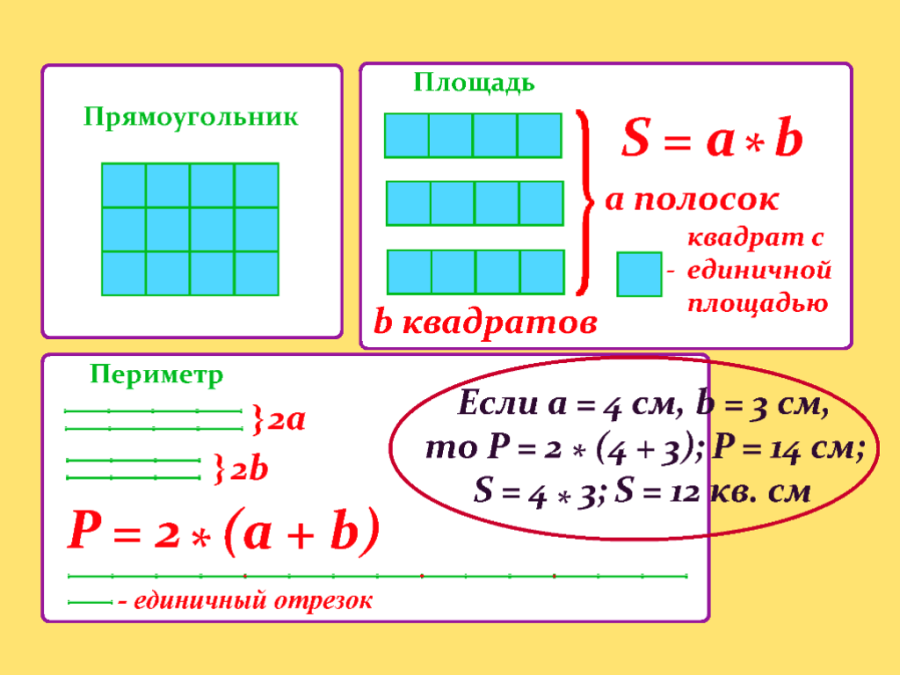 — М.: Дрофа, 2004.
— М.: Дрофа, 2004. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
 2, а длина 4 м? 9 по длине
2, а длина 4 м? 9 по длине