Периметр обозначается буквой: Периметр — урок. Математика, 2 класс.

Содержание

В каких единицах измеряется периметр. Периметр

Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.

Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.

Определение периметра

Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.

Измеряем периметр

Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.

Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.

Круг, квадрат, равносторонний треугольник

Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).

Инструкция

Источники:

как найти периметр abcd

Периметр – это сумма длин сторон какой-либо геометрической фигуры. Иными словами, если взять нить и выложить с ее помощью на столе, например, квадрат, а потом измерить длину этой нити, то полученная цифра и будет периметром данного квадрата. Все знают, что такое периметр, но не каждый может сразу сообразить, как его рассчитать.
Для измерения периметра разных фигур существуют различные способы.

Инструкция

Квадрат. Общеизвестно, что у квадрата есть 4 стороны и они . Поэтому для вычисления его периметра так:

где а – это длина одной стороны данной фигуры.

Проще говоря, измерьте одну из сторон квадрата и умножьте эту цифру на количество сторон, то есть на 4. В нашем случае равен 16 см (4*4).

Прямоугольник и ромб. У этих двух фигур только параллельные друг другу стороны равны, соответственно периметр определяется следующим образом:

где а и b – соприкасающиеся стороны. Таким образом, на нашем примере периметр прямоугольника равен 24 см (2*(8+4)).

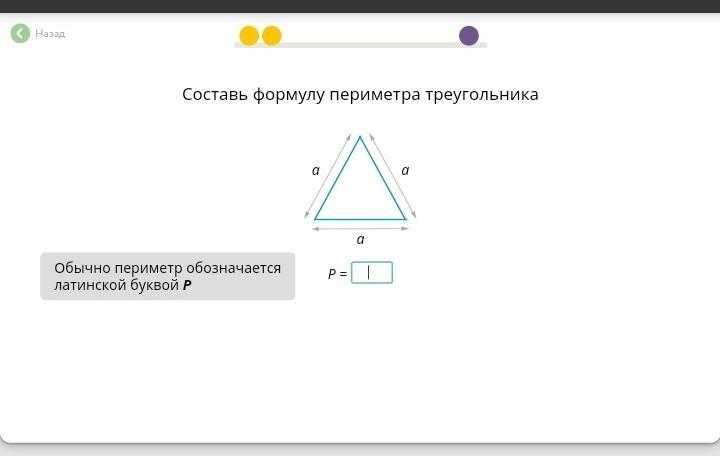
Треугольник. Поскольку треугольники бывают совершенно разными – равнобедренными, неправильными, с углами, то единственным верным способом периметр такой фигуры является формула:

То есть для вычисления периметра треугольника просто измерьте длины всех трех сторон и сложите полученные цифры.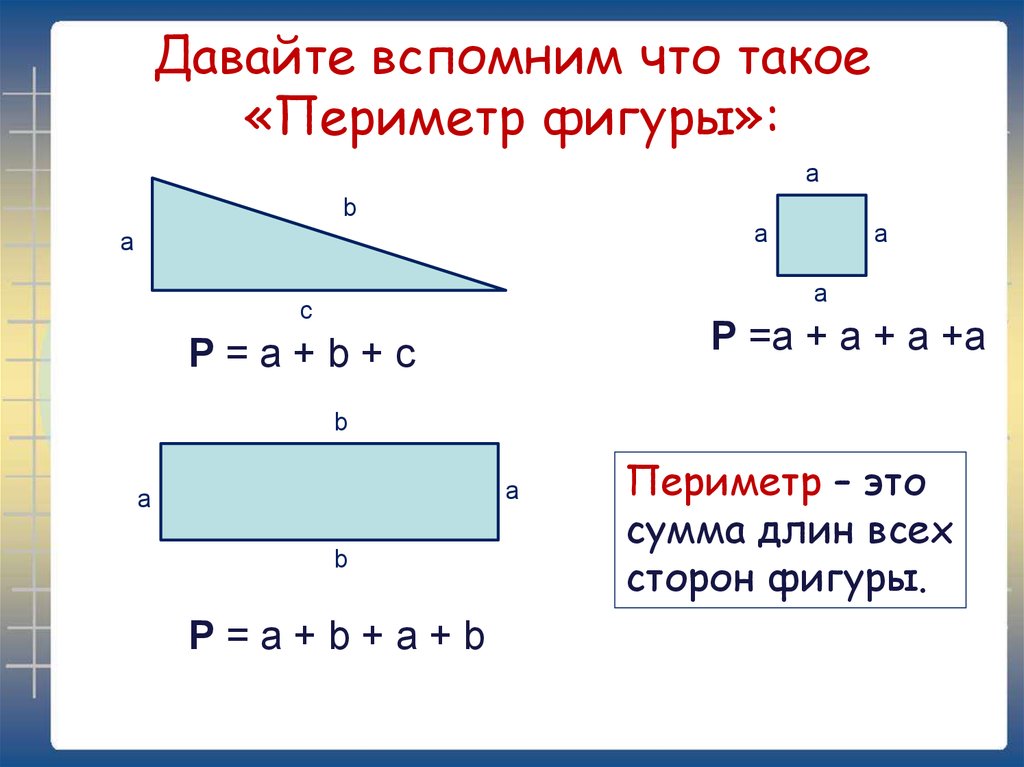 В нашем случае периметр треугольника равен 10,7 см (2+5+3,7).

Периметр называют длиной окружности, которая вычисляется по особой формуле:

где d – это окружности, а 3,14 – это число «пи», которое специально выведено учеными для определения периметра данной геометрической фигуры. Наш круг (см.) имеет 3 см, то есть периметр окружности равен 9,42см (3*3,14).

Источники:

как находить длину окружности

Ом в общем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину можно измерить, а для многих фигур и просто рассчитать, если известны длины соответствующих элементов.

Вам понадобится

— линейка или рулетка;
— прочная нить;
— роликовый дальномер.

Инструкция

Чтобы измерить произвольного многоугольника, измерьте при линейки или другим измерительным прибором все его стороны, а затем найдите их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, найдите периметр, сложив их вместе Р=5+3+7+4=19 см.

Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр обычной веревкой или ниткой. Для этого расположите ее так, она точно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если можно, просто обрежьте ее чтобы избежать путаницы. Затем при помощи рулетки или линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Обязательно следите за тем, чтобы нить максимально точно повторяла линию для большей точности результата.

Периметр сложной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в исходную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.

Периметр некоторых геометрических фигур вычисляйте. Например, чтобы найти периметр любого правильного многоугольника (выпуклого многоугольника, стороны которого ), длину стороны умножьте на количество углов или сторон (они равны).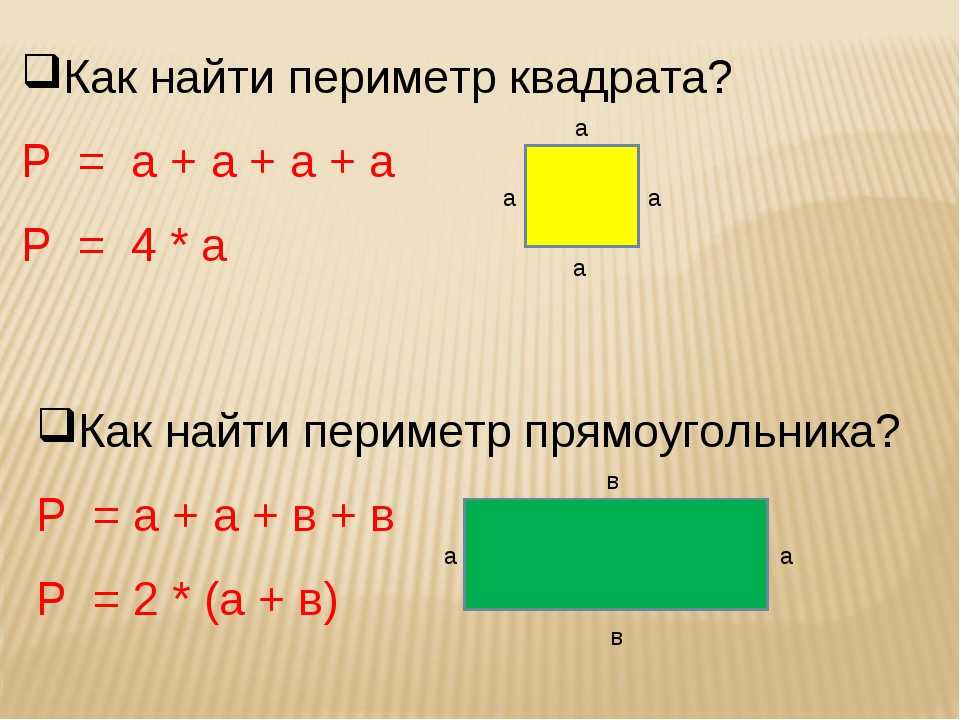

Чтобы найти периметр правильного треугольника со стороной 4 см умножьте это на 3 (Р=4∙3=12 см).

Чтобы найти периметр , сложите длины всех его сторон. Если не даны все стороны, а есть углы ними, найдите их по теореме синуса или косинуса. Если известны две стороны прямоугольного треугольника, третью найдите по теореме Пифагора и найдите их сумму. Например, если известно, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна √(3²+4²)=5 см. Тогда периметр Р=3+4+5=12 см.

Источники:

периметру

Для решения этой задачи методами векторной алгебры, вам необходимо знать следующие понятия: геометрическая векторная сумма и скалярное произведение векторов, а также следует помнить свойство суммы внутренних углов четырехугольника.

Вам понадобится

— бумага;
— ручка;
— линейка.

Инструкция

Вектор – это направленный отрезок, то есть величина, считающаяся заданной полностью, если задана его длина и направление (угол) к заданной оси. 2))=1/(sqrt2sqrt5), ф3=arcos(-1/sqrt(10))=п-ф1.
В соответствии с замечанием 2 — ф4=2п- ф1 — ф2- ф3=п/4.

Видео по теме

Обратите внимание

Замечание 1. В определении скалярного произведения используется угол между векторами. Здесь, например, ф2 — это угол между АВ и ВС, а между a и b этот угол п-ф2. сos(п- ф2)=- сosф2. Аналогично для ф3.
Замечание 2. Известно, что сумма углов четырехугольника равна 2п. Поэтому ф4=2п- ф1 — ф2- ф3.

Любая выпуклая и плоская геометрическая фигура имеет ограничивающую ее внутреннее пространство линию — периметр. У многоугольников он состоит из отдельных отрезков (сторон), сумма длин которых определяет протяженность периметра. Участок плоскости, ограниченный этим периметром, тоже может быть выражен через длины сторон и углы в вершинах фигуры. Ниже приведены соответствующие формулы для одного из видов многоугольников — параллелограмма.

Инструкция

Если в задачи даны длины двух смежных сторон параллелограмма (a и b) и величина угла между ними (γ), то этого будет достаточно для вычисления обоих параметров.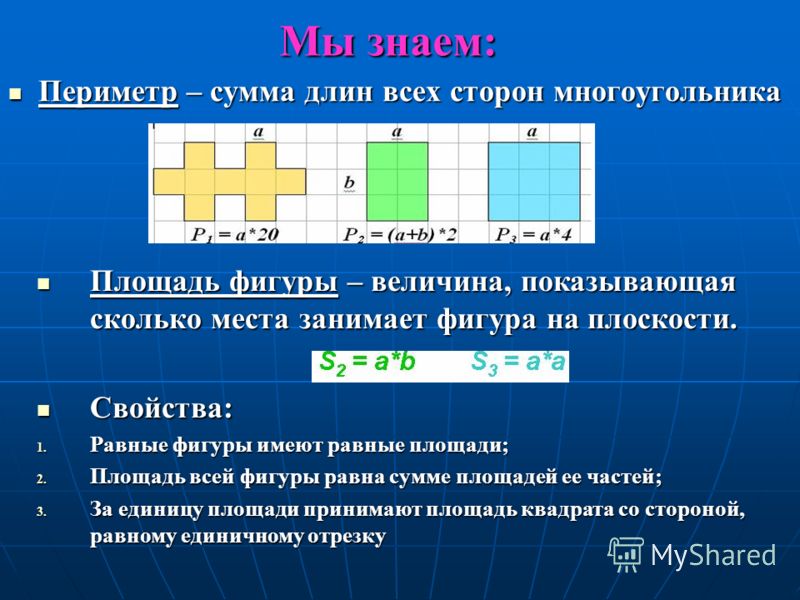 Для расчета периметра (P) четырехугольника сложите длины сторон и вдвое увеличьте полученное значение: P = 2*(a+b). Вычислять (S) фигуры придется с помощью тригонометрической функции — синуса. Перемножьте длины сторон, а результат умножьте на известного угла: S = a*b*sin(γ).

Если известна длина лишь одной из сторон (a) параллелограмма, но есть данные о (h) и величине угла (α) в любой из вершин , то это позволит и периметр (P) (S). Сумма всех углов в любом равна 360°, а в параллелограмме те из них, что лежат в противоположных вершинах, одинаковы. Поэтому для нахождения величины оставшегося неизвестным угла отнимите от 180° величину известного. После этого рассмотрите треугольник, составленный из высоты и лежащего напротив него угла, величины которых известны, а также неизвестной пока стороны. Примените к нему теорему синусов, и выясните, что длина стороны будет равна отношению высоты к синусу угла, лежащего напротив нее: h/sin(α).

После проведения предварительных расчетов предыдущего шага составьте нужные .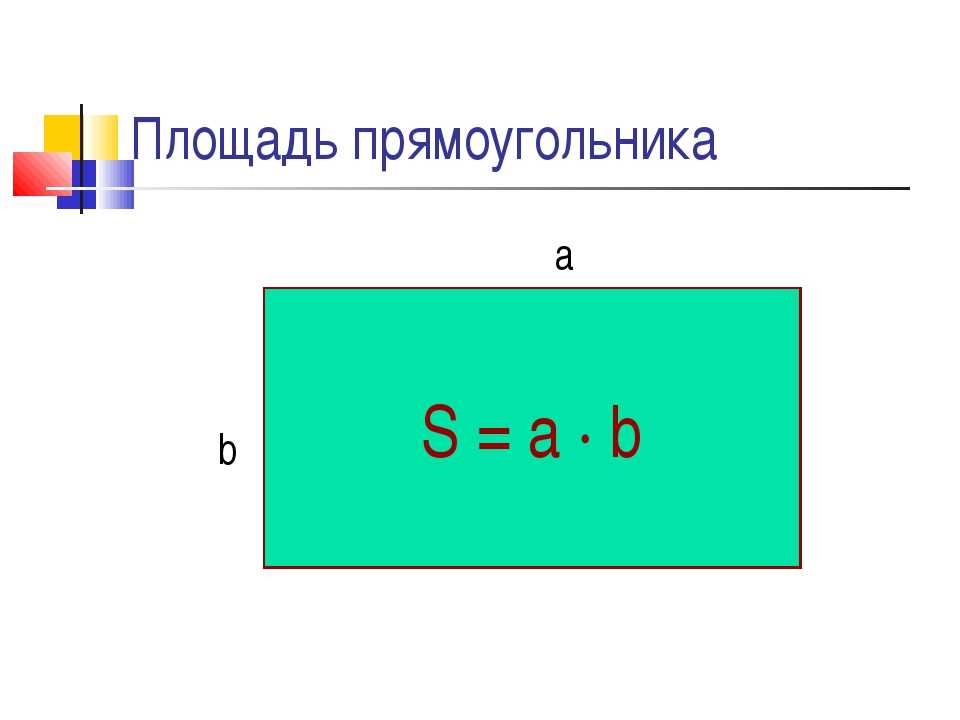 Подставьте полученное выражение в формулу из первого шага и получите равенство: P = 2*(a+h/sin(α)). В том случае, если высота соединяет две противоположные стороны параллелограмма, длина которых дана в исходных условиях, для нахождения площади просто перемножьте эти два значения: S=a*h. Если же это условие не соблюдено, то подставьте в формулу выражение для другой стороны, полученное в предыдущем шаге: S=a*h/sin(α).

Видео по теме

Среди основных задач аналитической геометрии на первом месте стоит представление геометрических неравенством, уравнением или системой тех или других. Это возможно благодаря применению координат. Опытный математик, только взглянув на уравнение, без труда скажет, какую геометрическую фигуру можно начертить.

Инструкция

Уравнением F (x, y) можно задать кривую или прямую линию при выполнении двух условий: если координаты точки, которая не принадлежит заданной линии, не удовлетворяют уравнению; если каждая точка искомой линии со координатами удовлетворяет этому уравнению.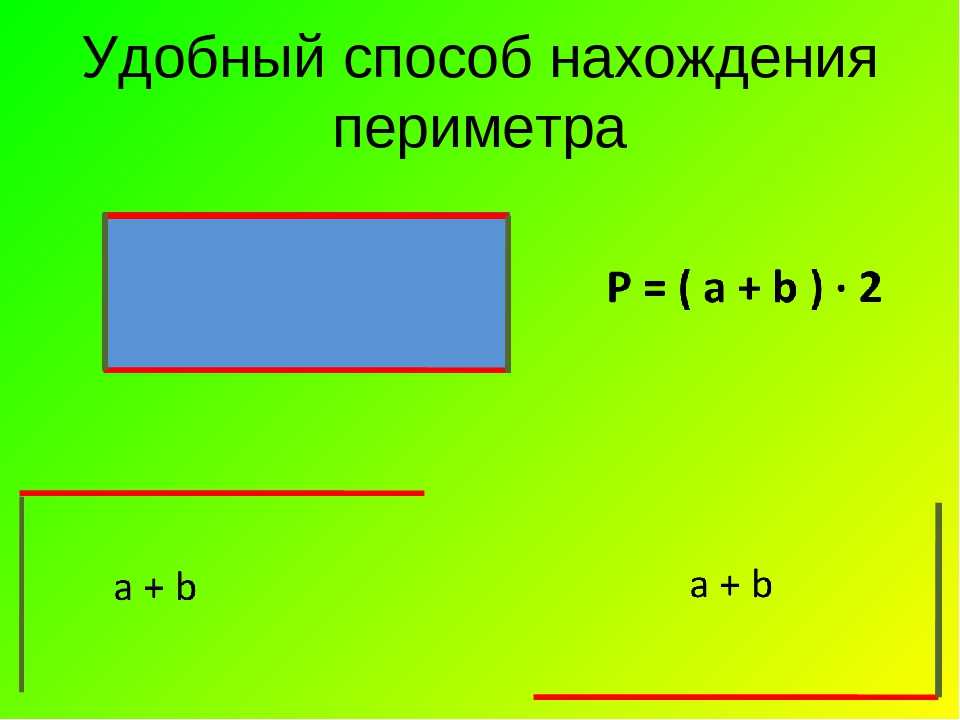

Уравнение вида x+√(y(2r-y))=r arccos (r-y)/r задает в декартовых координатах циклоиду – траекторию, которая описывается точкой на окружности c радиусом r. При этом окружность не по оси абсцисс, а катится. Какая при этом получается фигура, смотрите на рисунке 1.

Фигура, координаты точек которой задаются следующими уравнениями:
x=(R+r) cosφ — rcos (R+r)/r φ
y=(R+r) sinφ — rsin (R-r)/r φ,
называется эпициклоидой. Она траекторию, которую описывает точка на окружности с радиусом r. Эта окружность катится по другой окружности, имеющей радиус R, с внешней стороны. То, эпициклоида, смотрите на рисунке 2.

Существует несколько понятий периметра.

Геометрическое: всякая замкнутая плоскость имеет длину своих границ. И из области безопасности. То есть, периметром называют собственно охраняемую границу или территорию охраняемого объекта. Поскольку тема эта из рубрики «Обучение», а не из рубрики «Законы и безопасность», следует остановиться на геометрическом понятии периметра.

Итак, что такое периметр?

Этот вопрос почему-то ставит в тупик некоторых молодых людей. Они что, не учили этого в школе? Если какие-то математические (геометрические) формулы, которыми пичкают школяров, никогда не пригодятся в жизни, то знать, что такое периметр – просто необходимо, и это знание, можете не сомневаться, будет востребованным.

Каков периметр вашего дачного дома? А участка? От периметра зависит площадь и того, и другого. А если ваш огород, поле, сад имеет овальную форму или множество углов? Как вы узнаете их периметр?

Для начала следует заглянуть в словари и энциклопедии. И уяснить для себя, что включает в себя понятие «периметр».

Большой энциклопедический словарь дает такое определение периметру: это длина контура, который замкнут. Сумма длин сторон геометрической фигуры, к примеру, всех пяти сторон пятиугольника.

Скажем, имеется земельный участок, представляющий пятиугольник. Одна сторона простирается на 20 метров, другая – на 16, третья – на 4, четвертая – на 11 и пятая – на 6 метров.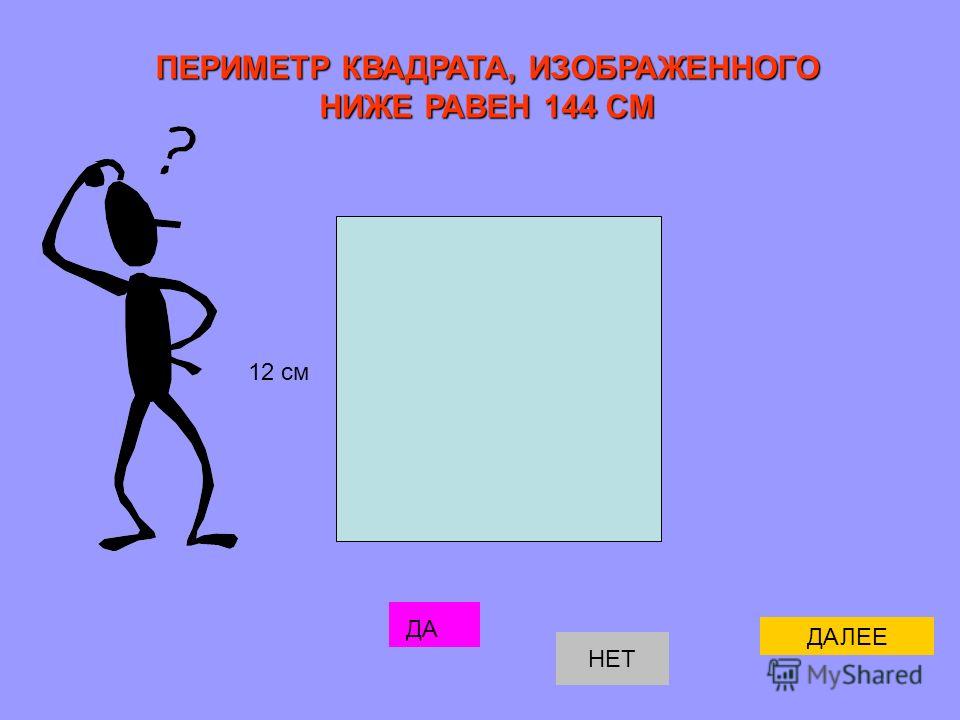

Каков периметр земельного участка? Простым арифметическим действием сложения мы вычисляем периметр земельного участка: 20 + 16 + 4 + 11 + 6 = 57 метров.

Словарь Ушакова дает такое объяснение понятию «периметр»: это сумма длин всех сторон плоской фигуры. Что мы уже и проиллюстрировали на вышеприведенном примере.

А как же окружность? Она ведь тоже плоская. Каков ее периметр, и как его вычислить?

Существует формула вычисления периметра (длины) окружности. Но для этого сначала надлежит вспомнить, что такое окружность, и какие она имеет элементы. А окружность – есть кривая, которая не только плоская и замкнутая, но еще и все ее точки расположены на одинаковом удалении от заданной точки, зовущейся центром.

Отрезок прямой, соединяющий этот центр с какой-либо точкой окружности, есть радиус (R).

Отрезок прямой, проходящий через центр окружности и соединяющий ее две точки, наиболее удаленные друг от друга, есть диаметр (D). Диаметр равен двум радиусам.

Отношение длины окружности к ее диаметру одинаково для любой окружности и равно постоянному числу 3, 14. .. Число это обозначается буквой π (пи).

Вот теперь можно и дать формулу вычисления периметра (длины) окружности: P = 2πR или π D.

Скажем, нам известен радиус окружности: 5 метров. Чему будет равен ее периметр?

Действия здесь будут следующие: диаметр (10 метров) умножаем на 3, 14. И получаем периметр окружности, равный 31, 4 метра.

Встречаются и более сложные фигуры, периметр которых необходимо узнать. Здесь для расчета периметра применяются методы математического анализа, что требует уже специальных знаний…

Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.

И как же найти периметр этих фигур?

Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .

Периметр обозначается заглавной латинской буквой Р .

Давайте рассмотрим несколько примеров.

Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:

Р = 15 + 17 + 10 + 10 + 20 + 15 = 87

Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:

Р = 15 × 2 + 10 × 2 + 17 + 20 = 87

Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :

Р(прямоугольника) = (а + б) × 2

То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:

Р = (5 + 3) × 2 = 16 см

А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?

Р(прямоугольника) = 2 × а + 2 × б

а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2

Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?

Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.

сторона б = (16 – 2 × 5) ÷ 2 = 3 см

Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:

Р(квадрата) = а × 4

Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:

Р(В) = 5 × 4 = 20 см

А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:

а = Р ÷ 4

Пример: Периметр квадрата 24 см. Чему равны его стороны?

а = 24 ÷ 4 = 6

Ответ: Стороны квадрата равны 6 см.

По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.

Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:

Р(равностороннего многоугольника) = а × n

Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:

Р(Д) = 6 × 5 = 30 см

Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.

Пери́метр (др. -греч. περίμετρον — окружность, др. -греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.

Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры , неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см.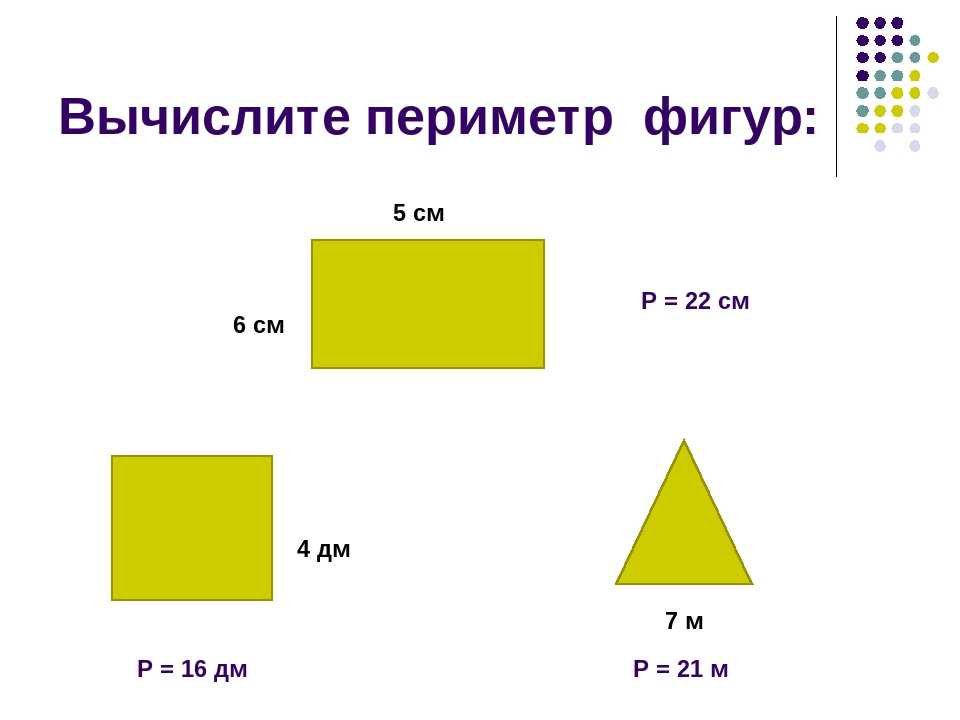 ниже). Фигуры с одинаковой площадью называются равновеликими.

Периметр фигуры обладает только одним параметром — протяжённостью, или длиной, выраженной в единицах длины: метр, ярд, аршин, локоть. Или производных от них: километр, сантиметр, дециметр.

Площадь фигуры обладает двумя параметрами — например, длиной и шириной, или радиусом и коэффициентом Пи, в зависимости от формы. Величина площади выражается в единицах в квадрате: квадратных метрах, гектарах, квадратных милях

Периметр и его определение

Периметром принято называть протяжённость границы плоской фигуры, состоящей из прямых отрезков, где начало каждого последующего примыкает к окончанию предыдущего.

Строго говоря, окружность тоже обладает периметром, но для криволинейных границ принято говорить о длине окружности, или длине дуги

Для определения длины периметра, необходимо измерить, или вычислить, длину каждой стороны фигуры, а затем суммировать полученные числа.

Площадь фигуры и её определение

Площадь простейших геометрических фигур определяется по формулам.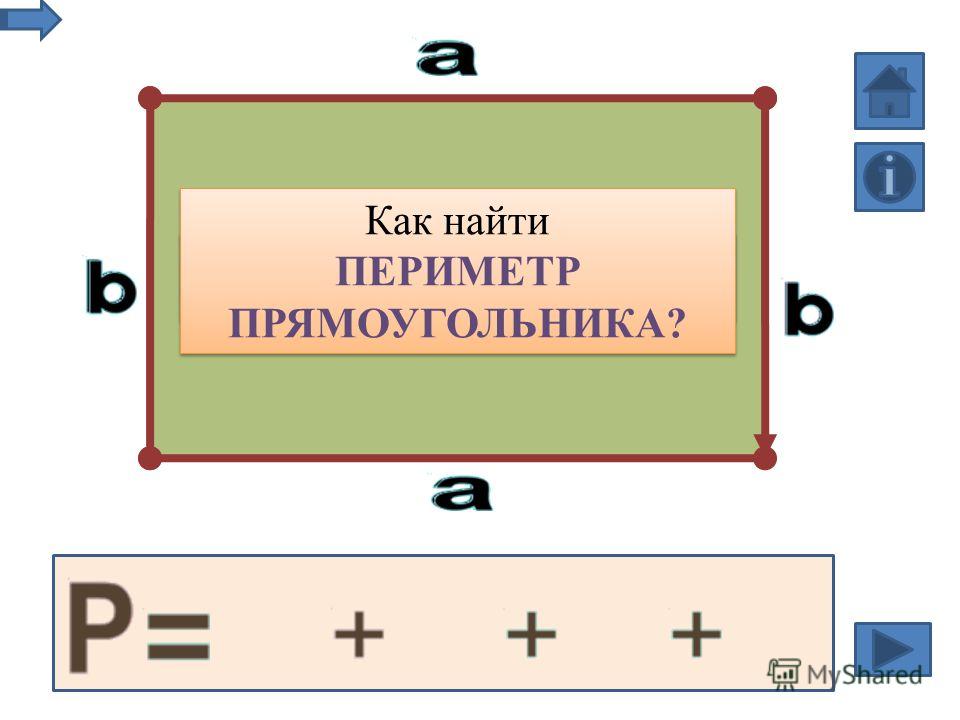

Площадь прямоугольника равна произведению длин сторон.
Площадь круга равна произведению квадрата радиуса на число Пи=3,1415
Свои формулы есть для треугольника, сектора, трапеции, параллелограмма.

Площадь сложных криволинейных фигур вычисляется интегралом. Взятие интеграла формулы, описывающей границу фигуры, даст в результате площадь. В этом и есть геометрический смысл интеграла — он вычисляет площадь, ограниченную графиком функции на заданном участке.

Сложная фигура, lkz которой нет общей формулы, для определения площади мысленно разбивается на простейшие фигуры. Площади простых фигур вычисляются и затем суммируются.

Периметр и площадь геометрической фигуры связаны и один параметр всегда может быть вычислен из другого с минимальными дополнительными данными.

Чем отличается периметр от площади? Что такое периметр

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.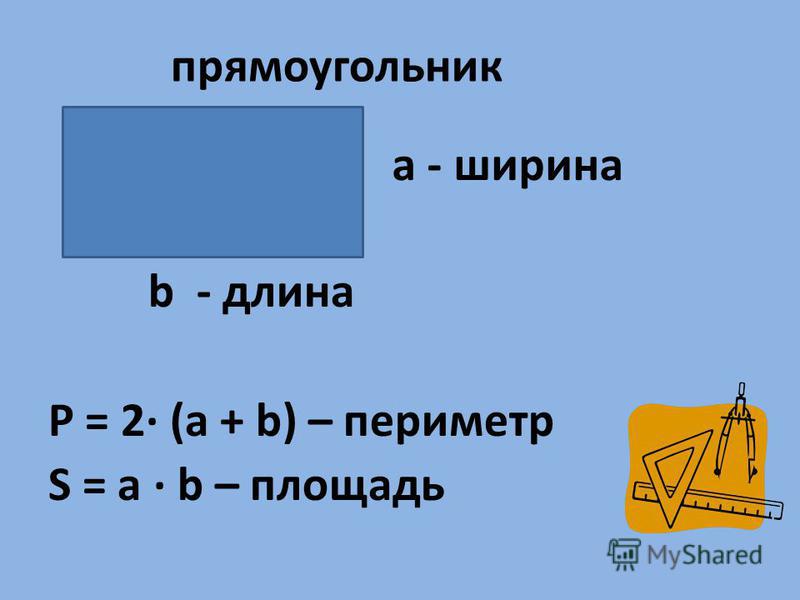 Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.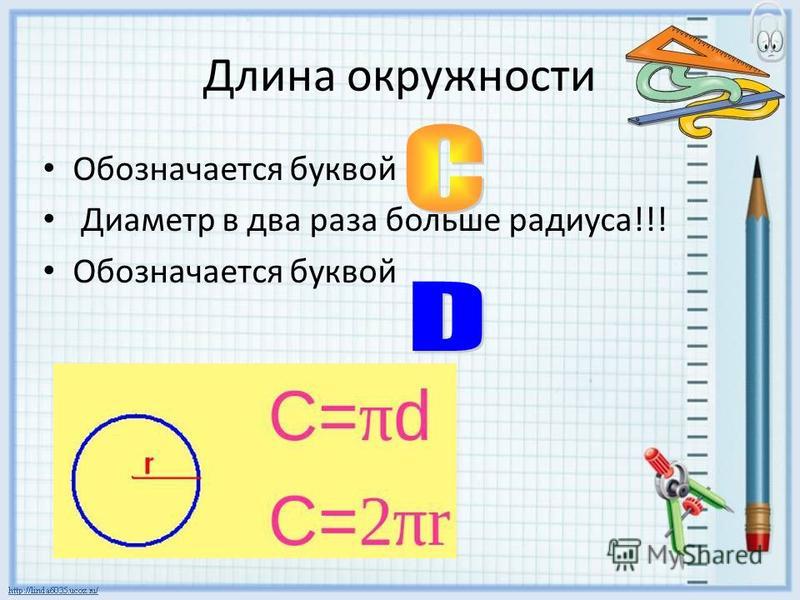

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.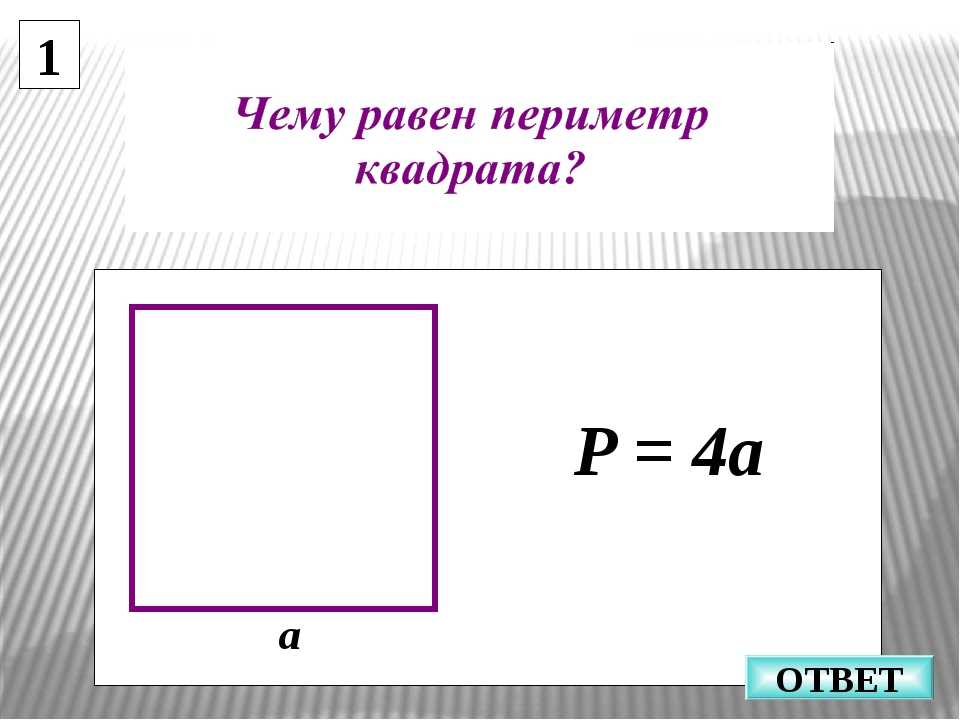
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Периметр и его определение

Площадь фигуры и её определение

Площадь простейших геометрических фигур определяется по формулам.

И как же найти периметр этих фигур?

Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .

Периметр обозначается заглавной латинской буквой Р .

Давайте рассмотрим несколько примеров.

Р = 15 + 17 + 10 + 10 + 20 + 15 = 87

Р = 15 × 2 + 10 × 2 + 17 + 20 = 87

Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

Р(прямоугольника) = (а + б) × 2

Р = (5 + 3) × 2 = 16 см

А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?

Р(прямоугольника) = 2 × а + 2 × б

а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2

Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?

сторона б = (16 – 2 × 5) ÷ 2 = 3 см

Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Р(квадрата) = а × 4

Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:

Р(В) = 5 × 4 = 20 см

а = Р ÷ 4

Пример: Периметр квадрата 24 см. Чему равны его стороны?

а = 24 ÷ 4 = 6

Ответ: Стороны квадрата равны 6 см.

Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:

Р(равностороннего многоугольника) = а × n

Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:

Р(Д) = 6 × 5 = 30 см

Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.

Определение периметра

Измеряем периметр

Круг, квадрат, равносторонний треугольник

Существует несколько понятий периметра.

Итак, что такое периметр?

Скажем, имеется земельный участок, представляющий пятиугольник. Одна сторона простирается на 20 метров, другая – на 16, третья – на 4, четвертая – на 11 и пятая – на 6 метров. Каков периметр земельного участка? Простым арифметическим действием сложения мы вычисляем периметр земельного участка: 20 + 16 + 4 + 11 + 6 = 57 метров.

А как же окружность? Она ведь тоже плоская. Каков ее периметр, и как его вычислить?

Отрезок прямой, соединяющий этот центр с какой-либо точкой окружности, есть радиус (R).

Отношение длины окружности к ее диаметру одинаково для любой окружности и равно постоянному числу 3, 14… Число это обозначается буквой π (пи).

Вот теперь можно и дать формулу вычисления периметра (длины) окружности: P = 2πR или π D.

Скажем, нам известен радиус окружности: 5 метров. Чему будет равен ее периметр?

Как рассчитать периметр фигуры. Периметр и площадь прямоугольника

На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.

На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.

Рассмотрим следующую геометрическую фигуру (рис. 1):

Рис. 1. Прямоугольник

Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.

Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.

Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.

Рассмотрим следующую задачу:

Задача 1 (рис. 2)

Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?

Рис. 2. Иллюстрация к задаче 1

Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.

Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.

Ответ: 30 метров.

Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).

Периметр любой фигуры измеряется в линейных единицах.

На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.

Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.

Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).

Список литературы

Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.

Festival.1september.ru ().
Nsportal.ru ().
Math-prosto.ru ().

Домашнее задание

Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
Найти периметр прямоугольника, если его полупериметр — 21 дм.

Периметр — это сумма длин всех сторон многоугольника.

Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

Прямоугольник – это четырехугольник.
Все параллельные стороны равны
Все углы = 90º.
Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

1 способ. Складываем все стороны. P = a + а + b + b
2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

: a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т. д.)

Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.

Как найти периметр обычного прямоугольника

Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:

Складываем все стороны.

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.

Решение (последовательность действий и рассуждения):

Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
Складываем все стороны (3 + 3 + 6 + 6) = 18 см.

Ответ: P = 18 см.

Второй способ заключается в следующем:

Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.

В рамках данной задачи получим такое решение:

2×(3 + 6) = 2×9 = 18.

Ответ: P = 18.

Как найти периметр прямоугольника – квадрат

Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:

Сложить все его стороны.
Умножить его сторону на 4.

Пример: Найти периметр квадрата, если его сторона = 5 см.

Так как нам известна сторона квадрата, мы сможем найти его периметр.

Складываем все стороны: 5 + 5 + 5 + 5 = 20.

Ответ: P = 20 см.

Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.

Ответ: P = 20 см.

Как найти периметр прямоугольника – онлайн-ресурсы

Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.

И как же найти периметр этих фигур?

Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .

Периметр обозначается заглавной латинской буквой Р .

Давайте рассмотрим несколько примеров.

Р = 15 + 17 + 10 + 10 + 20 + 15 = 87

Р = 15 × 2 + 10 × 2 + 17 + 20 = 87

Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

Р(прямоугольника) = (а + б) × 2

Р = (5 + 3) × 2 = 16 см

А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?

Р(прямоугольника) = 2 × а + 2 × б

а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2

Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?

сторона б = (16 – 2 × 5) ÷ 2 = 3 см

Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Р(квадрата) = а × 4

Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:

Р(В) = 5 × 4 = 20 см

а = Р ÷ 4

Пример: Периметр квадрата 24 см. Чему равны его стороны?

а = 24 ÷ 4 = 6

Ответ: Стороны квадрата равны 6 см.

Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:

Р(равностороннего многоугольника) = а × n

Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:

Р(Д) = 6 × 5 = 30 см

Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.

Немного теории:

Периметр — это длина геометрической фигуры по её внешней границе.

Периметр прямоугольника — это сумма длин его сторон.

Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.

Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.

Типовые математические и практические задачи:

Задача №1:

Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.

Решение:

Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.

Ответ: 30 см.

Задача №2:

Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.

Решение:

По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5
Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5

Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.

Задача №3 (практическая):

Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.

Решение:

Периметр комнаты = 2 * (5 + 3) = 16 метров
Количество плинтусов = 16 / 3 = 5,33 штук
Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно. Поэтому принимаем следующее целое число. Это шесть.

Ответ: Количество плинтусов 6 штук.

В заключение:

Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории.

На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.

2 класс. Математика. Периметр многоугольника — Периметр

Комментарии преподавателя

Повторение геометрических фигур

Внимательно посмотрите на рисунок. Какие фигуры на нем изображены?

Рис. 1.

На этом рисунке изображены прямоугольник, квадрат, четырехугольник и треугольник.

Как можно все эти фигуры назвать одним словом? Все эти фигуры – многоугольники.

Многоугольник – это замкнутая ломаная линия.

3. Задача №1 и знакомство с понятием периметр

Давайте решим следующую задачу.

Рис. 2.

Мы изобразили весь путь Кати в виде четырехугольника. Четырехугольник – это замкнутая линия. Чтобы узнать длину этой замкнутой линии, нужно знать длину каждого звена замкнутой линии и эти длины сложить. Длину Катиного пути можно представить в виде линии, которая состоит из четырех отрезков.

Рис. 3.

Зная длину каждого из отрезков, мы их сложим и узнаем длину Катиного пути.

2 + 1 + 1 + 2 = 6 (км)

Мы узнали, что Катя прошла 6 км. Но еще мы узнали периметр четырехугольника.

Периметр четырехугольника – это сумма длин его сторон.

4. Задача на тему периметр

Давайте посчитаем периметр еще одной фигуры – треугольника ABC.

В математике периметр обозначают буквой P (пэ).

Рис. 4.

Мы знаем, что периметр – это сумма длин сторон фигуры.

PΔ= a + b + c

Нам известно значение каждой из сторон. Сложив их, мы узнаем сумму длин сторон треугольника, то есть его периметр.

= AB + BC + AC

= 3 см + 4 см + 5 см = 12 см

5. Итоги урока

Мы узнали, что такое периметр многоугольника и научились его вычислять.

Список рекомендованной литературы

1. Александрова Э.И. Математика. 2 класс. М.: Дрофа – 2004.

2. Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. М.: Астрель – 2006.

3. Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. М.: Просвещение – 2012.

Дополнительные веб-ресурсы

1. Фестиваль педагогических идей «Открытый урок» (Источник).

2. Nsportal.ru (Источник).

3. Фестиваль педагогических идей «Открытый урок» (Источник).

Сделай дома

1. Найдите периметры фигур:

а)

б)

в)

2. Вычислите результаты выражений:
а) 3 + 4 + 7 б) 2 + 1 + 3 в) 5 + 5 + 1

3. Вычислите сумму удобным способом:
а) 10 + 12 + 8 + 20 б) 17 + 4 + 3 + 16 в) 9 + 7 + 21 + 13

3. Расставьте выражения так, чтобы результат одного выражения был началом другого:
1) 20 – 8
2) 32 + 7
3) 35 – 12
4) 66 – 22

*****************************************************

§1. Понятие «периметр»

Периметр – новое слово. Что же это такое?

Давайте отправимся в сказку «Золушка».

Помните момент, когда мачеха дала Золушке целый список поручений, чтобы та не смогла поехать на бал?

Давайте представим, что одно из поручений было измерить длину цветника, чтобы поставить вокруг него забор.

Как же Золушка справилась с этим заданием?

Цветник имеет форму прямоугольника.

Сначала Золушка измерила одну сторону цветника, она оказалась равна 16 метрам.

Затем измерила вторую сторону, ее длина была 8 метров.

Длина третей стороны – 16 метров и четвертой – 8 метров.

(Обратите внимание, противоположные стороны прямоугольника равны).

Затем Золушка сложила длины всех сторон, и у нее получилась длина всего цветника:

16 + 8 + 16 + 8 = 48 метров

В математике сумму длин всех сторон называют периметром.
Значит, периметр данного цветника равен 48 м.

Периметр многоугольника – это сумма длин всех сторон многоугольника.

Периметр обозначается заглавной буквой Р латинского алфавита.

Решение задач на нахождение периметра многоугольника

Итак, чтобы найти периметр многоугольника, нужно сложить длины всех его сторон.

Давайте решим задачи на нахождение периметра многоугольника.

Дан квадрат со стороной, равной 3 см.

Нужно найти его периметр.

Почему же у квадрата дана только одна сторона?

Вспомним, квадрат – это прямоугольник, у которого все стороны равны.

Значит, каждая сторона квадрата равна 3 см.

Найдем периметр.

Периметр – это сумма длин всех сторон многоугольника.

У квадрата четыре стороны, длина каждой равна 3 см, значит, нужно 3 сложить четыре раза.

Р = 3 см + 3 см + 3 см + 3 см = 12 см

Ответ: периметр квадрата равен 12 см.

Теперь найдем периметр треугольника.

У треугольника три стороны, складываем их длины:

Р = 7 см + 7 см + 4 см = 18 см

Ответ: периметр треугольника равен 18 см.

Изменим условие этой задачи и решим обратную ей задачу.

Периметр треугольника равен 18 см.

Длина одной стороны 7 см, второй – 7 см.

Найдите длину третей стороны.

Периметр треугольника – это сумма длин трех его сторон, значит,

чтобы найти третью сторону, нам нужно из значения периметра вычесть значения длин двух других сторон.

18 см – 7 см – 7 см = 4 см

Ответ: длина третей стороны треугольника равна 4 см.

Можно решать и более сложные задачи, зная, как находить периметр.

Найдем периметр многоугольника, изображенного на рисунке.

Посчитаем, сколько сторон у него.

Всего шесть сторон.

Значит, нам нужно сложить шесть чисел, представляющих длины сторон этого многоугольника.

Р = 2 см + 7 см + 5 см + 4 см + 3 см + 3 см = 24 см

Ответ: периметр многоугольника равен 24 см.

§3. Краткие итоги урока

Подведем итоги:

Периметр многоугольника – это сумма длин всех сторон многоугольника.
Периметр обозначается заглавной буквой Р латинского алфавита.
Чтобы найти длину неизвестной стороны многоугольника, нужно из периметра многоугольника вычесть известные длины всех других его сторон.

ИСТОЧНИКИ

http://interneturok.ru/ru/school/matematika/2-klass/chisla-ot-1-do-100-slozhenie-i-vychitanie/perimetr-mnogougolnika?seconds=0&chapter_id=2354

http://doc4web.ru/matematika/konspekt-uroka-perimetr-mnogougolnika-klass.html

Периметр многоугольника / Основы геометрии / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Основы геометрии
Периметр многоугольника

Любой многоугольник — это замкнутая ломаная линия.

Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.

Значит, периметр многоугольника — это сумма длин всех его сторон.

В математике периметр обозначают буквой P (пэ).

Периметр прямоугольника

Например, найдём периметр данного прямоугольника.

1 способ:

Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.

2 способ:

Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.

Формула для подсчета периметра прямоугольника:

(a + b) • 2

a – длина прямоугольника

b – ширина прямоугольника.

Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:

Периметр треугольника

Периметр квадрата

Первый способ (когда мы еще не знаем действие умножения):

Второй способ (когда мы изучили действие умножения):

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Круг. Шар. Овал

Треугольники

Многоугольники

Угол. Виды углов

Обозначение геометрических фигур буквами

Площадь фигуры

Окружность

Основы геометрии

Правило встречается в следующих упражнениях:

1 класс

Страница 4. Урок 3, Петерсон, Учебник, часть 3

Страница 5. Урок 3, Петерсон, Учебник, часть 3

Страница 87. Урок 44, Петерсон, Учебник, часть 3

2 класс

Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 39, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 53. Урок 27, Петерсон, Учебник, часть 1

Страница 3. Урок 1, Петерсон, Учебник, часть 2

Страница 28. Урок 10, Петерсон, Учебник, часть 2

Страница 87. Урок 36, Петерсон, Учебник, часть 2

3 класс

Страница 84, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 1

Страница 42. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы

Страница 33, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 46, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 20, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 13. Урок 4, Петерсон, Учебник, часть 1

Страница 41. Урок 15, Петерсон, Учебник, часть 1

Страница 18. Урок 7, Петерсон, Учебник, часть 2

Страница 39. Урок 15, Петерсон, Учебник, часть 2

4 класс

Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 70, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 41, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 48, Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 207, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 208, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 209, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 210, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 211, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

6 класс

Задание 389, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 428, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 430, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Найти его периметр и площадь.

Калькулятор вычисления периметра и площади геометрических фигур

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Что такое прямоугольник и квадрат

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D .

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором.

Какой длины будет забор?

Что такое площадь прямоугольника?

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

Для того, чтобы находить периметр и площадь прямоугольника, нужно знать формулы и главное — уметь применять их для решения задач — ведь они бывают разной сложности.

Очень часто при решении задач легкого уровня достаточно знать основные формулы и решить их просто подставляя нужные значения.

Если задачи посложнее и в их условии нет данных нужных для формулы, нужно их находить с помощью других алгебраических действий.

В этом случае можно навести следующий пример

нужно найти площадь прямоугольника, если его периметр равен 120 см, а стороны относятся как 2 к 3

сначала составляем уравнение , чтобы найти стороны используя при этом формулу периметра (P=2(а+b ):

2*(2х+3Х)=120 решаем его, х=12 значит стороны равны 24 см и 36 см и теперь уже подставляем значения в формулу площади S=ab и находим ее S=24*36=864 см.кв.

Площадь прямоугольника равна произведению длины и ширины и вычисляется по формуле a*b, где а и b -стороны прямоугольника. Периметр прямоугольника равен сумме всех его сторон и вычисляется по формуле a+b+a+b.

Нахождение площади прямоугольника — умножим длину прямоугольника на его ширину.

Нахождение периметра прямоугольника (сумма длин всех сторон) — простым сложением длин всех сторон, либо к длине продольной стороны прямоугольника, прибавляем длину поперечной и полученную сумму умножаем на два.

Если представить, что ваш огород прямоугольной формы и вам необходимо участок обложить забором, то наверное перед вами возникнет вопрос, а какой длины будет забор, чтобы правильно рассчитать расход стройматериалов. Вы сложите длины сторон забора и найдете ПЕРИМЕТР. Если зададитесь вопросом, какое количество земли нужно перекопать на этом участке, то придется искать ПЛОЩАДЬ, а для этого нужно будет перемножить длину на ширину участка, ведь как известно у прямоугольника противоположные стороны попарно равны. Не стоит забывать, что квадрат тоже прямоугольник, чтобы найти периметр квадрата, нужно длину умножить на 4, а площадь — длину стороны умножить на себя.

Вспомним школьный курс математики. Так периметр прямоугольника находится по формуле суммы двух его сторон умноженных на 2. То есть Р=2*(а+b), где а и b это стороны прямоугольника. Площадь, соответственно находится с помощью формулы S=a*b, где a и b также являются его сторонами.

Если не вдаваться в глубокие подробности, то найти площадь и периметр геометрической фигуры прямоугольник очень просто. Обозначим стороны такого прямоугольника латинскими буквами: a, b, c и d. Пусть a = c — это длина прямоугольника, а b и d — это ширина прямоугольника.

Площадь прямоугольника:

Периметр прямоугольника:

S = a + b + c + d

Периметр прямоугольника — это длины всех его сторон. Исходя из того, что у этой фигуры четыре стороны, или две пары, при этом противолежащие стороны равны друг другу, можно прийти к выводу, что уместно сложить значения двух разновеликих сторон и умножить полученное значение на два.

Площадь находится также просто: мы просто перемножаем разновеликие стороны.

Площадь вычисляется при умножении длинной стороны прямоугольника с короткой. А периметр-это (длин. сторона+ кор. сторона)*2

Можно пойти самым простым путем нахождения площади прямоугольника. А именно, умножить длину прямоугольника (как правило, это quot;aquot;) на ширину прямоугольника (как правило, это quot;Bquot;). А вот периметр ищем при помощи сложения всех сторон, или, проще говоря: 2a+2b

Прямоугольник это геометрическая фигура, а именно четырехугольник, у которого все углы прямые. Получается, что противоположные стороны равны друг другу.

Периметр прямоугольника это сумма длин всех сторон прямоугольника, либо сумма длины и ширины, умноженная на 2.

Периметр это длина всех сторон прямоугольника, то он измеряется в единицах длины: см, мм, м, дм, км.

P=AB+CD+AD+BC или P=2*(AB+AD).

Площадь измеряется квадратными единицами длины: м2, см2, дм2 и обозначается латинской буквой S.

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.

Площадь прямоугольника рассчитывается путем умножения его длины на ширину полученное произведение и будет площадь.

Периметр прямоугольника находится путем суммирования длины и ширины, полученную сумму нужно еще умножить на два, это и будет искомый периметр.

Если у прямоугольника заданы две противолежащие стороны, то все просто перемножаем их и получаем площадь, складываем и удваиваем и получаем периметр. Однако чаще в учебниках задают самый разнобой — сторону и периметр, сторону и площадь, сторону и диагональ. Как поступать в этих случаях.

Вот это идеальная задача.

Могут быть заданы сторона и диагональ. В этом случае находим вторую сторону по теореме Пифагора — как второй катет в треугольнике где гипотенуза диагональ прямоугольника.

В итоге мы имеем вот какие формулы для нахождения периметра прямоугольника:

А если по простому преобразовать эти же формулы, то получаются формулы для нахождения площади во всех вариантах задач:

Подписаться на сайт

Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P . Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Ответ: 40 см

P = 10+10+10+10

P =40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S= 100 см 2

Ответ: 10 0 см 2

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

P = (6+2) * 2

P = 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

S = 5*2

S =10см 2

Ответ: 10 см 2

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3. 141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L = 2*3,14*3

L =6 π

L=6*3.14

L = 18.84 см

P к = 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см 2 , м 2 , мм 2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Круг

Частные случаи

Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.

Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.

Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.

Многоугольник

Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:

— пентагон;
— гексагон;
восемь — октагон;
двенадцать — додекагон.

И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:

где n – количество сторон многоугольника, a – длина стороны.

Для определения площади используется выражение:

S = n/4 × a 2 × ctg(pi/n).

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.

Примеры из реальной жизни

Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.

Покраска забора

Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.

Отделка бахромой

Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:

Таким образом, нам понадобится 4 м бахромы для отделки платка.

Заключение

Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.

Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.

Основные понятия

Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.

Рассмотрим пример: по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.

Рис. 1. Земельный участок формой прямоугольника.

Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:

2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.

Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.

Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.

Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.

Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.

Формула периметра фигуры

Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:

$P = (a+b) * 2$, где а, b – стороны фигуры.

Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.

Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь. Тогда формула будет выглядеть следующим образом:

$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.

Рис. 3. Прямоугольник с сторонами a, b .

Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см. и 6 см.

Решение:

Используем формулу $P = (a+b)*2$

$P = (4+6)*2=20 см$

Таким образом, периметр фигуры $P = 20 см$.

Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.

Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.

Модуль 15 Раздел 3: Расчет сторон

Модуль 15 Раздел 3: Вычисление сторон

В этом разделе мы используем тригонометрические функции для вычисления длин сторон в прямоугольном треугольнике.

Тригонометрические функции

sin Θ =

cos Θ =

тан Θ =

Пример 1

Вычислите длину стороны, отмеченной x в этом треугольнике.

В этом вопросе мы используем противоположную сторону и гипотенузу . Эти две стороны появляются в формуле для SIN θ , поэтому мы начинаем с

SIN θ =

В этом случае это дает,

SIN 40 °	=
или	=
или	=
или	=
или	=
или	=
или	=
или	=
OR
x	= 8 × sin 40°
	= 5,142300877 см
	= 5,1 см до 1 Десятичного места

Пример 2

Вычисляйте длину побочной стороны.

В этом случае нас интересует сторона A B, которая является противоположной стороной, и стороной BC, которая является смежной стороной , поэтому мы используем формулу

tan Θ =

Для этой задачи мы имеем ,

tan 50°	=
so
x	= 9 × tan 50°
	= 10.72578233 cm
	= 10.7 cm to 1 decimal место

Пример 3

Вычислите длину гипотенузы этого треугольника.

В этом случае нам потребуется формула, связывающая смежную сторону и гипотенузу , поэтому мы используем cos Θ .

Starting with

cos Θ =

we can use the values from the triangle to obtain,

cos 20°	=
H × cos 20°	= 12
H	=
	= 12,77013327 см

Следовательно, гипотенуза имеет длину 12,8 см с точностью до 1 знака после запятой.

Упражнения

Вопрос 1

Используйте формулу для синуса, чтобы определить длину стороны, отмеченной x в каждом из следующих треугольников. В каждом случае дайте правильный ответ с точностью до 1 знака после запятой.

(а)

см

(б)

см

(в)

см

(г)

см

Вопрос 2

Используйте формулу косинуса, чтобы определить длину соседней стороны в каждом из следующих треугольников. Дайте свои ответы правильно с точностью до 1 знака после запятой.

(а)

см

(б)

см

(в)

см

(г)

см

Вопрос 3

Вычислите длину сторон, обозначенных буквами в каждом из следующих треугольников. Дайте каждый из ваших ответов правильно до 3-х значащих цифр.

(а)

х = см г = см

(б)

а = м B = M

(C)

x = CM

(D)

P = CM

(E)

Z = CM

(F)

Z = CM

(F)

7 = CM

(F)

7 = CM

(F)

7 = CM

(F)

88 = CM
(F) 9000
= CM
(E)
= CM
(E)
= CM
(E)
. = м
Вопрос 4
Вычислите длину гипотенузы каждого из следующих треугольников. Дайте каждый из ваших ответов правильно до 3-х значащих цифр.
(а)
см
(б)
см
(в)
см
(г)
см
Вопрос 5
Вычислите все длины, отмеченные буквами в следующих треугольниках. Дайте каждый из ваших ответов с точностью до 2 знаков после запятой.
(а)
а = см б = см
(б)
в = см д = см
(в)
д = см f = см
(d)
г = см ч = см
Вопрос 6
Лестница длиной 6 м прислонена к вертикальной стене. Угол между лестницей и горизонтальной поверхностью земли составляет 65°.
(a)
На каком расстоянии от стены находится основание лестницы?
Расстояние от подножия стены = м (с точностью до см)
(b)
Какова высота верха лестницы над землей?
Высота верха над землей = м (с точностью до см)
Вопрос 7
Лодка плывет 50 км по азимуту 070°.
(a)
Как далеко на восток проплывает лодка?
Расстояние на восток = км (с точностью до км)
Расстояние на восток = 50 × sin70° = 46,98463104 км = 47 км (с точностью до км)
(b)
Как далеко на север плывет лодка?
Расстояние на север = км (с точностью до км)
Расстояние на восток = 50 × cos70° = 17,10100717 км = 17 км (с точностью до км)
Вопрос 8
Вычислите периметр и площадь этого треугольника.
Дайте свои ответы правильно до 2 знаков после запятой.
Периметр =
Площадь =
Вопрос 9
Пандус имеет длину 6 м и расположен под углом 50° к горизонтали. Какова высота верха рампы? Дайте свой ответ с разумным уровнем точности.
Высота верха аппарели =
м Вопрос 10
Веревка протянута от окна в стене здания до точки на земле в 6 м от основания здания. Угол между веревкой и стеной здания равен 19°.
(a)
Какой длины веревка?
Длина веревки = м (с точностью до см)
6 ÷ sin19° = 18,42
2 м = 18,43 м (с точностью до см)
(b)
На какой высоте находится окно?
Высота окна = м (с точностью до см)
6 × tan19° = 17,42526527 м = 17,43 м (с точностью до см)
символов GD&T | Основы GD&T
Допуск формы
Прямолинейность
Используется для указания того, насколько прямой является цель.
Прямолинейность
Плоскостность
Используется для указания самой выступающей части и самой вогнутой части.
Плоскостность
Округлость
Используется для указания того, насколько близко должна быть цель к идеальному кругу.
Округлость
Цилиндричность
Используется для указания того, насколько прямой должна быть цель и насколько близко она должна быть к идеальному кругу.
Цилиндричность
Допуск профиля линии
Используется для указания того, насколько близка кривизна (поперечное сечение) к конструкции.
Допуск профиля линии
Допуск профиля плоскости
Используется для указания того, насколько кривизна (поверхность) близка к дизайну.
Допуск профиля плоскости
Допуск ориентации
Параллелизм
Используется для указания того, насколько точно две линии или плоскости параллельны базе.
Параллельность
Перпендикулярность
Используется для указания того, насколько точно цель перпендикулярна к исходной точке.
Перпендикулярность
Угловатость
Используется для указания точного наклона цели к системе отсчета.
Угловатость
Допуск местоположения
Истинное положение
Используется для указания того, насколько точно цель позиционируется по отношению к системе отсчета.
Истинное положение
Соосность
Используется для указания того, что оси двух цилиндров соосны (без отклонения центральных осей) относительно базы.
Соосность
Концентричность
Используется для указания того, что оси двух цилиндров соосны (без отклонения в центральных точках) относительно базы.
Концентричность
Симметрия
Используется для указания того, насколько симметрична цель относительно базы.
Симметрия
Допуск на биение
Круговое биение
Используется для указания биения любой части окружности при вращении цели.
Круговое биение
Полное биение
Используется для указания биения всей поверхности при вращении цели.
Полное биение
Требования к конверту
«E» означает «конверт». Этот символ указывает на взаимную зависимость допуска размера и геометрического допуска. Он задает оболочку совершенной формы.
Что такое?
Свободное состояние нежестких частей
«F» означает «свободное состояние». Этот символ указывает на деформацию, выходящую за пределы допуска по размеру или геометрического допуска в свободном состоянии.
Что такое?
Применение наименьшего материального состояния
«L» означает «наименее материальное состояние». Этот символ указывает на применение наименьших материальных условий.
Что такое?
Применение максимального состояния материала
«M» означает «максимальное состояние материала». Этот символ указывает на применение максимального состояния материала.
Что такое?
Индикация предполагаемой зоны допуска
«P» означает «проецируемая зона допуска». Этот символ указывает допуск, применяемый к выступу элемента.
Что такое?
Материал не требуется
Символ, используемый стандартом ANSI. Он представляет собой «независимо от размера элемента (RFS)». Этот символ был удален в ASME Y14.5-2009.
Индикация касательной плоскости (только ASME)
«T» означает «тангенциальная плоскость». Насколько наклонна плоскость, соприкасающаяся с поверхностью, к базовой плоскости в пределах заданной поверхности, обозначается параллелизмом. В отличие от параллелизма, это определяет выпуклость поверхности, а не вогнутость.
Допуск на неравномерное расположение профиля (только ASME)
«U» означает «неравномерно расположенный профиль». Это задает диапазон отклонения величины смещения от зоны допуска (предел зоны допуска) с точки зрения допуска профиля плоскости. «UZ» используется для аннотации в соответствии со стандартами ISO.
Элемент с допуском
Указание символов, допусков, типов геометрических допусков, положения и других требований.
Рамка управления функциями
Индикация исходной точки
Исходное положение.
Чертеж обозначения опорных элементов
Базовая цель
Точка, линия или зона для установки базы.
Базовые цели
Теоретически точный размер (TED)
Теоретически точный размер (TED)
Теория истинного положения (значение размера в прямоугольной рамке)
Общая зона допуска
«CZ» означает общую зону. Указание на то, что несколько элементов в разных положениях считаются одной зоной допуска.
Рамка управления функциями
Допуск профиля (периметр)
Средство для применения геометрического допуска к периметру элемента, указанного стрелкой.
Допуск формы и допуск местоположения (допуск профиля линии / допуск профиля плоскости)
Допуск профиля (полностью)
Средство применения геометрического допуска ко всему элементу, указанному стрелкой.
Допуск формы и допуск местоположения (допуск профиля линии / допуск профиля плоскости)
Подвижная базовая мишень (только ASME; предлагается для ISO)
Указанная целевая опорная точка и другие связанные с ней опорные точки могут быть перемещены. Например, даже когда деталь прикреплена к мишени, можно изменить форму мишени, мишень и базис можно переместить.
Точечная облицовка (только ASME)
Обработка, которая создает цековку, увеличивает еще одно коаксиальное отверстие.
Точечная облицовка
Статистическая погрешность (только ASME)
Спецификация, определяющая допуск для собранных компонентов в соответствии со статистикой. Применяя статистический допуск, можно увеличить допуск для каждого компонента, уменьшив зазор между компонентами и сопрягаемыми деталями. Хотя это может улучшить характеристики продукта и/или снизить производственные затраты, применение этого допуска требует надлежащего управления статистическими процессами в качестве предварительного условия.
Сравнение ISO и ASME
Непрерывная функция (только ASME)
«CF» означает «непрерывная функция». Это требование указывается, когда элементы должны быть геометрически обработаны как один элемент.
Сравнение ISO и ASME
Глоссарий Глоссарий
ИНДЕКС
Глава 2A — MUTCD, издание 2009 г.
Вернуться к текущей версии | Вернуться к части 2 Оглавление
Раздел 2A.01 Функция и назначение знаков
Поддержка:
01 В этом руководстве содержатся стандарты, рекомендации и варианты обозначения всех типов автомагистралей и частных дорог, открытых для общественного транспорта. Функции знаков заключаются в предоставлении правил, предупреждений и информации для участников дорожного движения. Слова, символы и стрелки используются для передачи сообщений. Знаки обычно не используются для подтверждения правил дорожного движения.
02 Подробные требования к знакам изложены в следующих главах Части 2:
Глава 2B — Знаки нормативных требований, заграждения и ворота
Глава 2C — Предупреждающие знаки и маркеры объектов
Глава 2D — Направляющие знаки для обычных дорог
Глава 2E — Направляющие знаки для автомагистралей и скоростных автомагистралей
Глава 2F — Знаки платных дорог
Глава 2G — Знаки преимущественной и контролируемой полосы движения
Глава 2H — Знаки общей информации
Глава 2I — Знаки общего обслуживания
Глава 2J — специальные служебные знаки (логотип)
Глава 2K — указатели направления, ориентированные на туристов
Глава 2L — Изменяемые знаки сообщений
Глава 2M — Знаки зон отдыха и культурных интересов
Глава 2N — Знаки аварийного управления
Стандарт:
03 Поскольку требования и стандарты для знаков зависят от конкретного типа автомагистрали, на которой они должны использоваться, должны применяться определения автомагистралей, скоростных автомагистралей, обычных дорог и дорог специального назначения, приведенные в Разделе 1A. 13. в Части 2.
Раздел 2A.02 Определения
Поддержка:
01 Определения и сокращения, применимые к знакам, приведены в Разделах 1A.13 и 1A.14.
Раздел 2A.03 Стандартизация применения
Поддержка:
01 Общепризнанно, что условия движения в городе отличаются от условий движения в сельской местности, и во многих случаях знаки наносятся и размещаются по-разному. Там, где это уместно и практично, в настоящем Руководстве излагаются отдельные рекомендации для городских и сельских условий.
Руководство:
02 Знаки следует использовать только в тех случаях, когда это оправдано инженерной оценкой или исследованиями, как указано в Разделе 1A.09.
03 Результаты инженерных исследований физических факторов и факторов дорожного движения должны указывать места, где знаки считаются необходимыми или желательными.
04 Геометрический дизайн проезжей части и применение знаков должны быть скоординированы таким образом, чтобы знаки можно было эффективно разместить, чтобы предоставить пользователю дороги любую необходимую нормативную, предупреждающую, руководящую и другую информацию.
Стандарт:
05 Каждый стандартный знак должен отображаться только для конкретной цели, предписанной в данном Руководстве. Определение конкретных знаков, которые должны применяться к конкретным условиям, должно производиться в соответствии с положениями, изложенными в Части 2. Перед любой новой автомагистралью, частной дорогой, открытой для общественного транспорта (см. определение в Разделе 1A.13), объездом или открыт временный маршрут для проезда населения, должны быть установлены все необходимые знаки. Знаки, требуемые дорожными условиями или ограничениями, должны быть удалены, когда эти условия перестают существовать или ограничения снимаются.
Раздел 2A.04 Чрезмерное использование знаков
Руководство:
01 Предупреждающие и предупредительные знаки следует использовать с осторожностью, поскольку эти знаки при чрезмерном использовании теряют свою эффективность. Если используются дорожные знаки и указатели направления, их следует использовать часто, поскольку их использование способствует повышению эффективности операций, информируя участников дорожного движения об их местонахождении.
Раздел 2A.05 Классификация знаков
Стандарт:
01 Знаки должны определяться по их функциям следующим образом:
Регулирующие знаки сообщают о правилах или правилах дорожного движения.
Предупреждающие знаки сообщают о ситуации, которая может быть неочевидной.
Указательные знаки показывают обозначения маршрутов, пункты назначения, направления, расстояния, услуги, достопримечательности и другую географическую, рекреационную или культурную информацию.
Поддержка:
02 Маркеры объектов определены в Разделе 2C.63.
Раздел 2A.06 Дизайн знаков
Поддержка:
01 В данном Руководстве показаны многие типичные стандартные знаки и указатели объектов, одобренные для использования на улицах, автомагистралях, велосипедных дорожках и пешеходных переходах.
02 В спецификациях на отдельные знаки и указатели объектов общий вид легенды, цвет и размер показаны в сопроводительных таблицах и иллюстрациях и не всегда подробно описываются в тексте.
03 Подробные чертежи стандартных знаков, указателей объектов, алфавитов, символов и стрелок (см. рис. 2D-2) приведены в книге «Стандартные дорожные знаки и разметка». Раздел 1A.11 содержит информацию о том, как получить эту публикацию.
04 Основные требования к знаку заключаются в том, чтобы он был разборчивым для тех, для кого он предназначен, и чтобы он был понятен вовремя, чтобы обеспечить надлежащую реакцию. К желательным атрибутам относятся:
Высокая видимость днем и ночью; и
Высокая разборчивость (буквы, символы или стрелки соответствующего размера, а также короткая легенда для быстрого понимания участником дорожного движения, приближающимся к знаку).
05 Определены стандартные цвета и формы, чтобы можно было быстро распознавать несколько классов дорожных знаков. Важны простота и единообразие дизайна, положения и применения.
Стандарт:
06 Термин «легенда» должен включать все словесные сообщения, а также символы и конструкции стрелок, предназначенные для передачи определенных значений.
07 Единообразие дизайна должно включать форму, цвет, размеры, надписи, границы и освещение или световозвращающую способность.
08 Стандартизация этих рисунков не исключает дальнейшего усовершенствования за счет незначительных изменений пропорций или ориентации символов, ширины границ или расположения словесных сообщений, но все формы и цвета должны соответствовать указанным.
09 Все символы должны быть безошибочно похожи или зеркально отображать принятые символы, все из которых показаны в книге «Стандартные дорожные знаки и разметка» (см. Раздел 1A.11). Символы и цвета не должны изменяться, если иное не предусмотрено настоящим Руководством. Все символы и цвета для знаков, не показанные в книге «Стандартные дорожные знаки и разметка», должны соответствовать процедурам экспериментирования и изменения, описанным в Разделе 1A.10.
Опция:
10 Хотя стандартный дизайн знаков с символами не может быть изменен, ориентация символа может быть изменена, чтобы лучше отражать направление движения, если это необходимо.
Стандарт:
11 В тех случаях, когда применяется стандартное текстовое сообщение, формулировка должна соответствовать данному Руководству.
12 В ситуациях, когда требуются словесные сообщения, отличные от тех, которые предусмотрены в настоящем Руководстве, знаки должны быть той же формы и цвета, что и стандартные знаки того же функционального типа.
Опция:
13 Государственные и местные дорожные службы могут разрабатывать специальные словесные информационные знаки в ситуациях, когда состояние дороги требует предоставления участникам дорожного движения дополнительной нормативной, предупреждающей или инструктивной информации, например, когда необходимо уведомить участников дорожного движения об особых правил или предупреждены о ситуации, которая может быть неочевидной. В отличие от цветов, которые не были назначены, или символов, которые не были одобрены для знаков, новые словесные сообщения могут использоваться без необходимости экспериментировать.
Стандарт:
14 За исключением случаев, предусмотренных в параграфе 16, и за исключением знака Carpool Information (D12-2) (см. Раздел 2I.11), интернет-адресов и адресов электронной почты, включая доменные имена и унифицированные указатели ресурсов (URL) , не должны отображаться на каких-либо знаках, дополнительных табличках, табличках (включая таблички с логотипами на табличках с особыми услугами) или табличках со сменными сообщениями.
Руководство:
15 Если иное не предусмотрено в настоящем Руководстве для конкретного знака и за исключением случаев, предусмотренных в параграфе 16, телефонные номера длиной более четырех символов не должны отображаться ни на каком знаке, дополнительной табличке, табличке (включая таблички с логотипом). на специальных служебных знаках) или изменяемый знак сообщения.
Опция:
16 Интернет-адреса, адреса электронной почты или телефонные номера, содержащие более четырех символов, могут отображаться на знаках, дополнительных табличках, табличках и знаках со сменными сообщениями, которые предназначены для просмотра только пешеходами, велосипедистами, пассажирами. припаркованных транспортных средств или водителей транспортных средств на низкоскоростных дорогах, где инженерная оценка указывает на то, что водители могут остановиться в транспортном потоке, чтобы прочитать сообщение.
Стандарт:
17 Пиктограммы (см. определение в разделе 1A.13) не должны размещаться на знаках, за исключением случаев, специально предусмотренных в настоящем Руководстве. Пиктограммы должны быть простыми, достойными и лишенными какой-либо рекламы. При использовании для обозначения политической юрисдикции (например, штата, округа или муниципальной корпорации) пиктограмма должна быть официальным обозначением, принятым юрисдикцией. При использовании для обозначения колледжа или университета пиктограмма должна быть официальной печатью, принятой учреждением. Запрещается размещать на вывесках графические изображения программ университетов или колледжей.
Раздел 2A.07 Световозвращение и освещение
Поддержка:
01 В настоящее время существует множество материалов для световозвращения и различные методы освещения знаков и указателей объектов. Постоянно появляются новые материалы и методы. Можно использовать новые материалы и методы, если знаки и маркеры объектов соответствуют стандартным требованиям к цвету как днем, так и ночью.
Стандарт:
02 Регулирующие, предупреждающие и направляющие знаки и указатели объектов должны быть световозвращающими (см. Раздел 2A.08) или освещаться, чтобы иметь одинаковую форму и одинаковый цвет как днем, так и ночью, если иное не предусмотрено в тексте обсуждения в настоящего Руководства для конкретного знака или группы знаков.
03 Считается, что требования к освещению знаков не удовлетворяются уличным или автомобильным освещением.
Опция:
04 Элементы знака могут быть подсвечены средствами, показанными в таблице 2A-1.
Таблица 2А-1. Освещение элементов знака
Средства освещения Элемент знака с подсветкой
Свет за вывеской
Символ или словесное сообщение
Фон
Символ, текстовое сообщение и фон (через полупрозрачный материал)
Присоединенный или независимо установленный источник света, для направления равномерного освещения на лицевую сторону знака
Вывеска целиком
Светоизлучающие диоды (СИД)
Символ или словесное сообщение
Части границы знака
Другие устройства или процедуры, которые выделяют форму, цвет или сообщение знака:
Светящаяся трубка
Волоконная оптика
Лампы накаливания
Люминесцентные панели
Символ или словесное сообщение
Вывеска целиком
05 Световозвращение элементов знака может быть достигнуто средствами, показанными в таблице 2А-2.
Таблица 2А-2. Световозвращение элементов знака
Средства световозвращения Элемент знака
Рефлекторные «кнопки» или аналогичные элементы Символ
Текстовое сообщение
Граница
Материал с гладкой герметичной внешней поверхностью поверх микроструктуры, отражающей свет Символ
Текстовое сообщение
Граница
Фон
06 Блоки светоизлучающих диодов (СИД) могут использоваться отдельно в легенде или символе знака и в рамке знака, за исключением сменных знаков сообщения, для улучшения заметности, повышения разборчивости легенд знаков и границы или предоставить изменяемое сообщение.
Стандарт:
07 За исключением случаев, предусмотренных в параграфах 11 и 12, ни отдельные светодиоды, ни группы светодиодов не должны размещаться на фоне знака.
08 При использовании светодиоды должны иметь максимальный диаметр 1/4 дюйма и должны быть следующих цветов в зависимости от типа знака:
Белый или красный, если используются со знаками СТОП или УХОД.
Белый, если используется с нормативными знаками, отличными от знаков СТОП или ДОХОД.
Белый или желтый, если используется с предупредительными знаками.
Белый, если используется с указателями.
Белый, желтый или оранжевый, если используются временные дорожные знаки.
Белый или желтый, если используется со школьными указателями.
09 При мигании все светодиодные блоки должны мигать одновременно с частотой более 50 и менее 60 раз в минуту.
10 Единообразие дизайна знака должно сохраняться без ухудшения видимости, разборчивости или понимания водителем как в дневное, так и в ночное время.
Опция:
11 Для знаков «СТОП» и «ВЫХОД» светодиоды могут быть размещены внутри рамки или в пределах одной ширины границы в пределах фона знака.
12 Для сигналов СТОП/МЕДЛЕННО (см. Раздел 6E.03), используемых сигнальщиками, и сигналов СТОП (см. Раздел 7D.05), используемых взрослыми регулировщиками, могут использоваться отдельные светодиоды или группы светодиодов.
Поддержка:
13 Другие методы повышения заметности стандартных знаков описаны в разделе 2A.15.
14 Информация об использовании световозвращающего материала на опоре знака содержится в Разделе 2A.21.
Раздел 2A.08 Поддержание минимальной световозвращающей способности
Поддержка:
01 Световозвращающая способность является одним из нескольких факторов, связанных с поддержанием видимости знака в ночное время (см. раздел 2A.22).
Стандарт:
02 Государственные учреждения или уполномоченные должностные лица должны использовать метод оценки или управления, предназначенный для поддержания световозвращающей способности знака на уровне или выше минимального уровня, указанного в Таблице 2A-3.
Тип покрытия
Таблица 2А-3. Минимальные поддерживаемые уровни световозвращения ¹
Цвет знака (ASTM D4956-04) Дополнительные критерии
Бисероплетение Призматическая пленка
я II III III, IV, VI, VII, VIII, IX, X
Белый на зеленом Вт*; G ≥ 7 Вт*; G ≥ 15 Вт*; G ≥ 25 Вт ≥ 250; G ≥ 25 Накладные расходы
Вт*; G ≥ 7 Вт ≥ 120; G ≥ 15 Установка на столбе
Черный на желтом
или
Черный на оранжевом г*; О* Д ≥ 50; О ≥ 50 ²
Д*; О* Д ≥ 75; О ≥ 75 ³
Белый на красном Вт ≥ 35; R ≥ 7 ⁴
Черный на белом Вт ≥ 50 —
Примечания:
¹ Минимальные поддерживаемые уровни световозвращения, указанные в этой таблице, указаны в единицах кд/лк/м ², измеренных под углом наблюдения 0,2° и входным углом -4,0°.
² Для текстовых знаков и знаков с мелкими символами размером не менее 48 дюймов и для жирных знаков всех размеров
³ Для текстовых знаков и знаков с мелкими символами размером менее 48 дюймов
⁴ Минимальный коэффициент контрастности знака ≥ 3:1 (белая световозвращающая способность ÷ красная световозвращающая способность)
* Этот тип листового материала не должен использоваться для данного цвета для данного применения.
Знаки жирного шрифта
W1-1, -2 – поворот и кривая
W1-3, -4 — обратный поворот и кривая
W1-5 – Извилистая дорога
W1-6, -7 — Большая стрела
W1-8 — Шеврон
W1-10 — Пересечение кривой
W1-11 — Кривая шпильки
W1-15 – Петля 270 градусов
W2-1 — перекресток
W2-2, -3 – второстепенная дорога
W2-4, -5 – T и Y пересечение
W2-6 — Круговой перекресток
W2-7, -8 — Двусторонние дороги
W3-1 – Стоп впереди
W3-2 – Предварительная доходность
W3-3 – Впереди сигнал
W4-1 — объединить
W4-2 – Концы полосы движения
W4-3 — добавлена полоса
W4-5 – Въезд на съезд с проезжей части
W4-6 — Выезд на проезжую часть с добавленной полосой
W6-1, -2 — Разделенное шоссе начинается и заканчивается
W6-3 — Двустороннее движение
W10-1, -2, -3, -4, -11, -12 – заблаговременное предупреждение о переезде
W11-2 – Пешеходный переход
W11-3, -4, -16-22 – Крупные животные
W11-5 – Сельскохозяйственное оборудование
W11-6 — Пересечение снегохода
W11-7 — Конный переход
W11-8 — Пожарная часть
W11-10 — Пересечение грузовика
W12-1 — Двойная стрела
W16-5P, -6P, -7P – таблички со стрелками
W20-7 — Флаггер
W21-1 — Рабочий
Знаки с мелкими символами (знаки-символы, не указанные как знаки жирным шрифтом)
Особые случаи
W3-1 – Остановка впереди: световозвращающая способность красного цвета ≥ 7
W3-2 – Урожай впереди: световозвращающая способность красного цвета ≥ 7; Белая световозвращающая способность ≥ 35
W3-3 – Сигнал впереди: световозвращающая способность красного цвета ≥ 7; Зеленая световозвращающая способность ≥ 7
W3-5 – Снижение скорости: световозвращающая способность белого цвета ≥ 50
Для знаков неромбовидной формы, таких как W14-3 (Зона запрещена для движения), W4-4P (Перекрестное движение не останавливается) или W13-1P, -2, -3, -6, -7 (Знаки, предупреждающие о превышении скорости) , используйте наибольший размер знака для определения надлежащего минимального уровня световозвращающей способности.
Служба поддержки:
03 Соответствие стандарту, указанному в параграфе 2, достигается путем наличия и использования метода для поддержания минимальных уровней, установленных в таблице 2A-3. При условии, что используется метод оценки или управления, агентство или должностное лицо, обладающее соответствующей юрисдикцией, будет соблюдать Стандарт в параграфе 2, даже если некоторые отдельные знаки не соответствуют минимальным уровням световозвращающей способности в конкретный момент времени.
Руководство:
04 За исключением тех знаков, которые конкретно указаны в параграфе 6, для поддержания световозвращающей способности знака следует использовать один или несколько из следующих методов оценки или управления:
Визуальный осмотр в ночное время. обученный инспектор знаков, проводящий визуальный осмотр с движущегося транспортного средства в ночных условиях. Знаки, которые визуально идентифицированы инспектором как имеющие световозвращающую способность ниже минимального уровня, должны быть заменены.
Измеренная световозвращающая способность знака — световозвращающая способность знака измеряется с помощью ретрорефлектометра. Знаки со световозвращающей способностью ниже минимального уровня должны быть заменены.
Ожидаемый срок службы знака — при установке знаков дата установки маркируется или записывается, чтобы был известен возраст знака. Возраст знака сравнивается с ожидаемым сроком службы знака. Ожидаемый срок службы знака основан на опыте ухудшения световозвращающей способности знака в географической зоне по сравнению с минимальными уровнями. Знаки старше ожидаемого срока эксплуатации подлежат замене.
Замена одеяла — все знаки в зоне/коридоре или определенного типа должны заменяться через определенные промежутки времени. Это избавляет от необходимости оценивать световозвращающую способность или отслеживать срок службы отдельных знаков. Интервал замены основан на ожидаемом сроке службы знака по сравнению с минимальными уровнями для материала с наименьшим сроком службы, используемого на затронутых знаках.
Контрольные знаки — Замена знаков в полевых условиях основана на характеристиках выборки контрольных знаков. Контрольные знаки могут быть небольшим образцом, расположенным на ремонтной площадке, или образцом знаков в поле. Контрольные знаки контролируются, чтобы определить окончание световозвращающего срока службы соответствующих знаков. Все полевые знаки, представленные контрольным образцом, должны быть заменены до того, как уровни световозвращения контрольного образца достигнут минимального уровня.
Другие методы — можно использовать другие методы, разработанные на основе инженерных исследований.
Поддержка:
05 Дополнительная информация об этих методах содержится в документе FHWA 2007 г. «Поддержание световозвращающей способности дорожных знаков» (см. раздел 1A.11).
Опция:
06 Дорожные службы могут исключить следующие знаки из руководств по поддержанию световозвращающей способности, описанных в этом разделе:
Знаки парковки, стоянки и остановки (серии R7 и R8)
Знаки для пешеходов/автостопщиков/переходов (серия R9, с R10-1 по R10-4b)
Знаки подтверждения
Все знаки с синим или коричневым фоном
Знаки велосипедных дорожек, предназначенные исключительно для велосипедистов или пешеходов
Раздел 2A.
09 Формы
Стандарт:
01 Особые формы, как показано в таблице 2A-4, должны использоваться исключительно для определенных знаков или серий знаков, если иное не предусмотрено в тексте настоящего Руководства для конкретного знака. или класс знаков.
Таблица 2А-4. Использование форм знаков
Форма Знаки
Октагон Стоп*
Равносторонний треугольник (на 1 точку вниз) Выход*
Круг Заблаговременное предупреждение о переезде*
Форма вымпела/ равнобедренный треугольник
(длинная ось горизонтальная) Нет прохождения*
Пентагон (указанный вверх) Предупреждающий знак школы (прямоугольные нижние углы)*
Дорожный знак округа (заостренные нижние углы)*
Крестовина
(два прямоугольника в конфигурации «Х») Железнодорожный переезд*
Алмаз Серия предупреждений
Прямоугольник (включая квадрат) Серия нормативных документов
Серия направляющих**
Предупреждение Серия
Трапеция Рекреационные и культурные интересы
Зона Серия
Знак национального лесного маршрута
* Этот знак должен иметь исключительно показанную форму.
** Серия путеводителей включает в себя общие услуги, специальные услуги, ориентированные на туристов направления, общую информацию, зоны отдыха и культурных интересов, а также знаки управления в чрезвычайных ситуациях.
Раздел 2A.10 Цвета знаков
Стандарт:
01 Цвета, используемые на стандартных знаках, и их конкретное использование на этих знаках должны соответствовать соответствующим разделам настоящего Руководства. Цветовые координаты и значения должны быть такими, как описано в 23 CFR, часть 655, подраздел F, приложение.
Техническая поддержка:
02 В качестве краткого справочника в Таблице 2A-5 показано обычное использование цветов знаков. Цветовые схемы на конкретных знаках показаны на иллюстрациях, расположенных в каждой соответствующей главе.
Таблица 2А-5. Распространенное использование цветов знаков
Тип знака Легенда Фон
Черный Зеленый Красный Белый Желтый Оранжевый Флуоресцентный желто-зеленый Флуоресцентно-розовый Черный Синий Коричневый Зеленый Оранжевый* Красный* Белый Желтый* Фиолетовый Флуоресцентный желто-зеленый Флуоресцентный розовый
Нормативные документы
   Запрет
   Разрешающий
Предупреждение
   Пешеходный
   Велосипед
Направляющая
   Межгосударственный маршрут
   Государственный маршрут
   Маршрут США
   Уездный маршрут
   Лесной маршрут
   Улица
   Назначение
   Исходное местоположение
Информация
   Путь эвакуации
   Дорожная служба
   Для отдыха
Временное управление дорожным движением
Управление инцидентами
Школа
Только учетная запись ETC ****
Сменные знаки сообщений
   Нормативно-правовой акт ***
   Предупреждение
   Временный контроль трафика
   Направляющая **
   Услуги автомобилиста **
   Управление инцидентами
   Школа, Пешеходная, Велосипедная
* Также можно использовать флуоресцентные версии этих фоновых цветов.
** Эти альтернативные цвета фона будут обеспечиваться пикселями с синей или зеленой подсветкой, чтобы подсвечивалась вся CMS, а не только легенда.
*** Красный цвет используется только для круга и косой черты или других красных элементов аналогичного статического нормативного знака.
**** Использование пурпурного цвета на знаках ограничено положениями параграфа 1 раздела 2F.03.
03 Если в данном Руководстве или в книге «Стандартные дорожные знаки и разметка» (см. раздел 1A.11) в качестве цвета указан белый цвет, подразумевается, что он включает серебристые световозвращающие покрытия или элементы, отражающие белый свет.
04 Цвета коралловый и светло-голубой зарезервированы для использования, которое будет определено в будущем Федеральным управлением автомобильных дорог.
05 Информация о цветовой маркировке пунктов назначения на указателях, в том числе указателях населенного пункта, содержится в главе 2D.
Опция:
06 Утвержденная флуоресцентная версия стандартного красного, желтого, зеленого или оранжевого цвета может использоваться в качестве альтернативы соответствующему стандартному цвету.
Раздел 2A.11 Размеры
Опора:
01 Книга «Стандартные дорожные знаки и разметка» (см. раздел 1A.11) предписывает детали дизайна до пяти различных размеров в зависимости от типа транспортного средства, включая велосипедные дорожки. Меньшие размеры предназначены для использования на велосипедных дорожках и некоторых других внедорожных условиях. Большие размеры предназначены для использования на автомагистралях и скоростных автомагистралях, а также могут использоваться для повышения безопасности и удобства участников дорожного движения на других объектах, особенно на многополосных разделенных автомагистралях и на неразделенных автомагистралях с пятью или более полосами движения и / или высокими скоростями. . Промежуточные размеры предназначены для использования на других типах шоссе.
Стандарт:
02 Должны использоваться размеры знаков, указанные в таблицах размеров знаков в различных частях и главах настоящего Руководства и в книге «Стандартные дорожные знаки и разметка» (см. Раздел 1A.11), если только инженерная оценка не определяет, что подходят другие размеры. За исключением случаев, предусмотренных в параграфе 3, когда инженерная оценка определяет, что размеры, меньшие предписанных размеров, подходят для использования, размеры знака не должны быть меньше минимальных размеров, указанных в настоящем Руководстве. Размеры, указанные в столбцах «Минимум», которые меньше размеров, указанных в столбцах «Обычные дороги» в различных таблицах размеров знаков в настоящем Руководстве, должны использоваться только на низкоскоростных дорогах, переулках и частных дорогах, открытых для общественного транспорта, где размер условных обозначений был бы достаточным для правил или предупреждений, или когда физические условия исключают использование больших размеров.
Опция:
03 Для переулков с ограниченными физическими условиями и использованием транспортных средств, которые ограничивают установку знака минимального размера (или знака стандартного размера дороги, если не указан минимальный размер), высота и ширина знака могут быть уменьшены на до 6 дюймов.
Руководство:
04 Размеры, указанные в столбцах «Автострада» и «Скоростная автомагистраль» в различных таблицах размеров знаков в данном Руководстве, следует использовать на автомагистралях и скоростных автомагистралях, а также для других высокоскоростных приложений на основе инженерной оценки, чтобы обеспечить более крупные знаки для увеличения видимость и узнаваемость.
05 Размеры, показанные в столбцах «Негабаритный» в различных таблицах размеров знаков в этом Руководстве, следует использовать для тех специальных приложений, где скорость, громкость или другие факторы приводят к условиям, когда требуется усиление выделения, улучшение распознавания или повышение разборчивости. , как определено инженерной оценкой или исследованием.
06 Увеличения сверх предписанных размеров следует использовать там, где требуется большая разборчивость или выразительность. Если используются знаки большего размера, чем предписанные размеры, общие размеры знаков следует увеличивать с шагом в 6 дюймов.
Стандарт:
07 Если инженерная оценка определяет, что размеры, отличные от предписанных размеров, подходят для использования, должны использоваться стандартные формы и цвета, а стандартные пропорции должны быть сохранены, насколько это практически возможно.
Руководство:
08 При установке дополнительных табличек со знаками большего размера необходимо также сделать соответствующее увеличение размера таблички и ее легенды. Результирующий размер бляшки должен быть приблизительно в той же относительной пропорции к знаку большего размера, как бляшка обычного размера к знаку обычного размера.
Раздел 2A.12 Символы
Стандарт:
01 Дизайн символов во всех случаях должен быть безошибочно похож на тот, что показан в данном Руководстве и в книге «Стандартные дорожные знаки и разметка» (см. Раздел 1A.11).
Поддержка:
02 Федеральное управление автомобильных дорог приняло новый дизайн символов на основе результатов исследований, направленных на определение понимания участников дорожного движения, заметности и удобочитаемости знаков.
03 Иногда переход от словесных сообщений к символам требует значительного времени для обучения и перехода общественности. Поэтому настоящее Руководство иногда включает практику использования информационных табличек для сопровождения новых знаков-символов.
Руководство:
04 Новые предупредительные или нормативные знаки, не легко узнаваемые публикой, должны сопровождаться информационными табличками.
Опция:
05 Учебные таблички можно оставлять на месте до тех пор, пока они находятся в рабочем состоянии.
06 Государственные и/или местные дорожные службы могут проводить исследования для определения понимания участниками дорожного движения, заметности и разборчивости знаков.
Руководство:
07 Хотя большинство стандартных символов ориентированы влево, зеркальные изображения этих символов следует использовать там, где обратная ориентация может лучше передать участникам дорожного движения направление движения.
Стандарт:
08 Символ, используемый для данной категории знаков (нормативных, предупреждающих или направляющих), не должен использоваться для знаков другой категории, за исключением случаев, специально разрешенных в данном Руководстве.
09 За исключением случаев, предусмотренных в параграфе 11, символ зоны рекреационного и культурного интереса (см. главу 2М) не должен использоваться на улицах или автомагистралях за пределами зон рекреационного и культурного интереса.
10 Символ путеводного знака зоны рекреационного и культурного интереса (см. главу 2M) не должен использоваться на каких-либо нормативных или предупреждающих знаках на улицах, дорогах или шоссе.
Опция:
11 Символ указателя зоны рекреационного и культурного интереса (см. Раздел 2M.04) может использоваться на дорожном указателе за пределами зоны отдыха и культурного интереса в дополнение к аналогичному словесному сообщению, для которого нет утвержденного символ для этого сообщения в главах с 2B по 2I или 2N.
Поддержка:
12 Раздел 2M.07 содержит положения об использовании символов рекреационных и культурных достопримечательностей для обозначения запрещенных действий или предметов в недорожных условиях.
Раздел 2A.
13 Словесные сообщения
Стандарт:
01 За исключением случаев, предусмотренных в Разделе 2A.06, во всех текстовых сообщениях должны использоваться стандартные формулировки и буквы, как показано в данном Руководстве и в книге «Стандартные дорожные знаки и разметка» (см. Раздел 1А.11).
Руководство:
02 Текстовые сообщения должны быть как можно короче, а буквы должны быть достаточно крупными, чтобы обеспечить необходимое расстояние для разборчивости. Следует использовать минимальное удельное соотношение 1 дюйм высоты буквы на 30 футов расстояния для удобочитаемости.
03 Сокращения (см. Раздел 1A.15) должны быть сведены к минимуму.
04 Сообщения Word не должны содержать точки, апострофы, вопросительные знаки, амперсанд и другие знаки пунктуации или символы, не являющиеся буквами, цифрами или дефисами, за исключением случаев, когда необходимо избежать путаницы.
05 Косая черта (наклонная черта или косая черта) предназначена для использования только для дробей и не должна использоваться для разделения слов в одной строке легенды. Вместо этого для этой цели следует использовать дефис, например «ГРУЗОВЫЕ МАШИНЫ — АВТОБУСЫ».
Стандарт:
06 Дроби должны отображаться с числителем и знаменателем, расположенными по диагонали относительно солидуса (наклонная линия или косая черта). Общая высота дроби измеряется от вершины числителя до нижней части знаменателя, каждая из которых совмещена по вертикали с верхним и нижним концами солидуса. Общая высота дроби определяется высотой цифр дроби и должна быть в 1,5 раза больше высоты отдельной цифры дроби.
Поддержка:
07 Книга «Стандартные дорожные знаки и разметка» (см. раздел 1A.11) содержит подробные сведения о расположении дробей на знаках.
Руководство:
08 Когда инициалы используются для обозначения аббревиатуры отдельных слов (например, «US» для маршрута в США), инициалы должны быть разделены пробелом между 1/2 и 3/4 буквы высота инициалов.
09 Когда межгосударственный маршрут отображается в текстовом виде вместо использования экрана маршрута, для ясности следует использовать дефис, например «I-50».
Стандарт:
10 Все надписи на знаках должны быть прописными буквами, как указано в книге «Стандартные дорожные знаки и разметка» (см. Раздел 1A.11), если иное не предусмотрено в настоящем Руководстве для конкретного знака или типа сообщения. .
11 Надписи на знаках названий мест, улиц и автомагистралей должны состоять из комбинации строчных букв с начальными прописными буквами.
Поддержка:
12 Высота буквы выражается в виде высоты прописной буквы. Для легенд смешанного регистра (состоящих из начальной прописной буквы, за которой следуют строчные буквы), высота строчных букв получается из указанной высоты начальной прописной буквы на основе заданного соотношения. Высота букв для надписей в смешанном регистре может быть выражена как в прописных, так и в строчных буквах, или только в терминах начальной прописной буквы. Когда высота строчной буквы указана или определена из предписанного соотношения, ссылка делается на номинальную высоту петли буквы. Термин высота петли относится к части строчной буквы, которая исключает любые восходящие или нисходящие основы или хвосты буквы, например, с буквами «d» или «q». Номинальная высота цикла равна фактической высоте незакругленной строчной буквы, форма которой не включает восходящие или нисходящие основы или хвосты, такие как буква «x». Закругленные части строчной буквы проходят немного выше и ниже базовых линий, проецируемых сверху и снизу такой неокругленной буквы, так что достигается появление единой высоты буквы в слове. Фактическая высота петли закругленной строчной буквы немного больше номинальной высоты петли, и эта дополнительная высота исключается из выражения высоты строчной буквы.
Стандарт:
13 При использовании легенды смешанного регистра высота строчных букв должна составлять 3/4 высоты начальной прописной буквы.
14 Уникальные формы букв для каждой серии Standard Alphabet нельзя растягивать, сжимать, деформировать или иным образом обрабатывать.
Поддержка:
15 Раздел 2D.04 содержит информацию о допустимых методах изменения длины слова для данной высоты буквы и серии.
Раздел 2A.14 Границы знака
Стандарт:
01 Если не указано иное, каждый знак, изображенный в данном Руководстве, должен иметь рамку того же цвета, что и легенда, на краю или непосредственно внутри него.
02 Углы окантовки всех знаков должны быть закруглены, кроме знаков СТОП.
Руководство:
03 Темная рамка на светлом фоне должна быть от края, а светлая рамка на темном фоне должна доходить до края знака. Рамка для 30-дюймовых вывесок со светлым фоном должна быть шириной от 1/2 до 3/4 дюйма, на расстоянии 1/2 дюйма от края. Для аналогичных знаков со светлой каймой следует использовать ширину 1 дюйм. Для других размеров ширина границы должна иметь аналогичные пропорции, но не должна превышать ширину штриха основной буквы знака. На знаках размером более 72 x 120 дюймов ширина границы должна быть 2 дюйма, а на больших знаках — 3 дюйма. За исключением знаков СТОП и других случаев, предусмотренных в Разделе 2E.16, углы знака должны быть закруглены до радиуса, совпадающего с радиусом границы.
Раздел 2A.15 Повышенная заметность для стандартных знаков
Опция:
01 На основании инженерной оценки, если требуется улучшение видимости стандартного регулирующего, предупреждающего или направляющего знака, может использоваться любой из следующих методов, при необходимости, для повышения заметности знака (см. рис. 2A-1):
Рисунок 2A-1 Примеры повышенной заметности для знаков
Увеличение размера стандартного регулирующего, предупреждающего или направляющего знака.
Дублирование стандартного регулирующего, предупреждающего или направляющего знака путем добавления второго такого же знака с левой стороны проезжей части.
Добавление сплошной желтой или флуоресцентно-желтой прямоугольной «панели заголовка» над стандартным нормативным знаком, при этом ширина панели соответствует ширине стандартного нормативного знака. Обозначение «УВЕДОМЛЕНИЕ», «ЗАКОН ШТАТА» или другой соответствующий текст может быть добавлен черными буквами на панели заголовка на период времени, определяемый техническим заключением.
Добавление НОВОЙ таблички (см. Раздел 2C.62) над новым стандартным нормативным или предупредительным знаком на период времени, определяемый техническим заключением, для привлечения внимания к новому знаку.
Добавление одного или нескольких красных или оранжевых флажков (из ткани или световозвращающей пленки) над стандартным нормативным или предупреждающим знаком, при этом флажки должны быть ориентированы под углом 45 градусов к вертикали.
Добавление сплошной желтой, сплошной флуоресцентной желтой или полосатой по диагонали черно-желтой (или черной и флуоресцентно-желтой) полосы световозвращающего листа шириной не менее 3 дюймов по периметру стандартного предупреждающего знака. Этого можно добиться путем размещения стандартного предупреждающего знака на фоне, размер которого на 6 дюймов больше размера стандартного предупреждающего знака.
Добавление предупреждающего маяка (см. раздел 4L.03) к стандартному нормативному (кроме знака «СТОП» или знаку ограничения скорости), предупреждающему или направляющему знаку.
Добавление маяка знака ограничения скорости (см. раздел 4L.04) к стандартному знаку ограничения скорости.
Добавление стоп-сигнала (см. Раздел 4L.05) к знаку СТОП.
Добавление блоков светоизлучающих диодов (LED) в символ или легенду знака или границы стандартного нормативного, предупреждающего или направляющего знака, как предусмотрено в Разделе 2A.07.
Добавление полосы световозвращающего материала к опоре знака в соответствии с положениями Раздела 2A.21.
Использование других методов, специально разрешенных для определенных знаков, как описано в других разделах данного Руководства.
Поддержка:
02 Повышение заметности знаков также может быть достигнуто за счет удаления ненужных и незаконных знаков с полосы отвода (см. Раздел 1A.08) и путем перемещения знаков для обеспечения лучшего расстояния между ними.
Стандарт:
03 НОВАЯ табличка (см. Раздел 2C.62) не должна использоваться отдельно.
04 Проблесковые огни не должны использоваться для повышения заметности дорожных знаков.
Раздел 2A.16 Стандартизация местоположения
Поддержка:
01 Стандартизация местоположения не всегда может быть достигнута на практике. Примеры высоты и поперечного расположения знаков для типовых установок показаны на рисунке 2А-2, а примеры расположения некоторых типичных знаков на перекрестках показаны на рисунках 2А-3 и 2А-4.
Рисунок 2A-2 Примеры расположения знаков по высоте и в поперечном направлении
Рисунок 2A-3 Примеры расположения некоторых типовых знаков на перекрестках
02 Примеры предварительной подписи на подходе к перекрестку показаны на рисунке 2A -4. Главы 2В, 2С и 2D содержат положения, касающиеся применения нормативных, предупреждающих и направляющих знаков соответственно.
Рисунок 2A-4 Относительное расположение нормативных, предупреждающих и направляющих знаков на подходе к перекрестку
Стандарт:
03 Знаки, требующие отдельного решения участника дорожного движения, должны располагаться на достаточном расстоянии друг от друга для принятия соответствующих решений. Одним из факторов, учитываемых при определении соответствующего интервала, должна быть вывешенная или 85-процентная скорость.
Руководство:
04 Знаки должны располагаться с правой стороны проезжей части, где их легко узнают и понимают участники дорожного движения. Знаки в других местах следует рассматривать только как дополнительные к знакам в обычных местах, если иное не предусмотрено настоящим Руководством.
05 Знаки должны устанавливаться индивидуально на отдельных столбах или креплениях, за исключением случаев, когда:
Один знак дополняет другой;
Маршрутные или указатели направления сгруппированы для разъяснения информации автомобилистам;
Не противоречащие друг другу нормативные знаки группируются, например, запрещающие повороты знаки, вывешенные с односторонним движением, или знак, регулирующий парковку, вывешенный со знаком ограничения скорости; или
На табличках с названиями улиц размещены знаки «стоп» или «уступи дорогу».
06 Знаки должны быть расположены таким образом, чтобы они:
Находились за пределами свободной зоны, если они не установлены на отрывной или поддающейся опоре (см. Раздел 2A.19),
Оптимизация видимости в ночное время,
Минимизация воздействия брызг грязи и мусора,
Не загораживать друг друга,
Не закрывать обзор приближающихся транспортных средств на главной улице для водителей, остановившихся на подъездах к второстепенным улицам, и
Не скрыты от глаз.
Опора:
07 Свободная зона – это общая придорожная граничная зона, начиная с края проезжей части, доступная для использования заблудившимися транспортными средствами. Ширина свободной зоны зависит от интенсивности движения, скорости и геометрии обочины. Дополнительную информацию можно найти в «Руководстве по проектированию обочины» AASHTO (см. Раздел 1A. 11).
Инструкции:
08 В связи с увеличением интенсивности движения и желанием предоставить участникам дорожного движения нормативную, предупредительную и инструктивную информацию, необходимо установить очередность установки знаков.
Служба поддержки:
09 Порядок приоритетности особенно важен, когда пространство для установки знаков ограничено и существует потребность в нескольких различных типах знаков. Перегружать участников дорожного движения слишком большим количеством информации нежелательно.
Инструкции:
10 Поскольку нормативная и предупредительная информация более важна для участника дорожного движения, чем путеводная информация, в случаях возникновения конфликтов следует отображать нормативные и предупреждающие знаки, расположение которых имеет решающее значение, а не направляющие знаки. Направляющие знаки сообщества и знаки подтверждения должны иметь более низкий приоритет в отношении размещения, чем другие направляющие знаки. Информация менее важного характера должна быть перемещена в менее важные места или опущена.
Опция:
11 В некоторых случаях, например, на поворотах направо, знаки могут быть размещены на срединных островках или на левой стороне дороги. Дополнительный знак, расположенный с левой стороны проезжей части, может использоваться на многополосной дороге, где движение по полосе справа может мешать обзору направо.
Руководство:
12 В городских районах, где есть пешеходные переходы, запрещается размещать знаки ближе чем в 4 футах от пешеходного перехода (см. рисунок D на рис. 2A-3).
Раздел 2A.17 Установка подвесных знаков
Указания:
01 Надземные знаки следует использовать на автомагистралях и скоростных автомагистралях, в местах, где желательна определенная степень контроля за использованием полосы движения, и в местах, где на обочине нет свободного места.
Поддержка:
02 Эксплуатационные требования существующей системы автомагистралей таковы, что дорожные знаки имеют значение во многих местах. Факторы, которые следует учитывать при установке дисплеев с потолочными знаками, не могут быть определены в конкретных числовых терминах.
Опция:
03 Следующие условия (не в порядке приоритета) могут быть рассмотрены в инженерном исследовании для определения полезности надземных знаков:
Интенсивность движения на уровне или близком к пропускной способности,
Сложная конструкция развязки,
Три и более полос в каждом направлении,
Ограниченное расстояние видимости,
Близко расположенные транспортные развязки,
Многополосные съезды,
Большой процент грузовых автомобилей,
Фон уличного освещения,
Высокоскоростной трафик,
Непротиворечивость местоположения знакового сообщения через ряд обменов,
Недостаточно места для табличек,
Перекресток двух автомагистралей и
Левые съезды.
04 Надземные переходы могут использоваться для поддержки надземных знаков.
Опора:
05 В некоторых случаях использование надземных конструкций в качестве опор для знаков может быть единственным практическим решением, обеспечивающим достаточное расстояние обзора. Использование таких конструкций в качестве опор для знаков могло бы устранить необходимость в фундаментах и опорах для знаков вдоль обочины.
Раздел 2A.18 Монтажная высота
Стандарт:
01 Положения этого раздела должны применяться, если иное специально не указано для конкретного знака или указателя объекта в другом месте настоящего Руководства.
Опора:
02 Требования к высоте установки маркеров объектов приведены в главе 2C.
03 В дополнение к положениям этого Раздела информацию, касающуюся минимальной высоты установки знаков в зависимости от характеристик при столкновении, можно найти в «Руководстве по проектированию придорожных сооружений» AASHTO (см. Раздел 1A.11).
Стандарт:
04 Минимальная высота, измеренная по вертикали от нижней части знака до отметки ближнего края тротуара, знаков, установленных на обочине дороги в сельской местности, должна составлять 5 футов (см. рис. 2А- 2).
05 Минимальная высота, измеренная по вертикали от низа знака до верха бордюра, или при отсутствии бордюра, измеренная по вертикали от низа знака до отметки ближнего края проезжей части, знаки, установленные на обочине дороги в деловых, коммерческих или жилых районах, где вероятны парковочные места или движение пешеходов, или где обзор знака может быть затруднен, должны составлять 7 футов (см. рис. 2A-2).
Опция:
06 Высота до низа вторичного знака, установленного под другим знаком, может быть на 1 фут меньше, чем высота, указанная в пунктах 4 и 5.
Стандарт:
07 Минимальная высота, измеренная по вертикали от нижней части знака до тротуара, знаков, установленных над тротуарами, должна составлять 7 футов.
08 Если низ дополнительного знака, установленного под другим знаком, установлен ниже 7 футов над пешеходным тротуаром или дорожкой (см. Раздел 6D.02), дополнительный знак не должен выступать более чем на 4 дюйма в пешеходную зону. .
Опция:
09 Знаки, которые размещаются на расстоянии 30 футов или более от края проезжей части, могут быть установлены на минимальной высоте 5 футов, измеренной по вертикали от нижней части знака до отметки ближнего края тротуара. .
Стандарт:
10 Указательные знаки на автомагистралях и скоростных автомагистралях должны быть установлены на минимальной высоте 7 футов, измеренной по вертикали от нижней части знака до отметки ближнего края тротуара. Все дорожные знаки, предупреждающие знаки и нормативные знаки на автомагистралях и скоростных автомагистралях должны быть установлены на высоте не менее 7 футов, измеренной по вертикали от нижней части знака до отметки ближнего края тротуара. Если второстепенный знак устанавливается ниже другого знака на автомагистрали или скоростной автомагистрали, основной знак должен быть установлен на высоте не менее 8 футов, а второстепенный знак должен быть установлен на высоте не менее 5 футов, измеренной по вертикали от нижней части знак на отметке ближнего края тротуара.
11 Если большие знаки площадью более 50 квадратных футов установлены на нескольких отрывных стойках, расстояние от земли до нижней части знака должно быть не менее 7 футов.
Опция:
12 Сборка маршрутных знаков, состоящая из маршрутного знака и вспомогательных знаков (см. Раздел 2D.31), может рассматриваться как единый знак для целей настоящего Раздела.
13 Высота установки может быть отрегулирована, когда опоры расположены у края полосы отвода на крутом обратном склоне, чтобы избежать иногда менее желательного варианта размещения знака ближе к проезжей части.
Стандарт:
14 Накладные знаки должны обеспечивать вертикальное расстояние не менее 17 футов до знака, светильника или знакового моста по всей ширине тротуара и обочин, за исключением тех случаев, когда конструкция, на которой должны быть установлены накладные знаки навесные или иные конструкции вдоль проезжей части вблизи конструкции знака имеют меньший вертикальный просвет.
Опция:
15 Если вертикальный просвет до других конструкций вдоль проезжей части рядом со знаком составляет менее 16 футов, вертикальный просвет до надземной конструкции знака или опоры может быть всего на 1 фут выше, чем вертикальный просвет до знака. другие конструкции для улучшения видимости надземных знаков.
16 В особых случаях может быть необходимо уменьшить расстояние до надземных знаков из-за нестандартных размеров в туннелях и других крупных сооружениях, таких как двухъярусные мосты.
Опора:
17 На рис. 2A-2 показаны некоторые примеры требований к монтажной высоте, содержащихся в этом разделе.
Раздел 2A.19 Боковое смещение
Стандарт:
01 Для опор подвесных знаков минимальное поперечное смещение от края обочины (или, если обочины нет, от края тротуара) до ближнего края подвесного знака опоры (консольные или знаковые мосты) должны быть 6 футов. Опоры надземных знаков должны иметь барьер или амортизационную подушку, чтобы защитить их, если они находятся в пределах свободной зоны.
02 Опоры знаков и указателей объектов, устанавливаемые на столбах, должны быть ударопрочными (отламываться, поддаваться или экранироваться продольным барьером или подушкой), если они находятся в пределах свободной зоны.
Руководство:
03 Минимальное боковое смещение для устанавливаемых на столбах знаков должно составлять 12 футов от края проезжей части. При наличии обочины шириной более 6 футов минимальное боковое смещение для устанавливаемых на столбах знаков должно составлять 6 футов от края обочины.
Опора:
04 Минимальные требования к боковому смещению для маркеров объектов приведены в главе 2C.
05 Минимальное боковое смещение предназначено для предотвращения ударов грузовых и легковых автомобилей, использующих обочины, о знаки или опоры.
Руководство:
06 Все опоры должны располагаться как можно дальше от края обочины. Следует использовать преимущество размещения знаков за существующими придорожными ограждениями, на надземных сооружениях или в других местах, которые сводят к минимуму воздействие транспортных средств на опоры знаков.
Опция:
07 Там, где это разрешено, знаки можно размещать на существующих опорах, используемых для других целей, таких как опоры светофоров, опоры дорожного освещения и опоры электропередач.
Стандарт:
08 Если знаки размещаются на существующих опорах, они должны соответствовать другим критериям размещения, указанным в данном Руководстве.
Опция:
09 Меньшие боковые смещения могут использоваться на соединяющих проезжей части или пандусах на развязках, но не менее чем на 6 футов от края проезжей части.
10 На обычных дорогах в районах, где нецелесообразно размещать знак с боковым смещением, предписанным настоящим Разделом, может использоваться боковое смещение не менее 2 футов.
11 Боковое смещение не менее 1 фута от поверхности бордюра может использоваться в деловых, коммерческих или жилых районах, где ширина тротуара ограничена или где существующие столбы расположены близко к бордюру.
Указания:
12 Опоры надземных знаков и опоры для знаков и указателей объектов, устанавливаемые на столбах, не должны заходить за полезную ширину тротуара или другого пешеходного объекта.
Опора:
13 На рисунках 2A-2 и 2A-3 показаны некоторые примеры требований к боковому смещению, содержащихся в этом разделе.
Раздел 2A.20 Ориентация
Указания:
01 Если в настоящем Руководстве не указано иное, знаки должны устанавливаться вертикально под прямым углом к направлению и лицом к движению транспорта, для обслуживания которого они предназначены.
02 Если зеркальное отражение от лицевой стороны знака встречается до такой степени, что ухудшает разборчивость, знак следует немного повернуть в сторону от дороги. Знаки, расположенные в 30 футах и более от края тротуара, должны быть обращены к дороге. На криволинейных трассах угол установки должен определяться направлением приближающегося транспорта, а не краем проезжей части в точке, где расположен знак.
Опция:
03 На уклонах лицевая сторона знака может быть наклонена вперед или назад относительно вертикального положения для улучшения угла обзора.
Раздел 2A.21 Стойки и крепления
Стандарт:
01 Стойки знаков, фундаменты и крепления должны быть сконструированы таким образом, чтобы удерживать знаки в надлежащем и постоянном положении, а также противостоять раскачиванию на ветру или смещению в результате вандализма.
Опора:
02 В последнем издании AASHTO «Спецификации несущих конструкций для дорожных знаков, светильников и светофоров» содержится дополнительная информация о стойках и монтаже (адрес AASHTO см. на стр. i).
Опция:
03 Если инженерная оценка указывает на необходимость привлечения внимания к знаку в ночных условиях, на опорах нормативных и предупреждающих знаков можно использовать полосу световозвращающего материала.
Стандарт:
04 Если на опоре знака используется полоса световозвращающего материала, она должна быть не менее 2 дюймов в ширину, она должна располагаться по всей длине опоры от знака в пределах 2 футов над краем проезжей части, а его цвет должен совпадать с цветом фона знака, за исключением того, что цвет полосы для знаков ПРОЕЗД и НЕ ВЪЕХАТЬ должен быть красным.
Раздел 2A.22 Техническое обслуживание
Руководство:
01 При проведении технического обслуживания необходимо учитывать правильное положение, чистоту, разборчивость и видимость в дневное и ночное время (см. Раздел 2A.09). Поврежденные или изношенные знаки, ворота или указатели объектов следует заменить.
02 Для обеспечения надлежащего технического обслуживания необходимо установить график осмотра (как днем, так и ночью), очистки и замены знаков, ворот и указателей объектов. Работников автомагистралей, правоохранительных органов и других государственных учреждений, чьи обязанности требуют, чтобы они передвигались по проезжей части, следует поощрять сообщать о любых поврежденных, испорченных или скрытых знаках, воротах или указателях объектов при первой же возможности.
03 Необходимо принять меры для того, чтобы сорняки, деревья, кустарники, а также строительные, ремонтные и коммунальные материалы и оборудование не закрывали лицо какого-либо знака или указателя объекта.
04 Должен поддерживаться регулярный график замены элементов освещения световой рекламы.
Раздел 2A.23 Обработка разделительных проемов для разделяемых автомагистралей с широкими разделительными участками
Указания:
01 Если разделяемые автомагистрали разделены разделительной шириной в среднем проеме в 30 футов или более, разделительные проемы должны обозначаться как два отдельных перекрестка.
Наверх
Разница между статистикой и параметром (со сравнительной таблицей и иллюстрацией)
Последнее обновление 1 сентября 2017 г. Surbhi S
В словаре статистики мы часто имеем дело с терминами параметр и статистика, которые играют жизненно важную роль в определении размера выборки. Параметр подразумевает краткое описание характеристик целевой совокупности. С другой стороны, статистика представляет собой суммарное значение небольшой группы населения, т. е. выборки.
Параметр берется из измерений единиц населения. В отличие от этого, статистика строится на основе измерения элементов выборки.
При изучении статистики важно понимать концепцию и различие между параметром и статистикой, так как они обычно неправильно истолковываются.
Содержание: Статистика и параметр
Сравнительная таблица
Определение
Ключевые отличия
Иллюстрация
Заключение
Сравнительная таблица
База для сравнения Статистика Параметр
Значение Статистика – это показатель, описывающий часть населения. Параметр относится к показателю, который описывает население.
Числовое значение Переменная и известная Фиксированная и неизвестная
Статистическая запись x̄ = Среднее значение выборки μ = Среднее значение генеральной совокупности
s = стандартное отклонение выборки σ = стандартное отклонение генеральной совокупности
p̂ = доля выборки P = доля населения
x = Элементы данных X = Элементы данных
n = размер выборки N = размер совокупности
r = коэффициент корреляции ρ = коэффициент корреляции

Определение статистики
Статистика определяется как числовое значение, полученное из выборки данных. Это описательная статистическая мера и функция выборочного наблюдения. Выборка описывается как часть совокупности, которая представляет всю совокупность во всех ее характеристиках. Обычно статистика используется для оценки определенного параметра населения.
Из данной совокупности можно сделать несколько выборок, и результат (статистика), полученный из разных выборок, будет различаться в зависимости от выборок.
Определение параметра
Фиксированная характеристика совокупности, основанная на всех элементах совокупности, называется параметром. Здесь население относится к совокупности всех рассматриваемых единиц, которые имеют общие характеристики. Это числовое значение, которое остается неизменным, так как каждый член населения опрашивается, чтобы узнать этот параметр. Он указывает истинное значение, полученное после проведения переписи.
Ключевые различия между статистикой и параметром
Разницу между статистикой и параметром можно четко провести по следующим основаниям:
Статистика есть характеристика небольшой части совокупности, т.е. выборки. Параметр представляет собой фиксированную меру, описывающую целевую совокупность.
Статистика представляет собой переменную и известное число, которое зависит от выборки населения, в то время как параметр представляет собой фиксированное и неизвестное числовое значение.
Статистические обозначения различны для параметров генеральной совокупности и статистики выборки, которые приведены ниже:
В параметре совокупности µ (греческая буква мю) представляет собой среднее значение, P обозначает долю населения, стандартное отклонение обозначается как σ (греческая буква сигма), дисперсия представлена как σ ² , размер совокупности обозначается как N, стандартная ошибка среднего значения представлено как σ _x̄ , стандартная ошибка пропорции обозначена как σ _p , стандартизованная переменная (z) представлена как (X-µ)/σ, коэффициент вариации обозначен как σ/µ.
В выборочной статистике x̄ (столбик x) представляет собой среднее значение, p̂ (штриховка) обозначает долю выборки, стандартное отклонение обозначается как s, дисперсия представлена как s ² , n обозначает размер выборки, стандартная ошибка среднего представлена как s _x̄ , стандартная ошибка пропорции обозначена как s _p , стандартизированная переменная (z) представлена (x-x̄)/s, коэффициент вариации обозначается s/(x̄)
Иллюстрация
Исследователь хочет узнать средний вес женщин в возрасте 22 лет и старше в Индии. Исследователь получает средний вес 54 кг из случайной выборки из 40 самок.
Решение : В данной ситуации статистикой является средний вес 54 кг, рассчитанный по простой случайной выборке 40 женщин в Индии, а параметром является средний вес всех женщин в возрасте 22 лет и старше.
Исследователь хочет оценить среднее количество воды, потребляемой подростками мужского пола в день. Из простой случайной выборки из 55 подростков мужского пола исследователь получает в среднем 1,5 литра воды.
Решение : В этом вопросе параметр представляет собой среднее количество воды, потребляемое всеми подростками мужского пола в день, тогда как статистика представляет собой среднее количество воды, потребляемое подростками мужского пола в среднем 1,5 литра в день, полученное из простой случайной выборки. из 55 подростков мужского пола.
Заключение
Подводя итоги обсуждения, важно отметить, что когда результат получен из совокупности, числовое значение известно как параметр. В то время как, если результат получен из выборки, числовое значение называется статистическим.
Другие типы учащихся — Приемная комиссия штата Джорджия
Прием

Заполните и отправьте заявку.
2
Оплатить регистрационный сбор
Штат Джорджия требует невозмещаемый сбор за подачу заявления в размере 60 долларов США, который может быть оплачен вместе с подачей заявления.
Онлайн-заявки обрабатываются только в том случае, если они сопровождаются комиссией через систему кредитной карты или расчетного счета. Бумажные заявки обрабатываются только при наличии чека или денежного перевода.
3
Предоставить необходимую документацию.
Предоставить официальные подтверждающие документы (аттестат о среднем образовании, баллы GED, баллы SAT/ACT, если таковые имеются).
4
Проверьте статус вашего заявления.
1
Заполните и отправьте онлайн-заявку о приеме на пост-бакалавриат.
2
Оплатить регистрационный сбор
Штат Джорджия требует невозмещаемый сбор за подачу заявления в размере 60 долларов США, который может быть оплачен вместе с подачей заявления.
Онлайн-заявки обрабатываются только в том случае, если они сопровождаются комиссией через систему кредитной карты или расчетного счета. Бумажные заявки обрабатываются только при наличии чека или денежного перевода.
3
Предоставить необходимую документацию.
Отправьте в Управление по приему студентов официальную стенограмму из учебного заведения, присуждающего вам степень бакалавра или выше. Студенческие копии стенограмм, открытые стенограммы и отправленные по факсу стенограммы не принимаются.
4
Проверьте статус своего заявления.
Сроки могут быть изменены. Мы не можем гарантировать решение по заявлениям и документам, полученным после указанных сроков. Обратите внимание, что заявки обрабатываются в порядке очереди, поэтому заявителям настоятельно рекомендуется подавать заявки как можно раньше.
1
Заполните и подайте онлайн-заявку на временный прием.
2
Оплатить регистрационный сбор
Штат Джорджия требует невозмещаемый сбор за подачу заявления в размере 60 долларов США, который может быть оплачен вместе с подачей заявления.
Онлайн-заявки обрабатываются только в том случае, если они сопровождаются комиссией через систему кредитной карты или расчетного счета. Бумажные заявки обрабатываются только при наличии чека или денежного перевода.
3
Отправьте письмо-разрешение, подписанное регистратором или академическим деканом вашего нынешнего учебного заведения, с рекомендацией вас в качестве временного студента.
В письме должен быть указан конкретный срок, в течение которого вы планируете учиться в Университете штата Джорджия.
В письме также может быть указан список курсов, которые необходимо пройти в Университете штата Джорджия.
Может быть приемлемо письмо о хорошей репутации от учреждений за пределами штата Джорджия.
Вот шаблон, который ваше учреждение может использовать для временного письма-запроса.
Временные/разрешительные письма можно отправить через проверку статуса заявки, отправить по электронной почте на адрес electronictranscript@gsu. edu, по факсу на номер 404-413-2235 или отправить нам по почте:
3
Прод.
Приемная комиссия бакалавриата
Университет штата Джорджия
P.O. Ящик 4009
Атланта, Джорджия 30302-4009
4
Проверьте статус своего заявления.
1
Должен подать заявку и предоставить всю необходимую документацию к установленному сроку, выполнить ВСЕ вступительные требования для выбранной программы обучения и быть принятым
2
Должен быть старше 62 лет на первую неделю семестра
3
Должен быть классифицирован как резидент Грузии в соответствии с требованиями Регентов для статуса проживания
Примечание: Абитуриент, получивший степень бакалавра и желающий пройти курсы бакалавриата, не будучи допущенным к программе получения степени, должен выполнить описанные выше шаги подачи заявки на получение степени бакалавра. Чтобы узнать о требованиях для поступления в аспирантуру, обратитесь к онлайн-информации об интересующей вас программе магистратуры. Преимущества GSU-62 не распространяются на курсы, предлагаемые Юридическим колледжем.
студентов GSU-62 не могут зарегистрироваться до первого дня поздней регистрации. Студенты ГСУ-62 не несут ответственности за стоимость обучения и обязательные платежи. Однако они несут ответственность за оплату лабораторных работ или расходных материалов для языковых курсов, музыки, науки и т. д.
Студенты GSU-62 имеют возможность отказаться от участия в программе, если они хотят зарегистрироваться до поздней регистрации. Учащимся, отказавшимся от участия, будет начислена обычная плата за обучение и сборы, и они не будут покрываться отказом. Студент будет обязан оплатить обучение и сборы до крайнего срока оплаты, если он решит отказаться от участия в программе GSU-62.
What Can We Help You With?Freshman ApplicantsHigh School Counselor LiaisonLatinx StudentsUndergraduate International StudentsHonorsFinancial Aid LiaisonHome-SchoolMetro Atlanta Private SchoolsState FarmTransitionTransferCampus VisitsGSU-62Non-traditionalPerimeter CollegePerimeter AcademyTransientVeteransAtlanta Public SchoolsDual EnrollmentPanther ExcellenceSuccess AcademyRe-entryPostbaccalaureateDistance LearningAppealsAthleticsSomething ElsePounce BackSummer Leadership AcademyKipp Enrollment Initiative
Choose Your County (Georgia Residents)ApplingAtkinsonBaconBakerBaldwinBanksBarrowBartowBen HillBerrienBibbBleckleyBrantleyBrooksBryanBullochBurkeButtsCalhounCamdenCandlerCarrollCatoosaCharltonChathamChattahoocheeChattoogaCherokeeClarkeClayClaytonClinchCobbCoffeeColquittColumbiaCookCowetaCrawfordCrispDadeDawsonDecaturDeKalbDodgeDoolyDoughertyDouglasEarlyEcholsEffinghamElbertEmanuelEvansFanninFayetteFloydForsythFranklinFulton — NorthFulton — SouthGilmerGlascockGlynnGordonGradyGreeneGwinnett — NorthGwinnett — SouthHabershamHallHaralsonHarrisHartHeardHenryHoustonIrwinJacksonJasperJeff DavisJeffersonJenkinsJohnsonJonesLamarLanierLaurensLeeLibertyLincolnLongLowndesLumpkinMaconMadisonMarionMcDuffieMcIntoshMeriwetherMillerMitchellMonroeMontgomeryMorganMurrayMuscogeeNewtonOconeeOglethorpePauldingPeachPickensPiercePikePolkPulaskiPutnamQuitmanRabunRandolphRichmondRockdaleSchleyScrevenSeminoleSpaldingStephensStewartSumterTalbotTaliaferroTattnallTaylorTelfairTerrellThomasTiftToombsTowns TreutlenTroupTurnerTwiggsUnionUpsonWalkerWaltonWareWarrenWashingtonWayneWebsterWheelerWhiteWhitfieldWilcoxWilkesWilkinsonWorth
Choose Your State or TerritoryAlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict of ColumbiaFlorida  -North Florida  -South FloridaHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaOhioOklahomaOregonPennsylvaniaPuerto RicoRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
Out Of State Action
Эл. 0003
Out of State Area: California, Puerto Rico
Andraea Capers
Помощник директора первого года набора
Телефон: 404-413-2170
Caper Двойная регистрация, связь с консультантами старших классов, частные школы Metro Atlanta
За пределами штата Районы: Аризона, Кентукки, Миссури, Монтана, Теннесси
Кензо Сарагоса-Цуру
Помощник директора, приветственный центр
Телефон: 404-413-2066
Электронная почта Kenzo Zaragoza-Curu
Специальность: Campus Pisitsity
Diana Kelley
9000 9000. 2007.shipertemant 9000.m.shipart.shipart
.0000.m.shiparder 9000.m.shipertist.3 9000.m.shipertment
.
Телефон: 404-413-2515
Эл.0008
Phone: 404-413-2037
Email Lan Nguyen
Specialty: Undergraduate International Students
Peace Li
Associate Director, International Recruitment
Phone: 404-413-2500
Эл. 0008
Phone: 404-413-5577
Email Ryan McLaughlin
Specialty: Honors
Tony Wahab
Assistant Director, Customer Management
Phone: 770-274-5208
Эл.0007 Советник по приему III
Эл. Территории за пределами штата: Арканзас, Колорадо, Гавайи, Иллинойс, Нью-Мексико, Северная Флорида, Юта, Вайоминг
Regina Daniels
Консультант по вопросам перевода
Телефон: 404-413-2045
Электронная почта Регина Дэниелс
Специальность: Совместная ферма, трансфер, переход
Michael Fackler
.
Донна Фрейзер
Консультант по приему первокурсников
Телефон: 678-891-4128
Эл.0003
Округа Джорджии: Бейкер, Брукс, Калхун, Чаттахучи, Клэй, Колкитт, Кук, Коуэта, Кроуфорд, ДеКалб, Декейтер, Догерти, Эрли, Грейди, Харрис, Ли, Лаундс, Мейкон, Марион, Меривезер, Миллер, Митчелл , Muscogee, Peach, Quitman, Randolph, Schley, Seminole, Stewart, Sumter, Talbot, Taylor, Terrell, Thomas, Tift, Troup, Webster, Worth
За пределами штата Области: Арканзас, Миссисипи, Монтана, Северная Дакота, Южная Дакота, Вайоминг
Джон Хэнсон
Советник по приему III
Эл. , Walker, Whitfield
Районы за пределами штата: Алабама, Невада, Северная Каролина, Орегон, Южная Каролина, Вашингтон
Эшли Холден
Консультант по вопросам перевода
Электронная почта Эшли Холден
Специальность: Трансфер, переход, ветераны
Daisy Huerta
Advision Consultor III
Finance Daisy Huerta
Specialty: Finany Finany yisy huerta
: Finany yisy huerta
: . Брантли, Брайан, Буллок, Баттс, Камден, Кэндлер, Чарльтон, Ковета, Эффингем, Эмануэль, Глинн, Харалсон, Херд, Дженкинс, Ламар, Либерти, Лонг, Макинтош, Монро, Пайк, Полк, Скревен, Апсон, Уэйн
Out of State Area: Айдахо, Индиана, штат Айова, Мичиган, Миннесота, Южная Флорида, Висконсин
Cameron Huggins
40413-2-23-232.
Телефон: 404-413-2-23-232.
.
Специальность: Посещения кампуса, первокурсники
Брианна Локхарт
Консультант по приему III
Эл.0003
Georgia Counties: Habersham, Rabun, Stephens, Towns
Out of State Areas: Connecticut, District of Columbia, Maryland, Virginia, West Virginia
Cameron Malveaux
Campus Visit Coordinator
Phone : 404-413-2065
Электронная почта Cameron Malveaux
Омар Нельсон
Консультант по приеме на новичок
Телефон: 404-413-2068
Электронная почта OMARSOSN 404-413-2068
.0003
Специальность: Абитуриенты-первокурсники, Kipp Enrollment Initiative, Pounce Back, Summer Leadership Academy
Округа Джорджии: Appling, Atkinson, Bacon, Ben Hill, Berrien, Bibb, Bleckley, Clayton, Clinch, Coffee, Crisp, Dodge , Дули, Эколс, Эванс, Файетт, Генри, Хьюстон, Ирвин, Джефф Дэвис, Джонсон, Ланье, Лоренс, Монтгомери, Пирс, Пуласки, Сполдинг, Таттналл, Телфэйр, Тумбс, Треутлен, Тернер, Твиггс, Уэр, Уилер, Уилкокс, Уилкинсон
За пределами штата Районы: Канзас, Луизиана, Небраска, Оклахома, Техас
Хейли Ричардсон
Консультант по приемной комиссии III
Haley Richardson
Specialty:
. Берк, Колумбия, Гласкок, Грин, Джаспер, Джефферсон, Джонс, Линкольн, Макдаффи, Морган, Оглторп, Патнэм, Ричмонд, Талиаферро, Уоррен, Вашингтон, Уилкс
Районы за пределами штата: Делавэр, Миннесота, Нью-Гэмпшир, Нью-Йорк Джерси, Нью-Йорк, Огайо, Пенсильвания, Род-Айленд, Вермонт
Aisha Snell
In-House Admissions Counselor
Phone: 678-891-2721
Email Aisha Snell
Specialty: Perimeter College
Peter Vleck
Freshman Admissions Counselor
Электронная почта Питера Влека
Специальность: Двойная регистрация, первокурсники
Округа Джорджии: Доусон, Форсайт, Фултон – Норт, Хабершам, Лумпкин, Рабун, Стивенс, Таунс, Юнион, Уайт
Out of State Area: Alabama, Nevada, Oregon, Washington
Donald Weatherington
Admission Consultor
Электронный телефон: 404-413-2038
Donaldtton
. Легкая атлетика
Друзелла Уайт
Специалист по регистрации
Телефон: 678-891-3238
Электронная почта Друзелла Уайт
Специальность: 0913 Колледж периметра
Нашли неработающую ссылку или нужно внести изменения на сайт? Заполните форму обратной связи на веб-сайте .
От одного студента-медика к другому
Тестирование поля зрения: от одного студента-медика к другому
Авторы: Джой Н. Кэрролл и Крис А. Джонсон, доктор философии.

Университет Айовы
Факультет офтальмологии и визуальных наук
Зрение представляет собой комбинацию различных измеримых функций: острота зрения, цветовое зрение, верньерная (выравнивание) острота, восприятие движения и изменение силы света (мерцание) или различия в силе света (контрастность). Острота зрения – это способность различать мелкие детали и отличать один объект от другого. Остроту зрения проверяют с помощью таблиц видения букв или изображений.
Изменения силы света воспринимаются как мерцание, а разница силы света от одного объекта к другому воспринимается как контраст [1]. Поле зрения охватывает всю видимую область пространства, в то время как взгляд направлен на какой-либо центральный объект. В этом руководстве объясняется тестирование поля зрения.
В нормальных дневных (фотопических) условиях самые маленькие или наименее интенсивные видимые объекты видны только в центральной части поля зрения. На периферии объекты должны быть крупнее или интенсивнее, чтобы их можно было идентифицировать. Нормальное поле зрения расширяется приблизительно на 100° височно (латерально), 60° назально, 60° вверх и 70° вниз [2]. Физиологическая скотома (слепое пятно) существует под углом 15° височно, где зрительный нерв выходит из глаза. Окончательное местоположение немного варьируется в зависимости от индивидуальных особенностей. Среднее слепое пятно имеет диаметр 7,5° с центром по вертикали на 1,5° ниже горизонтального меридиана [3]. См. рисунок 1. В условиях тусклого ночного освещения (скотопия) средняя периферия является наиболее чувствительной областью поля зрения.
Рисунок 1: Физиологическая скотома. Скотома представляет собой область повышенной пикселизации, указывающую на снижение остроты зрения. Рисунок 2: Пути ганглиозных клеток
Поле зрения соответствует топографическому расположению фоторецепторов в глазу. Когда фотоны света поглощаются фоторецепторными клетками сетчатки, цис-транс-изомеризация 11-цис-хромофора запускает каскад фототрансдукции, что приводит к гиперполяризации биполярных и горизонтальных клеток и, в конечном счете, к активации ганглиозных клеток, формирующих нервное волокно. слой [4]. Нервные волокна идут к диску зрительного нерва, где берет начало зрительный нерв. В головке зрительного нерва (также известной как диск зрительного нерва) нет фоторецепторов, только нервные волокна. Эта область соответствует физиологической скотоме.
Наибольшая плотность колбочковых (фотопических) фоторецепторов расположена в макуле. Аксоны ганглиозных клеток, которые в конечном итоге соединяются, образуя зрительный нерв, проходят горизонтально в виде папилломакулярного пучка от макулы к височной части диска зрительного нерва. Нервные волокна проходят вдоль срединного шва вдоль горизонтального меридиана. Ганглиозные клетки, возникающие височно от макулы, также должны перемещаться к диску зрительного нерва, не пересекая срединный шов. Для этого они должны огибать папилломакулярный пучок, образуя дугообразные волокна с соответствующим названием. Ганглиозные клетки, возникающие в областях сетчатки, носовой к диску, не должны огибать макулу дугой. Поэтому они ориентированы радиально, образуя довольно прямой путь к зрительному нерву. Дефекты полей зрения, возникающие в результате потери ганглиозных клеток, например, при глаукоме, соответствуют этим анатомическим паттернам.
Важно отметить, что координаты поля зрения противоположны координатам сетчатки. Свет, попадающий в глаз из височного поля зрения, улавливается фоторецепторами на назальной стороне сетчатки, а свет, попадающий из назального поля зрения, улавливается височными фоторецепторами. Точно так же свет из верхнего поля зрения поглощается нижней частью сетчатки и наоборот. Таким образом, у пациента с повреждением ганглиозных клеток в височной части сетчатки прогнозируется наличие носового дефекта поля зрения.
Распознавание поля зрения началось более 2000 лет назад, во времена Гиппократа, который распознал гемианопсию [5]. Поля зрения часто оценивают, просто закрыв один глаз и попросив пациента смотреть прямо вперед, используя периферийное зрение для идентификации объекта или количества пальцев, показанных исследователем. Поле часто проверяется только в четырех местах, что чувствительно только к большим дефектам поля. Этот метод тестирования называется конфронтационной оценкой поля зрения.
Количественная оценка полей зрения была разработана в девятнадцатом веке. Янник Бьеррум начал картировать поля зрения, прося пациентов определить, видели ли они белый объект на конце черной палочки перед черным экраном. Было протестировано несколько мишеней разного размера на палочке, что позволило эффективно отображать различия в размерах, необходимые для зрения в разных областях поля зрения. Этот метод тестирования, известный как касательный экран, измеряет только центральные 30° поля зрения [5].
Сетка Амслера — еще один инструмент для измерения центрального поля зрения, занимаемого макулой (примерно 8 градусов в диаметре). Тест состоит из карточки с пересекающимися горизонтальными и вертикальными черными линиями на белом фоне, которую держат на расстоянии 25 см или 40 см. При фиксации взгляда на точке в центре сетки больной идентифицирует размытые, отсутствующие или искаженные участки. Центральное зрение соответствует макуле, отсюда и использование сетки Амслера для клинического отслеживания макулярной патологии [5].
Рисунок 3: Пути света к сетчатке. Свет, идущий выше глаза, улавливается нижней частью сетчатки. Свет, исходящий из височной части глаза, обнаруживается носовой стороной сетчатки. Рисунок 4: Решетка Амслера
Метод тестирования всего поля зрения был разработан Гансом Гольдманном. Его чашеобразный периметр использует яркий свет в качестве целей, наложенных на белый фон. Мишени могут различаться по размеру, яркости и цвету. Периметрия Гольдмана требует, чтобы обученные периметристы измеряли и чертили поле зрения. Проблемы включают стоимость и межпериметрическую изменчивость [5]. На практике периметрия Гольдмана представляет собой форму кинетической периметрии: стимул равен переместил из-за края поля зрения в поле. Место, в котором стимул впервые виден, отмечает внешний периметр поля зрения для размера тестируемого стимула.
Автоматизированная периметрия была разработана в 1970-х годах. Как следует из названия, автоматизированная периметрия отображает поле зрения с помощью компьютера. Периметр Octopus, анализатор поля Хамфри и матрица Хамфри — вот лишь некоторые из доступных автоматизированных периметров. Хотя Octopus может выполнять модифицированную кинетическую периметрию, в большинстве случаев автоматизированная периметрия является статической: стационарные стимулы, различающиеся по размеру и интенсивности, предъявляются в определенных местах в пределах поля зрения [6].
Для успешного создания карты поля зрения любым методом должны быть выполнены несколько основных условий. Человек должен быть в состоянии удерживать постоянный взгляд в фиксированном месте в течение нескольких минут. Каждый глаз проверяется отдельно, в то время как противоположный глаз закрывается повязкой. Рефракционная коррекция должна быть сделана с помощью тестовой линзы. Нельзя носить очки, так как они могут вызывать ложные дефекты поля зрения из-за своей формы [6]. Кроме того, необходимо провести коррекцию пресбиопии, чтобы уменьшить аккомодационное напряжение. Стандартные корректировки для пресбиопии доступны только в зависимости от возраста. Для коррекции астигматизма >0,75 диоптрий необходимо использовать цилиндрическую линзу. Если веко или ресницы мешают зрительной оси, веко можно прикрепить скотчем ко лбу, чтобы убрать его с пути.
Во время тестирования поля зрения Хамфри (HVF) пациент кладет голову на опору для подбородка и фиксирует взгляд на центральной точке фиксации в большой белой чаше. Как указано выше, этот тест является примером статической периметрии. Он оценивает способность видеть неподвижный стимул, который остается на короткое время (200 мс) в поле зрения. Когда пациент видит предъявленный стимул, он нажимает кнопку на портативном пульте дистанционного управления. Различные места в пределах данной области поля зрения проверяются до тех пор, пока пороговое значение или интенсивность стимула, видимая в 50% случаев, не будет видна в каждом тестовом месте.
Стимулы различаются по размеру и интенсивности свечения. Размер Гольдмана III (около ½ градуса в диаметре) обычно используется, но размер Гольдмана V (приблизительно 2 градуса в диаметре) доступен для пациентов с пониженной остротой зрения (
Часто используется Шведский интерактивный пороговый алгоритм (SITA). SITA — это процедура прогнозирования, в которой используются байесовские статистические свойства, аналогичные методам, используемым для предоставления информации о погоде и прогнозов. SITA позволяет проводить более быстрый анализ, чем это было бы возможно без прогнозирования. Принимая во внимание результаты пользователя в близлежащих местах, стимулы, которые вряд ли будут замечены или очень вероятно будут замечены, не тестируются исчерпывающе. Вместо этого проверяются стимулы, которые, вероятно, близки к порогу.
Рисунок 5: Анализатор поля зрения Humphrey Рисунок 6: HVF 24-2. Предоставлено Майклом Уоллом, доктором медицины
Вся информация, представленная на распечатке поля зрения, важна. Информация о личности пациента, а также конкретный тест и размер стимула расположены в верхней части анализа. Важно убедиться, что дата рождения пациента была введена правильно, так как ошибка приведет к сравнению с нормой в неправильной возрастной группе.
Под именем пациента находится заявление, содержащее информацию о параметрах тестирования, например, «Центральный пороговый тест 24-2». Первое утверждение, «Центральные 24», указывает на то, что были проанализированы центральные 24 градуса поля зрения. Следующее число указывает, как сетка точек выровнена по визуальной оси. Число «1» указывает на то, что средние точки перекрывают горизонтальный и вертикальный меридианы. Число «2» указывает на то, что сетка точек охватывает эти меридианы. Это наиболее часто используемый параметр, так как легче оценить, относятся ли дефекты поля зрения к горизонтальной или вертикальной срединной линии.
Далее в отчете следуют показатели надежности, включая потери фиксации, ложноположительные и ложноотрицательные результаты. Потеря фиксации происходит, когда пациент сообщает, что видит стимул, представленный в прогнозируемой области физиологического слепого пятна. Ложноположительные результаты возникают, когда пациент нажимает кнопку при отсутствии стимула. Участники, стремящиеся угодить, иногда борются с высоким уровнем ложных срабатываний (т. Е. Они «счастливы к триггеру»). Ложноположительные результаты часто можно скорректировать простым утверждением, что многие стимулы не будут видны даже при нормальном зрении. Ложноотрицательные результаты возникают, когда пациент не видит в каком-либо месте значительно более яркий стимул, чем он был виден ранее. Ложноотрицательные результаты обычно являются результатом потери внимания или усталости, и их трудно исправить.
Визуальный порог — это интенсивность раздражителя, видимого в течение 50% времени в каждом месте. Пороговые значения каждой проверенной точки перечислены в децибелах на графике чувствительности. Более высокие числа означают, что пациент мог видеть более приглушенный свет и, следовательно, имел более чувствительное зрение в этом месте. Справа от числового графика чувствительности находится карта оттенков серого. На этой карте представлена чувствительность в поле зрения пациента, при этом более светлые области указывают на более высокую чувствительность, а более темные области отражают более низкую чувствительность. Чувствительность не сравнивается ни с одной нормативной базой данных. Таким образом, карта может привлечь внимание к неровностям в поле, но может свести к минимуму потери поля, если потери более однородны по всему полю. Следует проявлять осторожность, так как это может ввести в заблуждение в зависимости от того, где машина делает отсечку между различными оттенками серого. Необработанные пороговые данные всегда следует оценивать в сочетании с представлением в градациях серого.
Числовая карта полного отклонения сравнивает зрительную чувствительность пациента со средним нормальным человеком того же возраста. Полезно сравнить с возрастными нормальными порогами, поскольку чувствительность обычно постепенно снижается с возрастом. Положительные значения представляют области поля, где пациент может видеть более тусклые стимулы, чем средний человек этого возраста. Отрицательные значения представляют собой пониженную чувствительность по сравнению с нормальной.
Карта отклонений числового шаблона показывает несоответствия в пределах поля зрения пациента с поправкой на общее снижение зрительной чувствительности. Полезно показать локальные области потери чувствительности, скрытые внутри диффузно подавленного поля. Например, у человека с плотной катарактой пороговое значение может быть снижено по всему полю зрения, и это может скрывать более очаговые потери из-за сопутствующих заболеваний, таких как глаукома. Вместо того, чтобы сравнивать пороговые значения пациента с нормативной базой данных, анализ отклонения паттерна находит 7-ю наиболее чувствительную (85-й процентиль) некраевую точку пациента и присваивает ей нулевое значение [6]. Затем каждое другое тестовое место сравнивается с этим значением, чтобы скорректировать любую генерализованную депрессию. Было продемонстрировано, что этот метод лучше всего подходит для отделения распространенной или диффузной потери от локальной потери.
Самые нижние графики вероятностей представляют собой версии карт общего отклонения и отклонения шаблона в оттенках серого. Эти карты могут быть полезны для визуального представления статистической значимости расчетов общего и шаблонного отклонения. Карты в градациях серого следует интерпретировать только вместе с числовыми картами, чтобы избежать экстраполяции.
В правой части распечатки несколько полезных номеров. Тест полуполя глаукомы (GHT) сравнивает группы соответствующих точек выше и ниже горизонтального меридиана для оценки значимой разницы, которая может соответствовать глаукоме. Среднее отклонение (MD) — это среднее отклонение результатов пациента по сравнению с теми, которые ожидаются из нормативной базы данных для соответствующего возраста. В этом расчете центральные точки имеют больший вес, чем периферийные. Стандартное отклонение паттерна (PSD) представляет собой изображение очаговых дефектов. Он определяется путем сравнения разностей между соседними точками. Более высокие значения представляют большие очаговые потери, в то время как более низкие значения могут означать либо отсутствие потерь, либо диффузные потери. Краткосрочные колебания (SF) представляют собой расчет, отображающий изменчивость между повторными измерениями в одном и том же месте проведения испытаний. Высокий SF снижает надежность теста. Скорректированное стандартное отклонение шаблона (CPSD) корректирует PSD для SF. Если при тестировании одной и той же точки наблюдается высокая изменчивость (высокий SF), PSD получает меньший вес из-за пониженной прогностической ценности, и поэтому CPSD будет казаться ниже, чем PSD.
В нижней части распечатки HVF находится устройство отслеживания взгляда. Зрачок пациента контролируется во время тестирования, и каждый раз, когда зрачок перемещается (представляя потерю фиксации или выравнивание головы), регистрируется движение вверх. Потеря фиксации снижает точность исследования поля зрения, потому что аномалии не будут соответствовать ожидаемой анатомической области сетчатки, а некоторые могут быть полностью пропущены. Когда устройство отслеживания взгляда теряет вид зрачка (представляя моргание или опущенное верхнее веко), записывается движение вниз. Обструкция зрачков также может снизить точность результатов.
Периметрия поля зрения по Гольдману (GVF) не так широко доступна, как HVF, потому что для этого требуются опытные периметристы, которые вручную составляют карту поля зрения без помощи компьютерного алгоритма. Свет проецируется в белую чашу со стандартной интенсивностью фонового света. Проецируемый свет образует довольно круглый стимул. Доступны шесть размеров стимулов от 0,0625 мм2 (диаметр дуги около 6 минут) до 64 мм2 (диаметр около 2 градусов) при просмотре с расстояния 30 см, что является стандартным расстоянием между глазом пациента и стимулом на заднем плане. Используемый метод картирования общего поля представляет собой форму кинетической периметрии, когда стимул перемещается в поле зрения. Когда пациент видит стимул, он указывает на это низкотехнологичным методом. В Университете Айовы пациенту выдают шайбу с инструкциями постукивать шайбой по столу всякий раз, когда появляется раздражитель. Затем периметрист делает отметку в точке, где был замечен стимул. Чтобы учесть время реакции, хороший периметрист постоянно корректирует местоположение метки. По окончании проб отметки соединяют линиями, образуя плавные границы поля зрения, или изоптеры. Области пониженной чувствительности (скотомы) наносятся на карту противоположным способом, начиная с центра области потери и перемещая цель наружу как минимум в 8 направлениях (разные часы). Используемые разные цвета представляют стимулы разного размера и силы света.
Рисунок 7: Периметр Гольдмана Рисунок 8: Поле зрения Гольдмана. Предоставлено Крисом А. Джонсоном, доктором философии.
Конечным результатом GVF является диаграмма, похожая на топографическую карту. Аналогия, обычно используемая для концептуализации этих диаграмм, — это «остров видения». В этой аналогии поле зрения представляет собой остров с центральной вершиной, а высота коррелирует со зрительной чувствительностью в данном месте. В этой аналогии физиологическое слепое пятно представлено ямой или колодцем на острове. Изоптры обозначаются тремя знаками: римской цифрой, арабской цифрой и буквой. Римская цифра указывает размер стимула Гольдмана. Арабская цифра и буква обозначают затухание света. Комбинация «4е» используется при отсутствии затухания. Для каждого арабского числа меньше «4» свет ослабляется на 5 дБ. Для каждой буквы в алфавите, предшествующей «е», свет ослабляется на 1 дБ. В пределах изоптеры пациент может видеть свет такого размера и интенсивности. Scotomata представлены областями, заштрихованными сплошным цветом. Цвет представляет глубину скотомы или самый тусклый, самый маленький стимул, который пациент не может увидеть в этой области. Например, на изображении ниже физиологическое слепое пятно заштриховано оранжевым цветом, как у изоптер I2e. Это говорит о том, что пациент не может видеть стимул I2e в этой области, но может видеть более тусклый стимул I4e.
Потеря аксонов зрительного нерва при глаукоме в конечном итоге приводит к дефектам поля зрения, но эти дефекты могут быть незаметны до тех пор, пока не будет потерян значительный процент аксонов. После этой точки прогрессирования заболевания дальнейшее прогрессирование можно отслеживать с помощью серийных измерений полей зрения. Дефекты полей зрения, связанные с глаукомой, не являются специфическими для этого заболевания. Например, генерализованная депрессия всего поля — это изменение, связанное не только с глаукомой, но также может быть следствием катаракты. Дополнительные примеры глаукоматозных изменений включают, помимо прочего, фокальную депрессию, фокальное или генерализованное сужение поля зрения и обнажение слепых зон (снижение чувствительности непосредственно вокруг диска зрительного нерва) [7].
Scotomata — островки пониженной чувствительности в поле зрения, окруженные областями лучшего зрения. Островки в форме запятых называются скотомами Зейделя. Островки, дугообразные в виде дугообразных волокон, — это Бьеррум, или дугообразные скотомы. Те, которые влияют на центр зрения, являются центральными скотомами, а те, которые расположены вокруг центральных десяти градусов поля зрения, являются парацентральными скотомами. Если дефект расположен в области носа и простирается на десять градусов по горизонтальному меридиану в одной изоптере или на 5 градусов в нескольких изоптриях, это известно как назальная ступенька.
Терминальная стадия глаукомы может привести к дефекту верхнего или нижнего полушария или даже полной потере зрения, кроме центрального или височного островка зрения. Острота зрения (которая является показателем центрального зрения) может оставаться на уровне 20/20, но периферическое поле зрения может сильно уменьшаться.
Повреждение зрительных механизмов на различных участках зрительных путей от оптики и фоторецепторов до зрительных центров головного мозга приводит к различным формам и моделям выпадения поля зрения. Чтобы помочь вам правильно интерпретировать поля зрения, представлена таблица, в которой указаны классические закономерности потери поля зрения, связанные с повреждением различных зрительных структур, а также простая «поваренная книга» для интерпретации полей зрения, представленная в конце этого руководства. отчет. Пожалуйста, имейте в виду, что шаги «поваренной книги» должны выполняться в указанном порядке без ярлыков.
Таблица 1: Предлагаемые методы лечения нистагма[4]
Паттерны потери поля зрения Классическое расположение дефекта
Общее снижение чувствительности Помутнение сред (роговицы, хрусталика или стекловидного тела), снижение внимания
Сужение поля зрения Сетчатка, зрительный нерв, маленькие зрачки
Кольцевая скотома Дегенерация сетчатки
Центральная скотома Макула или зрительный нерв
Цекоцентральная скотома Пучок папилломакулярного нерва или близлежащая сетчатка в области между макулой и диском зрительного нерва
Дугообразная скотома Пучки нервных волокон дугообразных ганглиозных клеток сетчатки или сосудистая сеть сетчатки
Височный клин Носовые радиальные волокна сетчатки, входящие в зрительный нерв
Увеличение слепых зон Зрительный нерв
Множественные рассеянные дефекты сетчатка
Полуполя относительно горизонтального меридиана Пучки нервных волокон ганглиозных клеток сетчатки или, реже, сосудистая сеть сетчатки
Полуполя относительно вертикального меридиана Зрительный перекрест или задние зрительные пути
Битемпоральный Перекресток зрительных нервов
Одноименный Перекрест зрительных нервов или оптические лучи
Горизонтальный язычок Латеральное коленчатое тело
Конгруэнтные двусторонние дефекты Ближе к задней зрительной коре
Несовместимые двусторонние дефекты Ближе к перекресту зрительных нервов
«Небесный пирог» Височная доля
«Пирог на полу» Теменная доля
Дефекты «выбитые» Затылочная доля
Примечание редактора: в оригинальной версии классическое расположение несочетаемых и сочетающихся дефектов было изменено. Спасибо Терри Лу за информирование редакторов об этой ошибке. дек. 2021
Рисунок 9: Распространенные дефекты поля зрения. A: сужение поля зрения, B: кольцевая скотома, C: центральная скотома, D: цекоцентральная скотома, E: дугообразная скотома, F: височный клин, G: увеличение слепого пятна, H: множественные рассеянные дефекты, I: полуполя относительно горизонтальный меридиан, J: полуполя относительно вертикального меридиана, K: омонимичные, L: битемпоральные, N: несовместимые двусторонние дефекты, O: конгруэнтные двусторонние дефекты, P: «пирог в небе», Q: «пирог на полу», R : «Выбитые» дефекты
*Для получения наиболее точных результатов эти рекомендации необходимо выполнять в указанном порядке.
Ищите признаки ненадежных полей: много ли ложных срабатываний (> 15% при использовании SITA) или потери фиксации (> 33%)? Есть ли артефакт края линзы или нескорректированный птоз? Если поля кажутся надежными, перейдите к шагу 2.
Посмотрите на карту чувствительности, чтобы определить, находится ли поле в нормальных пределах. Если поля в пределах нормы, дальнейший анализ не проводится. Если в одном или обоих глазах наблюдаются аномальные поля, перейдите к шагу 3.
Присутствует ли повреждение поля зрения в одном или обоих глазах? Если поражен только один глаз, повреждение локализуется перед перекрестом зрительных нервов (то есть роговица, стекловидное тело, сетчатка или зрительный нерв только одного глаза). Повреждение полей зрения обоих глаз может быть связано с повреждением на уровне перекреста зрительных нервов и за его пределами или с отдельным повреждением зрительных путей каждого глаза перед перекрестом зрительных нервов.
Найдите область дефицита поля зрения. Обратитесь к диаграмме паттернов дефектов поля зрения, чтобы определить вероятную область повреждения зрительного пути.
Определите форму дефекта поля зрения. Обратитесь к таблице, чтобы определить вероятную область повреждения зрительного пути.
Сравните эти поля зрения с каждым из предыдущих тестов поля зрения пациента, чтобы определить прогрессирование потери поля зрения. Не срезайте путь, сравнивая эти поля только с самым последним полем зрения, так как это может ввести в заблуждение. Обычно для оценки прогрессирования заболевания необходимо шесть или более тестов поля зрения. Рассмотрите результаты в контексте результатов физического осмотра и результатов других тестов и визуализации.
Если есть сомнения, проконсультируйтесь с коллегами.
EyeWiki Американской академии офтальмологии
Общество визуализации и периметрии
Андерсон Д.Р. Стандартная периметрия. Ophthalmol Clin N Am 2003;16: 205-212. [PMID: 12809158]
Рамулу П. Стандартная автоматизированная периметрия. 2012. [Цитировано 29 мая 2013 г.]; Доступно на http://eyewiki.aao.org/Standard_Automated_Perimetry
Армалы МФ. Размер и расположение нормального слепого пятна. Арка Офтальмол. 1969 год; 81(2):192-201. [PMID: 5764683]
Пальчевск К. Химия и биология зрения. Журнал биологической химии 2012; 287(3): 1612-1619.
No related posts.