Периметр — что это такое
Обновлено 20 июля 2021 Просмотров: 82 274 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы подробно расскажем, что такое ПЕРИМЕТР, как он считается и каково его практическое применение.
Материал этот изучают в начальных классах школы, но далеко не всегда получается понятно объяснить простые вещи.
Что такое периметр
Периметр – это общая граница любой плоской геометрической фигуры. Измеряется в тех же величинах, что и стороны многоугольников.
У окружности тоже есть периметр. Хотя само слово в этом случае не применяют, говоря – длина окружности. Интересно, что само слово ПЕРИМЕТР изначально и обозначало окружность.
Так оно переводится с древнегреческого «περίμετρον». Но другой, более общий перевод – «измеряю вокруг», и тогда он подходит под все плоские геометрические фигуры как окружность, так и многоугольники.
youtube.com/embed/JprMHGEQqCU» allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Расчет периметра многоугольников
Считать периметр многоугольников очень просто. Надо всего лишь сложить длины всех сторон. И неважно, насколько замысловато выглядят сами фигуры.
Рассмотрим периметры самых популярных фигур.
Периметр треугольника
Как мы уже сказали, для расчета периметра треугольника надо просто сложить все его стороны.
Периметр обозначается латинской буквой «P». Он будет равен:
P = a + b + c
А если треугольник равносторонний или как его еще называют – правильный, то формула заметно упрощается.
P = a + a + a = 3a
Периметр прямоугольника
Отличительная черта прямоугольника – его противоположные стороны равны.
P = a + b + a + b = 2a + 2b = 2 (a + b)
Как и у треугольника, у прямоугольника есть частный случай, когда всего его стороны равны между собой. И всем известно, что называется такая фигура – квадрат.
И всем известно, что называется такая фигура – квадрат.
P = a + a + a + a = 4a
Периметр параллелограмма
Если кто забыл, то параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны между собой.
И периметр у него считается точно так же, как и у прямоугольника. Более того, прямоугольник – это частный случай параллелограмма.
P = a + a + b + b = 2a + 2b = 2 (a + b)
У параллелограмма есть еще один частный случай. Фигура, у которой все стороны равны. И называется она – ромб.
Его периметр считается точно так же, как и у квадрата.
P = a + a + a + a = 4a
Периметр трапеции
И еще одна фигура, которая частенько встречается в жизни. И ее изучению посвящены отдельные главы школьной программы. Трапеция – это четырехугольник, у которого только две стороны лежат на параллельных прямых.
P = a + b + c + d
Но есть и частный случай, который называется равнобедренной трапецией. У этой фигуры непараллельные стороны равны между собой и идут под одинаковым наклоном.
У этой фигуры непараллельные стороны равны между собой и идут под одинаковым наклоном.
P = a + b + c + c = a + b + 2c
Расчет длины окружности
Для расчета длины окружности, которая, по сути, и является периметром фигуры, есть своя формула. Вот только эту величину, в отличие от многоугольников, принято обозначать латинской буквой «L».
L = 2 π r
В этой формуле букой r обозначается радиус окружности, то есть расстояние от ее центра до границы. А буква π – это математическая постоянная, которая равна 3,14 (хотя на самом деле число знаков после запятой бесконечно).
Вместо заключения
Для чего в жизни нужно знать про ПЕРИМЕТР? Приведем самый простой пример.
Если вы на даче соберетесь поставить забор, вам нужно будет точно знать, сколько материала покупать. Для этого вы измерите свой участок по длине и ширине. Как правило, дачные участки имеют форму прямоугольников. Соответственно, после этого легко будет посчитать периметр:
P = 2L + 2W
где L – длина участка, а W – ширина. И уже с этими расчетами вы можете смело ехать в строительный магазин.
И уже с этими расчетами вы можете смело ехать в строительный магазин.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Нахождение периметра геометрических фигур — математика, уроки
УРОК МАТЕМАТИКИ ВО ВТОРОМ КЛАССЕ
Учитель начальных классов МКНО Рыспекова Дана Канаевна
Тема: Закрепление знаний. Нахождение периметра геометрических фигур.
Цель урока:
1. Закрепление знаний по теме «Периметр геометрических фигур»
2. Приобретение навыков работы студентов с интерактивной доской
Задачи:
Закрепить умение выполнять простейшие чертежи с помощью линейки и карандаша
Закрепить умения студентов находить периметр заданных фигур.
Продолжать работу над вычислительными навыками, используя устные приёмы вычисления.
Развивать умения решать задачи геометрического характера.

Развивать интеллектуальные и коммуникативные общеучебные умения.
Развивать умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять собственные ошибки, соотносить свои высказывания с поставленной проблемой и мнениями других детей
Развивать умения работы с интерактивной доской
План урока.
Организационный этап урока
Мотивация
Актуализация знаний
Постановка темы и цели урока
Применение и закрепление изученного материала
Практическая работа
Подведение итогов и результатов урока
Ход урока:
Организационный момент
Математику, друзья, не любить никак нельзя
Очень строгая наука, очень точная наука,
Интересная наука- математика!
Улыбнитесь друг другу, чтобы чувствовать себя увереннее и произнесем девиз нашего урока
Считать, решать, думать уверенно (слайд 3)
Мотивация к учебной деятельности
Учитель
— Математика — очень точная наука и нужно всегда помнить её правила.
3. Актуализация известного
— Чему мы учимся и что развиваем на уроке математики? Ответы детей
Не забывайте, что на уроке математики мы развиваем математическую речь, учимся доказывать, рассуждать. (слайд 4)
«Математику уже затем изучать надо, что она ум в порядок приводит» — сказал великий М.В. Ломоносов
Чтобы определить тему урока, ребята, я предлагаю вам решить круговые примеры на интерактивной доске.
Слайд 5
Начинаем работу:
+ 42 =
— 28 =
+ = 90
34 — = 26
+ =
Слайд 6 — поощрение
Открывается слайд 7 — фигуры
Учитель:
Какие геометрические фигуры вы видите на экране?
— Ответы
Какая фигура лишняя и почему?
— Круг
Чем отличаются остальные фигуры от круга?
— Имеют углы, стороны.
-Как назвать эти фигуры одним словом?
-Многоугольники
Слайд 8 . Замените фразу «Сумма длин сторон многоугольника» одним словом
— Периметр. Слайд 8-а
Молодцы, вы уже многое знаете, сегодня на уроке нам эти знания пригодятся.
4. Постановка темы и цели урока. Слайд 9
— Сможете ли вы сформулировать тему урока? (Ответы детей) слайд 9-а
Слайд «Нахождение периметра геометрических фигур»
Учитель:
Давайте вспомним формулы нахождения периметра геометрических фигур. Слайд 10
5. Задание 2. Найдите соответствие между формулой определения периметра и фигурой (интерактивная доска)
a+b+c a+a+a+a a+b+a+b a+b+c+d a+b+c+d+e
Делаем вывод:
слайд 11 открывается постепенно
Как найти периметр треугольника? Четырехугольника? Пятиугольника?
Р — сумма длин 3-х сторон
Р- сумма длин 4-х сторон
Р- сумма длин 5-ти сторон
Слайд 12-поощрение
Слайд 13.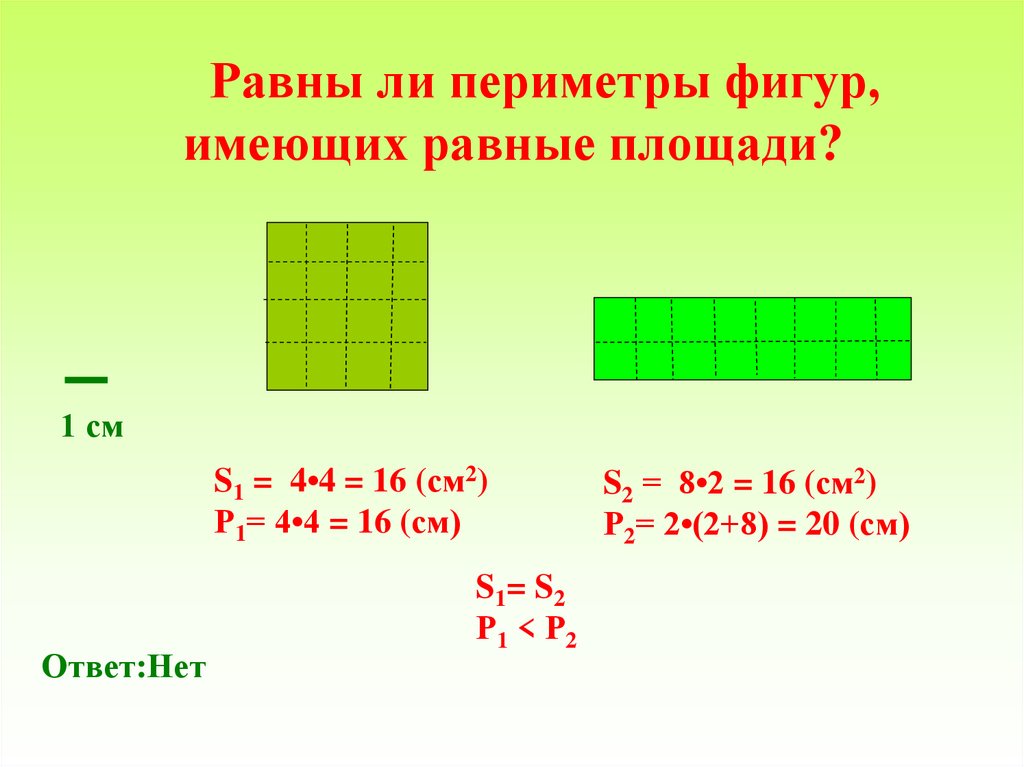 Давайте составим алгоритм нахождения периметра геометрических фигур
Давайте составим алгоритм нахождения периметра геометрических фигур
Какие шаги мы будем делать, чтобы определить периметр фигуры? Говорят дети, учитель открывает постепенно алгоритм нахождения периметра геометрической фигуры.
1. Выясняю, что это за фигура.
2. Вспоминаю правило нахождения Р этой фигуры.
3. Выполняю действия.
Используя алгоритм нахождения периметра геометрических фигур, выполним следующее задание. У каждого на парте лежит листок бумаги, разлинованный в клеточку.
Задание 3. Графический диктант. Построение на линованной бумаге.
В верхней части листа поставьте точку, от этой точки отсчитайте вправо 8 клеток, поставьте вторую точку. От второй точки отсчитайте вниз 4 клетки и поставьте 3 точку, от 3 точки отсчитайте влево 8 клеток и поставьте 4 точку. С помощью линейки соедините последовательно эти точки. Какая фигура получилась?
-Прямоугольник
-Запишите формулу периметра прямоугольника и найдите периметр полученной фигуры
Сколько нужно сделать измерений? Почему?
— 2, противоположные стороны равны.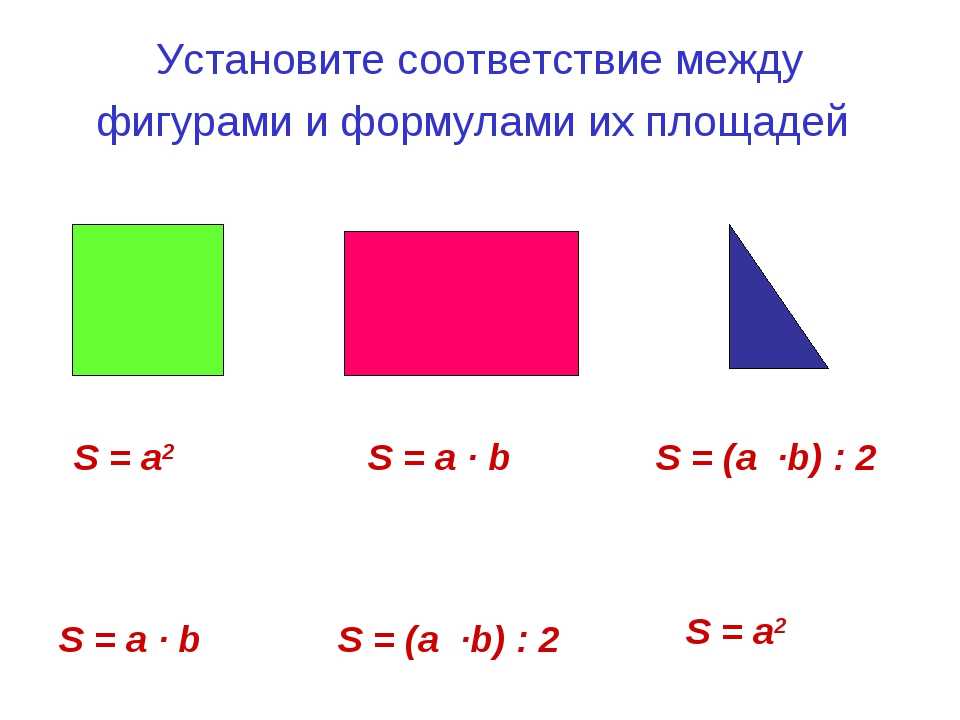 Ответ сравните с ответом на экране.
Ответ сравните с ответом на экране.
Слайд 14. Сравните ответы
Если все углы прямые,
И всего угла четыре,
Но, а по две стороны-
Противоположны и равны,
Этот четырехугольник назовем ……. прямоугольник
Он давно знакомый мой,
Каждый угол в нем — прямой.
Все четыре стороны одинаковой длины.
Что это за фигура?
— Квадрат
Найдите сторону квадрата с таким же периметром, как у вашего прямоугольника. Чему равна сторона квадрата?
Ответ сравните с ответом на экране (самопроверка) слайд 15
Солнышко слайд 16 – поощрение
Какие единицы измерения вы использовали при выполнении задания?
Задание № 4. На слайде 17 изображены картинки
Из предложенных единиц измерения выберите те, с помощью которых можно вычислить периметр и соедините стрелкой с соответствующим рисунком (интерактивная доска)
Кг, г, ц, тонна, см, м, дм, км, час, мин, сек (Сколько см в 1 дм и т.д.)
Книга — см
Стол — дм
Сад -м
Поле -км
От чего зависят выбор единиц измерения? – От размеров предмета
Назовите предметы, которые мы можем измерить с помощью метровой линейки
Поощрение слайд 18
6. Практическая работа (Предварительно студенты распределены на команды дифференцированно). Каждая команда получает свое практическое задание.
Практическая работа (Предварительно студенты распределены на команды дифференцированно). Каждая команда получает свое практическое задание.
Для того чтобы работа в группе была успешной, давайте вспомним соглашение при работе в группе.
Повторение критериев успеха при работе в группе. (слайд 19)
Соглашение при работе в группе
Работать дружно
Внимательно слушать друг друга
Помогать друг другу
Сотрудничать
Считаться с мнением группы
Уважительно относиться друг другу.
Аккуратно выполнять работу.
Задание команде № 1
Из предложенных геометрических фигур сконструируйте такую модель, чтобы можно было определить периметр каждой фигуры и найти периметр всей модели
Задание команде № 2
С помощью метровой линейки высчитайте длину ленты, необходимой для обшивки всех сторон ковра. (Как можно по-другому сформулировать вопрос? – Найти периметр)
(Как можно по-другому сформулировать вопрос? – Найти периметр)
Задание команде № 3
Перед вами чертеж двух комнат. Найдите длину потолочных галтелей, необходимых для ремонта двух комнат. Найдите значение слова «галтель» в словаре иностранных слов.
5 метров 3 метра
2 метра
4 метра
Задание для команды № 4
Найдите длину забора для садового участка четырехугольной формы, если его стороны равны 5 м, 6м, 8м, а четвертая сторона равна сумме первой и второй сторон. (Как можно по-другому сформулировать вопрос?)
Презентация работы групп
Открываются слайды – поощрения после каждой презентации 20-23
— Давайте подведем итоги урока
— Чему вы научились сегодня на уроке? (Применять на практике знания о нахождении периметра)
— Где пригодятся вам полученные знания?
Какие концепции мы применяли на уроке?
Ответственность
(мы несем ответственность каждый за себя, за группу и за весь класс)
Размышление
(откуда мы знаем про геометрические фигуры, про периметр – из уроков математики, из повседневной жизни)
Мы можем измерить периметры всех геометрических фигур, которые нас окружают
Изменение
(как это изменяется: при изменении размеров фигур, формы фигур изменяется значение периметра, алгоритм нахождения периметра сохраняется
Связь
(как это связано с другими предметами — познание мира, труд, физическая культура и др.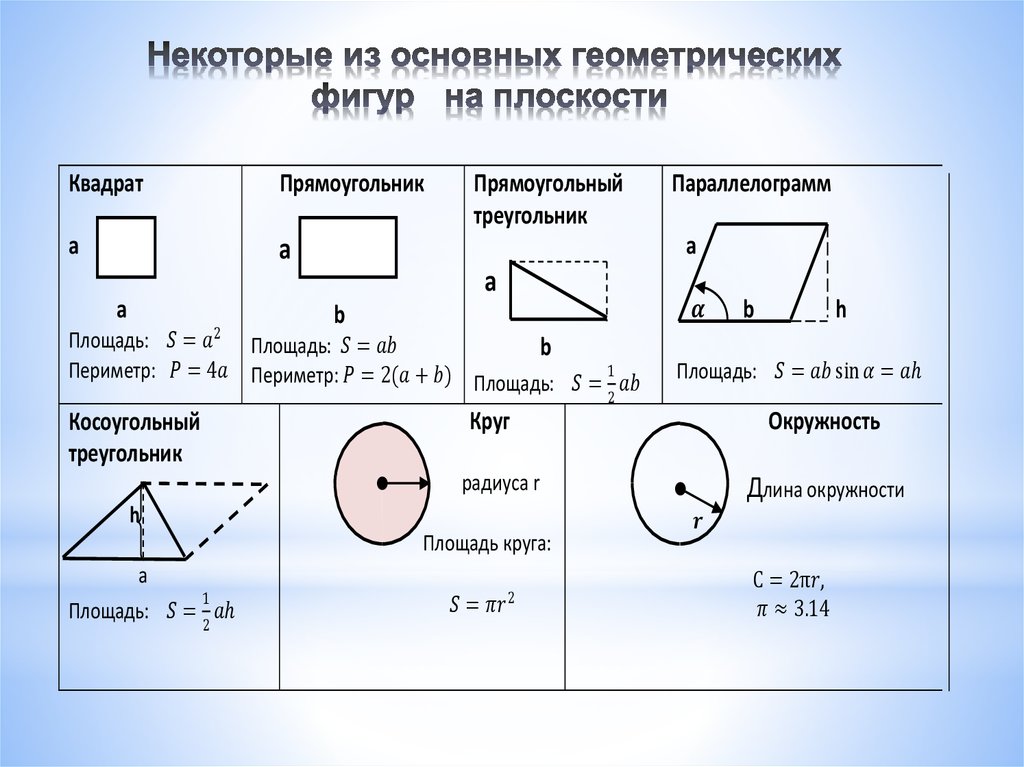 )
)
Как вы считаете, какими вы были сегодня на уроке? (устные ответы) докажите
Целеустремленными (достигли поставленной цели)
Трудолюбивыми (усердно работали на занятии)
Дружелюбными (дружно работали в группе)
Настойчивыми (справились со всеми заданиями, отстаивали свою точку зрения)
Воспитанными (хорошо себя вели)
Мыслящими (обдумывали решение)
Знающими (правильно выполнили все задания)
Рискованными, решительными (свободно выходили к доске с презентациями)
Теперь я предлагаю оценить свою работу на уроке. Подойдите к доске и покажите на «лестнице успеха» (Я знаю: все, много, мало) на какой ступени вы теперь находитесь
Благодарю всех за активную работу на уроке. Спасибо, молодцы. Слайд 24
Страница 6 из 6
Периметр | Периметр всех форм
В геометрии слово периметр используется для обозначения пути или длины. Слово «Периметр» происходит от двух греческих слов «ПЕРИ» (что означает «вокруг») и «МЕТР» (что означает «мера»). Периметр любой фигуры можно определить различными способами.
Слово «Периметр» происходит от двух греческих слов «ПЕРИ» (что означает «вокруг») и «МЕТР» (что означает «мера»). Периметр любой фигуры можно определить различными способами.
- Периметр любого многоугольника — это общее расстояние по внешней стороне многоугольника.
- Периметр фигуры равен сумме длин всех ее сторон.
- A Периметр — это длина границы фигуры.
- A Периметр — это длина контура фигуры.
Компьютерный периметр имеет множество практических применений. Например, с его помощью можно узнать число оборотов колеса, длину забора, окружающего двор или сад, отношение количества намотанной на катушку шерсти к периметру катушки, расстояние, пройденное бегуном по кругу. путь и т. д.
Формулы периметра (небольшое описание треугольника и прямоугольника, их формулы и диаграммы)
Периметр правильных фигур:
Периметр правильных многоугольников (фигура, у которой все стороны равны и все углы равны) определяется произведением числа сторон на длину стороны.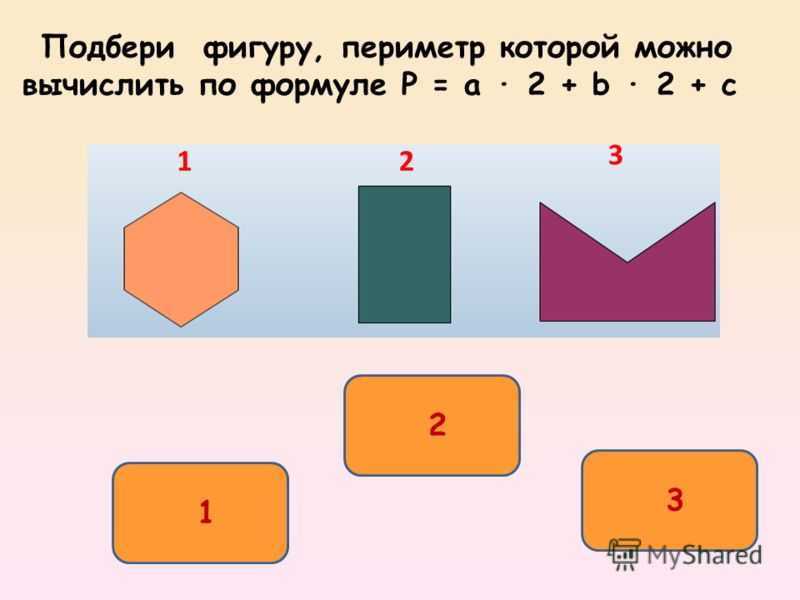
Периметр нескольких правильных многоугольников приведен ниже с диаграммами и формулами.
Пусть «s» будет длиной каждой стороны этих фигур.
Равносторонний треугольник:
Периметр = s + s + s
Периметр = 3 x s
Rhombus:
Периметр = S + S + S + S
Периметр = 4 x S
квадрат:
Периметр = S + S + S
Периметр = 4 x с
Регулярный Pentagon: Pentagon: Pentagon: Pentagon.
Периметр = S + S + S + S + S
Периметр = 5 x S
Обычный шестигран:
Периметр = S + S + S + S + S
Периметр = 6 x S
Периметр других фигур:
Другие фигуры, такие как прямоугольник, треугольник, параллелограмм, трапеция, воздушный змей, также имеют периметр. Ниже приведены диаграммы и формулы для них.
Прямоугольник:
Периметр = 2(l+b)
Где
l = длина прямоугольника
b = ширина прямоугольника
Треугольник + периметр a 900
Где a, b, c – длины каждой стороны.
Параллелограмм:
Периметр = 2(a+b)
Где
a = длина параллелограмма
b = ширина параллелограмма
Трапеция:
Периметр = a + b + c+ d
Где
a, b, c — длины каждой стороны.
Воздушный змей:
Периметр = 2(a+b)
Где
a — длина каждой стороны в одной паре
b — длина каждой стороны в другой паре
1 Окружность:
Периметр круга обычно называют окружностью.
Длина окружности = 2pi r, где: r — радиус окружности
Длина окружности = pi d, где: d — диаметр окружности.
Калькулятор среднего ускорения
Среднее ускорение — это изменение скорости объекта за определенный период времени. …
Калькулятор свободного падения
Когда объект падает на землю под действием гравитационной силы планеты, известно.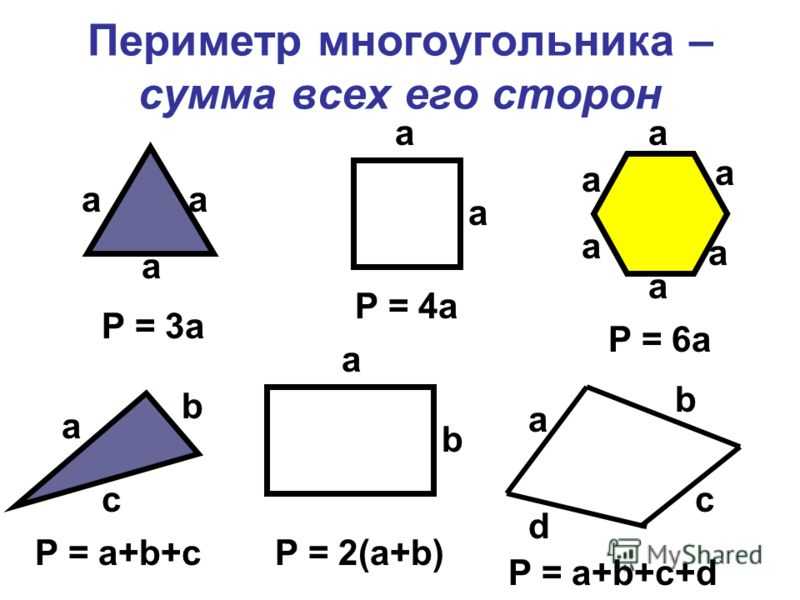 ..
..
Перестановка
В математике перестановку можно объяснить как расположение объектов в определенном порядке. Это упорядоченный…
Периметр прямоугольника
Прямоугольник можно представить как четырехугольник с четырьмя сторонами, противоположные стороны которого равны. В прямоугольнике
Периметр треугольника
Треугольником называется трехсторонний многоугольник, имеющий три вершины и три угла. Равносторонний треугольник…
Видео-урок: Периметр составной фигуры
Стенограмма видео
В этом видео мы научимся находить
периметры составных фигур. Составная фигура – это фигура, созданная
из двух и более фигур. Так, например, здесь на экране мы
составить составную фигуру, состоящую из двух прямоугольников. Мы также можем создавать более сложные
составные фигуры, состоящие из треугольников, полукругов или других двумерных фигур, таких как
параллелограммы или трапеции. Например, тот, что справа от
экран, который состоит из треугольника и полукруга.
Например, тот, что справа от
экран, который состоит из треугольника и полукруга.
Давайте начнем с обзора некоторых ключевых формулы, необходимые для вычисления периметров двумерных фигур. И в этот момент мы также вспомним что периметр фигуры — это расстояние вокруг ее края.
Во-первых, квадрат. У квадрата четыре стороны все равны
длина. Итак, если мы допустим длину стороны
квадрат равен 𝑠 единицам, тогда периметр будет равен четырем 𝑠 единицам. Это 𝑠 плюс 𝑠 плюс 𝑠 плюс s. Во-вторых, прямоугольник. В общем, это будет иметь длину 𝑙
единиц и ширина 𝑤 единиц. Таким образом, периметр, расстояние все
вокруг его края два 𝑙 плюс два 𝑤. В-третьих, для общего треугольника, если мы
обозначьте три стороны как единицы 𝑎, 𝑏 и 𝑐, тогда периметр будет равен 𝑎 плюс
𝑏 плюс 𝑐 единиц. В частном случае равностороннего
треугольников, у которых все три стороны имеют одинаковую длину, то периметр можно записать как
три 𝑠, где 𝑠 — длина стороны треугольника.
Далее круг. Периметр, который мы чаще называем длина окружности равна 𝜋𝑑 или двум 𝜋𝑟, где 𝑑 — диаметр окружность, а 𝑟 — радиус. И, наконец, пока полукруг, чей периметр состоит из изогнутой части или дуги и прямой линии. Изогнутая часть составляет половину окружности полного круга. Таким образом, мы можем записать это как 𝜋 умноженное на радиус. А прямая часть это диаметр круг, который мы можем записать как два 𝑟, что дает периметр 𝜋𝑟 плюс два 𝑟.
Теперь, когда мы рассмотрели ключевые формулы нам понадобится, давайте посмотрим на несколько примеров.
Определить периметр фигуры ниже.
Мы видим, что форма, в которой мы были
дана составная фигура. Он состоит из этих двух прямоугольников
соединенные вместе, или, может быть, вот эти два прямоугольника. Мы могли бы также думать об этом как о большем
прямоугольник, из которого вырезали меньший прямоугольник. В любом случае нам нужно определить его
периметр.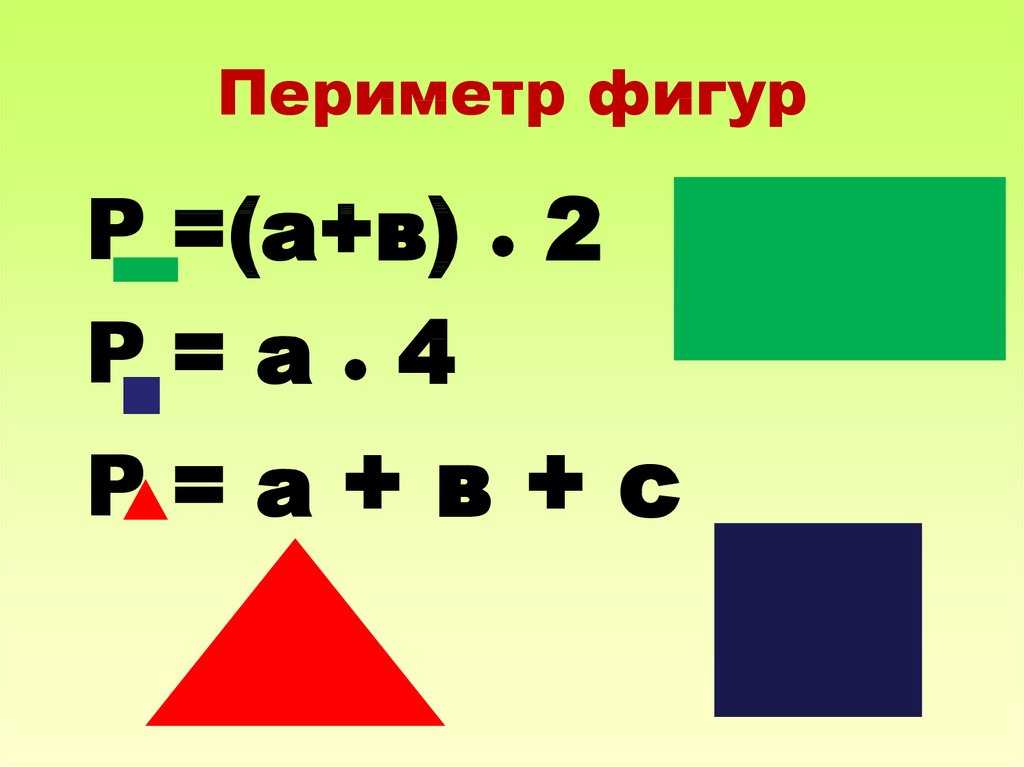
Теперь при расчете периметра такой формы, как эта, хорошей идеей будет начать с одного угла и проследить весь путь. вокруг края формы, чтобы убедиться, что мы не пропустили ни одной длины. Начнем с точки 𝐴. Периметр будет равен 𝐴𝐵 плюс 𝐵𝐶 плюс 𝐶𝐷 плюс 𝐷𝐸 плюс 𝐸𝐹 плюс 𝐹𝐴. И это все длины, которые нам нужны include, поскольку мы вернулись к исходной точке.
Нам дали на схеме первое четыре из этих длин. Их пять, семь, три и три сантиметров соответственно. Но нам не дали длины 𝐸𝐹 или 𝐹𝐴. Хотя мы можем их решить. Во-первых, 𝐸𝐹 будет разница между двумя вертикальными сторонами этой фигуры, 𝐴𝐵 минус 𝐶𝐷. Это пять минус три, что равно до двух сантиметров. 𝐹𝐴 будет разница между горизонтальные стороны фигуры. Это 𝐵𝐶 минус 𝐷𝐸, семь минус три, что равно четырем сантиметрам.
Теперь у нас есть длины всех шести
края нашей составной фигуры, и поэтому мы можем сложить их вместе. Пять плюс семь плюс три плюс три
плюс два плюс четыре равно 24.
Теперь обратите внимание, что этот периметр на самом деле такой же, как периметр полного прямоугольника 𝐴𝐵𝐶𝐺, если бы мы не удалили меньший прямоугольник 𝐹𝐸𝐷𝐺. И причина этого в том, что 𝐸𝐷 совпадает с длиной, которую мы удалили, 𝐹𝐺, а 𝐸𝐹 совпадает с длиной, которую мы удалили, 𝐷𝐺.
По этой причине мы могли бы вычислили периметр этой конкретной составной фигуры, используя формулу дважды длина плюс удвоенная ширина периметра исходного прямоугольника 𝐴𝐵𝐶𝐺.
Теперь рассмотрим пример с участием круги.
Определить периметр фигуры, используя 22 на семь, чтобы приблизить 𝜋.
Цифра, которую нам дали,
составная фигура. Он состоит из двух полукругов, соединенных
к любой стороне прямоугольника. Отслеживая наш палец полностью вокруг
края фигуры из заданной точки, мы видим, что периметр состоит из прямой
край; полукруглая дуга; еще одна линейка такой же длины, как и первая; и второй
полукруглая дуга, той же длины, что и предыдущая.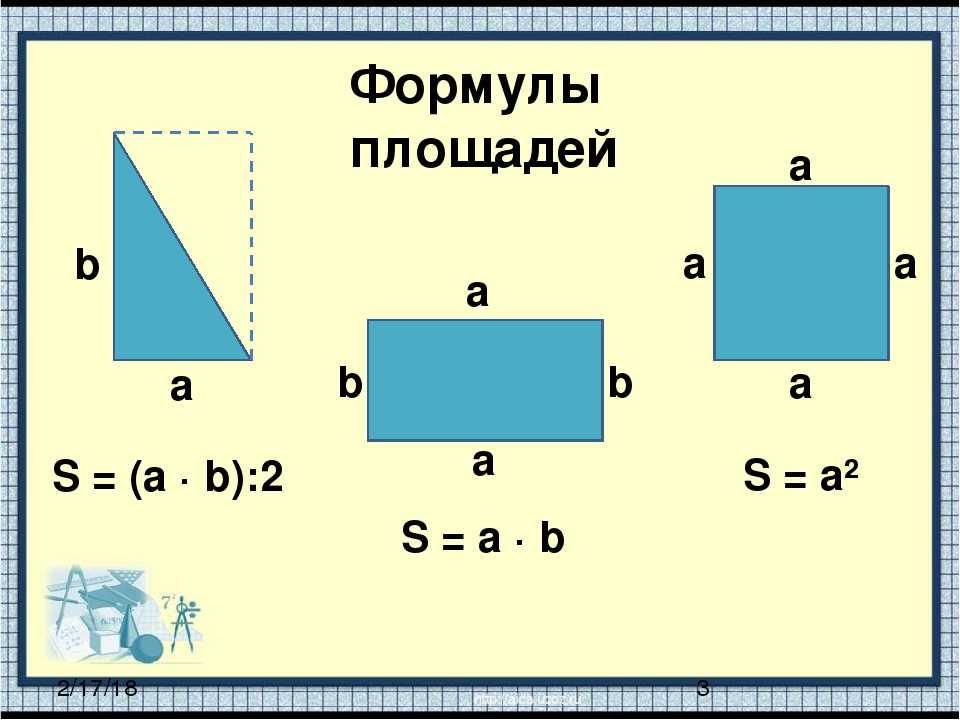
Из рисунка видно, что длина каждого прямого края 42 сантиметра. Таким образом, мы можем заменить эти значения напрямую. А как насчет длины этих двух полукруглые дуги? Ну а вместе эти две дуги сформируют полный круг. И мы знаем формулу расчета периметр или длина окружности в 𝜋 раз больше ее диаметра. Из рисунка мы видим, что диаметр нашего круга 49 сантиметров. Итак, длина окружности равна 49𝜋.
Теперь в вопросе сказано, что мы
следует использовать 22 на семь в качестве приближения для 𝜋. Это дает 49, умноженное на 22.
Семь. И тогда мы можем сократить фактор семь
в знаменателе с коэффициентом семь в числителе, что дает семь, умноженное на
22. Мы можем решить это, используя любой
метод умножения, который мы выбираем. Здесь я показал метод столбца, и он
дает 154. Таким образом, периметр фигуры становится равным 42.
плюс 154 плюс 42. Это 238. Единицы измерения периметра те же.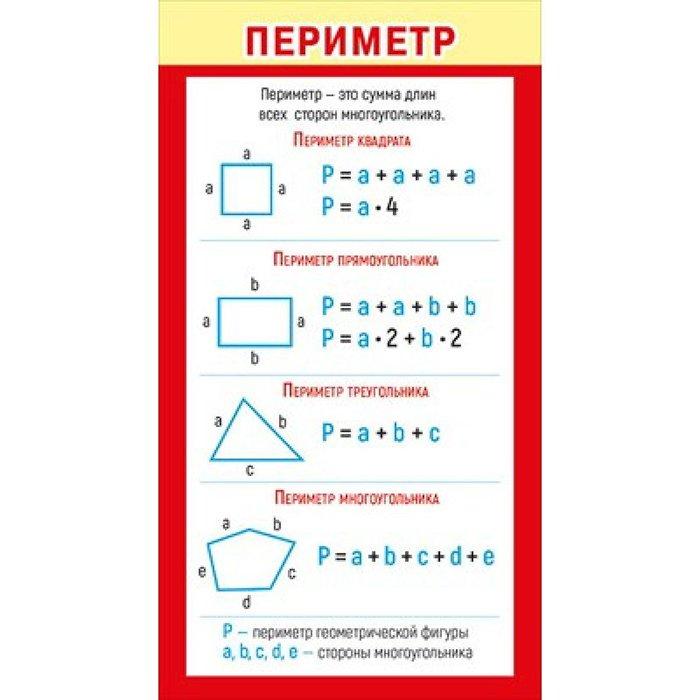 как единицы, указанные для отдельных длин в вопросе. Значит, это сантиметры. Обратите внимание, что поскольку мы использовали 22 вместо семи
в качестве приближения для 𝜋 нам не нужно было использовать калькулятор в этом вопросе.
как единицы, указанные для отдельных длин в вопросе. Значит, это сантиметры. Обратите внимание, что поскольку мы использовали 22 вместо семи
в качестве приближения для 𝜋 нам не нужно было использовать калькулятор в этом вопросе.
Теперь рассмотрим другой пример с составная фигура, состоящая из треугольника и полукруга.
Используйте 3.14, чтобы аппроксимировать 𝜋 и рассчитать периметр фигуры.
В этом вопросе нас попросили вычислить периметр составной фигуры, которая немного похожа на мороженое конус. У нас есть полукруг, который находится сверху треугольник. Обратите внимание, что разделительная линия между эти две фигуры — это третья сторона треугольника или прямой край полукруг — не является частью периметра, потому что он не является частью внешней стороны полного фигура. Периметр состоит из полуокружности и двух сторон треугольника.
Из рисунка видно, что
эти линии здесь, что треугольник равносторонний.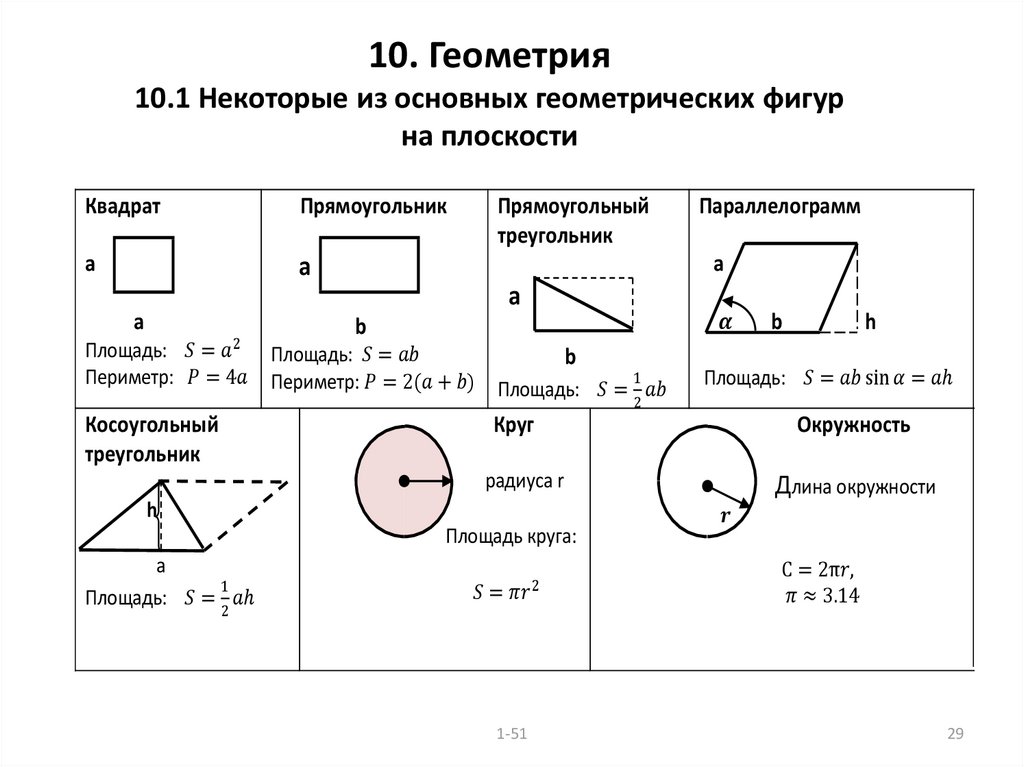 Все его стороны имеют одинаковую длину. Таким образом, каждая из двух прямых сторон равна 35
сантиметров в длину. Для дуги полукруга напомним, что
длина окружности в 𝜋 раз больше диаметра. Значит, длина дуги полукруга
будет половина этого. Уже 𝜋𝑑 больше двух. Диаметр этой окружности равен
как длина стороны треугольника. Это 35 сантиметров. Значит длина дуги полукруга равна 35𝜋
более двух или 35 более двух 𝜋.
Все его стороны имеют одинаковую длину. Таким образом, каждая из двух прямых сторон равна 35
сантиметров в длину. Для дуги полукруга напомним, что
длина окружности в 𝜋 раз больше диаметра. Значит, длина дуги полукруга
будет половина этого. Уже 𝜋𝑑 больше двух. Диаметр этой окружности равен
как длина стороны треугольника. Это 35 сантиметров. Значит длина дуги полукруга равна 35𝜋
более двух или 35 более двух 𝜋.
Теперь в вопросе сказано, что мы
необходимо использовать 3,14 в качестве приближения для 𝜋. Итак, наш периметр равен 35 на два.
умножить на 3,14 плюс 35 плюс 35. Чтобы получить 35 на два, умножить на
3,14 без калькулятора, мы можем сначала разделить 3,14 на два, чтобы получить 1,57, а затем умножить 35
на 1,57, используя любой удобный для нас метод умножения. Здесь я использовал метод сетки, чтобы найти
что 35 умножить на 1,57 равно 54,95. Итак, у нас есть 54,95 плюс 70 — это 35 плюс
35 — что равно 124,95.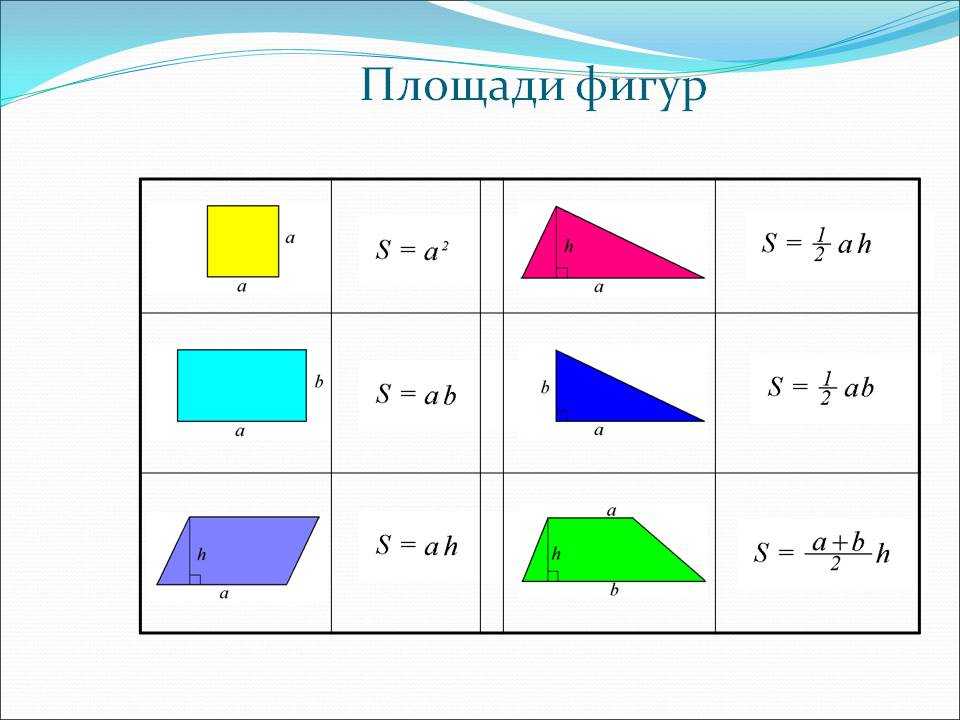 И единицы для этого периметра
такие же, как единицы длины в вопросе. Это сантиметры.
И единицы для этого периметра
такие же, как единицы длины в вопросе. Это сантиметры.
Потому что мы использовали 3,14 для аппроксимации 𝜋 тогда в этом вопросе не было нужды в калькуляторе. Хотя у нас были некоторые разумные сложные десятичные вычисления, чтобы работать.
Теперь рассмотрим немного больше сложный пример, когда вся фигура, периметр которой мы хотим вычислить, состоит из частей кругов.
На данном рисунке показаны два полукруга и две четверти другого круга. Найдите периметр заштрихованной области, принимая 3,14 в качестве приблизительного значения для 𝜋.
В этом вопросе у нас есть два
разные размеры круга. Отслеживание нашего пальца или ручки на всем пути
вокруг края фигуры мы видим, что она состоит сначала из дуги
полукруг. Тогда дуга разнокалиберной четверти
круг. Тогда дуга полуокружности, которая
конгруэнтное первому. И, наконец, дуга четверти окружности
которая конгруэнтна другой четверти окружности.
Итого то, что у нас есть, это полная окружность меньшего круга — это оранжевый — и половина окружности больший круг — это розовый. Мы знаем, что окружность Окружность можно найти по формуле 𝜋𝑑, где 𝑑 — диаметр окружности. Так что нам просто нужно определить диаметр каждого из этих кругов.
Из рисунка видно, что меньший круг имеет диаметр 39 сантиметров. Таким образом, его окружность и его вклад по периметру полной фигуры 39𝜋. Когда мы думаем о розовом круге, однако это измерение в 39 сантиметров является радиусом этого круга. То есть диаметр в два раза больше. Это 78 сантиметров. Окружность полного розового круга тогда будет 78𝜋. Но помните, у нас есть только половина длина окружности. Значит, длина полуокружности равна 78𝜋 больше двух.
На самом деле, тогда мы находим, что два значения
подобные. Обе окружности полностью оранжевые
круг и длина дуги полукруга для розового круга 39𝜋. В сумме имеем точный периметр
из 78𝜋. Но оглядываясь назад на предоставленную информацию
в вопросе нас просят использовать 3,14 в качестве приблизительного значения для 𝜋.
В сумме имеем точный периметр
из 78𝜋. Но оглядываясь назад на предоставленную информацию
в вопросе нас просят использовать 3,14 в качестве приблизительного значения для 𝜋.
Мы можем использовать метод столбца для разработки 314 умножить на 78, что даст 24492. Затем нам нужно разделить это значение на 100, чтобы дать ответ на десятичный расчет 3,14, умноженный на 78. Это дает значение 244,92. И единицы для этого периметра такие же, как единицы, указанные для отдельных длин в вопросе. Они сантиметры.
Давайте рассмотрим последний пример, который требует немного больше подхода к решению проблем.
На данном рисунке показан круг 𝑀 вписан в квадрат 𝐴𝐵𝐶𝐷. Площадь заштрихованной области цифра составляет два и одну треть квадратных сантиметров. Используя приближение 𝜋 равно 22 более семь, найдите периметр заштрихованной области.
Итак, первое, что мы замечаем, это то, что мы
на схеме вообще не указаны размеры. На самом деле, единственная информация, которую мы получили
с учетом того, что площадь заштрихованной области составляет две и одну треть квадратных сантиметров. Эта площадь будет равна площади
прямоугольника 𝐴𝐸𝐹𝐷 минус площадь полукруга.
На самом деле, единственная информация, которую мы получили
с учетом того, что площадь заштрихованной области составляет две и одну треть квадратных сантиметров. Эта площадь будет равна площади
прямоугольника 𝐴𝐸𝐹𝐷 минус площадь полукруга.
Посмотрим, сможем ли мы использовать это для решения некоторую информацию о размерах квадрата или круга. Начнем с того, что радиус нашего окружность равна 𝑟. Теперь этот радиус составляет половину диаметра круг. А так как диаметр круга равна длине стороны квадрата, то длина стороны квадрата будет равна двум 𝑟. Этот прямоугольник, 𝐴𝐷𝐹𝐸, поэтому имеет ширина 𝑟 единиц и длина две 𝑟 единиц. Его площадь, используя формулу длины умноженная на ширину площади прямоугольника, равна двум 𝑟 в квадрате.
Площадь полукруга будет равна половине
площадь полного круга радиуса 𝑟. Итак, 𝜋𝑟 в квадрате больше двух. Итак, мы имеем уравнение, включающее
радиус нашего круга. Два 𝑟 в квадрате минус 𝜋𝑟 в квадрате больше
два равно двум и одной трети. Мы можем разложить 𝑟 в квадрате из условий
в левой части, что дает два минус 𝜋 на два, все умноженное на 𝑟 в квадрате равно двум
и одна треть.
Два 𝑟 в квадрате минус 𝜋𝑟 в квадрате больше
два равно двум и одной трети. Мы можем разложить 𝑟 в квадрате из условий
в левой части, что дает два минус 𝜋 на два, все умноженное на 𝑟 в квадрате равно двум
и одна треть.
Теперь, в этот момент, мы помним, что мы попросили использовать приближение 𝜋 равно 22 на семь. Итак, 𝜋 разделить на два или 𝜋 умножить на половина — это то же самое, что 22 на семь, умноженное на половину, то есть 11 на семь. В то же время мы можем думать о целое число два как дробь 14 на семь. Итак, термины в скобках стать 14 на семь минус 11 на семь, что упрощается до просто три на семь или три седьмых.
Затем мы можем преобразовать смешанное число в
правую часть нашего уравнения, два и одну треть, в неправильную дробь. И это равно семи больше трех. Тогда, чтобы решить это уравнение, нам нужно
разделите обе части на три седьмых, чтобы оставить 𝑟 в квадрате слева
сторона. Предоставление 𝑟 в квадрате равно семи на три
разделить на три седьмых.
Предоставление 𝑟 в квадрате равно семи на три
разделить на три седьмых.
Но мы помним, что разделить на вместо дроби мы можем умножить ее на обратную. Итак, деление на три седьмых равно эквивалентно умножению на семь третей. И у нас есть, что квадрат 𝑟 равен семь на три умножить на семь на три. это 49больше девяти. Или мы можем написать семь вместо трех умножить на семь на три, как семь на три, все в квадрате.
Если 𝑟 в квадрате больше семи три в квадрате, затем, чтобы найти значение 𝑟, мы извлекаем квадратный корень из обеих сторон уравнение. И мы используем только положительное значение как 𝑟 является длиной. Итак, мы имеем, что 𝑟 больше семи. три. И мы нашли радиус нашего круг.
Теперь, когда мы знаем радиус
круг, мы также знаем длину стороны квадрата. Это вдвое больше этого значения, то есть на 14 больше.
три. И теперь мы можем вычислить
периметр заштрихованной области. Выбираем точку по периметру — так
Я выбрал точку 𝐹 — и далее, путешествуя по заштрихованной области, мы видим, что это
периметр состоит из 𝐹𝐷, 𝐷𝐴, 𝐴𝐸, а затем дуги полукруга. 𝐹𝐷 и 𝐴𝐸 семь больше трех
сантиметров, а 𝐷𝐴 составляет 14 на три сантиметра.
Выбираем точку по периметру — так
Я выбрал точку 𝐹 — и далее, путешествуя по заштрихованной области, мы видим, что это
периметр состоит из 𝐹𝐷, 𝐷𝐴, 𝐴𝐸, а затем дуги полукруга. 𝐹𝐷 и 𝐴𝐸 семь больше трех
сантиметров, а 𝐷𝐴 составляет 14 на три сантиметра.
Вспомним, что окружность полный круг равен двум 𝜋𝑟. Значит длина дуги полукруга равна половине это. Это просто 𝜋𝑟. Длина дуги полукруга равна поэтому 𝜋 умножить на семь на три.
Опять же, напомним, что нам нужно
используйте 22 на семь как наше приближение для 𝜋. И тогда мы можем сократить фактор семь
из числителя и знаменателя этих дробей. У нас осталось семь на три плюс 14
больше трех плюс семь больше трех плюс 22 больше трех. И так как все эти дроби имеют общие
знаменатель трех, они в сумме дают 50 на три. Затем мы можем преобразовать это в смешанный
количество. Это 16 и две трети. И единицы для этого периметра будут
сантиметры.