Первообразная. Интеграл. Формула Ньютона-Лейбница | Подготовка к ЕГЭ по математике
Математики любят всякому действию сопоставить противодействие.
Сложению противодействует вычитание, умножению – деление, возведению в степень – извлечение корня и т.п.
И противодействие дифференцированию (то есть взятию производной) есть! Это интегрирование.
Но давайте по порядку.
Первообразная
Первообразной функцией (также называют антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть .
Вычисление первообразной называется интегрированием.
Пример:
+ показать
Множество первообразных функций для называют неопределенным интегралом функции y = f(x) и обозначают :
Определенный интеграл
Определенный интеграл записывается так:
То есть у нас появляются границы интегрирования. – нижняя граница интегрирования, – верхняя.
Так вот формула Ньютона-Лейбница позволяет вычислять определенный интеграл следующим образом:
При вычислении первообразных вы можете пользоваться таблицей первообразных.
Пример:
+ показать
Вычислить интегралРешение:
Ответ: 0,25.
Геометрический смысл определенного интеграла
Сначала нам придется познакомиться с понятием «криволинейная трапеция».
Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой неотрицательной непрерывной функции , осью и прямыми :
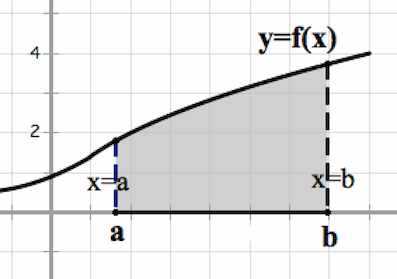
Так вот, с геометрической точки зрения площадь криволинейной трапеции, ограниченной графиком функции , осью и прямыми есть интеграл от на отрезке :
Примеры:
+ показать
1. Найти площадь фигуры, ограниченной графиком функции , осью и прямыми Решение: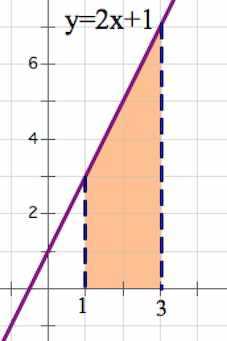
В общем-то, перед нами – прямоугольная трапеция с основаниями 3 и 7 и высотой 2.
Мы легко можем посчитать площадь трапеции по формуле :
.
Но, все же, мы посчитаем площадь через интеграл, а затем сверим результаты.
Итак,
Ну вот, все сошлось.
Ответ: 10.
Никто не спорит, здесь можно обойтись и без интеграла, но без него не обойтись в случаях, когда представляет из себя кривую, отличную от прямой линии.
2. Найти площадь фигуры, ограниченной графиком функции , осью и прямыми
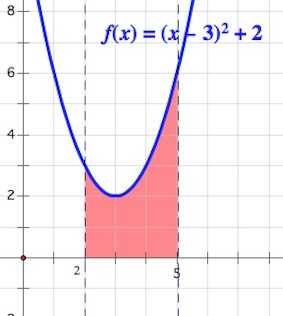
Решение:
Ответ:
egemaximum.ru
Первообразная | Математика | FANDOM powered by Wikia
В математическом анализе первоо́бразной (первообра́зной) или примити́вной функцией данной функции
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
- $ \int_a^b f(x)\, dx = F(b) — F(a). $
Это соотношение называется формулой Ньютона — Лейбница.
Благодаря этой связи множество первообразных данной функции f иногда называют общим интегралом или неопределённым интегралом f и записывают в виде интеграла без указания пределов:
- $ \int f(x)\, dx $
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая непрерывная функция f имеет первообразную F, которая представляется в виде интеграла от f с переменным верхним пределом:
- $ F(x) = \int_a^x f(t)\,dt. $функция F называется первообразной для функции f на заданном промежутке,если для всех Х из этого промежутка
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, f(x) = 2x sin (1/x) — cos(1/x) с f(0) = 0 не непрерывна при x = 0, но имеет первообразную F(x) = x² sin(1/x) с F(0) = 0.
Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:
- $ \int e^{-x^2}\,dx,\qquad \int \frac{\sin(x)}{x}\,dx,\qquad \int\frac{1}{\ln x}\,dx. $
Более развёрнутое изложение этих фактов можно отыскать в дифференциальной теории Галуа.
Свойства первообразной
- Первообразная суммы равна сумме первообразных
- Первообразная произведения константы и функции равна произведению константы и первообразной функции
- Достаточным условием для существования первообразной у заданной на отрезке функции $ f $ является непрерывность $ f $.
- Необходимыми условиями являются принадлежность функции $ f $ первому классу Бэра и выполнение для неё свойства Дарбу.
- У заданной на отрезке функции любые две первообразные отличаются на постоянную.
Техника интегрирования
Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого в нашем распоряжении имеется несколько методов:
- линейность интегрирования позволяет разбивать сложные интегралы на части,
- интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
- интегрирование по частям для операций с произведениями функций,
- метод обратной цепочки, особый случай интегрирования по частям
- метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
- алгоритм Риша (Risch algorithm),
- некоторые интегралы можно найти в таблице интегралов,
- при многоуровневом интегрировании можно использовать дополнительную технику, для примера см.двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
- вычислительные пакеты помогают автоматизировать некоторые или все вышеприведённые символические операции, что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
- если функция не имеет элементарной первообразной (например, exp(x²)), её интеграл может быть вычислен приближённо с помощью численного интегрирования.
Другие определения
Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной $ F’ $ и выполнения всюду равенства $ F'(x)=f(x) $, иногда в определении используют обобщения производной.
math.wikia.org
Первообразная и неопределенный интеграл
Константа интегрирования
Доказательство. Так как – первообразная функции , то по определению имеем, что
Рассмотрим функцию и покажем, что она также является первообразной для функции . Найдем производную:
То есть , а это означает, что и функция является первообразной для функции .
Что и требовалось доказать.
Правила нахождения первообразных
- Если – первообразная для функции , а – первообразная функции , то – первообразная функции .
- Если – первообразная для функции , а – некоторое число, то является первообразной для функции .
- Если является первообразной функции , а и – некоторые числа, то функция – первообразная для функции .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
📌 Первообразная — это… 🎓 Что такое Первообразная?
Первообра́зной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных, таких как или … и т. д.; таким образом семейство первообразных функции можно обозначить как , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
Это соотношение называется формулой Ньютона — Лейбница.
Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, с не непрерывна при , но имеет первообразную с .
Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:
Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.
Свойства первообразной
- Первообразная суммы равна сумме первообразных
- Первообразная произведения константы и функции равна произведению константы и первообразной функции
- Достаточным условием существования первообразной у заданной на отрезке функции является непрерывность на этом отрезке
- Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу
- У заданной на отрезке функции любые две первообразные отличаются на постоянную.
Техника интегрирования
Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:
- линейность интегрирования позволяет разбивать сложные интегралы на части,
- интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
- интегрирование по частям для операций с произведениями функций,
- метод обратной цепочки, особый случай интегрирования по частям,
- метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
- алгоритм Риша (en:Risch algorithm),
- некоторые интегралы можно найти в таблице интегралов,
- при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
- Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведённые символические операции, что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
- если функция не имеет элементарной первообразной (как, например, ), её интеграл может быть вычислен приближённо с помощью численного интегрирования.
Другие определения
Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной и выполнения всюду равенства , иногда в определении используют обобщения производной.
Примечания
Ссылки
См. также
dic.academic.ru
Первообразная функция и её свойства
⇐ ПредыдущаяСтр 7 из 10Следующая ⇒
Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если в каждой точке этого промежутка функция F(x) дифференцируема и выполняется равенство F ‘(x) = f(x).
Пример 1. Функция F (x) = sin x является первообразной функции f(x) = cos x на бесконечном промежутке (– ¥; +¥), так как
F’(x) = (sin x) ‘ = cos x = f(x) для x Î (– ¥;+¥).
Нетрудно убедиться, что функции F1(x) = sin x + 5 и F2(x) = sin x – 10 также являются первообразными функции f(x) = cos x для всех (– ¥;+¥), т.е. если для функции f(x) на некотором промежутке существует первообразная функции, то она не является единственной. Докажем, что множество всех первообразных для данной функции f(x) есть множество, которое задаётся формулой F(x) + C, где C – любая постоянная величина.
Теорема 1 (об общем виде первообразной). Пусть F(x) – одна из первообразных для функции f(x) на интервале (a;b). Тогда любая другая первообразная для функции f(x) на интервале (a;b) представлена в видеF( x) + C, где C – некоторое число.
Доказательство. Во-первых, проверим, что F(x) + C также является первообразной для функции f(x) на интервале (a;b).
По условию теоремы F(x) на интервале (a;b) является первообразной для функции f(x), поэтому выполняется равенство:
F ‘(x) = f(x) при любом xÎ (a;b).
Так как С – некоторое число, то
(F(x) + С) ‘ = F ‘(x)+С ‘ = F ‘(x) + 0 = f(x).
Отсюда следует: (F(x) + С)’ = f(x) при любом xÎ (a;b), а значит F(x) + С на интервале (a;b) является первообразной для функции f(x).
Во-вторых, проверим, что если F(x) и Ф(x) – две первообразные для функции
Обозначим j(x) = F(x) – Ф(x). Так как по предположению функции F(x) и Ф(x) первообразные на интервале (a;b) для функции f(x), то выполняются равенства: F ‘(x) = f(x) и Ф'(x) = f(x) при любом xÎ (a;b). Следовательно, j'(x) = F ‘(x) – Ф’ (x) = f(x) – f(x) = 0 при любом xÎ (a;b).
Функция j(x) непрерывна и дифференцируема при xÎ (a;b). Значит, на любом отрезке [x1; x2] Ì (a; b) функция j(x) удовлетворяет теореме Лагранжа: существует точка Î(x1; x2), для которой выполняется равенство:
j(x2) – j(x1) = j’ ( )× (x2 – x1) = 0×(x2 – x1) = 0
Þ j(x2) – j(x1) = 0 Þ j(x2) = j(x1) Þ j(x) = const.
Значит, F(x) – Ф(x) = const.
Итак, получили, что если известна одна первообразная F(x) для функции f(x) на интервале (a;b), то любая другая первообразная может быть представлена в виде F(x) + С, где С – произвольная постоянная величина. Такая форма записи первообразных носит название общего вида первообразной.
Понятие неопределённого интеграла
Определение 2. Множество всех первообразных для данной функции f(x) на интервале (a;b) называется неопределённым интегралом функции f(x) на этом интервале и обозначается символом:
В обозначении знак называется знаком интеграла, – подынтегральным выражением, – подынтегральной функцией, – переменной интегрирования.
Теорема 2. Если функция f(x) непрерывна на промежутке (a;b), то она имеет на промежутке (a;b) первообразную и неопределённый интеграл.
Замечание. Операция нахождения неопределённого интеграла от данной функции f(x) на некотором промежутке носит название интегрирования функции f(x).
Свойства неопределённого интеграла
Из определений первообразной F(x) и неопределённого интеграла от данной функции f(x) на некотором промежутке следуют свойства неопределённого интеграла:
1. .
2. .
3. , где С – произвольная постоянная.
4. , где k = const.
5.
Замечание. Все вышеперечисленные свойства верны при условии, что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.
Таблица основных неопределённых интегралов
Действие интегрирования является обратным действию дифференцирования, т.е. по заданной производной функции f(x) надо восстановить начальную функцию F(x). Тогда из определения 2 и таблицы производных (см. §4, п. 3, с. 24) получается таблица основных интегралов.
1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
10. .
11. .
12. .
13. .
14. .
15. .
16. .
В формулах 1-16 С – произвольная постоянная.
Замечание. Интеграл, взятый не от любой элементарной функции, является элементарной функцией. Примерами могут служить следующие интегралы, часто встречающиеся в задачах:
– интеграл Пуассона,
– интегралы Френеля,
– интегральный логарифм,
– интегральный косинус и синус.
Указанные функции существуют и имеют важное прикладное значение. Для этих функций составлены таблицы значений.
МЕТОДЫ ИНТЕГРИРОВАНИЯ
Рекомендуемые страницы:
lektsia.com
Интеграл и его применение. Первообразная
Пусть , функция дифференцируема. Функция называется первообразной функции , если .
Отыскание первообразной у функции носит название неопределенного интегрирования.
Обозначение. — неоднозначно.
: — одна из первообразных функции .
Свойства первообразной
1. Пусть — первообразная функции , . Тогда — первообразная функции .
Доказательство.
Обратное неверно.
2. Пусть , пусть и — первообразные функции . Тогда — постоянная функция.
Доказательство.
— функция с нулевой производной, заданная на промежутке. Значит, — постоянная функция.
3. Если — первообразная функции , — первообразная функции , то — первообразная функции .
Доказательство.
(последнее равенство справедливо с точностью до постоянной).
4. Пусть — первообразная функции , . Тогда — первообразная функции .
Доказательство.
5. Пусть — первообразная функции , — дифференцируемая функция. Тогда — первообразная функции .
Доказательство.
— формула замены переменной в неопределенном интеграле.
6. Пусть функции и дифференцируемы, пусть — первообразная функции . Тогда — первообразная функции .
Доказательство.
Формула интегрирования по частям
Таблица первообразных

hijos.ru
Первообразная | Царица Математика
Что такое первообразная
В более раннем материале был рассмотрен вопрос нахождения производной и были показаны её различные применения: вычисление углового коэффициента касательной к графику, решение задач на оптимизацию, исследование функций на монотонность и экстремумы. $\newcommand{\tg}{\mathop{\mathrm{tg}}\nolimits}$ $\newcommand{\ctg}{\mathop{\mathrm{ctg}}\nolimits}$ $\newcommand{\arctg}{\mathop{\mathrm{arctg}}\nolimits}$ $\newcommand{\arcctg}{\mathop{\mathrm{arcctg}}\nolimits}$
Рисунок 1.
Так же была рассмотрена задача нахождения мгновенной скорости $v(t)$ с помощью производной по заранее известному пройденному пути, выражаемому функцией $s(t)$.
Рисунок 2.
Очень часто встречается и обратная задача, когда нужно найти путь $s(t)$, пройденный точкой за время $t$, зная скорость движения точки $v(t)$. Если вспомнить, мгновенная скорость $v(t)$ находится, как производная от функции пути $s(t)$: $v(t)=s’(t)$. Значит, чтобы решить обратную задачу, то есть вычислить путь, нужно найти функцию, производная которой будет равна функции скорости. Но мы-то знаем, что производная пути и есть скорость, то есть: $s’(t) = v(t)$. Скорость равна произведению ускорения на время: $v=at$. Нетрудно определить, что искомая функция пути будет иметь вид: $s(t) = \frac{at^2}{2}$. Но это не совсем полное решение. Полное решение будет иметь вид: $s(t)= \frac{at^2}{2}+C$, где $C$ – некоторая константа. Почему именно так, будет рассказано далее. А пока проверим правильность найденного решения: $s'(t)=\left(\frac{at^2}{2}+C\right)’=2\frac{at}{2}+0=at=v(t)$.
Стоит заметить, что нахождение пути по скорости является физическим смыслом первообразной.
Полученная функция $s(t)$ называется первообразной функции $v(t)$. Довольно интересное и необычное название, не правда ли. В нём кроется большой смысл, который объясняет суть данного понятия и ведёт к его пониманию. Можно заметить, что в нём заключены два слова «первый» и «образ». Они говорят сами за себя. То есть это та функция, которая является исходной для имеющейся у нас производной. А мы по этой производной ищем ту функцию, которая была в начале, была «первой», «первым образом», то есть первообразную. Её иногда также называют примитивной функцией или антипроизводной.
Как нам уже известно, процесс нахождения производной называется дифференцированием. А процесс нахождения первообразной называется интегрированием. Операция интегрирования является обратной для операции дифференцирования. Верно и обратное утверждение.
Определение. Первообразной для функции $f(x)$ на некотором интервале называется такая функция $F(x)$, производная которой равна этой функции $f(x)$ для всех $x$ из указанного интервала: $F’(x)=f(x)$.
У кого-то может возникнуть вопрос: откуда в определении взялись $F(x)$ и $f(x)$, если изначально речь шла о $s(t)$ и $v(t)$. Дело в том, что $s(t)$ и $v(t)$ – частные случаи обозначения функций, имеющие в данном случае конкретный смысл, то есть это функция времени и функция скорости соответственно. То же самое и с переменной $t$ – она обозначает время. А $f$ и $x$ – традиционный вариант общего обозначения функции и переменной соответственно. Стоит обратить особое внимание на обозначение первообразной $F(x)$. Во-первых, $F$ – заглавная. Первообразные обозначаются заглавными буквами. Во-вторых, буквы совпадают: $F$ и $f$. То есть, для функции $g(x)$ первообразная будет обозначаться $G(x)$, для $z(x)$ – $Z(x)$. Вне зависимости от обозначений правила нахождения первообразной функции всегда одинаковы.
Рассмотрим несколько примеров.
Пример 1. Доказать, что функция $F(x)=\frac{1}{5}\sin5x$ является первообразной функции $f(x)=\cos5x$.
Для доказательства воспользуемся определением, а точнее тем фактом, что $F’(x)=f(x)$, и найдём производную функции $F(x)$: $F’(x)=(\frac{1}{5} \sin5x)’=\frac{1}{5}\cdot 5\cos5x= \cos5x$. Значит $F(x)=\frac{1}{5} \sin5x$ является первообразной $f(x)=\cos5x$. Что и требовалось доказать.
Пример 2. Найти, каким функциям соответствуют следующие первообразные: а) $F(z)=\tg z$; б) $G(l) = \sin l$.
Чтобы найти искомые функции, вычислим их производные:
а) $F’(z)=(\tg z)’=\frac{1}{\cos^2 z}$;
б) $G(l) = (\sin l)’ = \cos l$.
Пример 3. Какой будет первообразная для $f(x)=0$?
Воспользуемся определением. Подумаем, какая функция может иметь производную, равную $0$. Вспоминая таблицу производных, получаем, что любая постоянная будет иметь такую производную. Получаем, что искомая нами первообразная: $F(x)= C$.
Полученное решение можно объяснить геометрически и физически. Геометрически оно означает, что касательная к графику $y=F(x)$ горизонтальна в каждой точке этого графика и, значит, совпадает с осью $Ox$. Физически объясняется тем, что точка, имеющая скорость, равную нулю, остаётся на месте, то есть пройденный ею путь неизменен. Исходя из этого можно сформулировать следующую теорему.
Теорема. (Признак постоянства функций). Если на некотором промежутке $F’(x) = 0$, то функция $F(x)$ на этом промежутке постоянна.
Пример 4. Определить, первообразными каких функций являются функции а) $F_1 = \frac{x^7}{7}$; б) $F_2 = \frac{x^7}{7} – 3$; в) $F_3 = \frac{x^7}{7} + 9$; г) $F_4 = \frac{x^7}{7} + a$, где $a$ – некоторое число.
Используя определение первообразной, делаем вывод, что для решения этого задания нам нужно вычислить производные данных нам первообразных функций. При вычислении помним о том, что производная постоянной, то есть любого числа, равна нулю.
а) $F_1 =(\frac{x^7}{7})’= 7 \cdot \frac{x^6}{7} = x^6$;
б) $F_2 =\left(\frac{x^7}{7} – 3\right)’=7 \cdot \frac{x^6}{7}= x^6$;
в) $F_3 =(\frac{x^7}{7} + 9)’= x^6$;
г) $F_4 =(\frac{x^7}{7} + a)’ = x^6$.
Что мы видим? Несколько разных функций являются первообразными одной и той же функции. Это говорит о том, что у любой функции существует бесконечно много первообразных, и они имеют вид $F(x) + C$, где $C$ – произвольная константа. То есть операция интегрирования является многозначной в отличие от операции дифференцирования. Сформулируем на основании этого теорему, описывающую основное свойство первообразных.
Теорема. (Основное свойство первообразных). Пусть функции $F_1$ и $F_2$ являются первообразными функции $f(x)$ на некотором промежутке. Тогда для всех значений из этого промежутка справедливо следующее равенство: $F_2=F_1+C$, где $C$ – некоторая константа.
Факт наличия бесконечного множества первообразных можно интерпретировать геометрически. С помощью параллельного переноса вдоль оси $Oy$ можно получить друг из друга графики двух любых первообразных для $f(x)$. В этом заключается геометрический смысл первообразной.
Очень важно обратить внимание на то, что выбором константы $C$ можно добиться прохождения графика первообразной через определённую точку.

Рисунок 3.
Пример 5. Найти первообразную для функции $f(x)=\frac{x^2}{3}+1$, график которой проходит через точку $(3; 1)$.
Найдём сначала все первообразные для $f(x)$: $F(x)=\frac{x^3}{9}+x + C$.
Далее найдём такое число C, при котором график $y=\frac{x^3}{9}+x + C$ будет проходит через точку $(3; 1)$. Для этого подставим координаты точки в уравнение графика и решим его относительно $C$:
$1= \frac{3^3}{9}+3 + C$, $C=-5$.
Получили график $y=\frac{x^3}{9}+x-5$, который соответствует первообразной $F(x)=\frac{x^3}{9}+x-5$.
Таблица первообразных
Таблицу формул для нахождения первообразных можно составить, используя формулы нахождения производных.
| Функции | Первообразные |
| $0$ | $C$ |
| $1$ | $x+C$ |
| $a\in R$ | $ax+C$ |
| $x^n, n\ne1$ | $\displaystyle \frac{x^{n+1}}{n+1}+C$ |
| $\displaystyle \frac{1}{x}$ | $\ln|x|+C$ |
| $\sin x$ | $-\cos x+C$ |
| $\cos x$ | $\sin x+C$ |
| $\displaystyle \frac{1}{\sin^2 x}$ | $-\ctg x+C$ |
| $\displaystyle \frac{1}{\cos^2 x}$ | $\tg x+C$ |
| $e^x$ | $e^x+C$ |
| $a^x, a>0, a\ne1$ | $\displaystyle \frac{a^x}{\ln a} +C$ |
| $\displaystyle \frac{1}{\sqrt{1-x^2}}$ | $\arcsin x+C$ |
| $\displaystyle -\frac{1}{\sqrt{1-x^2}}$ | $\arccos x+C$ |
| $\displaystyle \frac{1}{1+x^2}$ | $\arctg x+C$ |
| $\displaystyle -\frac{1}{1+x^2}$ | $\arcctg x+C$ |
Проверить правильность составления таблицы можно следующим образом: для каждого множества первообразных, находящегося в правом столбце найти производную, в результате чего получатся соответствующие функции, стоящие в левом столбце.
Некоторые правила нахождения первообразных
Как известно, многие функции имеют более сложный вид, нежели указанные в таблице первообразных, и могут представлять собой любое произвольное сочетание сумм и произведений функций из этой таблицы. И тут возникает вопрос, как вычислять первообразные подобных функций. К примеру, из таблицы мы знаем, как вычислить первообразные $x^3$, $\sin x$ и $10$. А как, например, вычислить первообразную $x^3-10\sin x$? Забегая вперёд, стоит отметить, что она будет равна $\frac{x^4}{4}+10\cos x$.
1. Если $F(x)$ первообразная для $f(x)$, $G(x)$ – для $g(x)$, то для $f(x)+g(x)$ первообразная будет равна $F(x)+G(x)$.
2. Если $F(x)$ является первообразной для $f(x)$ и $a$ – константа, то для $af(x)$ первообразной будет $aF(x)$.
3. Если для $f(x)$ первообразной является $F(x)$, $a$ и $b$ – константы, то $\frac{1}{a} F(ax+b)$ первообразная для $f(ax+b)$.
Используя полученные правила мы можем расширить таблицу первообразных.
| Функции | Первообразные |
| $(ax+b)^n, n\ne1, a\ne0$ | $\displaystyle \frac{(ax+b)^n}{a(n+1)} +C$ |
| $\displaystyle \frac{1}{ax+b}, a\ne0$ | $\displaystyle \frac{1}{a}\ln|ax+b|+C$ |
| $e^{ax+b}, a\ne0$ | $\displaystyle \frac{1}{a} e^{ax+b}+C$ |
| $\sin(ax+b), a\ne0$ | $\displaystyle -\frac{1}{a}\cos(ax+b)+C$ |
| $\cos(ax+b), a\ne0$ | $\displaystyle \frac{1}{a}\sin(ax+b)+C$ |
Пример 5. Найти первообразные для:
а) $\displaystyle 4x^3+10x^7$;
б) $\displaystyle \frac{6}{x^5} -\frac{2}{x}$;
в) $\displaystyle 5\cos x+\sin(3x+15)$;
г) $\displaystyle \sqrt{x}-2\sqrt[3]{x}$.
а) $4\frac {x^{3+1}}{3+1}+10\frac{x^{7+1}}{7+1}+C=x^4+\frac{5}{4} x^8+C$;
б) $-\frac{3}{2x^4} -2\ln|x|+C$;
в) $5 \sin x — \frac{1}{3}\cos(3x + 15) + C$;
г) $\frac{2}{3}x\sqrt{x} — \frac{3}{2} x\sqrt[3]{x} + C$.
mathematike.ru
