Первообразная неопределенный интеграл: Первообразная. Неопределённый и определённый интегралы

2\) является первообразной для $f(x)=2x$, т.к. для любого $x$ производная $F'(x)=f(x)$.
2) Функция $F(x)=cos⁡x$ является первообразной для $f(x)=sin⁡x$, т.к. для любого $x$ производная $F'(x)=f(x)$.

Поиск производной данной функции называют дифференцированием.
Поиск первообразной данной функции называют интегрированием.
Дифференцирование и интегрирование являются взаимно обратными операциями.

Содержание

п.2. Основное свойство первообразной. Неопределенный интеграл

Каждая первообразная для функции $f(x)$ имеет вид $F(x)+C$, где $F(x)$ – одна из этих первообразных, $C$ – произвольная постоянная.

Действительно, по правилу нахождения производной суммы: $$ (F(x)+C)’=F'(x)+C’=f(x)+0=f(x) $$ Т.е. первообразная определена с точностью до константы.

Например:

Для $f(x)=sin⁡x$
Первообразными будут \begin{gather*} F(x)=cos⁡x,\ F(x)=cos⁡x+1, \\ F(x)=cos⁡x-2,\ F(x)=cos⁡x+0,100500 \end{gather*} и т.д.

Множество всех первообразных функции $f(x)$ называют неопределенным интегралом этой функции: $$ \int f(x)dx=F(x)+C $$

Например: $$ \int x^2 dx=\frac{x^3}{3}+C,\ \ \int \frac{dx}{\sqrt{x}}=2\sqrt{x}+C $$

п.

6}{3}-cosx+C\)

Постоянный множитель функции является постоянным множителем первообразной.
Если $F(x)$ является первообразной для $f(x)$,
то $kF(x)$ — первообразная для $kf(x)$.

Действительно $$ \left(kF(x)\right)’=kF'(x)=kf(x) $$
Например:
Найдем первообразную функции $y=5sinx+2=5\cdot sinx+2\cdot 1$
Первообразная для синуса $F_1(x)=-cosx$, первообразная для единицы $F_2(x)=⁡x$
Общая первообразная
$F(x)=-5cosx+2x$

Линейное преобразование аргумента функции.
Если $F(x)$ является первообразной для $f(x)$,
то для функции с аргументом $f(kx+b)$ — первообразной будет $\frac1k F(kx+b)$.

Действительно
Для $x$ получаем цепочку отображений: $x\rightarrow kx+b\rightarrow F(kx+b)$
По правилу дифференцирования сложной функции (см. §45 данного справочника) \begin{gather*} \left(\frac1k F(kx+b)\right)’=\frac1k\cdot F'(kx+b)\cdot (kx+b)’=\frac1k\cdot F'(kx+b)\cdot k=F'(kx+b)=\\ =f(kx+b) \end{gather*}
Например:
Найдем первообразную функции $y=sin(5x+2) $
Нам известно, что первообразная для $f(x)=sin⁡x,\ F=-cos⁡x$
При преобразовании аргумента $x\rightarrow 5x+2$ у новой первообразной будет новый аргумент и множитель $\frac1k=\frac15$. 4-4x+4\frac14 $$

Первообразная и неопределенный интеграл, их свойства

Определение первообразной

Для начала, дадим определение понятиям, которые будут использоваться в данном разделе. В первую очередь это первообразная функции. Для этого введем константу C.

Определение 1

Первообразная функции f(x) на промежутке (a; b) это такая функция F(x), при которое формула F'(x)=f(x) превращается в равенство для любого x из заданного промежутка.

Следует учитывать тот факт, что производная от константы C будет равна нулю, что позволяет нам считать верным следующее равенство F(x)+C’=f(x).

Получается, что функция f(x) имеет множество первообразных F(x)+C, для произвольной константы C. Эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла

Все множество первообразных функции f(x) можно назвать неопределенным интегралом этой функции. С учетом этого формула будет иметь вид ∫f(x)dx=F(x)+C. При этом, выражение f(x)dx является подынтегральным выражением, а f(x) – это подынтегральная функция. Подынтегральное выражение представляет собой дифференциал функции f(x).

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

Результатом неопределенного интегрирования будет не одна функция F(x), а множество ее первообразных F(x)+C.

Зная свойства производной, мы можем сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

∫f(x)dx’=F(x)+C’=f(x)

Производная результата интегрирования равна подынтегральной функции.

∫d(F(x))=∫F'(x)dx=∫f(x)dx=F(x)+C

Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

∫k·f(x)dx=k·∫f(x)dx, где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.

Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

∫f(x)±g(x))dx=∫f(x)dx±∫g(x)dx

Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.

Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:

k·∫f(x)dx’=k·∫d(x)dx’=k·f(x)∫f(x)dx±∫g(x)dx’=∫f(x)dx’±∫g(x)dx’=f(x)±g(x)

Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.

Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.

Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.

Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.

Рассмотрим пример.

Пример 1

Найдем первообразную функции f(x)=1x, значение которой равно единице при х=1.

Решение

Используя таблицу производных основных элементарных функций получаем

d(ln x)=(ln x)’dx=dxx=f(x)dx∫f(x)dx=∫dxx=∫d(ln(x))

Используя второе свойство ∫d(ln(x))=ln(x)+C, мы получаем множество первообразных ln(x)+C. При х=1 получим значение ln(1)+C=0+C=C. Согласно условию задачи, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид ln(x)+1.

Ответ: f(x)=1x=ln(x)+1

Пример 2

Необходимо найти неопределенный интеграл ∫2sinx2cosx2dx и проверить результат вычисления дифференцированием.

Решение

Используем для проведения вычислений формулу синуса двойного угла из курса тригонометрии 2sinx2cosx2=sin x, получим ∫2sinx2cosx2dx=∫sin xdx.

Используем таблицу производных для тригонометрических функций, получим:

d(cos x)=cos x’dx=-sin xdx⇒sin xdx=-d(cos x)

То есть, ∫sin xdx=∫(-d(cos x))

Используя третье свойство неопределенного интеграла, мы можем записать ∫-d(cos x)=-∫d(cos x).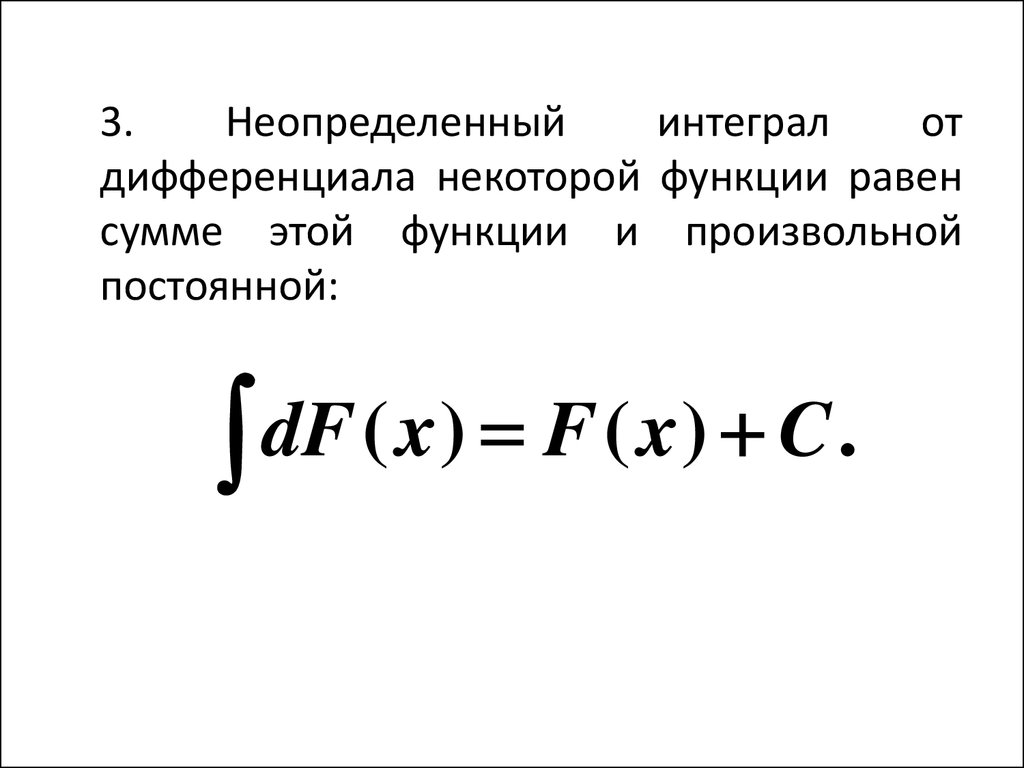

По второму свойству получаем -∫d(cos x)=-(cos x+C)

Следовательно, ∫2sin x2cosx2dx=-cos x-C.

Проверим полученный результат дифференцированием.

Продифференцируем полученное выражение:
-cos x-C’=-(cos x)’-(C)’=-(-sin x)=sin x=2sinx2cosx2

В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.

Ответ: ∫2sin x2cosx2dx=-cos x-C

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Подробнее эту тему мы рассмотрим в следующем разделе «Таблица первообразных (таблица неопределенных интегралов)».

Решение задач от 1 дня / от 150 р.

Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

5.1: Первообразные и неопределенное интегрирование

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 4178

Gregory Hartman et al.
Военный институт Вирджинии

Мы потратили много времени на рассмотрение производных функций и их приложений. В следующих главах мы начнем думать «в другом направлении». То есть, учитывая функцию $f(x)$, мы будем рассматривать функции $F(x)$ такие, что $F'(x) = f(x)$. Есть множество причин, по которым это окажется полезным: эти функции помогут нам вычислить площади, объемы, массу, силу, давление, работу и многое другое.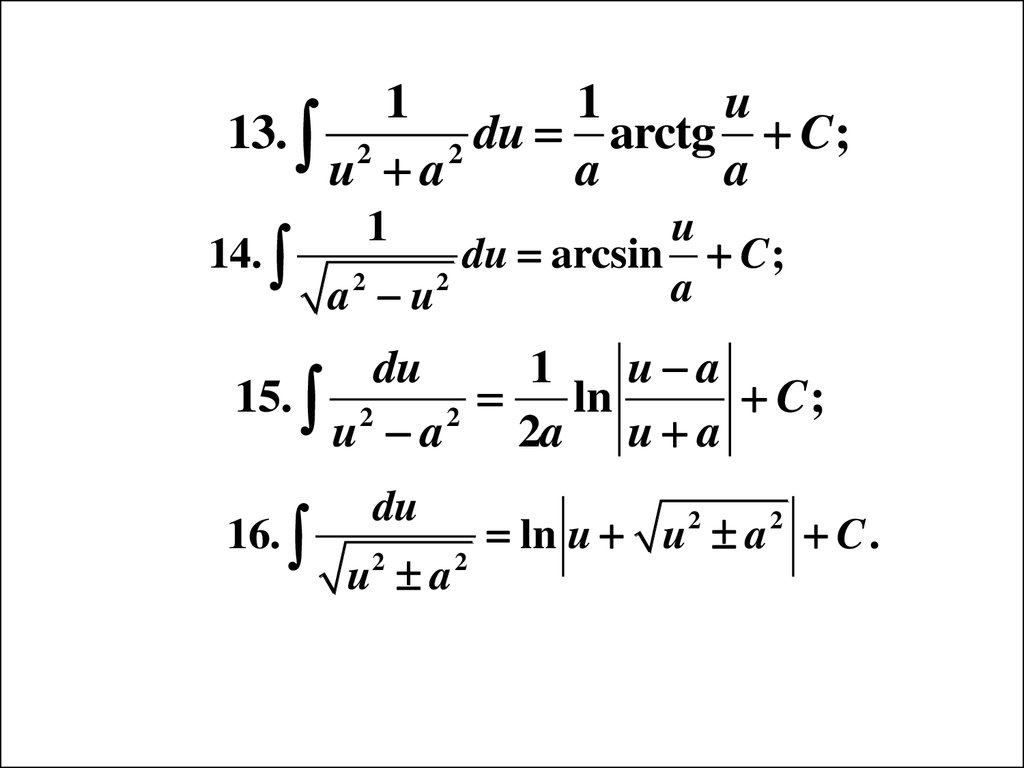

Для заданной функции $y=f(x)$ дифференциальным уравнением является уравнение, которое включает $y$, $x$ и производные от $y$. Например, простое дифференциальное уравнение: 92 + 123 456 789\) также имеет производную от $2x$. Дифференциальное уравнение $y’ = 2x$ имеет много решений. Это приводит нас к некоторым определениям.

Определение $\PageIndex{1}$: первообразные и неопределенные интегралы

Пусть задана функция $f(x)$. Первообразная функции $f(x)$ — это функция $F(x)$ такая, что $F'(x) = f(x)$.

Множество всех первообразных $f(x)$ есть неопределенный интеграл от $f$ , обозначаемый

$$\int f(x) \ dx.\]

Обратите внимание на наше определение: мы ссылаемся на как на первопроизводную $f$, в отличие от на первообразную $f$, поскольку всегда бесконечное число. Мы часто используем заглавные буквы для обозначения первообразных.

Зная одну первообразную $f$, мы можем найти бесконечно больше, просто добавляя константу. Это не только дает нам еще

первообразных, но и всех из них.

Теорема $\PageIndex{1}$: первообразные формы

Пусть $F(x)$ и $G(x)$ — первообразные $f(x)$. Тогда существует константа $С$ такая, что

$$G(x) = F(x) + C.\]

Для данной функции $f$ и одной из ее первообразных $F$ мы знаем , что все первообразных функции $f$ имеют вид $F(x) + C$ для некоторой константы $ С$. Используя определение $\PageIndex{1}$, мы можем сказать, что

$$\int f(x) \ dx = F(x) + C.\]

Давайте проанализируем это неопределенное целочисленное представление.

Рисунок $\PageIndex{1}$: Понимание обозначения неопределенного интеграла.

На рисунке $\PageIndex{1}$ показаны типичные обозначения неопределенного интеграла. Символ интегрирования $\int$ на самом деле представляет собой «удлиненную букву S», означающую «возьмите сумму». Позже мы увидим, как связаны суммы

и первообразных .

Функция, для которой мы хотим найти первообразную, называется подынтегральной функцией . Он содержит дифференциал переменной, по которой мы интегрируем. Символ $\int$ и дифференциал $dx$ не являются «форзацами» с зажатой между ними функцией; скорее, символ $\int$ означает «найти все первообразные следующего за ним», а функции $f(x)$ и $dx$ перемножаются; $dx$ не «просто сидит там».

Давайте попрактикуемся в использовании этих обозначений.

Пример $\PageIndex{1}$: вычисление неопределенных интегралов

Вычислить $\displaystyle \int \sin x\ dx.$

Решение

Нас просят найти все функции $F(x)$ такие, что $F'(x) = \sin Икс$. Некоторое размышление приведет нас к одному решению: $F(x) = -\cos x$, потому что $\frac{d}{dx}(-\cos x) = \sin x$.

Таким образом, неопределенный интеграл от $\sin x$ равен $-\cos x$ плюс постоянная интегрирования. Итак:

$$\int \sin x \ dx = -\cos x + C. \]

Часто задаваемый вопрос: «Что случилось с $dx$?» Непросветленный ответ: «Не беспокойтесь об этом. Это само пройдет». Полное понимание включает следующее.

Этот процесс антидифференциации действительно решает дифференциальный вопрос. Интеграл

$$\int \sinx\dx\]

представляет нам дифференциал $dy = \sin x\ dx$. Он спрашивает: «Что такое $y$?» Мы нашли множество решений, все вида $y = -\cos x+C$.

Пусть $dy = \sin x\ dx$, переписать

$$\int \sin x \ dx \quad \text{as}\quad \int dy.\]

Это вопрос: «Какие функции имеют дифференциал вида $dy$?» Ответ: «Функции вида $y+C$, где $C$ — константа». Что такое $у$? У нас есть много вариантов, все они отличаются на константу; самый простой выбор — $y = -\cos x$. 92+4х+5\).

Этот последний шаг «проверки нашего ответа» важен как с практической, так и с теоретической точки зрения. В общем, брать производные легче, чем находить первообразные, поэтому проверять нашу работу легко и важно по мере обучения.

Мы также видим, что производная от нашего ответа возвращает функцию под интегралом. Таким образом, мы можем сказать, что:

$$\frac{d}{dx}\left(\int f(x)\ dx\right) = f(x).\]

Дифференциация «отменяет» работу антидифференцировки.

Теорема 27 дала список производных общих функций, которые мы узнали к тому моменту. Мы повторяем здесь часть этого списка, чтобы подчеркнуть взаимосвязь между производными и первообразными. Этот список также будет полезен в качестве глоссария общих первообразных производных по мере нашего изучения.

Теорема $\PageIndex{2}$: производные и первообразные

92\большой)\)). Пример:

$$\int 5\cos x\ dx = 5\cdot\int \cos x\ dx = 5\cdot (\sin x+C) = 5\sin x + C.$$
На последнем шаге мы можно считать, что константа также умножается на 5, но «5 умножить на константу» все еще остается константой, поэтому мы просто пишем «$C$». 2+5x+C \end{выравнивание}\] 90+C\)»; скорее см. Правило №14.

Мы представляем антидифференцировку как «операцию, обратную» дифференцировке. Вот полезная цитата для запоминания: «Обратные операции делают противоположные вещи в обратном порядке».
При построении производной с помощью Степенного правила мы сначала умножаем на степень, затем секунд вычитаем из степени 1. Чтобы найти первообразную, выполните противоположные действия в обратном порядке: сначала прибавить единицу к степени, затем секунд разделить на степень.

Обратите внимание, что Правило №14 включает абсолютное значение $x$. Упражнения помогут читателю понять, почему это так; на данный момент знайте, что абсолютное значение важно и его нельзя игнорировать.

Задачи с начальными значениями

В разделе 2.3 мы видели, что производная функции положения дает функцию скорости, а производная функции скорости описывает ускорение. Теперь мы можем пойти «другим путем»: первообразная функции ускорения дает функцию скорости и т. д. Хотя существует только одна производная данной функции, существует бесконечное количество первообразных. Поэтому мы не можем спрашивать: «Что такое 92\). В момент времени $t=3$ падающий объект имел скорость $-10$ футов/с. Найдите уравнение скорости тела.

Решение

Мы хотим знать функцию скорости $v(t)$. Мы знаем две вещи:

Ускорение, т. е. $v'(t)=-32$, и
скорость в конкретный момент времени, т. е. $v(3) = -10$.

Используя первую часть информации, мы знаем, что $v(t)$ является первообразной $v'(t)=-32$. Итак, начнем с нахождения неопределенного интеграла от $-32$:

$$\int (-32)\ dt = -32t+C=v(t).\]

Теперь воспользуемся тем, что $v(3)=-10$, чтобы найти \(C\ ):

\[\begin{align} v(t) &= -32t+C \\ v(3) &= -10 \\ -32(3)+C &= -10\\ C &= 86 \end{align}\]

Таким образом, $v(t)= -32t+86$. Мы можем использовать это уравнение, чтобы понять движение объекта: когда $t=0$, объект имел скорость $v(0) = 86$ фут/с. Поскольку скорость положительна, объект двигался вверх.

Когда объект начал двигаться вниз? Сразу после $v(t) = 0$:

$$-32t+86 = 0 \quad \Rightarrow\quad t = \frac{43}{16} \приблизительно 2,69\text{s}.\]

Признать, что мы можем довольно много определить о путь объекта, зная только его ускорение и скорость в один момент времени.

Пример $\PageIndex{4}$: Решение задач с начальными значениями

Найти $f(t)$, учитывая, что $f»(t) = \cos t$, $f’ (0) = 3$ и $f(0) = 5$.

Решение

Начнем с нахождения $f'(t)$, которая является первообразной $f»(t)$:

$$\int f»(t)\ dt = \int \cos t\ dt = \sin t + C = f'(t).\]

Итак, $f'(t) = \sin t+C$ для правильного значения $C$. Нам дано, что $f'(0) = 3$, поэтому:

$$f'(0) = 3 \quad \Rightarrow \quad \sin 0+C = 3 \quad \Rightarrow \quad C= 3. \]

Используя начальное значение, мы нашли $f'(t) = \sin t+ 3.$

Теперь найдем $f(t)$ путем повторного интегрирования.

$$f(t)=\int f'(t) \ dt = \int (\sin t+3)\ dt = -\cos t + 3t + C.\]

Нам дано, что $ f(0) = 5$, поэтому

\[\begin{align} -\cos 0 + 3(0) + C &= 5 \\ -1 + C &= 5\\ C &= 6 \end{align}\]

Таким образом $ f(t) = -\cos t + 3t + 6$.

В этом разделе представлены первообразные и неопределенный интеграл. Мы обнаружили, что они необходимы при поиске функции с учетом информации о ее производной (производных). Например, мы нашли функцию положения по заданной функции скорости.

Авторы и ссылки

Грегори Хартман (Вирджинский военный институт). Свой вклад внесли Трой Симерс и Димплекумар Чалишаяр из VMI, а также Брайан Хейнольд из Университета Маунт-Сент-Мэри. Авторские права на этот контент защищены некоммерческой лицензией Creative Commons Attribution (BY-NC). http://www.apexcalculus.com/
Интегрировано Джастином Маршаллом.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Грегори Хартман (Вершина)
Лицензия
CC BY-NC
Показать страницу TOC
нет
Теги
1. производная
2. постоянное множественное правило
3. Правило различия
4. независимая переменная
5. силовое правило
6. Правило суммы

Антипроизводные APEX и неопределенное интегрирование

Рисунок 5.

1.1. Видео-введение в раздел 5.1

. Для заданной функции $y=f(x)\text{,}$ дифференциальное уравнение – это уравнение, которое включает $y\text{,}$ $x\text{ ,}$ и производные от $y\text{.}$ Например, простое дифференциальное уравнение:

\begin{уравнение*} у’ = 2x\текст{.} \end{уравнение*}

Решение дифференциального уравнения сводится к нахождению функции $y$, удовлетворяющей данному уравнению. Найдите минутку и рассмотрите это уравнение; можете ли вы найти функцию $y$ такую, что $y’ = 2x\text{?}$ 92 + 123{,}456{,}789\) также имеет производную от $2x\text{.}$ Дифференциальное уравнение $y’ = 2x$ имеет много решений. Это приводит нас к некоторым определениям.

Определение 5.1.2. Первообразные и неопределенные интегралы.

Пусть задана функция $f(x)$. Первообразная функции $f(x)$ — это функция $F(x)$ такая, что $\Fp(x) = f(x)\text{.}$

Множество всех первообразных $f(x)$ есть неопределенный интеграл от $f\text{,}$, обозначаемый

\begin{уравнение*} \int f(x) \,dx\text{. } \end{уравнение*}

Рисунок 5.1.3. Видеопрезентация определения 5.1.2

Обратите внимание на наше определение: мы ссылаемся на как на первопроизводную $f\text{,}$, а не на как на первопроизводную $f\text{,}$. ) так как всегда бесконечное количество. Мы часто используем заглавные буквы для обозначения первообразных.

Когда $f$ непрерывна, знание одной первообразной $f$ позволяет нам найти бесконечно больше, просто добавляя константу. Это не только дает нам еще первообразных, это дает нам всех из них. Это следствие теоремы дифференцирования о среднем значении, и мы уже встречались с этим результатом в теореме 3.2.11. Этот факт достаточно важен, чтобы мы переформулировали его, используя наш новый первообразный язык и обозначения.

Теорема 5.1.4. Антипроизводные формы.

Пусть $F(x)$ и $G(x)$ — первообразные непрерывной функции $f(x)$ на отрезке $I\text{.}$. Тогда существует постоянная $C$ такая, что на $I\text{,}$

\begin{уравнение*} G(x) = F(x) + C\text{. } \end{equation*}

Для заданной непрерывной функции $f$, заданной на интервале $I$, и одной из ее первообразных $F\text{,}$ мы знаем всех первообразных $ f$ на $I$ имеют вид $F(x) + C$ для некоторой константы $C\text{.}$ Используя определение 5.1.2, мы можем сказать, что

\begin{уравнение*} \int f(x) \,dx = F(x) + C \text{.} \end{уравнение*}

Давайте проанализируем это неопределенное целочисленное представление.

Рисунок 5.1.5. Первообразная запись

На рис. 5.1.5 показаны типичные обозначения неопределенного интеграла. Символ интегрирования $\int\text{,}$ на самом деле представляет собой «удлиненную букву S», означающую «возьмите сумму». Позже мы увидим, как связаны суммы и первообразных .

Функция, для которой мы хотим найти первообразную, называется подынтегральной функцией . Он содержит дифференциал переменной, по которой мы интегрируем. Символ $\int$ и дифференциал $dx$ не являются «подставками для книг», между которыми зажата функция; скорее, символ $\int$ означает «найти все первообразные следующего за ним», а функции $f(x)$ и $dx$ перемножаются; $dx$ не «просто сидит там».

Другим важным аспектом $dx$ является то, что он говорит нам, по какой переменной мы берем первообразную, во многом подобно тому, как $\lzo{x}$ означало бы брать производную по \ (x\text{,}\), а $\lzo{t}$ будет производной по отношению к $t\text{.}$

Давайте попрактикуемся в использовании этих обозначений.

Пример 5.1.6. Вычисление неопределенных интегралов.

Вычислить $\int \sin(x) \,dx\text{.}$

Решение.

Нас просят найти все функции $F(x)$ такие, что $\Fp(x) = \sin(x)\text{.}$ Некоторые размышления приведут нас к одному решению: $ F(x) = -\cos(x)\text{,}$, поскольку $\lzoo{x}{-\cos(x)} = \sin(x)\text{.}$

Таким образом, неопределенный интеграл от $\sin(x)$ равен $-\cos(x)\text{,}$ плюс постоянная интегрирования. Итак:

\begin{equation*} \int \sin(x) \,dx = -\cos(x) + C\text{.} \end{equation*}

Часто задаваемый вопрос: «Что случилось с $dx\text{?}$?» Неосведомленный ответ: «Не беспокойтесь об этом. Просто уходит». Полное понимание включает следующее.

Этот процесс антидифференцирования действительно решает дифференциал вопрос. Интеграл

\begin{уравнение*} \целое \sin(x) \,dx \end{уравнение*}

представляет нам дифференциал, $dy = \sin(x) \, dx\text{.}$ Он спрашивает: «Что такое $y\text{?}$». Мы нашли множество решений, все формы $y = -\cos(x) +C\text{.}$

Переписывание $dy = \sin(x)\,dx\text{,}$

\begin{уравнение*} \int \sin(x) \,dx \text{ as } \int\,dy\text{.} \end{уравнение*}

Это вопрос: «Какие функции имеют дифференциал вида $dy\text{?}$?» Ответ: «Функции вида $y+C\text{,}$, где $C\ ) является константой». Что такое \(y\text{?}$ У нас есть много вариантов, каждый из которых отличается константой; самый простой выбор: $y = -\cos(x)\text{.}$ 92+4x+5\text{.}\)

\begin{уравнение*} \lzoo{x}{\int f(x)\,dx} = f(x)\text{.} \end{уравнение*}

Дифференциация «отменяет» работу антидифференцировки.

Теорема 2.7.17 дала список производных общих функций, которые мы узнали на тот момент. Мы повторяем здесь часть этого списка, чтобы подчеркнуть взаимосвязь между производными и первообразными. Этот список также будет полезен в качестве глоссария общих первообразных производных по мере нашего изучения.

Теорема 5.1.8. Производные и антипроизводные.

Вот Общие правила дифференциации и их аналоги Общие неопределенные интегральные правила.

\начать{выравнивать*} \amp\lzoo{x}{cf(x)}=c\cdot\fp(x)\amp\amp\int c\cdot f(x)\,dx= c\cdot \int f(x)\, дх\\ \amp\lzoo{x}{f(x)\pm g(x)} =\fp(x)\pm g'(x)\amp\amp \int \big(f(x)\pm g(x) )\big)\,dx =\int f(x)\,dx\pm \int g(x)\,dx\\ \amp\lzoo{x}{C} = 0\amp\amp \int 0\,dx = C\\ \amp\lzoo{x}{x} = 1\amp\amp \int 1\,dx = \int dx = x+C\\ \amp\lzoo{x}{x^n} = n\cdot x^{n-1}\amp\amp \int x^n\,dx =\frac{1}{n+1}x^{n +1}+ C\quad(n\neq -1)\\ \amp\lzoo{x}{\sin(x)} = \cos(x)\amp\amp\int \cos(x) \,dx = \sin(x) +C\\ \amp\lzoo{x}{\cos(x)} = -\sin(x)\amp\amp \int \sin(x) \,dx = -\cos(x) +C\\ \amp\lzoo{x}{\tan(x)} = \sec^2(x)\amp\amp \int \sec^2(x) \,dx = \tan(x) +C\\ \amp\lzoo{x}{\csc(x)} = -\csc(x) \cot(x)\amp\amp \int \csc(x) \cot(x) \,dx = -\csc( х) +С\\ \amp\lzoo{x}{\sec(x)} = \sec(x) \tan(x)\amp\amp\int \sec(x) \tan(x) \,dx = \sec(x) +С\\ \amp\lzoo{x}{\cot(x)} = -\csc^2(x)\amp\amp \int \csc^2(x) \,dx = -\cot(x) +C\\ \amp\lzoo{x}{e^x} = e^x\amp\amp\int e^x\,dx = e^x+C\\ \amp\lzoo{x}{a^x} = \ln(a) \cdot a^x\amp\amp \int a^x\,dx = \frac{1}{\ln(a)}\cdot а^х+С\\ \amp\lzoo{x}{\ln(x)} = \frac1 x,\ x \gt 0\amp\amp \int \frac{1}x\,dx = \ln\abs{x}+C \end{выравнивание*} 92}\)). Пример:

\begin{уравнение*} \int 5\cos(x) \,dx = 5\cdot\int \cos(x) \,dx = 5\cdot (\sin(x) +C) = 5\sin(x) + C\text{ .} \end{уравнение*}

На последнем шаге мы можем считать, что константа также умножается на 5, но «5 умноженная на константу» все еще является константой, поэтому мы просто пишем «$C$».

\begin{уравнение*} \int \big(f(x)\pm g(x)\big)\,dx =\int f(x)\,dx\pm \int g(x)\,dx \end{уравнение*}

Это правило суммы/разности: мы можем разбивать интегралы на части, когда подынтегральная функция содержит члены, которые добавляются/вычитаются, как мы делали в примере 5.1.7. Итак: 90+С\)”; скорее смотрите последнее правило из списка.

Мы представляем антидифференцировку как «операцию, обратную» дифференцировке. Вот полезная цитата для запоминания:

«Обратные операции выполняют противоположные действия в обратном порядке».

При построении производной с помощью Степенного правила мы сначала умножаем на степень, затем секунду вычитаем из степени $1$. 2}} — (\sqrt{x} + 2)(x — 5) dx\) 92 — 10х\вправо) + С \end{выравнивание*}

Подраздел 5.1.1 Проблемы с начальным значением

В разделе 2.3 мы видели, что производная функции положения дает функцию скорости, а производная функции скорости описывает ускорение. Теперь мы можем пойти «другим путем»: первообразная функции ускорения дает функцию скорости и т. д. Пока есть только одна производная данной функции, первообразных бесконечно много. Поэтому мы не можем спрашивать: «Что такое скорость объекта, ускорение которого равно -32 ^футов ⁄ _{с ²} ?», поскольку существует более одного ответа.

Мы можем найти ответ , если вместе с вопросом предоставим дополнительную информацию, как это сделано в следующем примере. Часто дополнительная информация поступает в виде начального значения , значения функции, которое известно заранее.

Пример 5.1.10.

Найдите функцию $f(x)$ такую, что 92+\cos(x)+1\text{. }\)

Пример 5.1.12. Решение задач с начальными значениями.

Ускорение свободного падения падающего объекта составляет -32 ^футов ⁄ _{с ²} . В момент времени $t=3\text{,}$ падающий объект имел скорость -10 ^футов ⁄ _с . Найдите уравнение скорости тела.

Решение.

Мы хотим знать функцию скорости, $v(t)\text{.}$ Мы знаем две вещи:

Ускорение, т. е. $v'(t)= -32\text{ ,}$ и
скорость в определенное время, т. е. $v(3) = -10\text{.}$

Используя первую часть информации, мы знаем, что $v(t)$ является первообразной $v'(t)=-32\text{.}$. Итак, мы начнем с нахождения неопределенного интеграла от $-32\текст{:}$

\begin{уравнение*} \int (-32)\,dt = -32t+C=v(t)\text{.} \end{equation*}

Теперь мы используем тот факт, что $v(3)=-10$, чтобы найти $C\text{:}$

\begin{align*} v(t) \amp = -32t+C\\ v(3) \ампер = -10\\ -32(3)+С \amp = -10\\ С \амп = 86 \end{выравнивание*}

Таким образом, $v(t)= -32t+86\text{. }$ Мы можем использовать это уравнение, чтобы понять движение объекта: когда $t=0\text{,}$ объект скорость $v(0) = 86$ ^футов ⁄ _с . Поскольку скорость положительна, объект двигался вверх.

Когда объект начал двигаться вниз? Сразу после $v(t) = 0\text{:}$

\begin{equation*} -32t+86 = 0 \подразумевается t = \frac{43}{16} \приблизительно 2,69\text{s}\text{.} \end{equation*}

Признайте, что мы можем довольно многое определить о пути объекта, зная только его ускорение и скорость в определенный момент времени.

Пример 5.1.13. Решение задач с начальными значениями.

Найдите $f(t)\text{,}$ при условии, что $\fpp(t) = \cos(t)\text{,}$ $\fp(0) = 3$ и \ (ф(0) = 5\текст{.}\)

Решение.

Начнем с нахождения $\fp(t)\text{,}$, которая является производной от $\fpp(t)\text{:}$

\begin{align*} \int \fpp(t)\,dt \amp = \int \cos(t) \,dt\\ \amp = \sin(t) + C\\ \amp = \fp(t)\text{. } \end{align*}

Итак, $\fp(t) = \sin(t) +C$ для правильного значения $C\text{.}$ Нам дано, что $\fp( 0) = 3\текст{,}$ итак:

\begin{выравнивание*} \sin(0) +C \amp = 3\\ C \амп = 3\текст{.} \end{align*}

Используя начальное значение, мы нашли $\fp(t) = \sin(t) + 3\text{.}$ Теперь найдем $f(t)$ по снова интегрирование. Мы будем использовать другую константу интегрирования, так как мы уже определили $C$ равным $3$ выше.

\begin{уравнение*} f(t)=\int \fp(t) \,dt = \int (\sin(t) +3)\,dt = -\cos(t) + 3t + D\text{.} \end{equation*}

Нам дано, что $f(0) = 5\text{,}$ поэтому

\begin{align*} -\cos(0) + 3(0) + D \амп = 5\\ -1 + С \амп = 5\\ С \ ампер = 6 \end{выравнивание*}

Таким образом, $f(t) = -\cos(t) + 3t + 6\text{.}$

В этом разделе вводятся первообразные и неопределенный интеграл. Мы обнаружили, что они необходимы при поиске функции с учетом информации о ее производной (производных). Например, мы нашли функцию скорости по заданной функции ускорения.

В следующем разделе мы увидим, как положение и скорость неожиданно связаны площадями определенных областей на графике функции скорости. Затем, в разделе 5.4, мы увидим, как тесно связаны друг с другом площади и первообразные. Эта связь невероятно важна, на что указывает название теоремы, описывающей ее: Основная теорема исчисления.

Упражнения 5.1.2 Упражнения

Термины и понятия

1.

Дайте определение термину «первообразная» своими словами.

2.

Что более точно: «тот» первообразный $f(x)$ или «некий» первообразный $f(x)\text{?}$

3.

Используя свои слова, определите неопределенный интеграл от $f(x)\text{.}$

4.

Заполните пропуски: «Обратные операции выполняют действия по порядку».

5.

Что такое «задача начального значения»?

6.

Производная функции положения является функцией.

7.

Первообразная функции ускорения есть функция.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

Общие правила дифференцирования

Общие неопределенные правила интеграции