Задачи на вычисление площадей плоских фигур 11 класс онлайн-подготовка на Ростелеком Лицей
1. Повторение основных правил вычисления площадей плоских фигур
Повторение
Повторение начнем с основного определения. Что такое первообразная?
1. Определение. Функцию называют первообразной для функции на заданном промежутке , если для всех из выполняется равенство .
Пример. Мы умеем дифференцировать функцию .
Значит,
2. Основная задача интегрального исчисления:
Найти , зная – скорость ее изменения.
3. Если – одно из решений задачи, то – множество всех ее решений.
. Все это множество называется неопределенным интегралом.
Итак, нахождение первообразной – это восстановление функции по ее скорости.
Если физический прибор дает скорость, а мы находимся на борту или в автобусе, или в автомобиле и умеем интегрировать, то мы найдем путь. Если прибор дает ускорение, а мы умеем интегрировать, то мы найдем скорость. А если мы скорость проинтегрируем, мы получим расстояние. Если проинтегрировать по 3-м осям, то мы можем знать месторасположение летательного аппарата в каждый момент времени.
А если мы скорость проинтегрируем, мы получим расстояние. Если проинтегрировать по 3-м осям, то мы можем знать месторасположение летательного аппарата в каждый момент времени.
4. Формула Ньютона-Лейбница. Нахождение площади криволинейной трапеции, ограниченной графиком функции и тремя прямыми. Рис. 1.
Рис. 1. Нахождение площади криволинейной трапеции, ограниченной графиком функции и тремя прямыми
Вспомним, как мы искали площадь:
Разбили отрезок на одинаковых отрезков, заменили искомую площадь площадью поступенчатой ломаной, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили в пределе и
этот предел назвали определенным интегралом и обозначили его .
Таким образом, мы определили площадь, но еще находить ее численно не умели.
Как же мы численно смогли найти площадь криволинейной трапеции?
Рис. 2. Функция S(x)
Ввели функцию . Рис. 2. Каждому площадь под соответствующей частью кривой .
Мы доказали, что производная этой же функции . Значит – первообразная. И – приращение первообразных на отрезке То есть, можно взять первообразную в точке и отнять первообразную в точке . И таким образом получить формулу .
Значит – первообразная. И – приращение первообразных на отрезке То есть, можно взять первообразную в точке и отнять первообразную в точке . И таким образом получить формулу .
Итак, нахождение площади криволинейной трапеции – важное применение первообразной.
5. Выпишем формулу для вычисления площади криволинейной трапеции.
Найти площадь под кривой
. Рис. 3.
Площадь ищется следующим образом:
Рис. 3. Площадь под кривой
Повторим: Нужно найти одну из первообразных и взять пределы от a до b, – любая функция, важно, чтобы она была непрерывной
6. Далее с помощью первообразных мы научились находить площадь между двумя кривыми.
Постановка задачи: Найти площадь фигуры, ограниченной линиями.
Рис. 4.
Рис. 4. Площадь фигуры, ограниченной линиями
Площадь такой фигуры вычисляется следующим образом:
где – одна из первообразных разности .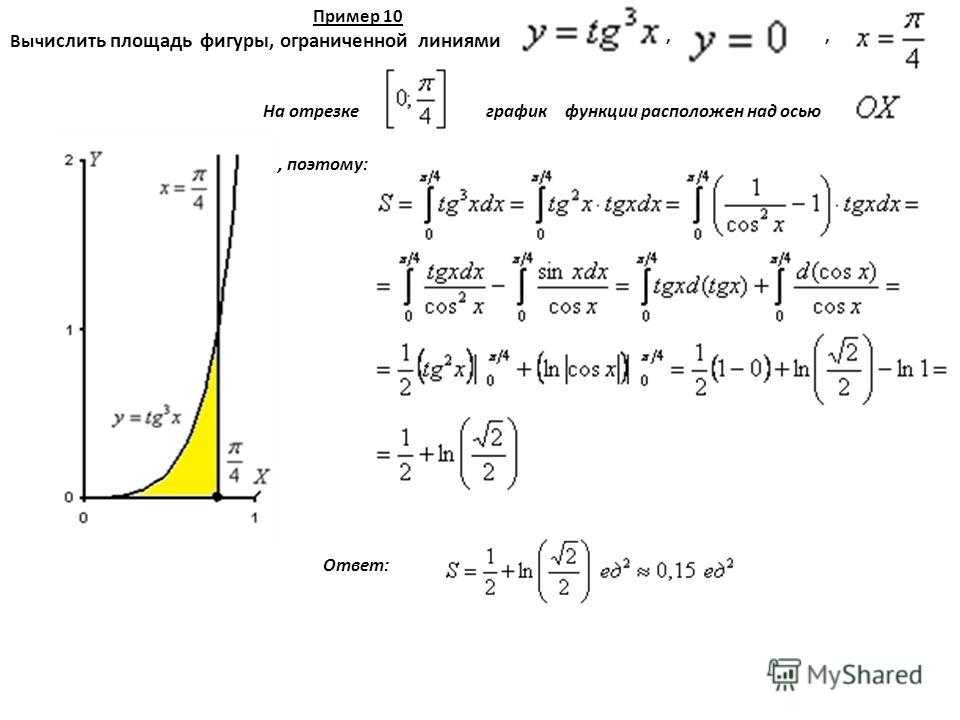
Таким образом, мы повторили опорные факты.
Перейдем к конкретным примерам и задачам на площадь. Вот первый из них:
2. Пример 1 — Задача вычислить площадь
Пример 1. Вычислите площадь фигуры, ограниченной линиями
. Рис. 5.
Рис. 5. Площадь фигуры, ограниченной линиями .
Решение.
В силу симметрии достаточно вычислить половину площади и удвоить ее. Так и поступим.
Искомая площадь:
Ответ:
3. Пример 2 — Задача вычислить площадь фигуры, ограниченной линиями
Пример 2. Вычислите площадь фигуры, ограниченной линиями
.
Рис. 6. Площадь фигуры, ограниченной линиями
Решение.
Речь идет о заштрихованной площади. Поступаем, как раньше. Сначала надо найти пределы интегрирования, то есть точки пересечения. Они легко находятся: это точки Значит, пределы интегрирования найдены. Площадь:
Площадь:
Ответ:
Следующая задача на площадь аналогичная, но решим ее по-иному.
4. Пример 3
Пример 3.
Вычислите площадь фигуры, ограниченной линиями
.
Решение.
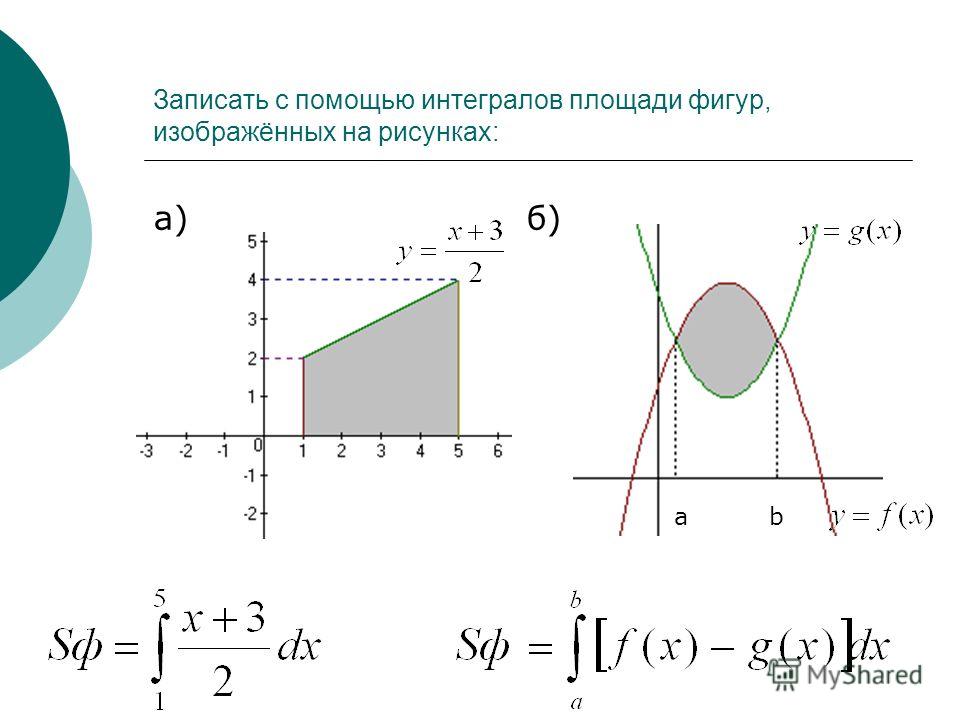
Сначала построим графики: рис. 7.
. График – парабола, ветви направлены вниз, корни . Вершина – .
График функции . Искомая площадь:
Рис. 7. Площадь фигуры, ограниченной линиями
Решим эту задачу следующим образом:
Сначала мы найдем площадь прямоугольника
Найдем площадь криволинейного треугольника
И вычтем площади. Получим искомую площадь.
Ответ:
Последнее действие
.
В следующей задаче имеем и кривую, и касательную к ней в точке.
5. Пример 4
Пример 4.
Вычислите площадь фигуры, ограниченной линиями:
Параболой , касательной к ней в точке с абсциссой , осью ;
Решение.
Итак, три линии образуют искомую площадь.
Первая линия, это известно.
Вторая – касательная в точке с абсциссой . Чтобы не отвлекаться от данной темы, мы воспользуемся данными предыдущих уроков, какая касательная была нами найдена .
Следующая прямая – ось . Получаем такую фигуру: рис. 8.
Рис. 8. Площадь фигуры, ограниченной линиями: параболой , касательной к ней в точке с абсциссой , осью
Находим ее площадь:
Пределы интегрирования: .
Ответ: .
Постановка следующей задачи нам уже известна.
6. Пример 5
Пример 5.
Найти массу неоднородного стержня , если плотность= sinx + 1. .
Решение.
Стержень помещен в координатной плоскости, как показано на рисунке:
Рис. 9. Стержень в координатной плоскости
В каждой точке плотность известна и меняется по закону= sinx + 1.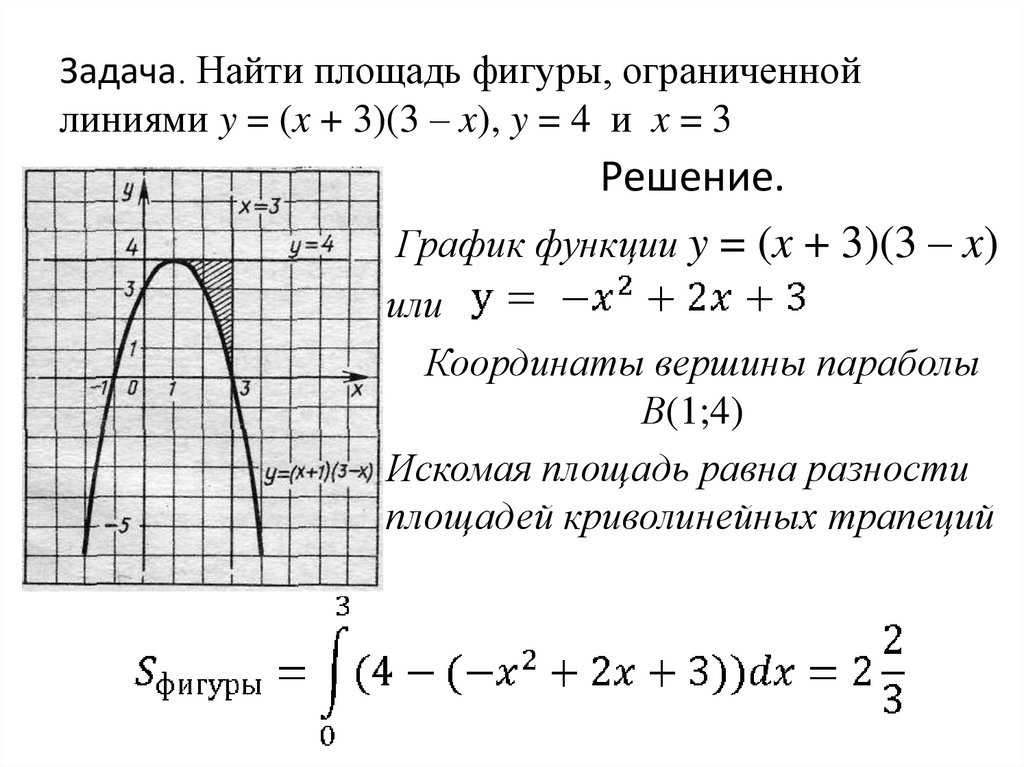 Чтобы найти массу, знаем, что надо найти площадь под этой плотностью. Площадь мы искать умеем:
Чтобы найти массу, знаем, что надо найти площадь под этой плотностью. Площадь мы искать умеем:
Ответ:
Следующая задача о движении точки по прямой.
7. Пример 6
Пример 6.
Найдите перемещение точки, если скорость меняется по закону . Рис. 10.
Решение.
Оси координат t,v:
Рис. 10. Перемещение точки
Нам нужно найти перемещение, значит, площадь под скоростью. Здесь задача настолько простая, что можно обойтись без интеграла.
Сделаем двумя способами:
С помощью интеграла:
Эту площадь можно найти как площадь прямоугольного треугольника:
Ответ:
Итак, мы рассмотрели задачи на вычисление площадей плоских фигур, далее перейдем к изучению корней и степеней.
Список литературы
- Мордкович А.
 Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Г. Алгебра и начала математического анализа. – М.: Мнемозина. - Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Mathprofi.ru (Источник).
- Dok.opredelim.com (Источник).
- School.xvatit.com (Источник).
Домашнее задание (задачи на площадь)
- Вычислить площадь фигуры, ограниченной графиком функции касательной к графику этой функции в точке и осью ординат.
- Вычислите массу участка стержня от , если его линейная плотность задается формулой
- Алгебра и начала анализа, Мордкович А.Г.: № 1018, 1026, 1027, 1038.
Вычисление площади поверхности / Двойной интеграл / 3dstroyproekt.
 2 } .$
2 } .$Далее:
Определение двойного интеграла
Механические приложения тройного интеграла
Теорема об аналоге СДНФ в Pk
Критерий полноты {формулировка}. Лемма о немонотонной функции
Введение
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Теорема об алгоритме распознавания полноты
Определение тройного интеграла. Теорема существования тройного интеграла
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Класс M. Теорема о замкнутости класса M
Скалярное поле, производная по направлению, градиент
Вычисление поверхностного интеграла первого рода
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному
Вычисление двойного интеграла. Двукратный интеграл
Двукратный интеграл
Класс $T_1$. Теорема о замкнутости класса $T_1$
Огравление $\Rightarrow $
23 сентября 2016, 09:39 проектирование км, кмд, кж Двойной интеграл 0 25695 0
Интегральный калькулятор | Лучшая онлайн-интеграция по частям Калькулятор
Знакомство с интегральным калькулятором
Наш усовершенствованный интегральный калькулятор — это наиболее полное интегральное решение в Интернете, с помощью которого вы можете выполнять множество операций интеграции. Вам нужно ввести функцию, переменную и границы, и все готово.
Калькулятор интегрирования с шагами позволяет изучить принципы расчета интегралов, не тратя слишком много времени. Вы можете вычислить интеграл, используя интегральный калькулятор с шагами, легко онлайн.
Точно так же вы можете найти калькулятор двойного интеграла на этом сайте. Калькулятор двойного интеграла показывает вам графики, графики, шаги и визуальное представление, что помогает вам изучить расширенные концепции двойного интегрирования.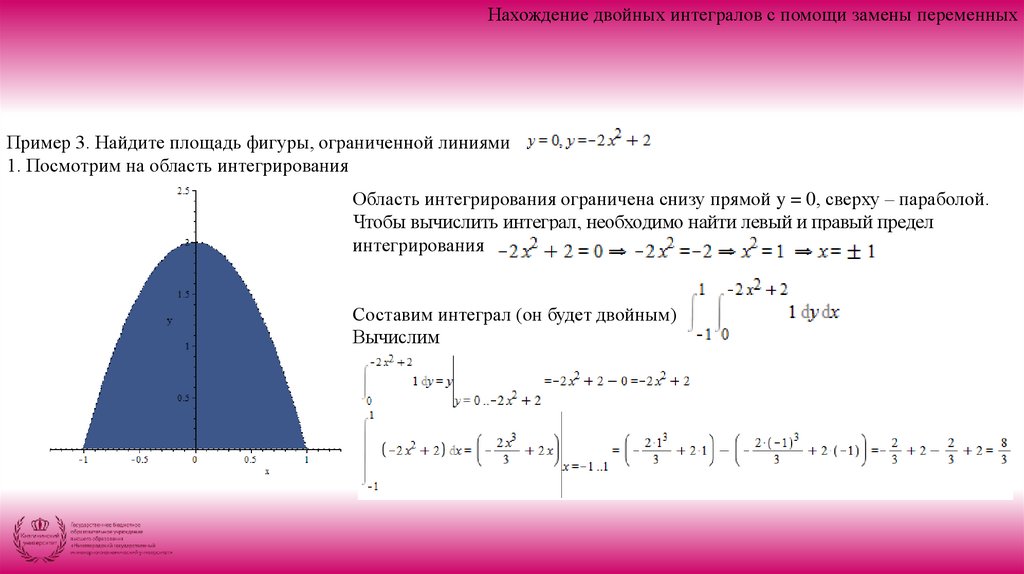
Есть много других полезных калькуляторов, которые можно использовать для получения выгоды. Точно так же вы можете определить объем тела вращения с помощью калькулятора метода шайбы и определить поперечные сечения тела вращения с помощью калькулятора метода диска.
Как решить Интеграция?
Чтобы найти определенный интеграл, вы должны сначала понять, что определенные интегралы имеют начальную и конечную точки, также известные как пределы или интервалы, представленные как (a,b) и расположенные сверху и снизу интеграла.
Мы можем обобщить интегралы на основе функций и областей, через которые выполняется интегрирование. Калькулятор интегрирования по частям с шагами помогает вычислять интегралы в цифровом виде.
Например, линейный интеграл выражается функциями двух или более переменных с заменой интервала интегрирования кривой, соединяющей две точки на интервале. 93$$
вычисление границ: 4
-3,4
-12
С другой стороны, неопределенный интеграл отличается от определенного из-за отсутствия у первого определенных пределов.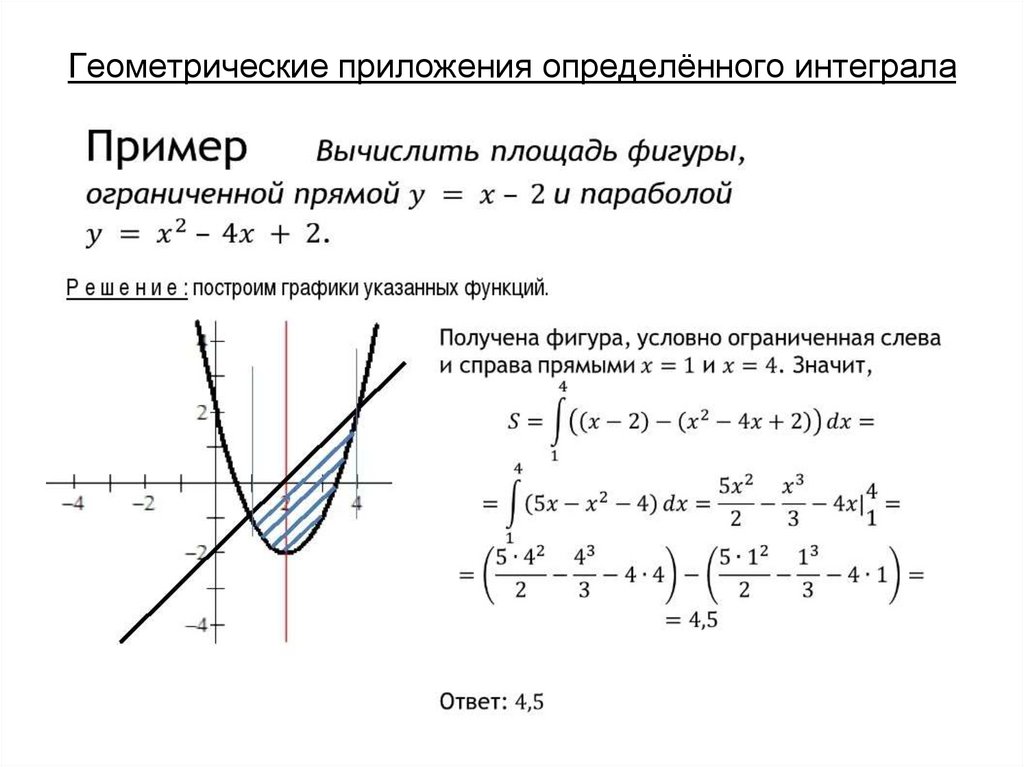
Неопределенный интеграл, таким образом, вычисляется по формуле:
$$\int f(x)dx$$
Вышеприведенный решатель интегрирования может вычислять неопределенный интеграл и определенный интеграл, но если вы хотите вычислить только неопределенный интеграл, найдите лучший Онлайн-калькулятор неопределенного интеграла.
Связанный: Найдите этот полезный блог, чтобы узнать об определенном интеграле и неопределенном интеграле
Как вычислить неправильный интеграл?
Одна из причин, по которой определенный интеграл становится несобственным, заключается в том, что один или оба предела достигают бесконечности. Калькулятор интегрального исчисления можно использовать для вычисления неправильных интегралов.
Этот интеграл затем решается путем превращения его в проблему пределов, где c случается приближаться к бесконечности или к отрицательной бесконечности. 9c$$
$$\lim_{c\to \infty} [-\frac {1}{c}] -(-\frac{1}{1})]$$
0+1
1
Поскольку ответ на несобственный интеграл конечен, мы считаем его сходящимся.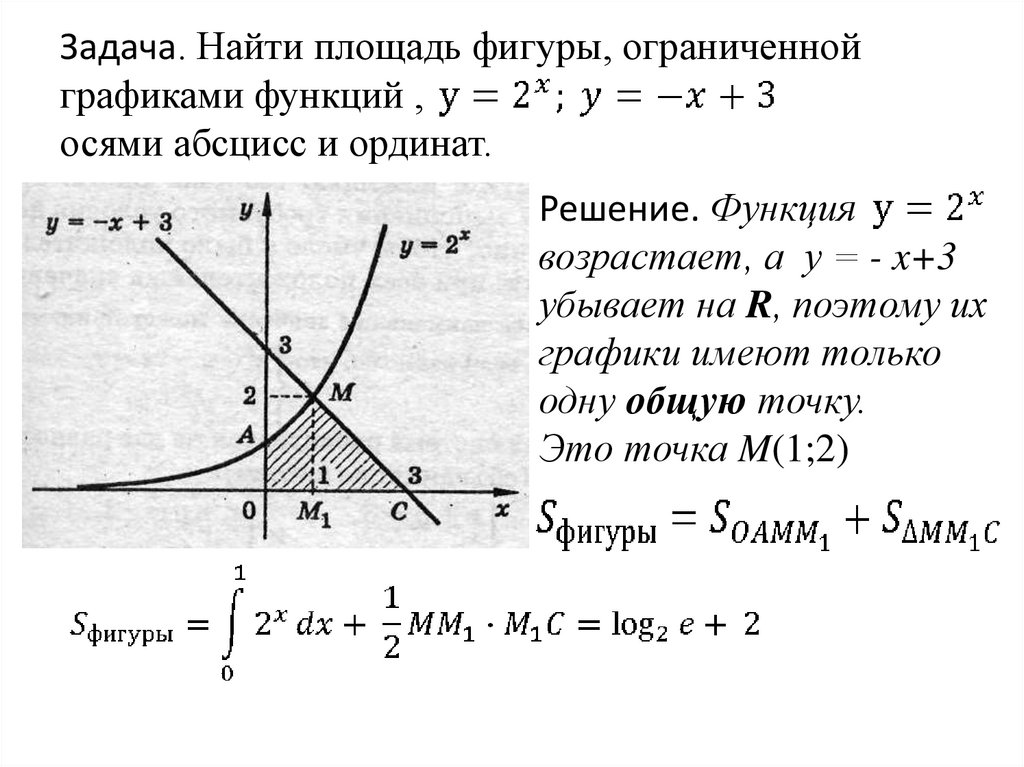
Если вы хотите вычислить только определенные интегралы, используйте этот лучший пошаговый онлайн-калькулятор определенных интегралов.
Связанный: Используйте калькулятор метода оболочки с шагами, чтобы легко найти объем тела вращения онлайн.
Как рассчитать непрерывную интеграцию?
Основная теорема исчисления устанавливает четкую связь между интегральным и дифференциальным исчислением. Наш интегральный калькулятор с шагами способен вычислить непрерывное интегрирование.
Если f(x) непрерывна для интервала a и b при заданной переменной x и G(x) является функцией в таком смысле, что dG/dx = f(x) для всех значений x в (a,b)
Пусть f непрерывна на интервале ‘y’. Выберите точку p в y, тогда функция f(x) будет определена как:
Пусть F(x) будет следующим 9c f(t)dt$$
Для вашего удобства и углубленного изучения множественных интегралов мы предлагаем один из самых быстрых калькуляторов тройных интегралов. Этот инструмент, несомненно, поможет вам вычислить определенные и неопределенные тройные интегралы онлайн, сделав несколько кликов.
Связанный: Понимание интегрирования неполной дробью за 5 минут!
Что такое интегральный калькулятор?
В течение многих лет существовал только один способ вычислить интегралы — вычисление вручную. В наши дни у нас есть много онлайн-калькуляторов интеграции, чтобы легко рассчитать стоимость интеграции. Большинство студентов обычно имеют прочные теоретические представления об исчислении. Таким образом, вычисление интегралов или производных на самом деле не проблема, когда у нас есть такие калькуляторы, как калькулятор интегрирования или калькулятор производных.
Однако это проблема, когда дело доходит до домашних заданий, когда ученики обычно получают массу задач, требующих решения интегралов. Для получения справки, пожалуйста, прочитайте статью, в которой говорится об интеграции, ее важности и различных методах.
Было бы неразумно повторно вычислять интегралы вручную. Калькулятор определенных интегралов удобен для решения сложных задач интегрирования.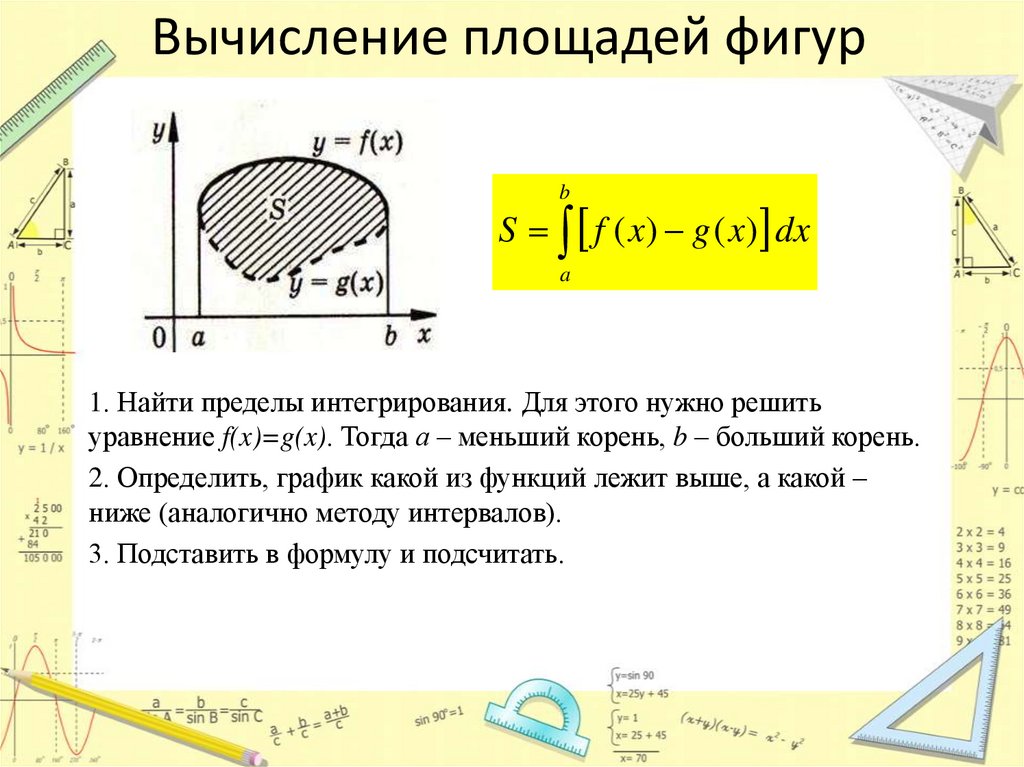 Он бесплатный и простой в использовании, и вы получаете ответ почти мгновенно, так как вы можете легко найти интегральный калькулятор с пошаговыми инструкциями в Интернете.
Он бесплатный и простой в использовании, и вы получаете ответ почти мгновенно, так как вы можете легко найти интегральный калькулятор с пошаговыми инструкциями в Интернете.
Также используйте другие полезные математические калькуляторы, которые важны для общих процессов интеграции. Подобно калькулятору преобразования Лапласа, вы можете преобразовать интеграл данной производной функции, а калькулятор преобразования Фурье позволяет преобразовать функцию времени в частоту.
Как найти лучший калькулятор интеграции?
В Интернете доступно множество интегральных калькуляторов, например, calculated, symbolab, wolframalpha и другие.
Однако наш интегральный калькулятор объема лучше, быстрее, обладает большей функциональностью и является лучшим калькулятором интеграции с пошаговыми инструкциями, доступными в Интернете. Узнайте о преимуществах использования нашего интегрального онлайн-калькулятора.
Когда вы вводите функцию, переменную, верхнюю и нижнюю границы пределов, наш интегральный решатель вычисляет интеграл и отображает все необходимые шаги, чтобы дать пользователю лучшее понимание вычисления интегрирования.
Вы также можете рассчитать интеграцию по вертикали и интеграцию по горизонтали в области кривых с помощью нашего интегрального онлайн-калькулятора с ограничениями.
Это еще не все. Наш интегральный решатель также отображает антипроизводные вычисления для пользователей, которые могут быть заинтересованы в математической концепции и шагах, связанных с интегрированием.
Кроме того, этот калькулятор интеграции по частям поставляется с визуализацией расчета с помощью интуитивно понятных графиков.
Связанный: Как найти объем тела вращения
Как использовать интегральный калькулятор с шагами?
Пользоваться калькулятором интегрирования по частям легко и быстро.
Выполните следующие шаги:
Шаг 1: Введите функцию
Для вычисления интегралов у вас должна быть правильная функция. Вам нужно ввести свою функцию в функциональную строку калькулятора интеграции. Существует также список «пример загрузки». Вы можете щелкнуть этот список, чтобы загрузить пример уравнения для пошагового расчета интегралов.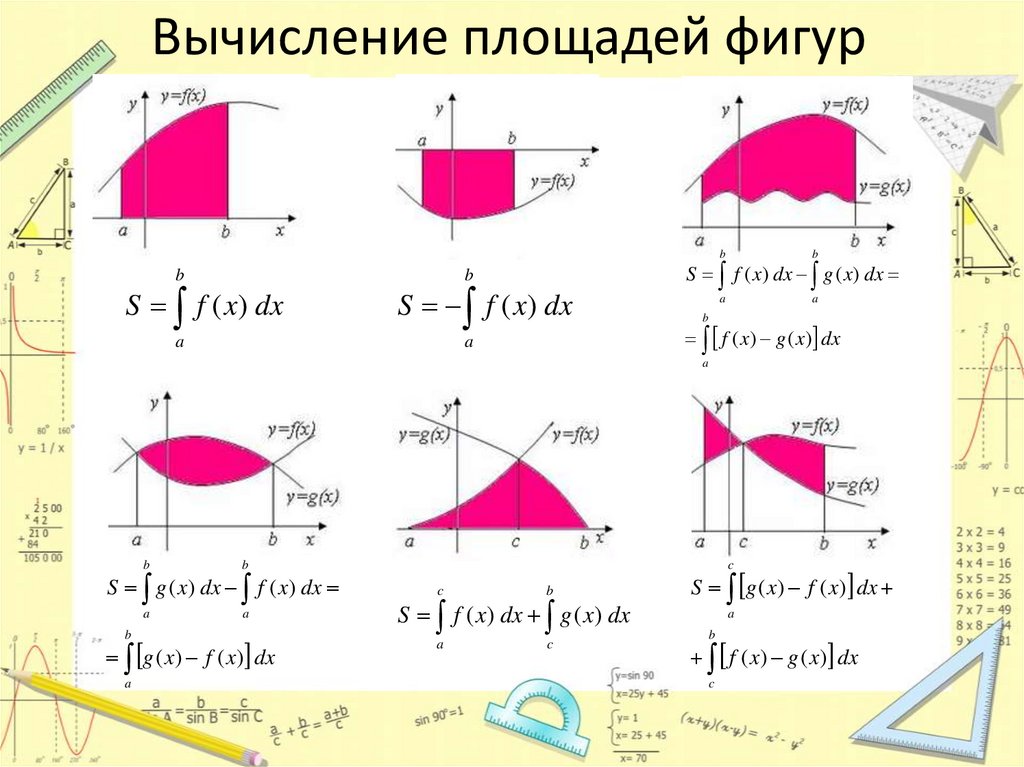
Шаг 2. Выберите переменную
Для вычисления интегралов можно использовать три переменные. Этими переменными являются x, y и z. Роль этих трех переменных отличается друг от друга, и все они по-разному влияют на общий результат. Вы можете выбрать переменные как x, y и z из раздела переменных.
Шаг 3: Дайте значение верхней границы
Верхняя граница — это значение, которое помогает нам суммировать интеграл при его максимальном значении. Верхняя граница обозначается как U, и ее определение имеет решающее значение в процессе интегрирования. Вы можете ввести верхнюю границу своего лимита в разделе верхней границы калькулятора верхней границы.
Шаг 4: Введите значение нижней границы
Нижняя граница — это наименьшее значение, которое мы установили для начала интегрирования. Чтобы получить точные результаты интегрирования, наименьшее значение интервала обозначается буквой L. Чтобы получить точные результаты интегрирования. Вам необходимо ввести фактическую сумму вашего нижнего лимита в разделе нижней границы калькулятора верхней и нижней границ.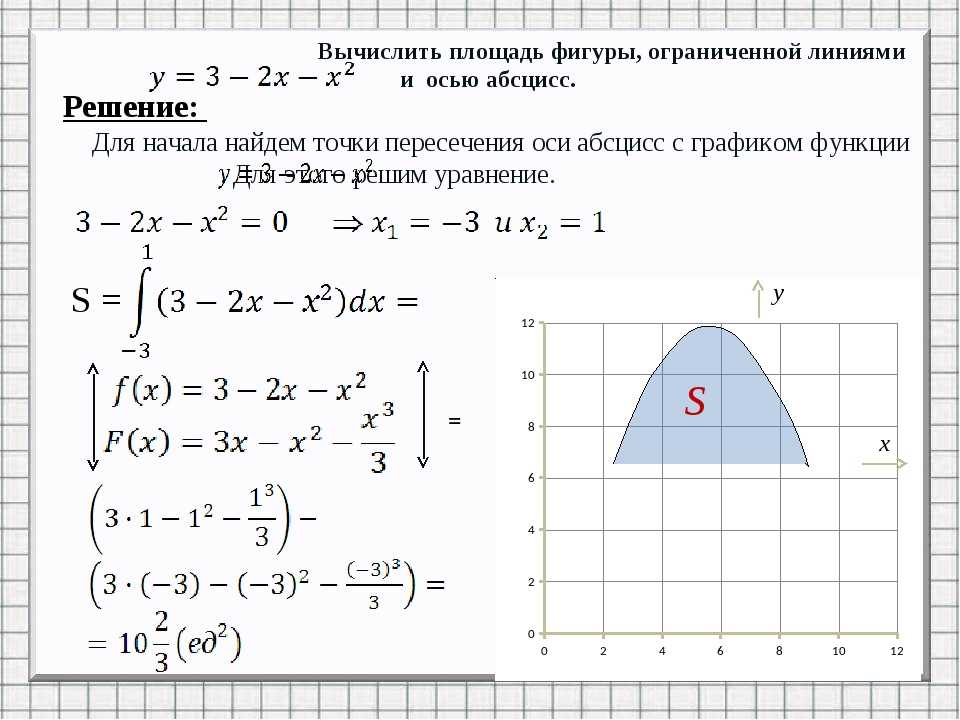
После выполнения всех вышеперечисленных шагов Нажмите кнопку «GO».
Сразу после нажатия на кнопку заработает наш интегральный калькулятор. Калькулятор интегрирования по частям покажет вам антипроизводную, интегральные шаги, дерево разбора и график вашего результата. Все эти функции и функции делают его лучшим калькулятором линейного интеграла для вычисления интеграла сложных задач интеграции.
По мере того, как вы вводите данные, под входными данными будет отображаться визуальное уравнение, где вы можете визуализировать, как ваши входные данные будут выглядеть в уравнении.
Часто задаваемые вопросы
Как вычислять интегралы?
Есть два типа интегралов, определенные и неопределенные интегралы. Вы можете решить их оба путем интеграции. Отличие состоит в том, что в определенных интегралах нужно ставить предельные значения после интегрирования, тогда как в неопределённых интегралах предельные значения ставить не нужно. 93 (1-х) дх \;=\; \left( 3 — \frac{9}{2} \right) \;-\; \влево( -4 -2 \вправо) \;=\; \frac{21}{2} $$
Итак, площадь под данной кривой равна 21/2.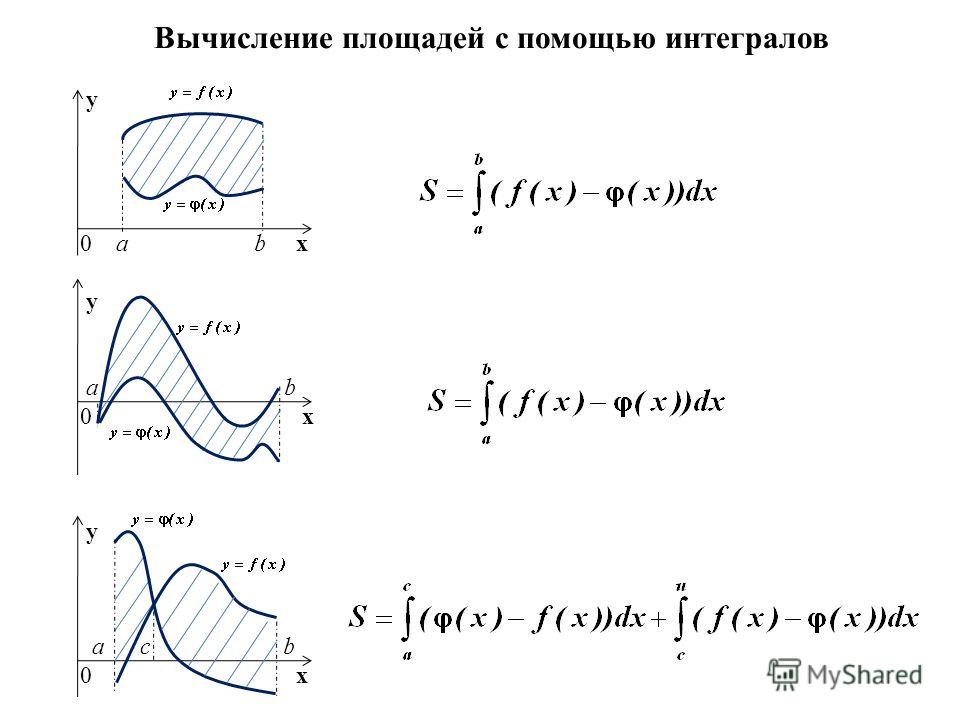 Мы можем убедиться в этом, оценив интегральный калькулятор для перекрестной проверки вашего ответа.
Мы можем убедиться в этом, оценив интегральный калькулятор для перекрестной проверки вашего ответа.
Калькулятор интеграла — отличный ресурс для вычислений такого типа, позволяющий сэкономить ваше время.
Чему равен интеграл от 1/x?
Интеграл от 1/x равен
$$ \int \frac{1}{x} dx \;=\; ln(x) + c $$
Получайте удовольствие от вычисления интегралов с помощью интегрального онлайн-калькулятора!
Другие онлайн-калькуляторы интеграции
На этом сайте есть много других пошаговых интегральных калькуляторов, которые вы можете использовать бесплатно. Эти инструменты:
- Калькулятор площади, ограниченной кривыми
- Калькулятор правил Симпсонов
- Калькулятор интеграла длины дуги
- Калькулятор длины дуги полярной кривой
- Калькулятор лимита суммы с шагами
Интегральный калькулятор | Лучшая онлайн-интеграция по запчастям Калькулятор
Знакомство с Калькулятором интегралов
Наш расширенный калькулятор интегралов — это наиболее полное решение для интегралов в Интернете, с помощью которого можно выполнять множество операций интегрирования.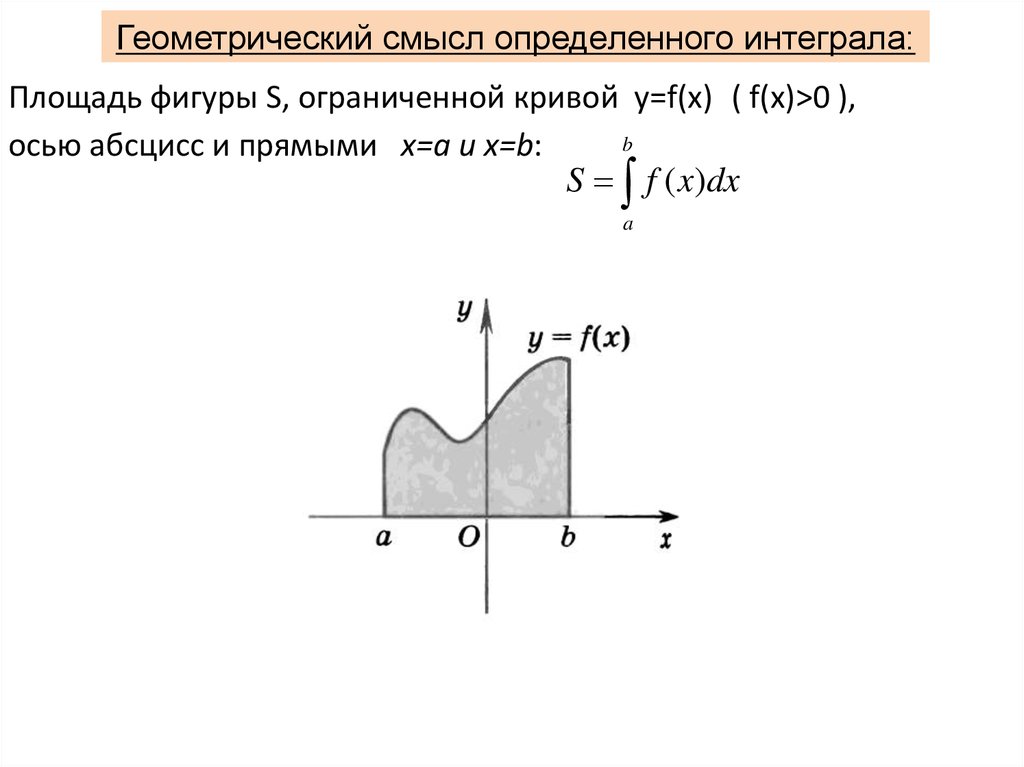 Вам нужно ввести функцию, переменную и границы, и все готово.
Вам нужно ввести функцию, переменную и границы, и все готово.
Калькулятор интегрирования с шагами позволяет изучить принципы расчета интегралов, не тратя слишком много времени. Вы можете вычислить интеграл, используя интегральный калькулятор с шагами, легко онлайн.
Точно так же вы можете найти калькулятор двойного интеграла на этом сайте. Калькулятор двойного интеграла показывает вам графики, графики, шаги и визуальное представление, что помогает вам изучить расширенные концепции двойного интегрирования.
Есть много других полезных калькуляторов, которые можно использовать для получения выгоды. Точно так же вы можете определить объем тела вращения с помощью калькулятора метода шайбы и определить поперечные сечения тела вращения с помощью калькулятора метода диска.
Как решить Интеграция?
Чтобы найти определенный интеграл, вы должны сначала понять, что определенные интегралы имеют начальную и конечную точки, также известные как пределы или интервалы, представленные как (a,b) и расположенные сверху и снизу интеграла.
Мы можем обобщить интегралы на основе функций и областей, через которые выполняется интегрирование. Калькулятор интегрирования по частям с шагами помогает вычислять интегралы в цифровом виде.
Например, линейный интеграл выражается функциями двух или более переменных с заменой интервала интегрирования кривой, соединяющей две точки на интервале. 93$$
вычисление границ: 4
-3,4
-12
С другой стороны, неопределенный интеграл отличается от определенного из-за отсутствия у первого определенных пределов.
Неопределенный интеграл, таким образом, вычисляется по формуле:
$$\int f(x)dx$$
Вышеприведенный решатель интегрирования может вычислять неопределенный интеграл и определенный интеграл, но если вы хотите вычислить только неопределенный интеграл, найдите лучший Онлайн-калькулятор неопределенного интеграла.
Связанный: Найдите этот полезный блог, чтобы узнать об определенном интеграле и неопределенном интеграле
Как вычислить неправильный интеграл?
Одна из причин, по которой определенный интеграл становится несобственным, заключается в том, что один или оба предела достигают бесконечности.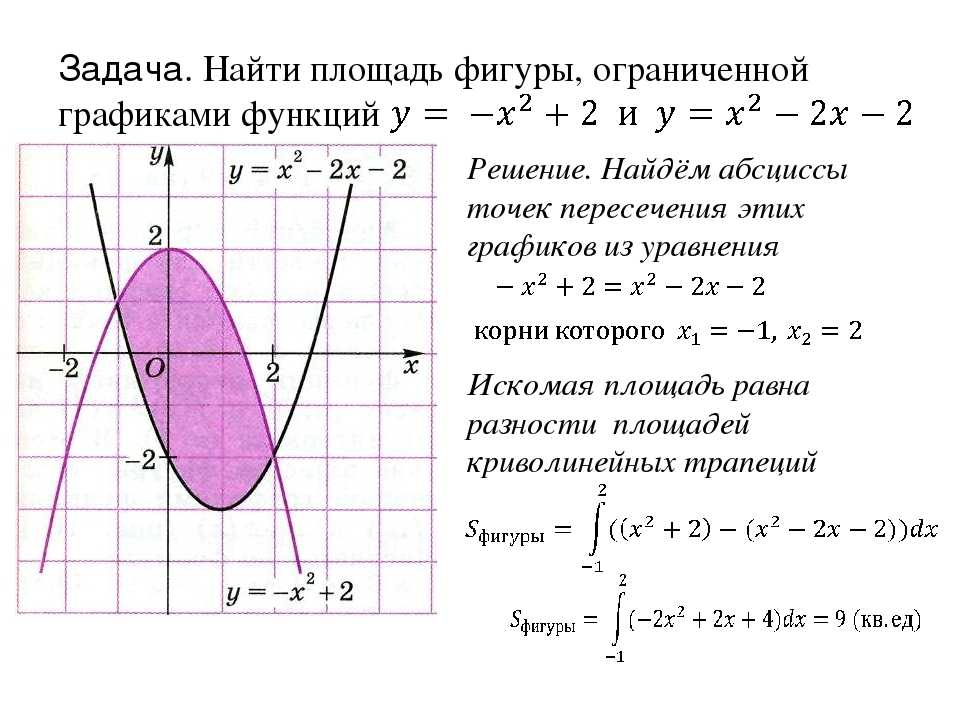 Калькулятор интегрального исчисления можно использовать для вычисления неправильных интегралов.
Калькулятор интегрального исчисления можно использовать для вычисления неправильных интегралов.
Этот интеграл затем решается путем превращения его в проблему пределов, где c случается приближаться к бесконечности или к отрицательной бесконечности. 9c$$
$$\lim_{c\to \infty} [-\frac {1}{c}] -(-\frac{1}{1})]$$
0+1
1
Поскольку ответ на несобственный интеграл конечен, мы считаем его сходящимся.
Если вы хотите вычислить только определенные интегралы, используйте этот лучший пошаговый онлайн-калькулятор определенных интегралов.
Связанный: Используйте калькулятор метода оболочки с шагами, чтобы легко найти объем тела вращения онлайн.
Как рассчитать непрерывную интеграцию?
Основная теорема исчисления устанавливает четкую связь между интегральным и дифференциальным исчислением. Наш интегральный калькулятор с шагами способен вычислить непрерывное интегрирование.
Если f(x) непрерывна для интервала a и b при заданной переменной x и G(x) является функцией в таком смысле, что dG/dx = f(x) для всех значений x в (a,b)
Пусть f непрерывна на интервале ‘y’. Выберите точку p в y, тогда функция f(x) будет определена как:
Выберите точку p в y, тогда функция f(x) будет определена как:
Пусть F(x) будет следующим 9c f(t)dt$$
Для вашего удобства и углубленного изучения множественных интегралов мы предлагаем один из самых быстрых калькуляторов тройных интегралов. Этот инструмент, несомненно, поможет вам вычислить определенные и неопределенные тройные интегралы онлайн, сделав несколько кликов.
Связанный: Понимание интегрирования неполной дробью за 5 минут!
Что такое интегральный калькулятор?
В течение многих лет существовал только один способ вычислить интегралы — вычисление вручную. В наши дни у нас есть много онлайн-калькуляторов интеграции, чтобы легко рассчитать стоимость интеграции. Большинство студентов обычно имеют прочные теоретические представления об исчислении. Таким образом, вычисление интегралов или производных на самом деле не проблема, когда у нас есть такие калькуляторы, как калькулятор интегрирования или калькулятор производных.
Однако это проблема, когда дело доходит до домашних заданий, когда ученики обычно получают массу задач, требующих решения интегралов. Для получения справки, пожалуйста, прочитайте статью, в которой говорится об интеграции, ее важности и различных методах.
Было бы неразумно повторно вычислять интегралы вручную. Калькулятор определенных интегралов удобен для решения сложных задач интегрирования. Он бесплатный и простой в использовании, и вы получаете ответ почти мгновенно, так как вы можете легко найти интегральный калькулятор с пошаговыми инструкциями в Интернете.
Также используйте другие полезные математические калькуляторы, которые важны для общих процессов интеграции. Подобно калькулятору преобразования Лапласа, вы можете преобразовать интеграл данной производной функции, а калькулятор преобразования Фурье позволяет преобразовать функцию времени в частоту.
Как найти лучший калькулятор интеграции?
В Интернете доступно множество интегральных калькуляторов, например, calculated, symbolab, wolframalpha и другие.
Однако наш интегральный калькулятор объема лучше, быстрее, обладает большей функциональностью и является лучшим калькулятором интеграции с пошаговыми инструкциями, доступными в Интернете. Узнайте о преимуществах использования нашего интегрального онлайн-калькулятора.
Когда вы вводите функцию, переменную, верхнюю и нижнюю границы пределов, наш интегральный решатель вычисляет интеграл и отображает все необходимые шаги, чтобы дать пользователю лучшее понимание вычисления интегрирования.
Вы также можете рассчитать интеграцию по вертикали и интеграцию по горизонтали в области кривых с помощью нашего интегрального онлайн-калькулятора с ограничениями.
Это еще не все. Наш интегральный решатель также отображает антипроизводные вычисления для пользователей, которые могут быть заинтересованы в математической концепции и шагах, связанных с интегрированием.
Кроме того, этот калькулятор интеграции по частям поставляется с визуализацией расчета с помощью интуитивно понятных графиков.
Связанный: Как найти объем тела вращения
Как использовать интегральный калькулятор с шагами?
Пользоваться калькулятором интегрирования по частям легко и быстро.
Выполните следующие шаги:
Шаг 1: Введите функцию
Для вычисления интегралов у вас должна быть правильная функция. Вам нужно ввести свою функцию в функциональную строку калькулятора интеграции. Существует также список «пример загрузки». Вы можете щелкнуть этот список, чтобы загрузить пример уравнения для пошагового расчета интегралов.
Шаг 2. Выберите переменную
Для вычисления интегралов можно использовать три переменные. Этими переменными являются x, y и z. Роль этих трех переменных отличается друг от друга, и все они по-разному влияют на общий результат. Вы можете выбрать переменные как x, y и z из раздела переменных.
Шаг 3: Дайте значение верхней границы
Верхняя граница — это значение, которое помогает нам суммировать интеграл при его максимальном значении. Верхняя граница обозначается как U, и ее определение имеет решающее значение в процессе интегрирования. Вы можете ввести верхнюю границу своего лимита в разделе верхней границы калькулятора верхней границы.
Верхняя граница обозначается как U, и ее определение имеет решающее значение в процессе интегрирования. Вы можете ввести верхнюю границу своего лимита в разделе верхней границы калькулятора верхней границы.
Шаг 4: Введите значение нижней границы
Нижняя граница — это наименьшее значение, которое мы установили для начала интегрирования. Чтобы получить точные результаты интегрирования, наименьшее значение интервала обозначается буквой L. Чтобы получить точные результаты интегрирования. Вам необходимо ввести фактическую сумму вашего нижнего лимита в разделе нижней границы калькулятора верхней и нижней границ.
После выполнения всех вышеперечисленных шагов Нажмите кнопку «GO».
Сразу после нажатия на кнопку заработает наш интегральный калькулятор. Калькулятор интегрирования по частям покажет вам антипроизводную, интегральные шаги, дерево разбора и график вашего результата. Все эти функции и функции делают его лучшим калькулятором линейного интеграла для вычисления интеграла сложных задач интеграции.

 Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Г. Алгебра и начала математического анализа. – М.: Мнемозина.